Polarization Division Multiplexing CV-QKD with Pilot-Aided Polarization-State Sensing
Abstract
1. Introduction
2. Scheme Description
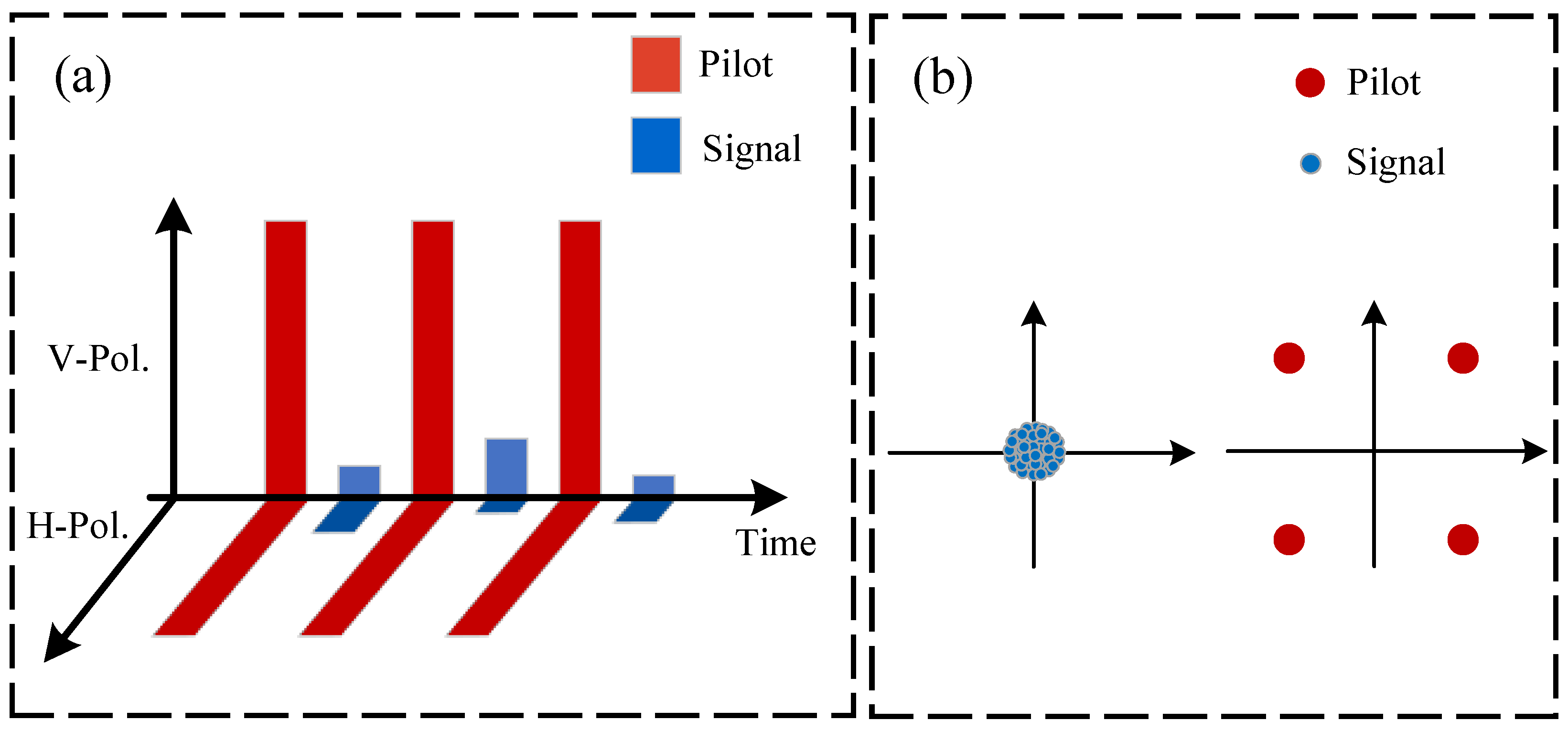
2.1. Scheme of the Dual-Channel CV-QKD
2.2. Noise Model of the PDM CV-QKD System
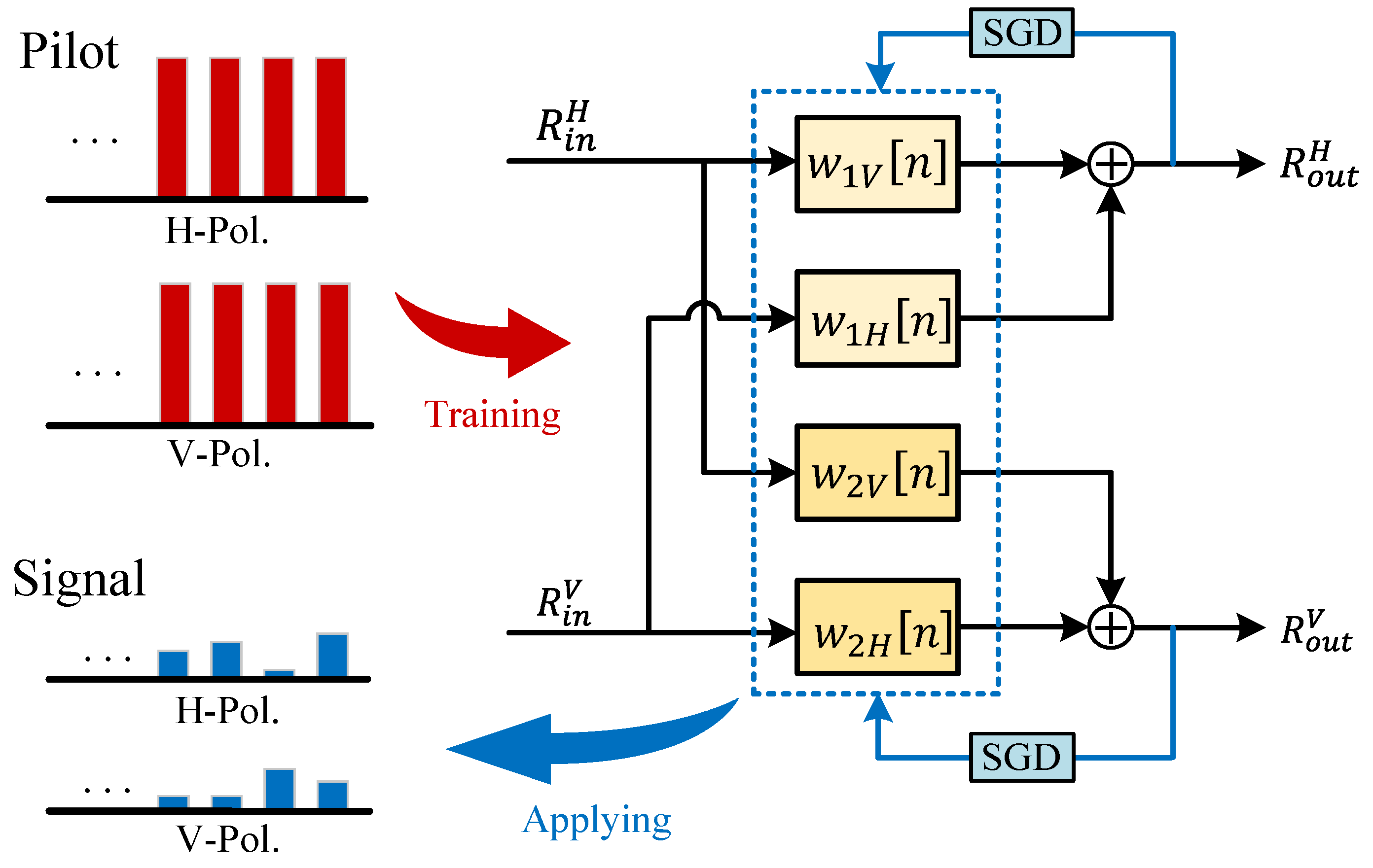
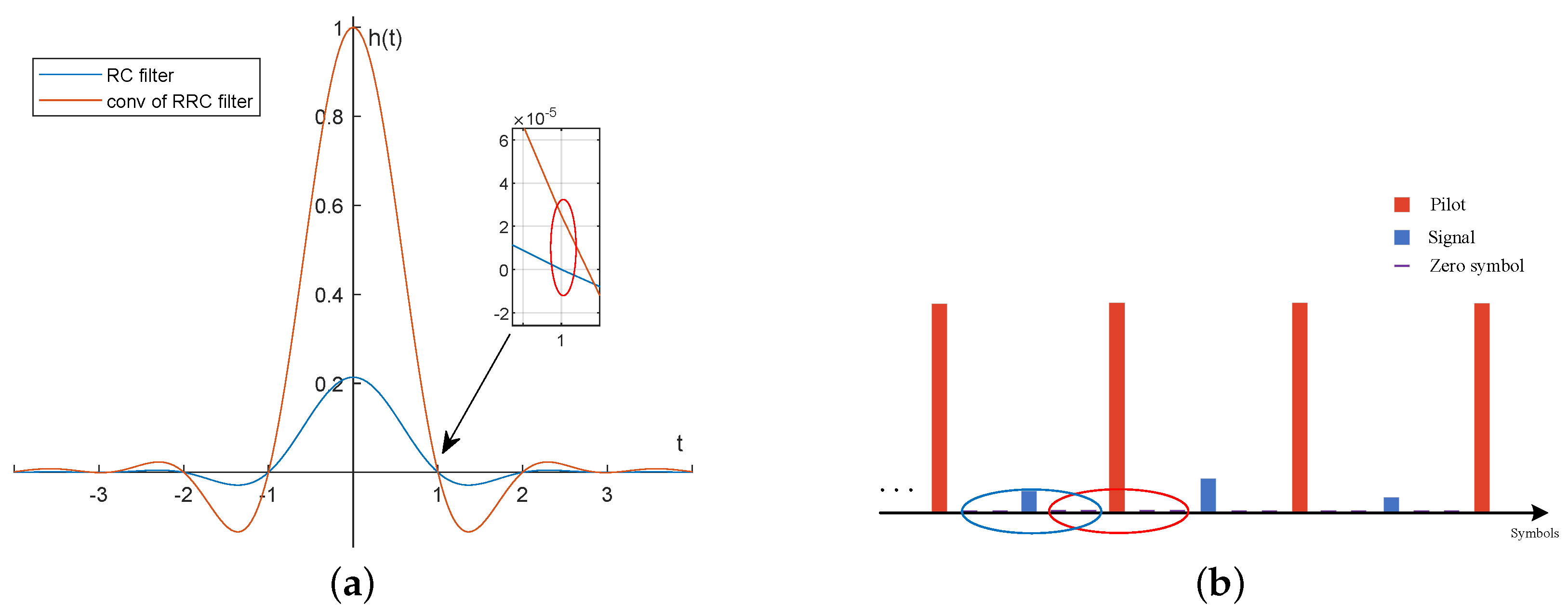
2.3. Noise-Suppression Based on Pilot-Aided CMA
| Algorithm 1 Pilot−aided CMA |
|
2.4. Phase Compensation
3. Experiment and Results
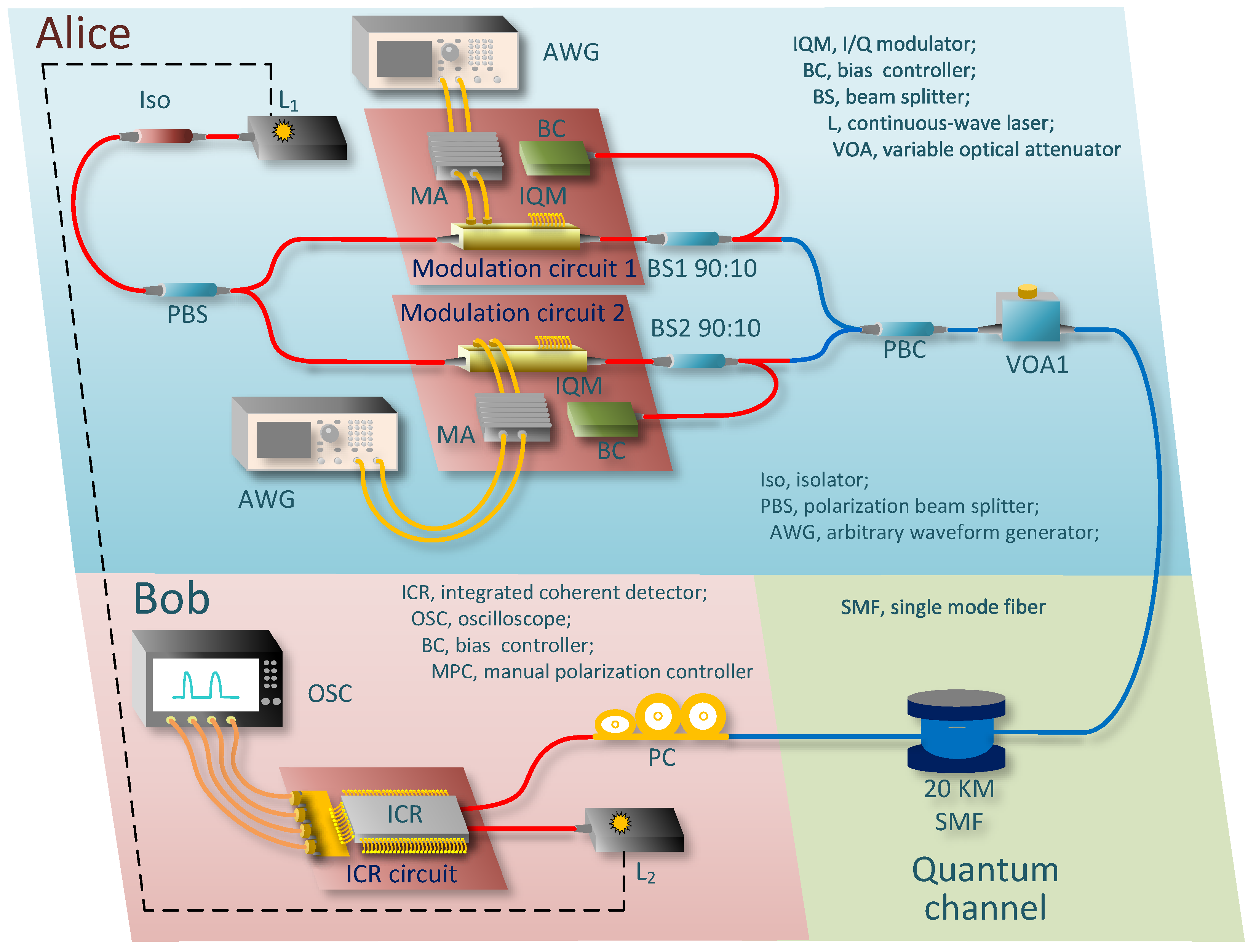
3.1. Experimental Setup
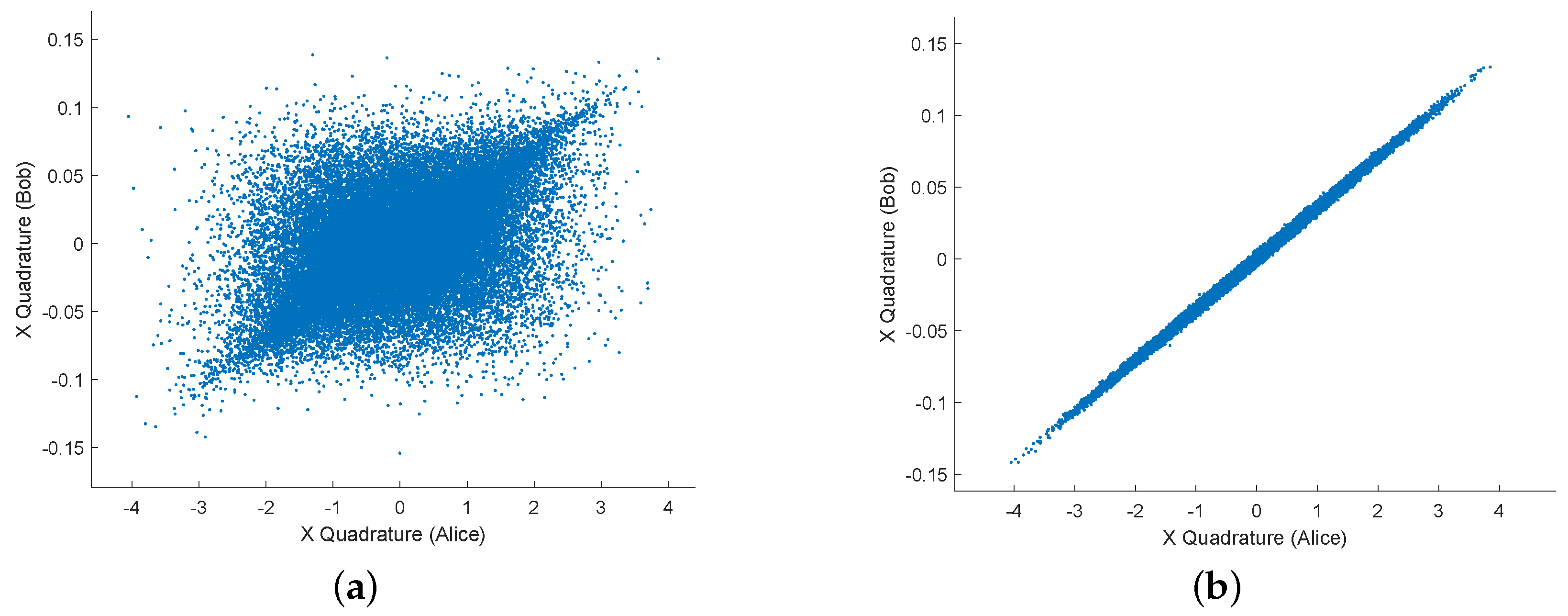
3.2. Noise-Suppression in Experiment
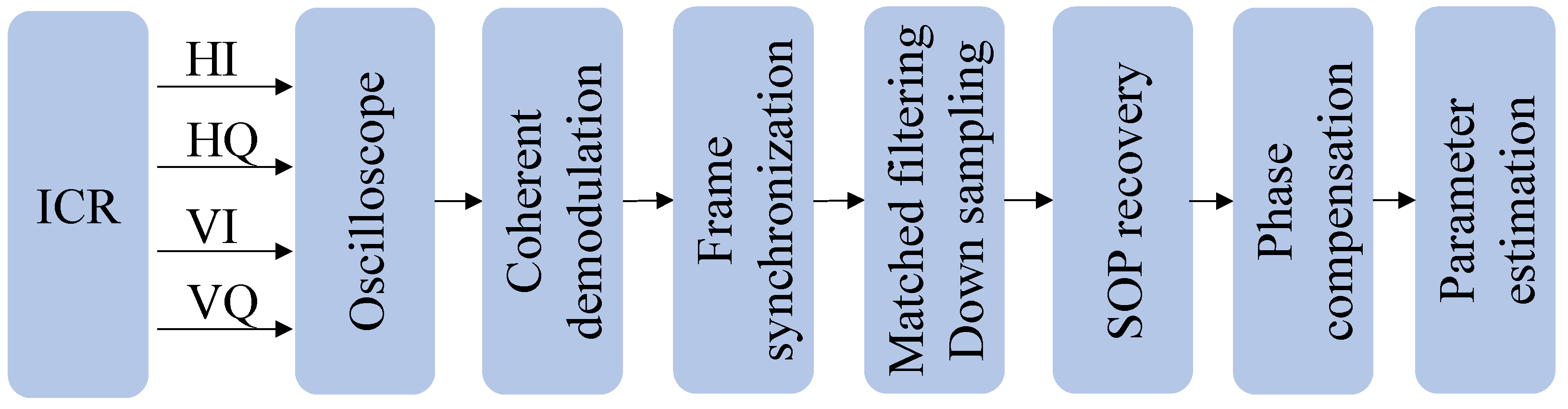
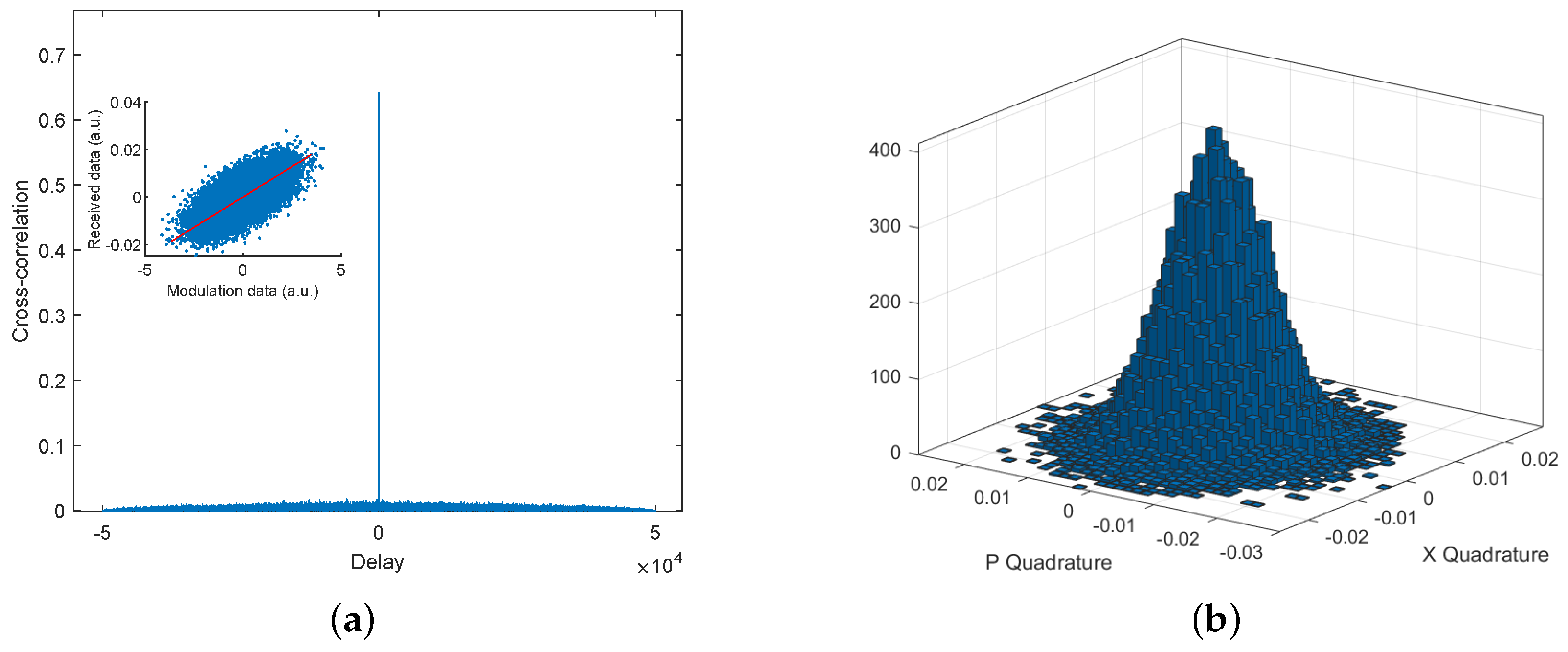
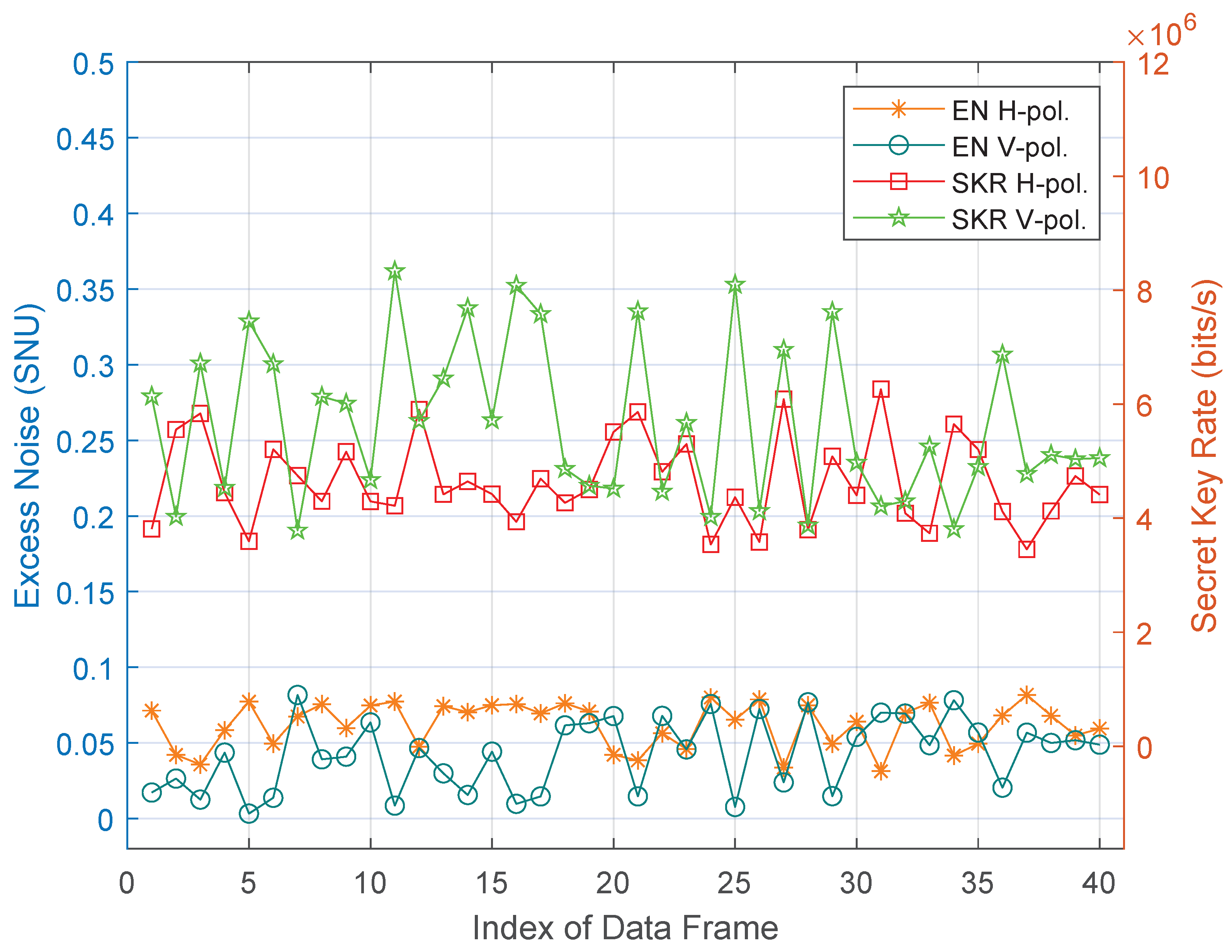
3.3. Data Acquisition and Offline Signal Processing
4. Discussion
- Two orthogonal polarizations can simultaneously carry both key and monitoring information.
- It is difficult for an attacker to precisely access information from both polarizations at the same time.
- Additional security checks are provided through the relative polarization relationship.
- The functions of key distribution and environmental monitoring can be decoupled.
- Real-time monitoring of channel fluctuations is possible.
- Quick response to abnormal polarization changes can be achieved.
- Interference can be identified by comparing the correlation between the two polarizations.
- Environmental noise and active attacks can be distinguished.
- Against intercept-resend attacks: Detection of polarization correlation.
- Against Trojan horse attacks: Real-time monitoring of channel anomalies.
- Against phase attacks: Utilizing the relative phase between the two polarizations.
- Against collective attacks: increasing the technical difficulty for attackers.
- Provides real-time feedback on channel status.
- Protocol parameters can be dynamically adjusted based on environmental changes.
- Enhances system adaptability and robustness.
- Optimizes the balance between key generation rate and security.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PDM | Polarization-division multiplexing |
| QKD | Quantum key distribution |
| CV-QKD | Continuous-variable quantum key distribution |
| SOP | State of the polarization |
| CMA | Constant modulus algorithm |
| LO | Local oscillator |
| LLO | Local-local oscillator |
Appendix A. Secret Key Rate of GMCS CV-QKD
References
- Lo, H.K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- García-Patrón, R.; Cerf, N.J. Unconditional Optimality of Gaussian Attacks against Continuous-Variable Quantum Key Distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef] [PubMed]
- Navascués, M.; Grosshans, F.; Acin, A. Optimality of Gaussian attacks in continuous-variable quantum cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef]
- Pirandola, S.; Braunstein, S.L.; Lloyd, S. Characterization of Collective Gaussian Attacks and Security of Coherent-State Quantum Cryptography. Phys. Rev. Lett. 2008, 101, 200504. [Google Scholar] [CrossRef]
- Renner, R.; Cirac, J.I. de Finetti representation theorem for infinite-dimensional quantum systems and applications to quantum cryptography. Phys. Rev. Lett. 2009, 102, 110504. [Google Scholar] [CrossRef]
- Leverrier, A.; García-Patrón, R.; Renner, R.; Cerf, N.J. Security of continuous-variable quantum key distribution against general attacks. Phys. Rev. Lett. 2013, 110, 030502. [Google Scholar] [CrossRef]
- Zhou, L.; Lin, J.; Jing, Y.; Yuan, Z. Twin-field quantum key distribution without optical frequency dissemination. Nat. Commun. 2023, 14, 928. [Google Scholar] [CrossRef]
- Hu, C.; Wang, W.; Chan, K.S.; Yuan, Z.; Lo, H.K. Proof-of-principle demonstration of fully passive quantum key distribution. Phys. Rev. Lett. 2023, 131, 110801. [Google Scholar] [CrossRef]
- Tene, A.G.; Kamdjou, A.M.S. Error correction based artificial neural network in multi-modes CV-QKD with simultaneous type-I and type-II parametric-down conversion entangled photon source. Opt. Commun. 2024, 565, 130681. [Google Scholar] [CrossRef]
- Zahidy, M.; Mikkelsen, M.T.; Müller, R.; Da Lio, B.; Krehbiel, M.; Wang, Y.; Bart, N.; Wieck, A.D.; Ludwig, A.; Galili, M.; et al. Quantum key distribution using deterministic single-photon sources over a field-installed fibre link. NPJ Quantum Inf. 2024, 10, 2. [Google Scholar] [CrossRef]
- Huang, D.; Lin, D.; Wang, C.; Liu, W.; Fang, S.; Peng, J.; Huang, P.; Zeng, G. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 2015, 23, 17511–17519. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Huang, P.; Zhou, Y.; Liu, W.; Ma, H.; Wang, S.; Zeng, G. High key rate continuous-variable quantum key distribution with a real local oscillator. Opt. Express 2018, 26, 2794–2806. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Pi, Y.; Huang, W.; Li, Y.; Shao, Y.; Yang, J.; Liu, J.; Zhang, C.; Zhang, Y.; Xu, B. High-speed Gaussian-modulated continuous-variable quantum key distribution with a local local oscillator based on pilot-tone-assisted phase compensation. Opt. Express 2020, 28, 32882–32893. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Wang, S.; Zeng, G. Polarization-state tracking based on Kalman filter in continuous-variable quantum key distribution. Opt. Express 2019, 27, 26689–26700. [Google Scholar] [CrossRef]
- Szafraniec, B.; Nebendahl, B.; Marshall, T. Polarization demultiplexing in Stokes space. Opt. Express 2010, 18, 17928–17939. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Pi, Y.; Shao, Y.; Huang, W.; Li, Y.; Xu, B. Polarization demultiplexing for CV-QKD system based on Stokes space. In Proceedings of the Quantum and Nonlinear Optics VIII. SPIE, Nantong, China, 10–19 October 2021; Volume 11905, pp. 84–89. [Google Scholar]
- Chin, H.M.; Jain, N.; Zibar, D.; Andersen, U.L.; Gehring, T. Machine learning aided carrier recovery in continuous-variable quantum key distribution. NPJ Quantum Inf. 2021, 7, 20. [Google Scholar] [CrossRef]
- Chin, H.M.; Hajomer, A.A.; Jain, N.; Andersen, U.L.; Gehring, T. Machine learning based joint polarization and phase compensation for CV-QKD. In Proceedings of the Optical Fiber Communication Conference. Optica Publishing Group, San Diego, CA, USA, 5–9 March 2023. [Google Scholar]
- Pan, Y.; Wang, H.; Shao, Y.; Pi, Y.; Ye, T.; Zhang, S.; Li, Y.; Huang, W.; Xu, B. Simple and fast polarization tracking algorithm for continuous-variable quantum key distribution system using orthogonal pilot tone. J. Light. Technol. 2023, 41, 6169–6175. [Google Scholar] [CrossRef]
- Feng, Y.; Li, L.; Lin, J.; Xu, H.; Zhang, W.; Tang, X.; Xi, L.; Zhang, X. Joint tracking and equalization scheme for multi-polarization effects in coherent optical communication systems. Opt. Express 2016, 24, 25491–25501. [Google Scholar] [CrossRef]
- Cui, N.; Zhang, X.; Zheng, Z.; Xu, H.; Zhang, W.; Tang, X.; Xi, L.; Fang, Y.; Li, L. Two-parameter-SOP and three-parameter-RSOP fiber channels: Problem and solution for polarization demultiplexing using Stokes space. Opt. Express 2018, 26, 21170–21183. [Google Scholar] [CrossRef] [PubMed]
- Qi, B.; Lougovski, P.; Pooser, R.; Grice, W.; Bobrek, M. Generating the local oscillator “locally” in continuous-variable quantum key distribution based on coherent detection. Phys. Rev. X 2015, 5, 041009. [Google Scholar] [CrossRef]
- Laudenbach, F.; Pacher, C.; Fung, C.H.F.; Poppe, A.; Peev, M.; Schrenk, B.; Hentschel, M.; Walther, P.; Hübel, H. Continuous-variable quantum key distribution with Gaussian modulation—The theory of practical implementations. Adv. Quantum Technol. 2018, 1, 1800011. [Google Scholar] [CrossRef]
- Faruk, M.S.; Savory, S.J. Digital signal processing for coherent transceivers employing multilevel formats. J. Light. Technol. 2017, 35, 1125–1141. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Li, L.; Zhou, Y.; Zeng, G. High key rate continuous-variable quantum key distribution using telecom optical components. New J. Phys. 2024, 26, 023002. [Google Scholar] [CrossRef]
- McDowell, E.J.; Cui, X.; Yaqoob, Z.; Yang, C. A generalized noise variance analysis model and its application to the characterization of 1/f noise. Opt. Express 2007, 15, 3833–3848. [Google Scholar] [CrossRef]
- Châtelain, B.; Laperle, C.; Roberts, K.; Chagnon, M.; Xu, X.; Borowiec, A.; Gagnon, F.; Plant, D.V. A family of Nyquist pulses for coherent optical communications. Opt. Express 2012, 20, 8397–8416. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. At. Mol. Opt. Phys. 2009, 42, 114014. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Wang, T.; Xu, Y.; Liu, X.; Li, L.; Zhang, B.; Liu, Y.; Huang, P.; Zeng, G. Polarization Division Multiplexing CV-QKD with Pilot-Aided Polarization-State Sensing. Mathematics 2024, 12, 3599. https://doi.org/10.3390/math12223599
Tan Z, Wang T, Xu Y, Liu X, Li L, Zhang B, Liu Y, Huang P, Zeng G. Polarization Division Multiplexing CV-QKD with Pilot-Aided Polarization-State Sensing. Mathematics. 2024; 12(22):3599. https://doi.org/10.3390/math12223599
Chicago/Turabian StyleTan, Zicong, Tao Wang, Yuehan Xu, Xu Liu, Lang Li, Beibei Zhang, Yuchao Liu, Peng Huang, and Guihua Zeng. 2024. "Polarization Division Multiplexing CV-QKD with Pilot-Aided Polarization-State Sensing" Mathematics 12, no. 22: 3599. https://doi.org/10.3390/math12223599
APA StyleTan, Z., Wang, T., Xu, Y., Liu, X., Li, L., Zhang, B., Liu, Y., Huang, P., & Zeng, G. (2024). Polarization Division Multiplexing CV-QKD with Pilot-Aided Polarization-State Sensing. Mathematics, 12(22), 3599. https://doi.org/10.3390/math12223599





