Abstract
In this study, a finite-time disturbance observer (FTDOB) with a new structure is originally put forward for the motion tracking problem of a class of nonlinear systems subject to model uncertainties and exogenous disturbances. Compared to existing disturbance estimator designs in the literature, in which the estimation error only converges to the origin asymptotically under assumptions that the first and/or second derivatives are vanishing, the suggested DOB is able to estimate the disturbance exactly in finite time. Firstly, uncertainties (parametric and unstructured uncertainties), unknown dynamics, and external disturbances in system dynamics are lumped into a generalized disturbance term that is subsequently estimated by the proposed DOB. Based on this, a DOB-based backstepping controller is synthesized to ensure high-accuracy tracking performance under various working conditions. The stability analysis of not only the DOB but also the overall closed-loop system is theoretically confirmed by the Lyapunov stability theory. Finally, the advantages of the proposed FTDOB and the FTDOB-based controller over other DOBs and existing DOB-based controllers are explicitly simultaneously demonstrated by a series of numerical simulations on a second-order mechanical system and comparative experiments on an actual DC motor system.
Keywords:
disturbance observer; finite-time convergence; tracking control; disturbances and uncertainties MSC:
93B52; 93B53; 93-05
1. Introduction
Improving the tracking performance and enhancing the robustness of nonlinear systems suffering from model uncertainties and external disturbances is a challenging task that has received considerable attention from the research community in recent decades [1,2,3,4]. Generally, sliding mode controllers [5] with high switching gains are considered the simplest way to suppress the adverse effects of these uncertainties and disturbances; however, using excessively high gains causes severe chattering or even leads to the instability of the closed-loop system [6]. Meanwhile, although developing control strategies using the backstepping control technique is most suitable for high-order nonlinear systems, system performance significantly degrades due to the existence of uncertainties and disturbances in system dynamics. High-gain backstepping controllers can be used to suppress these uncertainties and disturbances; however, they might cause system instability when excessive controller gains are employed. Consequently, advanced control techniques should be integrated into the backstepping control to avoid this obstacle. For instance, adaptive backstepping control approaches [7] can be viewed as a powerful method to cope with parametric uncertainties, and asymptotic stability can be achieved accordingly. In addition, in [8], a novel robust adaptive control framework was developed to deal with unknown control coefficients, indeterminate system parameters, and uncertain time delays in general uncertain time-delay nonlinear systems. Nonetheless, they are ineffective against unknown dynamics and exogenous disturbances. Therefore, investigating effective solutions to this problem requires further study.
To address unstructured uncertainties in controlled systems, universal approximators based on neural networks (NNs) and fuzzy logic systems (FLSs) have been developed and successfully employed in numerous studies in recent years [9,10,11,12,13,14]. For instance, in [12], adaptive NN was employed to approximate partially unknown dynamics of unmanned aerial vehicles and its weights were determined online by an adaptive law. In control theory, basis functions in Gaussian and sigmoid forms are normally used to predict function outputs, with weighting vectors updated online through adaptive laws derived from the closed-loop stability analysis using the Lyapunov theorem. However, applying these techniques in real-life applications faces challenges such as computational complexity, numerous tuning parameters, and the appropriate selection of basis functions. In [15], an adaptive direct fuzzy approach co-operated with a novel Lyapunov–Razumikhin function was applied to a class of high-order nonlinear delayed systems for reducing the computational complexity and learning time of the conventional method. Moreover, although NNs and FLSs can approximate nonlinear functions of system states and inputs, they are not effective in handling external disturbances that are independent of system states and naturally exist in dynamical systems.
To reduce the dependence on accuracy of the system model and improve system performance despite limited knowledge of system dynamics, Professor Jingqing Han introduced the active disturbance rejection control (ADRC) concept in the 1990s [16]. The core components of this framework are extended state observers (ESOs), which are designed to estimate both immeasurable states and lumped disturbances caused by model uncertainties and external disturbances. Recently, ESOs have been applied in various fields, including electro-hydraulic systems [17], marine vehicles [18], robotics [19,20,21], and so on [22,23]. It can be observed that high-gain ESOs are employed to enhance estimation accuracy and convergence speed; however, this can lead to peaking phenomena or even instability. Therefore, observer gains must be carefully selected to balance estimation performance and stability.
As an alternative estimation way to ESO designs for estimating disturbances in system dynamics, the disturbance observer (DOB) concept [24] was first introduced in the 1980s and broadly adopted in plentiful applications [25,26,27]. In particular, in [28], linear DOBs were developed to cope with external disturbances and approximation errors of FLS-based function estimators for a vehicular platoon system, and consequently, the distance between two consecutive vehicles was maintained in a predefined range. An adaptive sliding-mode DOB [29] was constructed to observe unknown disturbance for first-order nonlinear systems. However, according to the stability analysis of disturbance observers, only asymptotic stability is achieved when the first derivative of disturbance vanishes. In addition, for time-varying disturbances, estimation errors ultimately or finite-time converge to regions whose bounds can be adjusted based on the selection of observer gains and the changing rates of disturbances. To improve the convergence speed, a prescribed-time DOB was introduced in [30], whose convergence time was theoretically proven to be independent on the initial condition. However, it can be seen that the convergence speed of this DOB is achieved by simply employing high gains under a strict assumption that the first-order derivative of the lumped disturbance is completely known. Similarly, a novel DOB with zero estimation error within a specified time under the same assumption was also put forward in [31]. However, the effectiveness of these predefined-time DOBs was verified by numerical simulations only. In addition, the employment of excessively high gains for achieving a prescribed convergence time might not be feasible in practical applications.
Motivated by the above observations, this paper proposes a novel FTDOB and an FTDOB-based backstepping control algorithm for a class of nonlinear systems in the presence of not only model uncertainties but also exogenous disturbances. The main contributions of this research are as follows:
- (1)
- Firstly, a novel FTDOB with a simple structure is first introduced to exactly estimate the lumped disturbance caused by model uncertainties and external disturbances in system dynamics. In addition, the constructed DOB ensures the finite-time convergence of the estimation error.
- (2)
- Secondly, in light of the constructed FTDOB, a DOB-based control strategy is developed to achieve high-accuracy tracking performance by compensating the influence of the lumped disturbance in a feed-forward manner in the control design process.
- (3)
- Finally, the stability of the recommended observer and overall closed-loop system is analyzed by the Lyapunov theory, and the effectiveness of the proposed controller is confirmed by both comparative simulation and experiment results.
The remaining parts of this paper are organized as follows: the problem statement is given in Section 2. Section 3 presents the FTDOB design and the synthesis of the FTDOB-based backstepping controller, simultaneously. Subsequently, the stability of the overall closed-loop system is detailed in Section 4. Numerical simulations and experimental validation are provided in Section 5. Finally, Section 6 concludes this research.
2. Problem Formulation
Consider the following class of nonlinear systems
where y stands for system output; , , and denote the system states and state vector, respectively; and are known dynamical functions, u represents the control input; and reflexes the lumped disturbance that is constituted by model uncertainties and unknown external disturbances.
Remark 1.
In (1), and are dynamical functions that describe the system behavior based on nominal parameters and states, which can be determined through an off-line identification process. For the sake of simplicity, the adverse effects of parametric uncertainties, unknown dynamics, and external disturbances are collectively represented by a lumped disturbance . This disturbance will be addressed by the proposed disturbance observer in the subsequent section.
Control Objective: The main objective of this research work is to develop a new disturbance observer that is able to estimate the aforementioned lumped disturbance in finite time. Subsequently, a disturbance observer-based backstepping controller is designed to ensure that the system output follows any desired trajectories as closely as possible in the presence of model uncertainties and external disturbances.
To facilitate the control design, some assumptions are made, as follows:
Assumption 1.
The desired trajectory is sufficiently smooth, i.e., it has bounded derivatives up to the n-th order.
Assumption 2.
The lumped disturbance is bounded. There exists a positive constant D that satisfies .
Remark 2.
Assumption 1 on the reference trajectory is a basic condition when developing a backstepping controller and it can be found in numerous studies [4,11,12]. To construct model-based controllers for a dynamical system, the identified system model should be as simple as possible but it is able to capture accurately critical system behaviors at a specific level. In addition, for any control systems, the control input is restricted due to the limited force/torque generation ability. Therefore, the lumped disturbance caused by model uncertainties and external disturbances should be constrained so as to obtain a high-accuracy tracking performance.
Lemma 1
([32]). Suppose that there is a Lyapunov function radially unbounded such that
holds,
where and are positive constants; and . Then, the equilibrium is finite-time stable and the convergence time is given by
3. Disturbance-Observer Control Design
3.1. Finite-Time Disturbance Observer Design
For the sake of concise representation, d is used as a substitute for . To eliminate the influence of the lumped disturbance , a finite-time disturbance observer is developed as follows:
where and are the estimates of and d, respectively; denotes the estimation error; and represent positive observer gains; and stands for the standard signum function of •.
Theorem 1.
Proof.
Consider a candidate Lyapunov function as
From Lemma 1 and the appropriate selection of and , i.e., and , the estimation error converges to zero in finite time and there is no difference between and thereafter. Hence, the lumped disturbance d is accurately estimated by in finite time , defined by:
□
Remark 3.
Introducing an additional discontinuous term into the observer dynamics (4) enables the finite-time estimation performance of the proposed FTDOB. As presented in (8), the convergence time of the proposed DOB depends on the selection of the observer gains and . Specifically, the higher observer gains result in a faster convergence speed.
3.2. Disturbance Observer-Based Control Design
The control laws are constructed by using the traditional backstepping control framework. Tracking errors are defined as
where denotes the actual tracking error, are virtual tracking errors; and represent the virtual control laws to be designed.
The design procedure is presented as follows:
The virtual control law is designed as
where is an adjustable parameter.
Choosing as the Lyapunov function and taking the time derivative of it leads to
Step 2: Similarly, the dynamic of the tracking error is obtained as
where is the virtual control law that is designed as
where is an adjustable controller gain.
Selecting as a candidate Lyapunov function, then taking the derivative of it leads to
The control law in this step is constructed as
where are controller gains to be selected.
Choose the following Lyapunov function
Step n: The dynamic of the final tracking error is defined as
The control input, which guarantees high-accuracy tracking performance for the system (1), is designed as
where is the control parameter to be chosen.
4. Stability Analysis
Theorem 2.
Proof.
A Lyapunov function is chosen as
Applying Young’s inequality [33] leads to
□
According to Theorem 1, the disturbance estimation error converges to zero in finite time , when , (27) can be rewritten as
where
By integrating both sides of (28) with respect to time, we obtain
Hence, the Lyapunov function V converges to zero when t goes to infinity, i.e., . This completes the proof of Theorem 2.
Remark 4.
Theoretically, from (8) and (9), the observer gains and should be chosen as high as possible to not only eliminate the influence of the lump disturbance but also decrease the convergence time . However, the selection of excessive gain may cause severe chattering in the estimation. Therefore, to overcome this drawback and reduce the conservativeness of the tuning process, the sign function is replaced with the hyperbolic tangent function. Based on this, the disturbance observer (4) is modified as
where c is a positive constant.
Remark 5.
By replacing the discontinuous “sign” function with the continuous “tanh” function, the estimation performance of the proposed observer (4) can be improved in terms of chattering reduction, and finite-time boundedness estimation performance is achieved by the observer (30) accordingly. Therefore, ultimately uniformly bounded (UUB) performance of the closed-loop system is attained.
Remark 6.
It should be noted that the adoption of the “tanh” function instead of the “sign” function reduces the conservativeness of the observer-gain tuning process and partially relaxes the requirement given in Assumption 2. In addition, the constant c should be meticulously designed to ensure continuous estimation, achieve the desired convergence time, and minimize chattering in the estimated variable. Specifically, the higher value of c increases the estimation accuracy with the same value of , an excessively large value of c can lead to significant chattering.
5. Simulation and Experimental Verification
5.1. Numerical Simulations
Considering a mechanical system whose dynamics are given by
where and are system states, , , and are actual system parameters, denotes the term relating to the Coulomb friction that is strongly nonlinear and naturally exists in mechanical systems, reflexes external disturbances.
It should be pointed out that the actual system parameters in (31) cannot be exactly known in practical applications. However, nominal system parameters can be determined through experimental data by using system identification techniques. Herein, it is assumed that the nominal system parameters are identified as , , and . Hence, the nominal system dynamics for developing observers and control algorithms are as follows
where the lumped disturbance is defined as with and .
The following estimators for comparison of estimation performance in terms of convergence speed and estimation accuracy are employed as:
- (a)
- FTDOB: The proposed DOB (30), with observer gains being chosen as and , and the tuning parameter selected as .
- (b)
- LDOB: A linear disturbance observer, whose dynamics are given bywhere is the observer gain.
- (c)
- ESO: An extended state observer, which is adopted to estimate the lumped disturbance in (32), is designed aswhere stands for the observer gain, is the estimate of , and denotes the estimation of the lumped disturbance .
For a fair comparison, the equivalent observer gains of the three DOBs were employed. In addition, the external disturbance with different shapes were intentionally injected into the system dynamics (32) to evaluate the estimating capability of the above observers under open-loop and closed-loop control structures as follows:
5.1.1. Open-Loop Control Structure
In this case, an external control input was applied to the system (32). The estimation performance of the compared observers was investigated with the following case studies:
Case study 1: A square-pulse-like external disturbance with a magnitude of and a frequency of 0.5 was applied to the system dynamics described in (32). In this scenario, the lumped disturbance comprises parametric uncertainties, unknown dynamics, and external disturbances. The estimation performance and estimation errors of the compared observers are depicted in Figure 1 and Figure 2, respectively.

Figure 1.
The disturbance estimations of the compared observers with the square-pulse-like external disturbance.
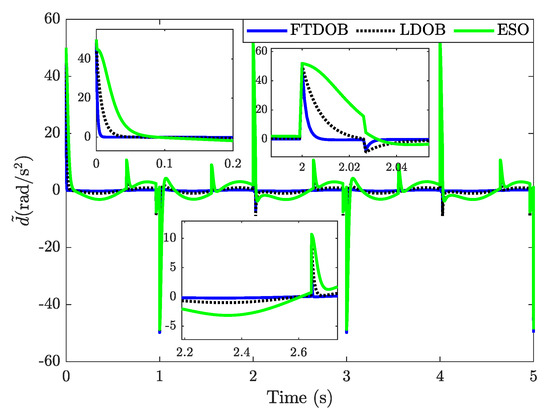
Figure 2.
The estimation errors of the compared observers with the square-pulse-like external disturbance.
As shown in Figure 1, all observers were able to accurately estimate the lumped disturbance at a specific level. In addition, chattering-free estimations were achieved by the FTDOB, LDOB, and ESO. The estimation performance in terms of convergence rate and accuracy of the observers were explicitly presented in Figure 2. From zoom-in sub-figures of Figure 2, it can be observed that when the disturbance abruptly changes, the proposed observer exhibits a faster convergence speed and higher accuracy compared to the LDOB. Meanwhile, the ESO performed the worst estimation performance with a slower rate of convergence and lower estimation accuracy. The results indicate that the performance of the ESO significantly degrades when dealing with fast-changing disturbances.
Case study 2: For further estimation performance evaluation, a sinusoidal-like external disturbance with a non-zero initial condition is intentionally injected into the system dynamics, which is mathematically formulated as . The estimation errors of the observers were presented in Figure 3. Similar to the first case study, the proposed observer (FTDOB) performs better estimation performance with respect to the convergence time and the estimation precision compared to the other compared observers. Since the disturbance estimation performance of the ESO depends on the accuracy of the state estimation, it obtained the worst performance.
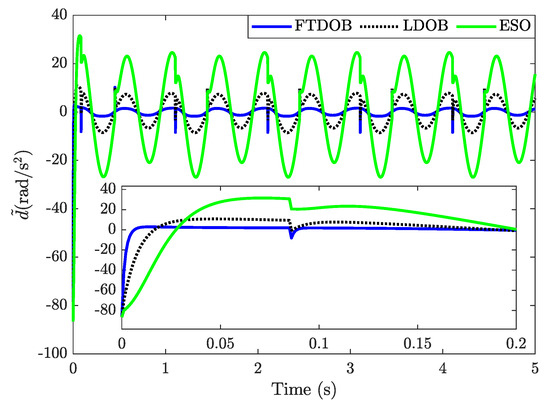
Figure 3.
The estimation errors of compared observers with the sinusoidal-like external disturbance.
5.1.2. Closed-Loop Control Structure
To evaluate the contribution of the proposed FTDOB in comparison to the LDOB and ESO, observer-based backstepping controllers were developed as follows:
where denotes the virtual control law, and reflex control errors, is the estimate of the lumped disturbance in (32), which is attained by the proposed FTDOB (30), LDOB (33), and ESO (34), and and are designed controller gains. Based on this, control algorithms including FTDOB-based controller (C1), LDOB-based controller (C2), and ESO-based controller (C3), are constructed accordingly.
A sinusoidal reference trajectory was adopted to assess not only the tracking performance of the above observer-based controllers but also the estimation capability of the considered observers in the presence of parametric difference between the actual system model (31) and the nominal system model (32), unmodeled dynamics, and external disturbance purposely inserted into the system.
The disturbance estimation errors of the FTDOB, LDOB, and ESO observers are presented in Figure 4. As shown, the results are similar to those obtained in previous case studies. In particular, the proposed FTDOB observer estimated the lumped uncertainty more precisely compared to the LDOB and the ESO observers. These estimates attained by these observers are subsequently used to compensate for the influence of the lumped disturbance in a feed-forward fashion, as given in (35). Furthermore, the tracking errors attained by the above controllers are depicted in Figure 5. Owing to the better estimation performance of the proposed FTDOB, the controller C1 achieved better tracking qualification in terms of tracking error in comparison with the other controllers (C2 and C3). For the time being, the controller C3 displayed the worst performance due to the poorer estimation performance of the ESO compared to the others.
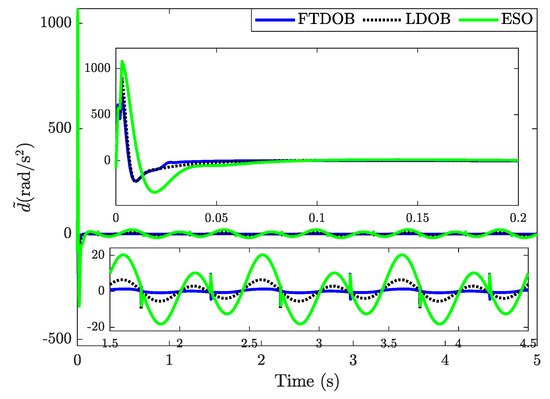
Figure 4.
The estimation errors of the compared estimators.
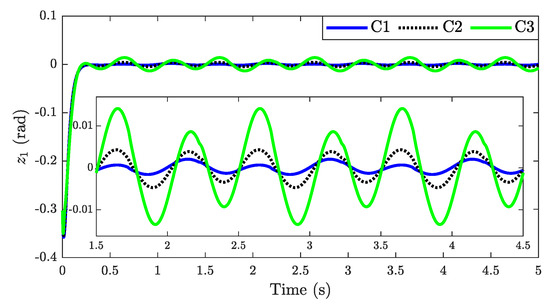
Figure 5.
The tracking errors of the compared observer-based controllers.
5.2. Experimental Validation
To confirm the feasibility and effectiveness of the recommended method, an actual DC motor system presented in Figure 6, was employed. A DC motor with a model, S6D15-24A, manufactured by SPG Co. Ltd., South Korea, which is powered by an MD-03 motor driver provided by Devantech Limited, England, was adopted. To measure the angular position and speed of the motor, an incremental encoder, E40H8-5000-3-V5, provided by Autonics company, South Korea, was utilized. In addition, an MDR-60-24 24VDC power source made by Meanwell company, Taiwan, was used to supply power to the overall motor system. Finally, an NI DAQ card, namely PCI 6229, from National Instruments company, was adopted to observe the angular position of the motor shaft from encoder signals and generate a control signal applied to the motor driver.

Figure 6.
The experimental platform of a DC motor.
The dynamics of this system is given by
where and are the angular position and speed of the motor shaft; u denotes the control voltage applying to the motor driver; with and are the nominal torque constant and rotor inertia of the DC motor, respectively; with as the nominal damping coefficient; with are the nominal Coulomb friction coefficient; presents the Coulomb effect; and represents the lumped disturbance caused by modeling errors and disturbance torque.
To evaluate the advantage of the proposed DOB over some reference DOB designed, distinct DOB-based controllers with the same control structure were developed and illustrated in Figure 7.
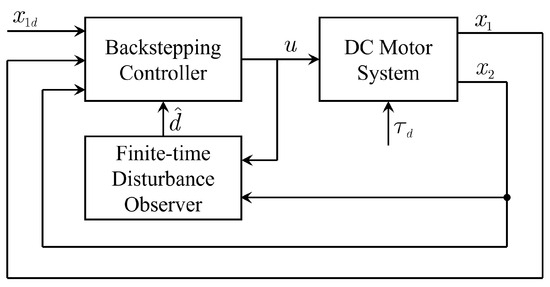
Figure 7.
The control scheme of compared controllers.
Main control laws of the three comparative disturbance observer-based controllers are designed based on the traditional backstepping framework as follows:
where , , controller gains are selected as and , and the estimation of the lumped disturbance is estimated by the following disturbance observers.
- (a)
- C1: The control algorithm with the proposed disturbance observer being designed to estimate the lumped disturbance in (36) as follows:where , , and observer gains are chosen as and .
- (b)
- C2 [34]: The linear disturbance observer (LDOB)-based controller (LDOB-BC) in which the dynamics of the LDOB are represented as:where z is the auxiliary variable and k reflexes the observer gain that is selected as .
- (c)
- C3 [35]: An extended state observer (ESO)-based controller, in which the dynamics of the constructed ESO are as follows:where and are estimates of and , respectively; denotes the estimation of ; and stands for the observer bandwidth to be selected. Herein, the observer bandwidth is chosen as .
Remark 7.
For a fair comparison, the observer gains of the proposed DOB, LDOB, and ESO are carefully tuned to achieve the best possible output tracking performance. In addition, the main controllers have the same structure and gains to verify the effectiveness of the proposed disturbance observer in comparison with well-known DOB designs.
To evaluate the tracking performance of three developed controllers, a sinusoidal reference trajectory was utilized. The tracking errors of three comparative controllers are presented in Figure 8. As shown in this figure, the proposed controller C1 exhibits better tracking performance compared to the C2 and C3 controllers, with smaller tracking errors and less fluctuation around the equilibrium. Although the ESO-BC controller only requires system output information by virtue of the ESO in the estimation of both angular velocity and lumped disturbance, it displays the worst performance due to the insufficient estimation accuracy. Theoretically, the estimation performance of the ESO can be improved by increasing the observer bandwidth; however, excessive observer bandwidth causes the peaking phenomenon or even leads to instability.
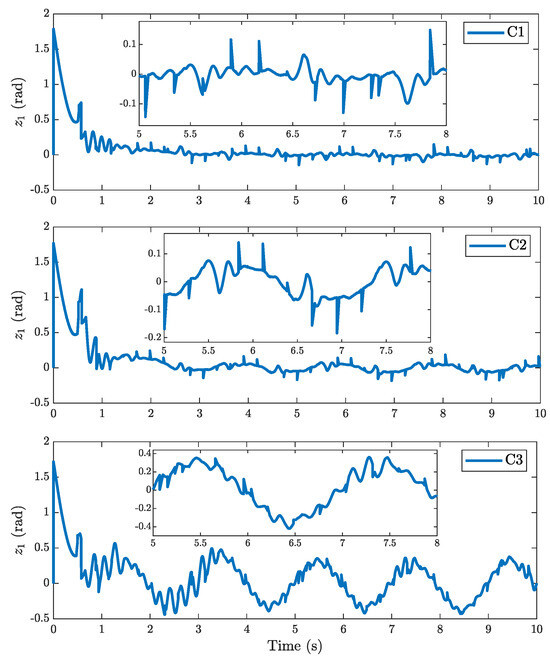
Figure 8.
Tracking errors of three comparative controllers.
For statistically evaluating the tracking performance of the three controllers, three performance indexes, including the maximal absolute tracking error, average tracking error, and standard derivation in the last two cycles, are given in Table 1. As given, the maximal absolute tracking error of the C1 controller is only 0.1484 (rad), while the values of the C2 and C3 controllers are 0.1857 (rad) and 0.4299 (rad), respectively. In terms of tracking accuracy and smooth response, the C1 controller achieves 0.0205 (rad) of the average tracking error and 0.0212 (rad) of the standard derivation. Meanwhile, the C2 and C3 controllers present a worse performance with the average tracking error and standard derivation of the tracking error, with values of 0.0420 (rad), 0.2094 (rad), 0.0261 (rad), and 0.1111 (rad), respectively.

Table 1.
Performance indexes of the three controllers.
The disturbance estimation and the control action of the proposed control method are provided in Figure 9 and Figure 10, respectively. As shown, the relatively smooth disturbance estimation was generated by using the proposed disturbance observer (38). Hence, continuous control action was achieved by the recommended control algorithm. In addition, owing to the higher accurate disturbance estimation compared to the LDOB and ESO, higher tracking performance was achieved by the proposed controller as a result.
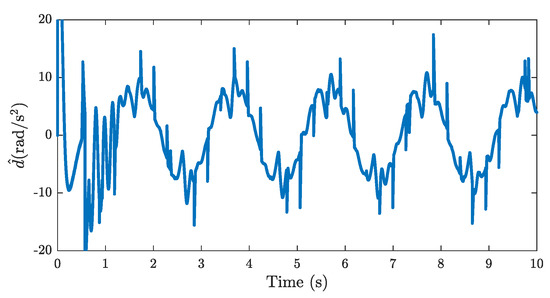
Figure 9.
Disturbance estimation of the proposed disturbance observer.
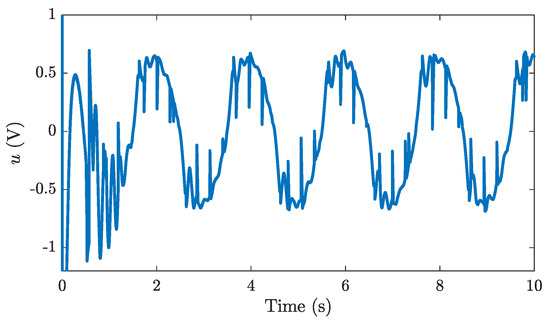
Figure 10.
Control input of the proposed controller.
6. Conclusions
In this research, a novel disturbance observer which is able to exactly estimate lumped disturbance constituted by model uncertainties and external disturbance in the system dynamics of a class of nonlinear systems in finite time, was developed. Based on this, a high-accuracy tracking control algorithm using the traditional backstepping framework was designed, in which the effect of the uncertainties and disturbances was sufficiently compensated in a feed-forward manner. Subsequently, the stability of the closed-loop system was explicitly verified by the Lyapunov theory. Finally, numerical simulation and experiment results were provided to demonstrate the feasibility and advantages of the proposed method over some existing observer-based controllers in the literature. Nevertheless, the system states and the upper bound of the lumped disturbance were assumed to be available in this study, therefore, these limitations will be investigated in future work.
Author Contributions
Conceptualization, M.H.N.; methodology, M.H.N.; software, M.H.N.; validation, M.H.N.; formal analysis, M.H.N.; investigation, M.H.N.; resources, M.H.N.; data curation, M.H.N.; writing—original draft preparation, M.H.N.; writing—review and editing, M.H.N.; visualization, M.H.N.; supervision, K.K.A.; project administration, K.K.A.; funding acquisition, K.K.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Regional Innovation Strategy (RIS) through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE) (2021RIS-003).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADRC | Active Disturbance Rejection Control |
| BSC | Backstepping Control |
| ESO | Extended State Observer |
| LDOB | Linear Disturbance Observer |
| FTDOB | Finite-Time Disturbance Observer |
References
- Zhang, J.; Nie, P.; Chen, Y.; Zhang, B. A Joint Acceleration Estimation Method Based on a High-Order Disturbance Observer. IEEE Robot. Autom. Lett. 2022, 7, 12615–12622. [Google Scholar] [CrossRef]
- Wang, C.; Guo, L.; Wen, C.; Zhu, Y.; Qiao, J. Adaptive Anti-Disturbance Control for a Class of Uncertain Nonlinear Systems with Composite Disturbances. IEEE Trans. Cybern. 2023, 54, 4241–4254. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control. 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, W.; Ge, S.S. Adaptive Fuzzy Control for Uncertain Strict-Feedback Nonlinear Systems with Full-State Constraints Using Disturbance Observer. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6145–6156. [Google Scholar] [CrossRef]
- Liu, X.; Su, X.; Li, R.; Shi, P. Anti-disturbance sliding mode control for uncertain nonlinear systems. Int. J. Control. 2023, 96, 3001–3011. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory And Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Landau, I.D.; Lozano, R.; M’Saad, M.; Karimi, A. Adaptive Control: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Liu, Z.-G.; Xue, L.; Sun, Z.-Y. A new robust adaptive tracking strategy to uncertain time-delay nonlinear systems with a general form. Automatica 2022, 146, 110560. [Google Scholar] [CrossRef]
- Xu, H.; Yu, D.; Liu, Y.J. Observer-Based Fuzzy Adaptive Predefined Time Control for Uncertain Nonlinear Systems with Full-State Error Constraints. IEEE Trans. Fuzzy Syst. 2024, 32, 1370–1382. [Google Scholar] [CrossRef]
- Lin, F.; Xue, G.; Qin, B.; Li, S.; Liu, H. Event-triggered finite-time fuzzy control approach for fractional-order nonlinear chaotic systems with input delay. Chaos Solitons Fractals 2023, 175, 114036. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Dao, H.V.; Ahn, K.K. Adaptive Robust Position Control of Electro-Hydraulic Servo Systems with Large Uncertainties and Disturbances. Appl. Sci. 2022, 12, 2. [Google Scholar] [CrossRef]
- Yu, G.; Reis, J.; Silvestre, C. Quadrotor Neural Network Adaptive Control: Design and Experimental Validation. IEEE Robot. Autom. Lett. 2023, 8, 2574–2581. [Google Scholar] [CrossRef]
- Truong, H.V.A.; Nguyen, M.H.; Tran, D.T.; Ahn, K.K. A novel adaptive neural network-based time-delayed estimation control for nonlinear systems subject to disturbances and unknown dynamics. ISA Trans. 2023, 142, 214–227. [Google Scholar] [CrossRef]
- Lin, F.; Xue, G.; Li, S.; Liu, H.; Pan, Y.; Cao, J. Finite-time sliding mode fault-tolerant neural network control for nonstrict-feedback nonlinear systems. Nonlinear Dyn. 2023, 111, 17205–17227. [Google Scholar] [CrossRef]
- Liu, Z.G.; Shi, Y.Y.; Sun, W.; Su, S.F. Direct Fuzzy Adaptive Regulation for High-Order Delayed Systems: A Lyapunov–Razumikhin Function Method. IEEE Trans. Cybern. 2024, 54, 1894–1906. [Google Scholar] [CrossRef]
- Han, J.-Q. Nonlinear design methods for control systems. IFAC Proc. Vol. 1999, 32, 1531–1536. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ahn, K.K. Output Feedback Robust Tracking Control for a Variable-Speed Pump-Controlled Hydraulic System Subject to Mismatched Uncertainties. Mathematics 2023, 11, 8. [Google Scholar] [CrossRef]
- Peng, Z.; Jiang, Y.; Liu, L.; Shi, Y. Path-Guided Model-Free Flocking Control of Unmanned Surface Vehicles Based on Concurrent Learning Extended State Observers. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4729–4739. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Li, T.; Yan, Y. Output Constrained Control of Lower Limb Exoskeleton Based on Knee Motion Probabilistic Model with Finite-Time Extended State Observer. IEEE/Asme Trans. Mechatron. 2023, 28, 2305–2316. [Google Scholar] [CrossRef]
- Yang, W.; Ding, S.; Ding, C. Fast Supertwisting Sliding Mode Control With Antipeaking Extended State Observer for Path-Tracking of Unmanned Agricultural Vehicles. IEEE Trans. Ind. Electron. 2024, 71, 12973–12982. [Google Scholar] [CrossRef]
- Sebastian, G.; Li, Z.; Crocher, V.; Kremers, D.; Tan, Y.; Oetomo, D. Interaction Force Estimation Using Extended State Observers: An Application to Impedance-Based Assistive and Rehabilitation Robotics. IEEE Robot. Autom. Lett. 2019, 4, 1156–1161. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, W.; Huang, W.; Xie, L.; Bi, K.; Zhu, Y. Combined Magnetic Field Decoupling and Disturbance Rejection Control of Microrobots Based on Extended State Observer. IEEE Robot. Autom. Lett. 2022, 7, 4032–4039. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Gu, S.; Zhao, L.; Li, Z. Modelling and Angle Tracking Control for Multi-Chamber Soft Bending Pneumatic Muscle. IEEE Robot. Autom. Lett. 2023, 8, 7647–7654. [Google Scholar] [CrossRef]
- Ohishi, K.; Nakao, M.; Ohnishi, K.; Miyachi, K. Microprocessor-Controlled DC Motor for Load-Insensitive Position Servo System. IEEE Trans. Ind. Electron. 1987, 1, 44–49. [Google Scholar] [CrossRef]
- Lee, W.; Chung, W.K. Disturbance-Observer-Based Compliance Control of Electro-Hydraulic Actuators with Backdrivability. IEEE Robot. Autom. Lett. 2019, 4, 1722–1729. [Google Scholar] [CrossRef]
- Lee, D.; Back, J.; Oh, S. Workspace Nonlinear Disturbance Observer for Robust Position Control of Flexible Joint Robots. IEEE Robot. Autom. Lett. 2024, 9, 4495–4502. [Google Scholar] [CrossRef]
- Xi, R.D.; Xiao, X.; Ma, T.N.; Yang, Z.X. Adaptive Sliding Mode Disturbance Observer Based Robust Control for Robot Manipulators Towards Assembly Assistance. IEEE Robot. Autom. Lett. 2022, 7, 6139–6146. [Google Scholar] [CrossRef]
- Li, K.; Li, Y. Disturbance-Observer Adaptive Fuzzy Performance Constraint Control for Vehicular Platoon System. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2462–2470. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhang, O.; Zhao, Y.; Chen, W.; Gao, Y. Adaptive Disturbance Observer-Based Fixed-Time Tracking Control for Uncertain Robotic Systems. IEEE Trans. Ind. Electron. 2024, 71, 14823–14831. [Google Scholar] [CrossRef]
- Que, N.; Deng, W.; Zhou, N.; Yao, J. Disturbance Observer Based Prescribed-Time Tracking Control of Nonlinear Systems with Non-Vanishing Uncertainties. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3131–3135. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Y.; Guo, G. Prescribed-Time Control of Vehicular Platoons Based on a Disturbance Observer. IEEE Trans. Circuits Syst. Express Briefs 2022, 69, 3789–3793. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Mitrinović, D.S.; Pečarić, J.E.; Fink, A.M. Young’s Inequality. In Classical and New Inequalities in Analysis; Mathematics and Its Applications (East European Series); Springer: Dordrecht, The Netherlands, 1993; Volume 61. [Google Scholar]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High-Gain Disturbance Observer-Based Backstepping Control with Output Tracking Error Constraint for Electro-Hydraulic Systems. IEEE Trans. Control. Syst. Technol. 2015, 23, 787–795. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. Adaptive Robust Control of DC Motors with Extended State Observer. IEEE Trans. Ind. Electron. 2014, 61, 3630–3637. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).