Dominion on Grids
Abstract
1. Introduction
2. Results
2.1. Dominion on Paths and Cycles
- 1.
- 2.
- 3.
- .
- 1.
- 2.
- 3.
2.2. An Optimization Problem
- 1.
- For , .
- 2.
- For , if , then .
- 3.
- If , then .
- 4.
- If , then .
- 5.
- If , then .
- 1.
- Both and satisfy the five restrictions in the Dominion Optimization Problem.
- 2.
- and .
- 3.
- .
- 4.
- and .
- 5.
- and .
2.3. Dominion on Ladder Graphs
- 1.
- 2.
- If n is odd, then is non-decomposible.
- 3.
- If n is even and , then can be decomposed to two non-decomposible vectors and for some odd integer k.
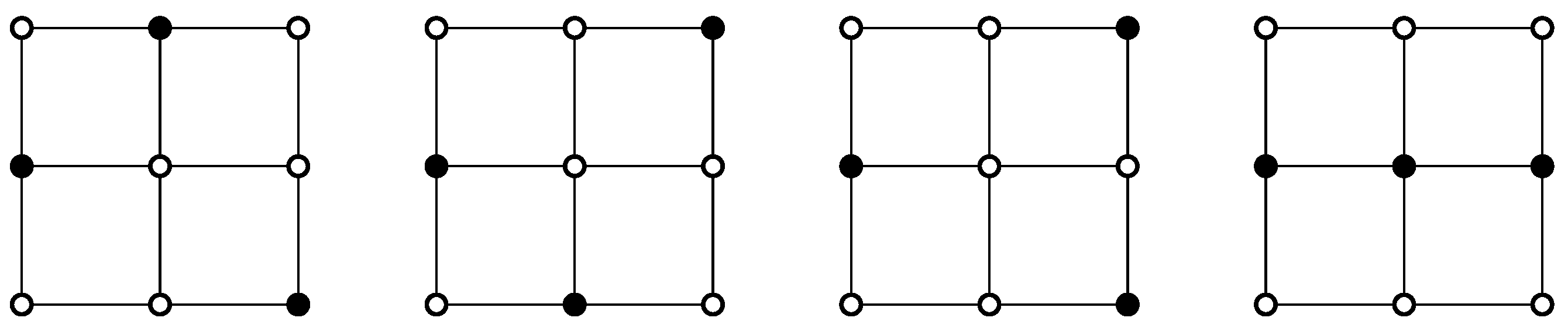
2.4. Dominion of Grid Graphs
- 1.
- , and
- 2.
- can be obtained from a vector of length by inserting copies of .
- 1.
- for .
- 2.
- for .
- 3.
- for .
- 4.
- for
- 1.
- If , then .
- 2.
- If , then .
- 3.
- If , then .
- 4.
- If , then
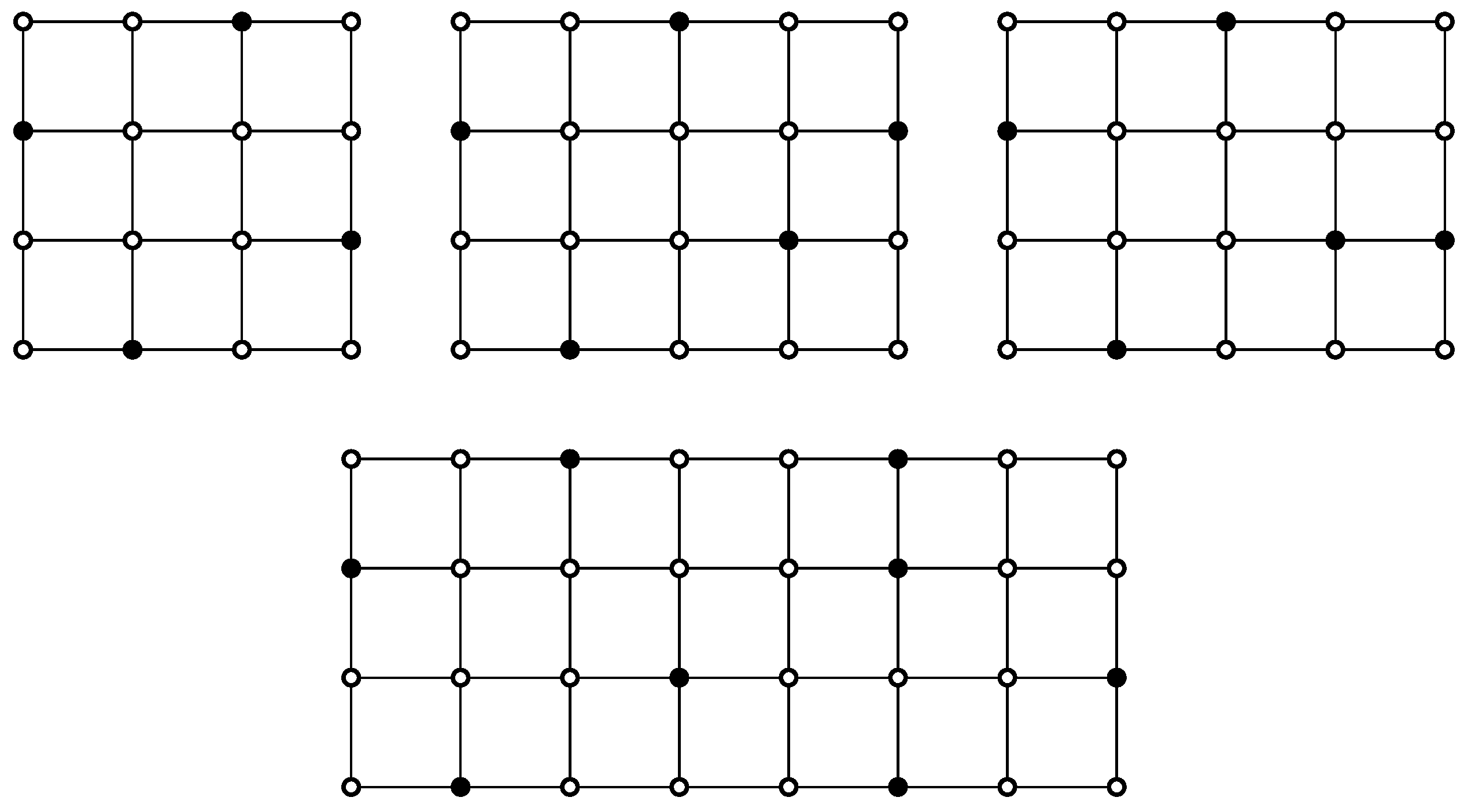
2.5. Dominion on Grids
- 1.
- or
- 2.
3. Conclusions and Future Research
- (a)
- (b)
- for
- (c)
- for
| import itertools as it |
| def Gamma(m,n): if m>n: m,n = n,m match m: case 1: return (n+2)//3 case 2: return (n+2)//2 case 3: return (3*n+4)//4 case 4: if n in (5,6,9): return n+1 else: return n case 5: if n==7: return (6*n+6)//5 else: return (6*n+8)//5 case 6: if n%7==1: return (10*n+10)//7 else: return (10*n+12)//7 case 7: return (5*n+3)//3 case 8: return (15*n+14)//8 case 9: return (23*n+20)//11 case 10: if n not in (13,16) and n%13 in (0,3): return (30*n+37)//13 else: return (30*n+24)//13 case 11: if n in (11,18,20,22,33): return (38*n+21)//15 else: return (38*n+36)//15 case 12: return (80*n+66)//29 case 13: if n%33 in (14,15,17,20): return (98*n+111)//33 else: return (98*n+78)//33 case 14: if n%22==18: return (35*n+40)//11 else: return (35*n+29)//11 case 15: if n%26==5: return (44*n+27)//13 else: return (44*n+40)//13 case _: return (m+2)*(n+2)//5-4 |
| def dom_vec(m,n): if n==1: yield [Gamma(m,1)] return seq = [0]*n def isValid(seq): if len(seq)==n: if sum(seq)!=Gamma(m,n): return False if 3*seq[-1]+seq[-2]<m: return False if len(seq)==2 and 3*seq[0]+seq[1]<m: return False if len(seq)>=3 and seq[-3]+3*seq[-2]+seq[-1]<m: return False if sum(seq)+Gamma(m,n-len(seq)-1)>Gamma(m,n): return False return True k = 0 while(k>=0): if k==n and isValid(seq): yield seq if k==n or seq[k]==m+1: k-=1 seq[k]+=1 else: if isValid(seq[:k+1]): if k<n-1: seq[k+1]=0 k+=1 else: seq[k]+=1 |
| def Zeta3p(n): m=3 def cnt_dom(seq,i=0,cov=(),nc=()): # tc for “to cover”; nc for “not covered” if i==len(seq): if len(nc)==0: return 1 else: return 0 cnt = 0 if len(nc)>seq[i]: return 0 for idx in it.combinations(list(set(range(m))-set(nc)),seq[i]-len(nc)): if i==0 and 1 not in idx: continue ncov = list(set(range(m))-set(cov)) for j in idx+nc: if j in ncov: ncov.remove(j) if j+1 in ncov: ncov.remove(j+1) if j-1 in ncov: ncov.remove(j-1) cnt += cnt_dom(seq,i+1,idx+nc,tuple(ncov)) return cnt cnt=0 for seq in dom_vec(m,n): cnt += cnt_dom(seq) return cnt |
| def Zeta(m,n): if m>n: m,n=n,m def cnt_dom(seq,i=0,cov=(),nc=()): # tc for “to cover”; nc for “not covered” if i==len(seq): if len(nc)==0: return 1 else: return 0 cnt = 0 if len(nc)>seq[i]: return 0 for idx in it.combinations(list(set(range(m))-set(nc)),seq[i]-len(nc)): ncov = list(set(range(m))-set(cov)) for j in idx+nc: if j in ncov: ncov.remove(j) if j+1 in ncov: ncov.remove(j+1) if j-1 in ncov: ncov.remove(j-1) cnt += cnt_dom(seq,i+1,idx+nc,tuple(ncov)) return cnt cnt=0 for seq in dom_vec(m,n): cnt += cnt_dom(seq) return cnt |
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; North-Holland: New York, NY, USA, 1976. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Domination in Graphs: Advanced Topics; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of Domination in Graphs; Chapman and Hall/CRC Pure and Applied Mathematics Series; Marcel Dekker, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Amir, H.K.; Reza, E.A. Application of dominating sets in wireless sensor networks. Int. J. Secur. Its Appl. 2013, 7, 185–202. [Google Scholar]
- Boutrig, R.; Chellali, M. A Note on a Relation Between the Weak and Strong Domination Numbers of a Graph. Opusc. Math. 2012, 32, 235–238. [Google Scholar] [CrossRef]
- Chaluvaraju, B.; Chellali, M.; Vidya, K.A. Perfect k-domination in graphs. Australas. J. Comb. 2010, 48, 175–184. [Google Scholar]
- Cockayne, E.J.; Dawes, R.M.; Hedetniemi, S.T. Total domination in graphs. Networks 1980, 10, 211–219. [Google Scholar] [CrossRef]
- Domke, G.S.; Hattingh, J.H.; Henning, M.A.; Markus, L.R. Restrained domination in trees. Discret. Math. 2000, 211, 1–9. [Google Scholar] [CrossRef]
- Beggas, F. Decomposition and Domination of Some Graphs: Data Structures and Algorithms. Ph.D. Thesis, Université Claude Bernard Lyon 1, Lyon, France, 2017. [Google Scholar]
- Harary, F.; Haynes, T.W. Double domination in graphs. Ars Comb. 2000, 55, 201–214. [Google Scholar]
- Henning, M.A. A survey of selected recent results on total domination in graphs. Discret. Math. 2009, 309, 32–63. [Google Scholar] [CrossRef]
- Livingston, M.; Stout, Q.F. Perfect Dominating Sets; University of Michigan, Computer Science and Engineering Division, Department of Electrical Engineering and Computer Science: Ann Arbor, MI, USA, 1990. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Yang, Y.; Ma, M. Minimum Connected Dominating Set Algorithms for Ad Hoc Sensor Networks. Sensors 2019, 19, 1919. [Google Scholar] [CrossRef] [PubMed]
- Allagan, J.; Benkam, B. Dominion of Some Graphs. Int. J. Math. Comput. Sci. 2021, 16, 1709–1720. [Google Scholar]
- Gray, O.E. Dominion on Ladders. Master’s Thesis, Elizabeth City State University, Elizabeth City, NC, USA, 2023. [Google Scholar]
- Alanko, S.; Crevals, S.; Isopoussu, A.; Östergård, P.R.; Pettersson, V. Computing the domination number of grid graphs. Electron. J. Comb. 2011, 18, 141. [Google Scholar] [CrossRef] [PubMed]



| m\n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 4 | 3 | 1 | 8 | 4 | 1 | 13 |
| 2 | 2 | 6 | 3 | 12 | 2 | 17 | 2 | 20 | 2 | 24 |
| 3 | 1 | 3 | 10 | 29 | 1 | 2 | 11 | 46 | 1 | 3 |
| 4 | 4 | 12 | 29 | 2 | 52 | 92 | 2 | 4 | 324 | 2 |
| 5 | 3 | 2 | 1 | 52 | 22 | 13 | 3 | 344 | 169 | 50 |
| 6 | 1 | 17 | 2 | 92 | 13 | 288 | 34 | 2 | 179 | 4683 |
| 7 | 8 | 2 | 11 | 2 | 3 | 34 | 2 | 34 | 148 | 2 |
| 8 | 4 | 20 | 46 | 4 | 344 | 2 | 34 | 52 | 96 | 560 |
| 9 | 1 | 2 | 1 | 324 | 169 | 179 | 148 | 96 | 32 | 24 |
| 10 | 13 | 24 | 3 | 2 | 50 | 4683 | 2 | 560 | 24 | 4 |
| m\n | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 1 | 19 | 6 | 1 | 26 | 7 | 1 | 34 | 8 |
| 2 | 2 | 28 | 2 | 32 | 2 | 36 | 2 | 40 | 2 | 44 |
| 3 | 12 | 60 | 1 | 4 | 16 | 78 | 1 | 5 | 21 | 103 |
| 4 | 10 | 8 | 2 | 16 | 32 | 18 | 22 | 74 | 90 | 60 |
| 5 | 8 | 2667 | 913 | 249 | 64 | 8 | 5611 | 1604 | 418 | 88 |
| 6 | 516 | 26 | 2091 | 32 | 2 | 358 | 27,739 | 732 | 42 | 4976 |
| 7 | 81 | 696 | 2 | 154 | 2315 | 2 | 261 | 6014 | 2 | 416 |
| 8 | 1640 | 3796 | 12,466 | 42,546 | 24 | 64 | 352 | 1416 | 5872 | 19,052 |
| 9 | 22 | 8 | 12,292 | 8892 | 6261 | 2464 | 1056 | 784 | 544 | 144 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Allagan, J.; Gao, S.; Malomo, O.; Gao, W.; Eyob, E. Dominion on Grids. Mathematics 2024, 12, 3408. https://doi.org/10.3390/math12213408
Su J, Allagan J, Gao S, Malomo O, Gao W, Eyob E. Dominion on Grids. Mathematics. 2024; 12(21):3408. https://doi.org/10.3390/math12213408
Chicago/Turabian StyleSu, Jianning, Julian Allagan, Shanzhen Gao, Olumide Malomo, Weizheng Gao, and Ephrem Eyob. 2024. "Dominion on Grids" Mathematics 12, no. 21: 3408. https://doi.org/10.3390/math12213408
APA StyleSu, J., Allagan, J., Gao, S., Malomo, O., Gao, W., & Eyob, E. (2024). Dominion on Grids. Mathematics, 12(21), 3408. https://doi.org/10.3390/math12213408








