Dominion on Grids

Abstract

The domination (number) of a graph $G=(V,E)$, denoted by $\gamma \left(G\right)$, is the size of the minimum dominating sets of $V\left(G\right)$, also known as $\gamma$-sets. As such, the dominion of G, denoted by $\zeta \left(G\right)$, counts all its $\gamma$-sets. We proved a conjecture from one of the authors on the dominion of cycles $C_{3k-1}$ and $C_{3k-2}$, $k\ge 2$. Further, we found the formulae and recurrence relations for the dominions of several grids, $G_{m,n}$, with $2\le m\le 4$ and other results when $m\le 9$ and $n\le 20$. In general, domination and dominion play important roles in assessing certain vulnerabilities of any given network system.

1. Introduction

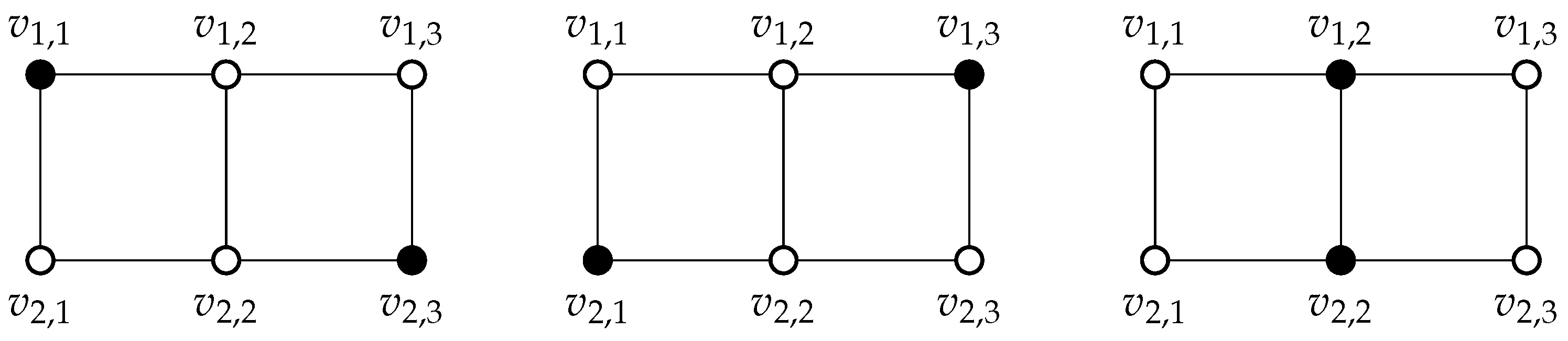
Throughout this article, the sequences of vertices denoted by $P_n:=v_1-v_2-\cdots -v_n$ and $C_n:=v_1-v_2-\cdots -v_n-v_1$ define a path and a cycle on $n\ge 2$ and $n\ge 3$ vertices, respectively. For other basic graph definitions, we refer the reader to [1]. A dominating set for a graph $G=(V,E)$ is a subset $S\subseteq V$ such that every vertex $v\in V$ is either in S or has a neighbor $u\in S$. A dominating set S is a minimal dominating set if no proper subset $S^{\prime }\subset S$ is a dominating set. The domination number$\gamma \left(G\right)$ of a graph G is the minimum cardinality among all the dominating sets of G. Variations in minimum dominating sets have been extensively researched. We recommend to the reader Haynes et al.’s books [2,3] and several other research works [4,5,6,7,8,9,10,11,12,13,14] on their applications. For simplicity, they are referred to as γ-sets in [15], and a graph may have multiple $\gamma$-sets. Thus, the dominion (number) of a graph $G=(V,E)$, denoted by $\zeta \left(G\right)$, is the number of its $\gamma$-sets. Figure 1 illustrates an example of a graph with $\gamma \left(G\right)=2$ and $\zeta \left(G\right)=3$.

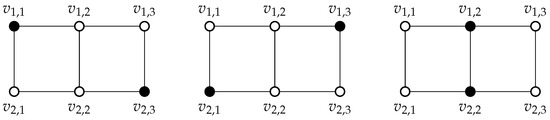
Figure 1. Illustration of the (3) possible $\gamma$-sets (each with two elements in solid color) of the ladder $G_{2,3}$.

In [16], Gray described several applications of the concepts of the dominion and domination of graphs related to wireless sensor networks, network security, social network analysis, distributed systems, and network optimizations. For instance, in network security, the domination of a network is the minimum number of nodes that need to be monitored to ensure the safety of the network system; as such, the critical assets within a network remain protected and the communications among these assets are not disrupted. Dominion, on the other hand, provides a network designer several different asset monitoring options in the event of a cyber attack. The greater the dominion value of a network system, the more resilient it is to any intrusion.

2. Results

2.1. Dominion on Paths and Cycles

Given a path $P_n$ and a cycle $C_n$, it is well known that $\gamma \left(P_n\right)=\gamma \left(C_n\right)=\lceil {\displaystyle \frac{n}{3}}\rceil$; see [17], for instance. From this, the following result was established in [15].

Theorem 1.

If $P_n$ denotes a path on $n\ge 3$ vertices, then, for $k\ge 2$, its dominions are

1. 

$\zeta \left(P_{3k}\right)=1$

2. 

$\zeta \left(P_{3k-1}\right)=k+1$

3. 

$\zeta \left(P_{3k-2}\right)={\displaystyle \frac{k^2+3k-2}{2}}$.

In this section, starting with the next lemma, we extend this result to cycles, which was a conjecture in [15]. First, we define ${\zeta }_v\left(G\right)$ as the number of $\gamma$-sets that contain v but do not contain its neighbor, i.e., any other vertex adjacent to v. Similarly, define ${\zeta }_{u,v}\left(G\right)$ as the number of $\gamma$-sets containing $u,v$ but not their neighbor.

Lemma 1.

Given a cycle on $n\ge 3$ vertices, $C_n$, the following relation holds

$$\zeta \left(C_n\right)=3{\zeta }_{v_1}\left(C_n\right)+4{\zeta }_{v_1,v_2}\left(C_n\right)-{\zeta }_{v_1,v_3}\left(C_n\right).$$

Proof. 

Let $C_n:=v_1-v_2-\cdots -v_n-v_1$ and S be a $\gamma$-set. We will focus on all cases over $v_1,v_2,v_3$. Note that no three consecutive vertices can be simultaneously in S. Hence, there are six cases. Three of them have two vertices in S, while the other three have one vertex in S.

Case 1. Suppose $v_2,v_3\in S$. Since no three consecutive vertices can be simultaneously in S, we have $v_1,v_4\notin S$. The number of such $\gamma$-sets is ${\zeta }_{v_2,v_3}\left(C_n\right)={\zeta }_{v_1,v_2}\left(C_n\right)$.

Case 2. Suppose $v_1,v_2\in S$. Similar to Case 1, the number of such $\gamma$-sets is ${\zeta }_{v_1,v_2}\left(C_n\right)$.

Case 3. Suppose $v_1,v_3\in S$ and $v_2\notin S$. If $v_4\in S$, then $v_3$ is covered as a neighbor and thus should not be in S due to minimality. Hence, $v_4\notin S$. Similarly, $v_n\notin S$. The number of such $\gamma$-sets is ${\zeta }_{v_1,v_3}\left(C_n\right)$.

Case 4. Suppose $v_2\in S$ and $v_1,v_3\notin S$. The number of such $\gamma$-sets is ${\zeta }_{v_2}\left(C_n\right)={\zeta }_{v_1}\left(C_n\right)$.

Case 5. Suppose $v_3\in S$ and $v_1,v_2\notin S$. If $v_4\notin S$, then the number of such $\gamma$-sets is ${\zeta }_{v_3}\left(C_n\right)-{\zeta }_{v_1,v_3}\left(C_n\right)={\zeta }_{v_1}\left(C_n\right)-{\zeta }_{v_1,v_3}\left(C_n\right)$. If $v_4\in S$, then the number of such $\gamma$-sets is ${\zeta }_{v_3,v_4}\left(C_n\right)={\zeta }_{v_1,v_2}\left(C_n\right)$. The total in this case is ${\zeta }_{v_1}\left(C_n\right)+{\zeta }_{v_1,v_2}\left(C_n\right)-{\zeta }_{v_1,v_3}\left(C_n\right)$.

Case 6. Suppose $v_1\in S$ and $v_2,v_3\notin S$. This result is similar to Case 5.

From Cases 1–6, the result follows. □

We now restate Conjecture 2.1 from [15] as the next theorem.

Theorem 2.

If $C_n$ denotes a cycle on $n\ge 3$ vertices, then, for $k\ge 2$, its dominions are

1. 

$\zeta \left(C_{3k}\right)=3$

2. 

$\zeta \left(C_{3k-1}\right)=3k-1$

3. 

$\zeta \left(C_{3k-2}\right)={\displaystyle \frac{(3k-2)(k+1)}{2}}.$

Proof. 

Let $C_n:=v_1-v_2-\cdots -v_n-v_1$ and let $k\ge 2$, and for the values of $\zeta \left(P_n\right)$ please see Theorem 1.

Case 1. This case is proved in [15]. In the context of this article, we present another proof of the result.

By definition, ${\zeta }_{v_1}\left(C_{3k}\right)$ refers to $\gamma$-sets that contain $v_1$ but not its neighbor. By removing $v_1$, $v_2$, $v_n$ from $C_{3k}$, we have a path on $3k-3$ vertices. Hence, ${\zeta }_{v_1}\left(C_{3k}\right)=\zeta \left(P_{3k-3}\right)$=1. Additionally, we have ${\zeta }_{v_1,v_2}\left(C_{3k}\right)=0$ and ${\zeta }_{v_1,v_3}\left(C_{3k}\right)=0$. By Lemma 1, we have $\zeta \left(C_{3k}\right)=3{\zeta }_{v_1}\left(C_{3k}\right)=3$.

Case 2. Similar to Case 1, we have ${\zeta }_{v_1}\left(C_{3k-1}\right)=\zeta \left(P_{3k-4}\right)$, ${\zeta }_{v_1,v_2}\left(C_{3k-1}\right)=0$, and ${\zeta }_{v_1,v_3}\left(C_{3k-1}\right)=\zeta \left(P_{3k-6}\right)$. By Lemma 1, we have $\zeta \left(C_{3k-1}\right)=3\zeta \left(P_{3k-4}\right)-\zeta \left(P_{3k-6}\right)=3k-1$.

Case 3. Following a similar argument as in the previous case, we have ${\zeta }_{v_1}\left(C_{3k-2}\right)=\zeta \left(P_{3k-5}\right)$, ${\zeta }_{v_1,v_2}\left(C_{3k-2}\right)=\zeta \left(P_{3k-6}\right)$, and ${\zeta }_{v_1,v_3}\left(P_{3k-2}\right)=\zeta \left(P_{3k-7}\right)$. By Lemma 1, we have

$$\begin{array}{cc}\hfill \zeta \left(C_{3k-2}\right)& =3\zeta \left(P_{3k-5}\right)+4\zeta \left(P_{3k-6}\right)-\zeta \left(P_{3k-7}\right)\hfill \\ \hfill & =3·{\displaystyle \frac{{(k-1)}^2+3(k-1)-2}{2}}+4-(k-1)\hfill \\ \hfill & ={\displaystyle \frac{3k^2+k-2}{2}}={\displaystyle \frac{(3k-2)(k+1)}{2}}.\hfill \end{array}$$

□

2.2. An Optimization Problem

This section considers grid graphs, or grids, for simplicity. An $m\times n$ grid $G_{m,n}$ has the vertex set $V=\{v_{i,j}:1\le i\le m,1\le j\le n\}$ with two vertices $v_{i,j}$ and $v_{i^{\prime },j^{\prime }}$ that are adjacent if $i=i^{\prime }$ and $|j-j^{\prime }|=1$ or if $j=j^{\prime }$ and $|i-i^{\prime }|=1$. The special case $G_{2,3}$ is well known as a ladder; see Figure 1 for an example. We denote ${\gamma }_{m,n}$ the cardinality of minimal dominating sets in $G_{m,n}$ and ${\zeta }_{m,n}$ the cardinality of $\gamma$-sets. Please refer to [17] for some original values of ${\gamma }_{m,n}\left(G_{m,n}\right)$.

We first consider the following combinatorial optimization problem.

Definition 1.

For $2\le m\le 4$ and $n\ge 1$, minimize $x_1+x_2+\cdots +x_n$ given the following (5) restrictions:

1. 

For $1\le i\le n$, $x_i\in \{0,1,2,\cdots ,m\}$.

2. 

For $1<i<n$, if $x_i=0$, then $x_{i-1}+x_{i+1}\ge m$.

3. 

If $x_1=0$, then $x_2=m$.

4. 

If $x_n=0$, then $x_{n-1}=m$.

5. 

If $n=1$, then $x_1=1$.

Let $A_n$ be the minimum sum of $x_1+x_2+\cdots +x_n$ under the above restrictions. Then, $A_n\le n$.

For easier reference, we call this optimization problem the Dominion Optimization Problem.

Lemma 2.

Let $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. If $n<m$, then $a_i=1$ for all i.

Proof. 

The statement is trivial when $n=1$.

For $n=2$, we have $m\ge 3$. If $a_1=0$, then $a_2=m$ and thus $A_2=m>2$. Hence, $a_1\ne 0$. Similarly, $a_2\ne 0$. Thus, $(a_1,a_2)=(1,1)$.

For $n=3$, we have $m=4$. If $a_1=0$, then $a_2=4$ and thus $A_3\ge 4>3$. Hence, $a_1\ne 0$. Similarly, $a_3\ne 0$. If $a_2=0$, then $A_3\ge a_1+a_3=4>3$. Hence, $a_2\ne 0$. Therefore, $(a_1,a_2,a_3)=(1,1,1)$. □

Definition 2.

From the Dominion Optimization Problem, if $(a_1,a_2,\cdots ,a_n)$ is a vector that minimizes $x_1+x_2+\cdots +x_n$ and there exists k such that $(a_1,a_2,\cdots ,a_k)$ minimizes $x_1+x_2+\cdots +x_k$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ minimizes $x_1+x_2+\cdots +x_{n-k}$, then we say $(a_1,a_2,\cdots ,a_n)$ is decomposible. We say $(a_1,a_2,\cdots ,a_n)$ can be decomposed to $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$. If $(a_1,a_2,\cdots ,a_n)$ is not decomposible, we say it is non-decomposible.

Lemma 3.

Let $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. Then, each of the following conditions implies that $(a_1,a_2,\cdots ,a_n)$ can be decomposed to $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$.

1. 

Both $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ satisfy the five restrictions in the Dominion Optimization Problem.

2. 

$a_k\ne 0$ and $a_{k+1}\ne 0$.

3. 

$(a_k,a_{k+1})=(0,0)$.

4. 

$(a_{k-1},a_k)=(m,0)$ and $n>k$.

5. 

$(a_k,a_{k+1})=(0,m)$ and $k>0$.

Proof. 

We just need to verify that all five restrictions in the Dominion Optimization Problem are satisfied for both $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ for each case.

It is straightforward to verify that the first four restrictions are inherited for each case. Additionally, restriction 5 is also satisfied due to minimality. Hence, we have the statement. □

Lemma 4.

Let $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. If $(a_1,a_2,\cdots ,a_n)$ is non-decomposible, then the values of each element alternate between zero and non-zero values.

Proof. 

This follows from parts 2 and 3 of Lemma 3. □

Lemma 5.

If $m=2$ and $(a_1,a_2,\cdots ,a_n)$ is non-decomposible, then

$(a_1,a_2,\cdots ,a_n)\in \{(0,2),(2,0),(0,2,0)\}$ or ${\left(a_i\right)}_{i=1}^n=(1,0,1,0,\cdots ,1)$.

Proof. 

Assume that $(a_1,a_2,\cdots ,a_n)\notin \{(0,2),(2,0),(0,2,0)\}$. Since $(a_1,a_2,\cdots ,a_n)$ is non-decomposible, by Lemma 4, its values must alternate between zero and non-zero. If it starts with zero, then $n>1$ and it starts with $(0,2)$. Since $(a_1,a_2,\cdots ,a_n)\ne (0,2)$, we have $n>2$ and it starts with $(0,2,0)$. Since $(a_1,a_2,\cdots ,a_n)\ne (0,2,0)$, we have $n>3$. By part 4 of Lemma 3, it is decomposible, which is a contradiction. Thus, $(a_1,a_2,\cdots ,a_n)$ does not start with zero. By a similar argument, it does not end with zero either. It follows that it starts and ends with non-zero elements. To minimize the sum, we have $(a_1,a_2,\cdots ,a_n)=(1,0,1,0,\cdots ,1)$. □

2.3. Dominion on Ladder Graphs

Definition 3.

Given a grid $G_{m,n}$ with $2\le m\le 4$ and $n\ge 1$, let S be a minimum dominating set. For $1\le i\le n$, let $a_i$ be the number of vertices from both S and Column i. Then, $(a_1,a_2,\cdots ,a_n)$ satisfies the five restrictions in the Dominion Optimization Problem. In this case, we call $(a_1,a_2,\cdots ,a_n)$ the minimum dominating vector.

Lemma 6.

Let $m=2$ and $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. Let $A_n=a_1+a_2+\cdots +a_n$.

1. 

$A_n=⌊{\displaystyle \frac{n}{2}}+1⌋$

2. 

If n is odd, then $(a_1,a_2,\cdots ,a_n)$ is non-decomposible.

3. 

If n is even and $n\ge 4$, then $(a_1,a_2,\cdots ,a_n)$ can be decomposed to two non-decomposible vectors $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ for some odd integer k.

Proof. 

Case 1. If n is odd, then, since the sum of $(1,0,1,0,\cdots ,1)$ is $⌊{\displaystyle \frac{n}{2}}+1⌋$, we have $A_n\le ⌊{\displaystyle \frac{n}{2}}+1⌋$. If n is even, consider a sequence with $a_1=1$ and the rest $(1,0,1,0,\cdots ,1)$. The sum is $⌊{\displaystyle \frac{n}{2}}+1⌋$. Hence, $A_n\le ⌊{\displaystyle \frac{n}{2}}+1⌋$. Since decomposition requires a non-smaller sum, we have $A_n=⌊{\displaystyle \frac{n}{2}}+1⌋$.

Case 2. Suppose that n is odd. Then $A_n={\displaystyle \frac{n-1}{2}}+1$. Assume on the contrary that $(a_1,a_2,\cdots ,a_n)$ can be decomposed to $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ for some k. If k is even, then $A_n=\left({\displaystyle \frac{k}{2}}+1\right)+\left({\displaystyle \frac{n-k-1}{2}}+1\right)={\displaystyle \frac{n-1}{2}}+2$, contradicting $A_n={\displaystyle \frac{n-1}{2}}+1$. Similarly, if k is odd, then $A_n=\left({\displaystyle \frac{k-1}{2}}+1\right)+\left({\displaystyle \frac{n-k}{2}}+1\right)={\displaystyle \frac{n-1}{2}}+2$, which is again a contradiction. Therefore, $(a_1,a_2,\cdots ,a_n)$ is non-decomposible.

Case 3. Suppose that n is even and $n\ge 4$. Then, $A_n={\displaystyle \frac{n}{2}}+1$. By the contrapositive statement of Lemma 5, ${\left(a_i\right)}_{i=1}^n$ is decomposible. Suppose that it can be decomposed to $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ for some k. If k is even, then $A_n=\left({\displaystyle \frac{k}{2}}+1\right)+\left({\displaystyle \frac{n-k}{2}}+1\right)={\displaystyle \frac{n}{2}}+2$, contradicting $A_n={\displaystyle \frac{n}{2}}+1$. Hence, k is odd. To obtain minimal sum, both $(a_1,a_2,\cdots ,a_k)$ and $(a_{k+1},a_{k+2},\cdots ,a_n)$ are non-decomposible. □

For $G_{2,n}$, note that there is exactly one dominating set with dominating sequence $(0,2,0)$. There are exactly two dominating sets with dominating sequence $(1,0,1,0,\cdots ,1)$.

Theorem 3.

${\zeta }_{2,n}=\left\{\begin{array}{cc}6\hfill & \mathit{if}n=2\hfill \\ 3\hfill & \mathrm{if}n=3\hfill \\ 12\hfill & \mathit{if}n=4\hfill \\ 17\hfill & \mathit{if}n=6\hfill \\ 2\hfill & \mathit{if}n\equiv 1(mod2)\mathit{and}n\ge 5\hfill \\ 2n+4\hfill & \mathit{if}n\equiv 0(mod2)\mathit{and}n\ge 8.\hfill \end{array}\right.$

Proof. 

Let S be a minimum dominating set and $(a_1,a_2,\cdots ,a_n)$ be the corresponding minimum dominating vector.

If n is odd, then, by Lemma 6, ${\left(a_i\right)}_{i=1}^n$ is non-decomposible. For $n\ge 5$, by Lemma 5, we have $(a_1,a_2,\cdots ,a_n)=(1,0,1,0,\cdots ,1)$. There are exactly two such minimum dominating sets. Hence, ${\zeta }_{2,n}=2$. For $n=3$, ${\left(a_i\right)}_{i=1}^n$ could also be $(0,2,0)$. Hence, ${\zeta }_{2,n}=2+1=3$.

Now, suppose that n is even. For $n=2$, any set of two vertices cover all the vertices. Hence, ${\zeta }_{2,2}=\left(\begin{array}{c}4\\ 2\end{array}\right)=6$. Now, suppose that $n\ge 4$. Then, by Lemma 6, $(a_1,a_2,\cdots ,a_n)$ can be decomposed to two non-decomposible vectors with length of odd integers, say $k_1$ and $k_2$. Hence, $n=k_1+k_2$. There are ${\displaystyle \frac{n}{2}}$ sets of non-negative odd integer solutions. For $n=4$, we have $k_1=1$ or $k_1=3$ and thus ${\zeta }_{2,4}=2·3+3·2=12$. For $n=6$, we have $k_1\in \{1,3,5\}$ and thus ${\zeta }_{2,6}=2·2+3·3+2·2=17$. Now, suppose $n\ge 8$. Then, ${\zeta }_{2,n}={\displaystyle \sum _{i=0}^{n/2-1}}{\zeta }_{2,2i+1}{\zeta }_{2,n-2i+1}=2n+4$. □

We note here that a proof of a partial result from Theorem 3 first appeared in [16], albeit using a very different technique.

2.4. Dominion of Grid Graphs $G_{3,n}$

Lemma 7.

Let $m=3$ and $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots x_n$ in the Dominion Optimization Problem. If $n\ge 5$, then there exists an integer k such that $(a_k,a_{k+1},a_{k+2},a_{k+3})=(1,0,2,0)$.

Proof. 

Let $A_n=a_1+a_2+\cdots a_n$. If $2\le n\le 4$, then $A_n=n$ and all elements are 1. For the case of $n=1$, we define $A_1=1$. Now, we suppose $n\ge 5$.

If there exists an index j such that $a_j\ne 0$ and $a_{j+1}\ne 0$, then, by Lemma 3, $(a_1,a_2,\cdots ,a_n)$ can be decomposed to $(a_1,a_2,\cdots ,a_j)$ and $(a_{j+1},a_{j+2},\cdots ,a_n)$. If both $j\le 4$ and $n-j\le 4$, then all elements in the vectors are 1. Hence, $A_n=n$. However, by setting $(x_1,x_2,x_3,x_4)=(1,0,2,0)$ and the rest to be 1, we obtain $A_n\le {\displaystyle \sum _{i=1}^n}{x}_i=n-1$, which is a contradiction. Hence, $j\ge 5$ or $n-j\ge 5$. We can prove the statement by demonstrating that it works for one of the sub-vectors with $\ge 5$ elements. We may assume that $j\ge 5$.

We may further assume that $(a_1,a_2,\cdots ,a_j)$ is non-decomposible. Hence, by Lemma 4, the values alternate between zero and non-zero elements. If $a_1=0$, then $a_2=3$ and thus it begins with $(0,3,0)$. By Lemma 3, it is decomposible, contradicting the assumption. Hence, $a_1\ne 0$. To minimize $A_n$, we have $a_3\le 2$. If $a_3=2$, then, to minimize $A_n$, we have $a_1=1$ and thus $(a_1,a_2,a_3,a_4)=(1,0,2,0)$. We now assume $a_3=1$. Then, $a_1=a_5=2$. If $n=5$, then $(a_1,a_2,\cdots ,a_5)=(2,0,1,0,2)$ and thus $A_5=2+0+1+0+2=5$, contradicting $A_5<5$. Hence, $n>5$ and thus $(a_3,a_4,a_5,a_6)=(1,0,2,0)$. □

We note here that it is shown in [17] that ${\gamma }_{3,n}=⌊{\displaystyle \frac{3n+4}{4}}⌋$ for all $n\ge 1$.

Lemma 8.

Let $m=3$ and $n\ge 2$. Let $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. Let $A_n=a_1+a_2+\cdots a_n$. Then,

1. 

$A_n={\gamma }_{3,n}$, and

2. 

$(a_1,a_2,\cdots ,a_n)$ can be obtained from a vector of length $\le 4$ by inserting $⌊{\displaystyle \frac{n}{4}}⌋$ copies of $(1,0,2,0)$.

Proof. 

For $1\le n\le 4$, we have $A_n=n=⌊{\displaystyle \frac{3n+4}{4}}⌋={\gamma }_{3,n}$. Hence, the statement is true for $n\le 4$. We may now assume $n\ge 5$. Then, by Lemma 7, there exists a sub-vector $(a_k,a_{k+1},a_{k+2},a_{k+3})=(1,0,2,0)$. Since $a_{k+2}\ne 3$, we have $n\ge k+4$ and $a_{k+4}\ge 1$. Hence, we can remove this sub-vector $(1,0,2,0)$ to obtain a vector of length $n-4$. Let $A_n$ be the minimum value and define $A_1=1$. Then, $A_n\ge 3+A_{n-4}$. Let $n=4k+r$ with $1\le r\le 4$. Then, recursively, we obtain $A_n\ge 3k+A_r=3k+r={\gamma }_{3,n}$.

Consider a vector beginning with k copies of $(1,0,2,0)$ and the rest to be 1; we obtain $A_n\le 3k+r=3k+⌊{\displaystyle \frac{3r+4}{4}}⌋=⌊{\displaystyle \frac{3n+4}{4}}⌋={\gamma }_{3,n}$. Hence, $A_n={\gamma }_{3,n}$. By reversing the process, we see that $(a_1,a_2,\cdots ,a_n)$ can be obtained from a vector of length $\le 4$ by inserting $⌊{\displaystyle \frac{n}{4}}⌋$ copies $(1,0,2,0)$. □

Theorem 4.

Given an integer $n\ge 1$ and let $G_{3,n}$ be a grid graph. Let $(a_1,a_2,\cdots ,a_n)$ be a minimum dominating vector of $G_{3,n}$. Then, $(a_1,a_2,\cdots ,a_n)$ minimizes $x_1+x_2+\cdots x_n$ in the Dominion Optimization Problem and $a_1+a_2+\cdots a_n={\gamma }_{3,n}$.

Proof. 

It is straightforward to verify that $(a_1,a_2,\cdots ,a_n)$ satisfies all five restrictions of the Dominion Optimization Problem. Since the corresponding vertex set is a dominating set, we have $a_1+a_2+\cdots +a_n={\gamma }_{3,n}$. By Lemma 8, ${\gamma }_{3,n}$ is the minimum sum of $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. Hence, $(a_1,a_2,\cdots ,a_n)$ minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. □

Given a grid graph $G_{3,n}$, we define ${\zeta }_{3,n}^{\prime }$, the number of $\gamma$-sets that contain $v_{2,1}$. Note that, by this definition, it is possible for such $\gamma$-set to contain its neighbors, such as $v_{1,1}$ and $v_{3,1}$.

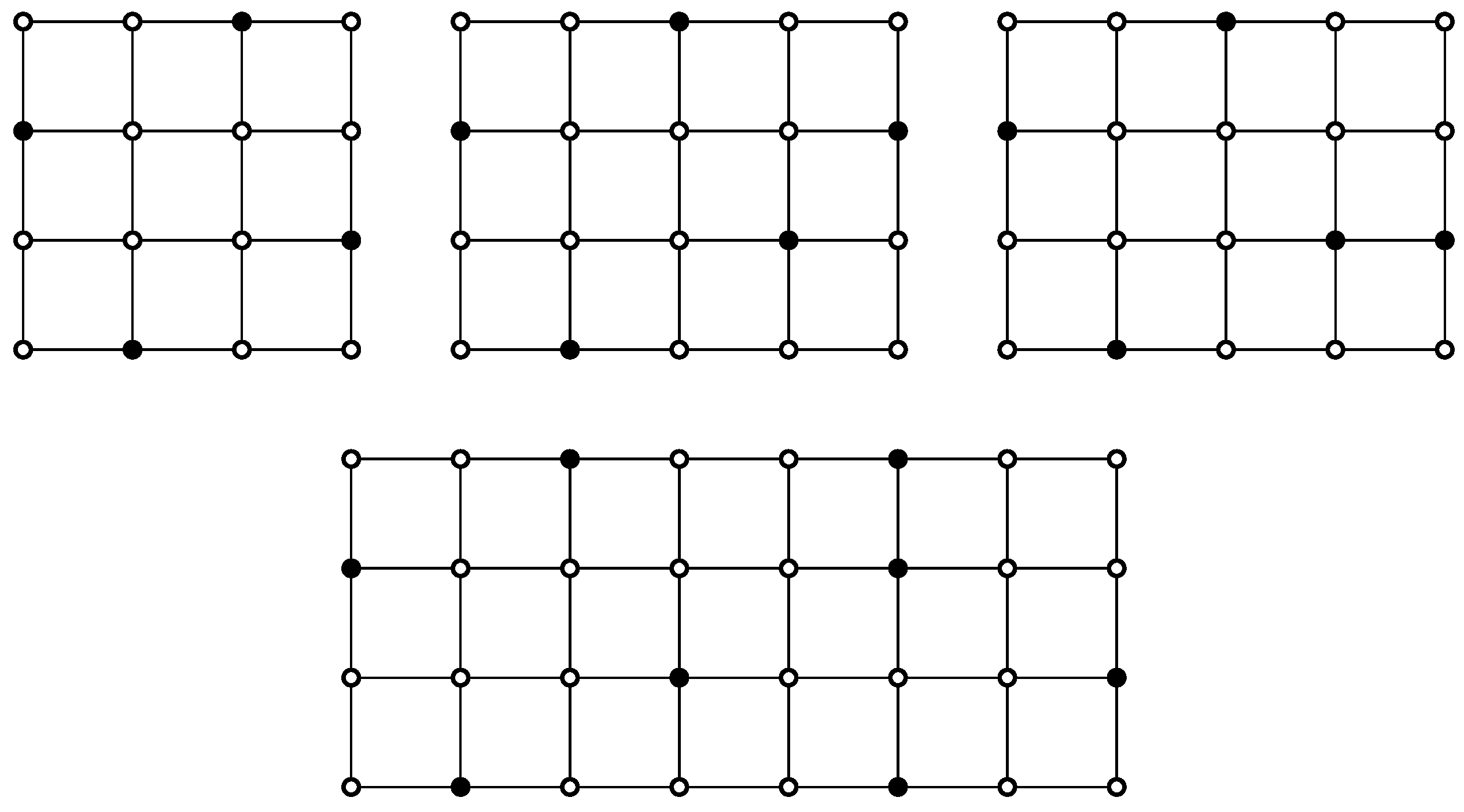
The dominion number increases rapidly as the values of $m,n$ increase. We use recursive arguments to generate and prove the remaining results in this article. As such, we derived a Python program, shown in the last section of the paper, to calculate the dominion numbers for some of those cases.

Lemma 9.

Given an integer $n\ge 1$ and a grid $G_{3,n}$,

1. 

${\zeta }_{3,4k+1}^{\prime }=1$ for $k\ge 0$.

2. 

${\zeta }_{3,4k+2}^{\prime }=k+1$ for $k\ge 0$.

3. 

${\zeta }_{3,4k+3}^{\prime }={\displaystyle \frac{(k+1)(k+2)}{2}}+3$ for $k\ge 0$.

4. 

${\zeta }_{3,4k}^{\prime }={\displaystyle \frac{k(k+1)(k+2)}{6}}+7k+9$ for $k\ge 3.$

Proof. 

Let S be a $\gamma$-set and $(a_1,a_2,\cdots ,a_n)$ be the corresponding minimum dominating vector.

Case 1. Note that ${\zeta }_{3,1}^{\prime }=1$. For $k\ge 1$, since $(a_1,a_2,\cdots ,a_n)$ begins with $(1,0,2,0)$, we have ${\zeta }_{3,4k+1}^{\prime }={\zeta }_{3,4k-3}^{\prime }$. Recursively, we obtain ${\zeta }_{3,4k+1}^{\prime }={\zeta }_{3,1}^{\prime }=1$.

Case 2. Note that ${\zeta }_{3,2}^{\prime }=1$. For $k\ge 1$, since $(a_1,a_2,\cdots ,a_n)$ begins with either $(1,0,2,0)$ or $(1,1,0,2,0)$, we have ${\zeta }_{3,4k+2}^{\prime }={\zeta }_{3,4k-2}^{\prime }+{\zeta }_{3,4k-3}^{\prime }={\zeta }_{3,4k-2}^{\prime }+1$. Recursively, we obtain ${\zeta }_{3,4k+2}^{\prime }=k+{\zeta }_{3,2}^{\prime }=k+1$.

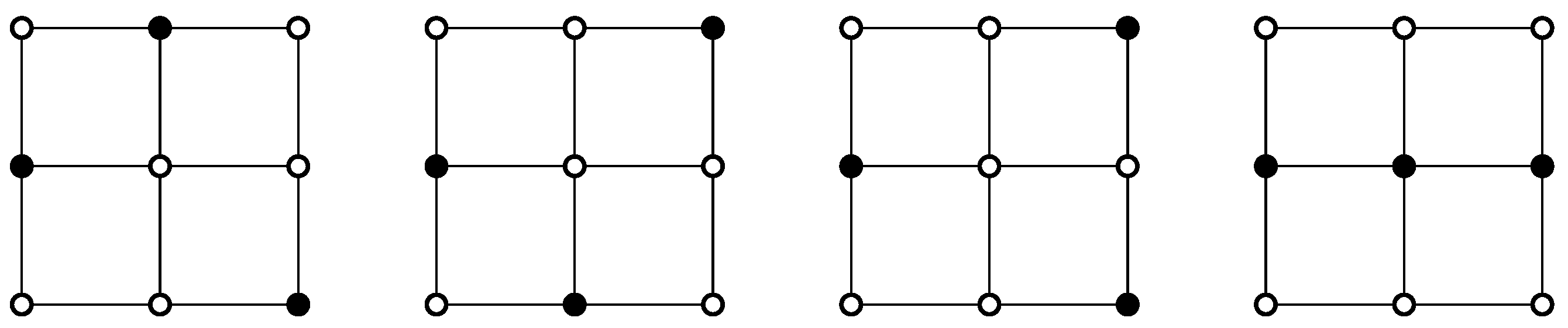
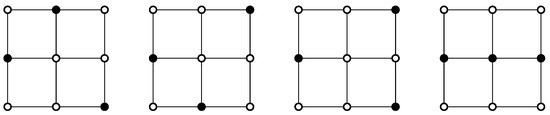
Case 3. For $k\ge 1$, since $(a_1,a_2,\cdots ,a_n)$ begins with $(1,0,2,0)$, $(1,1,0,2,0)$ or $(1,1,1,0,2,0)$, we have ${\zeta }_{3,4k+3}^{\prime }={\zeta }_{3,4k-1}^{\prime }+{\zeta }_{3,4k-2}^{\prime }+{\zeta }_{3,4k-3}^{\prime }={\zeta }_{3,4k-1}^{\prime }+(k+1)$. Recursively, we obtain ${\zeta }_{3,4k+3}^{\prime }=(k+1)+k+\cdots +2+{\zeta }_{3,3}^{\prime }={\displaystyle \frac{(k+1)(k+2)}{2}}-1+{\zeta }_{3,3}^{\prime }$. It can be verified by the Python program in the last section that ${\zeta }_{3,3}^{\prime }=4$. All four such $\gamma$-sets are shown in Figure 2. Hence, ${\zeta }_{3,4k+3}^{\prime }={\displaystyle \frac{(k+1)(k+2)}{2}}+3$.

Figure 2. All (4) possible $\gamma$-sets, including $v_{2,1}$ of the grid graph $G_{3,3}$.

Case 4. Note that $(a_1,a_2,\cdots ,a_n)$ begins with $(1,0,2,0)$, $(1,1,0,2,0)$, $(1,1,1,0,2,0)$, or $(a_1,a_2,a_3,1,0,2,0)$. Note that $(a_1,a_2,a_3,1)$ contains both $v_{2,1}$ and $v_{2,4}$. There are (5) such $\gamma$-sets, as shown in Figure 3. Hence, for $k\ge 3$, we have ${\zeta }_{3,4k}^{\prime }={\zeta }_{3,4k-4}^{\prime }+{\zeta }_{3,4k-5}^{\prime }+{\zeta }_{3,4k-6}^{\prime }+5{\zeta }_{3,4k-7}^{\prime }={\zeta }_{3,4k-4}^{\prime }+\left[{\displaystyle \frac{(k-1)k}{2}}+3\right]+(k-1)+5={\zeta }_{3,4k-4}^{\prime }+{\displaystyle \frac{k(k+1)}{2}}+7$. Recursively, we obtain ${\zeta }_{3,4k}^{\prime }={\displaystyle \sum _{i=3}^k}\left[{\displaystyle \frac{k(k+1)}{2}}+7\right]+{\zeta }_{3,8}^{\prime }={\displaystyle \sum _{i=1}^k}\left[{\displaystyle \frac{k(k+1)}{2}}+7\right]-8-10+{\zeta }_{3,8}^{\prime }={\displaystyle \frac{k(k+1)(k+2)}{6}}+7k-18+{\zeta }_{3,8}^{\prime }$. It can be verified by the Python program in the last section that ${\zeta }_{3,8}^{\prime }=27$. Hence, ${\zeta }_{3,4k}^{\prime }={\displaystyle \frac{k(k+1)(k+2)}{6}}+7k+9$.

Figure 3. All (5) possible $\gamma$-sets, including both $v_{2,1}$ and $v_{2,4}$ of the grid graph $G_{3,4}$.

□

Theorem 5.

Given $n\ge 2$ and a grid $G_{3,n}$.

1. 

If $n\equiv 1(mod4)$, then ${\zeta }_{3,n}=1$.

2. 

If $n\equiv 2(mod4)$, then ${\zeta }_{3,n}=⌊{\displaystyle \frac{n}{4}}⌋+1$.

3. 

If $n\equiv 3(mod4)$, then ${\zeta }_{3,n}=\left\{\begin{array}{cc}10\hfill & \mathit{if}n=3\hfill \\ 11\hfill & \mathit{if}n=7\hfill \\ {\displaystyle \frac{(n+1)(n+5)}{32}}+6\hfill & \mathit{if}n>7\hfill \end{array}\right.$.

4. 

If $n\equiv 0(mod4)$, then ${\zeta }_{3,n}=\left\{\begin{array}{cc}29\hfill & \mathit{if}n=4\hfill \\ 46\hfill & \mathit{if}n=8\hfill \\ 60\hfill & \mathit{if}n=12\hfill \\ {\displaystyle \frac{n(n+4)(n+8)}{384}}+{\displaystyle \frac{5n}{2}}+18\hfill & \mathit{if}n>12.\hfill \end{array}\right.$

Proof. 

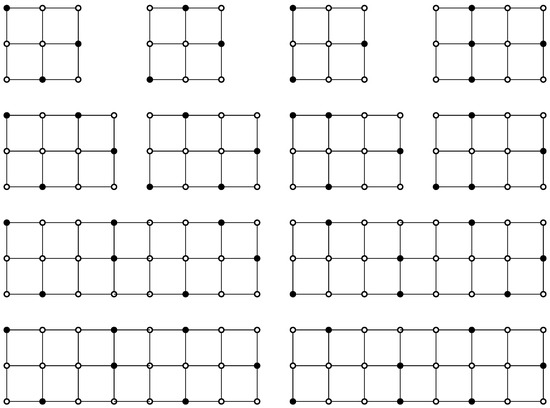
Let S be a $\gamma$-set and $(a_1,a_2,\cdots ,a_n)$ be the corresponding minimum dominating vector.

Case 1. Since $(a_1,a_2,\cdots ,a_n)$ begins with $(1,0,2,0)$, the vertex in S from Column 1 has to be $v_{2,1}$. Hence, ${\zeta }_{3,n}={\zeta }_{3,n}^{\prime }=1$.

Case 2. If $(a_1,a_2,\cdots ,a_n)$ begins with $(1,0,2,0)$, then $v_{2,1}\in S$. Otherwise, it ends with $(1,0,2,0,1)$. By reversing the sequence, we can see that the vertices are uniquely determined and that $v_{2,1}\in S$. Hence, ${\zeta }_{3,n}={\zeta }_{3,n}^{\prime }=⌊{\displaystyle \frac{n}{4}}⌋+1$.

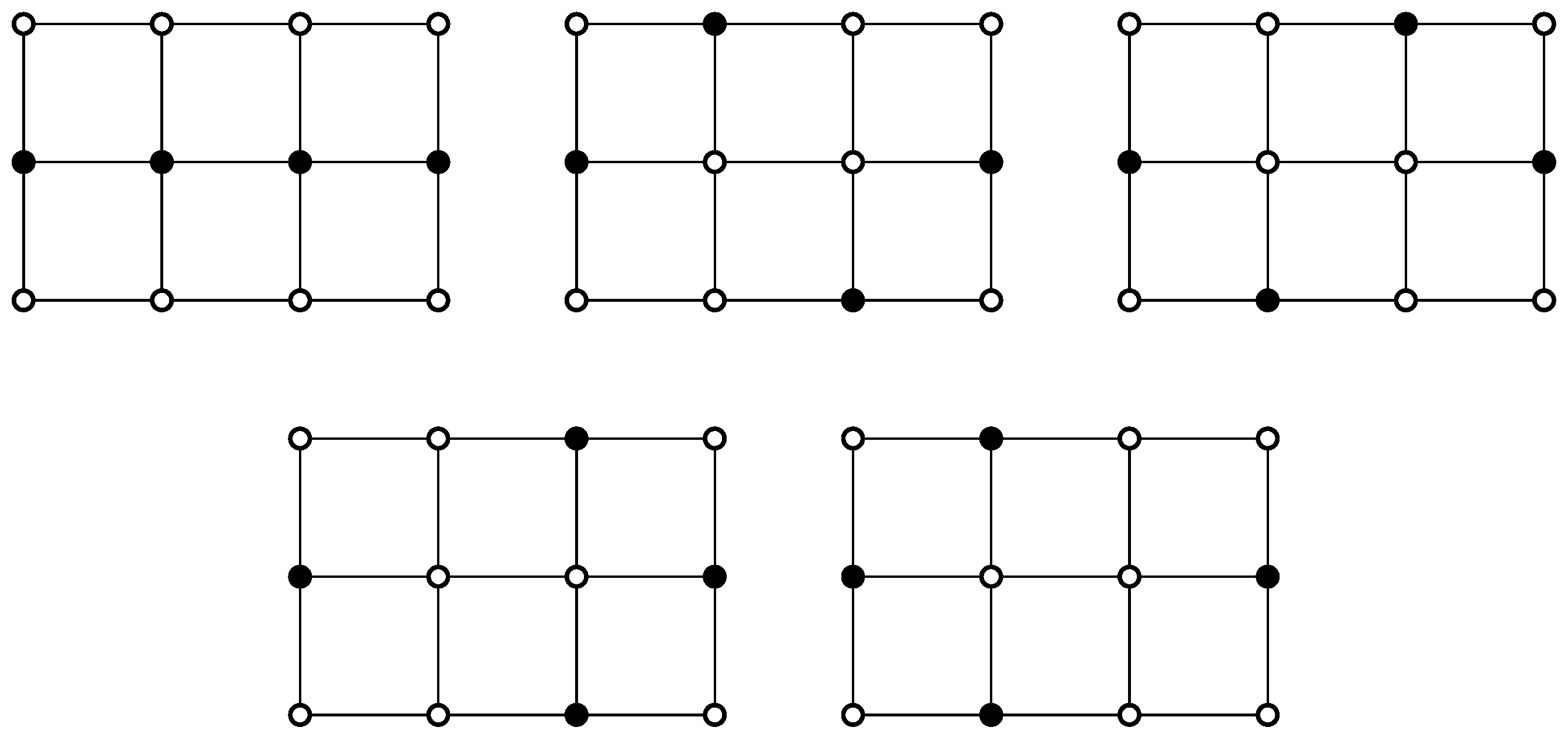
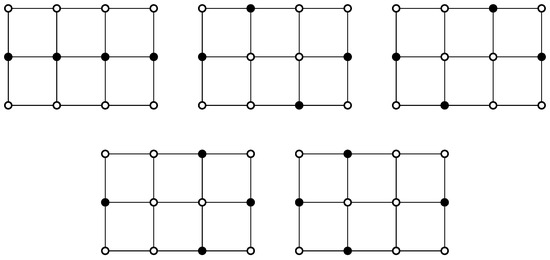
Case 3. For $n=3$ and $n=7$, the results can be verified by the programming results in the last section. We only focus on $n>7$. Consider the sequences that begin with $(a_1,a_2,1)$ such that $v_{2,1}\notin S$ and $v_{2,3}\in S$. There are 3 such $\gamma$-sets, as shown in Figure 4. Hence, ${\zeta }_{3,n}={\zeta }_{3,n}^{\prime }+3{\zeta }_{3,n-2}^{\prime }=\left[{\displaystyle \frac{(n+1)(n+5)}{32}}+3\right]+3={\displaystyle \frac{(n+1)(n+5)}{32}}+6$.

Figure 4. All $\gamma$-sets of grids $G_{3,n}$ as leading subset ending with the middle vertex in the last column.

Case 4. Similar to the previous case, we only focus on $n>12$. Based on the above case, there are 3 sequences beginning with $(a_1,a_2,1)$ such that $v_{2,1}\notin S$ and $v_{2,3}\in S$. As listed in Figure 4, there are 5 cases beginning with $(a_1,a_2,a_3,1)$ and 4 cases beginning with $(a_1,a_2,\cdots ,a_7,1)$. Hence, ${\zeta }_{3,n}={\zeta }_{3,n}^{\prime }+3{\zeta }_{3,n-2}^{\prime }+5{\zeta }_{3,n-3}^{\prime }+4{\zeta }_{3,n-7}^{\prime }$= $\left[{\displaystyle \frac{n(n+4)(n+8)}{384}}+{\displaystyle \frac{7n}{4}}+9\right]+3·{\displaystyle \frac{n}{4}}+5+4={\displaystyle \frac{n(n+4)(n+8)}{384}}+{\displaystyle \frac{5n}{2}}+18$. □

2.5. Dominion on Grids $G_{4,n}$

This section considers the grids $G_{4,n}$.

Lemma 10.

Given an integer $n\ge 4$, let $(a_1,a_2,\cdots ,a_n)$ be a vector that minimizes $x_1+x_2+\cdots +x_n$ in the Dominion Optimization Problem. Then, $(a_1,a_2,\cdots ,a_n)$ contains only copies of sub-vectors $(0,3,0)$ and $\left(1\right)$.

Proof. 

The result follows if there is no 0 element. We assume there exists 0 in $(a_1,a_2,\cdots ,a_n)$. We just need to show that every 0 in the vector belongs to some sub-vector $(0,3,0)$. We will show that this happens to the first 0 and then the rest follows recursively.

Suppose that k is the first index such that $a_k=0$. Note that $(0,0)$ is not allowed or it will lead to $(4,0,0,4)$, which can be replaced with $(1,1,1,1)$ for a smaller sum. Hence, $a_{k+1}\ne 0$. If $a_{k+1}=3$, then $a_{k+2}=0$ or $(a_{k-1},a_k,a_{k+1},a_{k+2})=(a_{k-1},0,3,a_{k+2})$ can be replaced with $(a_{k-1},1,1,a_{k+2})$ for a smaller sum. Hence, $(a_k,a_{k+1},a_{k+2})=(0,3,0)$. If $a_{k+1}=1$, then $a_{k-1}=3$ and thus $(a_{k-1},a_k)=(3,0)$ can be replaced with $(1,1)$ for a smaller sum. We now assume $a_{k+1}=2$. Hence, $a_{k-1}\ge 2$. If $a_{k+2}\ne 0$, then $(a_{k-1},a_k,a_{k+1})$ can be replaced with $(1,1,1)$ for a smaller sum. Hence, $a_{k+2}=0$ and $a_{k+3}\ge 2$. By a similar argument, we have $a_{k+4}=0$ and $a_{k+5}\ne 0$. In this case, $(a_{k-1},a_k,a_{k+1},a_{k+2},a_{k+3},a_{k+4})=(a_{k-1},0,a_{k+1},0,a_{k+3},0)$ can be replaced with $(1,1,1,1,1)$ with a smaller sum. Therefore, $a_{k+1}\ne 2$ and the result follows. □

Given a grid $G_{4,n}$, we define ${\zeta }_{4,n}^{\prime }$ as the number of $\gamma$-sets that contain n vertices.

Lemma 11.

Given a grid $G_{4,n}$ with a γ-set S, we have

1. 

$v_{2,1}\in S$ or $v_{3,1}\in S$

2. 

${\zeta }_{4,n}^{\prime }=\left\{\begin{array}{cc}0\hfill & \mathrm{if}n\le 3\hfill \\ 2\hfill & \mathrm{if}n=4\hfill \\ {\zeta }_{4,n-3}^{\prime }+2{\zeta }_{4,n-4}^{\prime }+{\zeta }_{4,n-7}^{\prime }\hfill & \mathrm{if}n\ge 5.\hfill \end{array}\right.$

Proof. 

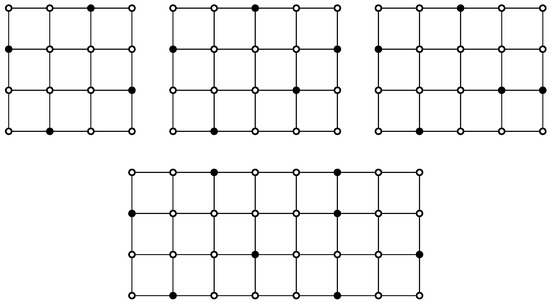
Case 1. Note that the corresponding dominating vector cannot begin with $(1,0)$ and thus it begins with $(1,1)$. If $v_{1,1}\in S$, then there is no way to cover both $v_{3,1}$ and $v_{4,1}$. So, $v_{1,1}\notin S$. Similarly, $v_{4,1}\notin S$. Hence, $v_{2,1}\in S$ or $v_{3,1}\in S$.

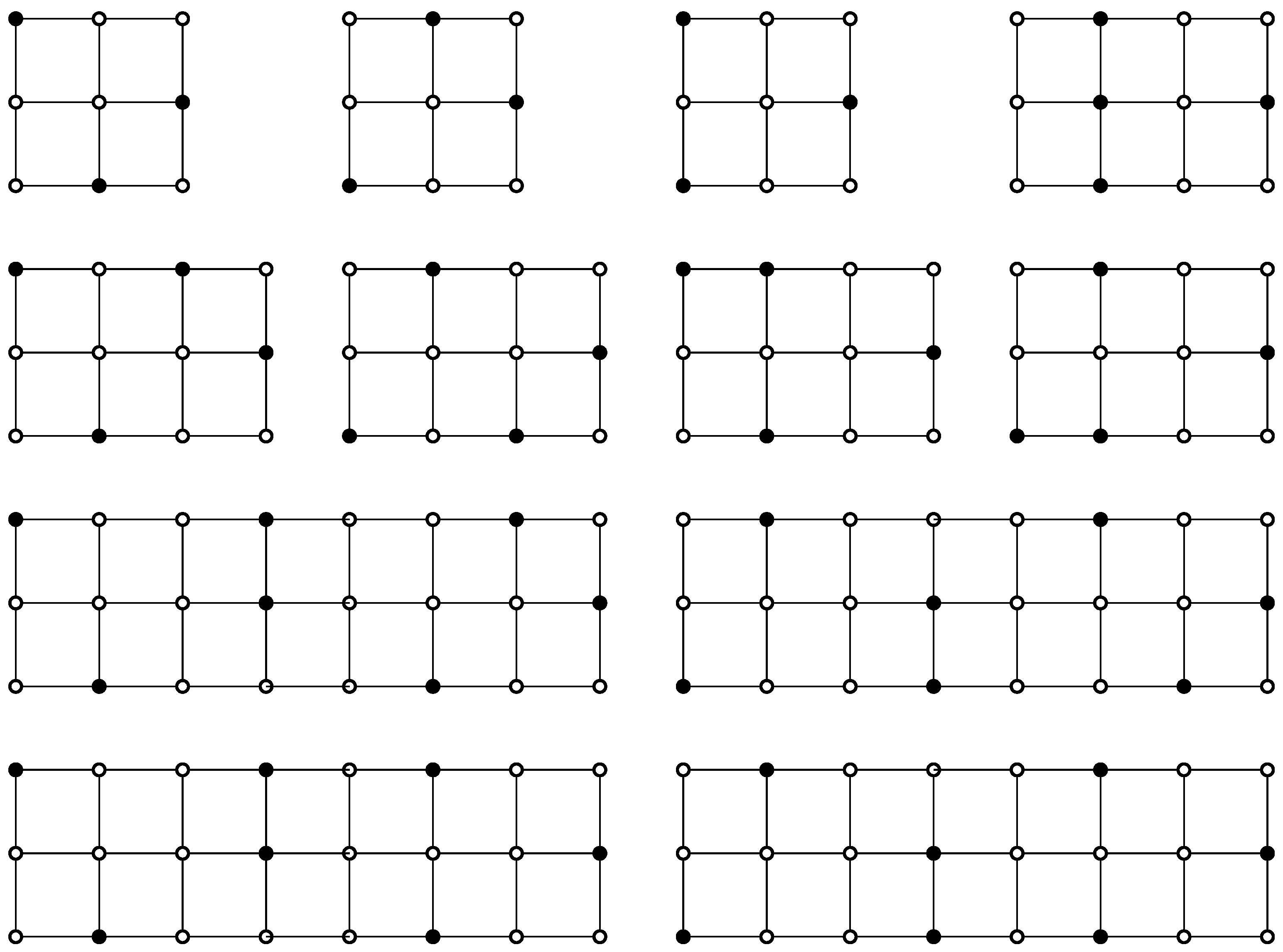
Case 2. Note that ${\gamma }_{4,1}={\gamma }_{1,4}=2$, ${\gamma }_{4,2}={\gamma }_{2,4}=3$, and ${\gamma }_{4,3}={\gamma }_{3,4}=4$. Hence, for $1\le n\le 3$, we have ${\gamma }_{4,n}>n$. It follows that ${\zeta }_{4,n}^{\prime }=0$ for $n\le 3$. We may assume $v_{2,1}\in S$. Note that the first graph in Figure 5 is the smallest $\gamma$-set that contains $v_{2,1}$. By symmetry, there is another one that contains $v_{3,1}$. These are the only two $\gamma$-sets with $n=4$. Hence, ${\zeta }_{4,4}^{\prime }=2$ and ${\zeta }_{4,n}^{\prime }=0$ for $n\le 3$. Also, note that Figure 5 provides all possible leading graphs containing $v_{2,1}$ that end with $v_{2,1}$ or $v_{3,1}$. Hence, we have ${\zeta }_{4,n}^{\prime }={\zeta }_{4,n-3}^{\prime }+2{\zeta }_{4,n-4}^{\prime }+{\zeta }_{4,n-7}^{\prime }$.

Figure 5. Four graphs that provide the leading portion of $\gamma$-sets of the grid graph $G_{4,n}$.

□

Theorem 6.

Given a grid graph $G_{4,n}$, we have ${\zeta }_{4,n}=\left\{\begin{array}{cc}52\hfill & \mathit{if}n=5\hfill \\ 92\hfill & \mathit{if}n=6\hfill \\ 324\hfill & \mathit{if}n=9\hfill \\ {\zeta }_{4,n}^{\prime }\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Proof. 

It is known in [17] that ${\gamma }_{4,n}=\left\{\begin{array}{cc}n+1\hfill & \mathrm{if}n=5,6,9\hfill \\ n\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

From this result, we have ${\zeta }_{4,n}={\zeta }_{4,n}^{\prime }$ if $n\ge 4$ and $n\ne 5,6,9$. Further, using a Python program, we find the exact values for ${\zeta }_{4,5}$, ${\zeta }_{4,6}$, and ${\zeta }_{4,9}$ and hence the result. □

3. Conclusions and Future Research

In this article, we proved a conjecture of one of the authors and found the dominions (formulae and recurrence relations) of several grids. In general, the notions of domination and dominion are important in ensuring the security of a network. They help network administrators to understand the vulnerabilities of a network and develop effective security measures to sustain an intruder’s attacks. The values of these two parameters, $\gamma$ and $\zeta$, offer to network administrators an analysis of the resilience of a network. Still, we found it very tedious to determine the $\zeta$ values of grids $G_{m,n}$ for larger $m\ge 5$. With a Python algorithm, we derived several exact values for $m\le 9$ and $n\le 20$. Table 1 and Table 2 summarize these results. From these results, follow the next conjecture.

Conjecture 1.

If ${\zeta }_{m,n}$ denotes the dominion of a grid $G_{m,n}$, then the following hold:

(a) 

${\zeta }_{5,5k+1}=\left\{\begin{array}{cc}13\hfill & \mathit{if}k=1\hfill \\ 8\hfill & \mathit{if}k\ge 2\hfill \end{array}\right.$

(b) 

${\zeta }_{6,7k+1}=2$ for $k\ge 1$

(c) 

${\zeta }_{7,3k+1}=2$ for $k\ge 1.$

Table 1. Dominion numbers ${\zeta }_{m,n}$ with $n\le 10$.

m\n	1	2	3	4	5	6	7	8	9	10
1	1	2	1	4	3	1	8	4	1	13
2	2	6	3	12	2	17	2	20	2	24
3	1	3	10	29	1	2	11	46	1	3
4	4	12	29	2	52	92	2	4	324	2
5	3	2	1	52	22	13	3	344	169	50
6	1	17	2	92	13	288	34	2	179	4683
7	8	2	11	2	3	34	2	34	148	2
8	4	20	46	4	344	2	34	52	96	560
9	1	2	1	324	169	179	148	96	32	24
10	13	24	3	2	50	4683	2	560	24	4

Table 2. Dominion numbers ${\zeta }_{m,n}$ with $11\le n\le 20$.

m\n	11	12	13	14	15	16	17	18	19	20
1	5	1	19	6	1	26	7	1	34	8
2	2	28	2	32	2	36	2	40	2	44
3	12	60	1	4	16	78	1	5	21	103
4	10	8	2	16	32	18	22	74	90	60
5	8	2667	913	249	64	8	5611	1604	418	88
6	516	26	2091	32	2	358	27,739	732	42	4976
7	81	696	2	154	2315	2	261	6014	2	416
8	1640	3796	12,466	42,546	24	64	352	1416	5872	19,052
9	22	8	12,292	8892	6261	2464	1056	784	544	144

We derived the Python program for the paper as follows. We defined the function Gamma(m,n) based on the $\gamma$ function result from [17]. We defined the function dom_vec(m,n) to generate all the potential minimum dominating vectors. We also defined Zeta(m,n) as the $\zeta$ function found in the article and used it to generate Table 1 and Table 2. Finally, we defined Zeta3p(n) to represent ${\zeta }_{3,n}^{\prime }$, which was later used to find ${\zeta }_{3,4}^{\prime }$ and ${\zeta }_{3,8}^{\prime }$ in the proof of Lemma 9.

import itertools as it

def Gamma(m,n):     if m>n: m,n = n,m     match m:         case 1: return (n+2)//3         case 2: return (n+2)//2         case 3: return (3*n+4)//4         case 4:             if n in (5,6,9): return n+1             else: return n         case 5:             if n==7: return (6*n+6)//5             else: return (6*n+8)//5         case 6:             if n%7==1: return (10*n+10)//7             else: return (10*n+12)//7         case 7: return (5*n+3)//3         case 8: return (15*n+14)//8         case 9: return (23*n+20)//11         case 10:             if n not in (13,16) and n%13 in (0,3): return (30*n+37)//13             else: return (30*n+24)//13         case 11:             if n in (11,18,20,22,33): return (38*n+21)//15             else: return (38*n+36)//15         case 12: return (80*n+66)//29         case 13:             if n%33 in (14,15,17,20): return (98*n+111)//33             else: return (98*n+78)//33         case 14:             if n%22==18: return (35*n+40)//11             else: return (35*n+29)//11         case 15:             if n%26==5: return (44*n+27)//13             else: return (44*n+40)//13         case _: return (m+2)*(n+2)//5-4

def dom_vec(m,n):     if n==1:         yield [Gamma(m,1)]         return     seq = [0]*n     def isValid(seq):         if len(seq)==n:             if sum(seq)!=Gamma(m,n): return False             if 3*seq[-1]+seq[-2]<m: return False         if len(seq)==2 and 3*seq[0]+seq[1]<m: return False         if len(seq)>=3 and seq[-3]+3*seq[-2]+seq[-1]<m: return False         if sum(seq)+Gamma(m,n-len(seq)-1)>Gamma(m,n): return False         return True     k = 0     while(k>=0):         if k==n and isValid(seq): yield seq         if k==n or seq[k]==m+1:             k-=1             seq[k]+=1         else:             if isValid(seq[:k+1]):                 if k<n-1: seq[k+1]=0                 k+=1             else:                 seq[k]+=1

def Zeta3p(n):     m=3     def cnt_dom(seq,i=0,cov=(),nc=()): # tc for “to cover”; nc for “not covered”         if i==len(seq):             if len(nc)==0: return 1             else: return 0         cnt = 0         if len(nc)>seq[i]: return 0         for idx in it.combinations(list(set(range(m))-set(nc)),seq[i]-len(nc)):             if i==0 and 1 not in idx: continue             ncov = list(set(range(m))-set(cov))             for j in idx+nc:                 if j in ncov: ncov.remove(j)                 if j+1 in ncov: ncov.remove(j+1)                 if j-1 in ncov: ncov.remove(j-1)             cnt += cnt_dom(seq,i+1,idx+nc,tuple(ncov))         return cnt     cnt=0     for seq in dom_vec(m,n):         cnt += cnt_dom(seq)     return cnt

def Zeta(m,n):     if m>n: m,n=n,m     def cnt_dom(seq,i=0,cov=(),nc=()): # tc for “to cover”; nc for “not covered”         if i==len(seq):             if len(nc)==0: return 1             else: return 0         cnt = 0         if len(nc)>seq[i]: return 0         for idx in it.combinations(list(set(range(m))-set(nc)),seq[i]-len(nc)):             ncov = list(set(range(m))-set(cov))             for j in idx+nc:                 if j in ncov: ncov.remove(j)                 if j+1 in ncov: ncov.remove(j+1)                 if j-1 in ncov: ncov.remove(j-1)             cnt += cnt_dom(seq,i+1,idx+nc,tuple(ncov))         return cnt     cnt=0     for seq in dom_vec(m,n):         cnt += cnt_dom(seq)     return cnt