Data-Driven Prescribed Performance Platooning Control Under Aperiodic Denial-of- Service Attacks

Abstract

This article studies a data-driven prescribed performance platooning control method for nonlinear connected automated vehicle systems (CAVs) under aperiodic denial-of-service (DoS) attacks. Firstly, the dynamic linearization technique is employed to transform the nonlinear CAV system into an equivalent linearized data model. Secondly, to improve the system’s transient performance, a prescribed performance transformation (PPT) scheme is proposed to transform the constrained output into the unconstrained one. In addition, an attack compensation mechanism is designed to reduce the adverse impact. Combining the PPT scheme and the attack compensation mechanism, the data-driven adaptive platooning control scheme is proposed to achieve the vehicular tracking control task. Lastly, the merits of the developed control method are illustrated by an actual simulation.

1. Introduction

With the improvement and maturity of new generation digital technologies such as artificial intelligence, Internet of Things, and 5G mobile communications, connected automated vehicle systems (CAVs) have become a new trend in the development of the automotive industry. For the purpose of dealing with the adverse impact generated by network attacks and event triggering, the authors of [1] develop a resilient event-triggered controller for CAVs. To reduce the resource consumption and pollution emissions, a hybrid model predictive control scheme for CAVs is developed in [2]. The authors of [3] develop a hierarchical collaborative tracking control strategy for CAVs to reduce traffic throughput and vehicle fuel efficiency in a complex traffic environment. In [4], the authors investigate the cooperative tracking control problem of dynamic event triggering for CAVs with various spacing strategies. To enhance the robustness of the vehicle system, the authors of [5] propose a recent robust control scheme by using an integral sliding mode. With the help of the barrier Lyapunov function, the authors of [6] study the fuzzy adaptive tracking control algorithm for heterogeneous CAVs with input saturation to ensure that collisions do not occur and to maintain communication between vehicles. For a vehicle steer-by-wire system under various parameters, the authors of [7] propose a robust control technique. To ensure collision avoidance and comfort assurance conditions, the authors of [8] propose a hierarchical control approach to address the prescribed performance lane-changing control problem for nonlinear vehicle platoons.

It is worth noting that, in practical applications, CAVs can exchange position and speed information with each other through the communication network. However, the communication network is very fragile and susceptible to cyber attacks, which will cause the controlled system to be in an unsafe state. In general, the network attacks can be divided into denial-of-service (DoS) attacks and false data injection (FDI) attacks. Differently from an FDI attack, which injects false attack signals into the system, the manner of DoS attacks is to destroy the information transmission channel, i.e., the data of the system cannot be timely transmitted to the controller. Until now, the safety of a vehicle system has been of wide concern [9,10,11,12,13,14]. The authors of [9] deal with the observer-based security consensus problem under DoS attacks. To deal with arbitrarily large parametric uncertainties, the authors of [10] develop a cooperative robust resilient output regulation control approach for linear uncertain multiagent systems (MASs) under DoS attacks. For mitigating the negative influence of DoS attacks, a novel security tracking control scheme of nonlinear autonomous ground vehicles in [11] is proposed. Due to the interaction information being affected by DoS attacks, the authors of [12] deal with the problem of security cooperative tracking control for nonlinear MASs suffering from DoS attacks. In [13], the authors propose a novel detection method on the basis of the adaptive Kalman filter bank to reduce the effect of FDI attacks. The authors of [14] introduce an adaptive boundary estimation mechanism during the back-stepping controller design process to reduce the adverse influence of FDI attacks. The authors of [15] propose a safe time-varying formation control framework for heterogeneous multiagent systems under the constraints of denial-of-service (DoS) attacks, noncooperative dynamic obstacles, and input saturation.

Although the above results can effectively mitigate the impact of attacks, they are all based on an accurate mathematical model. With the continuous progress of automobile intelligence and electrification, the dynamical modeling of CAVs is becoming more complex. For the purpose of addressing this problem, a model-free adaptive control (MFAC) algorithm is introduced. In the MFAC method [16,17,18,19], complex nonlinear systems can be transformed into the equivalent linear data model through applying the dynamic linearization technique (DLT). In addition, the design of a model-free adaptive controller relies merely on the system’s input and output information, not the architecture of the system itself. Up to now, the MFAC method has been used in a wide variety of applications, such as MASs [20,21], vehicular platooning systems (VPSs) [22,23], and cyber-physical systems (CPSs) [24]. Through employing the DLT, the authors of [20] develop a novel distributed MFAC strategy for MASs suffering from DoS attacks. In [21], a hierarchical distributed MFAC scheme is introduced to address the cooperative tracking control problem. The authors of [22,23] develop a novel MFAC method for nonlinear VPSs. The authors of [24] address the model-free adaptive tracking control problem for a class of discrete-time single-input single-output nonlinear systems under dynamic sparse attacks and measurement disturbances. Although the security cooperative control problem in the application of the MFAC algorithm has made great achievements, the above papers do not consider the safety problem for nonlinear CAVs under aperiodic DoS attacks. This will be one of the driving forces behind our research in this paper.

On the other hand, the above articles only consider the steady-state performance of the system, but do not consider the transient performance. Nevertheless, the transient performance of the system is also very valuable for the system itself. In an actual vehicular platooning control application, for the purpose of restricting the system’s transient performance within the prescribed boundaries and acquire a better tacking control effect, the prescribed performance control (PPC) method is firstly developed in [25] to increase the convergence speed and reduce overshoot. The primary goal of PPC is to limit the error or state of the system to a preset range by applying a strictly increasing function. Until now, the PPC method has gained wide attention [26,27,28]. Unlike the existing observer-based finite/fixed-time control methods, the authors of [26] develop the observer-based finite-time cooperative tracking control scheme for nonlinear MASs, where the time of convergence and the region of convergence can be pre-specified by the authors. Through the aid of back-stepping technology, the authors of [27] develop a novel adaptive tracking control method. The designed controller is able to guarantee the tracking control performance of the system as well as to reduce the communication burden. The authors of [28] propose a novel model-free path tracking controller that realizes appointed-time performance and reduces the communication burden. Until now, the PPC method has received great attention in the field of MFAC [29,30,31,32]. However, it has been noted that there is a fundamental characteristic of the above control methods that do not take into account the chattering generated by the sliding mode control (SMC) method. To this end, for the chatter problem caused by the SMC method, how to design a novel preset performance-based MFAC method that does not use the SMC scheme, especially for nonlinear CAVs, is a problem worthy of attention of this paper.

Enlightened by the previous discussions, this paper develops a data-driven prescribed performance platooning control strategy under aperiodic DoS attacks. Our major contributions in this articles are described below:

(1)

For nonlinear connected automated vehicle system (CAVs) under state constraint and aperiodic DoS attacks, the nonlinear CAV is converted into an equivalent linear data model by using the dynamic linearization technique (DLT). Moreover, to reduce the adverse effect of aperiodic DoS attacks, an attack compensation mechanism based on the latest received data is proposed, which greatly ensures the safe driving of nonlinear CAVs.

(2)

The existing data-driven prescribed performance platooning control methods [29,30,31,32] are based on the sliding mode control framework, which may cause chattering problems. Differently from them, a novel prescribed performance transformation strategy for nonlinear CAVs under aperiodic DoS attacks is developed to complete the vehicular tracking control task.

The rest of this paper is set out in the following. Firstly, the preliminaries and data-driven control algorithm design are shown in Section 2. In Section 3, we present the stability analysis of this paper. Then, the simulation description is presented in Section 4. Ultimately, our conclusion is illustrated in Section 5. To be more clear, Figure 1 is developed to describe each section of this article.

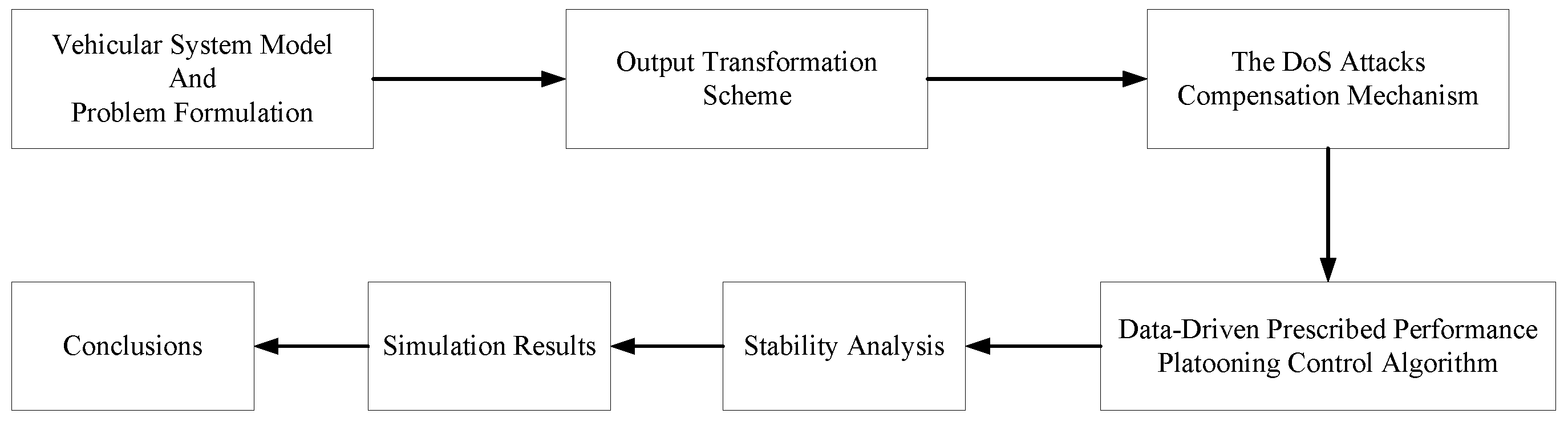
2. Preliminaries and Data-Driven Control Algorithm Design

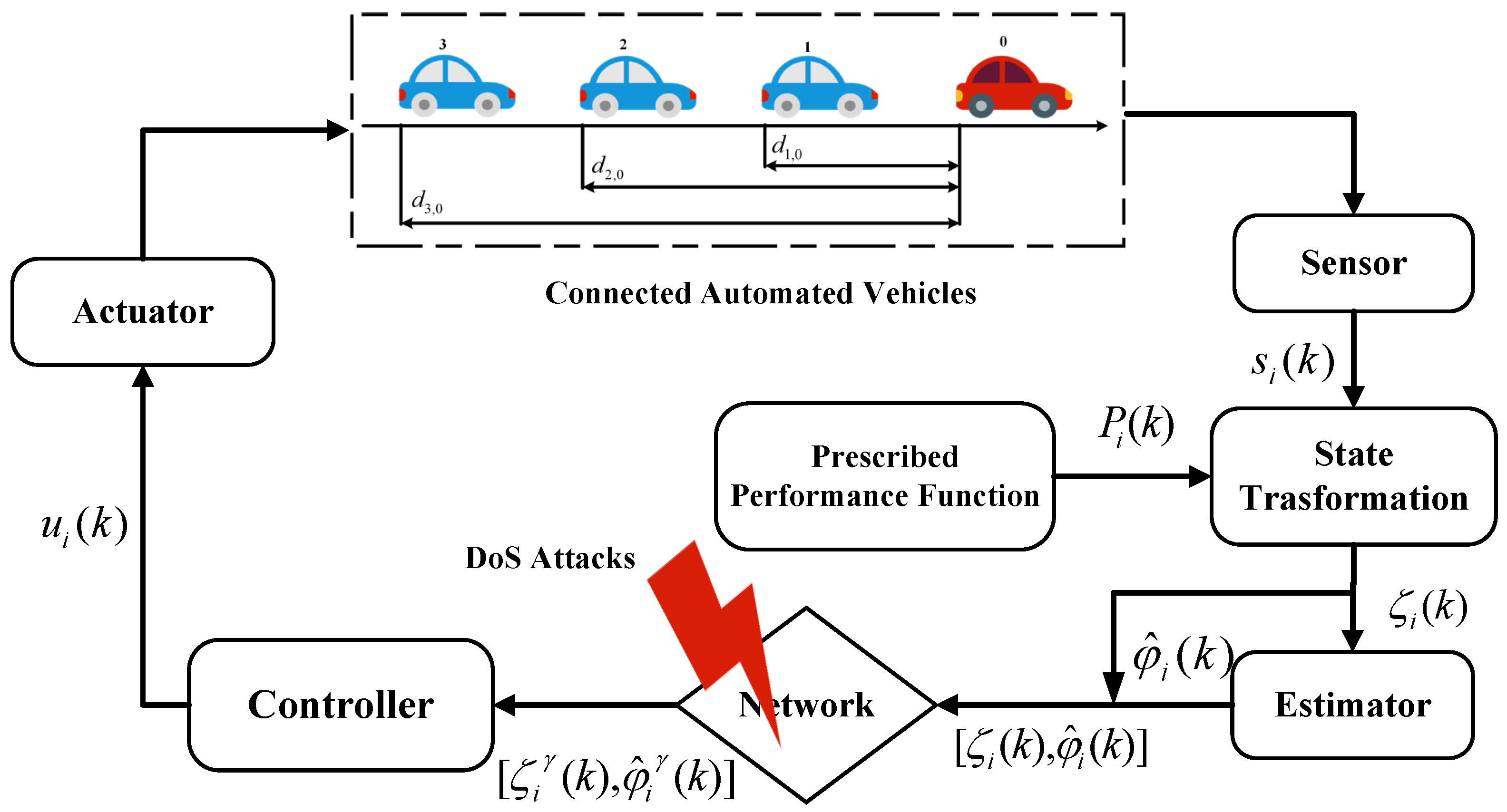
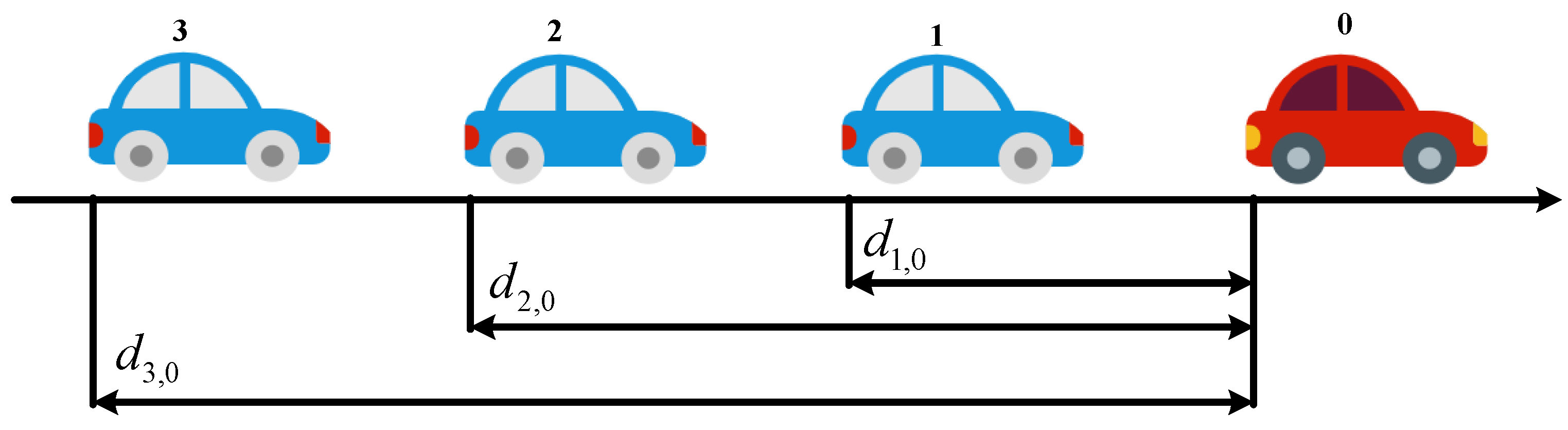
2.1. Connected Automated Vehicle System Model

In this paper, we consider $N+1$ connected automated vehicle systems (CAVs) driving in a platoon, which is made up of N follower vehicles and one leader vehicle; here, the dynamics model of the ith follower vehicle is defined as the following expression:

$$\begin{array}{cc}\hfill s_i(k+1)=& s_i\left(k\right)+T{\vartheta }_i\left(k\right)+{\displaystyle \frac{1}{2}}{T}^2(u_i\left(k\right)-F_i\left(k\right)),\hfill \\ \hfill {\vartheta }_i(k+1)=& {\vartheta }_i\left(k\right)+T(u_i\left(k\right)-F_i\left(k\right)),\hfill \end{array}$$

(1)

where T indicates the sampling time. Moreover, $s_i\left(k\right)$, ${\vartheta }_i\left(k\right)$, and $u_i\left(k\right)$ with $i=\{1,2,\dots ,N\}$ represent the position, speed, and the pulling/braking power of the ith follower vehicle, respectively. In addition, $F_i\left(k\right)$ is a nonlinear drag function that includes two terms, namely, a basis function $f_i^{\vartheta }\left({\vartheta }_i\left(k\right)\right)$ associated with velocity and an additional function $f_i^s\left(s_i\left(k\right)\right)$ related to the position. Here, the specific forms of $f_i^{\vartheta }\left({\vartheta }_i\left(k\right)\right)$ and $f_i^s\left(s_i\left(k\right)\right)$ are defined as the following two equations, respectively:

$$\begin{array}{cc}\hfill f_i^{\vartheta }\left({\vartheta }_i\left(k\right)\right)=& p_0\left(k\right)+p_1\left(k\right){\vartheta }_i\left(k\right)+p_2\left(k\right){\vartheta }_i^2\left(k\right)\hfill \\ \hfill f_i^s\left(s_i\left(k\right)\right)=& q_r\left(s_i\left(k\right)\right)+q_c\left(s_i\left(k\right)\right)+q_t\left(s_i\left(k\right)\right)\hfill \end{array}$$

(2)

with $p_0\left(k\right)$, $p_1\left(k\right)$, and $p_2\left(k\right)$ denoting the time-varying drag coefficients. Meantime, $q_r(·)$, $q_c(·)$, and $q_t(·)$ represent the drag relation to ramps, curves, and tunnels, respectively.

Combining (1) with (2), it is possible to obtain

$$\begin{array}{cc}\hfill s_i(k+1)=& s_i\left(k\right)+T{\vartheta }_i(k-1)+T^2{u}_i(k-1)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{T}^2{u}_i\left(k\right)-T^2{F}_{i1}(k-1)-{\displaystyle \frac{1}{2}}{F}_{i2}\left(k\right),\hfill \end{array}$$

(3)

where $F_{i1}(k-1)=p_0(k-1)+p_1(k-1){\vartheta }_i(k-1)+p_2(k-1){\vartheta }_i^2(k-1)+q_r\left(s_i(k-1)\right)+q_c\left(s_i(k-1)\right)+q_t\left(s_i(k-1)\right)$, and $F_{i2}\left(k\right)=p_0\left(k\right)+p_1\left(k\right){\vartheta }_i\left(k\right)+p_2\left(k\right){\vartheta }_i^2\left(k\right)+q_r\left(s_i\left(k\right)\right)+q_c\left(s_i\left(k\right)\right)+q_t\left(s_i\left(k\right)\right)$.

Correspondingly, the leader vehicle is able to be modeled in such a way that

$$\begin{array}{cc}\hfill s_0(k+1)=& s_0\left(k\right)+T{\vartheta }_0\left(k\right)\hfill \\ \hfill {\vartheta }_0(k+1)=& {\vartheta }_0\left(k\right)+T{F}_0\left(k\right)\hfill \end{array}$$

(4)

with $s_0\left(k\right)$ and ${\vartheta }_0\left(k\right)$ indicating the vehicular position and speed of leader. $F_0\left(k\right)$ denotes the nonlinear function.

It can be acquired from (3) that $s_i(k+1)=f_i\left(k\right)$, in which $f_i(·)$ denotes an unknown nonlinear function, containing the speeds ${\vartheta }_i\left(k\right)$, ${\vartheta }_i(k-1)$, positions $s_i\left(k\right)$, $s_i(k-1)$, and control inputs $u_i\left(k\right)$, $u_i(k-1)$.

The nonlinear function $f_i\left(k\right)$ of CAVs is able to be transformed to an equivalent linear data model with the CFDL technique through making the following assumptions about the nonlinear CAVs (1).

Assumption 1 

([16]). For unknown nonlinear function $f_i(·)$, the partial derivative of the nonlinear function $f_i(·)$ in relation to the control input $u_i\left(k\right)$ is continous.

Assumption 2 

([18]). Nonlinear CAVs (1) and (4) meet the generalized Lipschitz condition, namely, when $\Delta u_i\left(k\right)\ne 0$, then one can know that $|\Delta s_i(k+1)|\le {\tilde{\beta }}_i|\Delta u_i\left(k\right)|$ holds, in which $\Delta u_i\left(k\right)=u_i\left(k\right)-u_i(k-1)$, $\Delta s_i(k+1)=s_i(k+1)-s_i\left(k\right)$, and ${\tilde{\beta }}_i>0$ represents a constant.

Assumption 3 

([16]). From the perspective of realistic application, the system output increment $\Delta s_0\left(k\right)$ of the leader vehicle is supposed to be bounded, i.e., $|\Delta s_0\left(k\right)|\le {\varrho }_1$ with ${\varrho }_1>0$ being a constant, where $\Delta s_0\left(k\right)=s_0\left(k\right)-s_0(k-1)$.

Remark 1. 

Assumption 1 represents a basic restrictive condition employed in the nonlinear system [18,19,20]. Assumption 2 is used to illustrate the correlation between the system’s input and output increments.

Lemma 1 

([16]). For nonlinear CAVs, if Assumptions 1 and 2 can be satisfied, and $\Delta u_i\left(k\right)\ne 0$, then there exists a pseudo partial derivative (PPD) parameter that converts the nonlinear CAVs (1) to the form of the following input and output increments:

$$\Delta s_i(k+1)={\psi }_i^s\left(k\right)\Delta u_i\left(k\right),$$

(5)

where ${\psi }_i^s\left(k\right)$ denotes a time-varying and bounded PPD parameter, which satisfies $|{\psi }_i^s\left(k\right)|\le {\overline{c}}_i$.

Remark 2. 

In Lemma 1, we give the connection between the controller input increment and the output increment, that is to say, the output of CAVs changes identically with the input to CAVs. With the assistance of this one feature, in the following controller design, we use only the input and output information from the nonlinear CAVs.

2.2. Prescribed Performance Control Scheme Design

During the actual vehicle movement, the steady-state and transient performance of nonlinear CAVs play a key role. Here, for the purpose of ensuring the transient performance of nonlinear CAVs and achieve a preset performance under preset conditions, a prescribed performance transformation scheme is shown in this subsection. First of all, the position tracking error of nonlinear CAVs is designed as the following expression:

$$\begin{array}{c}\hfill e_i\left(k\right)=s_0\left(k\right)-s_i\left(k\right)-d_{i,0},\end{array}$$

(6)

where $d_{i,0}$ indicates the desired security distance between the ith follower and leader. Moreover, from Assumption 3, one can assume that $|s_0\left(k\right)|\le {\overline{s}}_0$.

For the output of nonlinear CAVs, the prescribed performance transformed scheme is developed as follows:

$$\begin{array}{c}\hfill -{\mathrm{\Pi }}_i\left(k\right)<s_i\left(k\right)<{\mathrm{\Pi }}_i\left(k\right),\end{array}$$

(7)

where ${\mathrm{\Pi }}_i\left(k\right)$ denotes the prescribed performance function.

Here, its specific expression is designed in the following form:

$$\begin{array}{cc}\hfill {\mathrm{\Pi }}_i(k+1)=& (1-{\kappa }_i){\mathrm{\Pi }}_i\left(k\right)+{\kappa }_i{\mathrm{\Pi }}_i(\infty ),\hfill \\ \hfill \underset{k\to \infty }{lim}{\mathrm{\Pi }}_i\left(k\right)=& {\mathrm{\Pi }}_i(\infty ),\hfill \end{array}$$

(8)

where the initial state of ${\mathrm{\Pi }}_i\left(0\right)$ satisfies $|{\mathrm{\Pi }}_i\left(0\right)|>|{\mathrm{\Pi }}_i(\infty )|>0$. ${\kappa }_i\in (0,1)$ represents the convergent rate.

For the purpose of ensuring that the tracking error $e_i\left(k\right)$ of vehicular position is capable of converging to the preset region, the following prescribed performance control scheme is formulated from (6) and (7):

$$\begin{array}{c}\hfill -{\mathrm{\Pi }}_i\left(k\right)-{\overline{s}}_0+d_{i,0}<e_i\left(k\right)<{\mathrm{\Pi }}_i\left(k\right)+{\overline{s}}_0-d_{i,0}.\end{array}$$

(9)

With a view to minimizing the complexity of the controller design process and strengthen the transient performance of the nonlinear CAVs, the strictly increasing function $\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)$ is able to be introduced to deal with the restricted vehicular tracking control problem (7). To this end, the output signal $s_i\left(k\right)$ is converted into the unconstrained one ${\delta }_i\left(k\right)$, namely,

$$\begin{array}{c}\hfill s_i\left(k\right)={\mathrm{\Pi }}_i\left(k\right)\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)\end{array}$$

(10)

with $\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)$ satisfying the following properties:

(i)

$\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)\in (-1,1)$ for any ${\delta }_i\left(k\right)$;

(ii)

${lim}_{k\to +\infty }\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)=1$, and ${lim}_{k\to -\infty }\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)=-1$.

In general, $\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)$ associated with ${\delta }_i\left(k\right)$ is designed as

$$\begin{array}{c}\hfill \mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)={\displaystyle \frac{e^{{\delta }_i\left(k\right)}-e^{-{\delta }_i\left(k\right)}}{e^{{\delta }_i\left(k\right)}+e^{-{\delta }_i\left(k\right)}}}.\end{array}$$

(11)

Then, the following equation can be acquired from (11):

$$\begin{array}{c}\hfill {\delta }_i\left(k\right)={\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{{\mathrm{\Pi }}_i\left(k\right)+s_i\left(k\right)}{{\mathrm{\Pi }}_i\left(k\right)-s_i\left(k\right)}}\right).\end{array}$$

(12)

Remark 3. 

It is noteworthy that the constrained output $s_i\left(k\right)$ can be converted into the unconstrained one through employing the strictly increasing function $\mathrm{{\rm Y}}\left({\delta }_i\left(k\right)\right)$. In addition, by adjusting the prescribed region, the position tracking error is also able to converge to the prescribed region (9), which significantly increases the transient performance of nonlinear CAVs.

Substituting $s_i(k+1)=f_i\left(k\right)$ into (12) yields

$$\begin{array}{c}\hfill {\delta }_i(k+1)={\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{{\mathrm{\Pi }}_i\left(k\right)+f_i\left(k\right)}{{\mathrm{\Pi }}_i\left(k\right)-f_i\left(k\right)}}\right),\end{array}$$

(13)

here, $f_i\left(k\right)=f_i\left(s_i\left(k\right),{\vartheta }_i\left(k\right),u_i\left(k\right)\right)$.

By analyzing (13), one can know that ${\delta }_i(k+1)$ denotes a nonlinear function related to the position $s_i\left(k\right)$, speed ${\vartheta }_i\left(k\right)$, control input $u_i\left(k\right)$, and prescribed performance function ${\mathrm{\Pi }}_i\left(k\right)$. Therefore, the new nonlinear function can be redeveloped as $\mathsf{\Phi }(·)$, i.e., ${\delta }_i(k+1)={\mathsf{\Phi }}_i[s_i\left(k\right),{\vartheta }_i\left(k\right),u_i\left(k\right),{\mathrm{\Pi }}_i\left(k\right)]$.

Lemma 2 

([20]). Through using the homeomorphism mapping method, one can know that ${\delta }_i\left(k\right)$ is the unconstrained output generated by the constrained output $s_i\left(k\right)$, namely, if Assumptions 1 and 2 hold, and $\Delta u_i\left(k\right)\ne 0$, there exists a PPD parameter that allows the unconstrained output ${\delta }_i\left(k\right)$ to be represented as the unconstrained linear data model below:

$$\Delta {\delta }_i(k+1)={\phi }_i\left(k\right)\Delta u_i\left(k\right),$$

(14)

where $|{\phi }_i\left(k\right)|\le {\phi }_s^{*}$ with ${\phi }_s^{*}>0$ being a constant. $\Delta {\delta }_i(k+1)={\delta }_i(k+1)-{\delta }_i\left(k\right)$.

Remark 4. 

The existing adaptive control schemes include virtual reference feedback tuning, iterative feedback tuning, and unfalsified control, which either require precise information about the system model or ignore, to varying degrees, the effect of linearization of the nonlinear function on the controller design. Differently from them, the model-free adaptive control method has a simple structure, moderate adjustable parameters, easy controller design, and direct use of system input and output data.

One thing worth noting is that it is quite difficult to obtain the real value of ${\phi }_i\left(k\right)$. To this end, the performance function is defined as the following expression:

$$\begin{array}{c}\hfill J\left[{\widehat{\phi }}_i\left(k\right)\right]=|\Delta {\delta }_i\left(k\right)-{\widehat{\phi }}_i\left(k\right)\Delta u_i{(k-1)|}^2+{\eta }_i{|{\widehat{\phi }}_i\left(k\right)-{\widehat{\phi }}_i(k-1)|}^2\end{array}$$

(15)

with ${\eta }_i>0$ denoting the penalty factor.

Further, the following PPD parameter estimation algorithm can be acquired through minimizing the above performance function (15):

$$\begin{array}{c}\hfill {\widehat{\phi }}_i\left(k\right)={\widehat{\phi }}_i(k-1)+{\displaystyle \frac{{\rho }_i\Delta u_i(k-1)[\Delta {\delta }_i\left(k\right)-{\widehat{\phi }}_i(k-1)\Delta u_i(k-1)]}{\Delta u_i^2(k-1)+{\eta }_i}}\end{array}$$

(16)

with ${\rho }_i\in [0,1)$ denoting the step-size factor.

For the purpose of optimizing system performance, the performance function is described as the following expression:

$$\begin{array}{c}\hfill J\left[u_i\left(k\right)\right]=|{\delta }_0\left(k\right)-d_{i,0}-{\delta }_i\left(k\right)-{\widehat{\phi }}_i\left(k\right)\Delta u_i{\left(k\right)|}^2+{\lambda }_i{|\Delta u_i\left(k\right)|}^2,\end{array}$$

(17)

where ${\delta }_0\left(k\right)$ is the transformed output of the leader.

Similar to the solution of (16), the following formula can be acquired from (17) that

$$\begin{array}{c}\hfill u_i\left(k\right)=u_i(k-1)+{\displaystyle \frac{{\tau }_i{\widehat{\phi }}_i\left(k\right)[{\delta }_0\left(k\right)-d_{i,0}-{\delta }_i\left(k\right)]}{{\widehat{\phi }}_i^2\left(k\right)+{\lambda }_i}},\end{array}$$

(18)

where the effects of ${\tau }_i$ and ${\lambda }_i$ are the same as ${\rho }_i$ and ${\eta }_i$.

2.3. Data-Driven Prescribed Performance Platooning Control Under Aperiodic DoS Attacks

The designed data-driven platooning control scheme of nonlinear CAVs is presented in Figure 2. From observation of Figure 2, it can be derived that the prescribed performance function $P_i\left(k\right)$ is introduced here to guarantee the system’s transient performance. Then, we can observe that the information $[{\delta }_i\left(k\right),{\widehat{\phi }}_i\left(k\right)]$ can be transmitted between the sensor and controller through the vehicle interaction network. Once the attacker launches the attack, the controller is unable to acquire the data from the sensor. An illustration of an aperiodic DoS attack is displayed in Figure 3. Here, $T_i^s\in \mathbb{N}$ and $T_i^e\in \mathbb{N}$ are introduced to show the beginning and the ending moment of the ith attack, respectively. Additionally, the red area is used to indicate that the system is attacked, and the green area is used to indicate that the system is not attacked at this time.

Moreover, to verify whether the attack occurs, the DoS attack indicator function ${\varrho }_i\left(k\right)$ is developed; the specific expression is designed as follows:

$${\varrho }_i\left(k\right)=\left\{\begin{array}{cc}\hfill 1,& k\in [T_{i-1}^e,T_i^s),\hfill \\ \hfill 0,& k\in [T_i^s,T_i^e),\hfill \end{array}\right.$$

(19)

where $[T_i^s,T_i^e)$, and $[T_{i-1}^e,T_i^s)$ represent the ith attack period and attack dormant interval. Based on which, the collection of all attack intervals in $[0,k]$ can be described as follows:

$$\begin{array}{c}\hfill {\mathrm{\Lambda }}_a(0,k)=\left\{\bigcup _{i\in N}[T_i^s,T_i^e]\right\}\bigcap [0,k].\end{array}$$

(20)

Moreover, the interval of no DoS attacks can be represented by

$$\begin{array}{c}\hfill {\mathrm{\Lambda }}_b(0,k)=[0,k]/{\mathrm{\Lambda }}_a(0,k),\end{array}$$

(21)

where $[0,k]/{\mathrm{\Lambda }}_a(0,k)$ represents a set which contains the set $[0,k]$ and does not contain the set ${\mathrm{\Lambda }}_a(0,k)$.

Assumption 4 

([33]). ${\mathrm{\Lambda }}_a(0,k)$ satisfies the following condition:

$$\left|{\mathrm{\Lambda }}_a(0,k)\right|\le {\mathrm{\Lambda }}_0+{\displaystyle \frac{k}{ϵ}},$$

(22)

where ${\mathrm{\Lambda }}_0$ indicates the original attack period parameter, which is used to deal with the situation where the CAV is attacked from the beginning. $ϵ>1$ denotes the attack interval coefficient that needs to be designed later.

According to (19), the following attack mechanism can be acquired:

$$\begin{array}{cc}\hfill {\delta }_i^{\varrho }\left(k\right)=& {\varrho }_i\left(k\right){\delta }_i\left(k\right)+(1-{\varrho }_i\left(k\right)){\delta }_i^{\varrho }(k-1),\hfill \\ \hfill {\widehat{\phi }}_i^{\varrho }\left(k\right)=& {\varrho }_i\left(k\right){\widehat{\phi }}_i\left(k\right)+(1-{\varrho }_i\left(k\right)){\widehat{\phi }}_i^{\varrho }(k-1).\hfill \end{array}$$

(23)

According to (16) and (18), and the attack compensation mechanism (22), the prescribed performance-based MFAC scheme for nonlinear CAVs with aperiodic DoS attacks is designed as follows:

$$\begin{array}{cc}\hfill {\widehat{\phi }}_i\left(k\right)=& {\widehat{\phi }}_i(k-1)+{\varrho }_i\left(k\right)\Delta u_i(k-1)\hfill \\ \hfill & \times {\displaystyle \frac{{\rho }_i[\Delta {\delta }_i\left(k\right)-{\widehat{\phi }}_i(k-1)\Delta u_i(k-1)]}{\Delta u_i^2(k-1)+{\eta }_i}},\hfill \end{array}$$

(24a)

$$\begin{array}{c}{\widehat{\phi }}_i\left(k\right)={\widehat{\phi }}_i\left(1\right),\mathrm{if}|{\widehat{\phi }}_i\left(k\right)|\le {\iota }_i,\mathrm{or}|\Delta u_i(k-1)|\le {\iota }_i\\ \mathrm{or}sign\left({\widehat{\phi }}_i\left(k\right)\right)\ne sign\left({\widehat{\phi }}_i\left(1\right)\right),\end{array}$$

(24b)

$$\begin{array}{c}\hfill u_i\left(k\right)=u_i(k-1)+{\displaystyle \frac{{\tau }_i{\widehat{\phi }}_i^{\varrho }\left(k\right)[{\delta }_0\left(k\right)-d_{i,0}-{\delta }_i^{\varrho }\left(k\right)]}{{{\widehat{\phi }}_i^{\varrho }\left(k\right)}^2+{\lambda }_i}},\end{array}$$

(25)

where ${\iota }_i$ represents an arbitrarily small positive constant.

Remark 5. 

It can be acquired that (24b) represents the reset condition of the estimation PPD parameter ${\widehat{\phi }}_i\left(k\right)$, which means the efficiency and feasibility of the PPD parameter estimation algorithm (24a) can be improved.

Remark 6. 

The existing prescribed performance-based data-driven control method [29,30,31], through constructing the sliding mode function, may cause the chattering problem. To deal with this problem, the prescribed performance function ${\mathrm{\Pi }}_i\left(k\right)$ of this paper is directly used in the cost functions (15) and (17), based on which, the position tracking error of CAVs can converge to the preset region.

Problem 1. 

For nonlinear CAVs (1), the objective of this article is to propose a prescribed performance-based MFAC strategy consisting of (24a)–(25) subject to aperiodic DoS attacks to guarantee the transformed output ${\delta }_i\left(k\right)$ is uniformly ultimately bounded. Mathematically, it is capable of converging to the following set, i.e., $\left\{{\delta }_i\left(k\right)\right|{lim}_{k\to \infty }\left|{\delta }_i\left(k\right)\right|\le {\delta }^{*}\}$.

3. Stability Analysis

In this part, our main purpose is to analyze the stability of CAVs. In order to present more clearly the control scheme designed in this paper, the whole control algorithm is shown in Algorithm 1.

Algorithm 1 Data-Driven Prescribed Performance Resilient Control Algorithm.

1: Select suitable parameters ${\tau }_i$, ${\lambda }_i$, ${\rho }_i$, ${\eta }_i$, ${\epsilon }_1$, and ${\epsilon }_2$. 2: The system’s state is constrained within the prescribed region (7). 3: The constrained state is converted into the unconstrained one (12). 4: The attack compensation mechanism (23) is designed to reduce the impact of attacks. 5: Updating ${\widehat{\phi }}_i\left(k\right)$ by using estimation algorithm (24a) and (24b). 6: Verify the reset conditions: if $|{\widehat{\phi }}_i\left(k\right)|<{\iota }_i\mathbf{or}|\Delta u_i(k-1)|<{\iota }_i\mathbf{or}sign\left({\widehat{\phi }}_i\left(k\right)\right)\ne sign\left({\widehat{\phi }}_i\left(1\right)\right)$, then ${\widehat{\phi }}_i\left(k\right)={\widehat{\phi }}_i\left(1\right)$. 7: Input leader ${\delta }_0\left(k\right)$, safety distance $d_{i,0}$, and compensation mechanism ${\widehat{\phi }}_i^{\varrho }\left(k\right)$ and ${\delta }_i^{\varrho }\left(k\right)$. 8: Update the control input $u_i\left(k\right)$ with (25) and output it.

The major theorem of this article is presented as follows.

Theorem 1. 

In accordance with Assumptions 1–4, Problem 1 can be addressed with the developed prescribed performance-based model-free adaptive resilient control algorithm subject to aperiodic DoS attacks made of (24a)–(25), if the parameters are chosen to meet ${\tau }_i\in [0,1)$, ${\lambda }_i>{\lambda }_{min}>0$ with ${\lambda }_{min}={\left({\displaystyle \frac{{\phi }_s^{*}}{2}}\right)}^2$, ${\rho }_i\in [0,1)$, ${\eta }_i>0$, ${\epsilon }_1\in (0,1)$, ${\epsilon }_2>1$, and

$$\begin{array}{c}\hfill 1<ϵ<{\displaystyle \frac{ln{\epsilon }_1-ln{\epsilon }_2}{ln{\epsilon }_1}}.\end{array}$$

(26)

Proof.

Throughout this segment, we will conduct the stability proofs, in which the proofs can be separated into the proceeding two main aspects: (i) proving the boundedness of estimation error of PPD parameter $e_{\phi i}\left(k\right)$; (ii) proving that the converted output ${\delta }_i\left(k\right)$ is bounded.

Part I: In the first place, the estimation error of the PPD parameter is defined as $e_{\phi i}\left(k\right)={\widehat{\phi }}_i\left(k\right)-{\phi }_i\left(k\right)$. Through subtracting ${\phi }_i\left(k\right)$ on both sides of (24a), it is possible to acquire

$$\begin{array}{cc}\hfill e_{\phi i}\left(k\right)=& {\widehat{\phi }}_i(k-1)-{\phi }_i\left(k\right)+\Delta u_i(k-1)\hfill \\ \hfill & \times {\displaystyle \frac{{\rho }_i[\Delta {\delta }_i\left(k\right)-{\widehat{\phi }}_i(k-1)\Delta u_i(k-1)]}{\Delta u_i^2(k-1)+{\eta }_i}}\hfill \\ \hfill =& \left(1-{\displaystyle \frac{{\rho }_i\Delta u_i^2(k-1)}{\Delta u_i^2(k-1)+{\eta }_i}}\right)e_{\phi i}(k-1)\hfill \\ \hfill & +{\phi }_i(k-1)-{\phi }_i\left(k\right).\hfill \end{array}$$

(27)

Taking absolute values for both sides of the above (27), the following expression can be acquired:

$$\begin{array}{cc}\hfill |e_{\phi i}\left(k\right)|\le & |1-{\displaystyle \frac{{\rho }_i\Delta u_i^2(k-1)}{\Delta u_i^2(k-1)+{\eta }_i}}|\left|e_{\phi i}(k-1)\right|\hfill \\ \hfill & +|{\phi }_i(k-1)-{\phi }_i\left(k\right)|.\hfill \end{array}$$

(28)

In addition, according to the reset condition (24b), one can obtain the minimum value of ${\displaystyle \frac{{\rho }_i\Delta u_i^2(k-1)}{\Delta u_i^2(k-1)+{\eta }_i}}$ is ${\displaystyle \frac{{\rho }_i{\iota }_i^2}{{\eta }_i+{\iota }_i^2}}$. Based on this, one can obtain

$$\begin{array}{c}\hfill |1-{\displaystyle \frac{{\rho }_i\Delta u_i^2(k-1)}{\Delta u_i^2(k-1)+{\eta }_i}}|\le 1-{\displaystyle \frac{{\rho }_i{\iota }_i^2}{{\eta }_i+{\iota }_i^2}}\triangleq {\theta }_i<1.\end{array}$$

(29)

Then, taking into account that the boundedness of ${\phi }_i\left(k\right)$ has been given in Lemma 2, it is possible to infer that $|{\phi }_i(k-1)-{\phi }_i\left(k\right)|\le 2{\phi }_s^{*}$.

Furthermore, considering these points, Equation (28) can be redeveloped as follows:

$$\begin{array}{cc}\hfill |e_{\phi i}\left(k\right)|\le & {\theta }_i\left|e_{\phi i}(k-1)\right|+2{\phi }_s^{*}\hfill \\ \hfill \le & {\theta }_i^2\left|e_{\phi i}(k-2)\right|+2{\phi }_s^{*}({\theta }_i+1)\hfill \\ \hfill \le & \cdots \hfill \\ \hfill \le & {\theta }_i^{k-1}\left|e_{\phi i}\left(1\right)\right|+{\displaystyle \frac{2{\phi }_s^{*}(1-{\theta }_i^{k-1})}{1-{\theta }_i}}.\hfill \end{array}$$

(30)

Therefore, according to (28)–(30), we can know that the boundedness of estimation error $e_{\phi i}\left(k\right)$ can be guaranteed. Further, dependent on the description of estimation error $e_{\phi i}\left(k\right)={\widehat{\phi }}_i\left(k\right)-{\phi }_i\left(k\right)$, we are capable of acquiring that ${\widehat{\phi }}_i\left(k\right)$ is ultimately uniformly bounded.

Part II: In this part, we will verify the transformed output ${\delta }_i\left(k\right)$ is ultimately uniformly bounded. In the first place, the transformed tracking error $e_{\delta i}\left(k\right)$ is determined in such a form that

$$\begin{array}{c}\hfill e_{\delta i}\left(k\right)={\delta }_0\left(k\right)-{\delta }_i\left(k\right)-d_{i,0}.\end{array}$$

(31)

According to the characteristics of aperiodic DoS, we will prove from the attack interval and non-attack interval, respectively.

(1)

When $k\in [T_{i-1}^e,T_i^s)$ and ${\varrho }_i\left(k\right)=1$, namely, the communication channel between the sensor and the controller is not subject to DoS attacks. On account of (14), (25), and (31), we can obtain

$$\begin{array}{cc}\hfill e_{\delta i}(k+1)=& {\delta }_0(k+1)-{\delta }_i\left(k\right)-{\phi }_i\left(k\right)\Delta u_i\left(k\right)-d_{i,0}\hfill \\ \hfill =& \Delta {\delta }_0(k+1)+e_{\delta i}\left(k\right)-{\displaystyle \frac{{\tau }_i{\phi }_i\left(k\right){\widehat{\phi }}_i\left(k\right)}{{\lambda }_i+{\widehat{\phi }}_i^2\left(k\right)}}{e}_{\delta i}\left(k\right)\hfill \\ \hfill =& \left(1-{\displaystyle \frac{{\tau }_i{\phi }_i\left(k\right){\widehat{\phi }}_i\left(k\right)}{{\lambda }_i+{\widehat{\phi }}_i^2\left(k\right)}}\right)e_{\delta i}\left(k\right)+\Delta {\delta }_0(k+1).\hfill \end{array}$$

(32)

Then, taking the absolute value on both sides of (32), it is possible to obtain that

$$\begin{array}{c}\hfill |e_{\delta i}(k+1)|\le {\displaystyle |}1-{\displaystyle \frac{{\tau }_i{\phi }_i\left(k\right){\widehat{\phi }}_i\left(k\right)}{{\lambda }_i+{\widehat{\phi }}_i^2\left(k\right)}}|+|\Delta {\delta }_0(k+1)|.\end{array}$$

(33)

According to the conditions given in Theorem 1 and Lemma 2, one can acquire that ${\tau }_i\in [0,1)$, ${\lambda }_i>{\lambda }_{min}>0$ with ${\lambda }_{min}={\left({\displaystyle \frac{{\phi }_s^{*}}{2}}\right)}^2$, and $|{\phi }_i\left(k\right)|\le {\phi }_s^{*}$. Based on this, the following inequality can hold:

$$\begin{array}{c}\hfill 0<H_i<\left|{\displaystyle \frac{{\tau }_i{\phi }_i\left(k\right){\widehat{\phi }}_i\left(k\right)}{{\lambda }_i+{\widehat{\phi }}_i^2\left(k\right)}}\right|<\left|{\displaystyle \frac{{\tau }_i{\phi }_s^{*}{\widehat{\phi }}_i\left(k\right)}{2\sqrt{{\lambda }_i}{\widehat{\phi }}_i\left(k\right)}}\right|<{\displaystyle \frac{{\tau }_i{\phi }_s^{*}}{2\sqrt{{\lambda }_i}}}={\tau }_i<1.\end{array}$$

(34)

Further, it yields

$$\begin{array}{c}\hfill 0<|1-{\displaystyle \frac{{\tau }_i{\phi }_i\left(k\right){\widehat{\phi }}_i\left(k\right)}{{\lambda }_i+{\widehat{\phi }}_i^2\left(k\right)}}|<1-H_i\triangleq {\varpi }_1<1.\end{array}$$

(35)

Furthermore, it follows from (35) that

$$\begin{array}{c}\hfill |e_{\delta i}(k+1)|<{\varpi }_1\left|e_{\delta i}\left(k\right)\right|+{\varrho }_1,\end{array}$$

(36)

where $|\Delta {\delta }_0(k+1)|\le {\varrho }_1$, in which the boundedness of $\Delta {\delta }_0(k+1)$ has been given in Assumption 3.

(2)

When $k\in [T_i^s,T_i^e)$ and ${\varrho }_i\left(k\right)=0$, namely, there exist DoS attacks.

According to (31), the following equation is capable of being acquired:

$$\begin{array}{c}\hfill e_{\delta i}(k+1)=\Delta {\delta }_0(k+1)+e_{\delta i}\left(k\right)-{\phi }_i\left(k\right)\Delta u_i\left(k\right).\end{array}$$

(37)

In addition, through taking absolute values for both sides of the above (37), it can be acquired that

$$\begin{array}{c}\hfill |e_{\delta i}(k+1)|<|e_{\delta i}\left(k\right)|+|{\mathrm{\Omega }}_i\left(k\right)|,\end{array}$$

(38)

where ${\mathrm{\Omega }}_i\left(k\right)=\Delta {\delta }_0(k+1)-{\phi }_i\left(k\right)\Delta u_i\left(k\right)$.

Taking into account the practical limitations of the physical structure of the vehicle, it is impossible to change the actuator too fast in actual application [22,23]. Based on this situation, the controller input increment is supposed to be bounded [34], namely, $|\Delta u_i\left(k\right)|\le {\overline{b}}_i$ with ${\overline{b}}_i>0$ being a constant. Moreover, the boundedness of $\Delta {\delta }_i(k+1)$ and ${\phi }_i\left(k\right)$ has already been given before. To this end, it is possible to acquire that ${\mathrm{\Omega }}_i\left(k\right)$ is bounded, namely, $|{\mathrm{\Omega }}_i\left(k\right)|\le {\varrho }_2$ with ${\varrho }_2>0$ being a constant.

On the basis of the above analysis, Equation (38) has been redesigned in the following form:

$$\begin{array}{c}\hfill |e_{\delta i}(k+1)|<{\varpi }_2\left|e_{\delta i}\left(k\right)\right|+{\varrho }_2,\end{array}$$

(39)

where ${\varpi }_2>1$.

According to (36) and (39), and the aperiodic DoS attack compensation mechanism, it is yielded that

$$|e_{\delta i}(k+1)|<\left\{\begin{array}{c}{\varpi }_1\left|e_{\delta i}\left(k\right)\right|+{\varrho }_1,k\in [T_{i-1}^e,T_i^s),\hfill \\ {\varpi }_2\left|e_{\delta i}\left(k\right)\right|+{\varrho }_2,k\in [T_i^s,T_i^e).\hfill \end{array}\right.$$

(40)

One thing worth noting is that there exist two situations for arbitrary time k, namely, $k\in [T_{i-1}^e,T_i^s)$ and $k\in [T_i^s,T_i^e)$. We assume that, when $k\in [T_i^s,T_i^e)$, the following specific derivation is capable of being obtained:

$$\begin{array}{cc}\hfill |e_{\delta i}(k+1)|<& {\varpi }_2\left|e_{\delta i}\left(k\right)\right|+{\varrho }_2\hfill \\ \hfill <& {\varpi }_2^2\left|e_{\delta i}(k-1)\right|+{\varpi }_2{\varrho }_2+{\varrho }_2\hfill \\ \hfill <& \cdots \hfill \\ \hfill <& {\varpi }_2^{k-T_i^s+1}\left|e_{\delta i}\left(T_i^s\right)\right|+{\sum }_{n=0}^{k-T_i^s}{\varpi }_2^n{\varrho }_2\hfill \\ \hfill <& {\varpi }_2^{k-T_i^s+1}({\varpi }_1|e_{\delta i}(T_i^s-1)|+{\varrho }_1)\hfill \\ \hfill & +{\sum }_{n=0}^{k-T_i^s}{\varpi }_2^n{\varrho }_2\hfill \\ \hfill <& {\varpi }_2^{k-T_i^s+1}({\varpi }_1^2|e_{\delta i}(T_i^s-2)|+{\varpi }_1{\varrho }_1+{\varrho }_1)+{\sum }_{n=0}^{k-T_i^s}{\varpi }_2^n{\varrho }_2\hfill \\ \hfill <& \cdots \hfill \\ \hfill <& {\varpi }_2^{k-T_i^s+1}{\varpi }_1^{T_i^s-T_{i-1}^e}\left|e_{\delta i}\left(T_{i-1}^e\right)\right|+{\sum }_{n=0}^{k-T_i^s}{\varpi }_2^n{\varrho }_2\hfill \\ \hfill & +{\varpi }_2^{k-T_i^s+1}{\sum }_{n=0}^{T_i^s-T_{i-1}^e-1}{\varpi }_1^n{\varrho }_1\hfill \\ \hfill <& \cdots \hfill \\ \hfill <& {\varpi }_1^{|{\mathrm{\Lambda }}_b(0,k)|}{\varpi }_2^{|{\mathrm{\Lambda }}_a(0,k)|}\left|e_{\delta i}\left(0\right)\right|+{\sum }_{n=1}^k{\varpi }_1^{k-n}\hfill \\ \hfill & \times {\varpi }_1^{-|{\mathrm{\Lambda }}_a(n,k)|}{\varpi }_2^{|{\mathrm{\Lambda }}_a(n,k)|}{\varrho }_s\hfill \end{array}$$

(41)

with ${\varrho }_s=max\{{\varrho }_1,{\varrho }_2\}$.

Moreover, when $k\in [T_{i-1}^e,T_i^s)$, we can obtain the same results. In addition, according to (20)–(22), one can acquire that $|{\mathrm{\Lambda }}_b(0,k)|=k-|{\mathrm{\Lambda }}_a(0,k)|$ and $|{\mathrm{\Lambda }}_a(0,k)|\le {\mathrm{\Lambda }}_0+{\displaystyle \frac{k}{ϵ}}$. Based on this, the following inequality can be acquired:

$$\begin{array}{c}\hfill |e_{\delta i}(k+1)|\\ \hfill <& {\varpi }_1^{k-|{\mathrm{\Lambda }}_a(0,k)|}{\varpi }_2^{|{\mathrm{\Lambda }}_a(0,k)|}\left|e_{\delta i}\left(0\right)\right|+{\sum }_{n=1}^k{\varpi }_1^{k-n}\hfill \\ \hfill & \times {\varpi }_1^{-|{\mathrm{\Lambda }}_a(n,k)|}{\varpi }_2^{|{\mathrm{\Lambda }}_a(n,k)|}{\varrho }_s\hfill \\ \hfill \le & e^{(k-|{\mathrm{\Lambda }}_a(0,k)\left|\right)ln{\varpi }_1+\left|{\mathrm{\Lambda }}_a(0,k)\right|ln{\varpi }_2}\left|e_{\delta i}\left(0\right)\right|\hfill \\ \hfill & +{\sum }_{n=1}^k{e}^{(k-n-|{\mathrm{\Lambda }}_a(0,k)\left|\right)ln{\varpi }_1+\left|{\mathrm{\Lambda }}_a(n,k)\right|ln{\varpi }_2}{\varrho }_s\hfill \\ \hfill \le & e^{(k-{\mathrm{\Lambda }}_0-{\displaystyle \frac{k}{ϵ}})ln{\varpi }_1+({\mathrm{\Lambda }}_0+{\displaystyle \frac{k}{ϵ}})ln{\varpi }_2}\left|e_{\delta i}\left(0\right)\right|\hfill \\ \hfill & +{\sum }_{n=1}^k{e}^{(k-n-{\mathrm{\Lambda }}_0-{\displaystyle \frac{k-n}{ϵ}})ln{\varpi }_1+({\mathrm{\Lambda }}_0+{\displaystyle \frac{k-n}{ϵ}})ln{\varpi }_2}{\varrho }_s\hfill \\ \hfill \le & e^{(ln{\varpi }_2-ln{\varpi }_1){\mathrm{\Lambda }}_0+[ln{\varpi }_1+{\displaystyle \frac{1}{ϵ}}(ln{\varpi }_2-ln{\varpi }_1)]k}\left|e_{\delta i}\left(0\right)\right|\hfill \\ \hfill & +{\sum }_{n=1}^k{e}^{(ln{\varpi }_2-ln{\varpi }_1){\mathrm{\Lambda }}_0+[ln{\varpi }_1+{\displaystyle \frac{1}{ϵ}}(ln{\varpi }_2-ln{\varpi }_1)](k-n)}{\varrho }_s\hfill \\ \hfill \le & e^{(ln{\varpi }_2-ln{\varpi }_1){\mathrm{\Lambda }}_0}{e}^{[ln{\varpi }_1+{\displaystyle \frac{1}{ϵ}}(ln{\varpi }_2-ln{\varpi }_1)]k}\left|e_{\delta i}\left(0\right)\right|\hfill \\ \hfill & +e^{(ln{\varpi }_2-ln{\varpi }_1){\mathrm{\Lambda }}_0}{\varrho }_s\hfill \\ \hfill & \times {\sum }_{n=1}^k{e}^{[ln{\varpi }_1+{\displaystyle \frac{1}{ϵ}}(ln{\varpi }_2-ln{\varpi }_1)](k-n)}.\hfill \end{array}$$

(42)

According to condition (26) presented in (1), one can obtain that $ln{\varpi }_1+{\displaystyle \frac{1}{ϵ}}(ln{\varpi }_2-ln{\varpi }_1)<0$. Based on this, it follows (42) that the tracking error $e_{\delta i}\left(k\right)$ can be shown to be uniformly bounded, i.e., $e_{\delta i}\left(k\right)$ is capable of converging to the following set: $\{e_{\delta i}\left(k\right)\left|\right|e_{\delta i}\left(k\right)|\le e^{(ln{\varpi }_2-ln{\varpi }_1){\mathrm{\Lambda }}_0}\left(\right|e_{\delta i}\left(k\right)|+{\varrho }_s\left)\right\}$.

Depending on the principle of homeomorphism mapping, the constrained output $-{\mathrm{\Pi }}_i\left(k\right)<s_i\left(k\right)<{\mathrm{\Pi }}_i\left(k\right)$ can be transformed into the unconstrained one ${\delta }_i\left(k\right)$. In addition, in accordance with the boundedness of $e_{\delta i}\left(k\right)$ and ${\delta }_0\left(k\right)$, one can conclude that the transformed output ${\delta }_i\left(k\right)$ is bounded. Furthermore, the boundedness of the constrained output $s_i\left(k\right)$ and tracking error $e_i\left(k\right)$ can be ensured through proving the converted output ${\delta }_i\left(k\right)$ is bounded. □

Remark 7. 

In [35] , the authors propose a new gain adaptation law for a discrete-time sliding mode. This method relaxes the assumption of a known bound and can tackle the uncertainty without any knowledge of the bound of uncertainty while overcoming the over- and under-estimation problems of switching gain. This method is worth learning and following and will be used in our future work.

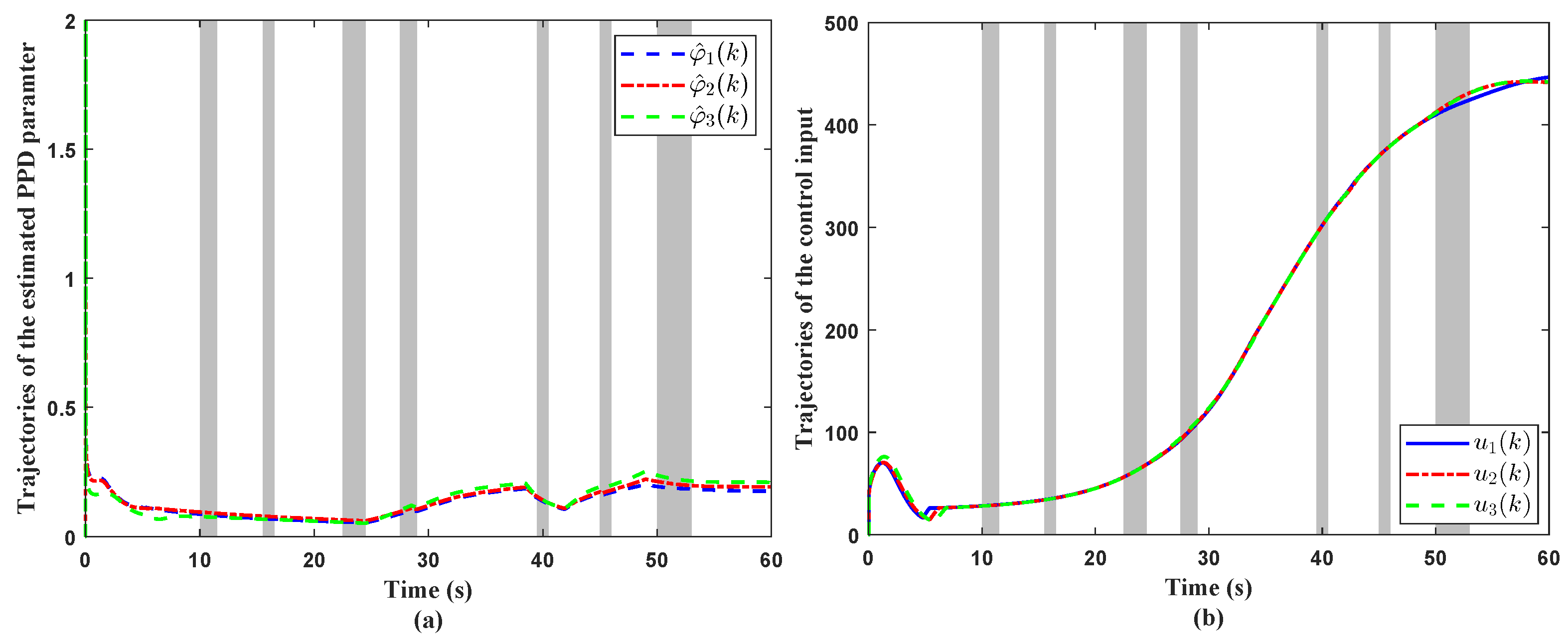
4. Simulation

In this segment, the designed preset performance-based model-free adaptive tracking control method of nonlinear CAVs subject to aperiodic DoS attacks is illustrated by a real-world simulation example.

The actual connected automated vehicle system is shown in Figure 4, which consists of three followers and one leader. Further, the dynamics model of the leader is designed as

$$\begin{array}{cc}\hfill s_0(k+1)=& s_0\left(k\right)+T{v}_0\left(k\right),\hfill \\ \hfill {\vartheta }_0(k+1)=& 2+{\displaystyle \frac{3.3}{1+e^{-0.0008k+5}}}.\hfill \end{array}$$

The position dynamics of the follower vehicle is designed as follows [23]:

$$\begin{array}{cc}\hfill s_i(k+1)=& s_i\left(k\right)+T{\vartheta }_i\left(k\right)+1/2T^2(u_i\left(k\right)-1.2\times {10}^{-4}{\vartheta }_i\left(k\right)\hfill \\ \hfill & -2.4\times {10}^{-6}{\vartheta }_i{\left(k\right)}^2-3{\vartheta }_i{\left(k\right)}^3-5\times {10}^{-5}{s}_i{\left(k\right)}^2).\hfill \end{array}$$

First of all, we will give the various parameters used in the numerical simulation. The specific values of the parameters are presented below. The starting positions of nonlinear CAVs are chosen as $s_i\left(1\right)=\left[\begin{array}{cccc}28.2& 20.2& 10& 0\end{array}\right]$ with $i=0,1,2,3$. The velocity dynamics equations for the follower vehicle are similar to the leader dynamics equations and are omitted here. Similarly, the starting speeds of nonlinear CAVs are chosen as ${\vartheta }_i\left(1\right)=\left[\begin{array}{cccc}2.08& 1.7& 1.7& 1.7\end{array}\right]$. The sampling time T is selected as $T=0.005$. The starting values of controller input $u_i\left(k\right)$ and PPD parameter ${\phi }_i\left(k\right)$ are respectively chosen as $u_i\left(1\right)=0$ and ${\phi }_i\left(1\right)=2$. In addition, it can be noticed by observing Figure 4 that, in the connected automated vehicle system model, the expected security distance is set to $d_{i,0}=\left[\begin{array}{ccc}6& 16& 26\end{array}\right]$. In the following, we will present the controller parameters of nonlinear CAVs, i.e., ${\rho }_i=\left[\begin{array}{ccc}0.58& 0.49& 0.51\end{array}\right]$, ${\eta }_i=\left[\begin{array}{ccc}3.31& 2.55& 3.51\end{array}\right]$, ${\tau }_i=\left[\begin{array}{ccc}0.83& 0.86& 0.81\end{array}\right]$, and ${\lambda }_i=\left[\begin{array}{ccc}0.74& 0.68& 0.72\end{array}\right]$. Then, the prescribed performance control parameters are set as ${\kappa }_i=0.0025$, ${\mathrm{\Pi }}_i(\infty )=0.50$, and ${\mathrm{\Pi }}_i\left(1\right)=3.5$. In addition, the parameters of attack duration time are selected as ${\epsilon }_1=0.9$ and ${\epsilon }_2=1.3$; one can obtain that $ϵ<3.49$. Then, we let $ϵ=3.19$ and ${\mathrm{\Lambda }}_0=10$; then, we have $|{\mathrm{\Lambda }}_a(0,12000)|<3771$. Therefore, the maximum duration time of DoS attacks is 18.855 s.

For the better highlighting of the superiority of the control scheme designed in this paper, here, a simulation comparison example [23] is used. Under the same controller parameters, model parameters, and aperiodic attacks, the control performance of the position and the speed tracking error can be illustrated through comparison with [23].

First of all, it follows from Figure 5a that the system’s estimated PPD parameter ${\widehat{\phi }}_i\left(k\right)$ of three connected automated vehicles can reach agreement, which indicates that the unknown PPD parameter ${\phi }_i\left(k\right)$ is exactly estimated through utilizing the developed PPD parameter estimation algorithm (24a) and (24b). In addition, the controller input (25) of this paper is exhibited in Figure 5b, which suggests that the system’s controller inputs are progressively more consistent suffering from the influence of DoS attacks.

The comparison between the control scheme developed in this paper and the control scheme in [23] is given in Figure 6 and Figure 7, in which the tracking trajectories of the position $s_i\left(k\right)$ and the position error $e_i\left(k\right)$ for nonlinear CAVs are illustrated. Through careful observation of Figure 6, it is possible to acquire that the follower vehicles can follow the trajectory of leaders in the existence of aperiodic DoS attacks and maintain a security distance between the vehicles, thus ensuring that no potential collision occurs. Nevertheless, collisions between vehicles may occur through using the control method [23]. Additionally, the tracking trajectories of the position tracking error $e_i\left(k\right)=s_0\left(k\right)-s_i\left(k\right)-d_{i,0}$ is illustrated in Figure 6. Through careful observation of Figure 6, it is possible to obtain that the position tracking error $e_i\left(k\right)$ is able to quickly converge to the predefined region, namely, the prescribed performance tracking control goal can be realized. However, by looking at Figure 7, it can be noticed that the position tracking error goes beyond the preset boundaries.

Through observing Figure 7, one can conclude, at the initial moment, the initial value of the tracking error of the position is within the preset range. In the proposed method, the position tracking error converges, completing bounded convergence within 60 s and forming a smaller error around 0. However, using the method in [23] would result in the position tracking error exceeding the preset range and eventually converging to a larger error bound within 60 s.

Finally, a numerical comparison is given in

Table 1. The comparison of convergence effect.

Comparative Parameters	Our Method	Method in [23]	Unit
Tracking error $e_i\left(k\right)$	$0.16$	$0.23$	m
Starting convergence time	10	38	second (s)

to demonstrate the superiority of the designed method. By looking at the table it can be obtained that our tracking error has a smaller value and has a shorter convergence time as compared to [23].

5. Conclusions

This paper focuses on the model-free adaptive vehicular tracking control problem for nonlinear CAVs under prescribed performance constraint and aperiodic DoS attacks. The constrained output of nonlinear CAVs is converted to an unconstrained output through utilizing a strictly incremental function. Then, the output of the previous moment is utilized to mitigate the adverse influence generated by aperiodic DoS attacks. On the basis of the above two points, a novel model-free adaptive prescribed performance tracking control strategy is developed. Ultimately, the superiority of the designed control algorithm is presented through simulation. In future work, we will focus on problems for nonlinear CAVs such as sliding mode control, saturation, faults, and collision problems.