Arbitrary Timestep Video Frame Interpolation with Time-Dependent Decoding

Abstract

Given an observed low frame rate video, video frame interpolation (VFI) aims to generate a high frame rate video, which has smooth video frames with higher frames per second (FPS). Most existing VFI methods often focus on generating one frame at a specific timestep, e.g., 0.5, between every two frames, thus lacking the flexibility to increase the video’s FPS by an arbitrary scale, e.g., 3. To better address this issue, in this paper, we propose an arbitrary timestep video frame interpolation (ATVFI) network with time-dependent decoding. Generally, the proposed ATVFI is an encoder–decoder architecture, where the interpolation timestep is an extra input added to the decoder network; this enables ATVFI to interpolate frames at arbitrary timesteps between input frames and to increase the video’s FPS at any given scale. Moreover, we propose a data augmentation method, i.e., multi-width window sampling, where video frames can be split into training samples with multiple window widths, to better leverage training frames for arbitrary timestep interpolation. Extensive experiments were conducted to demonstrate the superiority of our model over existing baseline models on several testing datasets. Specifically, our model trained on the GoPro training set achieved 32.50 on the PSNR metric on the commonly used Vimeo90k testing set.

1. Introduction

With the development of smart devices and high refresh-rate screen technology, recent mobile phones and computer monitors have enabled consumers to enjoy videos with high frames per second (FPS), which are much smoother than those with low FPS. However, high FPS video sources are scarce due to the high cost of capturing devices, data storage, and transfer bandwidth. Moreover, many existing videos taken in the past have low FPS due to the limits of capturing devices. To enhance the user experience when watching existing low FPS videos, video frame interpolation (VFI) aims to increase the video’s FPS by generating interpolated frames between the frames of a given input video. Recent years have witnessed much research attention and contributions from the community [1,2,3,4,5,6].

Given two consecutive input video frames with timesteps defined as 0 and 1, most existing VFI methods focus on the quality of the interpolated frame and can generate one frame at a specific timestep, e.g., 0.5, between each two frames of input video. As a consequence, these models often only perform $2\times$ interpolation, i.e., doubling the FPS of the input video. Although interpolation of $4\times$, $8\times$ is possible by applying these $2\times$ models in an iterative fashion, some problems still exist. First, arbitrary interpolation scales, e.g., $3\times$, cannot be realized due to the nature of $2\times$ interpolation in these methods. Second, iterative interpolation lacks shared computation among the interpolation of multiple frames, which may suffer from accumulated interpolation errors and also may lead to inconsistency between generated frames.

Recently, some researchers have focused on generating interpolated frames for arbitrary scales [7,8,9,10,11,12]. Most of these methods depend on scaling the estimated optical flow linearly according to the desired scale. However, this paradigm assumes that the motion is linear, which is not always the case in real-world motion scenarios. Moreover, these methods rely heavily on the precision of optical flow estimation, whose errors could yield artifacts in the final interpolated frames.

In this paper, we propose a new arbitrary timestep video frame interpolation (ATVFI) neural network model with interpolation time-decoding. Generally, our method is built on an encoder–decoder framework [13]. The decoder part of our model takes the interpolation timestep t as an extra input, indicating the relative time coordinate of the desired output frame with regard to input frames. The proposed model can relieve the above-mentioned problems from the following perspectives. First, since the timestep t can be arbitrarily given, the interpolated frame at any timestep can be obtained, and the FPS of the input video can be arbitrarily scaled. Second, the computation of each output frame only directly depends on (the features of) input frames, without dependency on any other output frames, and thus ATVFI is free from interpolation error accumulation. Compared to VFI methods [7,8,9,11,12], considering arbitrary interpolation scale, our ATVFI does not assume linear motion, and its motion estimation is accordingly learned from training samples.

Moreover, existing VFI methods leverage training videos by splitting them into samples of fixed-width windows [14]. To further leverage the high FPS video training set to match the arbitrary-scale interpolation fashion of our model, we propose a new data augmentation method, multi-width window sampling (MWWS), to split the videos into training samples with multiple window widths. This approach improves the variety of motion magnitude between input frames, as well as the possible values of timestep t during training. MWWS enables our model to adapt to different motion magnitudes and learn a continuous correspondence relationship from t to output frames, thus significantly boosting the performance of our proposed ATVFI.

To summarize, our contributions in this paper are listed as follows:

• A new arbitrary timestep video frame interpolation framework based on an encoder–decoder is proposed, where any interpolation timestep can be fed into the decoder part.
• We propose a new data augmentation method, i.e., multi-width window sampling, to better leverage the training set for interpolating videos at any interpolation scale.
• Extensive experiments are conducted to compare our method with state-of-the-art VFI methods, showing the effectiveness of the proposed framework and data augmentation.

2. Related Work

Existing mainstream methods of video frame interpolation can be generally categorized into flow-based methods [7,8,9,11,12,15,16,17,18,19,20,21,22,23,24,25,26], kernel-based methods [1,5,10,27,28,29,30], phase-based methods [31], and hallucination-based methods [2,3,14,32].

Kernel-based methods explicitly or implicitly estimate a convolution kernel for each target pixel, and then synthesize the interpolated frame by convolving over input frames. The concrete convolution operator may be adaptive convolution [27], separable convolution [1], AdaCoF [28,30], or deformable convolution [10], generalized deformable convolution [29]. Phase-based methods synthesize the interpolated frame from the estimated phase decomposition of it [31]. Hallucination-based methods directly synthesize the interpolated frame from blended features generated from PixelShuffle [2], 3D convolution [14], or 2D convolution with generative adversarial networks [32,33]. Flow-based methods first estimate the optical flow between input frames, then infer the optical flow between the intermediate frame and input frames, and finally synthesize the output frame based on the optical flow by warping the input frames or their features. Super SloMo [7] is a pioneering work under this setup. DAIN [8] incorporates a depth estimation module as extra information for handling occlusion. SoftSplat [16] leverages the Softmax operator to mix pixels and features during the forward warping operation. Heo and Jeong [26] combine max–min warping with forward warping. ABME [18] further estimates an asymmetric bilateral optical flow based on symmetric optical flow. QVI [19] and EQVI [20] leverage an extra two frames and refine optical flow based on the proposed quadratic motion assumption. AllAtOnce [21] further extends quadratic motion to cubic motion. IFRNet [11] gradually estimates bilateral optical flow together with intermediate features in a coarse-to-fine manner for mutual promotion of the two components. VFIformer [23] refines the warped frames with a Transformer [34] structure. UPR-Net [24] uses a unified pyramid recurrent network to estimate optical flow and synthesize frames. AMT [25] leverages bidirectional correlation volumes for all pairs of pixels in flow estimation and feature update.

Some existing methods are capable of arbitrary-scale interpolation and generate an interpolated frame at any given timestep t between input frames. For most flow-based methods, the bilateral optical flows between the intermediate frame and input frames can be simply obtained by scaling the optical flow between input frames by t [7,8,9,12]. IFRNet [11] takes t as input to the network to estimate optical flow. EDSC [10] is a kernel-based method using heterogeneous convolution [35] and deformable convolution [36] with separable filters.

3. Proposed Method

In this section, we describe our proposed ATVFI model. In the following, we first present the overall framework of the arbitrary-timestep video frame interpolation in Section 3.1, then the detailed network model architecture in Section 3.2, and finally our proposed data augmentation method named multi-width window sampling in Section 3.3. Please refer to the Supplementary Materials for the source code of our method.

3.1. Arbitrary Timestep VFI Framework

The goal of video frame interpolation is to generate intermediate frames for the moments between given video frames. Specifically, given two consecutive input frames, ${\mathit{I}}_0$ and ${\mathit{I}}_1$, the goal is to generate the frame ${\mathit{I}}_t$ at the given intermediate timestep t. Our ATVFI aims to model the continuous relationship between ${\mathit{I}}_t$ and any timestep $t\in [0,1]$, rather than fixed $t=0.5$, as in most existing VFI methods.

We model this relationship as a two-step process in an encoder–decoder framework. Firstly, given input frames ${\mathit{I}}_0$ and ${\mathit{I}}_1$, an encoder network $E_{\varphi }$ encodes them into latent representation $\mathit{z}$:

$$\mathit{z}=E_{\varphi }({\mathit{I}}_0,{\mathit{I}}_1).$$

(1)

Secondly, given $\mathit{z}$ and the desired timestep t, a decoder network $F_{\theta }$ decodes them into the target output frame ${\widehat{\mathit{I}}}_t$:

$${\widehat{\mathit{I}}}_t=F_{\theta }(\mathit{z},t).$$

(2)

3.2. Network Architecture

Our model follows a typical encoder–decoder framework of a U-Net [37] structure with skip connections, as shown in Figure 1.

3.2.1. Encoder of ATVFI

In the encoder of the ATVFI, a four-level pyramid network comprises the encoder part. The input frames are first concatenated on the channel axis, and then fed into the first level. Each level of the encoder part, named EncBlock, contains three convolution layers and one average pooling layer [38]. The latent feature $\mathit{z}$ consists of the output feature pyramid of all levels of the encoder network, as well as the input frames ${\mathit{I}}_0,{\mathit{I}}_1$ themselves.

Figure 1. Overall architecture of our ATVFI, which is built on encoder–decoder architecture. The details of warping parameter estimation modules (WPEMs) can be found in Figure 2.

Figure 1. Overall architecture of our ATVFI, which is built on encoder–decoder architecture. The details of warping parameter estimation modules (WPEMs) can be found in Figure 2.

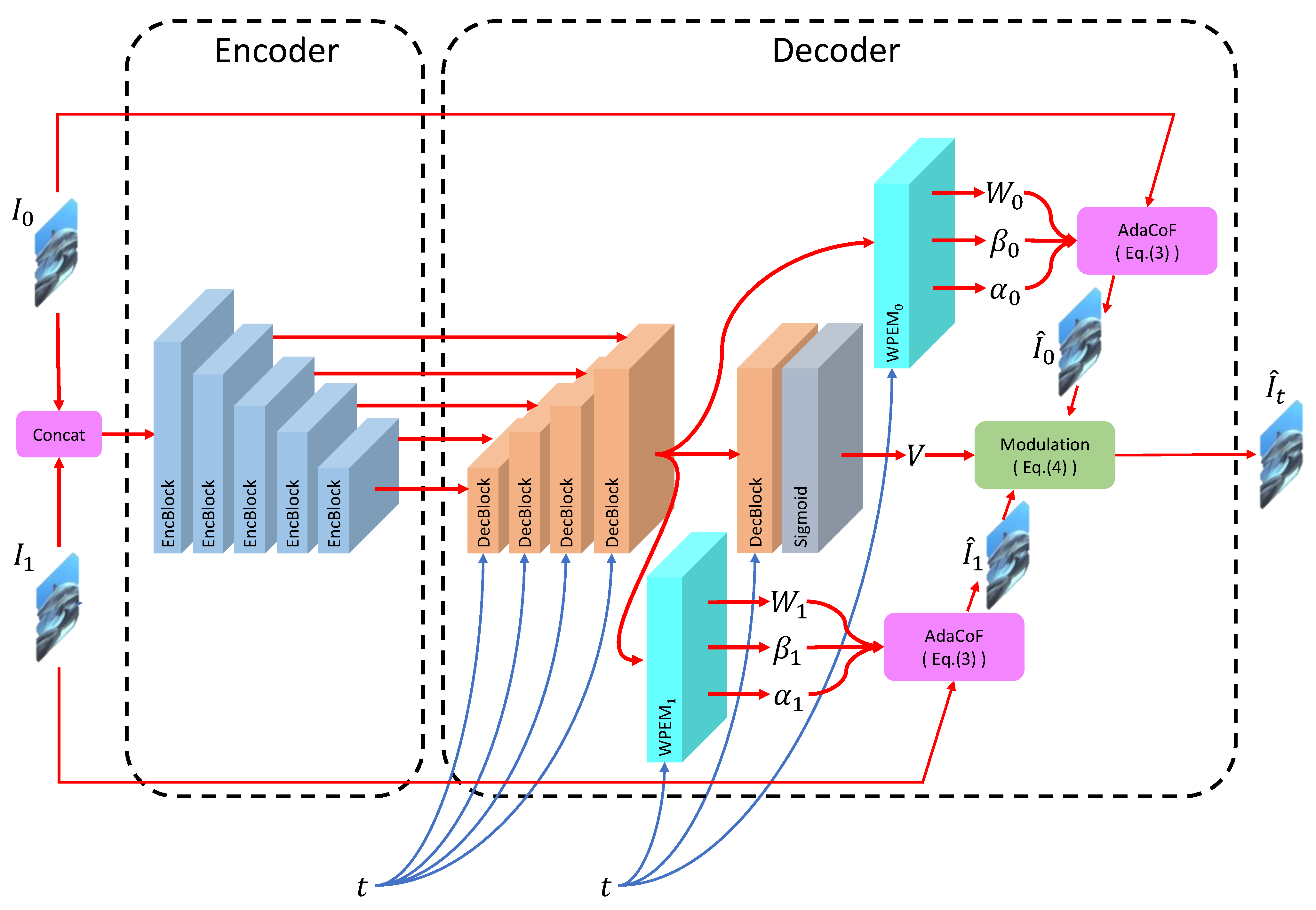
3.2.2. Decoder of ATVFI

As for the decoder of ATVFI, it is composed of a pyramid network, sub-networks for warping the input frames, and a fusion mechanism for the warped frames. The details are explained below.

Each level of the pyramid network, named DecBlock, has three convolution layers, followed by an upsampling layer and a convolution layer. The input of the first level is the concatenated tensor of two parts: the output feature of the last level of the encoder network, and a one-channel feature map with all values set to t. The input of each of the following levels is the concatenated tensor of three parts: the output feature of the corresponding encoder level via a skip connection, the output feature of the previous level of the decoder network, and the one-channel t-tensor, as mentioned above. In this way, the timestep is taken into account in the generation process of interpolated frames. In addition, the vanishing gradient problem [39] of the multi-layer network is addressed by the skip connections [40].

Then, two Warping parameter estimation modules (WPEMs, Figure 2), named ${\mathrm{WPEM}}_0$ for ${\mathit{I}}_0$ and ${\mathrm{WPEM}}_1$ for ${\mathit{I}}_1$, take t and the output feature of the pyramid network as input. Each WPEM has three sub-networks for calculating each parameter for the warping operator, including the warping kernel, $\mathit{W}$, and warping offsets, $\alpha ,\beta$. The basic architecture of these sub-networks is the same as DecBlock. The network for $\mathit{W}$ also has a Softmax layer appended. We employ the AdaCoF operator [28] as the warping operator, for its flexibility and simplicity, to warp both input frames ${\mathit{I}}_0,{\mathit{I}}_1$ into ${\widehat{\mathit{I}}}_0,{\widehat{\mathit{I}}}_1$. Specifically, given the kernel width K and dilation factor d as hyperparameters, the AdaCoF operator takes the properly padded input frame $I(i,j)$ of the original size $H\times W$, per-pixel convolution kernel $W(i,j,k,l)$, per-pixel vertical offsets $\alpha (i,j,k,l)$, and horizontal offsets $\beta (i,j,k,l)$ as input. The output image $\widehat{I}(i,j)$ of the AdaCoF operator is calculated as follows:     

$$\widehat{\mathit{I}}(i,j)=\sum _{k=0}^{K-1}\sum _{l=0}^{K-1}W(i,j,k,l)·\mathit{I}\left(i+dk+\alpha (i,j,k,l),j+dl+\beta (i,j,k,l)\right)$$

(3)

where $i,j$ are the coordinates of image pixels, and $k,l$ are the coordinates of the convolution kernel. In practice, the values in $\alpha$ and $\beta$ may not be integers, and the offset vector could point to positions other than grid points. Here, we use bilinear interpolation to obtain pixel values on those off-the-grid positions, which also make the warping operator differentiable; thus, the whole model could be trained end-to-end.

Figure 2. Architecture of the warping parameter estimation module (WPEM).

Figure 2. Architecture of the warping parameter estimation module (WPEM).

Finally, with t and the output feature of the pyramid network as input, a DecBlock followed by a Sigmoid function $\sigma \left(x\right)=\frac{1}{1+exp(-x)}$ is employed to calculate the per-pixel fusion factor $\mathit{V}$. Then, ${\widehat{\mathit{I}}}_0$ and ${\widehat{\mathit{I}}}_1$ are fused into the final image $\widehat{\mathit{I}}$ modulated by $\mathit{V}$ element-wisely, as a way to model the occlusion relationship between pixels. The modulation operation is calculated as follows:

$${\widehat{\mathit{I}}}_t(i,j)=\mathit{V}(i,j)·{\widehat{\mathit{I}}}_0(i,j)+(1-\mathit{V}(i,j))·{\widehat{\mathit{I}}}_1(i,j).$$

(4)

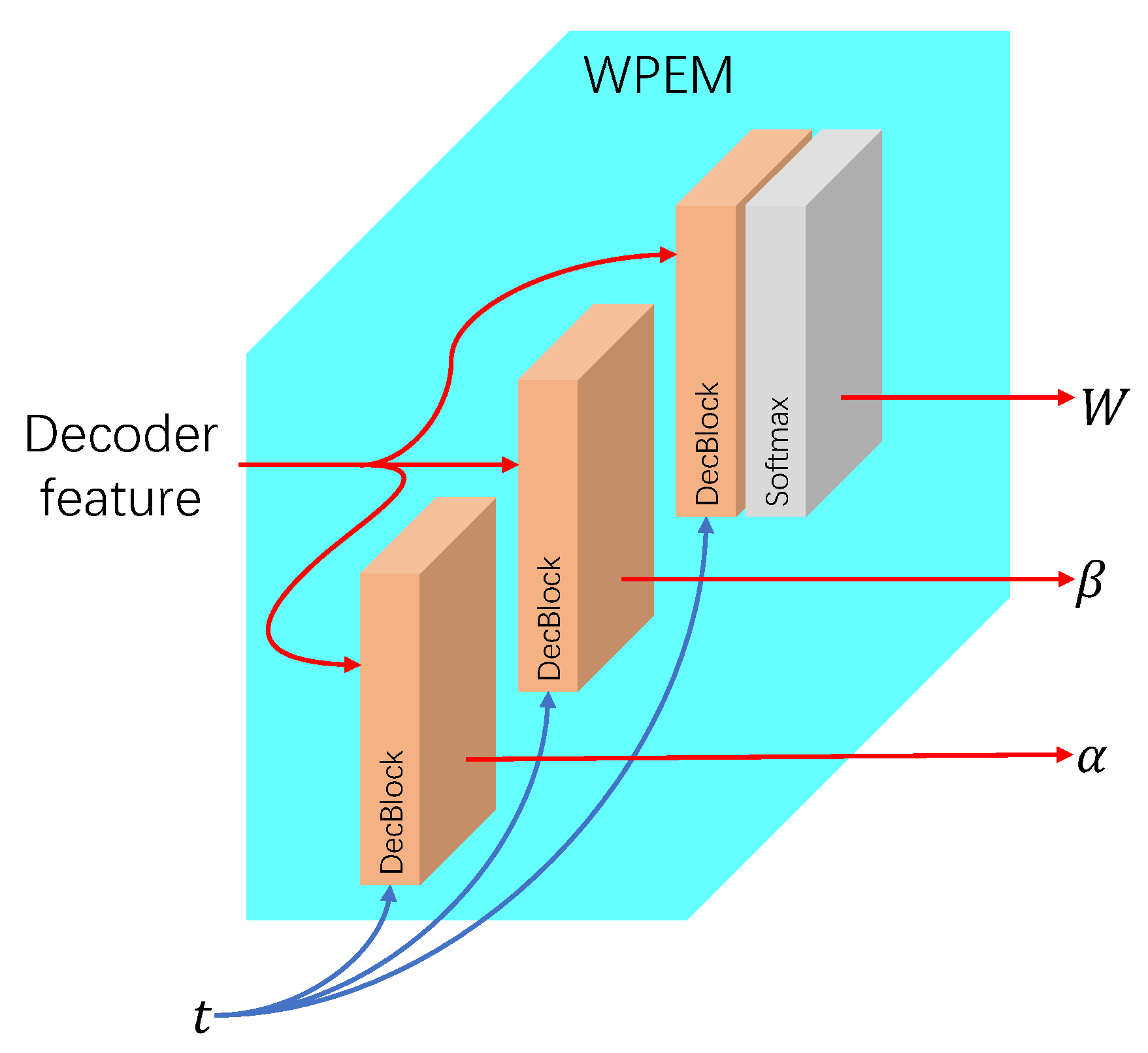
3.2.3. Algorithmic Explanation

In order to provide a comprehensive understanding of our model, we present the pseudocode representation of ATVFI in Algorithm 1. We aim to illustrate the step-by-step execution of the model, highlighting how each component plays its role in achieving the desired outcomes.

Algorithm 1: Pseudocode representation of ATVFI

1: function ATVFI(${\mathit{I}}_0,{\mathit{I}}_1,t$) 2:     ${\mathit{F}}_{e1}\leftarrow {\mathrm{EncBlock}}_1({\mathit{I}}_0,{\mathit{I}}_1)$ 3:     ${\mathit{F}}_{e2}\leftarrow {\mathrm{EncBlock}}_2\left({\mathit{F}}_{e1}\right)$ 4:     ${\mathit{F}}_{e3}\leftarrow {\mathrm{EncBlock}}_3\left({\mathit{F}}_{e2}\right)$ 5:     ${\mathit{F}}_{e4}\leftarrow {\mathrm{EncBlock}}_4\left({\mathit{F}}_{e3}\right)$ 6:     ${\mathit{F}}_{e5}\leftarrow {\mathrm{EncBlock}}_5\left({\mathit{F}}_{e4}\right)$

7:     ${\mathit{F}}_{d5}\leftarrow {\mathrm{DecBlock}}_5({\mathit{F}}_{e5},t)$ 8:     ${\mathit{F}}_{d4}\leftarrow {\mathrm{DecBlock}}_4({\mathit{F}}_{d5},{\mathit{F}}_{e5},t)$ 9:     ${\mathit{F}}_{d3}\leftarrow {\mathrm{DecBlock}}_3({\mathit{F}}_{d4},{\mathit{F}}_{e4},t)$ 10:   ${\mathit{F}}_{d2}\leftarrow {\mathrm{DecBlock}}_2({\mathit{F}}_{d3},{\mathit{F}}_{e3},t)$

11:   ${\alpha }_0,{\beta }_0,W_0\leftarrow {\mathrm{WPEM}}_0({\mathit{F}}_{d2},{\mathit{F}}_{e2},t)$ 12:   ${\widehat{\mathit{I}}}_0\leftarrow \mathrm{AdaCoF}({\mathit{I}}_0,{\alpha }_0,{\beta }_0,W_0)$ 13:   ${\alpha }_1,{\beta }_1,W_1\leftarrow {\mathrm{WPEM}}_1({\mathit{F}}_{d2},{\mathit{F}}_{e2},t)$ 14:   ${\widehat{\mathit{I}}}_1\leftarrow \mathrm{AdaCoF}({\mathit{I}}_1,{\alpha }_1,{\beta }_1,W_1)$

15:   $\mathit{V}\leftarrow \sigma \left({\mathrm{DecBlock}}_V({\mathit{F}}_{d2},{\mathit{F}}_{e2},t)\right)$ 16:   ${\widehat{\mathit{I}}}_t\leftarrow \mathit{V}·{\widehat{\mathit{I}}}_0+(1-\mathit{V})·{\widehat{\mathit{I}}}_1$ 17:   return ${\widehat{\mathit{I}}}_t$ 18: end function

3.3. Multi-Width Window Sampling

During training, the sampling process in high FPS videos of existing multi-frame interpolation methods only use a fixed-width window [10,14,21]. To be precise, given the window width W, frames from the training set video ${\mathit{I}}_0,{\mathit{I}}_1,\dots ,{\mathit{I}}_{n-1}$, and a proper sampling position index i, the input frames of a training sample are ${\mathit{I}}_i,{\mathit{I}}_{i+W}$ (for methods that require four frames as input, ${\mathit{I}}_{i-W},{\mathit{I}}_{i+2W}$ are also needed), and the ground-truth frames are ${\mathit{I}}_{i+1},{\mathit{I}}_{i+2},\dots ,{\mathit{I}}_{i+W-1}$. However, simply following such a sampling process in training our model would lead to limited motion magnitude. Moreover, the possible values of t would be limited to $1/W,2/W,\dots ,(W-1)/W$, whose values are at least $1/W$ apart from each other, which is not ideal for our model to learn a continuous mapping between t and the output frame.

To enrich the variety of motion magnitude between input frames, and to spread the possible values of t more continuously over $[0,1]$, we propose multi-width window sampling (MWWS). Firstly, for each window width W ranging from 2 to a certain maximum width $W_{\max }$, we perform a fixed window sampling of width W over the videos and obtain a set of training samples, ${\mathcal{D}}_W$. Secondly, we combine all sets to obtain the final training set: ${\mathcal{D}}_{\mathrm{MWWS}}={\bigcup }_{W=2}^{W_{\max }}{\mathcal{D}}_W$. In this way, the training samples in ${\mathcal{D}}_{\mathrm{MWWS}}$ gain not only a larger range of motion magnitude between input frames but also greater diversity and continuity of values of t, as illustrated in Figure 3.

4. Experiments

In this section, we perform a series of experiments on our proposed method. We first describe the basic experimental settings in Section 4.1, then we compare our proposed method to the related state-of-the-art frame interpolation methods, and analyze it quantitatively and qualitatively in Section 4.2; finally, we perform an ablation study on crucial components in our method in Section 4.3.

4.1. Basic Settings

Following common practice [8,10,28], our model is trained toward minimizing the ${\ell }_1$ norm of the distance between the output frame ${\widehat{\mathit{I}}}_t$ and the ground-truth frame ${\mathit{I}}_t$, by optimizing the following loss function:

$$\mathcal{L}=\sum _{i,j}\rho \left({\widehat{\mathit{I}}}_t(i,j)-{\mathit{I}}_t(i,j)\right)$$

(5)

where $\rho \left(x\right)=\sqrt{x^2+{ϵ}^2}$ is the Charbonnier function, with the constant $ϵ=0.001$. Since our model requires supervision of varied timesteps, which the commonly used Vimeo90k [41] triplet dataset lacks, we train our model on the training split of the GoPro [42] dataset, a collection of 240-fps 720p videos. MWWS with $W_{\max }=8$ is applied to our model during training by default. For a fair comparison with other methods, we retrain them on the GoPro training set. For different testing sets, we evaluate each method and report their peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) [43], calculated as follows:

$$\mathrm{PSNR}=10{log}_{10}\left(\frac{{255}^2}{\frac{1}{HW}{\sum }_{i=1}^H{\sum }_{j=1}^W{\left[{\widehat{\mathit{I}}}_t(i,j)-{\mathit{I}}_t(i,j)\right]}^2}\right)$$

(6)

$$\mathrm{SSIM}=\frac{(2{\mu }_O{\mu }_T+{ϵ}_1)(2{\sigma }_{OT}+{ϵ}_2)}{({\mu }_O^2+{\mu }_T^2+{ϵ}_1)({\sigma }_O^2+{\sigma }_T^2+{ϵ}_2)}$$

(7)

where ${\mu }_{\{O,T\}}$ and ${\sigma }_{\{O,T\}}$ represent the mean and deviation of the output image ${\widehat{\mathit{I}}}_t$ and target image ${\mathit{I}}_t$, respectively. ${\sigma }_{OT}$ represents the covariance between the two images. ${ϵ}_1$ and ${ϵ}_2$ are small constants to prevent the denominator from being zero.

4.2. Comparison with State-of-the-Art

In this section, we evaluate and compare our proposed method with state-of-the-art methods. We first compare them under the setting of the most common $2\times$ interpolation in Section 4.2.1 and the arbitrary-scale interpolation in Section 4.2.2. Then, we compare our method with an iterative version of the state-of-the-art $2\times$ interpolation methods in Section 4.2.3. Finally, we compare the methods qualitatively in Section 4.2.4.

4.2.1. $2\times$ Interpolation

For $2\times$ interpolation, we evaluate the competing methods on the Vimeo90k triplet [41], UCF [44], and Middlebury [45] testing sets. We group the baseline methods by their capability for arbitrary-scale interpolation. The results are presented in

Table 1. Comparison of the $2\times$ interpolation performance.

Method	Vimeo90k		Middlebury		UCF		Time (s)	Memory (GB)
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
SepConv [1]	29.76	0.874	29.60	0.848	29.18	0.899	0.011	0.76
AdaCoF [28]	31.98	0.920	32.40	0.906	31.56	0.935	0.011	0.76
CAIN [2]	30.32	0.885	29.12	0.830	28.99	0.892	0.019	0.97
VFIformer [23]	33.08	0.944	33.00	0.933	31.38	0.940	0.344	2.88
Super SloMo [7]	31.48	0.920	31.35	0.905	29.32	0.910	0.017	0.78
DAIN [8]	31.73	0.930	32.04	0.913	30.18	0.926	0.272	2.17
XVFI [9]	30.12	0.899	30.77	0.889	29.54	0.916	0.029	1.12
EDSC [10]	31.57	0.914	31.90	0.896	31.03	0.927	0.015	0.82
IFRNet [11]	32.23	0.927	32.89	0.925	31.52	0.935	0.007	0.79
RIFE [12]	30.41	0.885	31.66	0.897	31.48	0.935	0.006	0.78
UPR-Net [24]	31.73	0.920	31.95	0.911	30.98	0.932	0.021	0.85
AMT [25]	32.24	0.929	32.81	0.917	31.28	0.934	0.015	0.81
Ours	32.50	0.931	33.65	0.933	32.01	0.941	0.011	0.95

. It is shown that our model achieves the best results on PSNR and SSIM metrics on the UCF and Middlebury testing sets, and secures the second position on the Vimeo90k testing set. We also measure the inference speed and GPU memory consumption by running each method with frames from the Vimeo90k dataset on a workstation with a Core i7-8700K CPU and one Nvidia RTX2080Ti GPU. We measure the average running time and occupied GPU memory size over 100 runs.

4.2.2. Arbitrary-Scale Multi-Frame Interpolation

For arbitrary-scale multi-frame interpolation, we evaluate methods on GoPro [42] and Adobe240 [46] testing sets. Similar to the sampling process in MWWS, we sample from testing videos with different values of W and obtain testing sets of different interpolation scales from $3\times$ to $7\times$. We then report the performance of each one.

Table 2. Comparison of arbitrary-scale multi-frame interpolation performance results on GoPro.

Method	$3\times$		$4\times$		$5\times$		$6\times$		$7\times$
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Super SloMo [7]	35.39	0.969	34.10	0.957	32.80	0.941	31.64	0.923	30.50	0.902
DAIN [8]	30.70	0.922	29.35	0.893	27.67	0.862	26.65	0.837	25.65	0.811
EDSC [10]	35.52	0.967	34.17	0.955	32.84	0.940	31.69	0.923	30.57	0.902
XVFI [9]	31.21	0.928	29.69	0.901	27.90	0.872	26.80	0.847	25.80	0.825
IFRNet [11]	35.61	0.967	34.37	0.957	32.97	0.942	31.86	0.927	30.84	0.909
RIFE [12]	31.06	0.919	29.00	0.880	27.47	0.846	26.31	0.817	25.36	0.791
UPR-Net [24]	35.14	0.9633	34.06	0.955	32.92	0.942	31.98	0.928	30.94	0.910
AMT [25]	35.03	0.963	34.33	0.957	32.82	0.943	32.01	0.930	30.94	0.913
Ours	36.43	0.972	34.78	0.960	33.24	0.943	31.94	0.925	30.70	0.903

and

Table 3. Comparison of arbitrary-scale multi-frame interpolation performance results on Adobe240.

Method	$3\times$		$4\times$		$5\times$		$6\times$		$7\times$
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Super SloMo [7]	33.92	0.962	33.43	0.957	32.93	0.952	32.42	0.946	31.87	0.938
DAIN [8]	30.76	0.921	29.87	0.904	28.90	0.885	28.24	0.870	27.56	0.855
EDSC [10]	34.65	0.961	34.19	0.957	33.62	0.951	33.05	0.945	32.46	0.937
XVFI [9]	31.75	0.937	30.63	0.920	29.49	0.904	28.71	0.891	27.96	0.878
IFRNet [11]	35.32	0.966	34.69	0.962	33.93	0.954	33.21	0.948	32.59	0.940
RIFE [12]	31.79	0.931	30.44	0.910	29.40	0.891	28.56	0.874	27.84	0.858
UPR-Net [24]	34.72	0.964	34.28	0.960	33.71	0.954	33.17	0.948	32.53	0.939
AMT [25]	34.12	0.961	33.99	0.960	33.36	0.954	32.76	0.948	32.28	0.941
Ours	37.00	0.973	35.98	0.968	35.05	0.961	34.20	0.953	33.37	0.944

list the results of the GoPro and Adobe240 testing sets, respectively. Our model achieves the best results on all scale settings on the Adobe240 testing set and on most scale settings on the GoPro testing set.

4.2.3. Comparison with Iterative Interpolation

Iterative interpolation enables existing single-frame interpolation methods to generate more frames between input frames but suffers from deficiencies elaborated in Section 1. To compare our method with those under multi-frame interpolation settings, similar to Section 4.2.2, we sample from test videos with fixed window sizes $W=8$ and obtain testing sets for $8\times$ interpolation. The baseline single-frame interpolation models are applied iteratively, three times, to obtain seven interpolated frames. The results are presented in

Table 4. Comparison between our method and iterative interpolation.

Method	GoPro ($8\times$)		Adobe240 ($8\times$)
	PSNR	SSIM	PSNR	SSIM
SepConv [1] (iterative)	27.87	0.843	28.10	0.857
AdaCoF [28] (iterative)	29.34	0.877	31.27	0.918
CAIN [2] (iterative)	27.88	0.834	27.75	0.855
VFIformer [23] (iterative)	28.70	0.864	29.16	0.889
Ours	29.62	0.881	32.60	0.913

. Our model performs better than the iterative interpolation of any single-frame interpolation methods.

4.2.4. Qualitative Evaluation

We present several examples from the Vimeo90k testing set and compare the interpolated results visually, as shown in Figure 4. In the first example, our method generates the fingertip with clear edges and the strap loop with the correct shape and position. As for faces, our method generates background texture near the human face with the least blur and distortion.

4.3. Ablation Study

In this section, we conduct an ablation study on our proposed method. First, we test various designs of adopting the timestep in the decoder network in Section 4.3.1. Then, we analyze the effect of MWWS on our model in Section 4.3.2.

4.3.1. Method for Adopting the Timestep as Input

To explore more ways for our decoder network to adopt t as input, we compare the performance of our model (denoted as “Ours-original”) with the following decoder variants:

• Variant “Ours-lastonly”: Only the sub-networks in the warping modules adopt t as input, while the pyramid part of the decoder network only takes encoder features and previous-level decoder features as input.
• Variant “Ours-allconv”: Apart from the first convolution layer in each level of the decoder network, all other convolution layers also adopt t as extra input in the same way.

The results are presented in

Table 5. Comparison between ATVFI variants.

	Vimeo90k ($2\times$)		GoPro ($8\times$)		Adobe240 ($8\times$)
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Ours-original	32.50	0.931	29.62	0.881	32.60	0.935
Ours-lastonly	32.52	0.932	29.63	0.881	32.70	0.938
Ours-allconv	32.60	0.933	29.67	0.881	32.72	0.937

. The difference between different variants is minor, indicating that our model is robust in the choice of where to adopt t as input.

4.3.2. Effect of Multi-Width Window Sampling

To show the effectiveness of multi-width window sampling (MWWS) in augmenting the dataset, we compare our model with one trained on the GoPro dataset sampled by a fixed window width of 8 (denoted as “Ours (w/o MWWS)”). The results are presented in

Table 6. Results of the ablation study on MWWS.

	Vimeo90k ($2\times$)		GoPro ($8\times$)		Adobe240 ($8\times$)
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Ours	32.50	0.931	29.62	0.881	32.60	0.935
Ours (w/o MWWS)	31.46	0.909	29.39	0.877	31.83	0.924

. The large performance margin shows that the great variety of timestep values produced by MWWS is a crucial part of training our model.

5. Discussion and Conclusions

In this work, we proposed a new arbitrary timestep video frame interpolation (ATVFI) network model. The proposed ATVFI is built on an encoder–decoder architecture, where the interpolation timestep is fed as an extra input to the decoder, enabling ATVFI to interpolate video at any scale. For high-scale interpolation, this paradigm avoids error accumulation of iterative interpolation. Also, in contrast to flow-based methods that explicitly model motion as flows and assume linear motion, ATVFI models complex motion implicitly with the power of neural networks. For more supervision of motion magnitudes and correspondence between an output frame and its timestep, MWWS is proposed to split training samples with multiple window widths, which can better leverage training videos for arbitrary timestep video interpolation. Our ATVFI has been well evaluated on several testing datasets and achieved comparable results with state-of-the-art methods, notably a 32.50 on the PSNR metric on the Vimeo90k testing set.

In the future, our ATVFI could be further improved in terms of performance and efficiency. Currently, the warping parameters generated by WPEM are totally guided by the gradient from the differentiable AdaCoF operator during training. Although this works fine, the warping parameters could leverage some extra supervision, which could be, e.g., optical flow models pre-trained on large datasets. In addition, MWWS is unable to produce timestep t values that are very close to 0 and 1, as shown in Figure 3. How to produce training samples with such t values is left as future work. Furthermore, our ATVFI has the potential to be extended to handle more complicated tasks, e.g., joint video deblurring and arbitrary timestep video frame interpolation.