Gibbs–Appell Equations in Finite Element Analysis of Mechanical Systems with Elements Having Micro-Structure and Voids
Abstract
1. Introduction
2. Energy of Accelerations and Basic Notions
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mehdikhani, M.; Gorbatikh, L.; Verpoest, I.; Lomov, S.V. Voids in fiber-reinforced polymer composites: A review on their formation, characteristics, and effects on mechanical performance. Judd NCW and Wright WW. Voids and their effects on mechanical-properties of composites—Appraisal. J. Compos. Mater. 2019, 53, 1579–1669. [Google Scholar] [CrossRef]
- Rohatgi, V.; Patel, N.; Lee, L.J. Experimental investigation of flow-induced microvoids during impregnation of unidirectional stitched fiberglass mat. Polym. Compos. 1996, 17, 161–170. [Google Scholar] [CrossRef]
- Teodorescu-Draghicescu, H.; Scutaru, M.L.; Rosu, D.; Calin, M.R.; Grigore, P. New Advanced Sandwich Composite with twill weave carbon and EPS. J. Optoelectron. Adv. Mater. 2013, 15, 199–203. [Google Scholar]
- Marin, M.; Hobiny, A.; Abbas, I. The Effects of Fractional Time Derivatives in Porothermoelastic Materials Using Finite Element Method. Mathematics 2021, 9, 1606. [Google Scholar] [CrossRef]
- Schell, J.S.U.; Deleglise, M.; Binetruy, C.; Krawczak, P.; Ermanni, P. Numerical prediction and experimental characterisation of mesoscale-voids in liquid composite moulding. Compos. Part. A Appl. Sci. Manuf. 2007, 38, 2460–2470. [Google Scholar] [CrossRef]
- Helmus, R.; Kratz, J.; Potter, K.; Hubert, P.; Hinterhölzl, R. An experimental technique to characterize interply void formation in unidirectional prepregs. J. Compos. Mater. 2017, 51, 579–591. [Google Scholar] [CrossRef]
- Hernandez, S.; Sket, F.; Gonzalez, C.; Llorca, J. Optimization of curing cycle in carbon fiber-reinforced laminates: Void distribution and mechanical properties. Compos. Sci. Technol. 2013, 85, 73–82. [Google Scholar] [CrossRef]
- Campbell, F.C.; Mallow, A.R.; Browning, C.E. Porosity in carbon-fiber composites—An overview of causes. J. Adv. Mater. 1995, 26, 18–33. [Google Scholar]
- Naganuma, T.; Naito, K.; Kyono, J.; Kagawa, Y. Influence of prepreg conditions on the void occurrence and tensile properties of woven glass fiber-reinforced polyimide composites. Compos. Sci. Technol. 2009, 69, 2428–2433. [Google Scholar] [CrossRef]
- Gladysz, G.M.; Chawla, K.K. Intrinsic Voids in Polymers. Voids in Materials: From Unavoidable Defects to Designed Cellular Materials; Elsevier: Amsterdam, The Netherlands, 2015; pp. 37–48. [Google Scholar]
- Sung, B.J.; Yethiraj, A. Structure of void space in polymer solutions. Phys. Rev. E 2010, 81, 237. [Google Scholar] [CrossRef]
- Liang, J.; Chen, R.; Zhang, J.F. Geometry and statistics of voids in lattice polymers. Biophys. J. 2002, 82, 471A–477A. [Google Scholar]
- Nie, L.; Lee, K.; Liao, G.L. Void control in adhesive bonding using thermosetting polymer. Sens. Actuator A-Phys. 2011, 167, 398–405. [Google Scholar] [CrossRef]
- Lee, J.W.; Wang, C.S.; Price, G.E. Void Formation in Coagulated Rigid-Rod Polymer Thin-Films. Polymer 1995, 36, 955–958. [Google Scholar] [CrossRef]
- Gerhard-Multhaupt, R. Voided polymer electrets—New materials, new challenges, new chances. In Proceedings of the 11th International Symposium on Electrets (ISE 11), Melbourne, VIC, Australia, 3 October 2002; pp. 36–45. [Google Scholar]
- Murray, B.R.; Leen, S.B.; Bradaigh, C.M.O. Void distributions and permeability prediction for rotationally moulded polymers. Proc. Inst. Mech. Engineers. Part L-J. Mater.-Des. Appl. 2015, 229, 403–418. [Google Scholar] [CrossRef]
- Shen, T.F. Void damage model and service life prediction for solid high polymer. Chin. Sci. Bull. 2001, 46, 1842–1845. [Google Scholar] [CrossRef]
- Summerscales, J.; Fry, S.A. Poisson Ration in Fiber-Reinforced Polymer Composites with a High Void Content. J. Mater. Sci. Lett. 1994, 13, 912–914. [Google Scholar] [CrossRef]
- Wu, Y.N.; Shivpuri, R.; Lee, L.J. Effect of macro and micro voids on elastic properties of polymer composites. J. Reinf. Plast. Compos. 1998, 17, 1391–1402. [Google Scholar] [CrossRef]
- Hocine, N.A.; Hamdi, A.; Zairi, F. Experimental and finite element investigation of void nucleation in rubber-like materials. Int. J. Solids Struct. 2011, 48, 1248–1254. [Google Scholar] [CrossRef]
- Tang, J.-M.; Lee, W.I.; Springer, G.S. Effects of cure pressure on resin flow, voids, and mechanical properties. J. Compos. Mater. 1987, 21, 421–440. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, B.-M.; Wang, D.-F.; Wu, Z.-J. Effects of cure cycles on void content and mechanical properties of composite laminates. Compos. Struct. 2006, 73, 303–309. [Google Scholar] [CrossRef]
- Ghiorse, S. Effect of void content on the mechanical properties of carbon/epoxy laminates. Sample Q. 1993, 24, 54–59. [Google Scholar]
- Cinquin, J.; Triquenaux, V.; Rousne, Y. Porosity influence on organic composite material mechanical properties. In Proceedings of the 16th International Conference on Composite Materials (ICCM16), Kyoto, Japan, 8–13 July 2007. [Google Scholar]
- Hou, M.; Ye, L.; Mai, Y.-W. Effect of moulding temperature on flexure, impact strength and interlaminar fracture toughness of CF/PEI composite. J. Reinf. Plast. Compos. 1996, 15, 1117–1130. [Google Scholar] [CrossRef]
- Flavin, J.N.; Knops, R.J. Some decay estimates in continuum dynamics. J. Elast. 1987, 17, 249–264. [Google Scholar] [CrossRef]
- Goodman, M.A.; Cowin, S.C. A continuum theory for granular materials. Arch. Ration. Mech. Anal. 1972, 44, 249–266. [Google Scholar] [CrossRef]
- Chirita, S.; Arusoaie, A. Thermoelastic waves in double porosity materials. Eur. J. Mech. A Solids 2021, 86, 104177. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.; Marin, M. Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J. Taibah Univ. Sci. 2020, 14, 1369–1376. [Google Scholar] [CrossRef]
- Marin, M. On the minimum principle for dipolar materials with stretch. Nonlinear Anal. RWA 2009, 10, 1572–1578. [Google Scholar] [CrossRef]
- Modrea, A.; Vlase, S.; Calin, M.R.; Peterlicean, A. The influence of dimensional and structural shifts of the elastic constant values in cylinder fiber composites. J. Optoelectron. Adv. Mater. 2013, 15, 278–283. [Google Scholar]
- Vlase, S.; Teodorescu-Draghicescu, H.; Calin, M.R.; Serbina, L. Simulation of the elastic properties of some fibre-reinforced composite laminates under off-axis loading system. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 424–429. [Google Scholar]
- Öchsner, A. Computational Statics and Dynamics: An Introduction Based on the Finite Element Method; Springer: Singapore, 2020. [Google Scholar]
- Iesan, D. Thermoelastic Models of Continua; Kluwer Academic: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Nguyen, V.T.; Hwu, C. A Review on Modelling Polymer Composites via Anisotropic Viscoelasticity. J. Aeronaut. Astronaut. Aviat. 2021, 53, 387–402. [Google Scholar]
- Raju, K.; Tay, T.E.; Tan, V.B.C. A review of the FEM method for composites. Multiscale Multidiscip. Model. Exp. Des. 2021, 4, 1–24. [Google Scholar] [CrossRef]
- Sharma, A.; Bagha, A.K.; Shukla, D.K.; Bahl, S. Finite element model updating of metallic and composite structures-A state of the art review. AIMS Mater. Sci. 2021, 8, 390–415. [Google Scholar] [CrossRef]
- Jagadeesh, G.V.; Setti, S.G. A review on micromechanical methods for evaluation of mechanical behavior of particulate reinforced metal matrix composites. J. Mater. Sci. 2020, 55, 9848–9882. [Google Scholar] [CrossRef]
- Muzel, S.D.; Bonhin, E.; Guimaraes, N.M.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef] [PubMed]
- Teodorescu-Draghicescu, H.; Stanciu, A.; Vlase, S.; Scutaru, L.; Calin, M.R.; Serbina, L. Finite Element Method Analysis of Some Fibre-Reinforced Composite Laminates. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 782–785. [Google Scholar]
- Stanciu, A.; Teodorescu-Drǎghicescu, H.; Vlase, S.; Scutaru, M.L.; Calin, M.R. Mechanical behavior of CSM450 and RT800 laminates subjected to four-point bend tests. Optoelectron. Adv. Mater. Rapid Commun. 2012, 6, 495–497. [Google Scholar]
- Niculiţă, C.; Vlase, S.; Bencze, A.; Mihălcică, M.; Calin, M.R.; Serbina, L. Optimum stacking in a multi-ply laminate used for the skin of adaptive wings. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 1233–1236. [Google Scholar]
- Nunziato, J.W.; Cowin, S.C. Linear elastic materials with voids. J. Elast. 1983, 13, 125–147. [Google Scholar]
- Othman, M.I.A.; Fekry, M.; Marin, M. Plane waves in generalized magneto-thermo-viscoelastic medium with voids under the effect of initial stress and laser pulse heating. Struct. Eng. Mech. 2020, 73, 621–629. [Google Scholar]
- Chang, X.; Ren, M.F.; Li, T.; Guo, X. Evaluation of mechanical behaviour of unidirectional fibre-reinforced composites considering the void morphology. J. Reinf. Platics Compos. 2017, 36, 1817–1828. [Google Scholar] [CrossRef]
- Dong, C.S. Effects of Process-Induced Voids on the Properties of Fibre Reinforced Composites. J. Mater. Sci. Technol. 2016, 32, 597–604. [Google Scholar] [CrossRef]
- Erdman, A.G.; Sandor, G.N.; Oakberg, A. A General Method for Kineto-Elastodynamic Analysis and Synthesis of Mechanism. Journal of Engineering for Industry. ASME Trans. 1972, 94, 1193. [Google Scholar]
- Bagci, C. Elastodynamic Response of Mechanical Systems using Matrix Exponential Mode Uncoupling and Incremental Forcing Techniques with Finite Element Method. In Proceedings of the Sixth Word Congress on Theory of Machines and Mechanisms, New Delhi, India, 15–20 December 1983; p. 472. [Google Scholar]
- Bahgat, B.M.; Willmert, K.D. Finite Element Vibrational Analysis of Planar Mechanisms. Mech. Mach. Theory 1976, 11, 47. [Google Scholar] [CrossRef]
- Cleghorn, W.L.; Fenton, E.G.; Tabarrok, K.B. Finite Element Analysis of High-Speed Flexible Mechanisms. Mech. Mach. Theory 1981, 16, 407. [Google Scholar] [CrossRef]
- Christensen, E.R.; Lee, S.W. Nonlinear finite element modelling of the dynamics of unrestrained flexible structures. Comput. Struct. 1986, 23, 819–829. [Google Scholar] [CrossRef]
- Midha, A.; Erdman, A.G.; Frohrib, D.A. Finite element approach to mathematical modeling of high-speed elastic linkages. Mech. Mach. Theory 1978, 13, 603–618. [Google Scholar] [CrossRef]
- Nath, K.; Ghosh, A. Steady-state response of mechanism with elastic links by finite element methods. Mech. Mach. Theory 1980, 15, 199. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Öchsner, A.; Scutaru, M.L. Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Continuum Mech. Thermodyn. 2019, 31, 715–724. [Google Scholar] [CrossRef]
- Vlase, S. Dynamical Response of a Multibody System with Flexible Elements with a General Three-Dimensional Motion. Rom. J. Phys. 2012, 57, 676–693. [Google Scholar]
- Vlase, S.; Dănăşel, C.; Scutaru, M.L.; Mihălcică, M. Finite Element Analysis of a Two-Dimensional Linear Elastic Systems with a Plane “rigid Motion”. Rom. J. Phys. 2014, 59, 476–487. [Google Scholar]
- Deü, J.-F.; Galucio, A.C.; Ohayon, R. Dynamic responses of flexible-link mechanisms with passive/active damping treatment. Comput. Struct. 2008, 86, 258–265. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, X. Dynamic analysis of flexible linkage mechanisms under uniform temperature change. J. Sound. Vib. 2009, 319, 570–592. [Google Scholar] [CrossRef]
- Neto, M.A.; Ambrósio, J.A.C.; Leal, R. Composite materials in flexible multibody systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 6860–6873. [Google Scholar] [CrossRef]
- Piras, G.; Cleghorn, W.L.; Mills, J.K. Dynamic finite-element analysis of a planar high-speed, high-precision parallel manipulator with flexible links. Mech. Mach. Theory 2005, 40, 849–862. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the fundamental formulae of dynamics. Am. J. Math. 1879, 2, 49–64. [Google Scholar] [CrossRef]
- Appell, P. Sur une forme générale des equations de la dynamique. C.R. Acad. Sci. Paris. 1899, 1900, 129. [Google Scholar]
- Mirtaheri, S.M.; Zohoor, H. The Explicit Gibbs-Appell Equations of Motion for Rigid-Body Constrained Mechanical System. In Proceedings of the 2018 6th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 23–25 October 2018; pp. 304–309. [Google Scholar]
- Mehrjooee, O.; Dehkordi, S.F.; Korayem, M.H. Dynamic modeling and extended bifurcation analysis of flexible-link manipulator. Mech. Based Des. Struct. Mach. 2020, 48, 87–110. [Google Scholar] [CrossRef]
- Korayem, M.H.; Dehkordi, S.F. Motion equations of cooperative multi flexible mobile manipulator via recursive Gibbs-Appell formulation. Appl. Math. Model. 2019, 65, 443–463. [Google Scholar] [CrossRef]
- Shafei, A.M.; Shafei, H.R. A systematic method for the hybrid dynamic modeling of open kinematic chains confined in a closed environment. Multibody Syst. Dyn. 2017, 38, 21–42. [Google Scholar] [CrossRef]
- Amini, S.; Dehkordi, S.F.; Fahraji, S.H. Motion equation derivation and tip-over evaluations for K mobile manipulators with the consideration of motors mass by the use of Gibbs-Appell formulation. In Proceedings of the 5th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 25–27 October 2017. [Google Scholar]
- Korayem, M.H.; Dehkordi, S.F. Derivation of dynamic equation of viscoelastic manipulator with revolute-prismatic joint using recursive Gibbs-Appell formulation. Nonlinear Dyn. 2017, 89, 2041–2064. [Google Scholar] [CrossRef]
- Shafei, A.M.; Korayem, M.H. Theoretical and experimental study of dynamic load-carrying capacity for flexible robotic arms in point-to-point motion. Optim. Control. Appl. Methods 2017, 38, 963–972. [Google Scholar] [CrossRef]
- Marin, M.; Seadawy, A.; Vlase, S.; Chirila, A. On mixed problem in thermoelasticity of type III for Cosserat media. J. Taibah Univ. Sci. 2022, 16, 1264–1274. [Google Scholar] [CrossRef]
- Vlase, S.; Negrean, I.; Marin, M.; Scutaru, M.L. Energy of Accelerations Used to Obtain the Motion Equations of a Three- Dimensional Finite Element. Symmetry 2020, 12, 321. [Google Scholar] [CrossRef]
- Negrean, I.; Crișan, A.-D.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2020, 12, 95. [Google Scholar] [CrossRef]
- Vlase, S. Elimination of Lagrangian Multipliers. Mech. Res. Commun. 1987, 14, 17. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Mitrica, B. Dynamical Analysis of the Mechanical System with Two Degrees of Freedom Applied to the Transmission of the Wind Turbine. Math. Probl. Eng. 2016, 2016, 3821083. [Google Scholar] [CrossRef][Green Version]
- Vlase, S.; Marin, M.; Öchsner, A.; Itu, C. Elastic response of a hollow cylinder with voids and micropolar structure. Contin. Mech. Thermodyn. 2022, 34, 855–866. [Google Scholar] [CrossRef]
- Katouzian, M.; Vlase, S.; Scutaru, M.L. Finite Element Method-Based Simulation Creep Behavior of Viscoelastic Carbon-Fiber Composite. Polymers 2021, 13, 1017. [Google Scholar] [CrossRef]
- Iesan, D. A theory of thermoelastic materials with voids. Acta Mech. 1986, 60, 67–89. [Google Scholar] [CrossRef]
- Rusu, G. On existence and uniqueness in thermoelasticity of bodies with voids. Bull. Acad. Polon Sci. 1987, 35, 339–346. [Google Scholar]
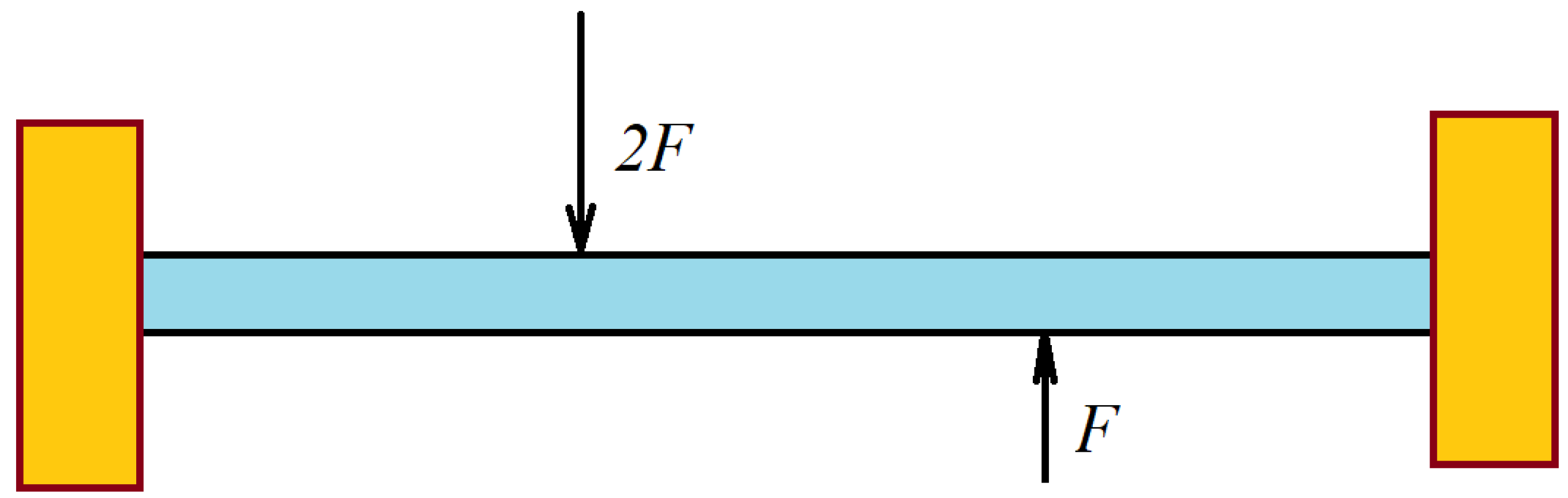
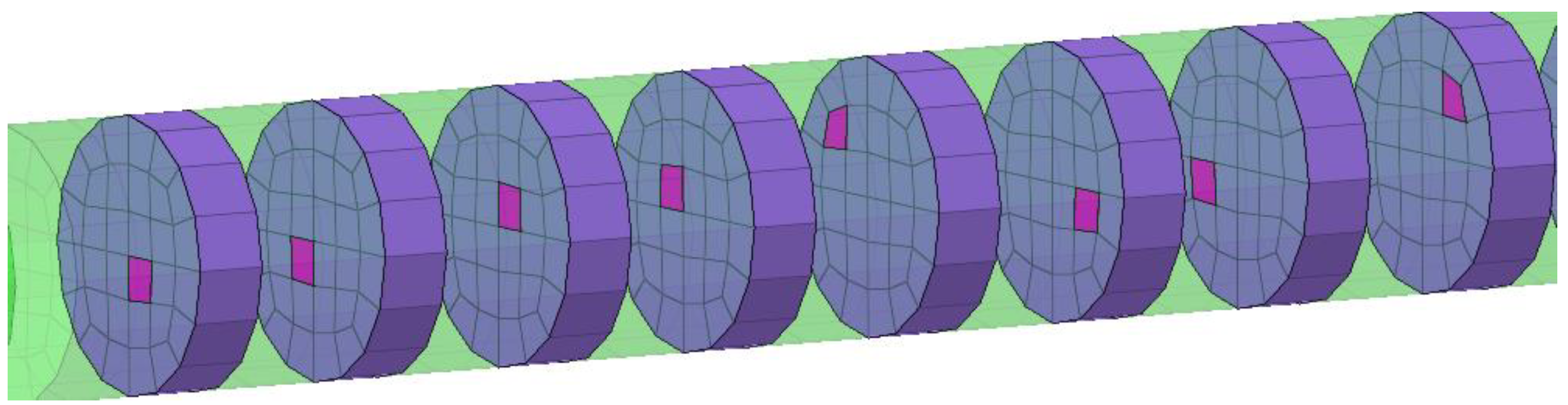


| Homogeneous Bar | 1% Voids | 2% Voids | 3% Voids | 4% Voids | |
|---|---|---|---|---|---|
| Displacements [mm] | 0.5126 | 0.5322 | 0.5524 | 0.5586 | 0.5723 |
| Variation of displacements [%] | ---- | 3.82 | 7.76 | 8.97 | 11.64 |
| von Mises stress [GPa] | 22.995 | 23.541 | 24.213 | 24.805 | 25.323 |
| Variation of von Mises stress [%] | ---- | 2.37 | 5.39 | 7.86 | 10.12 |
| Mode | Representation | Frequency for 0% Voids [Hz] | Frequency for 4% Voids [Hz] |
|---|---|---|---|
| 1 |  | 139.0319 | 139.9093 |
| 2 |  | 139.0319 | 139.9093 |
| 3 |  | 382.3166 | 382.3166 |
| 4 |  | 382.3166 | 382.3166 |
| 5 |  | 747.0574 | 747.0574 |
| 6 |  | 747.0574 | 747.0574 |
| 7 |  | 1229.853 | 1229.853 |
| 8 |  | 1229.853 | 1229.853 |
| 9 |  | 1828.136 | 1828.136 |
| 10 |  | 1828.136 | 1828.136 |
| Increase in Percentage of Voids | Reduction in Flexural Rigidity/[Reference] |
|---|---|
| 1% | 10%/[21] |
| 0% to 5% | 25%/[21] |
| 2.5% | 20%/[20] |
| 1% | 10%/[20] |
| 3% | 17%/[77] |
| 1% | 35%/[78] |
| 6% | 40%/[78] |
| Increase in Percentage of Voids | Variation of Displacement [%] | Variation of Von Mises Stress [%] |
|---|---|---|
| 0% | 0 | 0 |
| 1% | 3.82 | 2.37 |
| 2% | 7.76 | 5.39 |
| 3% | 8.97 | 7.86 |
| 4% | 11.64 | 10.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlase, S.; Marin, M.; Itu, C. Gibbs–Appell Equations in Finite Element Analysis of Mechanical Systems with Elements Having Micro-Structure and Voids. Mathematics 2024, 12, 178. https://doi.org/10.3390/math12020178
Vlase S, Marin M, Itu C. Gibbs–Appell Equations in Finite Element Analysis of Mechanical Systems with Elements Having Micro-Structure and Voids. Mathematics. 2024; 12(2):178. https://doi.org/10.3390/math12020178
Chicago/Turabian StyleVlase, Sorin, Marin Marin, and Calin Itu. 2024. "Gibbs–Appell Equations in Finite Element Analysis of Mechanical Systems with Elements Having Micro-Structure and Voids" Mathematics 12, no. 2: 178. https://doi.org/10.3390/math12020178
APA StyleVlase, S., Marin, M., & Itu, C. (2024). Gibbs–Appell Equations in Finite Element Analysis of Mechanical Systems with Elements Having Micro-Structure and Voids. Mathematics, 12(2), 178. https://doi.org/10.3390/math12020178








