Launching Point Estimation Using Inverse First-Order Pitch Programming
Abstract
1. Introduction
1.1. Related Work
1.2. Major Contribution
1.3. Organization
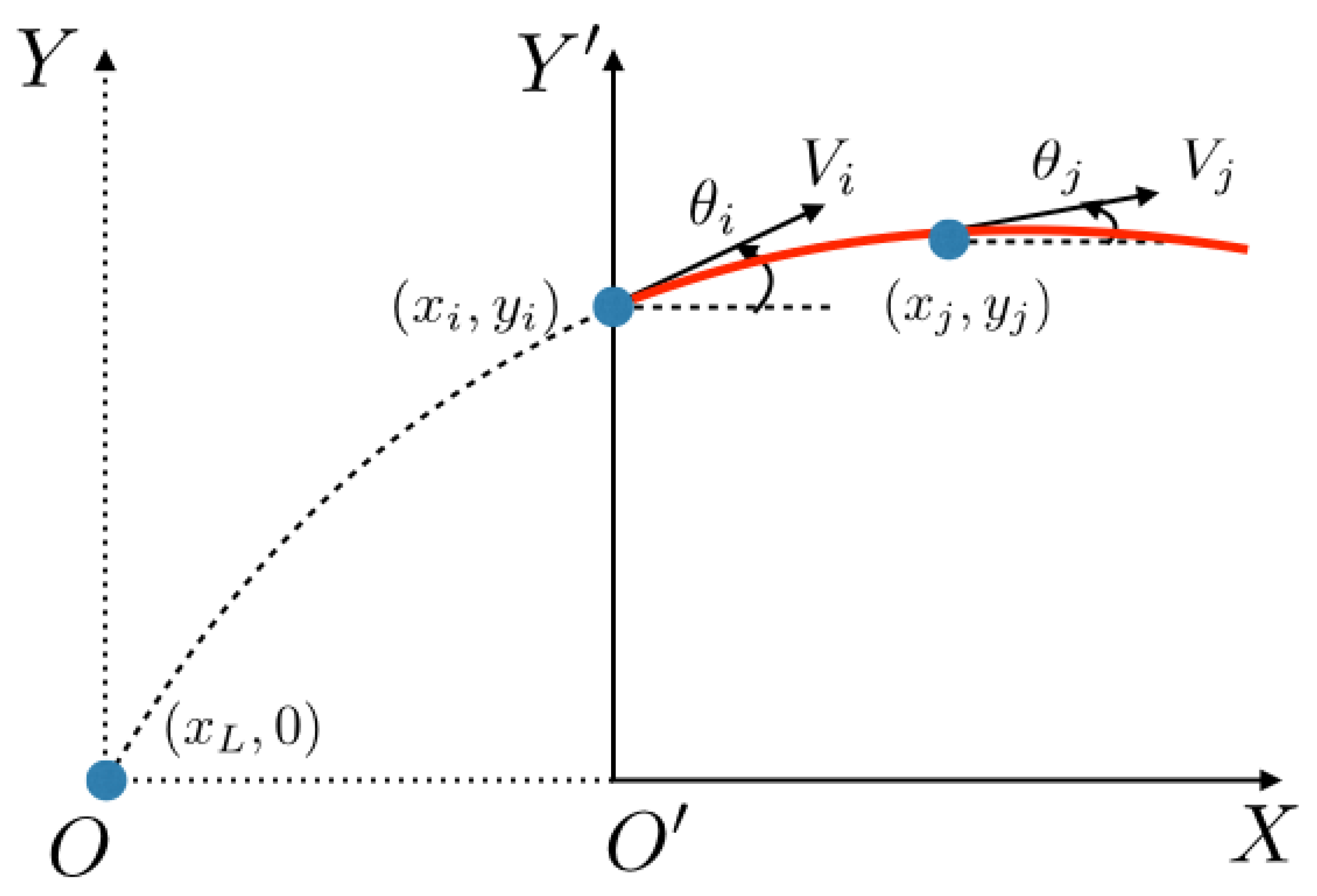
2. Problem Formulation
3. Analytic Solution of Launching Point
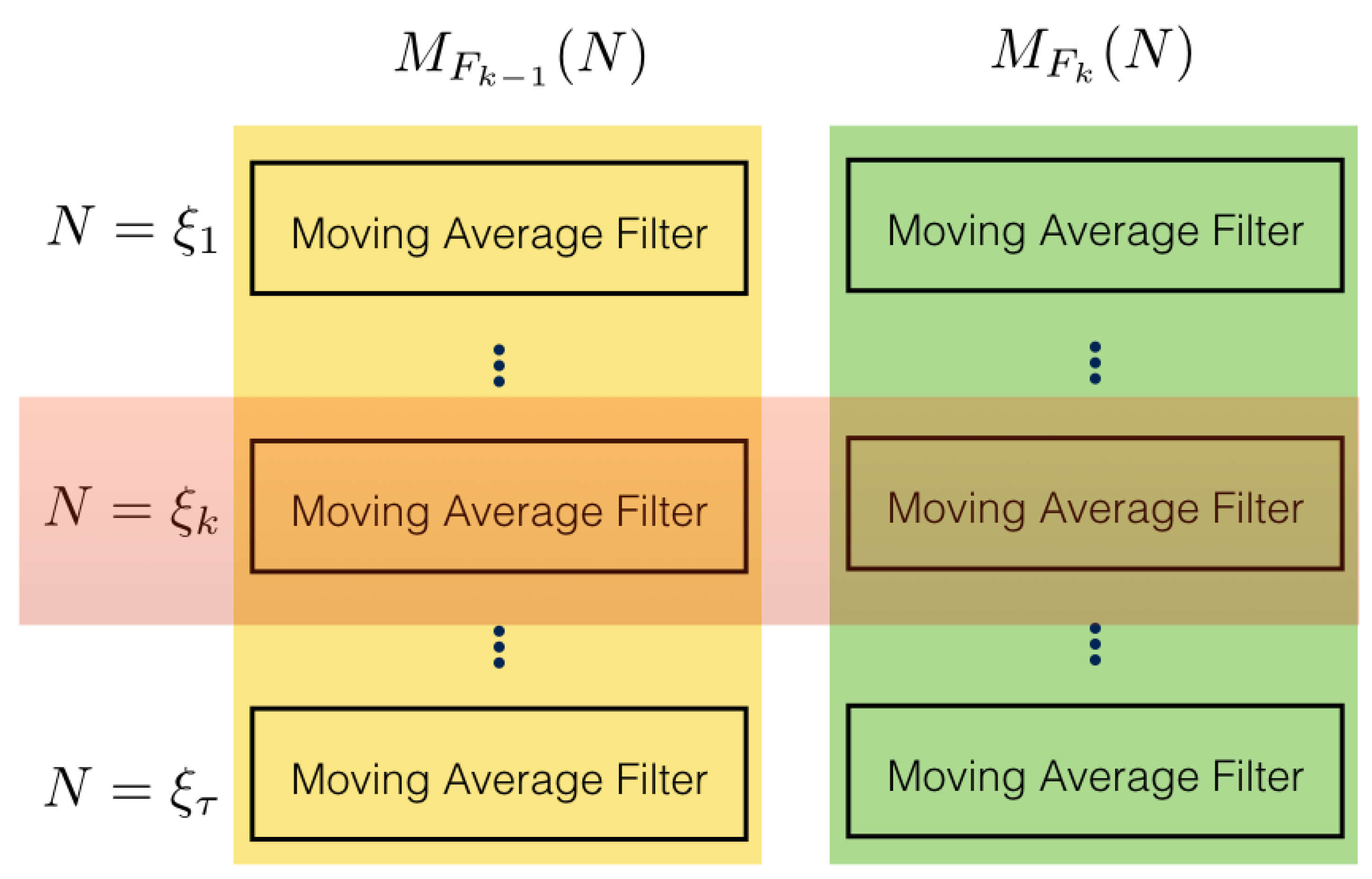
4. Two-Point Robust Measurement Selection (T-RMS)
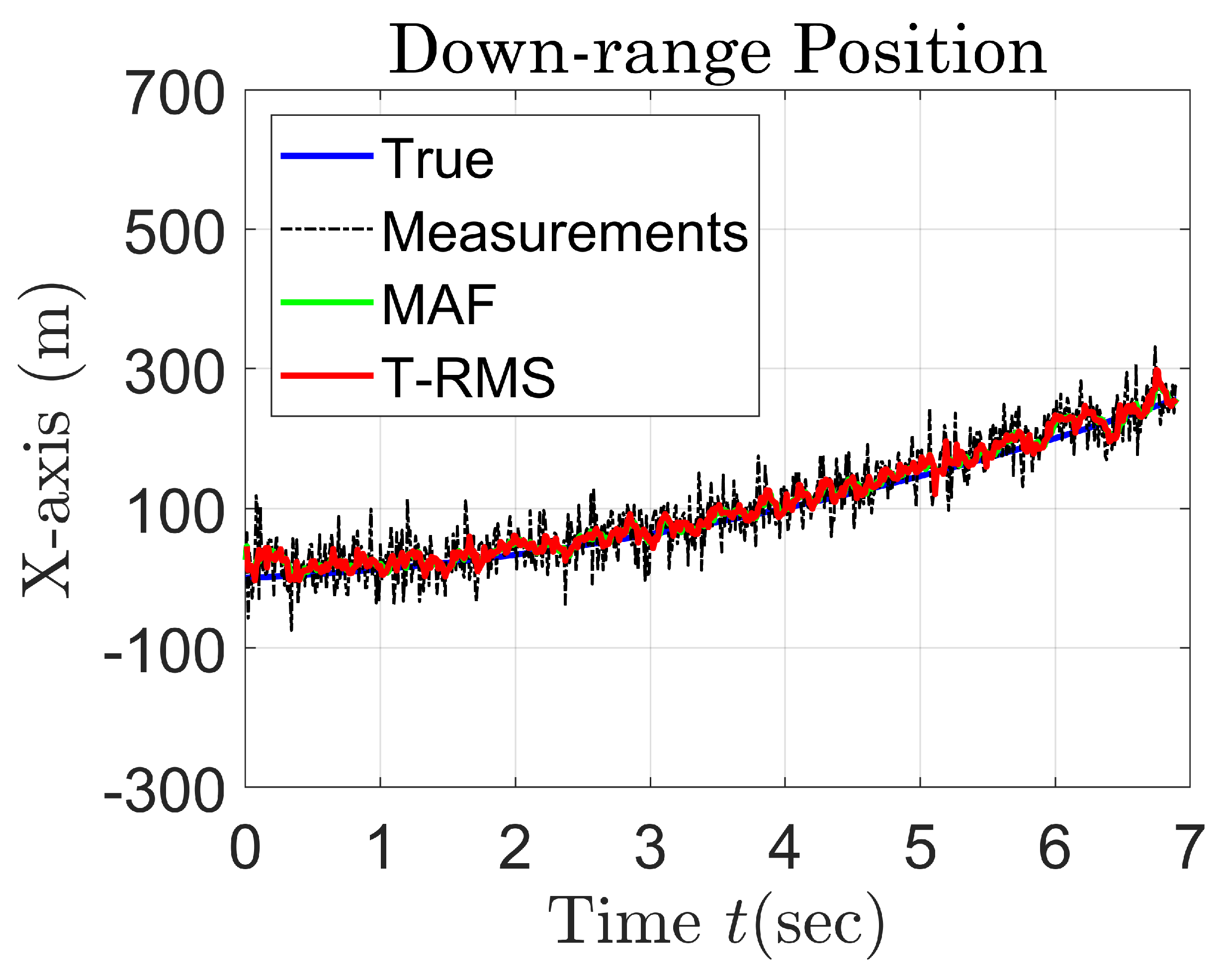
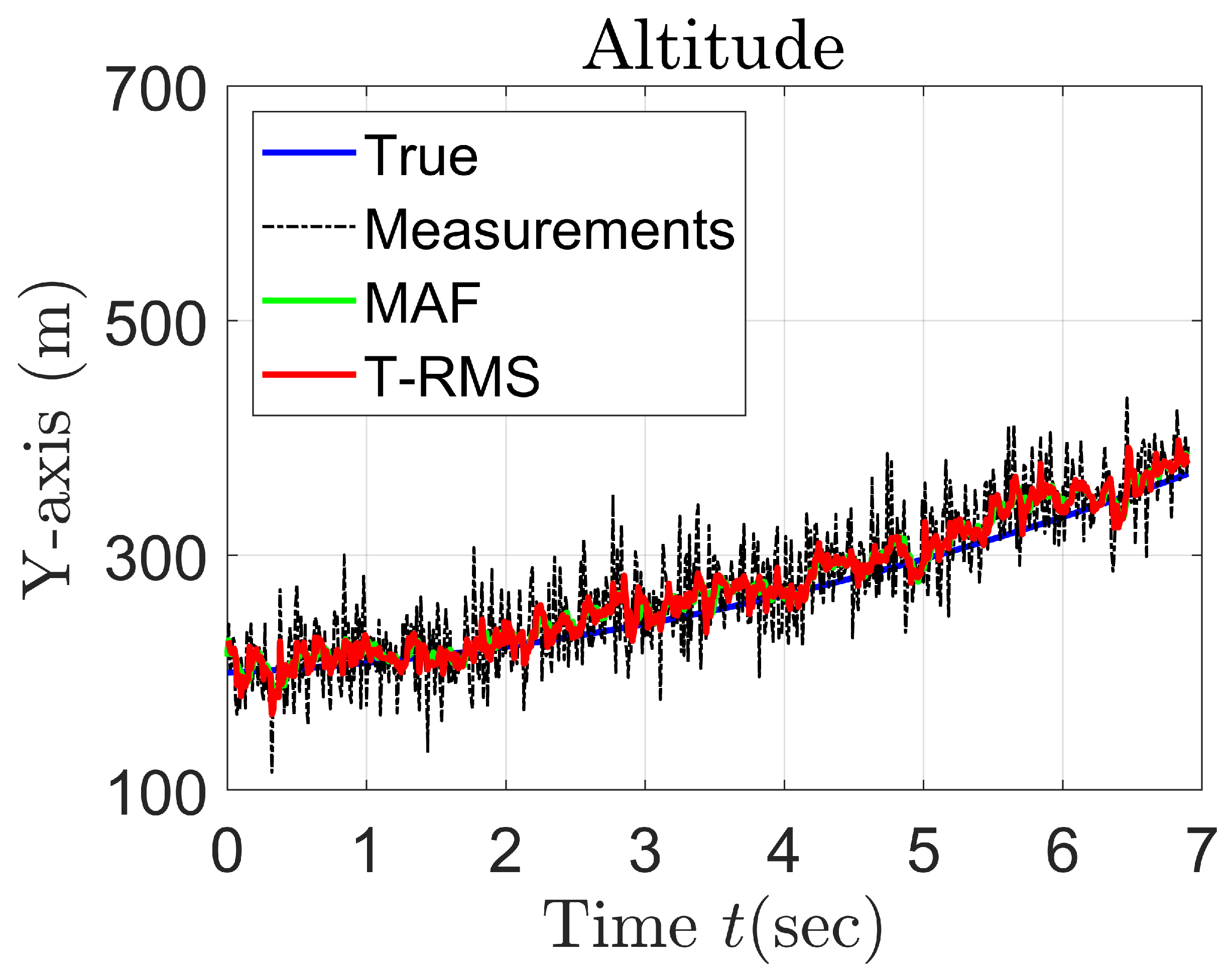
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ancel, E.; Capristan, F.M.; Foster, J.V.; Condotta, R. Real-time Risk Assessment Framework for Unmanned Aircraft System (UAS) Traffic Management (UTM). In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–17. [Google Scholar]
- Farina, A.; Timmoneri, L.; Vigilante, D. Classification and Launch-Impact Point Prediction of Ballistic Target via Multiple Model Maximum Likelihood Estimator (MM-MLE). In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006; pp. 802–806. [Google Scholar]
- Roonizi, A.K. An Efficient Algorithm for Maneuvering Target Tracking. IEEE Signal Process. Mag. 2020, 38, 122–130. [Google Scholar] [CrossRef]
- Yang, K.; Lu, Q.; Bar-Shalom, Y.; Willett, P.; Freund, Z.; Ben-Dov, R.; Milgrom, B. Estimation for a Thrusting/Ballistic Object with Mass Ejection from a Single Fixed Passive Sensor with Delayed Acquisition. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2786–2795. [Google Scholar] [CrossRef]
- Hough, M.E. Nonlinear Recursive Estimation of Boost Trajectories, Including Batch Initialization and Burnout Estimation. J. Guid. Control. Dyn. 2006, 29, 72–81. [Google Scholar] [CrossRef]
- Kim, J.K.; Kim, T.H.; Song, T.L. Launch Point Prediction Employing the Smoothing IPDA Algorithm in 3-D Cluttered Environments. Int. J. Control. Autom. Syst. 2015, 13, 808–815. [Google Scholar] [CrossRef]
- Nelson, E.; Pachter, M.; Musick, S. Projectile Launch Point Estimation from Radar Measurements. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 1275–1282. [Google Scholar]
- Chang, X.H.; Liu, X.M.; Hou, L.W.; Qi, J.H. Quantized Fuzzy Feedback Control for Electric Vehicle Lateral Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2331–2341. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, P.; Wang, Q.G.; Yu, L. Distributed non-fragile filtering for T-S fuzzy systems with event-based communications. Fuzzy Sets Syst. 2017, 306, 137–152. [Google Scholar] [CrossRef]
- Li, T.; Chen, H.; Sun, S.; Corchado, J.M. Joint Smoothing and Tracking Based on Continuous-Time Target Trajectory Function Fitting. IEEE Trans. Autom. Sci. Eng. 2019, 10, 1476–1483. [Google Scholar] [CrossRef]
- Tian, Z.; Yang, K.; Danino, M.; Bar-Shalom, Y.; Milgrom, B. Launch Point Estimation with a Single Passive Sensor without Trajectory State Estimation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 318–327. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.; Cho, S. F ast Parameterless Ballistic Launch Point Estimation based on k-NN Search. Def. Sci. J. 2014, 64, 41–47. [Google Scholar] [CrossRef][Green Version]
- Kim, J.; Lim, M.C.; Park, S.S.; Kim, I.; Choi, H.L. Ballistic Object Trajectory and Launch Point Estimation from Radar Measurements using Long-Short Term Memory Networks. In Proceedings of the 2019 7th International Conference on Robot Intelligence Technology and Applications (RiTA), Daejeon, Republic of Korea, 1–3 November 2019; pp. 26–31. [Google Scholar]
- Wiputgasemsuk, W. Projectile Launch Point Prediction via Multiple LSTM Networks. In Proceedings of the 19th International Conference on Computing and Information Technology (IC2IT 2023), Bangkok, Thailand, 18–19 May 2023; pp. 109–119. [Google Scholar]
- Brueh, R.G.; Need, T.E. Real-Time Launch Vehicles Steering Program Selection. In Proceedings of the AIAA Guidance and Control Conference, Stanford, CA, USA, 14–16 August 1972; pp. 1–7. [Google Scholar]
- Cho, S.; Shi, Y. Trajectory Shaping Based Pitch Programming. In Proceedings of the Korean Society for Aeronautical and Space Sciences Fall Conference, Jeju, Republic of Korea, 16–18 November 2022; pp. 358–359. [Google Scholar]
- Strang, G. Introduction to Linear Algebra; Wellesley–Cambridge Press: Wellesley, MA, USA, 2016. [Google Scholar]
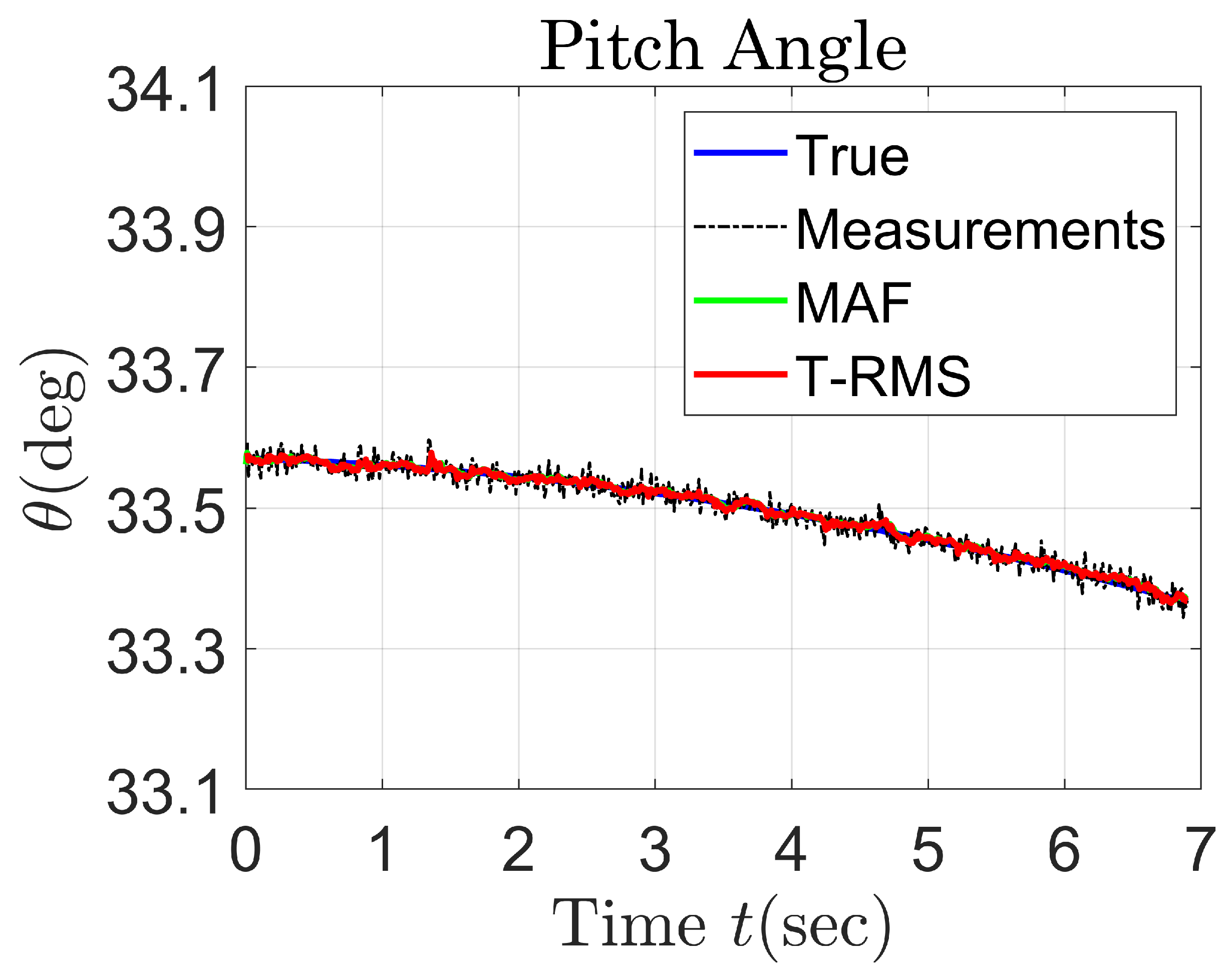
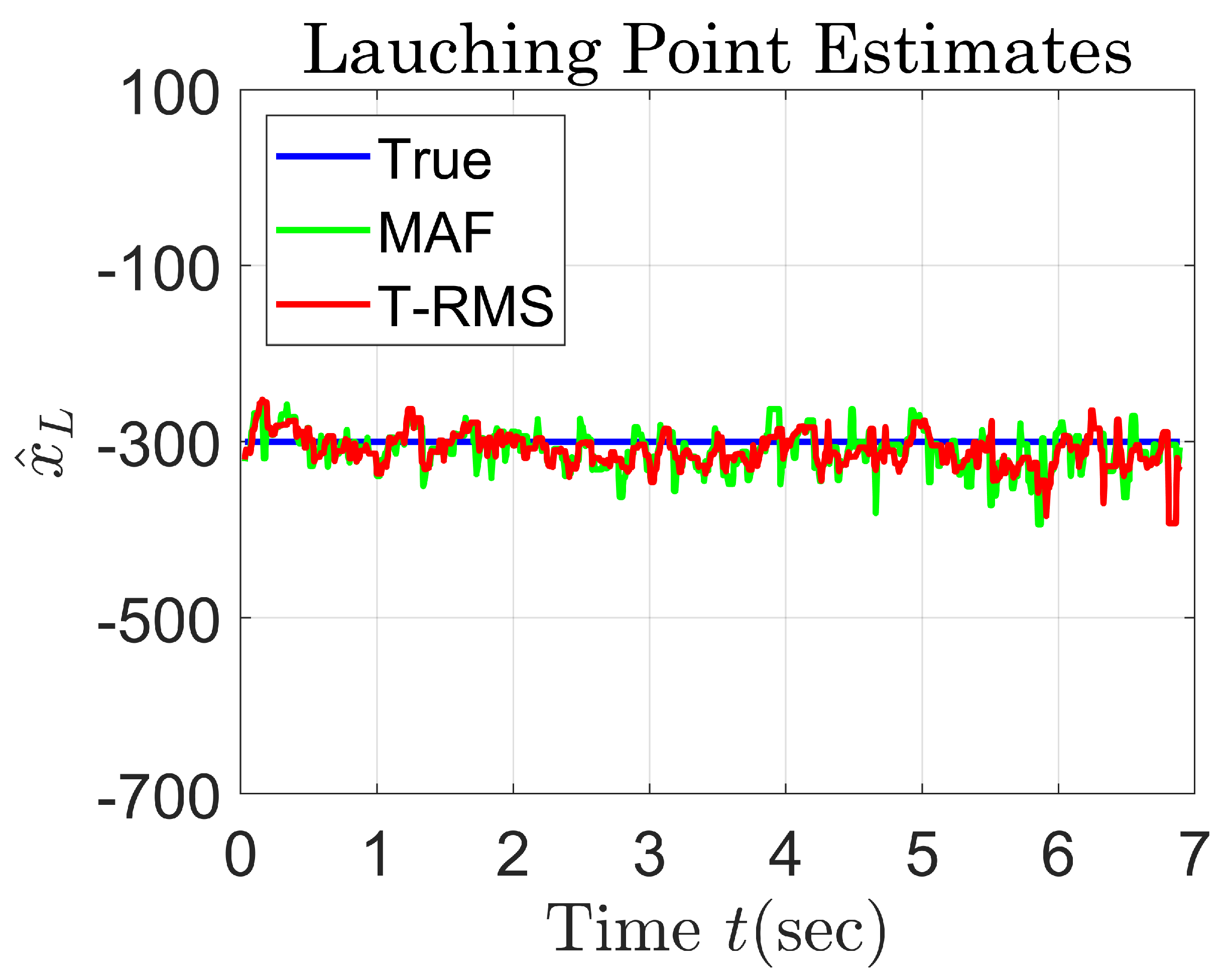

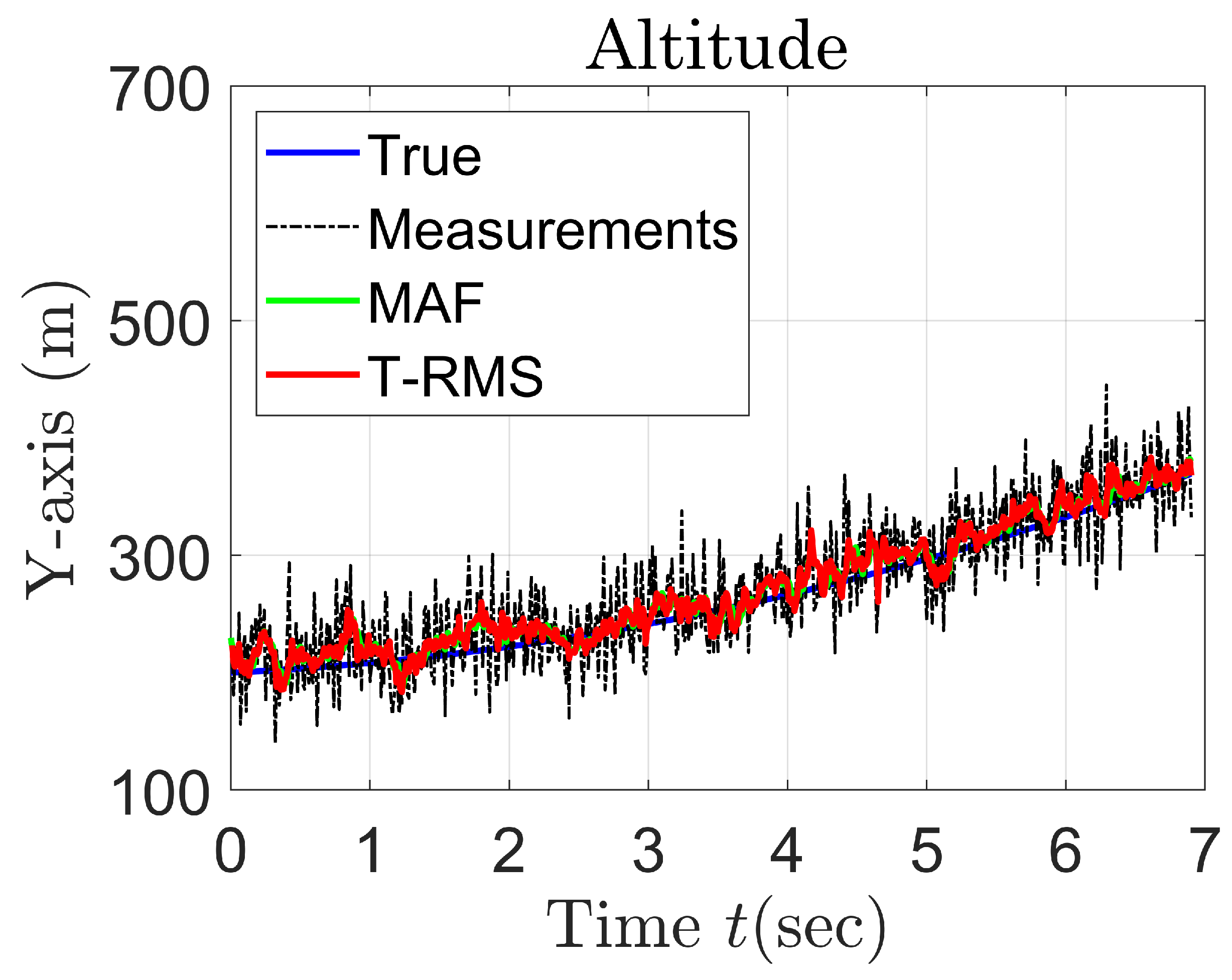
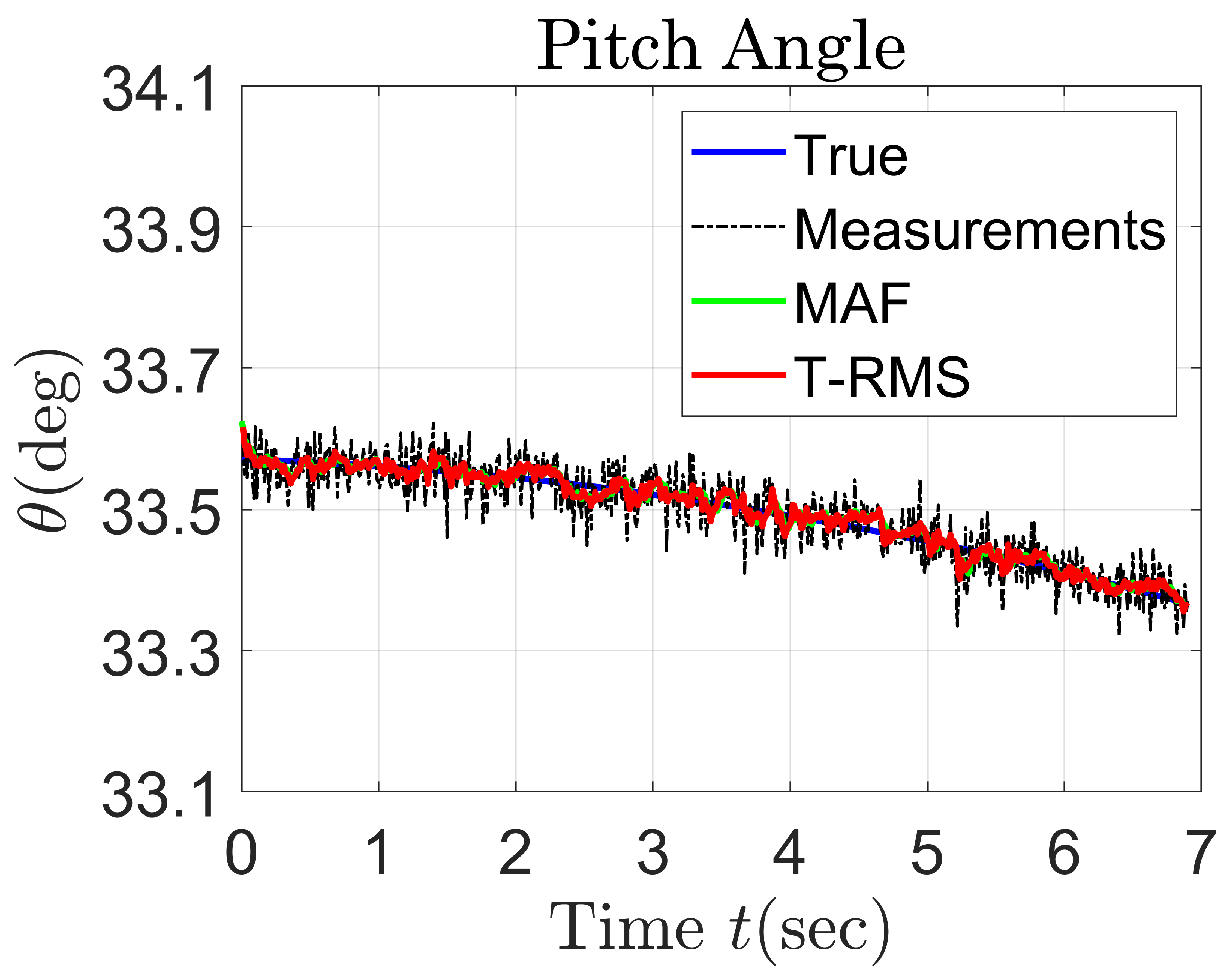
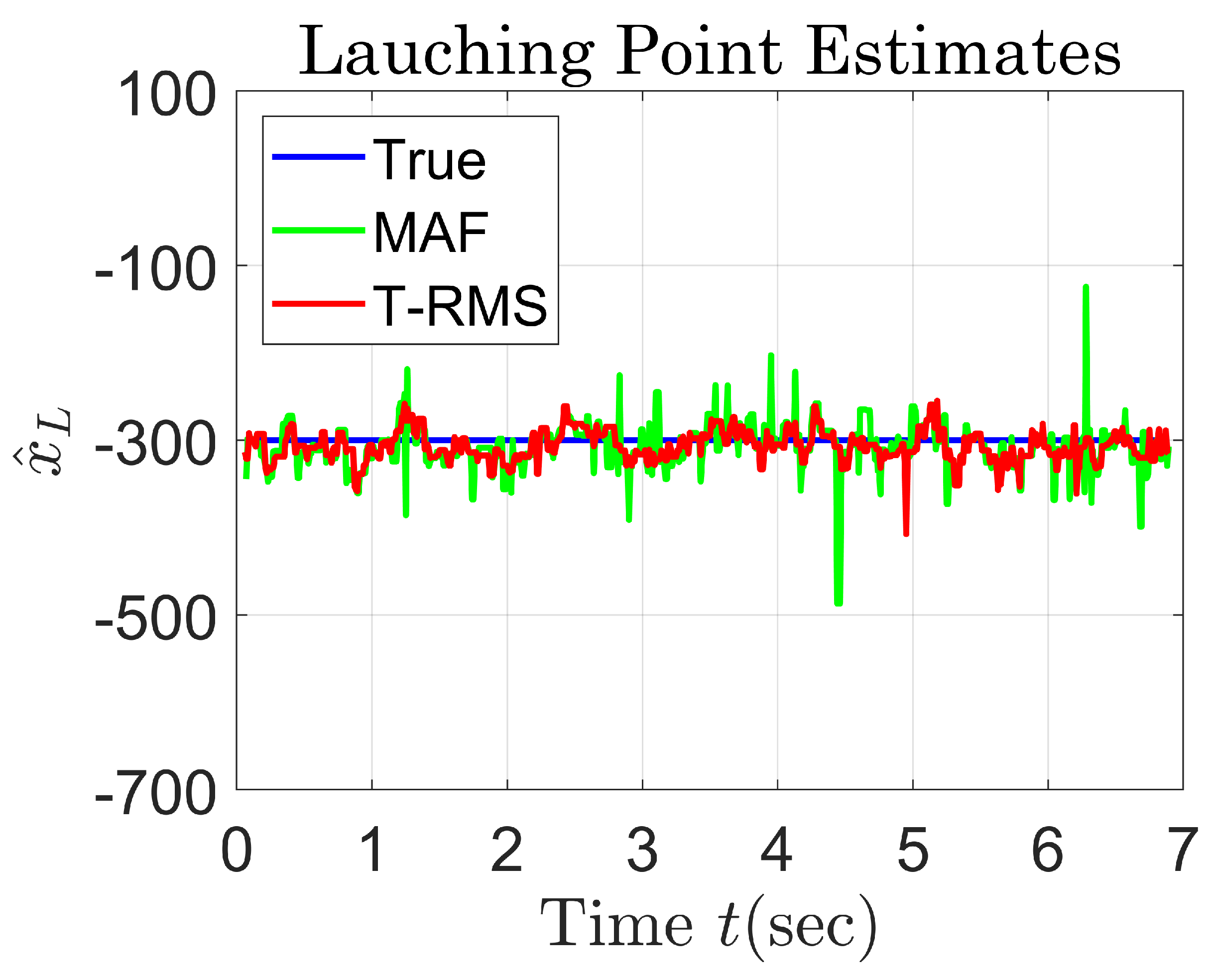
| Standard Deviation of Angle Noise | No Filter | MAF | T-RMS |
|---|---|---|---|
| 0.2 m rad | 59.4 m (19.8%) | 23.9 m (8.0%) | 21.9 m (7.3%) |
| 0.5 m rad | 62.0 m (20.7%) | 28.8 m (9.6%) | 18.7 m (6.2%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, S.; Song, T.L.; Choi, H.-J. Launching Point Estimation Using Inverse First-Order Pitch Programming. Mathematics 2024, 12, 2953. https://doi.org/10.3390/math12182953
Cho S, Song TL, Choi H-J. Launching Point Estimation Using Inverse First-Order Pitch Programming. Mathematics. 2024; 12(18):2953. https://doi.org/10.3390/math12182953
Chicago/Turabian StyleCho, Sungjin, Taek Lyul Song, and Hyeok-Jin Choi. 2024. "Launching Point Estimation Using Inverse First-Order Pitch Programming" Mathematics 12, no. 18: 2953. https://doi.org/10.3390/math12182953
APA StyleCho, S., Song, T. L., & Choi, H.-J. (2024). Launching Point Estimation Using Inverse First-Order Pitch Programming. Mathematics, 12(18), 2953. https://doi.org/10.3390/math12182953






