Reliability Analysis of (n, k)-Bubble-Sort Networks Based on Extra Conditional Fault

Abstract

Given a graph $G=\left(V\right(G),V(E\left)\right)$, a non-negative integer g and a set of faulty vertices $F\subseteq V\left(G\right)$, the g-extra connectivity of G, denoted by ${\kappa }_g\left(G\right)$, is the smallest cardinality of F, whose value of deletion, if exists, will disconnect G and give each remaining component at least $g+1$ vertices. The g-extra diagnosability of the graph G, denoted by $t_g\left(G\right)$, is the maximum cardinality of the set F of fault vertices that the graph can guarantee to identify under the condition that each fault-free component has more than g vertices. In this paper, we determine that g-extra connectivity of $(n,k)$-bubble-sort network $B_{n,k}$ is ${\kappa }_g\left(B_{n,k}\right)=n+g(k-2)-1$ for $4\le k\le n-1$ and $0\le g\le n-k$. Afterwards, we show that g-extra diagnosability of $B_{n,k}$ under the PMC model $(4\le k\le n-1$ and $0\le g\le n-k)$ and MM* model $(4\le k\le n-1$ and $0\le g\le min\{n-k-1,k-2\})$ is $t_g\left(B_{n,k}\right)=n+g(k-1)-1$, respectively.

1. Introduction

An interconnection network is typically modeled as an undirected graph $G=\left(V\right(G),E(G\left)\right)$, where the vertex and edge correspond to the processor and the link between two distinct processors, respectively. In the network, the failure of processors or links is inevitable. How to find the fault processors or links becomes the crucial problem to maintain the stability of such system. On 9 February 2001, the submarine cable between China and the United States was broken by the anchor hook of a fishing boat, which made a large number of domain names inaccessible. On 27 May 2015, an optical fiber was dug in Hangzhou, resulting in a large area of Alipay paralysis. In order to enable the system to operate normally when local faults occur, the concept of fault tolerance is proposed. Fault tolerance is the ability of the network to tolerate and recover from simultaneous failures of components and connections under normal operating conditions. Friedrich et al. [1] studied a strong network and fault tolerance setting. Fault diagnosis is the process of identifying faulty processors in a system. Many diagnostic models have been studied, such as PMC, BGM and MM (see references [2,3,4,5,6]). Among these models, the PMC model and the MM model are well known. In 1967, Preparata et al. [6] first introduced the PMC model. In this model, any two adjacent processors can be tested each other. The MM model, where the diagnosis is performed by sending the same task from one processor to its two adjacent processors and comparing the feedback results, was introduced by Maeng and Malek [4]. Sengupta and Dahbura [7] introduced a modification of the MM model, called the MM* model, in which each processor must test any pair of its neighboring processors. In recent years, some new fault-tolerant measures have been introduced. Zhang et al. [8], in 2016, proposed the g-extra diagnosability of a system, which requires that every component of $G-F$ has more than g processors. Moreover, they demonstrated the g-extra diagnosability of hypercubes under the PMC model and MM* model. There are many research works about the g-extra diagnosability (see [8,9,10,11]).

Let $F\subseteq V\left(G\right)$. If $G-F$ is disconnected or contains just one vertex, we call F a vertex cut. The connectivity of a graph G is defined as $\kappa \left(G\right)=\min \{|F||F\subseteq V\left(G\right)$ and F is a vertex cut}. The definition of connectivity implicitly assumes that the likelihood of any subset of the interconnection network experiencing simultaneous failures is the same. However, when a processor error occurs, not all processors adjacent to the processor will simultaneously lose their running ability in practical applications. In order to overcome this deficiency, Harary [12] introduced the concept of conditional connectivity by adding some restrictions on connected components. Additionally, the concept of g-extra connectivity was proposed by Fàbrega and Fiol [13], which restrains that each remaining component has at least $g+1$ vertices after removing the faulty vertex set. For recent results on the g-extra connectivity of the interconnection network, see [14,15,16,17,18].

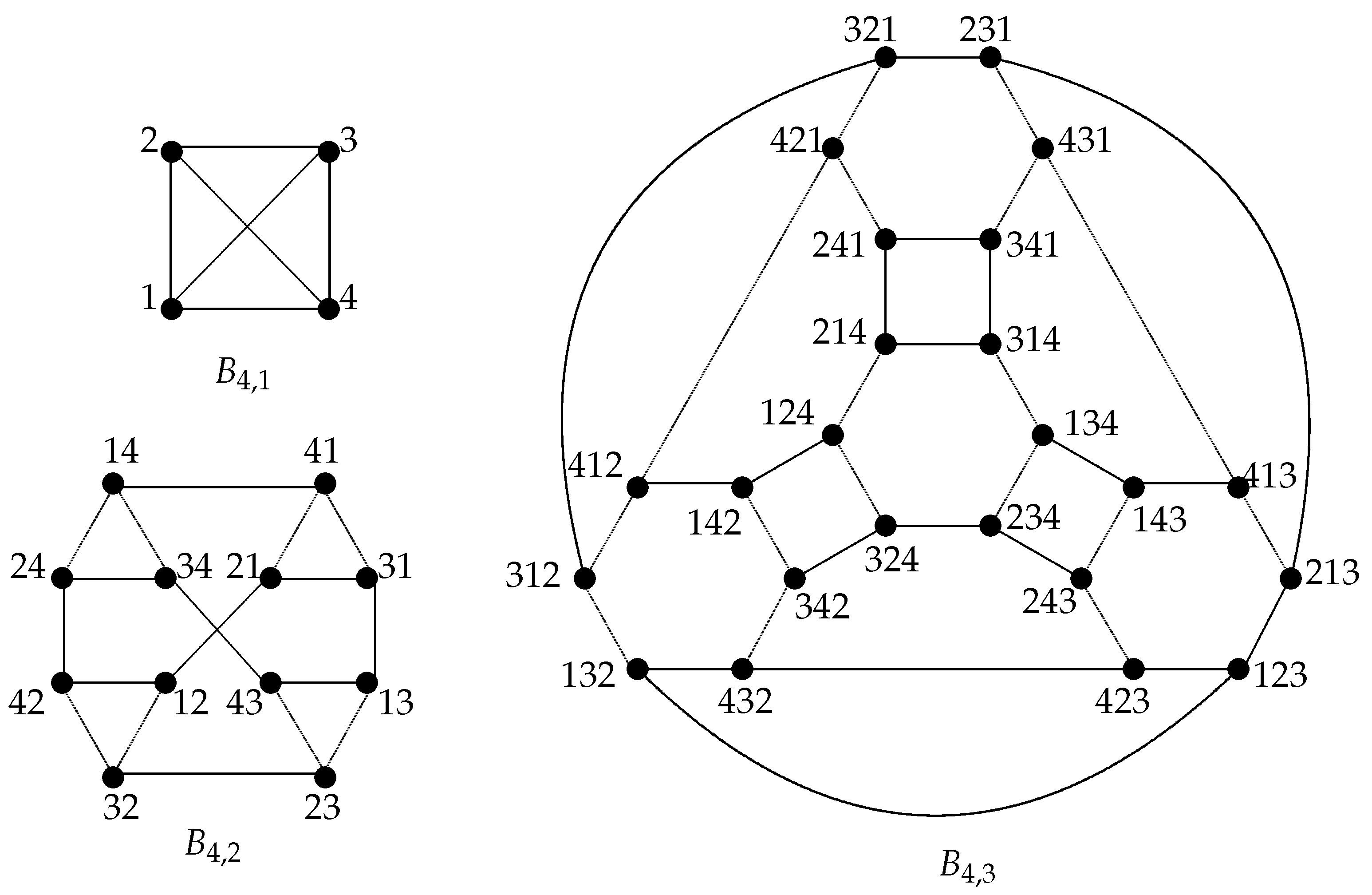
As a generalization of an n-dimensional bubble-sort graph $B_n$, the $(n,k)$-bubble-sort graph, namely $B_{n,k}$, was proposed by Shavash [19]. Considering the above ideas, we mainly study the g-extra connectivity of $(n,k)$-bubble-sort network $B_{n,k}$ that is ${\kappa }_g\left(B_{n,k}\right)=n+g(k-2)-1$ for $4\le k\le n-1$ and $0\le g\le n-k$. Afterwards, we show that g-extra diagnosability of $B_{n,k}$ under the PMC model $(4\le k\le n-1$ and $0\le g\le n-k)$ and the MM* model $(4\le k\le n-1$ and $0\le g\le min\{n-k-1,k-2\})$ is $t_g\left(B_{n,k}\right)=n+g(k-1)-1$, respectively.

2. Preliminaries

Let $G=\left(V\right(G),E(G\left)\right)$ be a simple connected graph, where $V\left(G\right)$ is the vertex set and $E\left(G\right)$ is the edge set. We denote the numbers of vertices and edges in G by $|V(G)|$ and $|E(G)|$. For any vertex $v\in V\left(G\right)$, $N_G\left(v\right)=\{u|(u,v)\in E\left(G\right)\}$ is the neighbor vertex set of v. We use $N_G\left[v\right]$ to denote the vertex set $N_G\left(v\right)\cup \left\{v\right\}$. For a subset S of $V\left(G\right)$, the graph induced by S, denoted by $G\left[S\right]$, has the vertex set $S\cap V\left(G\right)$ and the edge set $\left\{\right(u,v)|(u,v)\in E\left(G\right),u,v\in S\}$. We define $N_G\left(S\right)=\left({\bigcup }_{u\in S}N\left(u\right)\right)\setminus S$. We let $d_G\left(v\right)=|N_G\left(v\right)|$ be the degree of v and $\delta \left(G\right)=\min \{d_G\left(v\right)|v\in V\left(G\right)\}$ be the minimum degree of G. For any $v\in V\left(G\right)$, if $d_G\left(v\right)=k$, then G is k-regular. Let $F\subseteq V\left(G\right)$. We use $G-F$$(G\setminus F)$ to denote the subgraph of G with vertex set $V\left(G\right)-F$ and edge set $E\left(G\right)-\left\{\right(u,v)\in E(G)|\{u,v\}\cap F\ne \varnothing \}$. Let F be a vertex cut. The maximal connected subgraphs of $G-F$ are called components. Let $F_1$ and $F_2$ be two distinct subsets of $V\left(G\right)$, and let the symmetric difference $F_1▵F_2=(F_1\setminus F_2)\cup (F_2\setminus F_1)$. Let $a_1$, $a_2$ be two integers with $0\le a_1\le a_2$. Set $[a_1,a_2]=\{a|a$ is an integer with $a_1\le a\le a_2\}$. We follow [20] for terminologies and notations not defined here.

Definition 1

([19]). Let $n\ge 3$ be an integer and $k\in [1,n-1]$. The $(n,k)$-bubble-sort network $B_{n,k}$ (see Figure 1) has vertex set $V\left(B_{n,k}\right)$ and a vertex $p=p_1{p}_2\cdots p_k\in V\left(B_{n,k}\right)$ if and only if $p_i\in [1,n]$, and $p_i\ne p_j$ for $i\ne j$ with $i,j\in [1,k]$. Let $p^{\prime }=p_1^{\prime }{p}_2^{\prime }\cdots p_k^{\prime }\in V\left(B_{n,k}\right)$ with $p\ne p^{\prime }$. Then, $(p,p^{\prime })\in E\left(B_{n,k}\right)$ if and only if one of the following conditions hold:

(1) 

$p_m^{\prime }=p_{m+1}$, $p_{m+1}^{\prime }=p_m$ for some integer m with $m\in [1,k-1]$ and $p_i^{\prime }=p_i$ for every $i\in [1,m-1]\cup [m+2,k]$;

(2) 

$p_1^{\prime }\ne p_1$ and $p_i^{\prime }=p_i$ for every $i\in [2,k]$.

Obviously, $|V\left(B_{n,k}\right)|\hspace{0.17em}={\displaystyle \frac{n!}{(n-k)!}}$ and $B_{n,k}$ is a $(n-1)$-regular graph. We can find $B_{n,1}\cong K_n$ and $B_{n,n-1}\cong B_n$. Let $H_i$ be the induced subgraph of $B_{n,k}$ with $V\left(H_i\right)=\{p=p_1{p}_2\cdots p_k\in V\left(B_{n,k}\right)|p_k=i$ for every $i\in [1,n]$. Hence, $B_{n,k}$ can be decomposed into n subgraphs $H_i$ and $H_i\cong B_{n-1,k-1}$. In this paper, a set of vertices to be deleted is denoted as the faulty set F. Define $F\cap V\left(H_i\right)=F_i$ and $|F_i|\hspace{0.17em}=\hspace{0.17em}{f}_i$ for $1\le i\le n$. For an edge $(p,p^{\prime })\in E\left(B_{n,k}\right)$, if $(p,p^{\prime })$ satisfies $\left(1\right)$ of Definition 1, then $(p,p^{\prime })$ is called i-edge; otherwise, $(p,p^{\prime })$ is 1-edge.

Proposition 1

([21,22]). The $(n,k)$-bubble-sort network $B_{n,k}$ has the following properties:

(1) 

The set of all cross edges between any two subgraphs $H_i$ and $H_j$$(i\ne j\in [1,n\left]\right)$ is denoted by $E(i,j)$ with order $|E(i,j)|={\displaystyle \frac{(n-2)!}{(n-k)!}}$;

(2) 

Let $n\ge 4$, $2\le k\le n-2$ and $u,v\in V\left(B_{n,k}\right)$ with $u\ne v$. Then,

$$|N_{B_{n,k}}\left(u\right)\cap N_{B_{n,k}}\left(v\right)|\left\{\begin{array}{ccc}=n-k-1& & \mathit{if}(u,v)\in E\left(B_{n,k}\right)is1\text{-}edge;\\ \le 2& & \mathit{if}d(u,v)=2;\\ =0& & \mathit{otherwise}.\end{array}\right.$$

(3) 

$\kappa \left(B_{n,k}\right)=n-1$, where $2\le k\le n-1$;

(4) 

For any $u\in V\left(H_i\right)$ ($i\in [1,n]$), it has exactly one neighbor outside $H_i$, which is called the outside neighbor of u.

Definition 2

([13]). Given a graph G, a vertex set $F\subseteq V\left(G\right)$ is called a g-extra cut if every component of $G-F$ has at least $g+1$ vertices. A g-extra cut of G is a g-extra set F such that $G-F$ is disconnected. G is said to be g-extra connected if G has a g-extra cut. The minimum cardinality of g-extra cuts, denoted by ${\kappa }_g\left(G\right)$, is the g-extra connectivity of G.

Lemma 1

([6]). For any two distinct subsets $F_1$ and $F_2$ in a system $G=\left(V\right(G),E(G\left)\right)$, the sets $F_1$ and $F_2$ are distinguishable under the PMC model if and only if there exist a vertex $u\in V\left(G\right)-(F_1\cup F_2)$ and a vertex $v\in F_1▵F_2$ such that $(u,v)\in E\left(G\right)$ (Figure 2).

Lemma 2

([7]). For any two distinct subsets $F_1$ and $F_2$ in a system $G=\left(V\right(G),E(G\left)\right)$, the sets $F_1$ and $F_2$ are distinguishable under the MM* model if and only if one of the following conditions is satisfied (Figure 3).

(1) 

There are two vertices $u,w\in V\left(G\right)-(F_1\cup F_2)$ and there is a vertex $v\in F_1▵F_2$ such that $(u,w)\in E\left(G\right)$ and $(v,w)\in E\left(G\right)$;

(2) 

There are two vertices $u,v\in F_1-F_2$ and there is a vertex $w\in V\left(G\right)-(F_1\cup F_2)$ such that $(u,w)\in E\left(G\right)$ and $(v,w)\in E\left(G\right)$;

(3) 

There are two vertices $u,v\in F_2-F_1$ and there is a vertex $w\in V\left(G\right)-(F_1\cup F_2)$ such that $(u,w)\in E\left(G\right)$ and $(v,w)\in E\left(G\right)$;

3. The $\mathit{g}$-Extra Connectivity of $\mathbf{(}\mathit{n},\mathit{k}\mathbf{)}$-Bubble-Sort Network ${\mathit{B}}_{\mathit{n},\mathit{k}}$

In this section, we attempt to determine the size of g-extra connectivity of an $(n,k)$-bubble-sort network $B_{n,k}$.

Lemma 3.

${\kappa }_g\left(B_{n,k}\right)\le n+g(k-2)-1$ for $4\le k\le n-1$ and $0\le g\le n-k$.

Proof. 

We need to find a subset $X\subseteq V\left(B_{n,k}\right)$ such that $B_{n,k}\left[X\right]\cong K_{g+1}$. Obviously, X is located in the same subgraph. Without a loss of generality, let $X\subseteq V\left(H_i\right)$. Then, we get

$$\begin{array}{cc}\hfill |N_{B_{n,k}}\left(X\right)|& =\hspace{0.17em}|N_{B_{n,k}^i}\left(X\right)|+|N_{B_{n,k}}\left(X\right)\cap V(B_{n,k}-B_{n,k}^i)|\hfill \\ \hfill & =[n-k+1-|X|+(k-2)|X|]+|X|\hfill \\ \hfill & =n+g(k-2)-1.\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill |V\left(B_{n,k}\right)|-|N_{B_{n,k}}\left[X\right]|& ={\displaystyle \frac{n!}{(n-k)!}}-[(g+1)+n+g(k-2)-1]\hfill \\ \hfill & ={\displaystyle \frac{n!}{(n-k)!}}-[n+g(k-1)]\hfill \\ \hfill & >n(n-1)-[n+g(n-2\left)\right]\hfill \\ \hfill & =(n-g)(n-2)\hfill \\ \hfill & \ge k(n-2)\hfill \\ \hfill & >g,\hfill \end{array}$$

$B_{n,k}-N_{B_{n,k}}\left(X\right)$ is disconnected and $N_{B_{n,k}}\left(X\right)$ is a vertex-cut. Via Proposition 1 (4), every vertex in $H_i$ has exactly one outside neighbor. Since $B_{n,k}\left[X\right]\cong K_{g+1}$, we can find that the external neighborhoods of induced subgraph by X are within the same subgraph, denoted by $H_j$. Via Proposition 1 (3), $\kappa \left(B_{n-1,k-1}\right)=n-2>g+1$, $H_j-N_{B_{n,k}}\left(X\right)$ is connected for any $j\in [1,n]\setminus \left\{i\right\}$. Let the rest subgraphs in $B_{n,k}$, excluding subgraphs $H_i$ and $H_j$, be $B_{n,k}^P$; then, $V\left(B_{n,k}^P\right)\cap N_{B_{n,k}}\left(X\right)=\varnothing$ and $B_{n,k}^P-N_{B_{n,k}}\left(X\right)$ are connected. Via Proposition 1 (1), for any $p\in P$, $|E(j,p)|={\displaystyle \frac{(n-2)!}{(n-k)!}}>g+1$, there is an edge connecting $H_j-N_{B_{n,k}}\left(X\right)$ and $B_{n,k}^P-N_{B_{n,k}}\left(X\right)$. Thus, $B_{n,k}-H_i-N_{B_{n,k}}\left(X\right)$ is connected. For any vertex $x\in V(H_i-N_{B_{n,k}}\left[X\right])$, x has an outgoing neighbor, say $x^{\prime }$, and $x^{\prime }\notin N_{B_{n,k}}\left(X\right)\cap V(B_{n,k}-H_i)$. Thus, x is connected to $B_{n,k}-H_i-N_{B_{n,k}}\left(X\right)$. By the arbitrariness of x, $(B_{n,k}-H_i-N_{B_{n,k}}\left(X\right))\cup (H_i-N_{B_{n,k}}\left[X\right])=B_{n,k}-N_{B_{n,k}}\left[X\right]$ is connected. Therefore, $B_{n,k}-N_{B_{n,k}}\left(X\right)$ has two components, namely X and $B_{n,k}-N_{B_{n,k}}\left[X\right]$. Hence, $N_{B_{n,k}}\left(X\right)$ is a g-extra cut of $B_{n,k}$. So, $\kappa \left(B_{n,k}\right)\le n+g(k-2)-1$. □

Lemma 4.

For $3\le k\le n-1$. Let F be the set of vertices of $B_{n,k}$. If $|F|\le n+k-4$, then $B_{n,k}-F$ is either connected or has two components, one of which is a singleton.

Proof. 

This lemma is proved via induction on k. Let us consider the base case $k=3$ for removing $n-1$ vertices from $B_{n,3}$.

• Case 1. $f_i\le n-3$ for all i.

$H_i-F_i$ is connected for all i because $H_i$ is $(n-2)$-connected. Since only $n-1$ vertices are removed and s has n choices, there exists s such that $f_s=0$. Thus, $f_i+f_s\le n-3$ for any $i\ne s$. We can see that at most, $n-3$ vertices are deleted in $V\left(H_i\right)\cup V\left(H_s\right)$. There are ${\displaystyle \frac{(n-2)!}{(n-3)!}}=n-2$ edges between $H_i$ and $H_s$, and since $n-2>n-3$, one of these edges is retained in $B_{n,3}-F$. By the arbitrariness of i, there is an edge between $H_i-F_i$ and $H_s-F_s$ for all $1\le i\le n$, so $B_{n,3}$ is connected.

• Case 2. $f_i\ge n-2$ for some i.

Since ${\sum }_{i=1}^n{f}_i\le n-1$ and $f_i\ge n-2$, one faulty vertex is outside of $H_i$, at most. Hence, $B_{n,k}-F$ has a component Y that includes every $H_j-F_j$ for $j\ne i$. According to Proposition 1 (4), each vertex in $H_i-F_i$ has an outside neighbor, so it also belongs to Y unless that outside neighbor is in $F-F_i$. There is at most one vertex in $F-F_i$, so all but one of the vertices of $B_{n,k}-F$ belong to Y. Thus, the base case has been proved.

Now suppose that for all pairs ($n,k$), $k<k^{\prime }$ and $3\le k\le n-1$ for $k^{\prime }\ge 4$, the statement holds, and consider removing up to $n+k^{\prime }-4$ vertices from $B_{n,k^{\prime }}$, where $n>k^{\prime }$. We will consider two cases.

• Case 1. $f_i\le n-3$ for all i.

Since $H_i$ is $(n-2)$-connected, $H_i-F_i$ is connected for all i. For any $1\le i\ne j\le n$, there are ${\displaystyle \frac{(n-2)!}{(n-k^{\prime })!}}\ge (n-2)(n-3)\ge 2(n-2)>n+k^{\prime }-4$ independent edges between $H_i$ and $H_j$, but only a total of $n+k^{\prime }-4$ vertices are removed, leaving one edge between $H_i-F_i$ and $H_j-F_j$; thus, $B_{n,k}-F$ is connected.

• Case 2. $f_i\ge n-2$ for some i.

Assume there exists $j\ne i$ such that $f_j\ge n-2$. Then, $n+k^{\prime }-4=|F|\ge f_i+f_j\ge 2n-4>n+k^{\prime }-4$ is a contradiction. Then, we get $f_j\le n-3$ for any $j\ne i$, which implies that $H_j-F_j$ is connected. All the $H_j-F_j$, $j\ne i$, belong to a large component, say Y, in $B_{n,k}-F$ due to the same argument as Case 1. If $f_i\le (n-1)+(k^{\prime }-1)-4=n+k^{\prime }-6$, according to the inductive hypothesis, $H_i-F_i$ is either connected, which is similar to Case 1, or there are two components, one of which is a singleton. Since, at most, $n+k^{\prime }-6$ vertices were deleted from $H_i$, and only one vertex remained in the small component, there is at least

$${\displaystyle \frac{(n-1)!}{(n-k^{\prime })!}}-(n+k^{\prime }-6)-1\ge (n-1)(n-2)(n-3)-n-k^{\prime }+5\ge (n-1)\times 3\times 2-n-k^{\prime }+5>2n$$

vertices in the large component; in other words, at least $2n$ independent edges are present. Since $|F|-|F_i|<n+k^{\prime }-4<2n$, the large component of $H_i-F_i$ is part of Y, and, at most, one vertex does not belong to Y. If $f_i=n+k^{\prime }-5$ or $f_i=n+k^{\prime }-4$, due to the fact that only one or zero vertex outside of $H_i$ can be removed, the proof is similar to Case 2 of the base case. Thus, the proof is complete. □

Lemma 5

([23]). Let $n\ge 4$. If F is a set of vertices of $B_{n,n-1}$ with $|F|\le 3n-8$, then $B_{n,n-1}-F$ is connected or has a large component and small components with, at most, two vertices in total.

Lemma 6.

For any subset $F\subseteq V\left(B_{n,k}\right)$ with $|F|\le n+2k-6$ where $3\le k\le n-1$. Then, $B_{n,k}-F$ is connected or has a large component and small components having, at most, two vertices in total.

Proof. 

When $k=n-1$, we can obtain a bubble-sort graph $B_n$. Lemma 5 holds due to the removal of up to $n+2k-6=3n-8$ vertices from $B_{n,n-1}$. Now let us consider $k<n-1$. We proceed via induction on k. Firstly, we consider the base case $k=3$ of deleting n vertices from $B_{n,3}$. Let us consider the following two cases:

• Case 1. $f_i\le n-3$ for all i.

In this case, all of the $H_i-F_i$ are connected because $B_{n-1,2}$ is $(n-2)$-connected. For all i, if $f_i=1$, then all the $H_i-F_i$ are part of one large component. Otherwise, since ${\sum }_{i=1}^n{f}_i\le n$, there exists some s such that $f_s=0$. Then, we obtain $f_i+f_s\le n-3$ for any $i\ne s$. There are ${\displaystyle \frac{(n-2)!}{(n-3)!}}=n-2$ edges between $H_i$ and $H_j$$(j\ne i)$ by Proposition 1 (1), so an edge remains between $H_i-F_i$ and $H_s-F_s$. Hence, $B_{n,3}-F$ is connected.

• Case 2. $f_i\ge n-2$ for some i.

Since ${\sum }_{i=1}^n{f}_i\le n$ and $f_i\ge n-2$, two faulty vertices, at most, are outside of $H_i$. Hence, $B_{n,k}-F$ has a component Y that includes all $H_j-F_j$$(j\ne i)$ except possibly the components of $H_i-F_i$. According to Proposition 1 (4), each vertex in $H_i$ has an external neighbor. Conversely, assuming that at least three vertices in $H_i-F_i$ do not belong to Y, then each of these outer neighbors must be in F. This means that $|F|-|F_i|\ge 3$, which is a contradiction. Thus, two vertices, at most, do not belong to Y, and the base case is proved.

Now suppose that for all pairs ($n,k$), $k<k^{\prime }$ and $3\le k\le n-1$ for $k^{\prime }\ge 4$, the statement holds, and consider removing up to $n+2k^{\prime }-6$ vertices from $B_{n,k^{\prime }}$, where $k^{\prime }\le n-2$. We will consider three cases.

• Case 1. $f_i\le n-3$ for all i.

Thus, every $H_i-F_i$ is connected. There are ${\displaystyle \frac{(n-2)!}{(n-k^{\prime })!}}\ge (n-2)(n-3)$ independent edges between $H_i-F_i$ and $H_j-F_j$$(i\ne j)$. Since $4\le k^{\prime }\le n-2$ implies that $n\ge 6$, we can obtain $(n-2)(n-3)\ge 3(n-2)>n+2k^{\prime }-6$. Then, for any pair $(i,j)$, there is an edge between $H_i-F_i$ and $H_j-F_j$. Hence, $B_{n,k}-F$ is connected.

• Case 2. $f_i\ge n-2$ for exactly one i where $1\le i\le n$.

It means that for $j\ne i$, $H_j-F_j$ is connected and every $H_j-F_j$ belongs to a large component Y in $B_{n,k}-F$. If $f_i\ge n+2k^{\prime }-8$, then $|F|-|F_i|\le 2$; so, at most, two vertices are not in Y regarding Case 2 of the base case. If $f_i\le n+2k^{\prime }-9=(n-1)+2(k^{\prime }-1)-6$, then we can apply the inductive hypothesis to get that $H_i-F_i$ is connected or has a big component and small components with at most two vertices in total. If it is connected, we follow the method of Case 1; then, $B_{n,k}-F$ is connected. Otherwise, we find that the large component will be part of a Y. Since the number of edges outside $H_i$, ${\displaystyle \frac{(n-1)!}{(n-k^{\prime })!}}=(n-1)(n-2)\cdots (n-k^{\prime }+2)(n-k^{\prime }+1)$. Since $k^{\prime }\ge 4$, ${\displaystyle \frac{(n-1)!}{(n-k^{\prime })!}}\ge (n-1)(n-2)(n-3)$ is greater than the number of vertices removed plus the number of vertices in small components, which is at most $n+2k^{\prime }-6+2<3n<(n-1)\times 3\times 2<(n-1)(n-2)(n-3)$. Therefore, at most, two vertices do not belong to Y, and the proof is complete.

• Case 3. $f_i\ge n-2$ for more than one i.

Assume there exist three integers $i,j,s$ such that $f_i,f_j,f_s\ge n-2$. Then

$$n+2k^{\prime }-6\ge |T|\ge f_i+f_j+f_s\ge 3(n-2)>n+2k^{\prime }-6,$$

which is a contradiction. Therefore, there are exactly two positive integers $i,j$, such that $f_i,f_j\ge n-2$ and $H_s-F_s$ are connected for $s\ne i,j$. All of the $H_s-F_s$ belong to a large component Y in $B_{n,k}-F$ for $s\ne i,j$. If $f_i\ge (n-1)+(k^{\prime }-1)-3$ or $f_j\ge (n-1)+(k^{\prime }-1)-3$, then

$$f_i+f_j\ge (n-1)+(k^{\prime }-1)-3+(n-2)=2n+k^{\prime }-7>n+2k^{\prime }-6.$$

At most, $n+2k^{\prime }-6$ vertices are removed, which is a contradiction. Thus, $f_i,f_j\le (n-1)+(k^{\prime }-1)-4$. Hence, according to Lemma 4 for $H_i-F_i$ and $H_j-F_j$, each has at most one vertex that is not connected to Y. According to the same argument as in Case 2, the large components of both $H_i-F_i$ and $H_j-F_j$ are part of Y; so, at most, two vertices do not belong to Y, and our statement is proven. □

Lemma 7.

Let $3\le k\le n-1$ and $0\le g\le n-k$. If $F\subseteq V\left(B_{n,k}\right)$ with $|F|\le n+g(k-2)-2$, then $B_{n,k}-F$ is connected or contains a large component and small components with g vertices at most.

Proof. 

First, we solve the base case $k=3$ of removing up to $n+g-2$ vertices. We have two cases:

• Case 1. $f_i\le n-3$ for all $1\le i\le n$.

Every $H_i-F_i$ is connected in this case. There are $n-2$ edges between $H_j$ and $H_s$ for $j\ne s$. Thus, if $f_j+f_s\le n-3$ for all $j\ne i$, then there will be an edge between $H_j-F_j$ and $H_s-F_s$. If $f_i=n-3$ for some i, then we cannot get $f_j\ge 1$ for all $j\ne i$ because ${\sum }_{j=1}^n{f}_j\ge (n-1)+f_i=2n-4>n+g-2$. Therefore, there exists $s\ne i$ such that $f_s=0$. For every $j\ne s$, we have $f_j+f_s\le n-3$. If $f_i\le n-4$ for all $1\le i\le n$, then there exists s such that $f_s\le 1$; otherwise, $|F|\ge 2n>n+g-1$ is a contradiction. We consider this $f_s$ and then $f_j+f_s\le n-3$ for all $j\ne s$. In summary, regardless of the type, we can get $f_j+f_s\le n-3$ for all $j\ne i$; thus, there is an edge between $H_j-F_j$ and $H_s-F_s$ for every $j\ne s$, which shows that $B_{n,3}-F$ is connected.

• Case 2. $f_i\ge n-2$ for some i.

Since ${\sum }_{i=1}^n{f}_i\le n+g-2$ and $f_i\ge n-2$ for some i, then we will get ${\sum }_{i\ne j}{f}_i\le g\le n-3$. Thus, all the $H_j-F_j$$(j\ne i)$ belong to a large component of $B_{n,k}-F$, say Y. Since each vertex in $H_i$ has an outside neighbor and at most g vertices are removed outside $H_i$, at most g vertices do not belong to Y. This case is proven.

Now we suppose $k\ge 4$. We use induction on g. When $g=0$ and $|F|\le n-2$, then $B_{n,k}-F$ is connected by Proposition 1 (3). When $g=1,2$, the cases are true via Lemmas 4 and 6, respectively. Suppose that the statement holds for all $g<g^{\prime }$ for some $3\le g^{\prime }\le n-k$. Let us prove the case of $g=g^{\prime }$ via induction on k. The base case $k=3$ is completed above, so suppose that the declaration is true for all $k<k^{\prime }$ for some $k^{\prime }\ge 4$ and consider that when reached, $n+g^{\prime }(k^{\prime }-2)-2$ vertices are removed from $B_{n,k^{\prime }}$. There are two cases:

• Case 1. $f_i\ge (n-1)+g^{\prime }(k^{\prime }-3)-1$ for some $1\le i\le n$.

In this case, $|F|-|F_i|\le g^{\prime }\le n-k^{\prime }<n-3$. Thus, there is a large component Y in $B_{n,k^{\prime }}-F$ containing all the $H_j-F_j$ for $j\ne i$. Since every vertex in $H_i$ has an outside neighbor and ${\sum }_{j\ne i}{f}_i\le g^{\prime }$, at most $g^{\prime }$ vertices do not belong to Y, as desired.

• Case 2. $f_i\le (n-1)+g^{\prime }(k^{\prime }-3)-2$ for all $1\le i\le n$.

We will construct the function $F\left(x\right)=2x$.

As $n+g^{\prime }{k}^{\prime }-F(g^{\prime }+1)<n+(g^{\prime }+1)(k^{\prime }-2)\le n+(n-k^{\prime }+1)(k^{\prime }-2)\le n+n(n-3)=n(n-2)$, we can get inequality

$$n(n-2)>n+g^{\prime }{k}^{\prime }-F(g^{\prime }+1).$$

Thus, at least one of the n subgraphs has a number of faulty vertices less than or equal to $n-3$. Moreover, there exists some s such that $f_s\le n-3$. Since $H_s$ is (n − 2)-connected, we can find that $H_s-F_s$ is connected. We can still use the inductive hypothesis on $n-1, g^{\prime }$ and $k^{\prime }-1$ because $f_i\le (n-1)+g^{\prime }(k^{\prime }-1)-F(g^{\prime }+1)$ and $(n-1)-(k^{\prime }-1)=n-k^{\prime }\ge g^{\prime }$; thus, for any $1\le i\le n$, $H_i-F_i$ consists of a large component and small components containing at most $g^{\prime }$ vertices in total. Hence, we require

$$g^{\prime }+n+g^{\prime }{k}^{\prime }-F(g^{\prime }+1)<{\displaystyle \frac{(n-2)!}{(n-k^{\prime })}}.$$

However, $k^{\prime }\ge 4$, so ${\displaystyle \frac{(n-2)!}{(n-k^{\prime })!}}\ge (n-2)(n-3)$. Despite this,

$$\begin{array}{cc}\hfill g^{\prime }+n+g^{\prime }{k}^{\prime }-F(g^{\prime }+1)& =g^{\prime }(k^{\prime }-1)+n-2\hfill \\ \hfill & \le (n-4)(n-2)+n-2=(n-2)(n-3).\hfill \end{array}$$

We use two inequalities, $g^{\prime }\le n-k^{\prime }\le n-4$ and $k^{\prime }-1\le n-2$. Therefore, this equality is true if and only if these two inequalities are true. However, the first inequality takes an equal sign, which implies that $k^{\prime }=4$, and then the second takes an equal sign, which means that $n=5$. Then, going back to the first inequality, we can get $g^{\prime }=n-4=1$, which is contradictory to the hypothesis that $g^{\prime }\ge 3$. So, this inequality strictly holds. By the arbitrariness of i, there is an edge between the large component of $H_i-F_i$ and $H_s-F_s$ for all $i\ne s$. Then, all these large components belong to a large component of $B_{n,k^{\prime }}-F$.

Next, we prove that the small components contain at most $g^{\prime }$ vertices in total. Suppose, on the contrary, that at least $g^{\prime }+1$ vertices are in the small components. Let us construct another function $h\left(x\right)=(n-1)+(x-1)(k^{\prime }-1)-F\left(x\right)$. Assume $H_i-F_i$ is disconnected for any i and let $q_i$ be the total number of vertices in the small components of $H_i-F_i$. At most, $g^{\prime }$ vertices are disconnected in any $H_i-F_i$, so $q_i\le g^{\prime }$. Since ${\sum }_{i=1}^n{q}_i\ge g^{\prime }+1$ and $g^{\prime }\ge 3$, then at least two of these $q_i$ are positive. So, we let $q_1,q_2,\dots ,q_j$ ($j\ge 2$) be at least 1. According to the induction hypothesis, we can get that if $f_i\le h\left(x\right)$, then for any integer $x-1\le g^{\prime }$, there are at most $x-1$ vertices in the small components of $H_i$. Thus, for all integers $m\le q_i$, we have $f_i>h\left(m\right)$. Otherwise, $f_i\le h\left(m\right)$; thus, at most, $m-1\le q_i-1$ vertices are in the small components of $H_i-F_i$, which contradicts to the fact the small components have a total of $q^{\prime }$ vertices. Since ${\sum }_{i=1}^n{q}_i\ge g^{\prime }+1$, we can choose $p_i$ for $1\le i\le j$, such that ${\sum }_{i=1}^j{p}_i=g^{\prime }+1$ and $p_i\le q_i$ for all i. This means that for $1\le i\le j$, we can get $f_i>h\left(p_i\right)$.

For $1\le i\le j$, the sum of the $f_i$ does not exceed the total number of removed vertices, so

$$\begin{array}{cc}\hfill n+g^{\prime }{k}^{\prime }-F(g^{\prime }+1)& \ge \sum _{i=1}^j{f}_i\hfill \\ \hfill & \ge \sum _{i=1}^j(h\left(p_i\right)+1)\hfill \\ \hfill & =\sum _{i=1}^j(n+(p_i-1)(k^{\prime }-1)-F\left(p_i\right))\hfill \\ \hfill & =jn+(k^{\prime }-1)\sum _{i=1}^j(p_i-1)-\sum _{i=1}^{j}F\left(p_i\right).\hfill \end{array}$$

Since ${\sum }_{i=1}^j{p}_i=g^{\prime }+1$, this implies ${\sum }_{i=1}^j(p_i-1)=g^{\prime }+1-j$. Then,

$$n+g^{\prime }{k}^{\prime }-F(g^{\prime }+1)\ge jn+(k^{\prime }-1)(g^{\prime }+1-j)-\sum _{i=1}^{j}F\left(p_i\right)$$

Equivalently,

$$\sum _{i=1}^{j}F\left(p_i\right)-F(g^{\prime }+1)+g^{\prime }+1\ge (j-1)(n-k^{\prime })+j.$$

Using $F\left(x\right)=2x$ and ${\sum }_{i=1}^j{p}_i=g^{\prime }+1$, we can find that $g^{\prime }+1-j\ge (j-1)(n-k^{\prime })$, where $j\ge 2$. Since $j\ge 2$ and $g^{\prime }\le n-k^{\prime }$, we get $(j-1)(n-k^{\prime })\ge n-k^{\prime }\ge g^{\prime }>g^{\prime }+1-j$, which is a contradiction. Therefore, there are at most $g^{\prime }$ vertices in the small components. The proof of this lemma is complete. □

According to Lemma 7, we can easily obtain the following Lemma.

Lemma 8.

${\kappa }_g\left(B_{n,k}\right)\ge n+g(k-2)-1$ for $3\le k\le n-1$ and $0\le g\le n-k$.

Theorem 1.

The g-extra connectivity of $(n,k)$-bubble-sort network $B_{n,k}$ is ${\kappa }_g\left(B_{n,k}\right)=n+g(k-2)-1$ for $4\le k\le n-1$ and $0\le g\le n-k$.

4. The $\mathit{g}$-Extra Diagnosability of $\mathbf{(}\mathit{n},\mathit{k}\mathbf{)}$-Bubble-Sort Network ${\mathit{B}}_{\mathit{n},\mathit{k}}$

Lemma 9

([24]). Let G be a n-regular graph and g be an integer with $0\le g\le n$. If G satisfies the following two conditions:

(1) 

$|V\left(G\right)|>2({\kappa }_g\left(G\right)+g)$;

(2) 

There exists a subgraph $A\subseteq G$ with $|V(A)|=g+1$, and $N_G\left(A\right)$ is the minimum g-extra cut of G.

Then, the g-extra diagnosability of G under the PMC model is $t_g\left(G\right)={\kappa }_g\left(G\right)+g$.

Via Lemma 9, we have the following theorem:

Theorem 2.

Let $4\le k\le n-1$, $n\ge 5$ and $0\le g\le n-k$. Then, $t_g\left(B_{n,k}\right)=n+g(k-1)-1$ under the PMC model.

Proof. 

For $4\le k\le n-1$, $n\ge 5$ and $0\le g\le n-k$, we have

$$\begin{array}{cc}\hfill |V\left(B_{n,k}\right)|-2[\left({\kappa }_g\left(B_{n,k}\right)\right)+g]& ={\displaystyle \frac{n!}{(n-k)!}}-2[n+g(k-2)-1+g]\hfill \\ \hfill & >0\hfill \end{array}$$

Thus, Condition (1) in Lemma 9 holds. There exists a subgraph $A\subseteq B_{n,k}$ with $|V(A)|=g+1$; thus, $N_{B_{n,k}}\left(V\left(A\right)\right)$ is a minimum g-extra cut of $B_{n,k}$ via Lemma 3. Then, we have $B_{n,k}$, which is $t_g\left(B_{n,k}\right)=n+g(k-1)-1$ under the PMC model. □

Lemma 10

([25]). Let G be a n-regular graph and g be an integer with $0\le g\le n$, where $n\ge 4$. If G satisfies the following three conditions:

(1) 

${\kappa }_g\left(G\right)\ge n$ and $|V\left(G\right)|>4({\kappa }_g\left(G\right)+g)-n+1$;

(2) 

There exists a connected subgraph $A\subseteq G$ such that $|V(A)|=g+1$ and $N_G\left(A\right)$ is the minimum g-extra cut of G;

(3) 

$|N_G\left(S\right)|\ge {\kappa }_g\left(G\right)+g$ for any connected subgraph $S\subseteq G$ with $|V(S)|\ge g+2.$ then, under the MM* model, the g-extra diagnosability of G is $t_g\left(G\right)={\kappa }_g\left(G\right)+g$.

Lemma 11.

Let $S\subseteq V\left(B_{n,k}\right)$ with $|S|=g+1$, where $3\le k\le n-1$, $0\le g\le n-k$. Then, $|N_{B_{n,k}}\left(S\right)|\ge n+g(k-2)-1$.

Proof. 

This lemma is proved via induction on $|S|$. It is clear that the result is true for $g=0$. Suppose that the result is true for all S with $|S|\le g$. Next, we will show that for S with $|S|=g+1$, the result holds.

Since $g\ge 1$, $|S|\ge 2$. We can find that for any two vertices $u=u_1{u}_2\cdots u_k$, $v=v_1{v}_2\cdots v_k\in V\left(B_{n,k}\right)$, there exists at least one coordinate that is different from u and v. $B_{n,k}$ can be decomposed into n subgraphs along dimension k. Assume that $S_1=S\cap V\left(B_{n,k}^i\right)$ and $S_2=S\cap V(B_{n,k}-B_{n,k}^i)$.

If $S_1\ne \varnothing$ and $S_2=\varnothing$, we consider the minimum value of the neighborhood; then, $B_{n,k}\left[S\right]=B_{n,k}\left[S_1\right]\cong K_{g+1}$. Thus,

$$\begin{array}{c}|N_{B_{n,k}}\left(S\right)|= |N_{B_{n,k}}\left(S_1\right)|\hfill \\ = |N_{B_{n,k}^i}\left(S_1\right)|+|N_{B_{n,k}-B_{n,k}^i}\left(S_1\right)|\hfill \\ =[n-(k-1+g+1)+(k-2\left)\right(g+1\left)\right]+(g+1)\hfill \\ =n+g(k-2)-1,\hfill \end{array}$$

the lemma holds.

If $S_1\ne \varnothing$ and $S_2\ne \varnothing$, we assume that $|S_1|\hspace{0.17em}=x$ with $1\le x\le g$; then, $|S_2|\hspace{0.17em}=g+1-x$. By carrying out induction hypothesis, we have

$$|N_{B_{n,k}^i}\left(S_2\right)|\hspace{0.17em}\ge \hspace{0.17em}n-1+(x-1)(k-1-2)-1,$$

and

$$\begin{array}{c}|N_{B_{n,k}-B_{n,k}^i}\left(S_2\right)|\hspace{0.17em}=\hspace{0.17em}|N_{B_{n,k}}\left(S_2\right)|-|N_{B_{n,k}^i}\left(S_2\right)|\hfill \\ \ge n+(g+1-x-1)(k-2)-1-(g+1-x).\hfill \end{array}$$

Thus, we have

$$\begin{array}{c}|N_{B_{n,k}}\left(S\right)|\hspace{0.17em}\ge \hspace{0.17em}|N_{B_{n,k}^i}\left(S_1\right)|+|N_{B_{n,k}-B_{n,k}^i}\left(S_2\right)|\hfill \\ \ge [n-1+(x-1\left)\right(k-1-2)-1]+[n+(g-x\left)\right(k-2)-1-(g+1-x\left)\right]\hfill \\ =2n-4+(k-3)(g-1).\hfill \end{array}$$

Note that

$$2n-4+(k-3)(g-1)-[n+g(k-2)-1]=n-g-k\ge 0$$

for $0\le g\le n-k$, we have

$$|N(V\left(A\right))|\ge n+g(k-2)-1.$$

Therefore, this lemma holds. □

Theorem 3.

Let $4\le k\le n-1$, $n\ge 5$ and $0\le g\le min\{n-k-1,k-2\}$. Then, g-extra diagnosability of $B_{n,k}$ under the MM* model is $t_g\left(B_{n,k}\right)=n+g(k-1)-1$

Proof. 

By Definition 1, $|V\left(B_{n,k}\right)|\hspace{0.17em}={\displaystyle \frac{n!}{(n-k)!}}$, and $B_{n,k}$ is $(n-1)$-regular. By Theorem 1, we know that ${\kappa }_g\left(B_{n,k}\right)=n+g(k-2)-1$ for $4\le k\le n-1$ and $0\le g\le n-k$.

$$\begin{array}{cc}\hfill |V\left(B_{n,k}\right)|-4[\left({\kappa }_g\left(B_{n,k}\right)\right)+g]+(n-1)-1& ={\displaystyle \frac{n!}{(n-k)!}}-4[n+g(k-2)-1+g]+n-2\hfill \\ \hfill & ={\displaystyle \frac{n!}{(n-k)!}}-(3n+4g(k-1)-2)\hfill \\ \hfill & >0\hfill \end{array}$$

Then, Condition (1) for Lemma 10 is satisfied. By Lemma 3, there is a subgraph $A\subseteq B_{n,k}$ such that $A\cong K_{1,g}$ and $N_{B_{n,k}}\left(A\right)$ is a minimum g-extra cut of $B_{n,k}$; thus, Condition (2) of Lemma 10 is true. By Lemma 11, $|N_{B_{n,k}}\left(S\right)|\ge n+(g+1)(k-2)-1$ for any subgraph $S\in B_{n,k}$ and $|V(S)|=g+2$. When $0\le g\le k-2$, we can get $|N_{B_{n,k}}\left(S\right)|\ge n+(g+1)(k-2)-1\ge {\kappa }_g\left(B_{n,k}\right)+g$. Then, three conditions of Lemma 10 are true. Hence, for $4\le k\le n-1$ and $0\le g\le min\{n-k-1,k-2\}$, $B_{n,k}$ is $t_g\left(B_{n,k}\right)=n+g(k-1)-1$ under the MM* model. □

5. Conclusions

The connectivity and diagnosability of interconnection networks are two indexes that are needed to measure the fault tolerance of interconnection networks, which are of great significance to their design and maintenance. In this paper, we give the values of g-extra connectivity and g-extra diagnosability of an $(n,k)$-bubble-sort network $B_{n,k}$. Using g-extra connectivity and g-extra diagnosability to analyze $B_{n,k}$ not only improves its fault tolerance but also provides high reliability. Therefore, g-extra connectivity is superior to traditional connectivity in evaluating the reliability of an $(n,k)$-bubble-sort network. When the $(n,k)$-bubble-sort network $B_{n,k}$ is used to model the topological structure of interconnection networks, the results can provide a more accurate measurement of the tolerance of a fault network. Based on this study, researchers can explore the g-extra connectivity and g-extra diagnosability of other networks.