Strong Convergence of Euler-Type Methods for Nonlinear Fractional Stochastic Differential Equations without Singular Kernel
Abstract
1. Introduction
1.1. Important Properties of
1.2. Motivational Background
1.3. Organization of the Paper
2. Convergence, Continuity, and Uniqueness of the Solution for Equation (2)
- (i)
- Suppose that are both one-sided Lipschitz nonlinear continuous functions and, in addition, the function b is Lipschitz nonlinear continuous function with respect to u, respectively, i.e., for , then there exists a constant depending only on R, such that ; it holds that
- (ii)
- We assume that the nonlinear term b is measurable a.e., t, and that there exists such that
- (iii)
- Let , the space of functions that are differentiable and continuous on the interval such that there is such that
3. Strong Convergence of the Euler–Maruyama Scheme
3.1. Derivation of the Scheme
3.2. Auxiliary Equation and Its Error Estimates
3.3. Error Estimate of the Euler–Maruyama Scheme
4. Numerical Results and Simulations
4.1. Strong Convergence of the Euler–Maruyama Scheme
- Find the reference solution at because the analytical solution is unknown a priori;
- In the numerical experiment, the inputs for the simulation are:
- the time interval ;
- ;
- ;
- with the initial condition ;
- Define the corresponding grid and notice that
- ;
- ;
- Compute the variable order using
- Compute the sample mean of the error as follows:
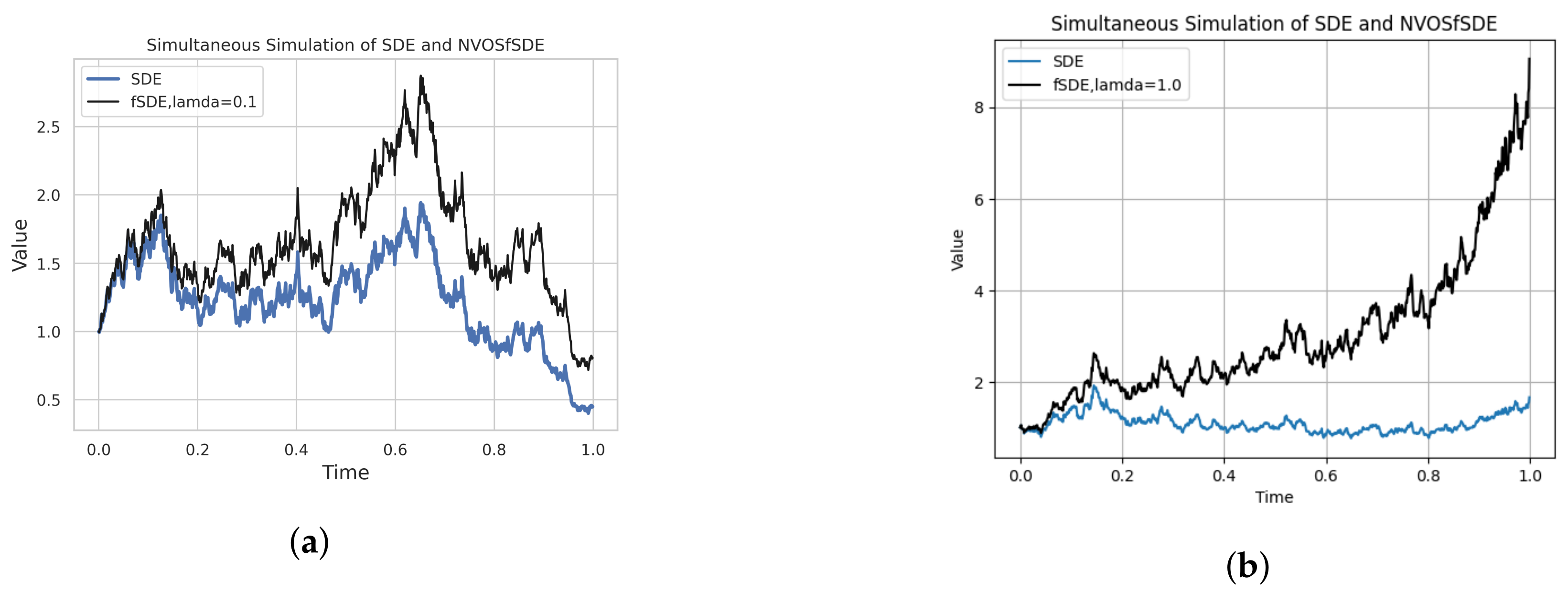
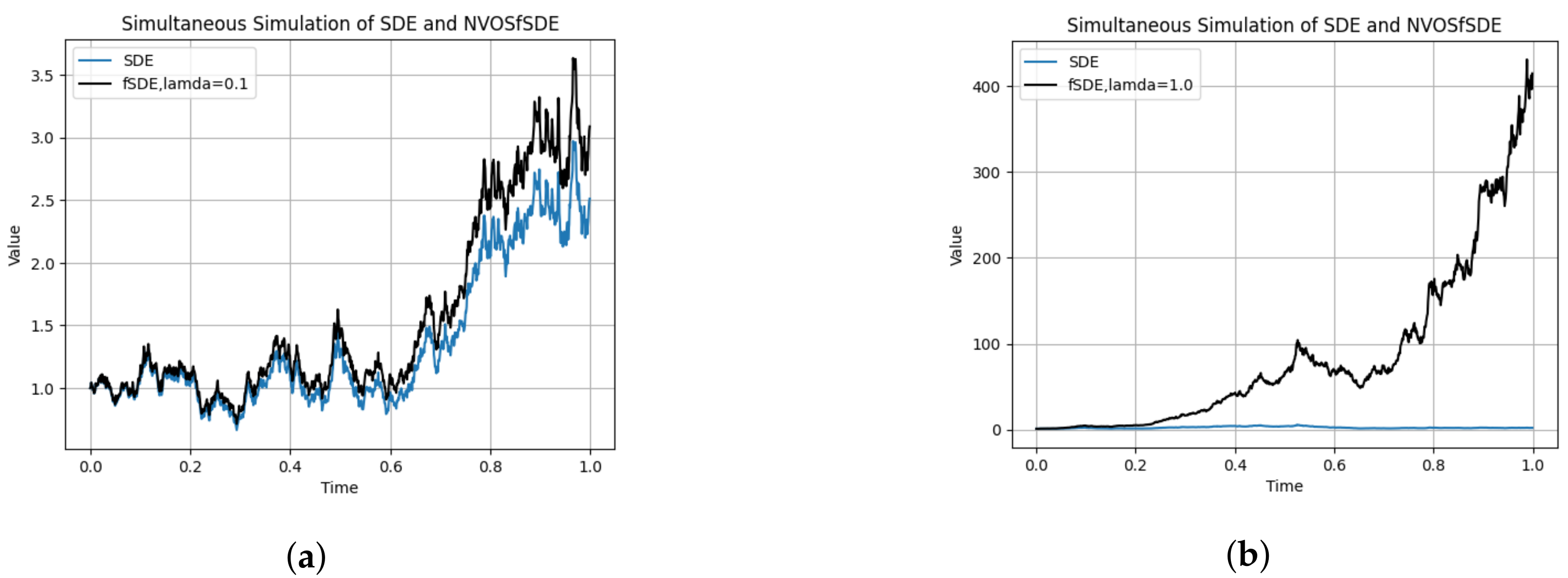
4.2. Performance of the Variable-Order FSDE
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (i)
- A one-parameter function of the Mittag-Leffler function type is defined in [58] by setting
- (ii)
- A two-parameter function of Mittag-Leffler function type is defined in [58] by setting
References
- Diethelm, K.; Ford, N.J. The analysis of fractional differential equations. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Gulgowski, J.; Stefański, T.P. On applications of fractional derivatives in electromagnetic theory. In Proceedings of the 23rd International Microwave and Radar Conference (MIKON), Warsaw, Poland, 5–8 October 2020; pp. 13–17. [Google Scholar]
- Gulgowski, J.; Stefański, T.P.; Trofimowicz, D. On applications of elements modelled by fractional derivatives in circuit theory. Energies 2020, 13, 5768. [Google Scholar] [CrossRef]
- Hilfer, R. Mathematical and physical interpretations of fractional derivatives and integrals. In Handbook of Fractional Calculus with Applications 1; De Gruyter: Berlin, Germany, 2019; pp. 47–85. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Kaltenbacher, B.; Rundell, W. Some inverse problems for wave equations with fractional derivative attenuation. Inverse Probl. 2021, 37, 045002. [Google Scholar] [CrossRef]
- Zhou, Y. Fractional Evolution Equations and Inclusions: Analysis and Control; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Duan, Y.; Jiang, Y.; Wei, Y.; Zhou, J. The solution of stochastic evolution equation with the fractional derivative. Phys. Scr. 2024, 99, 025219. [Google Scholar] [CrossRef]
- Bashar, M.H.; Ghosh, S.; Rahman, M.M. Dynamical exploration of optical soliton solutions for M-fractional Paraxial wave equation. PLoS ONE 2024, 19, e0299573. [Google Scholar] [CrossRef]
- Aksoy, E.; Kaplan, M.; Bekir, A. Exponential rational function method for space–time fractional differential equations. Waves Random Complex Media 2016, 26, 142–151. [Google Scholar] [CrossRef]
- Ghany, H.A.; Hyder, A.A.; Zakarya, M. Exact solutions of stochastic fractional Korteweg de-Vries equation with conformable derivatives. Chin. Phys. B 2020, 29, 030203. [Google Scholar] [CrossRef]
- Han, T.; Li, Z.; Wen, J.; Yuan, J. Classification of All Single Traveling Wave Solutions of (3 + 1)-Dimensional Jimbo-Miwa Equation with Space-Time Fractional Derivative. Adv. Math. Phys. 2022, 2022, 2466900. [Google Scholar] [CrossRef]
- Zou, G.A.; Wang, B. Stochastic Burgers’ equation with fractional derivative driven by multiplicative noise. Comput. Math. Appl. 2017, 74, 3195–3208. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M.K. A generalized definition of the fractional derivative with applications. Math. Probl. Eng. 2021, 2021, 9444803. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Iqbal, N.; Albalahi, A.M.; Abouelregal, A.E.; Atta, D.; Ahmad, H.; El-Morshedy, M. Brownian motion effects on analytical solutions of a fractional-space long–short-wave interaction with conformable derivative. Results Phys. 2022, 35, 105371. [Google Scholar] [CrossRef]
- Martínez, F.; Kaabar, M.K. A Novel Theoretical Investigation of the Abu-Shady-Kaabar Fractional Derivative as a Modeling Tool for Science and Engineering. Comput. Math. Methods Med. 2022, 2022, 4119082. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Li, Z.; Zhang, K. Exact solutions of the stochastic fractional long—Short wave interaction system with multiplicative noise in generalized elastic medium. Results Phys. 2023, 44, 106174. [Google Scholar] [CrossRef]
- Han, T.; Zhao, Z.; Zhang, K.; Tang, C. Chaotic behavior and solitary wave solutions of stochastic-fractional Drinfel’d-Sokolov-Wilson equations with Brownian motion. Results Phys. 2023, 51, 106657. [Google Scholar] [CrossRef]
- Peng, C.; Zhao, L. Dynamic effects on traveling wave solutions of the space-fractional long-short-wave interaction system with multiplicative white noise. Results Phys. 2023, 53, 106931. [Google Scholar] [CrossRef]
- Singh, B.K.; Kumar, A. New approximate series solutions of conformable time-space fractional Fokker-Planck Equation via two efficacious techniques. Partial. Differ. Eq. Appl. Math. 2022, 6, 100451. [Google Scholar] [CrossRef]
- Kim, H.; Sakthivel, R.; Debbouche, A.; Torres, D.F. Traveling wave solutions of some important Wick-type fractional stochastic nonlinear partial differential equations. Chaos Solitons Fractals 2020, 131, 109542. [Google Scholar] [CrossRef]
- Guo, B.; Pu, X.; Huang, F. Fractional Partial Differential Equations and Their Numerical Solutions; World Scientific: Singapore, 2015. [Google Scholar]
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. Siam J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Shu, J.; Li, P.; Zhang, J.; Liao, O. Random attractors for the stochastic coupled fractional Ginzburg-Landau equation with additive noise. J. Math. Phys. 2015, 56, 102702. [Google Scholar] [CrossRef]
- Guner, O.; Aksoy, E.; Bekir, A.; Cevikel, A.C. Different methods for (3 + 1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation. Comput. Math. Appl. 2016, 71, 1259–1269. [Google Scholar] [CrossRef]
- Cresson, J.; Szafrańska, A. Comments on various extensions of the Riemann-Liouville fractional derivatives: About the Leibniz and chain rule properties. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 104903. [Google Scholar] [CrossRef]
- El-Nabulsi, A.R. Fractional derivatives generalization of Einstein’s field equations. Indian J. Phys. 2013, 87, 195–200. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Modifications at large distances from fractional and fractal arguments. Fractals 2010, 18, 185–190. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Gravitons in fractional action cosmology. Int. J. Theor. Phys. 2012, 51, 3978–3992. [Google Scholar] [CrossRef]
- Koeller, R. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Pedjeu, J.C.; Ladde, G.S. Stochastic fractional differential equations: Modeling, method and analysis. Chaos Solitons Fractals 2012, 45, 279–293. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, X.; Zhang, Z.; Wang, H. Strong convergence of a Euler-Maruyama scheme to a variable-order fractional stochastic differential equation driven by a multiplicative white noise. Chaos Solitons Fractals 2021, 142, 110392. [Google Scholar] [CrossRef]
- Sakamoto, K.; Yamamoto, M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 2011, 382, 426–447. [Google Scholar] [CrossRef]
- Ahmadova, A.; Mahmudov, N.I. Strong convergence of a Euler—Maruyama method for fractional stochastic Langevin equations. Math. Comput. Simul. 2021, 190, 429–448. [Google Scholar] [CrossRef]
- Ding, X.L.; Nieto, J.J. Analytical solutions for multi-time scale fractional stochastic differential equations driven by fractional Brownian motion and their applications. Entropy 2018, 20, 63. [Google Scholar] [CrossRef]
- Doan, T.S.; Huong, P.T.; Kloeden, P.E.; Vu, A.M. Euler–Maruyama scheme for Caputo stochastic fractional differential equations. J. Comput. Appl. Math. 2020, 380, 112989. [Google Scholar] [CrossRef]
- Dong, J.; Du, N.; Yang, Z. A distributed-order fractional stochastic differential equation driven by Levy noise: Existence, uniqueness, and a fast EM scheme. Chaos: Interdiscip. J. Nonlinear Sci. 2023, 33, 023109. [Google Scholar] [CrossRef]
- Huang, J.; Shao, L.; Liu, J. Euler–Maruyama methods for Caputo tempered fractional stochastic differential equations. Int. J. Comput. Math. 2024, 2024, 1–19. [Google Scholar] [CrossRef]
- Li, X.; Yang, X. Error estimates of finite element methods for stochastic fractional differential equations. J. Comput. Math. 2017, 35, 346–362. [Google Scholar]
- Li, M.; Dai, X.; Huang, C. Fast Euler–Maruyama method for weakly singular stochastic Volterra integral equations with variable exponent. Numer. Algorithms 2023, 92, 2433–2455. [Google Scholar] [CrossRef]
- Xiao, A.; Dai, X.; Bu, W. Well-posedness and EM approximation for nonlinear stochastic fractional integro-differential equations with weakly singular kernels. arXiv 2019, arXiv:1901.10333. [Google Scholar]
- Yu, Y. Convergence of Relative Entropy for Euler-Maruyama Scheme to Stochastic Differential Equations with Additive Noise. Entropy 2024, 26, 232. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; Huang, J. A fast Euler-Maruyama method for fractional stochastic differential equations. J. Appl. Math. Comput. 2023, 69, 273–291. [Google Scholar] [CrossRef]
- Abou-Senna, A.; Al Nemer, G.; Zhou, Y.; Tian, B. Convergence Rate of the Diffused Split-Step Truncated Euler–Maruyama Method for Stochastic Pantograph Models with Levy Leaps. Fractal Fract. 2023, 7, 861. [Google Scholar] [CrossRef]
- Agrawal, N.; Hu, Y. Jump models with delay—Option pricing and logarithmic Euler-Maruyama scheme. Mathematics 2020, 8, 1932. [Google Scholar] [CrossRef]
- Batiha, I.M.; Abubaker, A.A.; Jebril, I.H.; Al-Shaikh, S.B.; Matarneh, K. A numerical approach of handling fractional stochastic differential equations. Axioms 2023, 12, 388. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, X. Wellposedness and regularity of the variable-order time-fractional diffusion equations. J. Math. Anal. Appl. 2019, 475, 1778–1802. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, Z.; Wang, H. Analysis of a nonlinear variable-order fractional stochastic differential equation. Appl. Math. Lett. 2020, 107, 106461. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- De Espíndola, J.J.; Bavastri, C.A.; de Oliveira Lopes, E.M. Design of optimum systems of viscoelastic vibration absorbers for a given material based on the fractional calculus model. J. Vib. Control. 2008, 14, 1607–1630. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Pardoux, É. Equation Aux Derivees Partielles Stochastiques non Lineaires Monotones. PhD Thesis, Universite Paris, Paris, France, 1975. [Google Scholar]
- Nouri, K.; Ranjbar, H.; Torkzadeh, L. Solving the stochastic differential systems with modified split-step euler-maruyama method. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105153. [Google Scholar] [CrossRef]
- Jia, J.; Yang, Z.; Wang, H. Analysis and numerical approximation for a nonlinear hidden-memory variable-order fractional stochastic differential equation. East Asian J. Appl. Math. 2022, 12, 673–695. [Google Scholar] [CrossRef]
- Jia, J.; Zheng, X.; Fu, H.; Dai, P.; Wang, H. A fast method for variable-order space-fractional diffusion equations. Numer. Algorithms 2020, 85, 1519–1540. [Google Scholar] [CrossRef]
- Lord, G.J.; Powell, C.E.; Shardlow, T. An Introduction to Computational Stochastic PDEs; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Podlubny, I.; Thimann, K.V. (Eds.) Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1st ed.; Mathematics in Science and Engineering 198; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Zheng, X.; Wang, H.; Fu, H. Well-posedness of fractional differential equations with variable-order caputo-fabrizio derivative. Chaos Solitons Fractals 2020, 138, 109966. [Google Scholar] [CrossRef]
- Zhang, Z.; Karniadakis, G.E. Numerical Methods for Stochastic Partial Differential Equations with White Noise; Springer: Berlin/Heidelberg, Germany, 2017; Volume 196. [Google Scholar]
- Le Gall, J.F.; Le Gall, J.F. Brownian motion and partial differential equations. In Brownian Motion, Martingales, and Stochastic Calculus; Springer: Berlin/Heidelberg, Germany, 2016; pp. 185–208. [Google Scholar]
- Shao, J. New integral inequalities with weakly singular kernel for discontinuous functions and their applications to impulsive fractional differential systems. J. Appl. Math. 2014, 2014, 252946. [Google Scholar] [CrossRef]
| (0.2, 0.1) | (0.6, 0.3) | (0.8, 0.5) | ||||
|---|---|---|---|---|---|---|
| N | k | k | k | |||
| 8 | 4.40 | 0.00 | 4.73 | 0 | 8.77 | 0 |
| 16 | 4.38 | 0.0070642 | 5.04 | 0.0924739 | 9.49 | 0.1148251 |
| 32 | 4.33 | 0.0141644 | 5.12 | 0.0222736 | 9.72 | 0.0334769 |
| 64 | 4.25 | 0.0284441 | 4.96 | 0.0445478 | 9.39 | 0.0494342 |
| 128 | 4.08 | 0.0570356 | 4.47 | 0.1524107 | 8.22 | 0.1926919 |
| 256 | 3.78 | 0.1109219 | 3.97 | 0.1714552 | 8.22 | 0.00 |
| 0.5 | 0.4 | 0.2 | ||||
| (0.2, 0.1) | (0.6, 0.3) | (0.8, 0.5) | ||||
|---|---|---|---|---|---|---|
| N | k | k | k | |||
| 16 | 4.38 | 0.009004 | 5.04 | 0.08139 | 9.49 | 0.1234129 |
| 32 | 4.33 | 0.00900 | 5.12 | 0.02227360 | 9.72 | 0.0231000 |
| 64 | 6.25 | 0.03411000 | 4.96 | 0.0445478 | 9.39 | 0.0494342 |
| 128 | 4.08 | 0.32949910 | 4.47 | 0.1524107 | 8.22 | 0.1926919 |
| 0.5 | 0.4 | 0.2 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.; Abebe, M.A.; Nazir, T. Strong Convergence of Euler-Type Methods for Nonlinear Fractional Stochastic Differential Equations without Singular Kernel. Mathematics 2024, 12, 2890. https://doi.org/10.3390/math12182890
Ali Z, Abebe MA, Nazir T. Strong Convergence of Euler-Type Methods for Nonlinear Fractional Stochastic Differential Equations without Singular Kernel. Mathematics. 2024; 12(18):2890. https://doi.org/10.3390/math12182890
Chicago/Turabian StyleAli, Zakaria, Minyahil Abera Abebe, and Talat Nazir. 2024. "Strong Convergence of Euler-Type Methods for Nonlinear Fractional Stochastic Differential Equations without Singular Kernel" Mathematics 12, no. 18: 2890. https://doi.org/10.3390/math12182890
APA StyleAli, Z., Abebe, M. A., & Nazir, T. (2024). Strong Convergence of Euler-Type Methods for Nonlinear Fractional Stochastic Differential Equations without Singular Kernel. Mathematics, 12(18), 2890. https://doi.org/10.3390/math12182890






