Rigid Polynomial Differential Systems with Homogeneous Nonlinearities

Abstract

Planar differential systems whose angular velocity is constant are called rigid or uniform differential systems. The first rigid system goes back to the pendulum clock of Christiaan Huygens in 1656; since then, the interest for the rigid systems has been growing. Thus, at this moment, in MathSciNet there are 108 articles with the words rigid systems or uniform systems in their titles. Here, we study the dynamics of the planar rigid polynomial differential systems with homogeneous nonlinearities of arbitrary degree. More precisely, we characterize the existence and non-existence of limit cycles in this class of rigid systems, and we determine the local phase portraits of their finite and infinite equilibrium points in the Poincaré disc. Finally, we classify the global phase portraits in the Poincaré disc of the rigid polynomial differential systems of degree two, and of one class of rigid polynomial differential systems with cubic homogeneous nonlinearities that can exhibit one limit cycle.

1. Introduction and Statement of the Main Result

The rigid differential systems in the plane ${\mathbb{R}}^2$ with a focus or a center at the origin of coordinates can be written in the form

$$\dot{x}={\displaystyle \frac{dx}{dt}}=-y+xF(x,y),\dot{y}={\displaystyle \frac{dy}{dt}}=x+yF(x,y),$$

(1)

where $F(x,y)$ is a smooth real function. Such differential systems have been studied by several authors; see, for instance, [1,2,3,4,5,6,7,8]. Gasull, Prohens and Torregrosa [9] in 2005 classify the phase portraits of the rigid cubic polynomial differential systems in the Poincaré disc.

Our objective here is to study the dynamics of the rigid polynomial differential systems with homogeneous nonlinearities of arbitrary degree in the Poincaré disc. From Equation (1), a rigid polynomial differential system with homogeneous nonlinearities of degree $n>1$ in the plane ${\mathbb{R}}^2$ can be written in the form

$$\dot{x}=-y+x(\lambda +P(x,y)),\dot{y}=x+y(\lambda +P(x,y)),$$

(2)

where $P(x,y)$ is a homogeneous polynomial of degree $n-1$.

Roughly speaking, the Poincaré disc ${\mathbb{D}}^2$ is the closed unit disc in the plane ${\mathbb{R}}^2$, where its interior has been identified with the whole plane ${\mathbb{R}}^2$ and its boundary, the circle ${\mathbb{S}}^1$, has been identified with the infinity of ${\mathbb{R}}^2$. Note that in the plane ${\mathbb{R}}^2$, we can go or come from infinity in as many directions as the circle ${\mathbb{S}}^1$ has points. A polynomial differential system defined in ${\mathbb{R}}^2$ can be extended analytically to the Poincaré disc ${\mathbb{D}}^2$. In this way, we can study the dynamics of the polynomial differential systems in a neighborhood of infinity. In Appendix A, we summarize how to work in the Poincaré disc.

Our main result is the following theorem and two propositions.

Theorem 1.

The following statements hold for the differential systems (2).

(a) 

If $\lambda =0$, then systems (2) have no limit cycles.

(b) 

If $\lambda \ne 0$, then systems (2) have at most one limit cycle.

(c) 

Define $B={\int }_0^{2\pi }P(cos\theta ,sin\theta )d\theta =0$. If $\lambda B<0$ and λ is sufficiently small, then n is odd and systems (2) have one limit cycle, stable if $\lambda >0$, and unstable if $\lambda <0$.

(d) 

If ${\lambda }^2+B^2\ne 0$ and $aB\ge 0$, then systems (2) have no periodic orbits.

Statements (c) and (d) were proved by Gasull and Torregrosa in Theorem 1.1 of [7]. Here, we prove statements (a) and (b) at the end of Section 2, and we present a new proof of statement (c).

Proposition 1.

System (2) has a unique equilibrium point $p=(0,0)$ at the origin of coordinates.

(a) 

If $\lambda \ne 0$, then p is a focus, stable if $\lambda <0$, and unstable if $\lambda >0$.

(b) 

If $\lambda =0$ and $B={\int }_0^{2\pi }P(cos\theta ,sin\theta )d\theta =0$, then p is a center.

(c) 

If $\lambda =0$ and $B\ne 0$, then p is a weak focus, unstable if $B<0$, and stable if $B>0$.

Statement (b) is also due to Gasull and Torregrosa; see again Theorem 1.1 of [7]. We present another proof of statement (b).

Proposition 2.

All points of the infinity of the differential system (2) are equilibrium points.

(a) 

The infinite equilibrium point $(u,0)$ of the local chart $U_1$ in the Poincaré compactification of the differential system (2) is the α-limit (resp. ω-limit) of one orbit of system (2) if $P(1,u)>0$ (resp. $P(1,u)<0$). If $P(1,u)=0$, then, either the infinite equilibrium point $(u,0)$ is simultaneously the α-limit and ω-limit of two orbits of system (2), or no orbit has the infinite equilibrium point $(u,0)$ as the α-limit and ω-limit set.

(b) 

The infinite equilibrium point $(0,0)$ of the local chart $U_2$ in the Poincaré compactification of the differential system (2) is the α-limit (resp. ω-limit) of one orbit of system (2) if $P(0,1)>0$ (resp. $P(0,1)<0$). If $P(0,1)=0$, then, either the infinite equilibrium point $(0,0)$ is simultaneously the α-limit and ω-limit of two orbits of system (2), or no orbit has the infinite equilibrium point $(0,0)$ as the α-limit and ω-limit set.

Propositions 1 and 2 are proved in Section 2.

In the following propostions, we provide the phase portraits of the rigid quadratic polynomial differential systems.

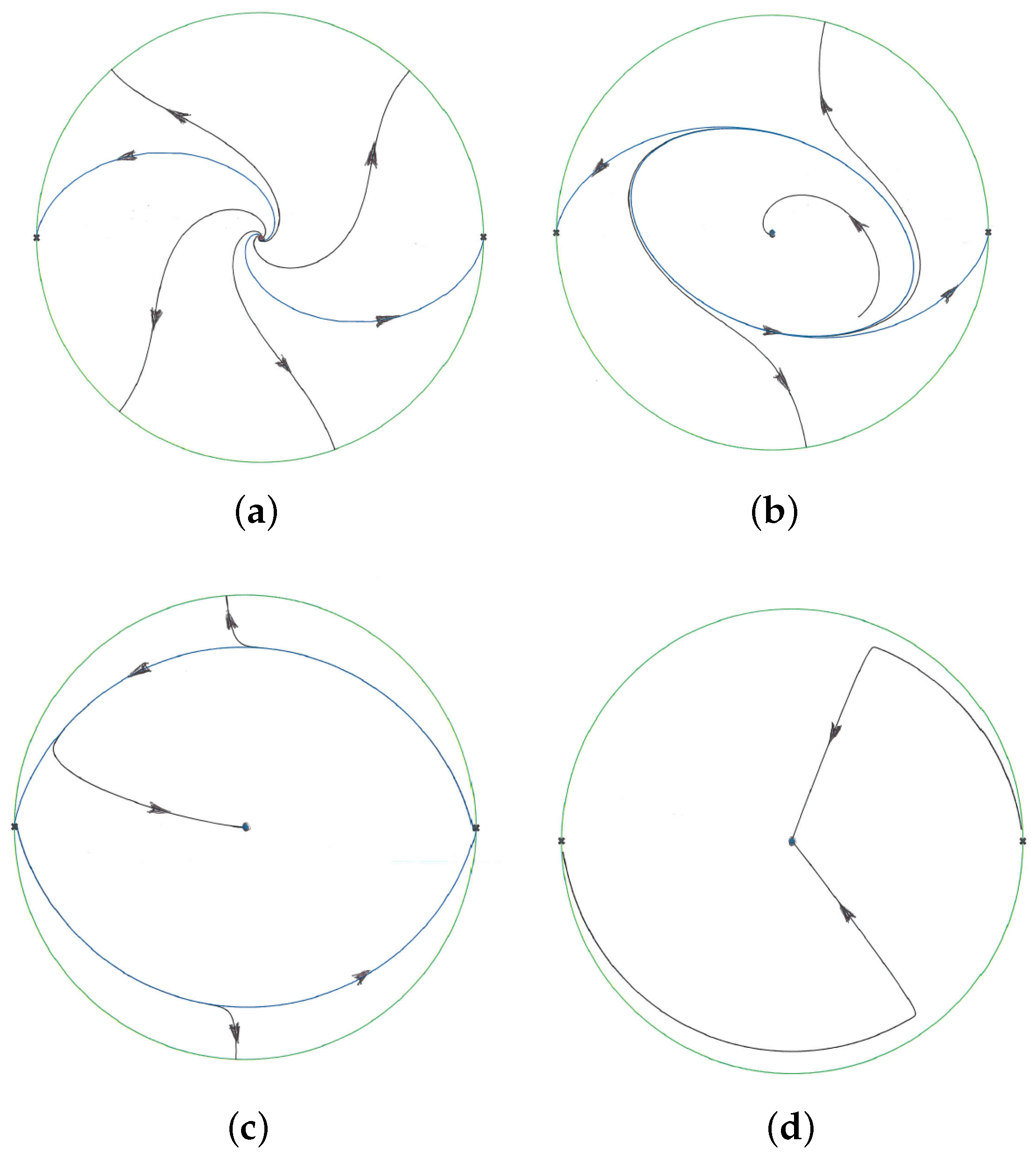
Proposition 3.

The phase portraits of the rigid quadratic polynomial differential systems in the Poincaré disc are topologically equivalent to one of the two phase portraits of Figure 1, perhaps reversing the sense of all its orbits.

Figure 1. Phase portraits of the differential system (2) with $n=2$ in the Poincaré disc: (a) when $\lambda =0$ and (b) when $\lambda >0$. If $\lambda <0$, then, we have the phase portrait (b) but its orbits are travelled in the converse sense. The infinity of the phase portraits (a) and (b) is filled with equilibrium points.

Proposition 4.

The following statements hold for the rigid cubic polynomial systems with homogeneous nonlinearities (2) with $P(x,y)=y^2$.

(a) 

If $\lambda \ge 0$, the origin is a global attractor; see Figure 2a.

Figure 2. Phase portraits of the differential system (2) with $P(x,y)=y^2$ in the Poincaré disc: (a) when $\lambda \ge 0$, (b) when $\lambda =-1$, (c) for the value $\lambda ={\lambda }^{*}$, where the family of the limit cycles that exist for $0<\lambda <{\lambda }^{*}$ ends in a graphic, and (d) for a value of $\lambda >{\lambda }^{*}$. The infinity of these phase portraits is filled with equilibrium points.

(b) 

An unstable limit cycle bifurcates from the origin when $\lambda =0$; see this limit cycle for the value $\lambda =-1$ in Figure 2b.

(c) 

The λ-family of unstable limit cycles ends in a graphic having two equilibria at infinity; see Figure 2c.

(d) 

See the phase portrait of the system after missing the graphic in Figure 2d.

Propostions 3 and 4 are proved in Appendix A.

In what follows, we give more information about the references cited in this paper. In paper [8], as in papers [1,2], the authors used commutators for studying rigid centers. In paper [3], the centers of a family of cubic polynomial differential systems were studied. In books [10,11,12,13] are the results that we use in this paper. In papers [4,5,6], the authors studied different polynomial differential systems with rigid centers. The authors of papers [7,9] studied the same rigid systems that we study, and in this paper, we comment on the differences of their results with our results. Reference [14] is cited because there Poincaré introduced what we call now the Poincaré compactification for studying the dynamics of the polynomial differential systems in a neighborhood of infinity.

2. Proofs

For the basic notions of focus, center, $\alpha$-limit, $\omega$-limit and limit cycle that appear in this paper see, for instance, book [11].

We write the differential system (2) in polar coordinates $(r,\theta )$ where $x=rcos\theta$ and $y=rsin\theta$, and we obtain the system

$$\dot{r}=r\lambda +r^{n}P(cos\theta ,sin\theta ),\dot{\theta }=1.$$

(3)

Taking $\theta$ as the new time, the differential system (3) becomes the differential equation

$$r^{\prime }={\displaystyle \frac{dr}{d\theta }}=r\lambda +r^{n}P(cos\theta ,sin\theta ).$$

(4)

Proposition 5.

Consider the differential Equation (4).

(a) 

If $\lambda =0$, Equation (4) has the first integral

$$H(r,\theta )=r^{1-n}+(n-1){\int }_0^{\theta }P(coss,sins)ds.$$

(b) 

If $r(\theta ,r_0)$ denotes the solution of Equation (4) such that $r(0,r_0)=r_0>0$, then

$$r(\theta ,r_0)={\left(e^{-(n-1)\lambda \theta }\left(r_0^{1-n}-(n-1){\int }_0^{\theta }{e}^{(n-1)\lambda s}P(coss,sins)ds\right)\right)}^{{\displaystyle \frac{1}{1-n}}}.$$

(5)

Proof. 

Let $r\left(\theta \right)$ be an arbitrary solution of the differential Equation (4). Since

$${\displaystyle \frac{dH\left(r\right(\theta ),\theta )}{d\theta }}={\displaystyle \frac{\partial H(r,\theta )}{\partial r}}{\displaystyle \frac{dr\left(\theta \right)}{d\theta }}+{\displaystyle \frac{\partial H(r,\theta )}{\partial \theta }}=0,$$

the function $H(r,\theta )$ is a first integral of Equation (4). Statement (a) is proved.

We verify that $r(\theta ,r_0)$ is a solution of the differential Equation (4) through the direct substitution of the expression of $r(\theta ,r_0)$, given in (5), into the differential Equation (4). Thus, statement (b) is proved. □

In the next proposition, we study the finite equilibrium points of the differential systems (2).

Proof of Proposition 1. 

Since $x\dot{y}-y\dot{x}=x^2+y^2$, it follows that p is the unique equilbrium point of system (2).

The eigenvalues of the Jacobian matrix of the system at p are $\lambda \pm i$. If $\lambda \ne 0$, by the Hartman–Grobman Theorem (see, for instance, [10], or Theorem 2.15 of [11]), p is a focus, stable if $\lambda <0$, and unstable if $\lambda >0$. Thus, statement (a) is proved.

If $\lambda =0$, from statement (b) of Proposition 5, the solution $r(\theta ,r_0)$ of Equation (4) becomes

$$r(\theta ,r_0)={\left(r_0^{1-n}-(n-1){\int }_0^{\theta }P(coss,sins)ds\right)}^{{\displaystyle \frac{1}{1-n}}}.$$

(6)

Then,

$$r(2\pi ,r_0)={\left(r_0^{1-n}-(n-1){\int }_0^{2\pi }P(coss,sins)ds\right)}^{{\displaystyle \frac{1}{1-n}}}.$$

(7)

From (6) and (7), it follows that $r(0,r_0)=r_0=r(2\pi ,r_0)$ if and only if $B=0$. Thus, statement (b) follows. If $B\ne 0$, then from (6) and (7), if follows that we have a weak focus, unstable if $B<0$, and stable if $B>0$, and hence statement (c) is proved. □

Now, we study the infinite equilbrium points of the differential systems (2). For studying these equilibrium points, we shall use the notation and results of Appendix A.1. Thus, we recall that for analyzing the local phase portraits at the infinite equilibrium points, we only need to study the infinite equilibrium points of the local chart $U_1$ and the origin of the local chart $U_2$.

Proof of Proposition 2. 

From Appendix A.1, the differential system (2) in the local chart $U_1$ is written as

$$\dot{u}=(1+u^2)v^{n-1},\dot{v}=v\left((1-\lambda )u{v}^{n-1}-P(1,u)\right).$$

Therefore, all the points $(u,0)$ of the infinity contained in the chart $U_1$ are equilibrium points. Rescaling the time, we eliminate the common factor v between $\dot{u}$ and $\dot{v}$, and we obtain the differential system

$$\dot{u}=(1+u^2)v^{n-2},\dot{v}=(1-\lambda )u{v}^{n-1}-P(1,u).$$

So, $\dot{v}{|}_{v=0}=-P(1,u)$. From here statement (a) follows.

In the local chart $U_2$, system (2) is written as

$$\dot{u}=-(1+u^2)v^{n-1},\dot{v}=-v\left((1+\lambda )u{v}^{n-1}+P(u,1)\right).$$

Therefore, the origin $(0,0)$ of the chart $U_1$ is an equilibrium point. Consequently, all the points of the infinity are equilibrium points. Again, rescaling the time, we eliminate the common factor v between $\dot{u}$ and $\dot{v}$, and we obtain the differential system

$$\dot{u}=-(1+u^2)v^{n-2},\dot{v}=-(1+\lambda )u{v}^{n-1}-P(u,1).$$

So, $\dot{v}{|}_{u=v=0}=-P(0,1)$. This proves statement (b). □

After determining the local phase portraits at the finite and infinite equilibrium points of the differential system (2), in order to obtain the global phase portraits in the Poincaré disc of this differential system, we need to control their possible limit cycles. Of course, if $\lambda =0$, it is clear that the differential systems (2) have no limit cycles. Now, we shall prove that when $\lambda \ne 0$, the differential systems (2) have no periodic orbits, and, consequently, no limit cycles. First, we recall the following well known result.

Proof of Theorem 1. 

When $\lambda =0$, since the first integral $H(r,\theta )$ given in statement (a) of Proposition 5 is defined in the whole plane ${\mathbb{R}}^2$ except at the origin of coordinates, the differential system (2) cannot have limit cycles; otherwise, by continuity, the first integral will be constant in a neighborhood of the limit cycle, and this is not the case for the function $H(r,\theta )$. This proves statement (a).

From statement (b) of Proposition 5, for every $r_0>0$, the solution $r(\theta ,r_0)$ of the differential Equation (4) such that $r(0,r_0)=r_0$ verifies that

$$r(2\pi ,r_0)={\left(e^{-(n-1)\lambda 2\pi }\left(r_0^{1-n}-(n-1){\int }_0^{2\pi }{e}^{(n-1)\lambda s}P(coss,sins)ds\right)\right)}^{{\displaystyle \frac{1}{1-n}}}.$$

If the solution $r(\theta ,r_0)$ is periodic, then $r(2\pi ,r_0)=r_0$. From this equation, we obtain the unique solution that

$$r_0={\left({\displaystyle \frac{e^{2\pi \lambda }-e^{2n\pi \lambda }}{(n-1)e^{-2\pi \lambda }{\int }_0^{2\pi }{e}^{(n-1)\lambda s}P(coss,sins)ds}}\right)}^{{\displaystyle \frac{1}{n-1}}}.$$

So, if there exists a periodic solution this is unique, consequently, it is a limit cycle. Statement (b) is proved.

Now, assume $\lambda B<0$. We have

$${\int }_0^{2\pi }{cos}^p\theta {sin}^q\theta d\theta =0,$$

if p or q is odd (see formulas 2.5111 and 2.5114 of [12]), and

$${\int }_0^{2\pi }{cos}^p\theta {sin}^q\theta d\theta ={\displaystyle \frac{(q-1)!!(p-1)!!}{2^{p/2}(p/2)|(q+p)(q-2+p)\cdots (2+p)}}\ne 0,$$

if p and q are even (see formulas 2.5121 and 2.5122 of [12]). As usual $(q-1)!!=(q-1)(q-3)\cdots 1$ when q is even. Therefore, since $B={\int }_0^{2\pi }P(cos\theta ,sin\theta )d\theta \ne 0$ and $P(x,y)$ is a homogeneous polynomial of degree $n-1>0$, it follows that n is odd.

For completing the proof of statement (c), we shall use the averaging theory of first order; see Appendix A.2.

Assume that $\lambda >0$. Then, in the differential Equation (4), we change the variable r by $r=R{\lambda }^{{\displaystyle \frac{1}{n-1}}}$, and then we obtain the differential equation

$$R^{\prime }=\lambda (R+R^{n}P[cos\theta ,sin\theta ])=:\lambda F(\theta ,R).$$

(8)

If $\lambda$ is sufficiently small, we can apply the averaging theory of first order with $\lambda =\epsilon$, $\mathbf{x}=R$. $t=\theta$ and $T=2\pi$. Then

$$f\left(R\right)={\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }F(\theta ,R)d\theta =R+{\displaystyle \frac{R^n}{2\pi }}{\int }_0^{2\pi }P(cos\theta ,sin\theta )d\theta =:R+{\displaystyle \frac{R^n}{2\pi }}B.$$

The unique positive zero of the averaged function $f\left(R\right)$ is $R^{*}={(-B/\left(2\pi \right))}^{1/(1-n)}$, and since $f^{\prime }\left(R^{*}\right)=1-n<0$, from Appendix A.2, it follows that the differential Equation (8) with $\lambda >0$ sufficiently small has a stable limit cycle $R(\theta ,\lambda )$ such that $R(0,\lambda )R^{*}$ when $\lambda =0$.

Now, assume $\lambda <0$. Then, performing the change of variables $r=R{(-\lambda )}^{{\displaystyle \frac{1}{n-1}}}$ in the differential Equation (4), and working as in the case where $\lambda >0$, we obtain that the differential Equation (8) with $\lambda <0$ sufficiently small has an unstable limit cycle $R(\theta ,\lambda )$ such that $R(0,\lambda ){(B/\left(2\pi \right))}^{1/(1-n)}$ when $\lambda \to 0$. This completes the proof of the proposition. □

3. Phase Portraits

Now, we shall prove Propositions 3 and 4.

Proof of Proposition 3. 

From Proposition 1, the differential system (2) for $\lambda =0$ and $B=0$ has a center at the origin of coordinates. Moreover, this differential system by Theorem 1 has no limit cycles, and by Proposition 2, we know its dynamics at infinity. Therefore, its phase portrait in the Poincarè disc is given in Figure 2a. That is, the origin is a global repeller.

Now, assume that either $\lambda \ne 0$, or $\lambda =0$ and $B\ne 0$. Now, from Proposition 1, the differential system (2) has a focus at the origin of coordinates, stable if $\lambda <0$ and unstable if $\lambda >0$. By statement (a) of Theorem 1, when $\lambda =0$, the system has no limit cycles, and when $\lambda \ne 0$, by statement (c) of Theorem 1, since the degree of the system is $n=2$, it also has no limit cycles. Again, by Proposition 2, we know its dynamics at infinity. Hence, its phase portrait in the Poincarè disc is given in Figure 2b. □

Proof of Proposition 4. 

Applying the arguments of the proof of Proposition 2 to the rigid systems (2) with $P(x,y)=y^2$ and $\lambda \ge 0$, it follows that each infinite singular point is the $\omega$-limit of a unique orbit, so infinity is an attractor. For these rigid systems, we have

$$B={\int }_0^{2\pi }P(cos\theta ,sin\theta )d\theta ={\int }_0^{2\pi }{cos}^2\theta d\theta =\pi .$$

Then, by statement (d) of Theorem 1, when $\lambda \ge 0$ these systems have no periodic orbits. Since the origin of coordinates is the unique equilibrium point of these systems and it is an unstable hyperbolic focus for $\lambda >0$ and a weak unstable focus for $\lambda =0$, we obtain that their phase portraits in the Poincaré disc are given in Figure 2a. Thus, statement (a) is proved.

For $\lambda <0$, we have that $\lambda B<0$, and if $\lambda$ is sufficiently small, by statement (c) of Theorem 1, an unstable limit cycle bifurcates from the equilibrium localized at the origin of coordinates. This proves statement (b).

The limit cycle bifurcating from the origin increasis with $\lambda$, because $\lambda$ is a rotating parameter as it was already observed in [7]; for more details on rotating families of differential systems see, for instance, Chapter 8 of [11]. Since the unique finite equilibrium is at the origin, this $\lambda$-family of limit cycles can only end in a graphic with equilibrium points at infinity. Due to the fact that systems (2) with $P(x,y)=y^2$ are invariant under the symmetry $(x,y)\to (-x,-y)$, the infinite equilibrium points of that graphic are diametrally opposite in the Poincaré disc. Studying the infinite equilibrium points as we did in the proof of Proposition 2, there are only two infinite equilibrium points that are simultaneously the $\alpha$-limit and $\omega$-limit of two orbits, so the mentioned graphic has only these two infinite equilbrium points. Hence, statement (c) follows.

Since the parameter $\lambda$ is a rotating parameter, after missing the graphic, no more limit cycles can exist. Studying the infinite equilibrium points as in the proof of Proposition 2, we obtain that each infinite equilibrium is the $\alpha$-limit of a unique orbit, and so infinity is a repeller. Taking into account that the unique finite equilibrium point is a stable focus, we obtain the phase portrait of Figure 2d. That is, the origin is a global attractor. □

4. Conclusions

We have studied the dynamics of planar rigid polynomial differential systems with homogeneous nonlinearities of arbitrary degree. Thus, in Theorem 1, we have characterized when such a rigid system does or does not have a limit cycle, and the kind of stability of the limit cycle when it exists.

In this class of rigid systems, we have determined the local phase portraits of their finite and infinite equilibrium points in the Poincaré disc, in Propositions 1 and 2, respectively.

The phase portraits of the rigid quadratic polynomial differential systems in the Poincaré disc are classified in Proposition 3, while in Proposition 4, we provide the phase portraits in the Poincaré disc of one class of rigid polynomial differential systems with cubic homogeneous nonlinearities that can exhibit one limit cycle.

A nice objective for the future is to classify the phase portraits in the Poincaré disc of all rigid polynomial differential systems of degree 4; here, we classified the ones of degree 2, and in reference [7], the ones of degree 3 were classified.

Appendix A.1. Poincaré Compactification of Polynomial Differential Systems in ${\mathbb{R}}^2$

In order to study the dynamics of a polynomial differential system in the plane ${\mathbb{R}}^2$ near infinity, we need its Poincaré compactification. This tool was created by Poincaré in [14]; for more details, see Chapter 5 of [11].

Consider the polynomial differential system

$$\dot{x}=P(x,y),\dot{y}=Q(x,y),$$

(A1)

where P and Q are polynomials, with d being the maximum of the degrees of the polynomials P and Q.

We consider the plane $\{(x_1,x_2,1); x_1,x_2\in \mathbb{R}\}$ of ${\mathbb{R}}^3$ identified with the plane ${\mathbb{R}}^2$, where we have the differential system (A1). This plane is tangent at the nord pole $(0,0,1)$ of the 2-dimensional sphere ${\mathbb{S}}^2=\{(x_1,x_2,x_3)\in {\mathbb{R}}^3; x_1^2+x_2^2+x_3^2=1\}$. We define the northern hemisphere $H_{+}=\{(x_1,x_2,x_3)\in {\mathbb{S}}^2; x_3>0\}$, the southern hemisphere $H_{-}=\{(x_1,x_2,x_3)\in {\mathbb{S}}^2; x_3<0\}$, and the equator ${\mathbb{S}}^1\equiv \{(x_1,x_2,x_3)\in {\mathbb{S}}^2; x_3=0\}$ of the sphere ${\mathbb{S}}^2$.

In order to study a vector field over ${\mathbb{S}}^2$, we consider six local charts that cover the whole sphere ${\mathbb{S}}^2$. So, for $i=1,2,3$, let

$$U_i=\{(x_1,x_2,x_3)\in {\mathbb{S}}^2; x_i>0\} \mathrm{and} V_i=\{(x_1,x_2,x_3)\in {\mathbb{S}}^2; x_i<0\}.$$

Consider the diffeomorphisms ${\phi }_i:U_i⟶{\mathbb{R}}^2$ and ${\psi }_i:V_i⟶{\mathbb{R}}^2$ given by

$${\phi }_i(x_1,x_2,x_3)={\psi }_i(x_1,x_2,x_3)=\left({\displaystyle \frac{x_j}{x_i}},{\displaystyle \frac{x_k}{x_i}}\right)$$

with $j,k\ne i$ and $j<k$. The sets $(U_i,{\phi }_i)$ and $(V_i,{\psi }_i)$ are the local charts over ${\mathbb{S}}^2$.

Let $f^{\pm }:{\mathbb{R}}^2⟶H_{\pm }$ be the central projections from the tangent plane ${\mathbb{R}}^2$ at the point $(0,0,1)$ of the sphere ${\mathbb{S}}^2$ to ${\mathbb{S}}^2$ given by

$$f^{\pm }(x_1,x_2)=\pm \left({\displaystyle \frac{x_1}{\Delta (x_1,x_2)}},{\displaystyle \frac{x_2}{\Delta (x_1,x_2)}},{\displaystyle \frac{1}{\Delta (x_1,x_2)}}\right)$$

where $\Delta (x_1,x_2)=\sqrt{x_1^2+x_2^2+1}$. In other words, $f^{\pm }(x_1,x_2)$ is the intersection of the straight line through the points $(0,0,0)$ and $(x_1,x_2,1)$ with $H_{\pm }$. Moreover, the maps $f^{\pm }$ induce over $H_{\pm }$ vector fields analytically conjugated with the vector field of the differential system (A1). Indeed, $f^{+}$ induces on $H_{+}=U_3$ the vector field $X_1\left(y\right)=D{f}^{+}\left({\phi }_3\left(y\right)\right)X\left({\phi }_3\left(y\right)\right)$, and $f^{-}$ induces on $H_{-}=V_3$ the vector field $X_2\left(y\right)=D{f}^{-}\left({\psi }_3\left(y\right)\right)X\left({\psi }_3\left(y\right)\right)$. Note that $f^{+}={\phi }_3^{-1}$ and $f^{-}={\psi }_3^{-1}$. Thus, we obtain a vector field on ${\mathbb{S}}^2\setminus S^1$ that admits an analytic extension $p\left(X\right)$ on ${\mathbb{S}}^2$. The vector field $p\left(X\right)$ on ${\mathbb{S}}^2$ is called the Poincaré compactification of the vector field $X=(P,Q)$.

Denote $(u,v)={\phi }_i(x_1,x_2,x_3)={\psi }_i(x_1,x_2,x_3)$. Then, the expression of the differential system associated to the vector field $p\left(X\right)$ in the chart $U_1$ is

$$u^{\prime }=v^d\left[Q\left({\displaystyle \frac{1}{v}},{\displaystyle \frac{u}{v}}\right)-uP\left({\displaystyle \frac{1}{v}},{\displaystyle \frac{u}{v}}\right)\right], v^{\prime }=-v^{d+1}P\left({\displaystyle \frac{1}{v}},{\displaystyle \frac{u}{v}}\right).$$

The expression of $p\left(X\right)$ in $U_2$ is

$$u^{\prime }=v^d\left[P\left({\displaystyle \frac{u}{v}},{\displaystyle \frac{1}{v}}\right)-uQ\left({\displaystyle \frac{u}{v}},{\displaystyle \frac{1}{v}}\right)\right], v^{\prime }=-v^{d+1}Q\left({\displaystyle \frac{u}{v}},{\displaystyle \frac{1}{v}}\right).$$

The expression of $p\left(X\right)$ in $U_3$ is

$$u^{\prime }=P(u,v), v^{\prime }=Q(u,v).$$

For $i=1,2,3$, the expression of $p\left(X\right)$ in the chart $V_i$ differs from the expression in $U_i$ only by the multiplicative constant ${(-1)}^{d-1}$.

Note that we can identify the infinity of ${\mathbb{R}}^2$ with the equator ${\mathbb{S}}^1$. Two points for each direction in ${\mathbb{R}}^2$ provide two antipodal points of ${\mathbb{S}}^1$. An equilibrium point of $p\left(X\right)$ on ${\mathbb{S}}^1$ is called infinite equilibrium point and an equilibrium point on ${\mathbb{S}}^2\setminus {\mathbb{S}}^1$ is called a finite equilibrium point. Observe that the coordinates of the infinite equilibrium points are of the form $(u,0)$ on the charts $U_1,V_1,U_2$, and $V_2$. Thus, if $(x_1,x_2,0)\in {\mathbb{S}}^1$ is an infinite equilibrium point, then its antipode $(-x_1,-x_2,0)$ is also a infinite equilibrium point.

The image of the closed northern hemisphere of ${\mathbb{S}}^2$ under the projection $(x_1,x_2,x_3)\to (x_1,x_2,0)$ is the Poincaré disc, denoted by ${\mathbb{D}}^2$.

Appendix A.2. The Averaging Theory of First Order

This theory deals with the problem of finding T-periodic solutions for a T-periodic differential system depending on a small parameter $\epsilon$. For more details about the averaging theory of first order for finding periodic orbits, see Theorems 11.5 and 11.6 of [13].

We consider the differential system

$$\dot{\mathbf{x}}\left(t\right)=\epsilon F(t,\mathbf{x})+{\epsilon }^{2}G(t,\mathbf{x},\epsilon ),$$

(A2)

where $\mathbf{x}\in D\subset {\mathbb{R}}^n$, D is an open set, $t\ge 0$, the functions F, G, $\partial F/\partial \mathbf{x}$, ${\partial }^{2}F/\partial {\mathbf{x}}^2$ and $\partial G/\partial \mathbf{x}$ are defined, continous and bounded by a constant M (independent of $\epsilon$) in $[0,\infty )\times D$, $0\le \epsilon \le {\epsilon }_0$; and F and G are T-periodic in t (T independent of $\epsilon$). If p is a zero of the averaged function

$$f\left(\mathbf{x}\right)={\displaystyle \frac{1}{T}}{\int }_0^{T}F(t,\mathbf{x})dt,$$

such that

$${\left|{\displaystyle \frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}}\right|}_{\mathbf{x}=p}\ne 0,$$

then for a sufficiently small $\left|\epsilon \right|$, there exists a T-periodic limit cycle $\mathbf{x}(t,\epsilon )$ of system (A2) such that $\mathbf{x}(0,\epsilon )\to p$ as $\epsilon \to 0$. Moreover, if all eigenvalues of the Jacobian matrix

$${\left.{\displaystyle \frac{\partial f\left(\mathbf{x}\right)}{\partial \mathbf{x}}}\right|}_{\mathbf{x}=p}$$

have negative real parts, the corresponding periodic solution $\mathbf{x}(t,\epsilon )$ is asymptotically stable for a sufficiently small $\epsilon$. If one of these eigenvalues has a positive real part, $\mathbf{x}(t,\epsilon )$ is unstable.

That is, the simple zeros of the averaged function $f\left(\mathbf{x}\right)$ provide the initial conditions for T-periodic limit cycles of the differential system (A2).