Study of Cayley Digraphs over Polygroups

Abstract

In this paper we introduce Cayley digraphs associated to finitely generated polygroups, where the vertices correspond to finite products of the generators of polygroups and the edges to multiplication by vertices and generators. We investigate some properties of the Cayley digraphs, emphasizing connectivity and existence of cycles for each vertex of the Cayley digraphs. Particularly, we identify Cayley digraphs on polygroups derived from conjugate classes of dihedral groups. Moreover, we examine some fundamental illustrative examples of Cayley digraphs through the class of gmg-polygroups.

1. Introduction

Cayley diagrams are one of many representations of finite groups. They provide a means of representing a group diagrammatically and various properties of groups, including commutativity, can be extracted from the graph. The Cayley diagram also provides sufficient information to test isomorphism between groups, and thus is a useful tool for recognizing the type of a given group [1]. Arthur Cayley in [1] introduced the concept of a graph for a given group $G,$ according to a generating subset S, namely the set of labeled oriented edges $(g,g·s)$, for every g in G and s in S. Such a graph is called a directed Cayley graph or Cayley digraph of G. Once a Cayley digraph has been constructed for G, it is possible to obtain algorithmic solutions to the following problems: describing a complete set of rewrite rules for $G,$ relative to some lexicographic plus length ordering on the words of S; obtaining a set of defining relations for G in terms of S and finding a word in S of minimal length that represents a specified element of G [2]. Recent works show many different ways of associating graphs to finite groups, most of which were inspired by a question posed by P. Erdos [3]. These differences lie in the adjacency criterion used to relate two group elements constituting the set of vertices of such a graph. Some essential authors in this context are A. Abdollahi [4], A. Ballester-Bolinches et al. [5] and A. Lucchini [6]. In algebraic graph theory it has been shown that all Cayley graphs are vertex-transitive and the converse is not true in general. The Petersen graph is a vertex-transitive graph which is not a Cayley graph. A characterization for all unlabeled and undirected Cayley graphs is Sabidussi’s theorem, which states that a graph is a Cayley graph if and only if its automorphism group contains a regular subgroup. A generalization of the concept of a group is the concept of a hypergroup, that was introduced by Marty in 1934 [7]. In a group, the composition of two elements is an element, while in a hypergroup, the composition of two elements is a nonempty set. One of the important classes of hypergroups are polygroups, with their properties being close to groups [8]. Polygroups are used in color algebra, combinatorics, lattices and graphs. Surveys of the theory of polygroups can be found in the work of Davvaz [9]. D. Heidari et al. studied the concept of generalized Cayley graphs over polygroups, or so-called GCP-graphs, and proved some of their properties in order to answer the question of which simple graphs are GCP-graphs. Moreover, they proved that every simple graph of order at most five is a GCP-graph [10]. In [11] F. Arabpur et al. studied the generalized Cayley graph $\left(gCay\right(P,S\left)\right)$ (undirected graphs or simple graphs) on finitely generated polygroups and made a connection between finitely generated polygroups and geodesic metric spaces. Furthermore, a hyperaction of polygroup on $\left(gCay\right(P,S\left)\right)$ introduced and proved that the generalized Cayley graphs of a polygroup by two different generators are quasi-isometric. Finally, they expressed a connection between finitely generated polygroups and geodesic metric spaces. N. Abughazalah et al., in [12], studied simple graphs that are generalized Cayley graphs over LA-polygroups, and investigated some of their properties to show that each simple graph of order three, four and five is a GCLAP-graph. Until now, all research papers were written on Cayley graphs of polygroups related to undirected graphs. In this paper we introduce generalized Cayley directed graphs for the class of polygroups, i.e., $GCaydi\overrightarrow{(P,\prod S)},$ where P is a polygroup and S is a finitely generated subset of P, which is not necessarily symmetric, that is, $S^{-1}\ne S$. The generalized Cayley directed graph is called minimal if S is a minimal generator of P. In this case the minimal general Cayley directed graph is denoted by $Caydi\overrightarrow{(P,\prod S)}$ and it is called the Cayley digraph of P. Throughout the paper we give many examples of digraphs on some finite polygroups. We investigate the existence a path between every pair of vertices of a Cayley digraph of a polygroup, and we prove that the Cayley directed graph $Caydi\overrightarrow{(P,\prod S)}$ is connected. Furthermore, we show the existence of a cycle for each vertex of the Cayley directed graph. Finally, we focus on the polygroups of conjugacy classes of a group G and characterize the Cayley digraph of dihedral group $D_n.$ The dihedral group is the group of symmetries of a regular polygon which includes rotations and reflections. The motivation of this paper is to extend the notions of algebraic graph theory by polygroups such as the generalized Cayley digraph, the Cayley digraph of a polygroup and the connectivity of the Cayley digraphs. This extension allows us to specify more graphs and extend the class of Cayley graphs. Also, we can study the Cayley digraphs of polygroups for interconnection networks and extend Sabidussi’s theorem and Frucht’s theorem for this class of polygroups.

2. Preliminaries

In this chapter we recall some basic notions of hyperstructure theory and graph theory [13], which will be used throughout the paper. Surveys of the theory of hyperstructures can be found in the works of Corsini [14], Corsini and Leoreanu [15], Vougiouklis [16], and for the theory of polygroups, in the work of Davvaz [9].

Definition 1 

([7]). Let H be a nonempty set and $\ast :H\times H⟶{\mathcal{P}}^{\ast }\left(H\right)$ be a hyperoperation. The couple $(H,\ast )$ is called a hypergroupoid. For any two nonempty subsets A and B of H and $x\in H$, we define

$$A\ast B=\bigcup _{a\in A,b\in B}a\ast b,A\ast x=A\ast \left\{x\right\},x\ast A=\left\{x\right\}\ast A.$$

A hypergroupoid $(H,\ast )$ is called a hypergroup if for all $a,b,c$ of H, it satisfies the following conditions:

(1) 

$(a\ast b)\ast c=a\ast (b\ast c)$, which means that

$$\bigcup _{u\in a\ast b}u\ast c=\bigcup _{v\in b\ast c}a\ast v,$$

(2) 

$a\ast H=H=H\ast a$.

Definition 2 

([14]). Let $(H,\ast )$ be a hypergroup and $\varnothing \ne K\subseteq H$. We say that $(K,\ast )$ is a subhypergroup of H if for all $x\in K$ we have $K\ast x=K=x\ast K$.

Let $(H,\ast )$ be a hypergroup, and an element $e_r$ (resp. $e_l$) of H is called a right identity $e_r$ (resp. left identity $e_l$) if for all $x\in H,$ $x\in x\ast e_r$$(x\in e_l\ast x)$. An element e is called a two-side identity, or for simplicity, an identity, if for all $x\in H$, $x\in x\ast e\cap e\ast x$. A right identity $e_r$ (resp. left identity $e_l$) of H is called a scalar right identity (resp. scalar left identity) if for all $x\in H$, $x=x\ast e_r(x=e_l\ast x)$. An element e is called a scalar identity if for all $x\in H$, $x=x\ast e=e\ast x$. An element $x^{\prime }\in H$ is called a right inverse (resp. left inverse) of x in H if $e_r\in x\ast x^{\prime }$ for some right identities and $e_r$ in $H(e_l\in x^{\prime }\ast x)$. An element $x^{\prime }\in H$ is called an inverse of $x\in H$ if $e\in x^{\prime }\ast x\cap x\ast x^{\prime }$ for some identities in H. We denote the set of identities of H by $E\left(H\right)$ and the set of inverses of a by $i\left(a\right)$. Moreover, we have the following definition.

Definition 3 

([17]). Let $(H,\ast )$ be a hypergroup, and $x\in H$ be given. Then the following assertions hold.

(i) 

Suppose that $e_r$ is a right scalar identity of H and there exists $(n,m,k)\in {\mathbb{N}}^3$ such that $e_r\in x^n\ast {(x^m\ast {x^{\prime }}^m)}^k\cap {(x^m\ast {x^{\prime }}^m)}^k\ast x^n$, where $e_r\in x\ast x^{\prime }$; then we define $O_r(x,x^{\prime })$ = $min\{s>0|\exists (k,m)\in {\mathbb{N}}^2:e_r\in x^s\ast {(x^m\ast {x^{\prime }}^m)}^k\cap {(x^m\ast {x^{\prime }}^m)}^k\ast x^s\}$ and moreover, $O_r\left(x\right)=min\left\{O_r(x,x^{\prime })\right|e_r\in x\ast x^{\prime }\}$ is the right order of x. If such an $(n,m,k)$ does not exist, we say $O_r\left(x\right)=\infty$.

(ii) 

If $e_l$ is a left scalar identity of a hypergroup H, and there exists $(n,m,k)\in {\mathbb{N}}^3$ such that $e_l\in x^n\ast {({x^{″}}^m\ast x^m)}^k\cap {({x^{″}}^m\ast x^m)}^k\ast x^n\}$, where $e_l\in x\ast x^{″}$, then $O_l(x,x^{″})$ = $min\{s>0|\exists (k,m)\in {\mathbb{N}}^2:e_l\in x^s\ast {({x^{″}}^m\ast x^m)}^k\cap {({x^{″}}^m\ast x^m)}^k\ast x^s\}$. Moreover, we have $O_l\left(x\right)=min\{O_l(x,x^{″})|e_l\in x^{″}\ast x\}$ is the left order of x. If such an $(n,m,k)$ does not exist, we say $O_l\left(x\right)=\infty$.

(iii) 

If e is a scalar identity of H and $O_l\left(x\right)=O_r\left(x\right)$, we say $O\left(x\right)=O_l\left(x\right)=O_r\left(x\right)$ is order of x and otherwise we say $O\left(x\right)$ does not exist.

For any $a,b\in H$, we define $a/b=\{x\mid a\in x\ast b\}$ and $a\backslash b=\{y\mid b\in a\ast y\}$. Now let A be a nonempty subset of hypergroup $(H,\ast )$. Denote $A_0=A\cup (A\ast A)\cup (A/A)\cup (A\backslash A)$ and $A_{n+1}=A_n\cup (A_n\ast A_n)\cup (A_n/A_n)\cup (A_n\backslash A_n),$ where $n\in \mathbb{N},$$A/B={\cup }_{a\in A,b\in B}a/b$ and $A\backslash B={\cup }_{a\in A,b\in B}a\backslash b$.

Definition 4 

([14]). Let $(H,\ast )$ be a hypergroup. Then the subhypergroup A of H is closed to the right (resp. closed to the left) if $\forall a\in H$, $\forall (x,y)\in A^2$, and from $y\in x\ast a$ (resp. $y\in a\ast x$) follows $a\in A$. We say that A is closed if it is closed to the right and the left.

Theorem 1 

([14]). Let $(H,\ast )$ be a hypergroup and $A\subseteq H$. Then $<A>={\cup }_{n\ge 0}{A}_n$ is the least closed subhypergroup of H.

If $H=<A>$ and A is a finite set ($\left|A\right|<\infty$), then we say that the hypergroup $(H,\ast )$ is finitely generated hypergroup.

A polygroup or quasi-canonical hypergroup is a special kind of hypergroup. Polygroups were introduced by P. Corsini, and later, they were studied by P. Bonansinga and Ch.G. Massouros [18], Cristea [19] and others. The hypergroup $(P,·)$ is called a polygroup if the following conditions hold:

Definition 5 

([9]). A polygroup $(P,·)$ is a nonempty set equipped with a hyperoperation “·” with the following properties:

(1) 

$(a·b)·c=a·(b·c),\forall a,b,c\in P,$

(2) 

$\exists !e_p\in E\left(P\right)$ such that $e_p·a=a=a·e_p,\forall a\in P,$

(3) 

$\forall a\in P\exists !b\in i\left(a\right)$ such that $e_p\in a·b.$ We denote $b=a^{-1},$

(4) 

$a\in b·c\Rightarrow b\in a·c^{-1},c\in b^{-1}·a,\forall a,b,c\in P$.

Definition 6 

([9]). Let $(P,·)$ be a polygroup. A nonempty subset K of P is a subpolygroup if:

(1) 

$x,y\in K$ implies that $x·y\subseteq K$;

(2) 

$x\in K$ implies that $x^{-1}\in K$.

A subpolygroup N is normal if $N·x=x·N$ (or $x^{-1}·N·x\subseteq N$), for all $x\in P$.

We say that $(P,·)$ is a proper polygroup if there exist elements $a,b$ in P such that $|a·b|\ne 1$.

Proposition 1. 

Let $(P,·)$ be a polygroup such that $|a·a^{-1}|=1$, for all $a\in P$. Then P is a group.

Proof. 

Let $\{c,b,\alpha ,\beta \}\subseteq P$. Then we have

$$\{\alpha ,\beta \}\subseteq c·b⟹\alpha \in c·b⟹b\in c^{-1}·\alpha$$

$$⟹\beta \in c·b\subseteq c·c^{-1}·\alpha =\alpha .$$

Thus $\alpha =\beta$ and so $|c·b|=1,$ for all $(c,b)\in P^2$. Hence the polygroup $(P,·)$ is not proper. □

Definition 7 

([9]). Let X be a nonempty subset of a polygroup P and $\left\{A_i\right|i\in J\}$ be the family of all subpolygroups of P which contain X. Then we have

$${\cap }_{i\in J}{A}_i=<X>=\cup \{x_1^{{\epsilon }_1}·\dots ·x_k^{{\epsilon }_k}|x_i\in X,k\in \mathbb{N},{\epsilon }_i\in \{-1,1\}\}.$$

If $X=\{x_1,x_2,\dots ,x_n\}$, then the subpolygroup $<X>$ is denoted $<x_1,\dots ,x_n>$. The finitely generated polygroup P = $<x_1,\dots ,x_n>$ is called good if for all $a,b\in P$, $\left|ab\right|<\infty$.

Proposition 2. 

Let $(P,·)$ be a finite polygroup and $x\in P$. Then x has a finite order, i.e., there is a natural number $n_x$ such that $e_p\in x^{n_x}$.

Proof. 

Let $(P,·)$ be a finite polygroup and $x\in P$. There exists $(r,s)\in {\mathbb{N}}^2$ ($r>s$) such that $x^r\cap x^s\ne \varnothing .$ If $y\in x^r\cap x^s$, then $e_p\in y·y^{-1}\subseteq x^r·x^{-s}\subseteq x^{r-s}·x^s·x^{-s}.$ Thus $O\left(x\right)=n_x⩽r-s.$ □

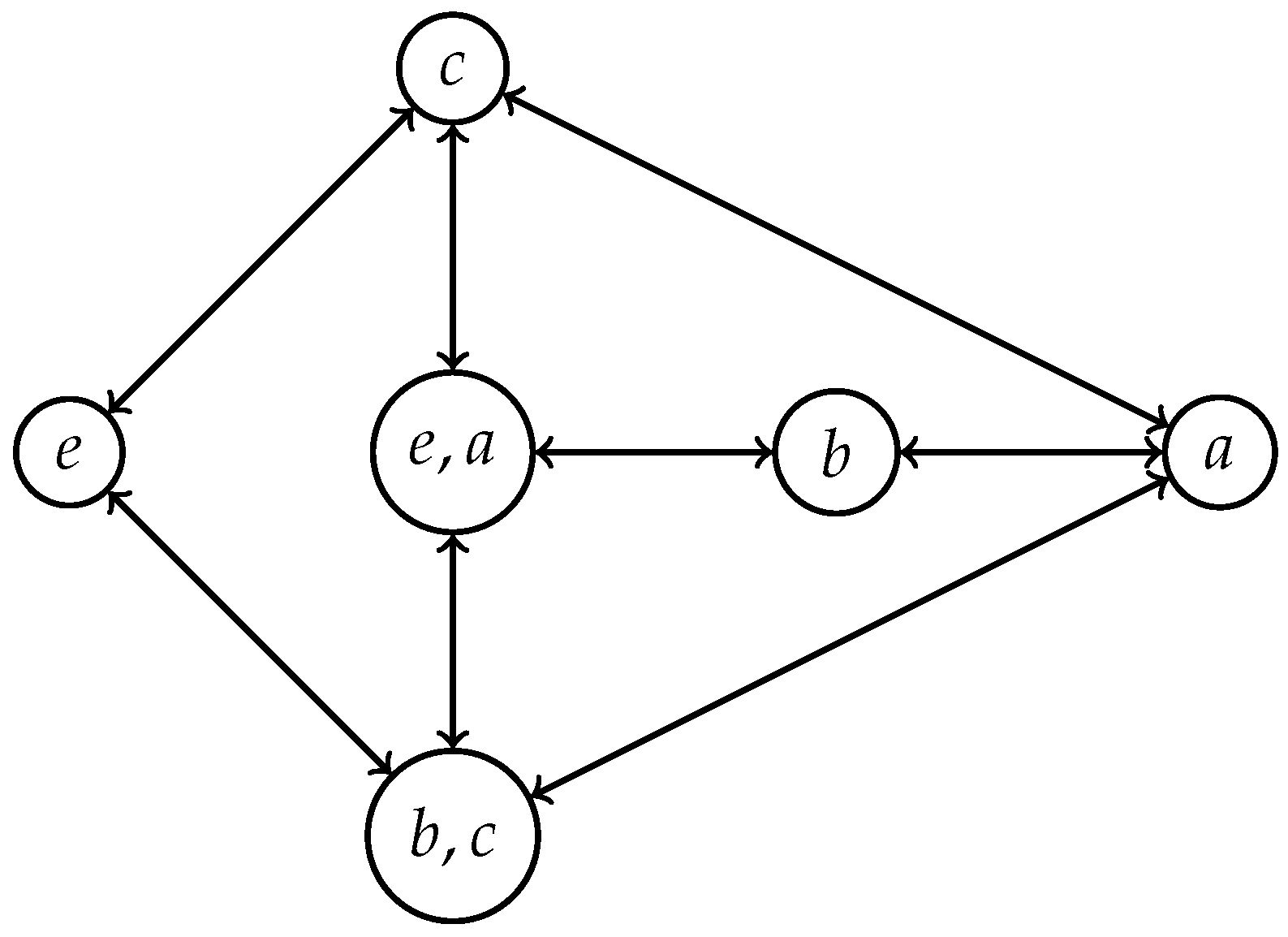
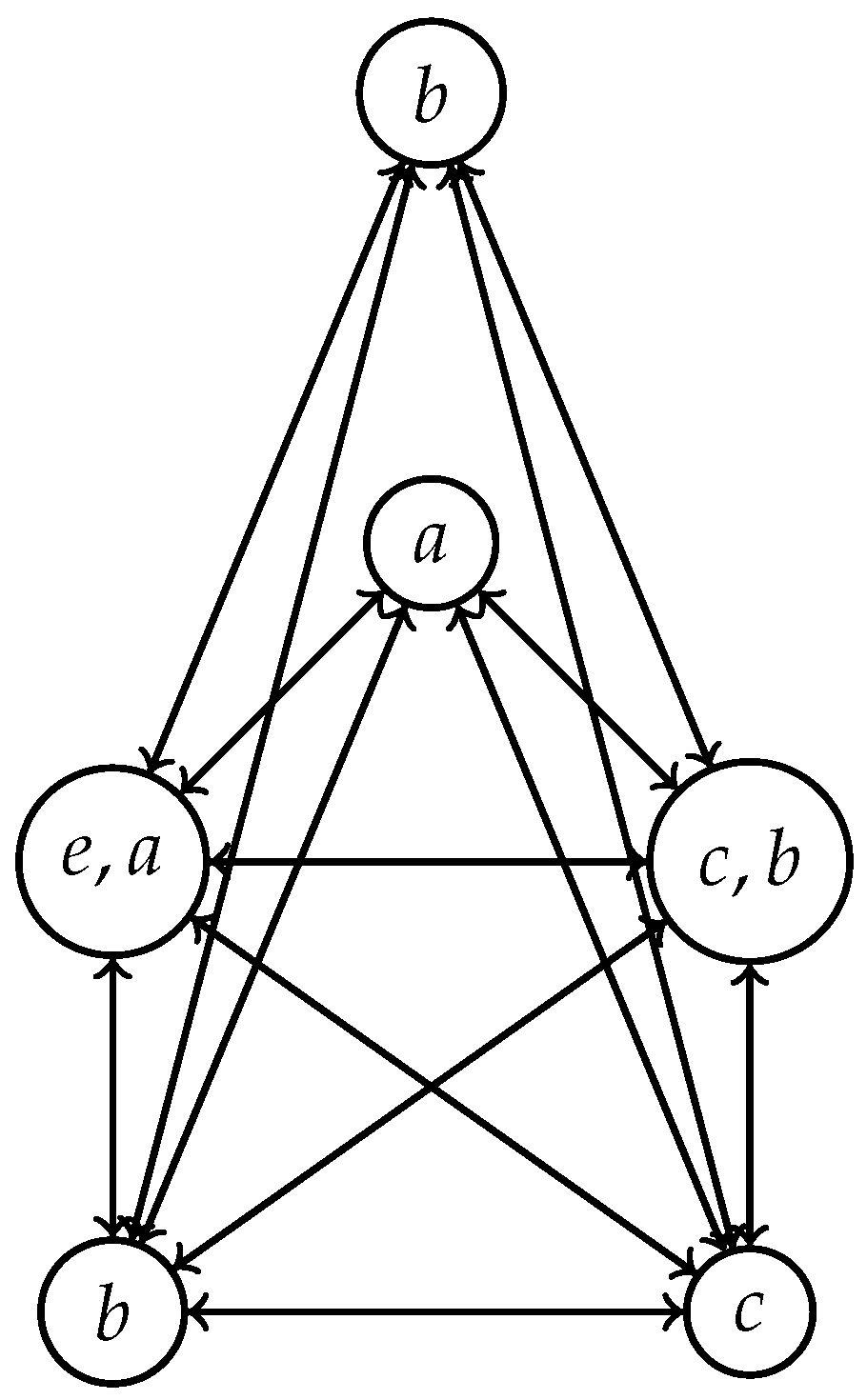
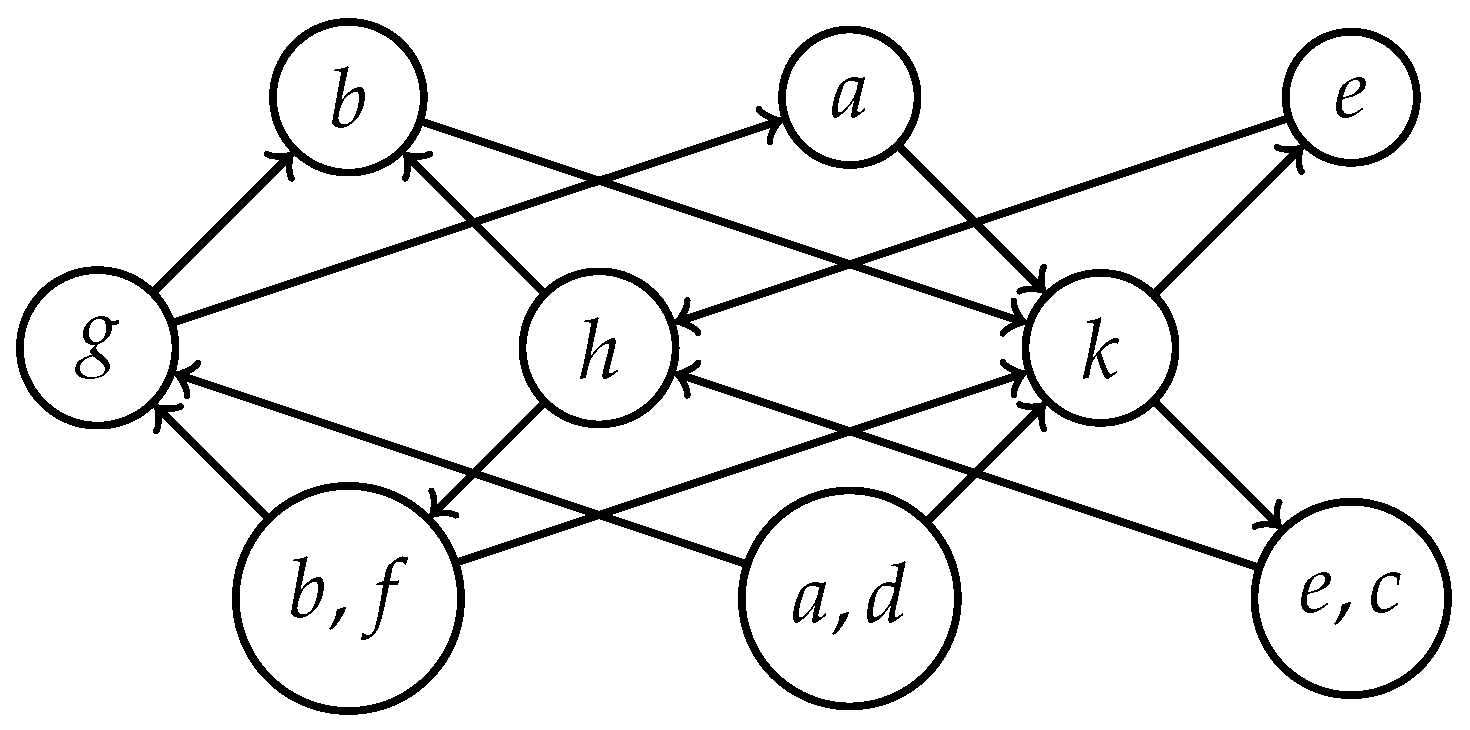
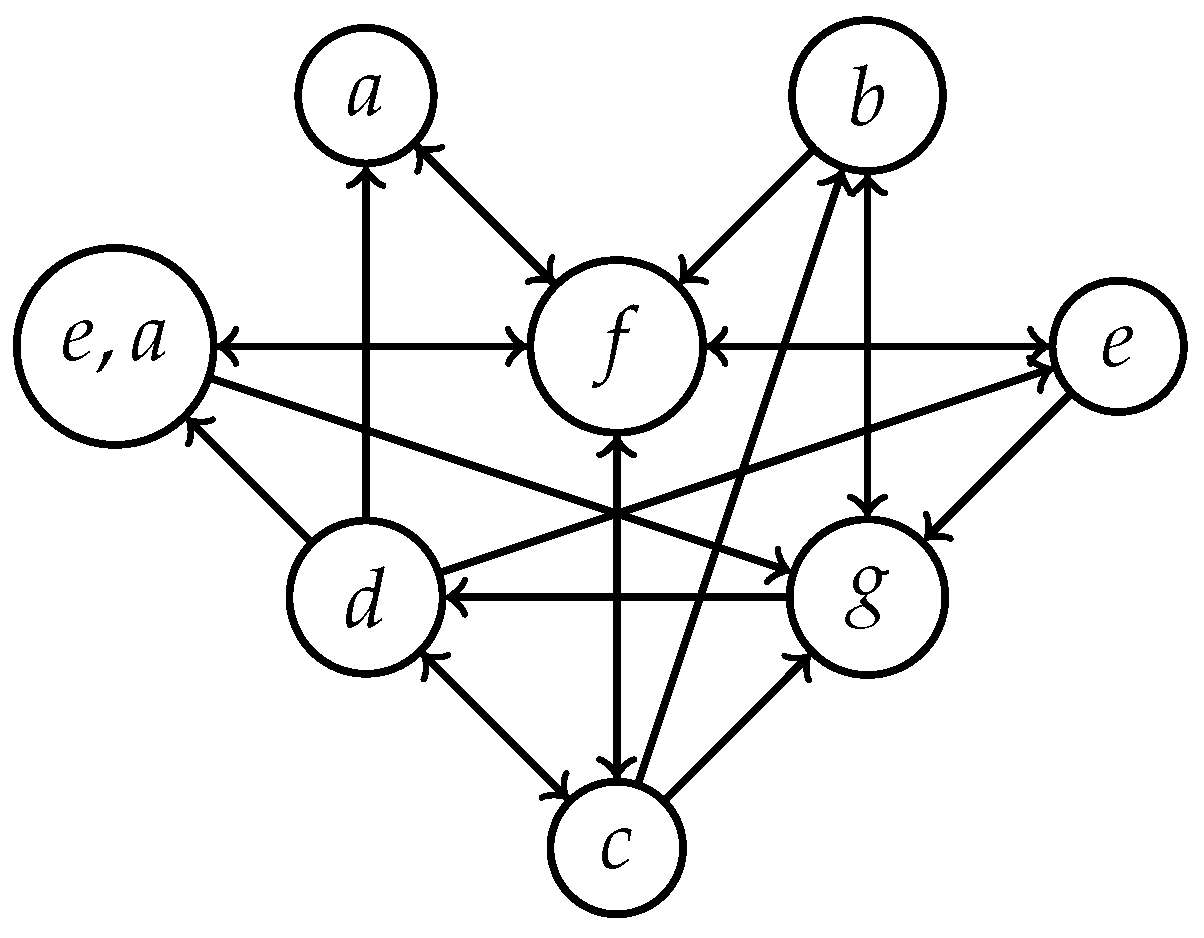
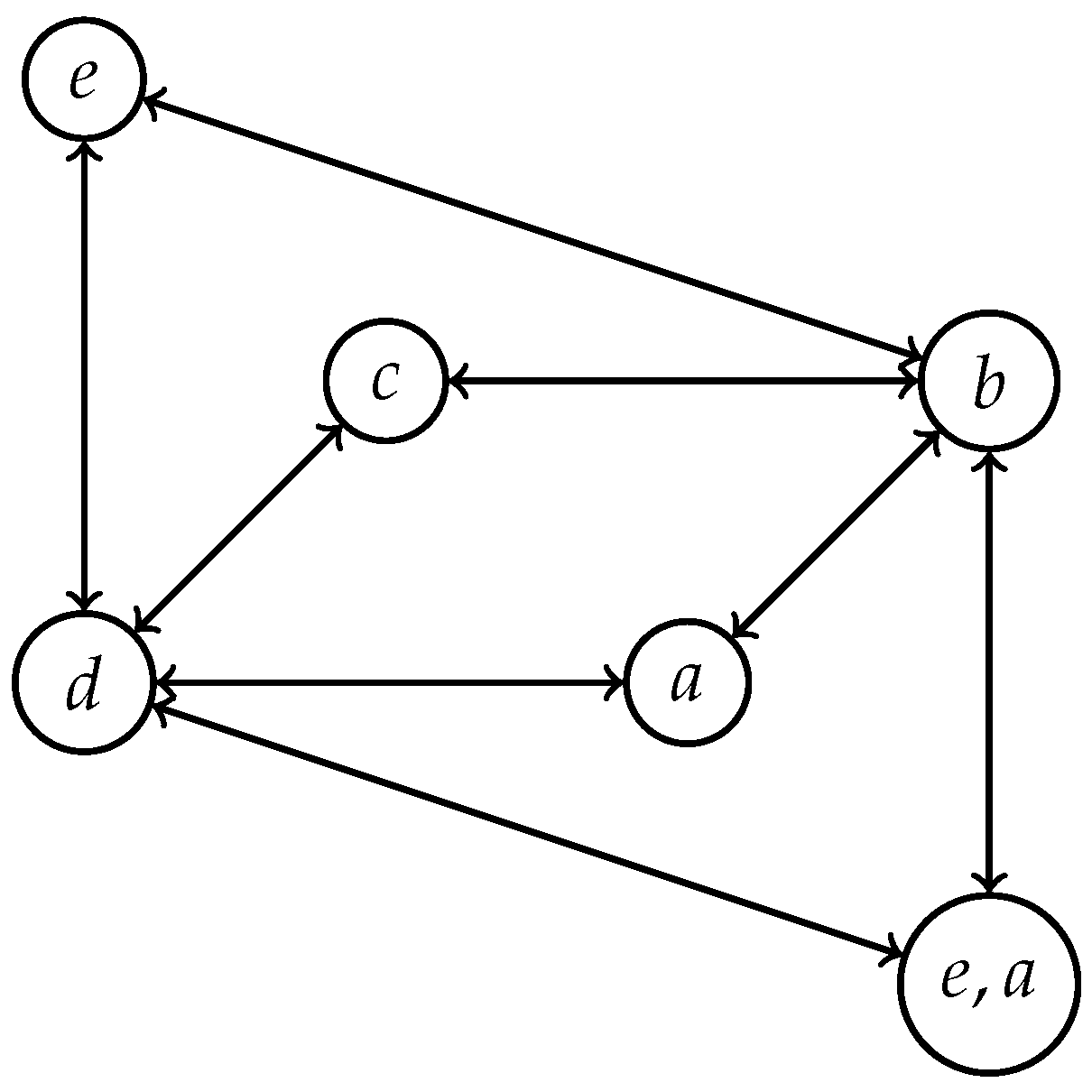
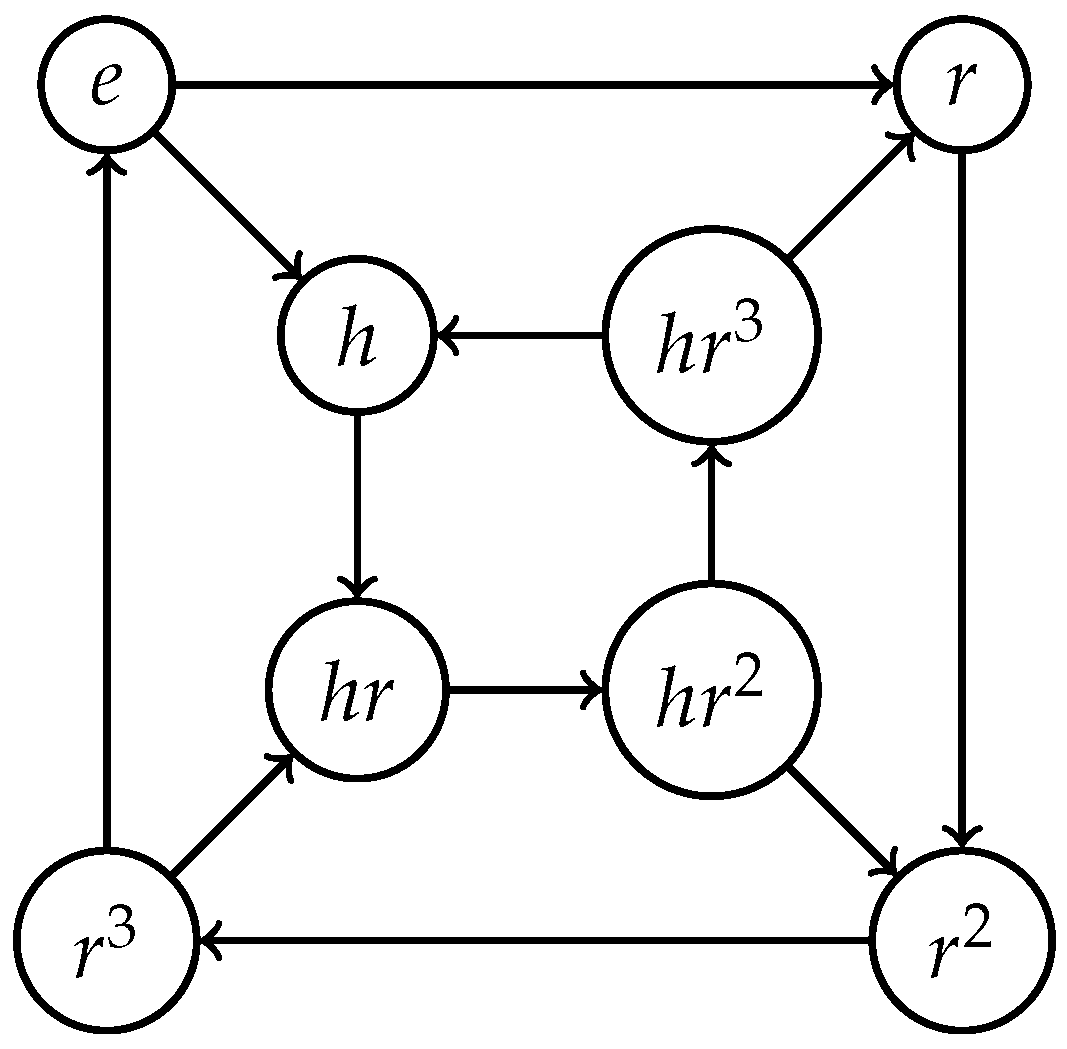
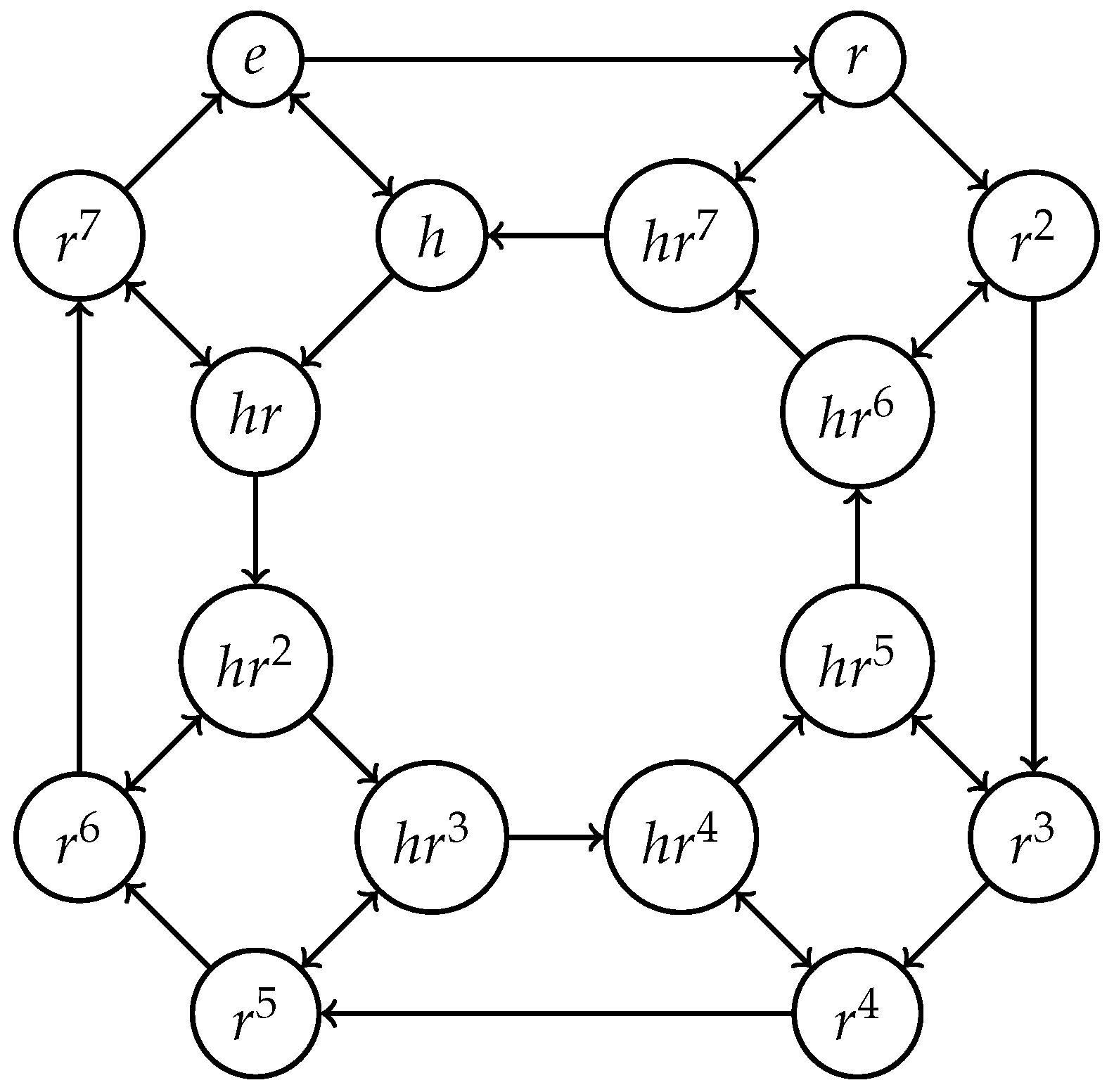
3. On Cayley Directed Graphs of Polygroups

A polygroup, or quasi-canonical hypergroup, is a special kind of a hypergroup introduced by Corsini and later studied by Bonansinga and Corsini [18]. Polygroups satisfy all conditions of canonical hypergroups except the commutativity. Comer introduced this class of hypergroups independently, using the name of polygroups [20]. He emphasized the importance of polygroups by analyzing them in connections to graphs, relations, Boolean and cylindric algebras. For more study about polygroup theory we refer to the work of Davvaz [9]. In this section we introduce generalized Cayley directed graphs for the class of good minimal generated polygroups. We give many examples of digraphs on some finite polygroups. We also investigate the existence of a path between each pair of vertices of Cayley digraph of a polygroup and we prove that the Cayley directed graph, $Caydi\overrightarrow{(P,\prod S)}$, is connected. Moreover, we show the existence of a cycle for each vertex of the Cayley directed graph [21,22].

Definition 8. 

Let $(P,·)$ be a polygroup and $S=\{s_1,s_2,\dots ,s_n\}$ be a nonempty finite subset of P. Then we say that S is a good minimal generator of P, if the following conditions are valid:

(1) 

$P=<s_1,s_2,\dots ,s_n>$ is a good finitely generated polygroup.

(2) 

$\forall s\in S,<S-\left\{s\right\}>\ne P$.

In this case we say P is a good mimimal generated polygroup or, for simplicity, gmg-polygroup and denote P = $<<s_1,s_2,\dots ,s_n>>$.

Definition 9. 

Let P = $<S>$ be a finitely generated polygroup.

(I) 

The generalized Cayley digraph of P with respect to S, which is denoted by $GCaydi\overrightarrow{(P,\prod S)}$, is the pair $(V\overrightarrow{(P,\prod S)}$, $E\overrightarrow{(P,\prod S)})$, where

(1) 

$\prod S$ is the set of all finite products of elements of S and $S^{-1}.$ A finite product $U\in \prod S$ is called positive if $U=s_1{s}_2\dots s_k$, where $s_i\in S$ ($\forall j,1⩽j⩽k$), i.e., U is a finite product of elements of S.

(2) 

$\mathcal{V}$ = $V\overrightarrow{(P,\prod S)}$ is the set of vertices consisting of distinct elements of P and $\prod S$.

(3) 

$\mathcal{E}$ = $E\overrightarrow{(P,\prod S)}$ = {$(U,V)$|$U^{-1}V\cap S\ne \varnothing ,$ $U,V\in \mathcal{V}$, for all $U\ne V$}. An ordered pair $(U,V)$ is an edge with direction from U to V and is called an $arc.$

(II) 

The generalized Cayley digraph $GCaydi\overrightarrow{(P,\prod S)}$ is called minimal if S is a good minimal generator of P. In this case we denote P = $<<S>>$. Moreover, the minimal generalized Cayley digraph is denoted by $Caydi\overrightarrow{(P,\prod S)}$ and is called a Cayley digraph of P.

Definition 10. 

Let K = $<T>$ and P = $<S>$ be two finitely generated polygroups. We say $GCaydi\overrightarrow{(K,\prod T)}$ is a sub-Cayley digraph of $GCaydi\overrightarrow{(P,\prod S)}$ and is denoted by $GCaydi\overrightarrow{(K,\prod T)}<GCaydi\overrightarrow{(P,\prod S)}$, if $V\overrightarrow{(K,\prod T)}\subseteq V\overrightarrow{(P,\prod S)}$ and $E\overrightarrow{(K,\prod T)}\subseteq E\overrightarrow{(P,\prod S)}$.

Proposition 3. 

Let P be a polygroup and S and $S^{\prime }$ are finite generators of P. If $S\subseteq S^{\prime }$, then $GCaydi\overrightarrow{(P,\prod S)}<GCaydi\overrightarrow{(P,\prod S^{\prime })}$.

Proof. 

The proof is straightforward. □

Example 1. 

Let the polygroup $(P,·)$ be as follows:

$$\begin{array}{ccccc}·& e& a& b& c\\ e& e& a& b& c\\ a& a& \{e,a\}& c& \{b,c\}\\ b& b& c& e& a\\ c& b& \{b,c\}& a& \{e,a\}\end{array}$$

P is generated by $\left\{c\right\}$. Then we have $\prod \left\{c\right\}=\left\{c,\{e,a\},\{b,c\}\right\}$, $\mathcal{V}$ = $V\overrightarrow{(P,\prod S)}=\{e,a,b,c,\{e,a\},$$\{b,c\}\}$ and the $Caydi\overrightarrow{(P,\prod \{c\left\}\right)}$ is as in Figure 1.

Moreover, P is generated by $\{a,b\}$. Then we have $\prod \{a,b\}=\left\{e,a,b,c,\{e,a\},\{b,c\}\right\}$, and the $Caydi\overrightarrow{(P,\prod \{a,b\left\}\right)}$ looks like Figure 2.

Definition 11. 

For two distinct vertices $U,V\in \mathcal{V}$ in $Caydi\overrightarrow{(P,\prod S)}$, we say:

(1) 

An ordered pair $(U,V)$ is a directed adjacent and denoted by $\overrightarrow{(U,V)}$ (or $UV$ and say the direction is from U to V), where $(U,V)$ is an arc in $Caydi\overrightarrow{(P,\prod S)}$.

(2) 

An ordered pair $(U,V)$ is symmetrically adjacent and denoted by $\{U,V\}$, where both $(U,V)$ and $(V,U)$ are arcs in $Caydi\overrightarrow{(P,\prod S)}$.

(3) 

An ordered pair $(U,V)$ is oriented adjacent and denoted by $[U,V]$ whenever $(U,V)$ is an arc in $Caydi\overrightarrow{(P,\prod S)}$, but $(V,U)$ is not an arc in $Caydi\overrightarrow{(P,\prod S)}$.

Definition 12. 

For two vertices (not necessarily distinct) $U,V\in \mathcal{V}$ in $Caydi\overrightarrow{(P,\prod S)}$:

(1) 

A simple walk $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)}$ is a sequence of vertices $U=U_1,U_2,\dots ,U_k=V$ in $\mathcal{V}$, beginning with U and ending with V such that consecutive vertices $U_i,U_{i+1}$ for $1\le i\le k-1$ are direction-adjacent in $Caydi\overrightarrow{(P,\prod S)}$.

(2) 

A simple walk $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)}$ in which no vertex is repeated is called a path.

(3) 

Two vertices $U,V$ are connected if there is a path $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)}$. Moreover, a $Caydi\overrightarrow{(P,\prod S)}$ itself is connected if every pair of vertices is connected.

Definition 13. 

For two vertices (not necessarily distinct) $U,V\in \mathcal{V}$ in $Caydi\overrightarrow{(P,\prod S)}$:

(1) 

A directed walk $U⟶V$ in $Caydi\overrightarrow{(P,\prod S)}$ is a sequence of vertices $U=U_1,U_2,\dots ,U_k=V$ in $\mathcal{V}$, beginning with U and ending at V such that consecutive vertices $U_i,U_{i+1},$ for $1\le i\le k-1,$ are arcs $\overrightarrow{(U_i,U_{i+1})}$ in $Caydi\overrightarrow{(P,\prod S)}$.

(2) 

A directed walk $U⟶V,$ in $Caydi\overrightarrow{(P,\prod S)},$ in which no vertex is repeated, is called a directed path.

Definition 14. 

For two vertices (not necessarily distinct) $U,V\in \mathcal{V}$ in $Caydi\overrightarrow{(P,\prod S)}$:

(1) 

A symmetric walk $U⟷V$ in $Caydi\overrightarrow{(P,\prod S)}$ is a sequence of vertices $U=U_1,U_2,\dots ,U_k=V$ in $\mathcal{V}$, beginning with U and ending with V such that consecutive vertices $U_i,U_{i+1},$ for $1\le i\le k-1$ are symmetrically adjacent in $\mathcal{V}$.

(2) 

A symmetric walk $U⟷V$ in $Caydi\overrightarrow{(P,\prod S)}$ in which no vertex is repeated is called a symmetric path.

(3) 

Two vertices $U,V$ are symmetrically connected if there is a symmetric path $U⟷V$ in $Caydi\overrightarrow{(P,\prod S)}$. A $Caydi\overrightarrow{(P,\prod S)}$ itself is symmetrically connected if every pair of vertices are symmetrically connected.

Definition 15. 

For two vertices (not necessarily distinct) $U,V\in \mathcal{V}$ in $Caydi\overrightarrow{(P,\prod S)}$:

(1) 

An oriented walk $U⟼V$ in $Caydi\overrightarrow{(P,\prod S)}$ is a sequence of vertices $U=U_1,U_2,\dots ,U_k=V$ in $\mathcal{V}$, beginning with U and ending with V such that consecutive vertices $U_i,U_{i+1},$ for $1\le i\le k-1$ are oriented adjacent $[U_i,U_{i+1}]$ in $Caydi\overrightarrow{(P,\prod S)}$.

(2) 

An oriented $U⟼V$ walk in $Caydi\overrightarrow{(P,\prod S)}$, in which no vertices are repeated, is called an oriented path.

Lemma 1. 

Let P = $<<S>>$ be a gmg-polygroup. Then,

(1) 

for every finite product $U\in \prod S,$ there is a path $e_p\sim U$ in $Caydi\overrightarrow{(P,\prod S)}$;

(2) 

for every pair of finite products $U,V\in \prod S,$ there is a path $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)}$.

Proof. 

(1)

Let U = $s_1^{t_1}\dots s_n^{t_n}\in \prod S,$ for some $s_1,\dots ,s_n\in S$ and $t_i\in \{-1,1\}$. We prove the first part of the Lemma by induction on n. If $n=1$ there is a path $e_p\sim s_1^{t_1}$. Now suppose there is a path $e_p\sim s_1^{t_1}\dots s_k^{t_k}$, where $s_1,\dots ,s_k\in S$ and $t_i\in \{-1,1\}$. We need to show that there is a path $e_p\sim s_1^{t_1}\dots s_{k+1}^{t_{k+1}}$, for every $s_{k+1}\in S$ and $t_{k+1}\in \{-1,1\}$. If $t_{k+1}=1$, then the arc ($s_1^{t_1}\dots s_k^{t_k}$,$s_1^{t_1}\dots s_{k+1}^{t_{k+1}})\in Caydi\overrightarrow{(P,\prod S)}$. Now suppose that $t_{k+1}=-1$, then the arc ($s_1^{t_1}\dots s_{k+1}^{t_{k+1}}$,$s_1^{t_1}\dots s_k^{t_k})\in Caydi\overrightarrow{(P,\prod S)}$ is the edge that we need. Therefore, we have the path $e_p\sim s_1^{t_1}\dots s_{k+1}^{t_k+1},$ which is constructed with the path $e_p\sim s_1^{t_1}\dots s_k^{t_k}$ and the consecutive vertices $s_1^{t_1}\dots s_{k+1}^{t_{k+1}}$, and $s_1^{t_1}\dots s_k^{t_k}$.

(2)

It is sufficient to show that for every pair of vertices $U,V\in \mathcal{V}$, there is a path $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)}$. By part (1) there are the paths $e_p\sim U$, $e_p\sim V$. Therefore, there is a path $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)}$.

□

Theorem 2. 

The Cayley directed graph $Caydi\overrightarrow{(P,\prod S)}$ is connected.

Proof. 

Let $x,y\in \mathcal{V}$ be two vertices in $Caydi\overrightarrow{(P,\prod S)}$. Then, we consider the following two cases:

(1)

If $x,y\in \prod S$. By the previous Lemma there is a path $x\sim y$ in $Caydi\overrightarrow{(P,\prod S)}$. Thus x and y are connected.

(2)

If $x\notin \prod S$ or $y\notin \prod S$, then we have $x\in P$ or $y\in P$. Without losing the generality of the proof, let $x\in P$. There is a finite product $U=s_1^{t_1}\dots s_n^{t_n}\in \prod S,$ such that $x\in U$, for some $s_1,\dots ,s_n\in S$ and $t_i\in \{-1,1\}$. Now let $s\in S$, then $x,Us$ are adjacent because $e_p\in x^{-1}Us$. Further, $Us$ is a finite product of elements of S; then, by the previous Lemma there is a path $e_p\sim Us$ in $Caydi\overrightarrow{(P,\prod S)}$. Consequently, there is the path $x\sim e_p$, consisting of adjacent vertices $(x,Us)$ and path $Us\sim e_p$ in $Caydi\overrightarrow{(P,\prod S)}$. Similarly, we have the path $y\sim e_p$ and so the path $x\sim y,$ exists.

□

Definition 16. 

For two distinct vertices $U,V\in \mathcal{V}$ in $Caydi\overrightarrow{(P,\prod S)}$:

(1) 

A cycle on vertices $U,V$ is a path $U\sim V$ in $Caydi\overrightarrow{(P,\prod S)},$ and it consists a sequence of consecutive vertices $U=U_1,U_2,\dots ,U_n=V,$$n⩾3,$ and the arc $UV$ or $VU.$

(2) 

A directed cycle on vertices U,V is a directed path $U⟶V$ in $Caydi\overrightarrow{(P,\prod S)},$ and it consists of consecutive vertices $U=U_1,U_2,\dots ,U_n=V,$ and directed adjacent $(V=U_n,U=U_1)$.

(3) 

A symmetric cycle on vertices U,V is a symmetric path $U⟷V,$ in $Caydi\overrightarrow{(P,\prod S)},$ and it consists of consecutive vertices $U=U_1,U_2,\dots ,U_n=V,$ and symmetricaly adjacent $\{V=U_n,U=U_1\}$.

(4) 

An oriented cycle on vertices U,V is an oriented path $U⟼V$ in $Caydi\overrightarrow{(P,\prod S)},$ and it consists of consecutive vertices $U=U_1,U_2,\dots ,U_n=V,$ and oriented adjacent $[V=U_n,U=U_1]$.

Example 2. 

Let $P=\{e,a,b,c,d,f,g,h,k\}$. Consider the polygroup $(P,·)$, where · is defined on P as follows:

$$\begin{array}{cccccccccc}·& e& a& b& c& d& f& g& h& k\\ e& e& a& b& c& d& f& g& h& k\\ a& a& b& e& d& f& c& h& k& g\\ b& b& e& a& f& c& d& k& g& h\\ c& c& d& f& e& a& b& g& h& k\\ d& d& f& c& a& b& e& h& k& g\\ f& f& c& d& b& e& a& k& g& h\\ g& g& h& k& g& h& k& \{e,c\}& \{a,d\}& \{b,f\}\\ h& h& k& g& h& k& g& \{a,d\}& \{b,f\}& \{e,c\}\\ k& k& g& h& k& g& h& \{b,f\}& \{e,c\}& \{a,d\}\end{array}$$

It is easy to see that $P=<<\left\{h\right\}>>$. Then $Caydi\overrightarrow{(P,\{h\left\}\right)}$ looks like Figure 3.

In this example there exists an oriented cycle for each of the vertices of $Caydi\overrightarrow{(P,\prod S)}$.

Proposition 4. 

Let $P=<<S>>$ be a finite gmg-polygroup. Then for every $U\in \prod S$, there exists a positive product $W=s_1{s}_2\dots s_k\in \prod S,$ consisting of U.

Proof. 

Let $U=s_1^{t_1}\dots s_k^{t_k}\in \prod S$, where $s_1,\dots ,s_k\in S$ and $t_i\in \{-1,1\}$, $1\le i\le k$. If $t_j=-1$, then $s_i^{t_j}\subseteq s_j^{n_{s_j}-1}$, for every $1\le j\le k$, where $n_{s_j}$ is the order of $s_j$ in the polygroup of $P.$ We define the positive product $W=w_1{w}_2\dots w_k$, where

$$w_j=\left\{\begin{array}{cc}{s}_j\hfill & t_j=1,\hfill \\ {s_j}^{n_{s_j}-1}\hfill & t_j=-1,\hfill \end{array}\right.$$

for every $1\le j\le k$. We have $U\subseteq W$. □

Proposition 5. 

Suppose that $P=<<S>>$ is a gmg-polygroup. If $U\in \prod S,$ and $Us=U$ (resp. $U=sU$), for every $s\in S$, then $U=P$.

Proof. 

If $U=Us$, for every $s\in S$, then there exists the positive product $W\in \prod S,$ that $U^{-1}\subseteq W$. Hence $U=U{s}^{n_s}W$⊇$U{s}^{n_s}{U}^{-1}$⊇$\left\{e_p\right\}$. Indeed, $e_p\in s^{n_s}$. Therefore $S\subseteq U$. Now let $x\in P$; there exists $D\in \prod S,$ such that $x\in D$. Thus $x\in D\subseteq UD=U,$ and so $P=U$ holds. □

Definition 17. 

In $Caydi\overrightarrow{(P,\prod S)},$ the cycle $U_1,U_2,\dots ,U_n$ is called rotational if $n⩾3,$ and $U_n$ is in the form of $U_1{s}^t$ or $s^t{U}_1,$ in which $s\in S$ and $t\ge 1$.

Proposition 6. 

Let $P=<<S>>$ be a gmg-polygroup and $\left|P\right|\ge 3$. Moreover, suppose that $U\in \prod S,$ and $Us\ne P$ (resp. $sU\ne P$), for some $s\in S$. Then there exists a rotational cycle in $Caydi\overrightarrow{(P,\prod S)},$ starting with U.

Proof. 

Let $x,y,z$ be distinct elements in P and $Us\ne P$, for some $s\in S$. There exists $s\in S$ such that $Us\ne U.$ Now we have the paths $U\sim x$, $x\sim y$, $y\sim z,$ and $z\sim Us.$ So we have the rotational cycle $U,\dots ,x,\dots ,y,\dots ,z,\dots ,Us$ in $Caydi\overrightarrow{(P,\prod S)},$ which starts with U. □

Corollary 1. 

Suppose that $P=<<S>>$ is a gmg-polygroup and $\left|P\right|\ge 3$. If $a\in P,$ then there exists a cycle in $Caydi\overrightarrow{(P,\prod S)},$ which starts with a.

Proof. 

Let $a\in P$; then there exists $U\in \prod S,$ such that $a\in U$. Now consider the cycle $a,\dots ,U,\dots ,Us$ in $Caydi\overrightarrow{(P,\prod S)},$ in which $a\sim U$ is a path and $U\sim Us$ is the rotational cycle, for some $s\in S$. □

Corollary 2. 

Let $P=<<S>>$ be a gmg-polygroup. Then for every vertex $v\in \mathcal{V},$ there exists a cycle in Caydi$\overrightarrow{(P,\prod S)}$ which starts with v.

Remark 1. 

If $P=<<S>>$ is a proper polygroup of order 2, then the $Caydi\overrightarrow{(P,\prod S)}$ is a cycle. Indeed, the only proper polygroup of order 2 is as below:

$$\begin{array}{ccc}·& e& a\\ e& e& a\\ a& a& \{e,a\}\end{array}$$

We can see that $S=\left\{a\right\}$ is the only minimal generator of P and the $Caydi\overrightarrow{(P,\prod \{a\left\}\right)}$ looks like Figure 4.

Definition 18. 

Let P = $<<S>>$ be a gmg-polygroup. Then we say S is symmetric whenever the $Caydi\overrightarrow{(P,\prod S)}$ is symmetrically connected.

Remark 2. 

Let P = $<<S>>$ be a gmg-polygroup and $S^{-1}=S$. Then S is symmetric.

Example 3. 

Let $P=\{e,a,b,c,d,f,g\}$. Consider the polygroup $(P,·)$, where · is defined on P as follows:

$$\begin{array}{cccccccc}·& e& a& b& c& d& f& g\\ e& e& a& b& c& d& f& g\\ a& a& e& b& c& d& f& g\\ b& b& b& \{e,a\}& d& c& g& f\\ c& c& c& g& \{e,a\}& f& d& b\\ d& d& d& f& b& g& c& \{e,a\}\\ f& f& f& d& g& b& \{e,a\}& c\\ g& g& g& c& f& \{e,a\}& b& d\end{array}$$

It is easy to see that P = $<<S>>$, $where$ S = {f, g}. $Inthiscasewehave$ S ≠ S⁻¹. $Indeed,$ S⁻¹ = {f, d}. $The$ $Caydi\overrightarrow{(P,\prod \{f,g\})}$ is as in Figure 5, which is not symmetrically connected.

Proposition 7. 

Suppose that $P=<<S>>$ is a gmg-polygroup. If P is finite and the $Caydi\overrightarrow{(P,\prod S)}$ is not symmetrically connected, then there exists a directed cycle in $Caydi\overrightarrow{(P,\prod S)},$ that the union of its vertices is a subpolygroup of P.

Proof. 

Since $Caydi\overrightarrow{(P,\prod S)}$ is not symmetrically connected, there exists $s\in S$ such that $s\ne s^{-1}$. Now let the directed cycle $s,s^2,s^3,\dots ,s^{n_s},$ where $n_s$ is the order of s in P. We have ${\bigcup }_{i=1}^{n_s}{s}^i$ as a subpolygroup of $P.$ □

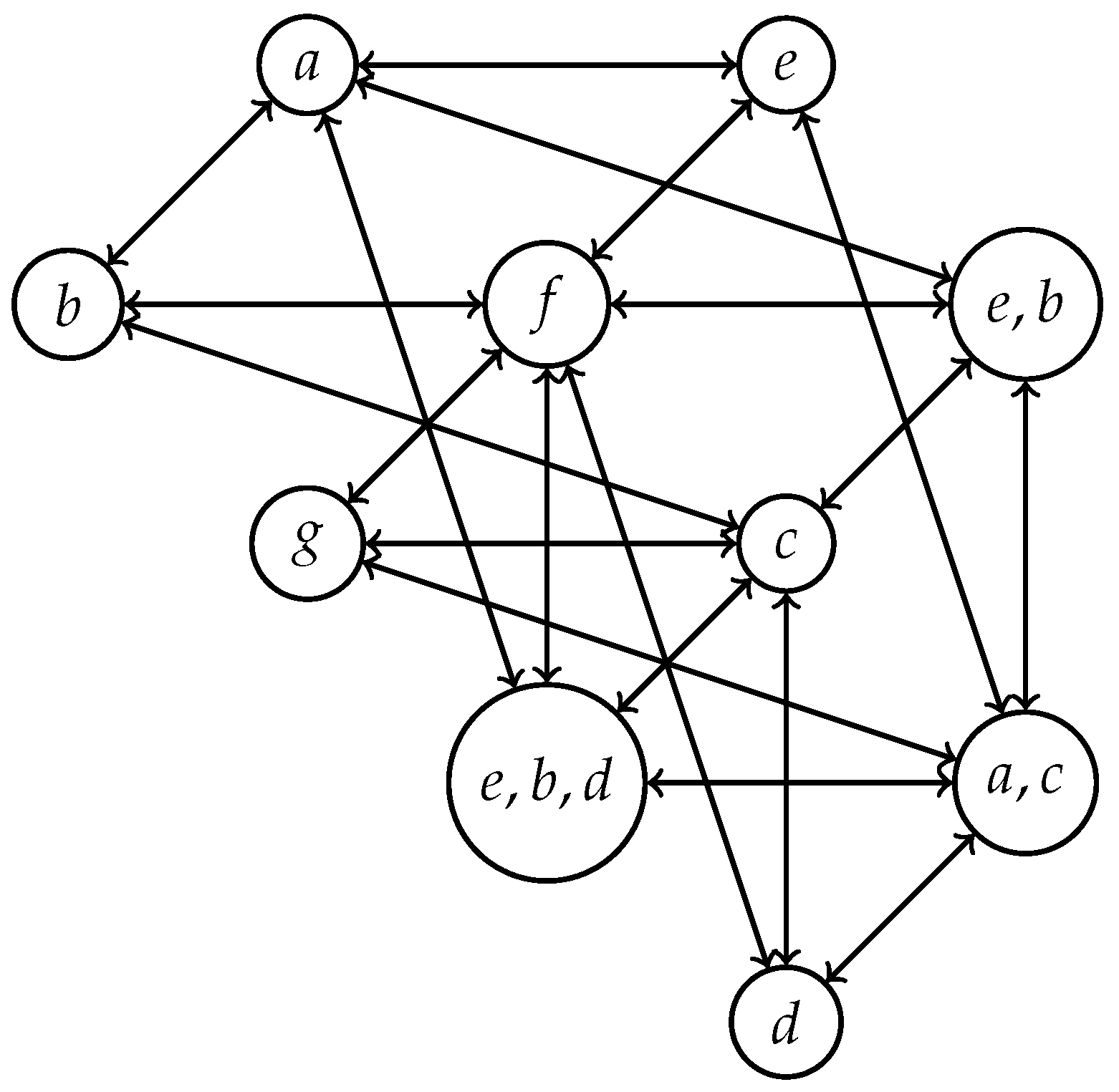
4. Polygroups Derived from Conjugacy Classes of Groups

Let G be a group and $a\in G$. We set $a^G=\left\{ga{g}^{-1}\right|g\in G\}$ and say the conjugate class of a is in G. We set all conjugate classes of elements in G by $\overline{G}$. In this section we focus on the polygroups of conjugacy classes of a group G which is introduced for the first time by H. Campaigne in [23], and we characterize the Cayley directed graph associated from the group of symmetries of a regular polygon which includes rotations and reflections, which is shown by $D_n.$

Theorem 3 

([23]). Let $(G,·)$ be a group and $\overline{G}$ be the set of all conjugate classes of G. Then $(\overline{G},\ast )$ is a polygroup, where for two elements $a^G$ and $b^G$ in $\overline{G}$,

$$a^G\ast b^G=\{c^G:c^G\subseteq a^G·b^G\}.$$

Example 4. 

Let G be the dihedral group

$$D_4=<r,h|r^4=h^2=1,h^{-1}rh=r^{-1}>=\{1,r,r^2,r^3,h,hr,h{r}^2,h{r}^3\}.$$

We have five conjugacy classes consisting of $e=\left\{1\right\},a=\left\{r^2\right\},b=\{r,r^3\},c=\{hr,h{r}^3\},d=\{h,h{r}^2\}.$ The polygroup $(\overline{G},\ast )$ is as below and it is generated by $S=\{b,d\}.$

$$\begin{array}{cccccc}·& e& a& b& c& d\\ e& e& a& b& c& d\\ a& a& e& b& c& d\\ b& b& b& \{e,a\}& d& c\\ c& c& c& d& \{e,a\}& b\\ d& d& d& c& b& \{e,a\}\end{array}$$

Moreover, we have $\prod S=\{b,c,d,\{e,a\left\}\right\}$, $\mathcal{V}=V\overrightarrow{(P,\prod S)}=\{e,a,b,c,d,\{e,a\}\}$ and the $Caydi\overrightarrow{(\overline{G},\prod \{b,d\})}$ is symmetrically connected and looks like Figure 6.

Also the $Caydi\overrightarrow{(D_4,\prod \{r,h\})}$ is as in Figure 7.

Proposition 8. 

Let $G=<S>$ be a finitely generated group on S. Then $\overline{G}=<\overline{S}>$ is a finitely generated polygroup, where $\overline{S}=\left\{S^G\right|s\in S\}$.

Proof. 

Let $a^G\in \overline{G}.$ Then there exist $s_1,s_2,\dots ,s_n$ in $S^{\pm 1}$ such that $a=s_1·\dots ·s_n.$ Thus $a^G\subseteq s_1^G·\dots ·s_n^G$ and so $a^G\in s_1^G\ast \dots \ast s_n^G\subseteq <\overline{S}>$. □

Proposition 9. 

Let $G=<S>$ be a finitely generated group. Then

(1) 

if $(a,b)\in E\overrightarrow{(G,\prod S)}$, then $(a^G,b^G)\in E\overrightarrow{(\overline{G},\prod \overline{S})}.$

(2) 

The $Caydi\overrightarrow{(\overline{G},\prod \overline{S})}$ is symmetrically connected.

Proof. 

(1) Let $(a,b)\in G^2$ and $a·b\in S$. Then there exist $s_1,s_2,\dots ,s_n$ in $S^{\pm 1}$ such that $a^{-1}·b=s_1·\dots ·s_n.$ Hence ${\left(a^{-1}\right)}^G·b^G={\left(a^G\right)}^{-1}·b^G\subseteq s_1^G·\dots ·s_n^G$ and so ${\left(a^G\right)}^{-1}\ast b^G\cap s_1^G\ast \dots \ast s_n^G\ne \varnothing$. Consequently $(a^G,b^G)\in E\overrightarrow{(\overline{G},\prod \overline{S})}.$

(2) Since $\overline{G}$ is a commutative polygroup we have $(a^G,b^G)\in E\overrightarrow{(\overline{G},\prod \overline{S})}$ if and only if $(b^G,a^G)\in E\overrightarrow{(\overline{G},\prod \overline{S})}.$ Thus $Caydi\overrightarrow{(\overline{G},\prod \overline{S})}$ is symmetrically connected. □

In abstract algebra a dihedral group is a group of symmetries of a regular polygon which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups and they play an important role in group theory, geometry and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. We use the notion $D_n$ for a dihedral group of a regular $n\text{-}$polygon and define:

$$D_n=<<a,b>>=<a,b|a^n=b^2=1,b^{-1}ab=a^{-1}>,(n\ge 3).$$

Let $0\le k\le n$, we denote $c_k=c_{-k}=c_{n-k}=\{a^{-k},a^k\}$, $A_o=\left\{a^{2k+1}b\right|0\le k\le n-1\}$, $A_e=\left\{a^{2k}b\right|0\le k\le n-1\}$ and $A=\{b,ab,a^{2}b,\dots ,a^{n-1}b\}$. Then the conjugate classes of $D_n$ are as below:

(1)

If $n=2m+1$, we have $\overline{D_n}=\{\left\{1\right\},\{a^{-1},a\},\dots ,\{a^{-m},a^m\},\{b,ab,a^{2}b,\dots ,a^{2m}b\}\}=\{c_0,c_1,\dots ,c_m,A\}$.

(2)

If $n=2m$, we have $\overline{D_n}=\{\left\{1\right\},\{a^{-1},a\},\dots ,\{a^{-(m-1)},a^{m-1}\},\left\{a^m\right\},\left\{a^{2k}b\right|0\le k\le m-1\},\left\{a^{2k+1}b\right|0\le k\le m-1\}=\{c_0,c_1,\dots ,c_m,A_o,A_e\}$.

Theorem 4. 

Let $(\overline{D_n},\ast )$ be the commutative polygroup of conjugacy classes of $D_n$. Then we have:

(1) 

$c_1^{2k}=\{c_0,c_2,\dots ,c_{2k}\}$ and $c_1^{2k+1}=\{c_1,c_3,\dots ,c_{2k+1}\}$, for all $k\ge 0$.

(2) 

If $n=2m+1,$ then $A^2=\{c_0,c_1,c_2,\dots ,c_m\}$ and $A\ast c_k=A,$ for all $k\ge 0$. In this case $\overline{D_n}=<<A>>.$

(3) 

If $n=2m$, then $c_1\ast A_e=A_o$, $c_1\ast A_o=A_e$, $A_e^2=A_o^2=\{c_0,c_2,c_4,\dots \}$ and $A_e\ast A_o=\{c_1,c_3,c_5,\dots \}.$ In this case $\overline{D_n}=<<c_1,A_e>>.$

Proof. 

(1) Let $c_i,c_j\in \overline{D_n}$. Then we have $c_i\ast c_j=\{c_{i+j}$, $c_{j-i}\},$ where $c_{i+j}=c_t,$ and $i+j{\equiv }_{n}t.$ Hence $c_1^{2k}=\{c_0,c_2,\dots ,c_{2k}\}$ and consequently $c_1^{2k}\ast c_1=c_1^{2k+1}=\{c_1,c_3,\dots ,c_{2k+1}\},$ for all $k\ge 0.$ (2) If $n=2m+1,$ and $a^{i}b,a^{j}b\in A,$ then by the relation of the dihedral group $D_n$ we have $a^{i}b·a^{j}b=a^{i-j}.$ Thus $A·A=\{a,a^2,a^3,\dots ,a^{n-1}\}$ and so $A\ast A=A^2=\{c_0,c_1,c_2,\dots ,c_m\}.$ Moreover, $a^{i}b·a^j=a^{i-j}b.$ Consequently, $A·a^j=A$ and so $A\ast c_k=A,$ for all $k\ge 0$. Also, the equality $\overline{D_n}=<<A>>$ holds. (3) The proof is the same as part (2). □

Theorem 5. 

Let $(\overline{D_n},\ast )$ be the commutative polygroup of conjugacy classes of $D_n$. Then,

(1) 

If $n=2m+1$ and $\overline{D_n}=<<A>>,$ then $V\overrightarrow{(\overline{D_n},\prod A)}=\{c_0,c_1,\dots ,c_m,A,A^2\}.$

(2) 

If $n=2m$ and $\overline{D_n}=<<c_1,A_e>>,$ then

$$V\overrightarrow{(\overline{D_n},\prod \{c_1,A_e\})}=\{c_0,c_1,\dots ,c_m,A_e,A_o,c_1^2,\dots ,c_1^m\}.$$

Proof. 

(1) Let $n=2m+1$. According to Theorem 4, we have:

$$A^k=\left\{\begin{array}{cc}{A}^2=\{c_0,c_1,c_2,\dots ,c_m\},\hfill & k=2t,\hfill \\ A\hfill & k=2t+1\hfill \end{array}\right.$$

Hence $\prod A=\{A,A^2\}$ and so $V\overrightarrow{(\overline{D_n},\prod A)}=\{c_0,c_1,\dots ,c_m,A,A^2\}.$

(2) Now let $n=2m$. Using part (3) of Theorem 4 we have $\overline{D_n}=<<c_1,A_e>>.$ Moreover, according to part (1) $c_1^{m+i}=c_1^i,$ for all $i\ge 2$, and so $c_1^2,\dots ,c_1^m$ are distinct subsets of $\prod \{c_1,A_e\}.$ Hence $V\overrightarrow{(\overline{D_n},\prod \{c_1,A_e\})}=\{c_0,c_1,\dots ,c_m,A_e,A_o,c_1^2,\dots ,c_1^m\}.$ □

Example 5. 

Let G be the dihedral group,

$$D_8=<r,h|r^8=h^2=1,h^{-1}rh=r^{-1}>.$$

We have five conjugate classes consisting of $e=\left\{1\right\},a=\{r^{-1},r\},b=\{r^{-2},r^2\},c=\{r^{-3},r^3\},$$d=\left\{r^4\right\},f=\{h,h{r}^2,h{r}^4\},g=\{hr,h{r}^3\}.$ The polygroup $(\overline{G},\ast )$ is as below and it is generated by $S=\{a,f\}.$

$$\begin{array}{cccccccc}·& e& a& b& c& d& f& g\\ e& e& a& b& c& d& f& g\\ a& a& \{e,b\}& \{a,c\}& b& c& f& g\\ b& b& \{a,c\}& \{e,b\}& a& b& f& g\\ c& c& b& a& \{e,b\}& a& g& f\\ d& d& c& b& a& e& f& g\\ f& f& g& f& g& f& \{e,b,d\}& \{a,c\}\\ g& g& f& g& f& g& \{a,c\}& \{e,b,d\}\end{array}$$

Moreover, we have $\prod S=\{a,f,\{e,b\},\{a,c\},\{e,b,d\},g\},$ $\mathcal{V}=V\overrightarrow{(P,\prod S)}=\{e,a,b,c,d,,f,g,\{e,b\},\{a,c\},\{e,b,d\}\}$ and the $Caydi\overrightarrow{(\overline{G},\prod \{a,f\})}$ is symmetrically connected and it looks like Figure 8.

Also the $Caydi\overrightarrow{(D_8,\prod \{r,h\})}$ is as in Figure 9.

5. Conclusions

Polygroups are a generalization of groups in which the composition of any two elements is a nonempty set. By using polygroups, we have introduced in this paper a new digraph called the Cayley digraph of a polygroup as an extension of the Cayley digraph of a group introduced by D. Witte. Moreover, we extend the notion of Cayley (di)graphs to the general framework of polygroups. The motivation for considering polygroups lies in their unique and intriguing algebraic properties. This extension allows us to specify more graphs and extend Sabidussi’s theorem for the class of polygroups. Finaly, we can study the Cayley digraphs of polygroups for interconnection networks. An important outcome of this paper is the fact that we show the connectivity of the Cayley digraph of gmg-polygroups. This research direction is open to new studies, for instance by studying some other properties related to degrees of vertices, number of edges, girth, Eulerian and Hamiltonian cycles in the Cayley digraphs of a polygroup and also analysis of the Cayley digraph for some classes of polygroups.