Explicit Analysis for the Ground Reaction of a Circular Tunnel Excavated in Anisotropic Stress Fields Based on Hoek–Brown Failure Criterion
Abstract
1. Introduction
2. Problem Description
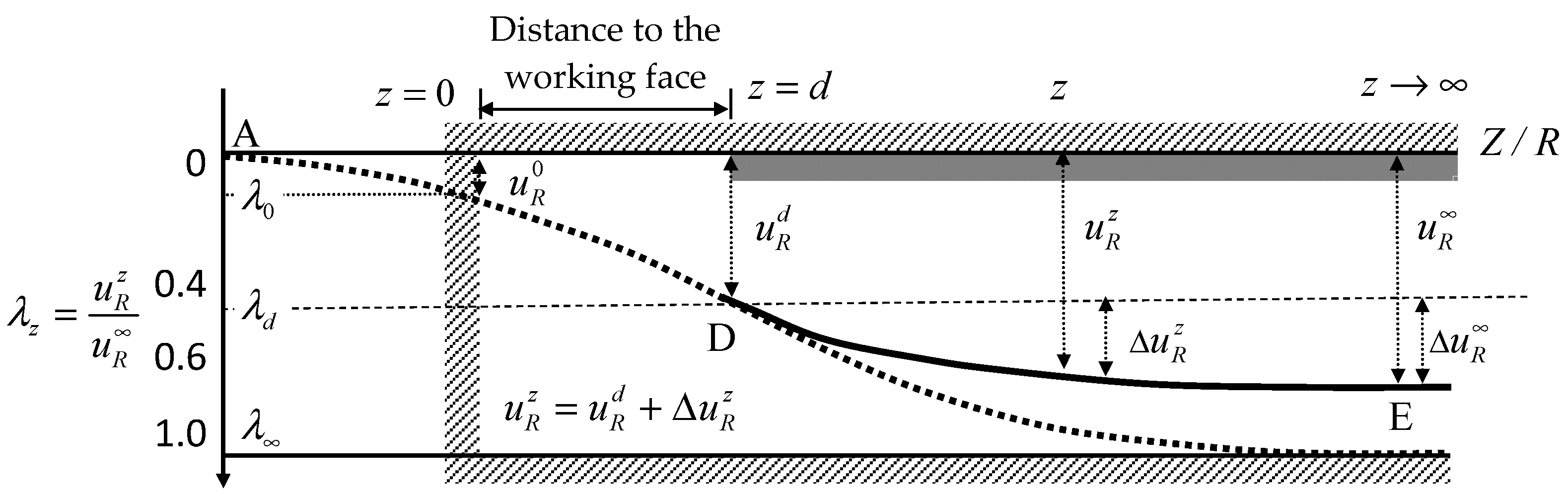
2.1. Correlation between Confinement Loss and the Advancing Excavation of Tunnels
2.2. Variations in Stress around a Circular Tunnel
- (1)
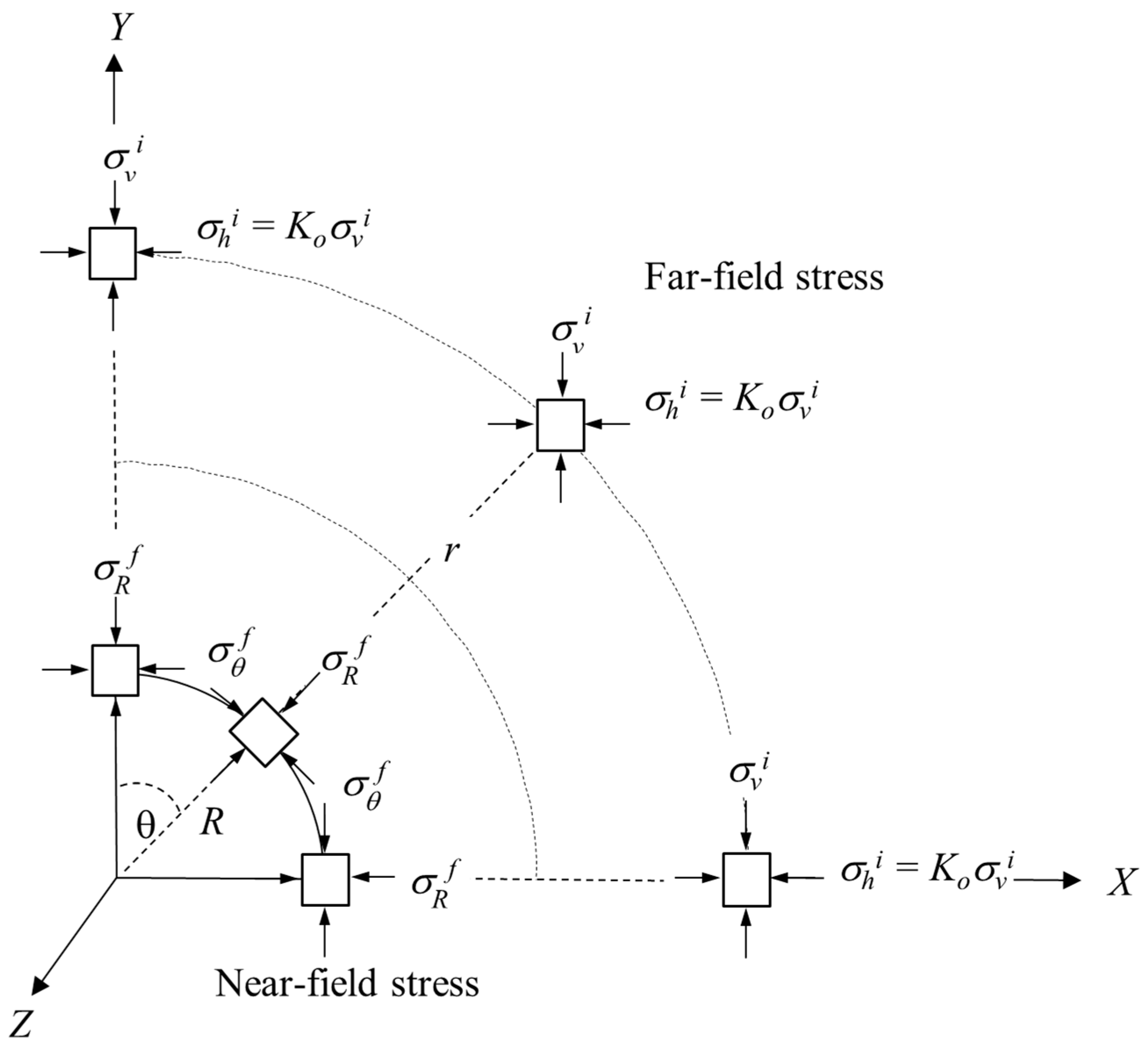
- Stresses in the far field (initial in situ stresses, as r → ∞): Before tunnel excavation, the stresses within the rock masses are in equilibrium and mirror the lithostatic stresses, remaining constant in the surrounding medium of the tunnel. Thus, the initial anisotropic stress within the rock masses can be illustrated as depicted in Figure 3 and represented by the following equation:where , , and are the initial radial stress, the initial tangential stress, and the vertical stress in the polar coordinates (r, θ), respectively. Moreover, the coefficients k1 = 1 + K0, k2 = (1 − Ko)cosθ, and Ko is the lateral stress ratio (Ko = σh/σv = horizontal stress/vertical stress).
- (2)
- Stresses in the near field (final stresses or boundary stresses at the tunnel periphery, R ≤ r < ∞): Upon tunnel excavation, the stresses at any given point within the rock masses surrounding the tunnel undergo alteration. These altered stresses can be determined using the Kirsch solutions, outlined as follows:where and are the final radial stress and the final tangential stress around the tunnel proximity, respectively.
3. Derivation of Stress/Displacement Equations in the Plastic Region
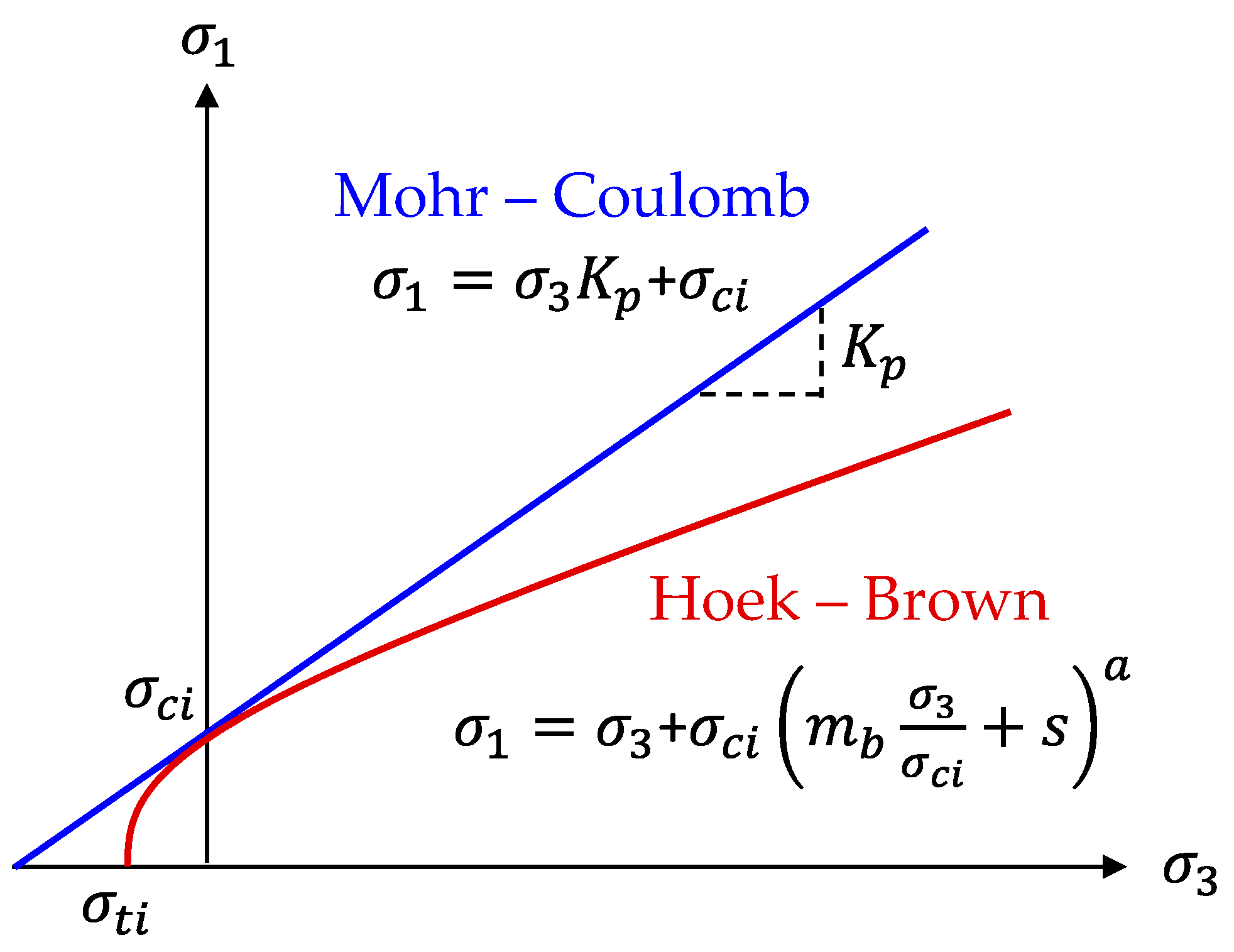
3.1. Derivation of the Confinement Loss in Elastic Limit with the Non-Linear Failure Criteria
3.2. Derivation of the Plastic Radius
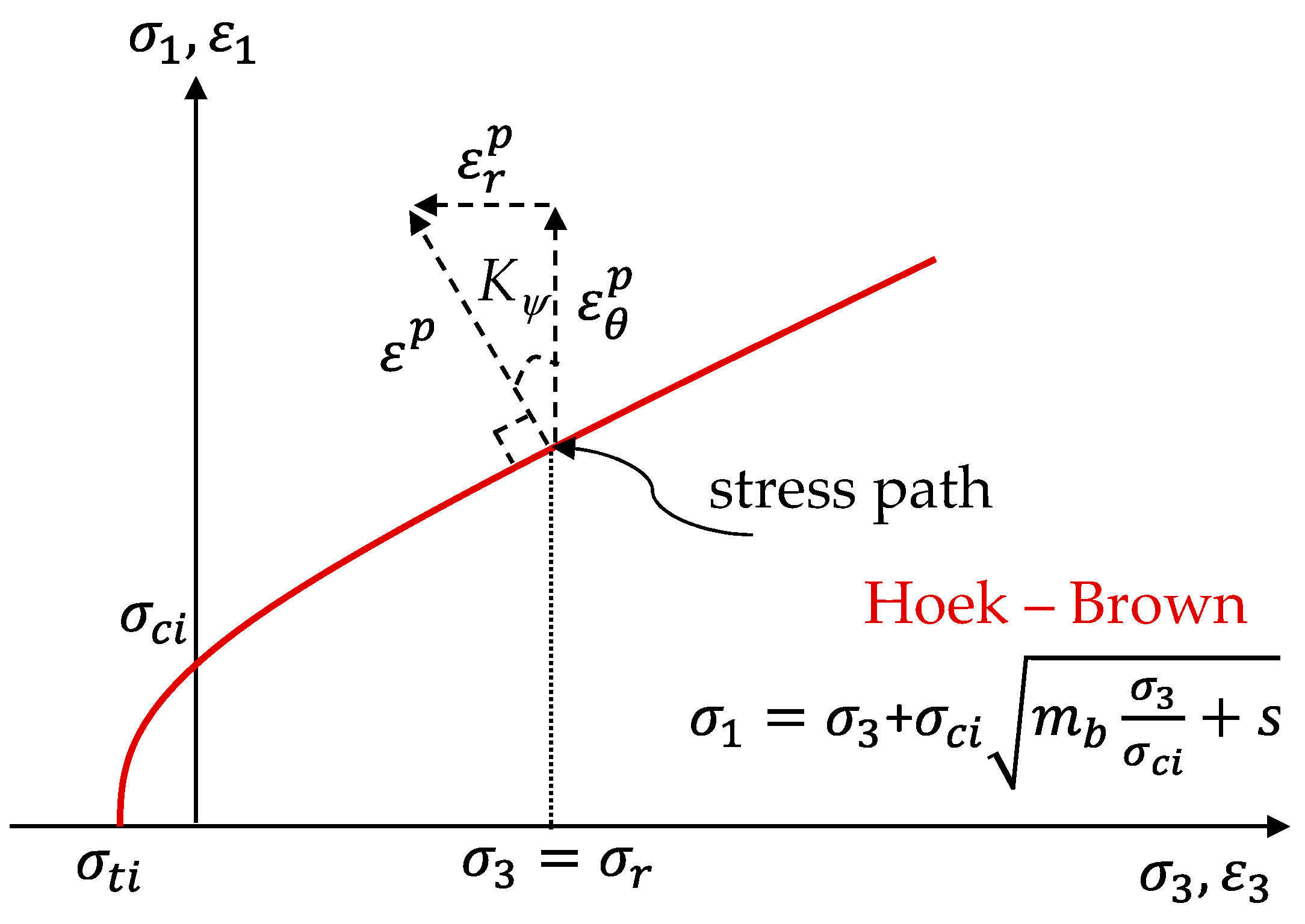
3.3. Derivation of Stress in the Plastic Region
3.4. Derivation of Displacement in the Plastic Region
- (1)
- Homogeneous solution ():
- (2)
- Particular solution ():
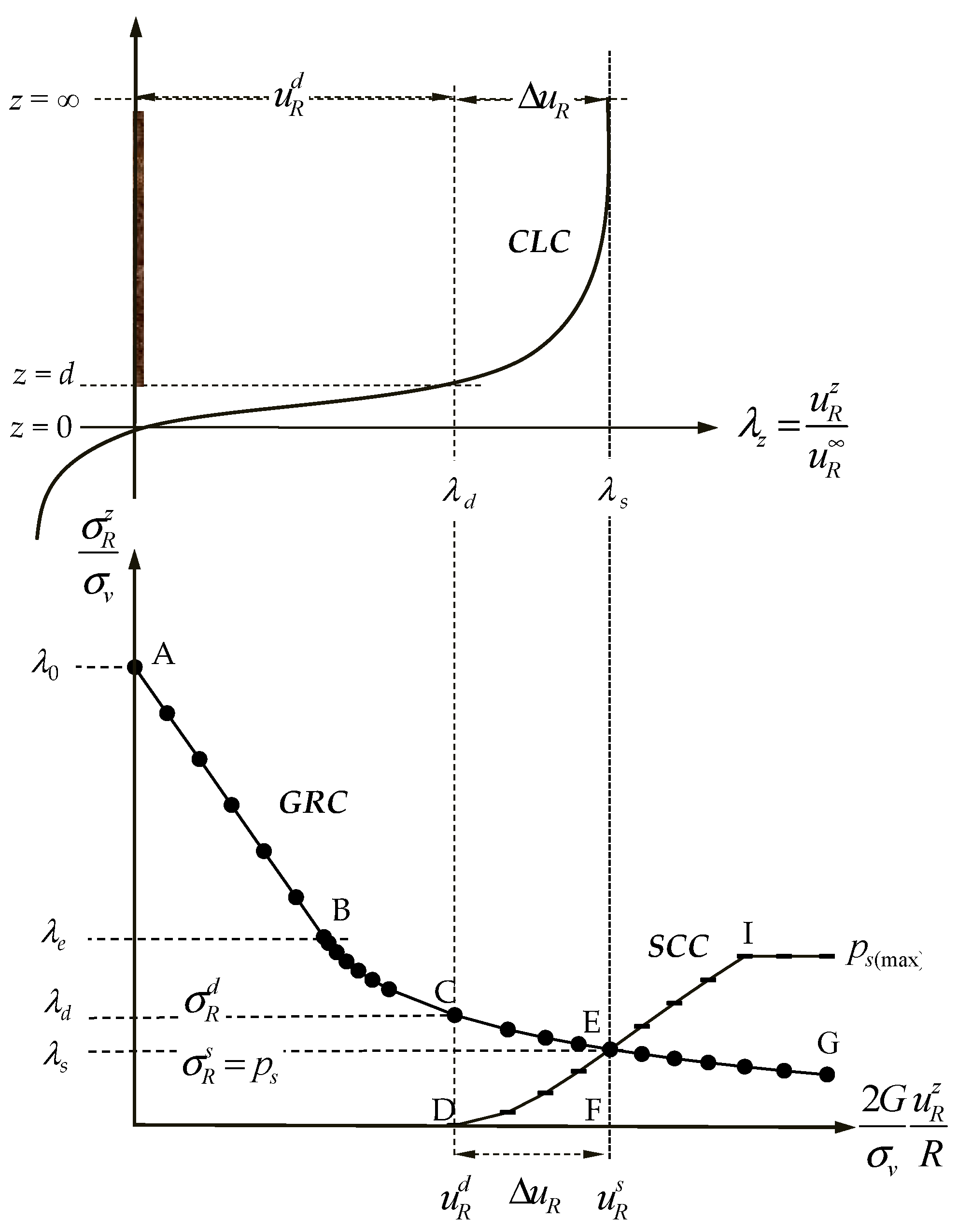
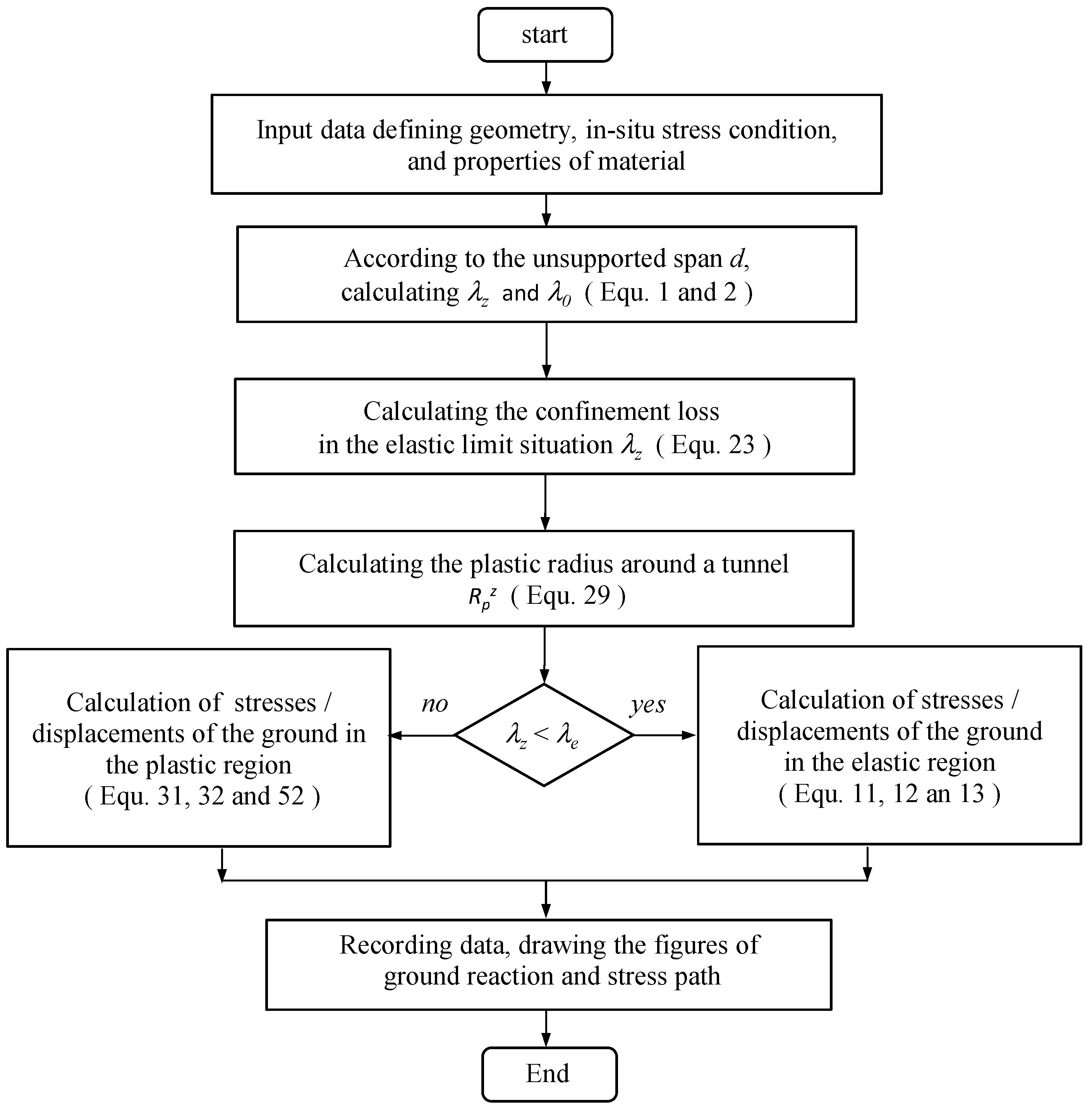
4. Utilization of an Incremental Procedure for the Analytical Solution
Calculation Steps in the Incremental Procedure Method
- (1)
- Input data: This relates to the data of the initial in situ stress, geometry of the tunnel, material properties, and unsupported distance.
- (2)
- To estimate the confinement loss λz at a certain distance z from the tunnel working face, one can use a given value of λz as a chosen effect of the unsupported distance of tunnel excavation. Therefore, λz can be determined from the Equation (1).
- (3)
- Dividing the confinement loss λz by n segments, the incremental step λ can be expressed as
- (4)
- Calculating each step value of λ as
- (5)
- Attaining the final value
- (6)
- According to Equation (23), estimate the confinement loss in the elastic limit situation (λe).
- (7)
- If , it means that the stress state is in the elastic region and that the radial and tangential stresses/displacements can be calculated with Equations (11)–(13).
- (8)
- If , it means that the stress state is in the plastic region and that the plastic radius Rp can be calculated with Equation (29). Once one obtains this value Rp, the procedure automatically substitutes into Equations (31), (32) and (52) for the radial and tangential stresses, and the radial displacement, respectively.
- (9)
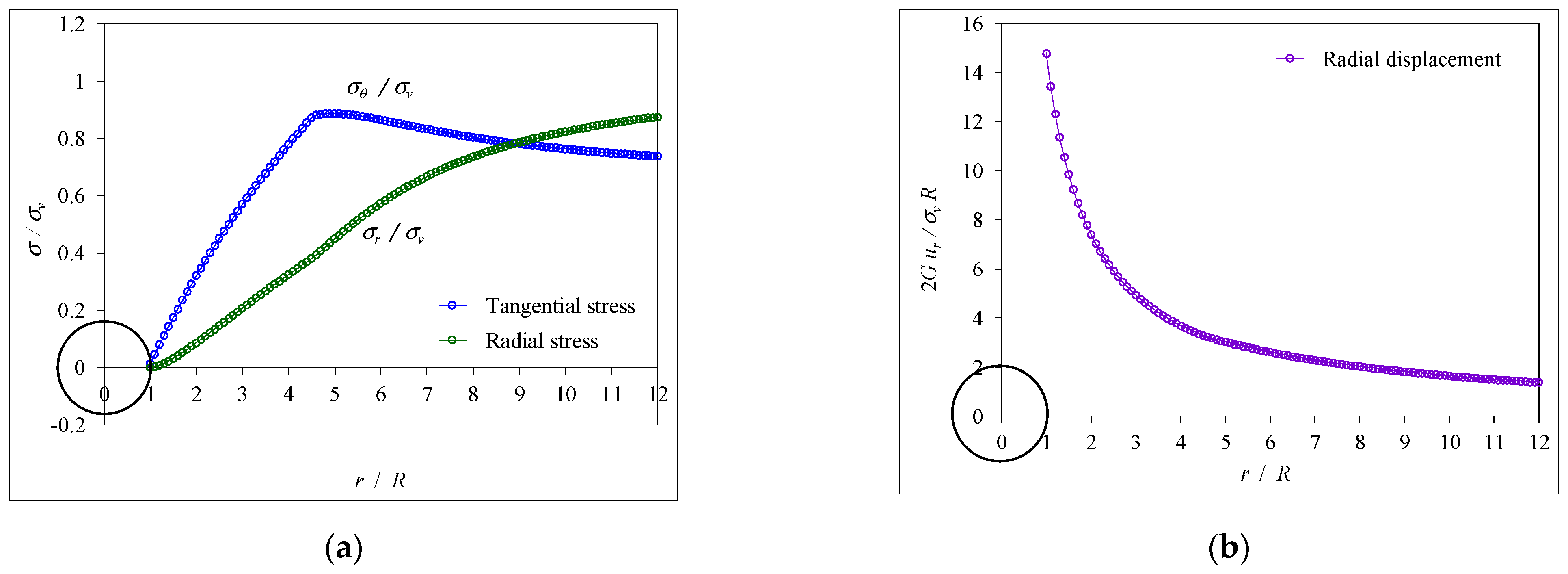
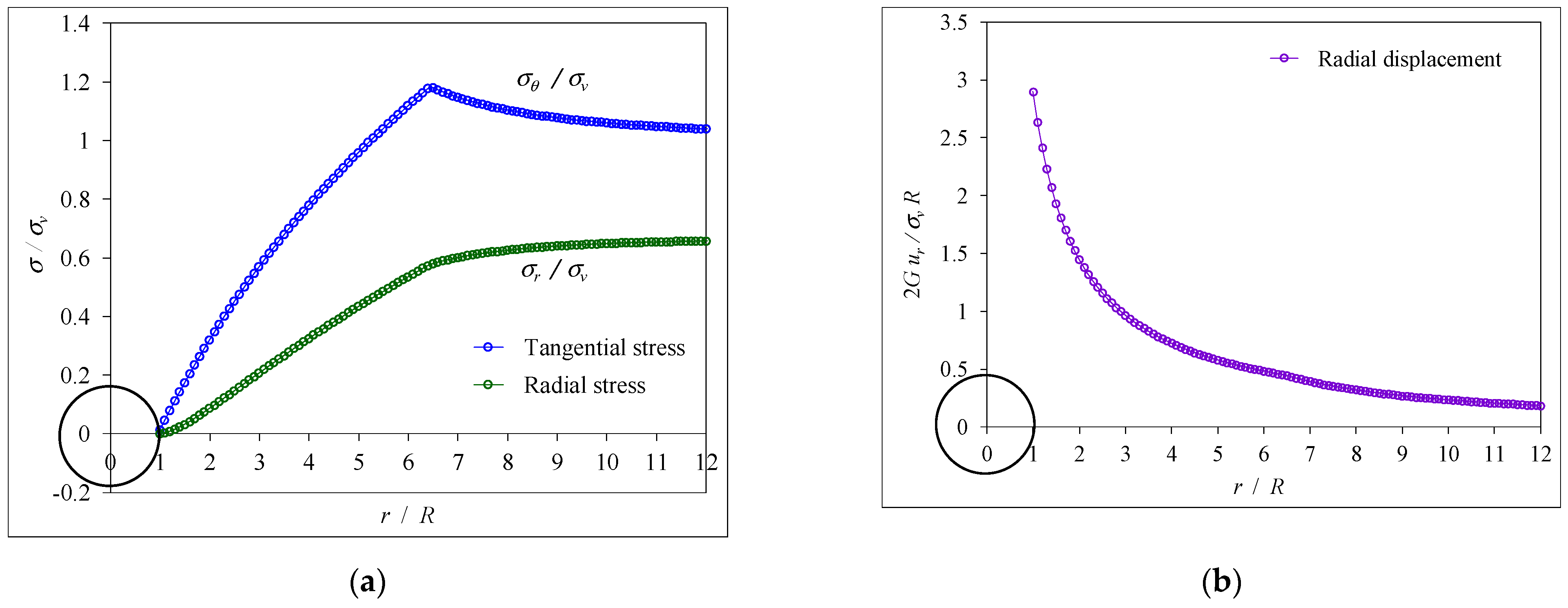
- Recording the calculated data relates to the representation of the distribution of stresses/displacements (), (), and () on the cross-section of the tunnel and () at the intrados of the tunnel.
- (10)
- When i < n − 1, repeat steps (4) through (10).
- (11)
- When i = n − 1, the process is not repeated, and the data from each step is recorded.
- (12)
- Drawing the distribution of stresses/displacements at the intrados and on the cross-section of the tunnel.
5. Comparison of Results between the Findings of This Study and Published Data
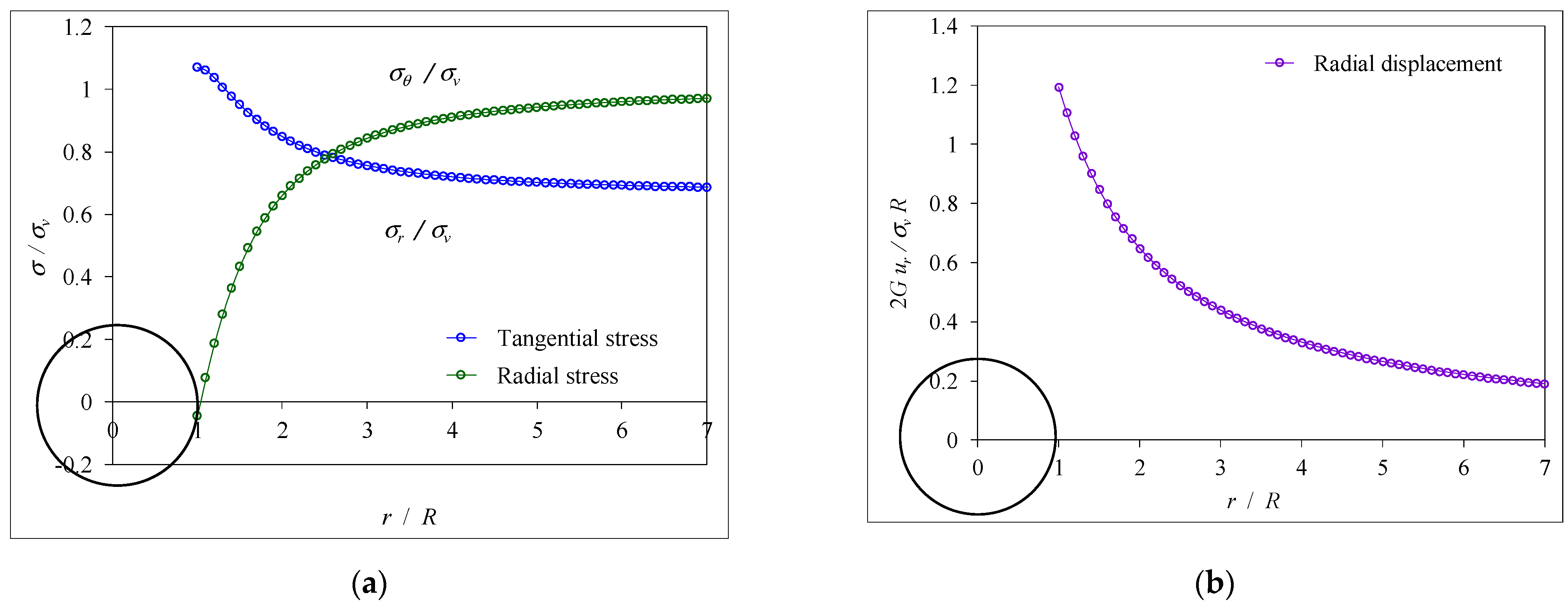
5.1. Stress/Displacement in the Elastic Region
- (1)
- When λ = 0 (), it indicates that the dimensionless radial stress (σr/σv) and tangential stress (σθ/σv) used in the calculation were, respectively, 1 and 0.67 in the initial anisotropic stress state as shown the horizontal line on the right side in Figure 9a;
- (2)
- When 0 < λ < 1.0 (), it describes that the stresses were also in the elastic region, the radial and tangential stresses increased with the increase of the confinement loss, and both stresses were separated along the horizontal axis (r/R);
- (3)
5.2. Stress/Displacement in the Plastic Region
- (1)
- When λ = 0 (), it indicates that the stresses were in the initial stress state as shown in the horizontal line on the right side in Figures; the radial stress (σh/σv) and tangential stress (σθ/σv) used in the calculation were 0.67 and 1.0, respectively.
- (2)
- When 0 (), it describes that the stresses were in the elastic region, and the radial and tangential stresses increased with the increase of the confinement loss, and both stresses were separated along the horizontal axis (r/R).
- (3)
- When (), the plastic radius appeared, and stresses were at the elastic-plastic interface. The radial stress began to change the curvature, and the tangential stress attained the maximum value.
- (4)
- When (), it indicates that the stresses are in the plastic region, and this leads to both the radial stress and tangential stress being decreased steeply.
- (5)
- Until (), the radial stress becomes zero and the tangential stress is equal to the coefficient proposed by the Hoek–Brown failure criterion.
6. Conclusions
- (1)
- A coherent closed-form analytical solution has been derived for the elastic–perfectly plastic analysis of a circular tunnel within rock masses governed by the Hoek–Brown non-linear failure criterion, considering anisotropic in situ stress.
- (2)
- The agreement between published results and the proposed closed-form solutions using the explicit procedure was excellent within elastic–perfectly plastic media. The percentage error for radial displacement ranged from 0.93% to 1.18% in the elastic region and from 3.28% to 5.51% in the plastic region. Additionally, the percentage error for the radius of the plastic zone ranged from 4.99% to 5.6%.
- (3)
- An incremental approach within the explicit analysis method (EAM) was proposed to model the advancing excavation of the tunnel face. This method calculates stresses and displacements at each step, facilitating the generation of ground reaction curves, stress paths at the intrados of the tunnel, and stress/displacement distributions across tunnel cross-sections.
- (4)
- The fluctuation of stresses during tunnel excavation can primarily be explained by the stress gradient, which represents the disparity between far-field and near-field stresses around the tunnel. This gradient can be computed using incremental assumptions in numerical analysis, with the confinement loss considered as a portion of the stress gradient.
- (5)
- Confinement loss in the elastic limit was determined by the peak strength parameters of the rock masses and initial vertical stress.
- (6)
- The plastic radius was influenced by the peak strength parameters of the rock masses, confinement loss in the elastic limit, and dependency on confinement loss. Increased confinement loss resulted in a larger plastic radius, reducing both radial and tangential stress while increasing radial displacement in the plastic region.
- (7)
- The incremental procedure method proposed herein accommodates the nonlinear failure criterion of the rock masses. It not only serves as a valuable tool for analyzing circular tunnels under isotropic stress conditions but also holds promise for simulating tunnel behavior under anisotropic stress conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panet, M. Calcul du souténement des tunnels à section circulaire par la method convergence-confinement avec un champ de contraintes initiales anisotrope. Tunn. Et Ouvrages Souterr. 1986, 77, 228–232. [Google Scholar]
- Panet, M. Le Calcul des Tunnels par la Méthode de Convergence-Confinement; Presses de l’Ecole Nationale des Ponts et Chaussées: Paris, France, 1995. [Google Scholar]
- Panet, M. Recommendations on the Convergence-Confinement Method; Association Française des Tunnels et de l’Espace Souterrain (AFTES): Paris, France, 2001; pp. 1–11. Available online: https://tunnel.ita-aites.org/media/k2/attachments/public/Convergence-confinement%20AFTES.pdf (accessed on 28 September 2023).
- Panet, M.; Sulem, J. Convergence-Confinement Method for Tunnel Design; Springer: Berlin, Germany, 2022; Available online: https://link.springer.com/book/10.1007/978-3-030-93193-3 (accessed on 29 January 2023).
- Lee, Y.L.; Hsu, W.K.; Lee, C.M.; Xin, Y.X.; Zhou, B.Y. Direct calculation method for the analysis of non-linear behavior of ground-support interaction of circular tunnel using convergence–confinement approach. Geotech. Geol. Eng. 2021, 39, 973–990. [Google Scholar] [CrossRef]
- Lee, Y.L.; Hsu, W.K.; Chou, P.Y.; Hsieh, P.W.; Ma, C.H.; Kao, W.C. Verification and comparison of direct calculation method for the analysis of ground-support interaction of a circular tunnel excavation. Appl. Sci. 2022, 12, 1929. [Google Scholar] [CrossRef]
- Oreste, P.P. Analysis of structural interaction in tunnels using the convergence-confinement approach. Tunnell Undergr. Space Technol. 2003, 18, 347–363. [Google Scholar] [CrossRef]
- Oreste, P. The convergence–confinement method: Roles and limits in modern geomechanical tunnel design. Am. J. Appl. Sci. 2009, 6, 757–771. [Google Scholar] [CrossRef]
- Cui, L.; Zheng, J.; Zhang, R.; Lai, H. A numerical procedure for the fictitious support pressure in the application of the convergence-confinement method for circular tunnel design. Int. J. Rock Mech. Min. Sci. 2015, 78, 336–349. [Google Scholar] [CrossRef]
- Brown, E.; Bray, J.; Ladanyi, B.; Hoek, E. Ground response curves for rock tunnels. J. Geotech. Eng. ASCE 1983, 109, 15–39. [Google Scholar] [CrossRef]
- Brady, B.; Brown, E. Rock Mechanics for Underground Mining; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Wang, Y. Ground response of a circular tunnel in poorly consolidated rock. J. Geotech. Eng. ASCE 1996, 122, 703–708. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabasi, Y. Ground reaction analyses in conventional tunnelling excavation. Tunnell Undergr. Space Technol. 2007, 22, 230–237. [Google Scholar] [CrossRef]
- Alejano, L.R.; Rodriguez-Dono, A.; Alonso, E.; Fdez-Manín, G. Ground reaction curves for tunnels excavated in different quality rock masses showing several types of post-failure behavior. Tunnell Undergr. Space Technol. 2011, 24, 689–705. [Google Scholar] [CrossRef]
- Mousivand, M.; Maleki, M.; Nekooei, M.; Msnsoori, M.R. Application of convergence-confinement method in analysis of shallow non-circular tunnels. Geotech. Geol. Eng. 2017, 35, 1185–1198. [Google Scholar] [CrossRef]
- Rocksupport. Rock Support Interaction and Deformation Analysis for Tunnels in Weak Rock; Tutorial Manual of Rocscience Inc.: Toronto, ON, Canada, 2004; pp. 1–76. [Google Scholar]
- Rodríguez, R.; Díaz-Aguado, M.B. Deduction and use of an analytical expression for the characteristic curve of a support based on yielding steel ribs. Tunnell Undergr. Space Technol. 2013, 33, 159–170. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Engen, M. The support characteristic curve for blocked steel sets in the convergence-confinement method of tunnel support design. Tunnell Undergr. Space Technol. 2017, 69, 233–244. [Google Scholar] [CrossRef]
- Oke, J.; Vlachopoulos, N.; Diederichs, M. Improvement to the convergence-confinement method: Inclusion of support installation proximity and stiffness. Rock Mech. Rock Eng. 2018, 51, 1495–1519. [Google Scholar] [CrossRef]
- De La Fuente, M.; Taherzadeh, R.; Sulem, J.; Nguyen, X.S.; Subrin, D. Applicability of the convergence-confinement method to full-face excavation of circular tunnels with stiff support system. Rock Mech. Rock Eng. 2019, 52, 2361–2376. [Google Scholar] [CrossRef]
- Lee, Y.L. Explicit analysis for the ground-support interaction of circular tunnel excavation in anisotropic stress fields. J. Chin. Inst Eng 2020, 43, 13–26. [Google Scholar] [CrossRef]
- Bernaud, D.; Rosset, G. The new implicit method for tunnel analysis. Int. J. Num. Anal. Meth. Geomech. 1996, 20, 673–690. [Google Scholar] [CrossRef]
- Humbert, P.; Dubouchet, A.; Fezans, G.; Remaud, D. CESAR-LCPC, un progiciel de calcul dédié au génie civil. Bull. Lab. Ponts Chaussées 2005, 256, 7–37. Available online: https://www.ifsttar.fr/collections/BLPCpdfs/blpc_256-257_7-37.pdf (accessed on 25 October 2023).
- González-Nicieza, C.; Álvarez-Vigil, A.E.; Menéndez-Díaz, A.; González-Palacio, C. Influence of the depth and shape of a tunnel in the application of the convergence-confinement method. Tunnell Undergr. Space Technol. 2008, 23, 25–37. [Google Scholar] [CrossRef]
- Vlachopoulos, N.; Diederichs, M. Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels. Rock Mech. Rock Eng. 2009, 42, 131–146. [Google Scholar] [CrossRef]
- Mousivand, M.; Maleki, M. Constitutive models and determining methods effects on application of Convergence-Confinement method in underground excavation. Geotech. Geol. Eng. 2017, 36, 1707–1722. [Google Scholar] [CrossRef]
- Zhao, K.; Bonini, M.; Debernardi, D.; Janutolo, M.; Barla, G.; Chen, G. Computational modelling of the mechanised excavation of deep tunnels in weak rock. Comput. Geotechics 2015, 66, 158–171. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J Geotech. Eng. ASCE 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Underground Excavations in Rock. CRC Press: London, UK, 1980. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek–Brown failure criterion—2002 edition. Proc NARMS-Tac. 2020, 1, 267–273. Available online: https://static.rocscience.cloud/assets/verification-and-theory/RSData/Hoek-Brown-Failure-Criterion-2002-Edition.pdf (accessed on 1 January 2023).
- Carranza-Torres, C.; Fairhurst, C. The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 1999, 36, 777–809. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C. Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek–Brown failure criterion. Tunnell Undergr. Space Technol. 2000, 15, 187–213. [Google Scholar] [CrossRef]
- Carranza-Torres, C. Elasto-plastic solution of tunnel problems using the generalized form of the Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2004, 41, 480–491. [Google Scholar] [CrossRef]
- Sharan, S.K. Exact and approximate solutions for displacements around circular openings in elastic-brittle plastic Hoek-Brown rock. Int. J. Rock Mech. Min. Sci. 2005, 42, 542–549. [Google Scholar] [CrossRef]
- Park, K.H.; Kim, Y.J. Analytical solution for a circular opening in an elastic–brittle–plastic rock. Int. J. Rock Mech. Min. Sci. 2006, 43, 616–622. [Google Scholar] [CrossRef]
- Serrano, A.; Olalla, C.; Reig, I. Convergence of circular tunnels in elastoplastic rock masses with non-linear failure criteria and non-associated flow laws. Int. J. Rock Mech. Min. Sci. 2011, 48, 878–887. [Google Scholar] [CrossRef]
- Shen, B.; Barton, N. The disturbed zone around tunnels in jointed rock masses. Int. J. Rock Mech. Min. Sci. 1997, 34, 117–125. [Google Scholar] [CrossRef]
- Sharan, S.K. Elastic–brittle–plastic analysis of circular openings in Hoek–Brown media. Int. J. Rock Mech. Min. Sci. 2003, 40, 817–824. [Google Scholar] [CrossRef]
- Lee, Y.L.; Ma, C.H.; Lee, C.M. An improved incremental procedure for the ground reaction based on Hoek-Brown failure criterion in the tunnel convergence-confinement method. Mathematics 2023, 11, 3389. [Google Scholar] [CrossRef]
- Kirsch, G. Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre: The theory of elasticity and the needs of the strength of materials. Z. Des Vereines Dtsch. Ingenieure 1898, 42, 797–807. [Google Scholar]
- Sharan, S.K.; Naznin, R. Linearization of the Hoek-Brown failure criterion for non-hydrostatic stress fields. In Proceedings of the Eighth International of the Conference on Engineering Computational Technology, Scotland, UK, 4–7 September 2012; Available online: https://webapp.tudelft.nl/proceedings/ect2012/pdf/sharan.pdf (accessed on 10 February 2023).


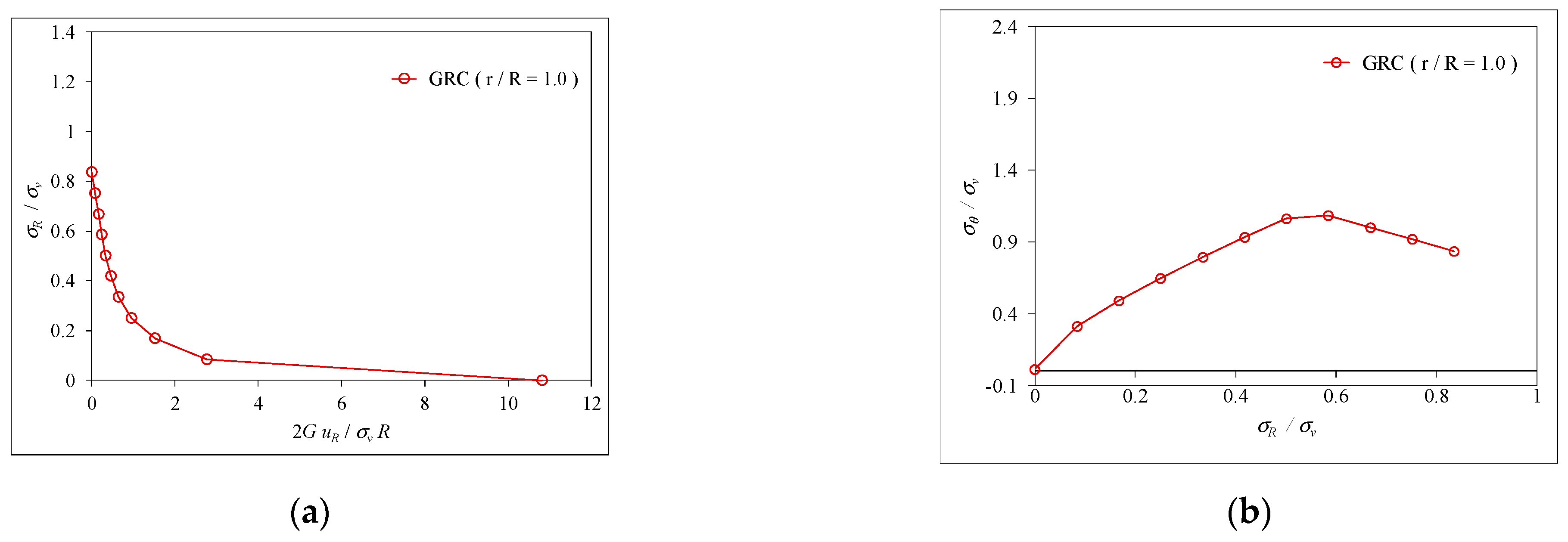
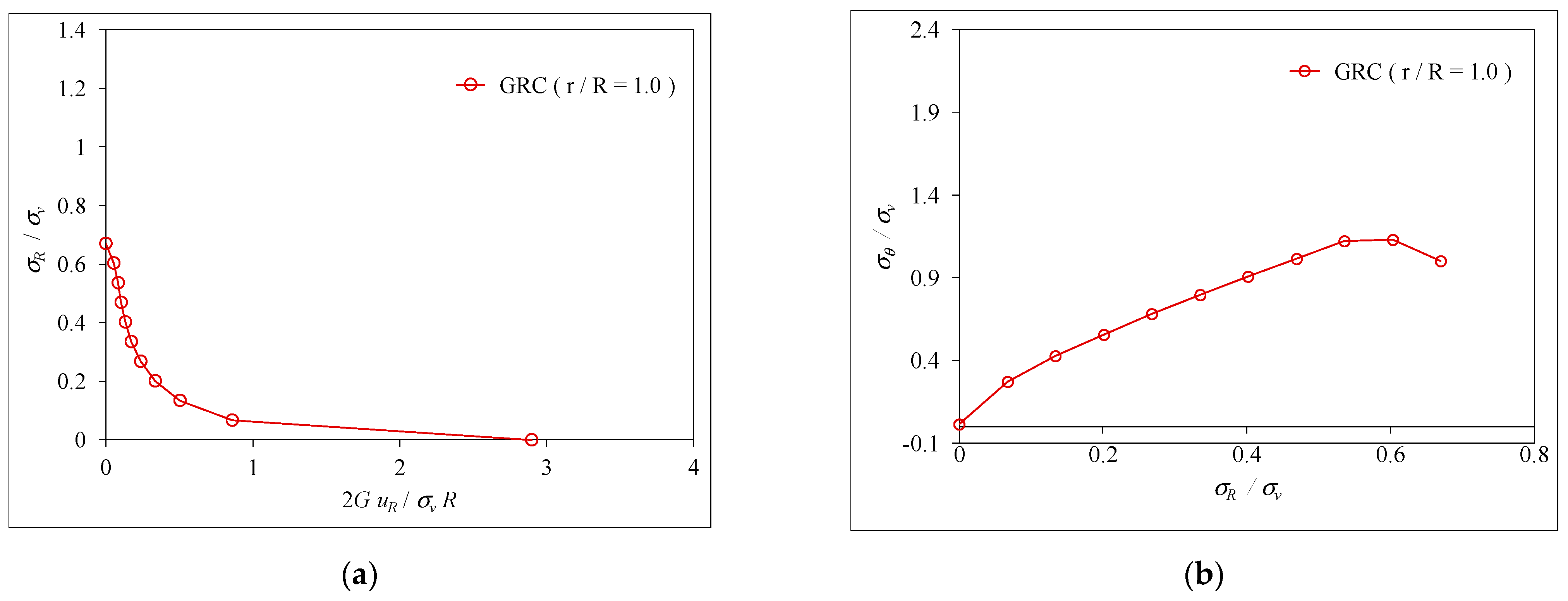

| Reference | Sharan and Naznin [41] | ||||
|---|---|---|---|---|---|
| Parameter | Case I | Case II | Case III | Case IV | Case V |
| E (GPa) | 60 | 90 | 40 | 5.5 | 27.6 |
| ν | 0.2 | 0.2 | 0.2 | 0.25 | 0.2 |
| mi | 10.84 | 16 | 7.5 | 17 | 15 |
| GIS | 89 | 90 | 79 | 50.08 | 50.31 |
| D | 0 | 0 | 0 | 0 | 0 |
| σci (MPa) | 210 | 200 | 300 | 30 | 69 |
| Kψ | 0 | 0 | 0 | 0 | 0 |
| R (m) | 10.0 | 10.0 | 4.0 | 5.0 | 6.1 |
| Published Studies | Radial Displacement, uR (m) | Plastic Zone Radius, Rp (m) | EAM Radial Displacement, uR (mm) (Error * %) | EAM Plastic Zone Radius, Rp (m) (Error * %) |
|---|---|---|---|---|
| Case I | 0.09 | N/A | 0.0909 (1.0%) | N/A |
| Case II | 0.05 | N/A | 0.0505 (0.93%) | N/A |
| Case III | 0.11 | N/A | 0.1113 (1.18%) | N/A |
| Case IV | 0.24 | 21.5 | 0.2268 (5.51%) | 22.705 (5.60%) |
| Case V | 0.038 | 14.3 | 0.0368 (3.28%) | 15.014 (4.99%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-L.; Chen, C.-S.; Lee, C.-M. Explicit Analysis for the Ground Reaction of a Circular Tunnel Excavated in Anisotropic Stress Fields Based on Hoek–Brown Failure Criterion. Mathematics 2024, 12, 2689. https://doi.org/10.3390/math12172689
Lee Y-L, Chen C-S, Lee C-M. Explicit Analysis for the Ground Reaction of a Circular Tunnel Excavated in Anisotropic Stress Fields Based on Hoek–Brown Failure Criterion. Mathematics. 2024; 12(17):2689. https://doi.org/10.3390/math12172689
Chicago/Turabian StyleLee, Yu-Lin, Chih-Sheng Chen, and Chi-Min Lee. 2024. "Explicit Analysis for the Ground Reaction of a Circular Tunnel Excavated in Anisotropic Stress Fields Based on Hoek–Brown Failure Criterion" Mathematics 12, no. 17: 2689. https://doi.org/10.3390/math12172689
APA StyleLee, Y.-L., Chen, C.-S., & Lee, C.-M. (2024). Explicit Analysis for the Ground Reaction of a Circular Tunnel Excavated in Anisotropic Stress Fields Based on Hoek–Brown Failure Criterion. Mathematics, 12(17), 2689. https://doi.org/10.3390/math12172689







