Abstract
In this work, we aim to explore the superconvergence of a modified nonconforming cut finite element method with rectangular meshes for elliptic problems. Boundary conditions are imposed via the Nitsche’s method. The superclose property is proven for rectangular meshes. Moreover, a postprocessing interpolation operator is introduced, and it is proven that the postprocessed discrete solution converges to the exact solution, with a superconvergence rate . Finally, numerical examples are provided to support the theoretical analysis.
MSC:
65N12; 65N15; 65N30
1. Introduction
Boundaries/interfaces with time or involving complex geometries arise in many engineering applications and physical phenomena problems. Cut finite element methods (CutFEM) have been developed to solve PDEs whose solutions involve jumps, kinks, singularities and other locally non-smooth features within elements. This method not only retains the accuracy and robustness of a standard finite element method, but also relaxes the mesh, which is independent of the geometric description. Over the past few decades, cut finite element methods have been applied to many problems [1,2,3,4,5,6]. We also refer to the overview article [7] and the references therein.
Note that superconvergence of the finite element method is quite popular in practice, and several types have been studied in the past few decades. There are two main techniques within the framework of superconvergence. One technique is the interpolation approximation, which has two ingredients: the supercloseness between the numerical solution and the finite element canonical interpolant, and the global superconvergence between the exact solution and a postprocessed solution. This technique has been studied for conforming finite elements [8,9,10,11] and nonconforming finite elements [12,13]. The other one uses some equivalences, and involves translating the superconvergence of the original problems into the superconvergence of some mixed problems—for example, the equivalence between the Crouzeix–Raviart method and the lower order Raviart–Thomas (RT) method for the Poisson equation [14], and the equivalence between the the nonconforming Rannacher–Turek (NCRT) element and RT element for elliptic equations [15].
For the NCRT element, based on the interpolation approximation technique, it has been shown in [12] that the supercloseness between the numerical solution and the finite element interpolation holds only under square meshes. To overcome this barrier, many modified NCRT elements [12,13,16] have been proposed. In this work, we study the cut finite element method, based on the five-node nonconforming element developed in [12,13]. The main contribution is that a postprocessing operator is designed, and the superconvergence order is proven for elliptic problems based on the nonconforming CutFEM under rectangular meshes.
The remainder of this paper is organized as follows. In Section 2, we formulate the modified nonconforming CutFEM. The supercloseness is presented in Section 3. A postprocessing operator and the global superconvergence are analyzed in Section 4. Some numerical results are shown in Section 5 to verify the theoretical results. The conclusions are given in the last section. Throughout this paper, C is used to denote generic positive constants, which are independent of h, the location of the boundary to the mesh. Moreover, stands for .
2. The Model Problem and the Finite Element Formulation
Consider the following elliptic problem with a bounded and simply connected domain under a smooth boundary :
where f is a smooth function, and is the Dirichlet boundary function prescribed on .
Remark 1.
For and , it is well known that the variational formulation of (1) has a unique solution . In the following analysis of superconvergence, we assume that for the solution .
For domain , we first define a fictitious domain , such that . Let be a family of non-overlapping rectangles that cover the domain . For any , we define as , and denote . Note that any element is considered closed. Define the set of cut elements by . In particular, for , we denote , and . Denote the set of all interior edges of by . Denote uncut and cut edges by and , respectively, which are defined as , and . Further, the set of extended edges is denoted by
Define .
We define a weak space:
Let denote the reference element with four vertices , , and . Denote the bilinear function as an isomorphism from to K by
where are four vertices of element K, and are the basis functions of the standard conforming bilinear finite element space, which can be written as
Denote the finite element space of modified nonconforming elements with support in by
where , if .
We now give the finite element formulation based on the weak formulation of Problem (1). Firstly, the average on the cut edges is defined by
with , .
The modified nonconforming cut finite element method is to find such that
where is the bilinear form on and is the linear function on , defined by
and
where is the unit outward normal vector on the boundary , and are positive numbers.
We introduce the energy norm on the space as
with
From the proof of Lemma 6 in [2], the following inequality can be directly obtained.
Lemma 1.
Suppose that h is sufficiently small. For any , we have
where .
To analyze the convergence and superconvergence, we need an extension result (see Chapter VI, Section 2 of [17], or Chapter 6 of [18]). We continuously extend the solution of (1) to to obtain a function , such that
and
It is easy to obtain the following inconsistency equation:
Assume that and are large enough; it is easy to find that the coercivity of holds, which can be proven similarly to Theorems 4.1 and 4.2 of [19]. Then, the a priori error estimate for the modified nonconforming CutFEM holds:
3. Supercloseness Analysis
In this section, we will show the supercloseness result between the gradient of the finite element solution and the gradient of the interpolation of the exact solution. Firstly, for any element K, define a local interpolation operator by and , where . Denote by the interpolation operator over by and . From the interpolation theory in [20] and the above extension properties, the following approximation estimate holds:
where and .
For element and , and are constants, and then and , through the definition of . Similarly to the proof of Theorem 3.1 of [21], we have the following Lemma.
Lemma 2.
Let u be the solution of the interface problem, and be the interpolation of u, defined as above. If , then for all ,
Theorem 1.
Let be the finite element solution of the discrete problem, and be the interpolation of u. If , then
Proof.
Using the coercivity of , we have
From Lemma 2, the first term on the right hand can be estimated via
From Lemma 3.1 of [12], the following consistency error estimate holds:
Remark 2.
From the definition of , Lemma 1, and Theorem 1, we obtain
4. Postprocessing and Superconvergence
In this section, we will use a postprocessing operator defined in [13], and apply it to our fictitious domain. The global superconvergence for the modified nonconforming cut finite element method to elliptic problems will be analyzed. For this purpose, we assume that is obtained from by dividing each element M of into four congruent rectangles . Define an operator on , , and define the local operator by
where are four edges of M. From Lemma 3.2 of [13], we obtain the following Lemma, which presents the properties of operator .
Lemma 3.
The interpolation operator satisfies
Now, we give some notations. For partition , we define and . Let . Note that there might exist an element which is not in for and (see Figure 1 for an illustration). For each element , in order to obtain superconvergence, we need expand the value from into M. For but , there is and . Let be the projection. Take
with
where is the continuous extension of and is the basis function of . Further, we define
where the average is the convex combination
with weights , such that and , and . For , let . It is easy to find that
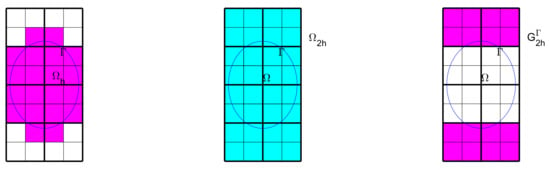
Figure 1.
Illustration of definitions of , , , and for domain . Partitions (fine meshes) and (coarse meshes) of domain . Left: elements in (magenta area). Middle: elements in (cobalt blue area). Right: elements in (magenta area).
For , we define a postprocessing operator by . Then, we can obtain the following main superconvergence result in this work.
Proof.
We decompose as . Then, the triangle inequality implies that
where the last equality uses the definition of and Lemma 3, and then we obtain . From Lemma 3 and the extension properties, we have
5. Numerical Examples
In this section, we will consider several numerical examples to verify the theoretical results given in the previous section. In these examples, we will test the convergence rate, supercloseness result and superconvergence rate based on square meshes and different rectangular meshes. We summarize our experimental results in tables, displaying the following errors: .
5.1. Example 1
In this example, we consider the elliptic problem with a circular boundary with center and radius . Define domain . Choose the fictitious domain , and let f be chosen such that the exact solution is . The performance for errors of , and with square and rectangular meshes are shown in Table 1. Firstly, it shows errors of , , and versus square meshes with and , respectively. It is observed that our formulation converges with the optimal rate for , and with rate for and , which support Theorems 1 and 2. Secondly, the performance for errors of , and , based on two different rectangular meshes, are also tested. It is shown that the convergence rate of is , and the convergence orders for and are , which are also coincide with the theoretical analysis.

Table 1.
Rates of errors for Example 1 based on square and rectangular meshes with penalty parameters .
5.2. Example 2
In this example, we consider an elliptic boundary condition. The boundary curve is the zero level set of the following function: . Define domain , and let the fictitious domain . We choose the exact solution . The numerical results for , , and , based on square and rectangular meshes with , are presented in Table 2, which shows the same convergence, supercloseness, and superconvergence rates as the theoretical analysis.

Table 2.
Rates of errors for Example 2 based on square and rectangular meshes with penalty parameters .
5.3. Example 3
In this example, we choose a more complicated boundary. The boundary curve is the zero level set of the following function: . Let domain , and the fictitious domain . The exact solution is set to be . Table 3 displays the convergence rates of , , and for our formulation based on square and rectangular meshes with . We also observe the same convergence, supercloseness, and superconvergence phenomena for three meshes as predicted in our theoretical analysis.

Table 3.
Rates of errors for Example 3 based on square and rectangular meshes with penalty parameters .
In the three examples, the performance of errors , and on both the square meshes and rectangular meshes is tested. The numerical results show that the nonconforming cut finite element method converge with optimal rate for and with order of convergence for and , which is accordant with our theoretical results.
6. Conclusions
In this work, we have studied the superconvergence of the modified nonconforming cut finite element method to solve elliptic problems on rectangular meshes. We have proven that the supercloseness rate between the gradient of the numerical solution and the gradient of exact solution’s interpolation is . Through a constructed postprocessing operator, we have proven that the error between the exact gradient and the postprocessed gradient with rate . Numerical examples with squares and rectangular meshes have been provided to illustrate the theoretical results.
Author Contributions
Methodology, X.H. and F.S.; Writing—original draft, X.H.; Writing—review & editing, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work of the first author is supported by the National Natural Science Foundation of China grant 12201312. The work of the second author is supported by the National Natural Science Foundation of China grant 12201303.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the anonymous referees for their insightful suggestions and comments, which lead to a great improvement of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hansbo, A.; Hansbo, P. An unfitted finite element method, based on Nitsche’s method, for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 5537–5552. [Google Scholar] [CrossRef]
- Burman, E.; Hansbo, P. Fictitious domain finite element methods using cut elements: I. A stabilized Lagrange multiplier method. Comput. Methods Appl. Mech. Eng. 2010, 199, 2680–2686. [Google Scholar] [CrossRef]
- Hansbo, P.; Larson, M.G.; Zahedi, S. A cut finite element method for a Stokes interface problem. Appl. Numer. Math. 2014, 85, 90–114. [Google Scholar] [CrossRef]
- Huang, P.; Wu, H.; Xiao, Y. An unfitted interface penalty finite element method for elliptic interface problems. Comput. Methods Appl. Mech. Eng. 2017, 323, 439–460. [Google Scholar] [CrossRef]
- Wang, N.; Chen, J. A nonconforming Nitsche’s extended finite element method for Stokes interface problems. J. Sci. Comput. 2019, 81, 342–374. [Google Scholar] [CrossRef]
- Massing, A.; Schott, B.; Wall, W.A. A stabilized Nitsche cut finite element method for the Oseen problem. Comput. Methods Appl. Mech. Eng. 2018, 328, 262–300. [Google Scholar] [CrossRef]
- Burman, E.; Claus, S.; Hansbo, P.; Larson, M.G.; Massing, A. CutFEM: Discretizing geometry and partial differential equations. Int. J. Numer. Methods Eng. 2015, 104, 472–501. [Google Scholar] [CrossRef]
- Lin, Q.; Yan, N. The Construction and Analysis of High Effciency Finite Element Methods; Hebei University Publishers: Baoding, China, 1996. (In Chinese) [Google Scholar]
- Zienkiewicz, O.C.; Zhu, J.Z. The superconvergent patch recovery and a posteriori error estimates. I. the recovery technique. Int. J. Numer. Methods Eng. 1992, 33, 1331–1364. [Google Scholar] [CrossRef]
- Naga, A.; Zhang, Z. A posteriori error estimates based on the polynomial preserving recovery. SIAM J. Numer. Anal. 2004, 42, 1780–1800. [Google Scholar] [CrossRef]
- Bank, R.E.; Xu, J.; Zheng, B. Superconvergent derivative recovery for lagrange triangular elements of degree p on unstructured grids. SIAM J. Numer. Anal. 2007, 45, 2032–2046. [Google Scholar] [CrossRef]
- Lin, Q.; Tobiska, L.; Zhou, A. Superconvergence and extrapolation of non-conforming low order finite elements applied to the poisson equation. IMA J. Numer. Anal. 2005, 25, 160–181. [Google Scholar] [CrossRef]
- Mao, S.; Chen, S.; Shi, D. Convergence and superconvergence of a nonconforming finite element on anisotropic mehses. Int. J. Numer. Anal. Model. 2007, 4, 16–38. [Google Scholar]
- Hu, J.; Ma, R. Superconvergence of both the Crouzeix-Raviart and morley elements. Numer. Math. 2016, 132, 491–509. [Google Scholar] [CrossRef]
- Li, Y. Superconvergent flux recovery of the Rannacher-Turek nonconforming element. J. Sci. Comput. 2021, 87, 32. [Google Scholar] [CrossRef]
- Ming, P.; Shi, Z. Superconvergence studies of quadrilateral nonconforming rotated Q1 elements. Int. J. Numer. Anal. Model. 2006, 3, 322–332. [Google Scholar]
- Stein, E. Singular Integrals and Differentiability Properties of Functions; Princeton University Press: Princeton, NJ, USA, 1970; Volume 30. [Google Scholar]
- Gilbarg, D.; Trudinger, N.S. Elliptic Partial Differential Equations of Second Order, 2nd ed.; Springer: Berlin, Germany, 1983; Volume 224. [Google Scholar]
- He, X.; Song, F.; Deng, W. A well-conditioned, nonconforming Nitsche’s extended finite element method for elliptic interface problems. Numer. Math. Theory Methods Appl. 2020, 13, 99–130. [Google Scholar]
- Arnold, D.; Boffi, D.; Falk, R. Approximation by quadrilateral elements. Math. Comput. 2002, 71, 909–922. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Ji, H.; Wang, H. Superconvergence of unfitted rannacher-turek nonconforming element for elliptic interface problems. Appl. Numer. Math. 2024, 203, 32–51. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).