Using ArcFace Loss Function and Softmax with Temperature Activation Function for Improvement in X-ray Baggage Image Classification Quality

Abstract

Modern aviation security systems are largely tied to the work of screening operators. Due to physical characteristics, they are prone to problems such as fatigue, loss of attention, etc. There are methods for recognizing such objects, but they face such difficulties as the specific structure of luggage X-ray images. Furthermore, such systems require significant computational resources when increasing the size of models. Overcoming the first and second disadvantage can largely lie in the hardware plane. It needs new introscopes and registration techniques, as well as more powerful computing devices. However, for processing, it is more preferable to improve quality without increasing the computational power requirements of the recognition system. This can be achieved on traditional neural network architectures, but with the more complex training process. A new training approach is proposed in this study. New ways of baggage X-ray image augmentation and advanced approaches to training convolutional neural networks and vision transformer networks are proposed. It is shown that the use of ArcFace loss function for the task of the items binary classification into forbidden and allowed classes provides a gain of about 3–5% for different architectures. At the same time, the use of softmax activation function with temperature allows one to obtain more flexible estimates of the probability of belonging, which, when the threshold is set, allows one to significantly increase the accuracy of recognition of forbidden items, and when it is reduced, provides high recall of recognition. The developed augmentations based on doubly stochastic image models allow one to increase the recall of recognizing dangerous items by 1–2%. On the basis of the developed classifier, the YOLO detector was modified and the mAP gain of 0.72% was obtained. Thus, the research results are matched to the goal of increasing efficiency in X-ray baggage image processing.

1. Introduction

Nowadays, the task of ensuring security in areas of mass gathering of people is becoming more and more urgent. Such areas include subway stations, railway stations, bus stations, airports, concert halls, stadiums, etc. At the same time, when it comes to air transportation, the requirements for permitted baggage are usually stricter than in other places. For example, even scissors or water in medium and big containers are prohibited to carry on board. At the same time, the flow of people in airports is quite large, and the security check can take a long time. It leads in some cases to problems with boarding the flight.

It should be noted that baggage and hand luggage inspection require both hardware to register X-ray images and software to display them on the screen of the inspection operator. Different kinds of introscopes are used for registration [1], and the processed images show a picture different from the optical images which are widely known in traditional image processing tasks. There may be overlaps and gaps of different objects, which lead to additional difficulties to the operator. Moreover, there may be a somewhat nonstandard color gamut of images.

The result of the screening process is either the admission of a passenger’s baggage for boarding with all authorized items, or the seizure of a prohibited item and taking appropriate measures. Automating the process of deciding on the presence or absence of prohibited items in baggage or hand luggage is an important and urgent task. The solution of this task will help one to cope with human error and speed up the screening process. However, such systems will need to meet high quality standards and have extremely high accuracy values. Currently, the most likely use case seems to be the introduction of such systems as decision support tools.

Practice shows that the use of modified activation and loss functions allows us to obtain an improvement in the quality of the classification task in optical images without complicating the architecture. The motivation of this paper is also the need to improve the classification accuracy of prohibited items in X-ray luggage images without complication of neural network architectures. This is due to the need to provide real-time operation and high-accuracy requirements at the same time. The goal is to generally improve the algorithms for classification of prohibited items through new approaches to training neural networks. The objectives of research included the development of a new generative algorithm for image augmentation without the use of deep generative networks, the modification of the training process of neural networks by changing the loss functions, and comparative analysis of the performance quality of the proposed and known solutions. For this purpose, it is possible to use additional augmentation algorithms based on doubly stochastic models and new loss function ArcFace, which has not been previously used in the processing of X-ray images of luggage.

2. Related Works

First, it is necessary to review the existing solutions in the field of recognizing prohibited baggage items. It should be noted that the cost of an error, especially when the system skips the prohibited item, can be very expensive. Thus, it was not possible to find actually implemented and functioning systems during the literature review. However, there are developments, mainly based on neural networks, which demonstrate good results. Let us consider them.

In modern science publications, to combat fatigue and loss of concentration of operators, the authors offer a number of solutions for the development of automated computer vision systems [2,3,4,5,6]. The authors note that the most important is the indicator of detection recall, and such developments are aimed at preventing the sneaking of prohibited items on board. Dr. Harris D.H. considers a system of detection of 6 classes of dangerous objects, among which are knives, bombs, guns, etc. [7]. The authors manage to get high performance based on the YOLO neural network. In [8], special attention is paid to the inspection process. It is noted that when entering the airport to the gate, each passenger is obliged to place luggage on the conveyor belt. Then the luggage goes through the registration device, and in the end a security operator performs a visual search in manual mode and makes the final decision.

Despite the apparent simplicity of the decision making, it is indeed quite complex, which is influenced by various factors [9,10,11]. One of the main problems is the very large class imbalance. In practice, more than 90% of the luggage that passes through does not contain prohibited items. This suggests that in more than 9 out of 10 cases, the operator marks the baggage as “allowed” (safe) and lets it through. Therefore, in cases where prohibited items are present, there is a risk of missing them. The study of the changing trend from safe to dangerous luggage resulted in a decrease in the quality of the operator’s work, as shown in studies [12,13,14].

Due to the importance of the class imbalance issue, it is definitely important to note the methods that are used to combat this situation. An entire technology has been developed to combat this problem. It allows specialists to create fake X-ray images by projecting prohibited items onto luggage images. This technology is called Threat Image Projection (TIP). TIP is known as a good practice used at leading airports around the world. The use of TIP can create fictitious threat images (FTI) and keep the concentration of security operators at a high level after a long time [15,16,17]. On the other hand, in terms of the development of neural networks and computer vision technologies, there is an interesting challenge of recognizing such fake forbidden items. However, it will not be considered in this article.

It should be noted that the use of TIP technology creates additional opportunities for obtaining feedback to characterize the performance of inspection operators. Actually, it is known for such images when and where the prohibited item was projected. Thus, it is possible to count the number of correct and incorrect operator responses. But the main feature of this approach is the artificial convergence of the number of examples in the classes of “prohibited” and “allowed” baggage. In some studies [18,19], it is suggested to use TIP for additional motivation and certification of aviation security officers. Moreover, studies [20,21] confirmed the positive impact of TIP technology for employee motivation. The authors conclude that the cognitive performance of the screening operators is improved and also note that in real-world conditions this approach will also improve the quality of detection.

There are known cases when TIP is used as a real system for assessing the effectiveness of security personnel in a number of airports [15,16,17]. To pass the test positively, an operator must overcome a certain threshold in terms of the proportion of correct answers. In case an operator fails the test, sanctions can be applied to the operator or, on the contrary, additional training can be organized. In [22], the authors note that operators with low scores on the TIP test passing assessment were sent for remedial training. In order to re-admit such employees, they must pass the test successfully.

The second approach is more classical for data science and is called augmentation. The importance of data augmentation for class balance is not diminished in the case of computer vision systems. Augmentation technologies play a crucial role in such a case [23,24,25]. Moreover, TIP-like technology is already being used to validate computer vision systems. In [26], a specialized effect on a neural network at the input is considered, which results in obtaining an erroneous label at the output. In [26], methods for detecting such injections are also considered.

An alternative direction of research is related to improving the quality of deep learning models. In this case, as was mentioned earlier, such models try to achieve maximum values in terms of recall. The modern systems are based on the best computer vision models [27,28,29,30]. Traditionally, the same tasks are solved as in the case of optical images. First of all, these are the tasks of classification [31] and object detection in X-ray images of luggage [32]. Next in popularity is the task of segmentation of such images [33].

It should also be noted that researchers often pay attention to the problems of optimizing the performance of such systems [34,35,36], since it is necessary to operate them only in real time. Usually, optimization leads to a loss of model quality, and an additional task of finding a compromise between speed and accuracy arises.

Fang C. et al. [37] proposed a novel few-shot SVM-constraint threat detection model, named FSVM, which aims to detect unseen contraband items using only a small number of labeled samples. Rather than simply fine-tuning the original model, FSVM embeds a differentiable SVM layer to back-propagate the supervised decision information into the preceding layers. Additionally, a combined loss function incorporating SVM loss is created as an additional constraint. The key idea of the authors is to more deeply integrate the support vector machine mechanism into the model architecture, instead of just superficial fine-tuning. This allows the system to be efficiently trained for prohibited item detection even with limited labeled data. The proposed approach differs from a straightforward fine-tuning of the base model. FSVM embeds a differentiable SVM component that enables backpropagation of the supervised classification information to earlier layers of the network. Moreover, the authors devise a combined objective function that includes the SVM loss as an additional regularizer.

Han L. et al. [38] proposed an approach to address the limitations of existing methods for X-ray image object detection. The existing techniques suffer from low accuracy and poor generalization, mainly due to the lack of large-scale, high-quality datasets. To address this gap, the authors provided a new large-scale X-ray image dataset for object detection, named LSIray. This dataset consists of high-quality X-ray images of luggage and 21 types of objects with varying sizes. Importantly, LSIray covers some common categories that were neglected in previous research, thus offering more realistic and rich data resources for X-ray image object detection. Additionally, the authors proposed an improved model based on YOLOv8, called SC-YOLOv8. This model incorporates two new modules. The first is CSPnet Deformable Convolution Network Module (C2F_DCN), and the second is Spatial Pyramid Multi-Head Attention Module (SPMA). The C2F_DCN module utilizes deformable convolution, which can adaptively adjust the position and shape of the receptive field to accommodate the diversity of targets. The SPMA module adopts a spatial pyramid head attention mechanism, allowing the model to leverage feature information from different scales and perspectives to enhance the representation ability of the detected objects.

Jing B. et al. [39] propose a novel method called EM-YOLOv7 to better detect prohibited items in security X-ray images, which are characterized by challenging visual features. Experimental results on the SIXray dataset show that EM-YOLOv7 outperforms YOLOv5, YOLOv7, and other state-of-the-art models, achieving 4% and 0.9% higher detection accuracy, respectively. The authors propose the EM-YOLOv7 method, which represents an effective solution for the task of prohibited item detection in security X-ray imagery, surpassing previous approaches through its innovative architectural components.

As for augmentation methods, Jang H. and colleagues [40] developed a novel data augmentation technique aimed at enhancing the training of semantic segmentation models for X-ray-based applications. The method generates synthetic X-ray images by blending actual X-ray scans of nuclear items with X-ray cargo background images. To evaluate the effectiveness of this augmentation approach, the researchers trained representative semantic segmentation models and performed extensive experiments, assessing both the quantitative and qualitative performance improvements enabled by the proposed technique. However, it is not clear whether such a method can work with nuclear items or not. Anyway, other augmentation techniques in the latest studies are only based on generative artificial intelligence.

However, the analysis also shows that at least two issues have been rather poorly addressed in the literature. First, researchers usually use standard convolutional neural network architectures to solve the baggage X-ray processing problem and do not apply modified activation and loss functions. Second, the distribution of the output layer of the network will be close to 0 and 1, which makes the system relatively nonflexible, and it is the technology of making flexible predictions that is of more interest. This problem and additional augmentation algorithms will be discussed in this article. First, the data and the modified methods will be considered, and then the next chapter will discuss the results, which turned out to be very interesting in the course of the experiments.

3. Materials and Methods

Let us consider the binary classification problem as the main task, for which most of the modifications will be made.

The available dataset was prepared jointly with the Ulyanovsk Civil Aviation Institute named after Boris Bugaev (Ulyanovsk, Russia). It contains 12,562 images and is not balanced. In particular, the dataset contains 8471 images for allowed baggage items and 4091 images for prohibited baggage items. As processing, the Ulyanovsk Civil Aviation Institute performed registration of different images and then made preprocessing to normalize the images and crop only the objects of interest.

Figure 1 shows examples of images of different classes.

From Figure 1 it is possible to conclude that the baggage items themselves from different classes are very heterogeneous. It makes the training task difficult. Moreover, developing a multi-class recognizer is also problematic due to the strong imbalance of the different items.

Let us use the following augmentation options: no augmentations, traditional Albumentations augmentations [23], and augmentations based on the doubly stochastic image model [41,42]. Let us consider it in more detail.

Let a random field be given as $X$. For its implementation in the simplest case, a bivariate autoregressive model can be used [41]:

$$\begin{array}{l}X(i,j)={\rho }_x(i,j)X(i-1,j)+{\rho }_y(i,j)X(i,j-1)-{\rho }_x(i,j){\rho }_y(i,j)X(i-1,j-1)+\\ +{\sigma }_x\sqrt{[1-{\rho }_x^2(i,j)][1-{\rho }_y^2(i,j)]}\xi (i,j).\end{array}$$

(1)

Here ${\rho }_x$ is random field of correlation along the row; ${\rho }_y$ is random field of correlation along the column; ${\sigma }_x$ is standard deviation of the main random field; $\xi$ is random field providing random additive; $(i,j)$ is pixel coordinate by row and by column.

To generate random correlation fields a similar model is used [41]:

$$\begin{array}{l}{\rho }_k(i,j)=r_{kx}{\rho }_k(i-1,j)+r_{ky}{\rho }_k(i,j-1)-r_{kx}{r}_{ky}{\rho }_k(i-1,j-1)+\\ +{\sigma }_{\rho k}\sqrt{(1-r_{kx}^2)(1-r_{ky}^2)}{\varsigma }_k(i,j)\end{array},$$

(2)

where $r_{kx}$ and $r_{ky}$ are row and column correlation coefficients for auxiliary fields along the k-th axis, respectively; ${\sigma }_{\rho k}$ is standard deviation for the random correlation field along the k-th axis; ${\varsigma }_k$ is random additive field for the k-th axis, $k$ is parameter defining the generated correlation field (either row correlations, then $k=x$, or column correlations, then $k=y$).

Parameter estimation of such a model can be performed as shown in [43]. Figure 2 shows an example of augmentation using the proposed model. On the left is the original image, and on the right is the augmented image. It is possible to see that the images are very close to each other, and it is easy to classify the augmented image for the human eye.

Thus, it is necessary to perform the generation of a new image based on the reference image, which is fed to the input of the augmentation model. Then the parameters of the doubly stochastic model are estimated. It should be noted that the correlation field for row and column, as well as the mean and variance fields, are actually estimated. This provides a different set of internal parameters at each point of the generated pixel. Otherwise, the model works as a classical random field regression model. That is, at high values of correlation across the row, the brightness of a new pixel is generated close to the brightness of the one neighboring pixel, or neighboring pixels group across the row (similarly for the column), and at high variance the model becomes more random in values. The average is needed to provide greater closeness to real images and plays an important role. However, all generated elements are then normalized from 0 to 255 anyway, giving us a new image at the output of the augmenter. At the same time, the speed is much faster than generative neural networks. In other words, it takes a much less time to create the new image.

Also, a training process modification is proposed in this article. Binary cross-entropy is most commonly used in binary classification tasks. In this case, usually the last layer is activated using a sigmoid, and the output itself can be interpreted as the probability of belonging to a positive class. In our case, such a class can be a forbidden object. It is clear that the alternative probability (for the class of allowed item) is calculated by subtracting the predicted probability from 1 (full probability is equal to 1). Then it is possible to write the loss function based on binary cross-entropy as following [38]:

$$\log loss={\displaystyle \frac{-1}{N}}{\displaystyle \sum _{i=1}^N(y_i\times \log (p_i)+(1-y_i)\times \log (1-p_i))}.$$

(3)

Here $y_i$ is the true label of positive class membership for the i-th example of training data; $p_i$ is the probability value of belonging to a positive class for the i-th example of training data, obtained as a result of the inference of the neural network model.

Thus, the model receives large penalties if it predicts a value that can be interpreted as an incorrect answer at the 0.5 threshold. But the penalties for predicting, for example, 0.3 instead of 0 are rather small, because the final answer will be correct with such a prediction and a threshold of 0.5.

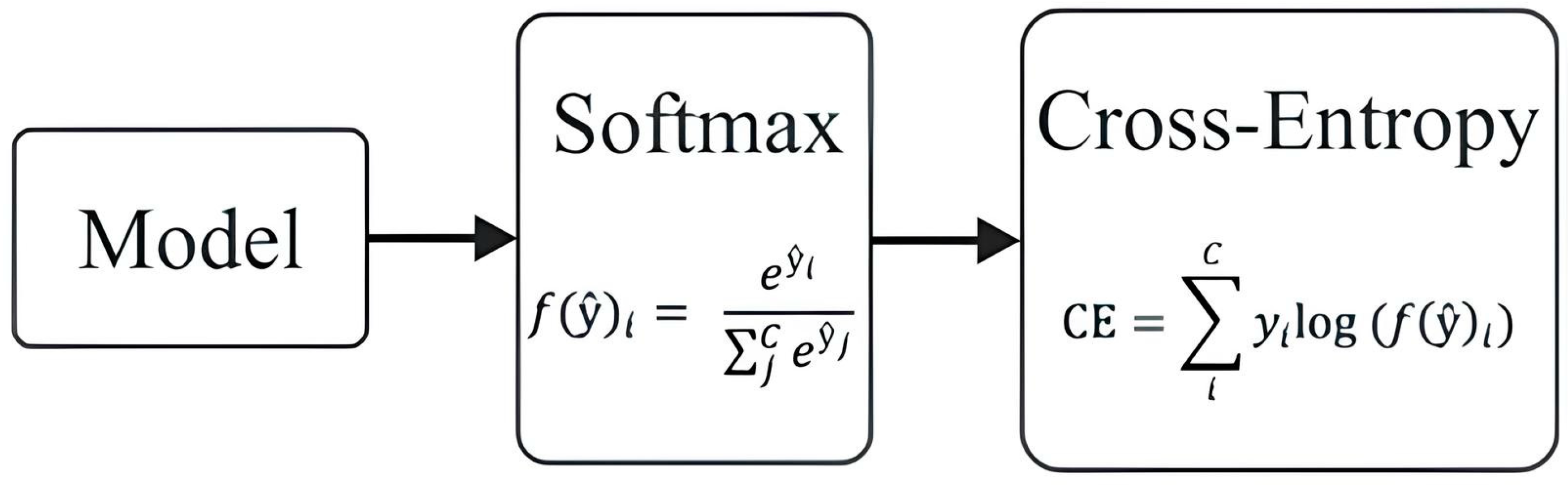
A development of the sigmoid function is the softmax activation function [44], which is needed to interpret the probabilities of belonging to a set of classes. At the same time, it can also be applied to the problem with two classes. The relationship between logits (outputs of not activated last layer), activation function and loss function, is presented in Figure 3.

Let us rewrite the expression for sofrmax again [44] as in Figure 3:

$$f({\widehat{y}}_i)={\displaystyle \frac{e^{{\widehat{y}}_i}}{{\displaystyle \sum _{j=1}^C{e}^{{\widehat{y}}_j}}}}.$$

(4)

Here ${\widehat{y}}_i$ is value of the i-th logit of the last layer of the neural network before activation; $C$ is number of classes.

It is clear that in (4) the sum of all outputs will be equal to 1. This is valid also for the case $C=2$.

By analogy with expression (3), let us rewrite the cross-entropy loss for the task with multiple classes [44]:

$$CE={\displaystyle \sum _{j=1}^C{y}_i\log (f{(\widehat{y})}_i)}.$$

(5)

It should be noted that under the logarithm, it is necessary to use the activation function, because it gives the final predictions on the neural network output. In a standard situation, it is possible to substitute expression (3), and the result for cross-entropy will coincide with the result for sigmoid. Let us use a more advanced transformation, which was proposed in the task of face identification and is called ArcFace [45]:

$$f({\widehat{y}}_i)={\displaystyle \frac{e^{{\widehat{y}}_i+m}}{{\displaystyle \sum _{j=1,j\ne i}^C{e}^{{\widehat{y}}_j}}+e^{{\widehat{y}}_i+m}}},$$

(6)

where ${\widehat{y}}_i$ is value of the i-th logit of the last layer of the neural network before activation, $C$ is number of classes, and $m$ is margin.

It would be more useful to add a margin in the form of an angle factor, which would move the logit vectors for different classes farther apart [45]:

$$f({\widehat{y}}_i)={\displaystyle \frac{e^{s\cos ({\theta }_{\widehat{y}i}+m)}}{{\displaystyle \sum _{j=1,j\ne i}^C{e}^{s\cos ({\theta }_{\widehat{y}j})}}+e^{s\cos ({\theta }_{\widehat{y}i}+m)}}}.$$

(7)

Here it was suggested to add a vector of model parameters needed for optimization $\theta$. And let us also introduce some standardization coefficient $s$.

The main parameter is the margin $m$, which provides the deviation of each class from all others in the extracted feature space. However, too large a value of the parameter $m$ could lead to bad results, so that the classes would be mixed even worse. However, it is better to implement angular deviation, so that this parameter is responsible for the angle and its optimization is simplified.

Thus, the ArcFace function ensures that each class is more removed relative to the others. The ArcFace loss function is designed to improve the discriminative power of the learned feature embeddings in classification tasks, such as face recognition. It achieves this by introducing an additive angular margin penalty between the embeddings of different classes. Typically, in a classification problem, the similarity between an input feature embedding and the reference embeddings of each class is computed, often using cosine similarity, and the class with the highest similarity score is predicted as the output. The ArcFace loss aims to increase the angular distance between the embeddings of different classes by adding a margin to the cosine similarity score of the ground truth class. Specifically, the ArcFace loss function penalizes the model when the cosine similarity between the input embedding and the reference embedding of the ground truth class is not sufficiently larger than the cosine similarities with the reference embeddings of other classes. This angular margin penalty is applied in the log-softmax formulation of the loss function, which normalizes the similarity scores to obtain a valid probability distribution over the classes.

The use of normalized embeddings (i.e., unit-length feature vectors) in the ArcFace loss also helps to simplify the optimization process, as the cosine similarity scores are bounded between −1 and 1. This property allows the model to focus on learning the relative angular relationships between the embeddings, rather than their absolute magnitudes. By minimizing this loss function during training, the model learns to push the embeddings of different classes further apart in the angular space, improving the overall classification performance, particularly in face recognition applications.

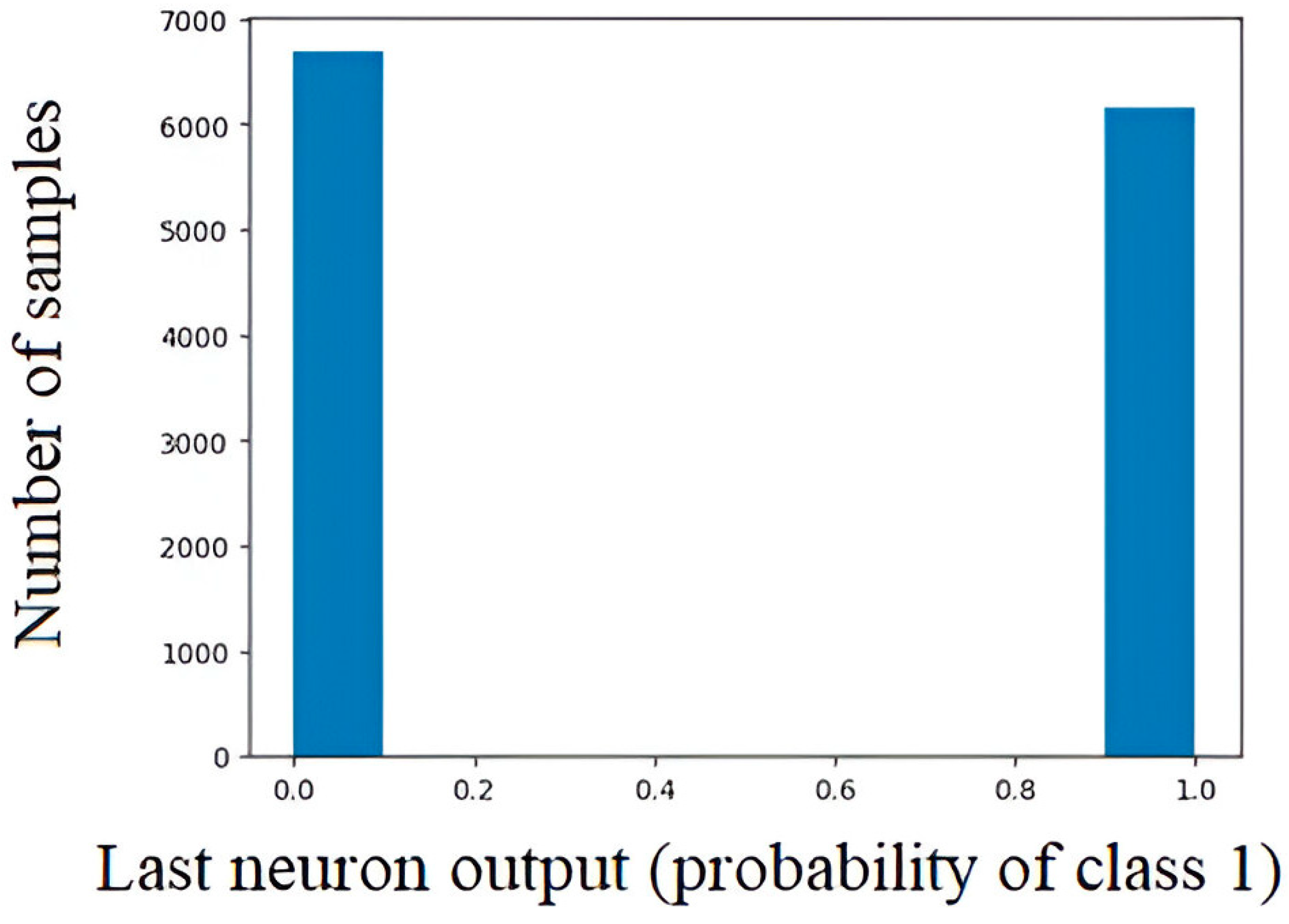
Another important aspect is the fact that the training takes place at a partitioning that produces as correct answers probabilities 0 and 1. Due to this, the models are trained such that most of the predictions are distributed around 0 and 1. This makes the fuzzy logic system [46] more predictable. To avoid this problem, it is possible to apply not just softmax function to calculate probabilities, but to use softmax with temperature [46]:

$$\mathrm{soft}\max {(x)}_i={\displaystyle \frac{e^{\raisebox{1ex}{$y_i$}\!\left/ \!\raisebox{-1ex}{$T$}\right.}}{{\displaystyle \sum _{i=1}^N{e}^{\raisebox{1ex}{$y_i$}\!\left/ \!\raisebox{-1ex}{$T$}\right.}}}}$$

(8)

where $T$ characterizes the temperature. Thus, we can equalize the probability distribution at the output.

The larger the temperature value $T$, the closer the output layer distribution is to a uniform distribution.

Let us consider the results that the proposed modifications provide.

4. Results and Discussion

Let us compare known convolutional neural network architectures and vision transformer architectures.

Table 1. Comparison of recall metrics for prohibited items.

Model	No Augmentations	Standard Augmentations	Our Augmentations
VGG-16	0.76	0.78	0.79
VGG-16 + ArcFace	0.79	0.81	0.83
ResNet50	0.82	0.83	0.84
ResNet50 + ArcFace	0.86	0.88	0.91
ViT	0.89	0.91	0.91
ViT + ArcFace	0.90	0.89	0.91
SWIN	0.93	0.94	0.94
SWIN + ArcFace	0.96	0.97	0.97

shows the different models and their quality scores on the recall metric for forbidden items. The quantity of augmentations everywhere is 10%.

The experiments were performed in the Python programming language using the pytorch framework and the numpy and pandas libraries. ASUS TUF FX504 laptop (CPU Intel Core i7-8750H, 16 GB RAM) with GPU NVIDIA GeForce GTX 1060, 6 GB was used as a computing device. Taking into account the memory size, a batch size of 8 images was chosen.

Transfer learning technology for the architectures already available in pytorch was used. However, in the first case, the cross-entropy function was used as the loss function, and in the second case, the proposed modified loss function implemented using numpy was applied.

Regarding the dataset, validation on a proprietary dataset was performed at the presented earlier special dataset and other known benchmarks.

The analysis of the data presented in Table 1 shows that the proposed methods improve the quality within individual models in general.

At the same time, augmentations have a better effect on networks with convolutional architecture, while ArcFace provides a gain in recall characteristics for all architectures.

The developed classifier was implemented on the additional layer of YOLO instead of ResNet, and experiments were performed. Since the SWIN model showed the best metrics, testing was performed for it, for YOLO with basic ResNet and YOLO without the additional classifier.

The results for the version YOLOv7m (medium) and YOLOv10m (medium) model were compared. The comparative performance is summarized in

Table 2. Comparison of detection models based on YOLOv7.

Model	mAP	IoU
YOLOv7	0.629	0.788
YOLOv7 + ResNet	0.647	0.788
YOLOv7 + SWIN(ArcFace)	0.654	0.788

(YOLOv7) and

Table 3. Comparison of detection models based on YOLOv10.

Model	mAP	IoU
YOLOv10	0.638	0.832
YOLOv10 + ResNet	0.671	0.832
YOLOv10 + SWIN(ArcFace)	0.688	0.832

(YOLOv10). For the detection task, the original dataset from which the subjects were sliced for classification was used. It amounted to a volume of 2542 images with more than 10,000 subjects. The metric used as the main detection metric was the metric of mean area precision (mAP).

It is possible to see that the intersection over union (IoU) metric depends only on model type and IoU is higher for YOLOv10. The analysis of the presented results allows us to conclude that the introduction of an additional classifier provides an increase in the quality of detection of the prohibited objects by about 1% compared to the use of ResNet. However, the problem of transformer architectures is their slow speed of operation. And the metrics for YOLOv10 are better. The value of mAP was 0.714 for GroundingDINO model, but this model is very slow.

Finally, let us consider the application of the softmax function with temperature for activation. At $T=0.1$ we obtain distant distributions (Figure 4); increasing $T=1.5$ brings the probabilities at both ends closer (Figure 5).

Smoothing distributions also provides a recall gain if a threshold even lower than 0.5 is used for further classification. Studies of a test dataset have shown that applying functions with temperature in the neighborhood of 0.5 allows up to 1.2% gain in the recall of forbidden object detection compared to the traditional softmax function. However, these studies are expected to be more thorough in the future.

Table 4. Comparison of activation functions.

Function	Recall	Precision
Softmax	0.971	0.874
Softmax with temperature (T = 0.5)	0.979	0.869
ReLu	0.862	0.782
Tanh	0.931	0.855

presents results using different activation functions.

Table 4 shows that using temperature, it is possible to increase recall of prohibited items classification, but precision deceases a little.

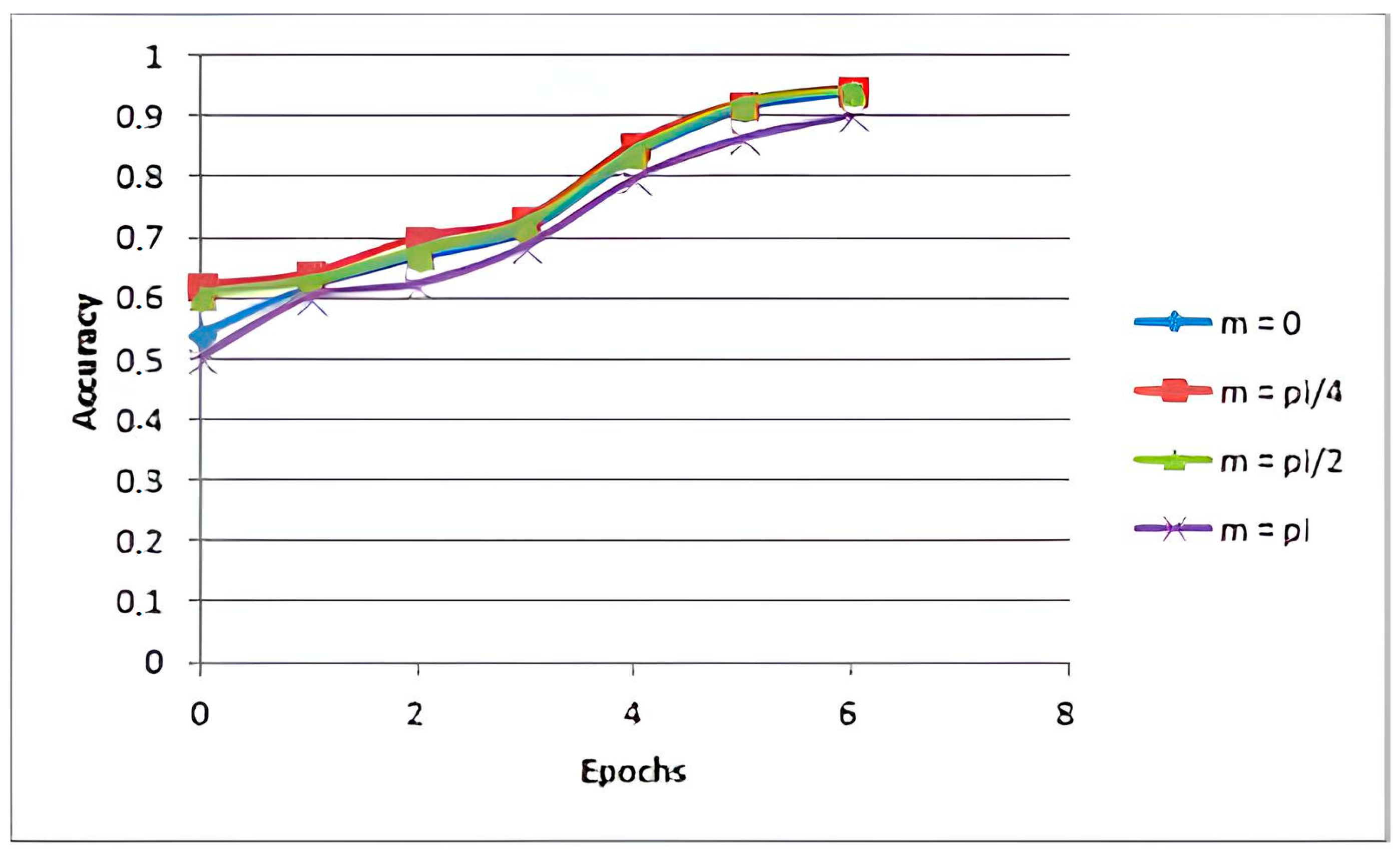
Also, for the proposed learning function, the stability of the models was tested by applying the modified loss function. The analysis was performed for different values of the margin $m$. As a result, it was found that the learning curves converge, i.e., the method is stable. Figure 6 demonstrates accuracy for different margins.

To ensure that the proposed solutions are adequate, we chose other datasets and checked the results. We used the Kaggle Suitcase/Luggage Dataset [47] and the HiXray dataset [48].

Table 5. Detection results on Kaggle Suitcase/Luggage Dataset.

Model	mAP
YOLOv7 + ArcFace	0.589
YOLOv7	0.521
YOLOv10 + ArcFace	0.596
YOLOv10	0.563

and

Table 6. Detection results on HiXray dataset.

Model	mAP
YOLOv7 + ArcFace	0.714
YOLOv7	0.687
YOLOv10 + ArcFace	0.722
YOLOv10	0.701

compare results for mAP metric for the first and second dataset, respectively. It should be noted that the training included 20 epochs with default hyperparameters.

The key finding from the tables is that the integration of the ArcFace loss function into the YOLOv7 and YOLOv10 object detection models results in improved detection performance compared to the standalone YOLO models. Specifically, on the Kaggle Suitcase/Luggage Dataset, the YOLOv7 + ArcFace model achieves mAP of 0.589, which is higher than the mAP of 0.521 achieved by the standalone YOLOv7 model, and the YOLOv10 + ArcFace model achieves a mAP of 0.596, which is higher than the mAP of 0.563 achieved by the standalone YOLOv10 model. Similarly, on the HiXray dataset, the YOLOv7 + ArcFace model achieves a mAP of 0.714, which is higher than the mAP of 0.687 achieved by the standalone YOLOv7 model, and the YOLOv10 + ArcFace model achieves a mAP of 0.722, which is higher than the mAP of 0.701 achieved by the standalone YOLOv10 model.

However, there are some limitations for this approach. First, the approach can exhibit biases towards certain subgroups within the data, leading to disparities in performance and fairness concerns. The model’s vulnerability to adversarial attacks is also a common issue, where carefully crafted perturbations can cause misclassifications. The dependence on the quality and diversity of the training data is a fundamental challenge, as biases in the data can lead to suboptimal performance in real-world scenarios. Scaling the approach to handle large-scale problems can be computationally expensive, as the computational cost may increase with the size of the reference database or problem complexity. Additionally, the widespread deployment of such systems raises privacy and ethical concerns, which need to be carefully addressed. Finally, improving the generalization of the approach to handle novel or unseen inputs is an important research direction, as it can enhance the robustness and versatility of the system. Addressing these limitations is crucial for developing reliable, fair, and ethically-aligned machine learning and deep learning-based solutions.

So, the proposed methods demand future optimization for choosing the margin parameter value, and it will be discussed in the next publications.

5. Conclusions

Thus, in this article, neural network layers and target functions have been modified in training neural networks for binary classification of luggage X-ray images. The computational cost of the approach for face recognition is primarily dominated by the feature extraction network, whose complexity scales with the network architecture and input image size. The embedding calculation and cosine similarity computation between the input and reference embeddings also contribute to the overall cost, with the latter scaling linearly with the size of the reference database. However, the additional computations for the ArcFace loss function are relatively insignificant compared to the other components. The exact computational requirements will depend on the specific implementation and hardware, but the optimization of the feature extraction network is crucial for achieving efficient face recognition using the ArcFace approach. A method for augmenting such images using doubly stochastic random field models is proposed, showing gains to the quality of the models in the sense of a recall metric. The results obtained are also translated to models of object detection in X-ray baggage and hand luggage images. Studies of the proposed algorithms on other datasets have also shown their robustness and high metrics in recognizing prohibited baggage items. Initial experiments using softmax with temperature have shown its potential in the task of baggage image classification. In particular, this approach helps one to increase recall value. But more in-depth studies on this issue are planned in future works.