The Connection between Der(
Abstract
1. Introduction
2. Preliminaries
2.1. The Algebras and
2.2. Iterated Ore Extension
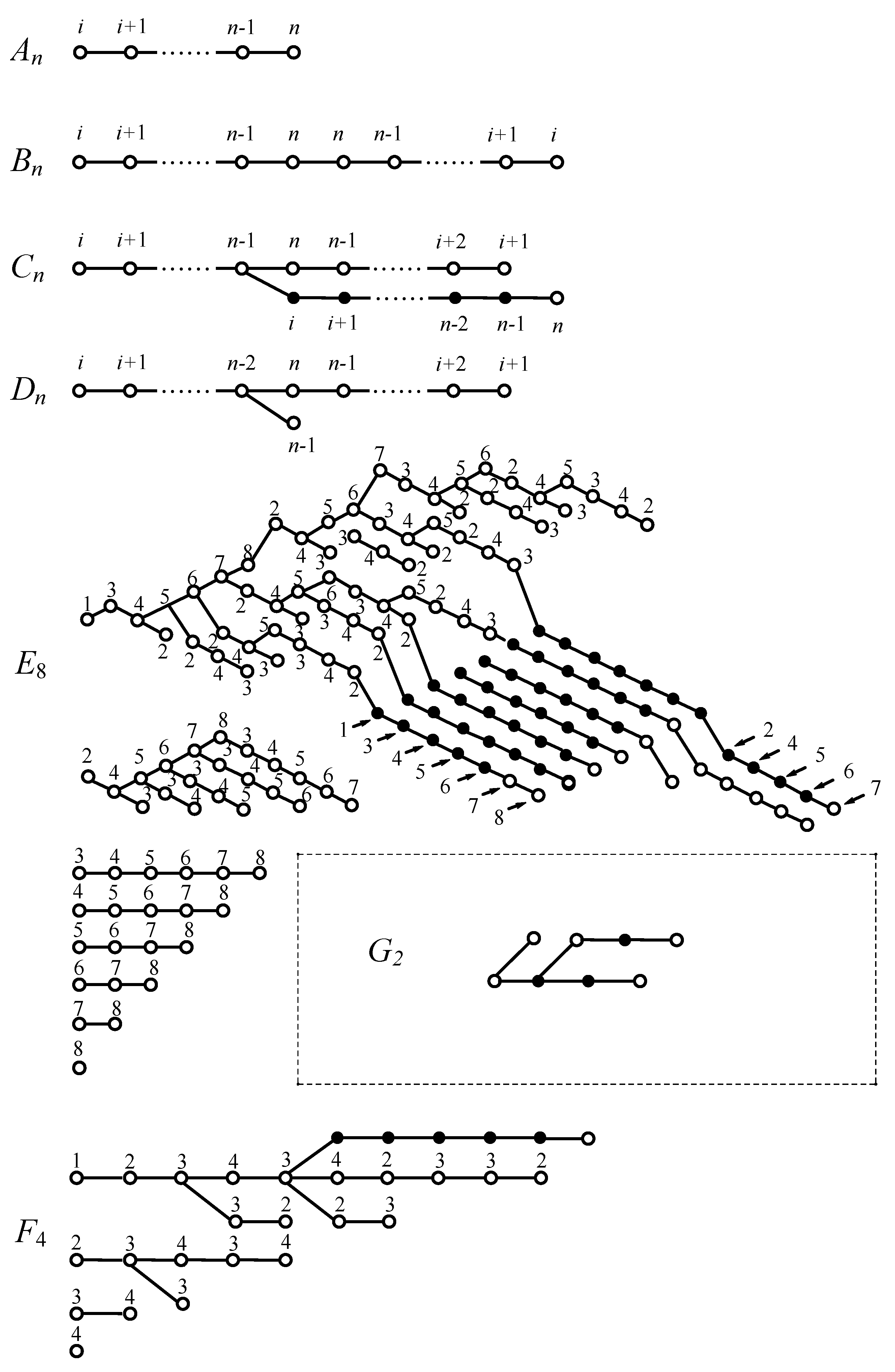
3. Derivations of Iterated Ore Extension
4. The Relationship between and
4.1. Derivations of Quantum Groups
4.2. Obtain Der from Der
- (i)
- , for all ;
- (ii)
- for all ;
- (iii)
- The greatest common divisor of all is equal to 1.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Drinfel’D, V. Hopf algebras and quantum Yang-Baxter equation. Dokl. Akad. 1985, 32, 254–258. [Google Scholar]
- Benkart, G.; Witherspoon, S. A Hopf structure for down-up algebras. Math. Z. 2001, 238, 523–553. [Google Scholar] [CrossRef]
- Benkart, G.; Witherspoon, S. Quantum group actions, twisting elements, and deformations of algebras. J. Pure Appl. Algebra 2007, 208, 371–389. [Google Scholar] [CrossRef]
- Bergeron, N.; Yun, G.; Hu, N. Drinfel’d doubles and Lusztig’s symmetries of two-parameter quantum groups. J. Algebra 2006, 301, 378–405. [Google Scholar] [CrossRef]
- Bergeron, N.; Yun, G.; Hu, N. Representations of two-parameter quantum orthogonal groups and symplectic groups. AMS/IP Stud. Adv. Math. 2007, 39, 1–21. [Google Scholar]
- Hu, N.; Shi, Q. The two-parameter quantum group of exceptional type G2 and Lusztig’s symmetries. Pac. J. Math. 2007, 230, 327–345. [Google Scholar] [CrossRef]
- Hu, N.; Wang, X. Convex PBW-type Lyndon bases and restricted two-parameter quantum groups of type B. J. Geom. Phys. 2010, 6, 430–453. [Google Scholar] [CrossRef]
- Hu, N.; Pei, Y. Notes on two-parameter quantum groups (II). Commun. Algebra 2012, 40, 3202–3220. [Google Scholar] [CrossRef]
- Hu, N.; Pei, Y. Notes on two-parameter quantum groups, (I). Sci. China Ser. Math. 2008, 51, 1101–1110. [Google Scholar] [CrossRef]
- Fan, Z.; Li, Y. Two-Parameter quantum algebras, canonical bases, and categorifications. Int. Math. Res. Not. 2015, 16, 7016–7062. [Google Scholar] [CrossRef][Green Version]
- Lalonde, P.; Arun, R. Standard Lyndon bases of Lie algebras and enveloping algebras. Trans. Am. Math. Soc. 1995, 347, 1821–1830. [Google Scholar] [CrossRef]
- Elle, S. Classification of relation types of Ore extensions of dimension 5. Commun. Ina. 2017, 45, 1323–1346. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Y.; Tang, X.
The Connection between Der(
Zhong Y, Tang X.
The Connection between Der(
Zhong, Yongyue, and Xiaomin Tang.
2024. "The Connection between Der(
Zhong, Y., & Tang, X.
(2024). The Connection between Der(






