Modeling and Rotation Control Strategy for Space Planar Flexible Robotic Arm Based on Fuzzy Adjustment and Disturbance Observer
Abstract
1. Introduction
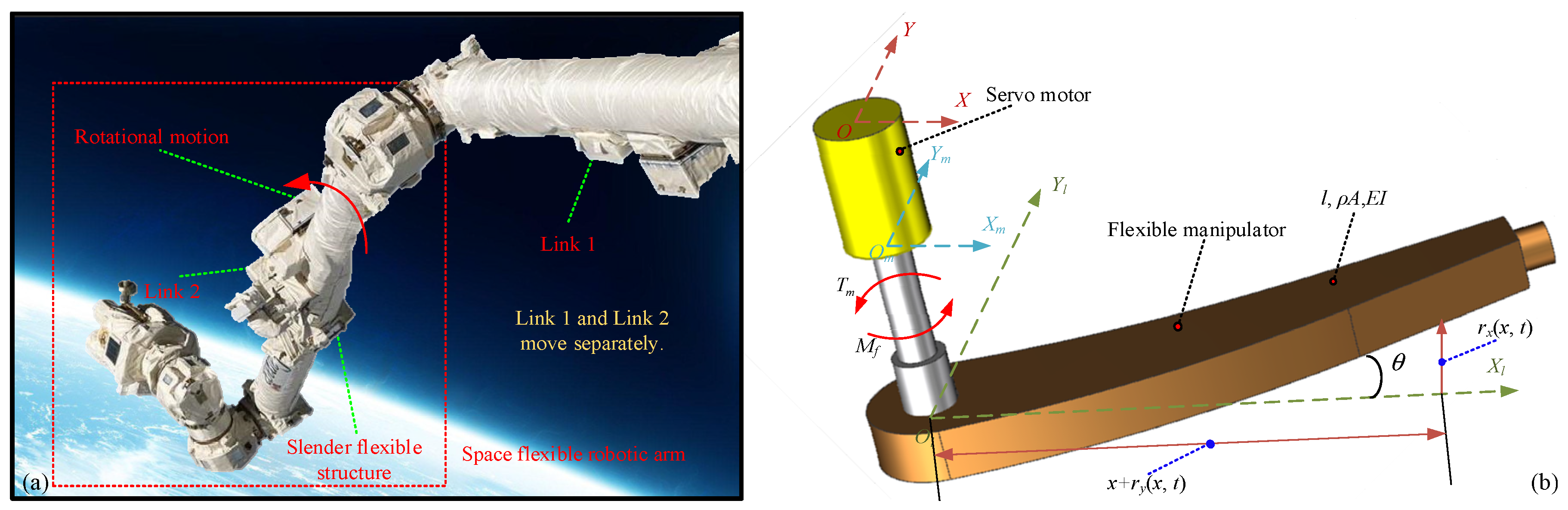
2. Modelling Dynamics for the SFRA
2.1. Friction Modeling
2.2. Dynamic Modeling
2.3. Dynamical Model Simplification
2.3.1. 1D1M Simplification Model
2.3.2. NNTs Simplification Model
3. Accuracy Evaluation of the Simplified Model
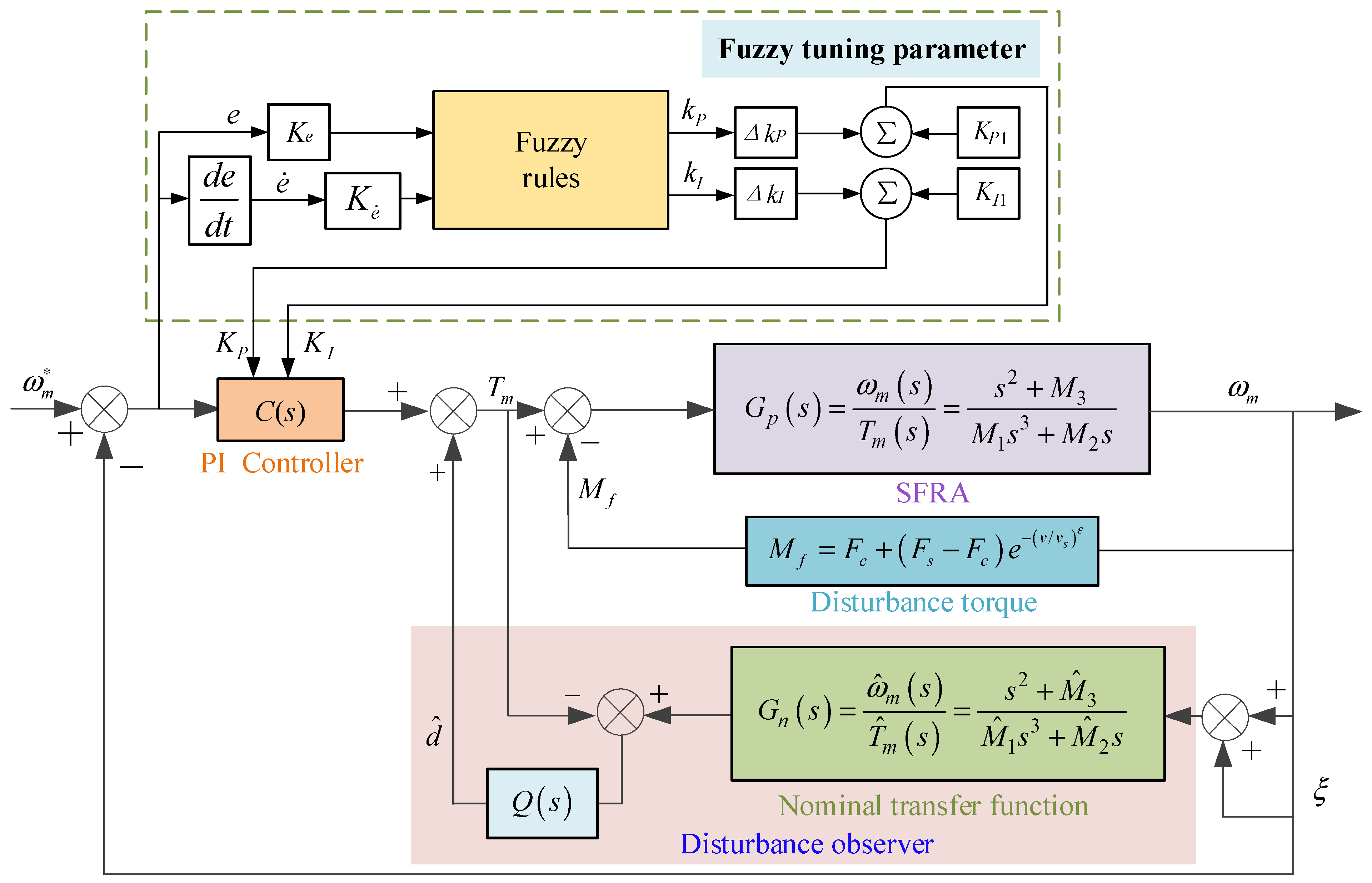
4. Fuzzy PI Control Based on Disturbance Observer
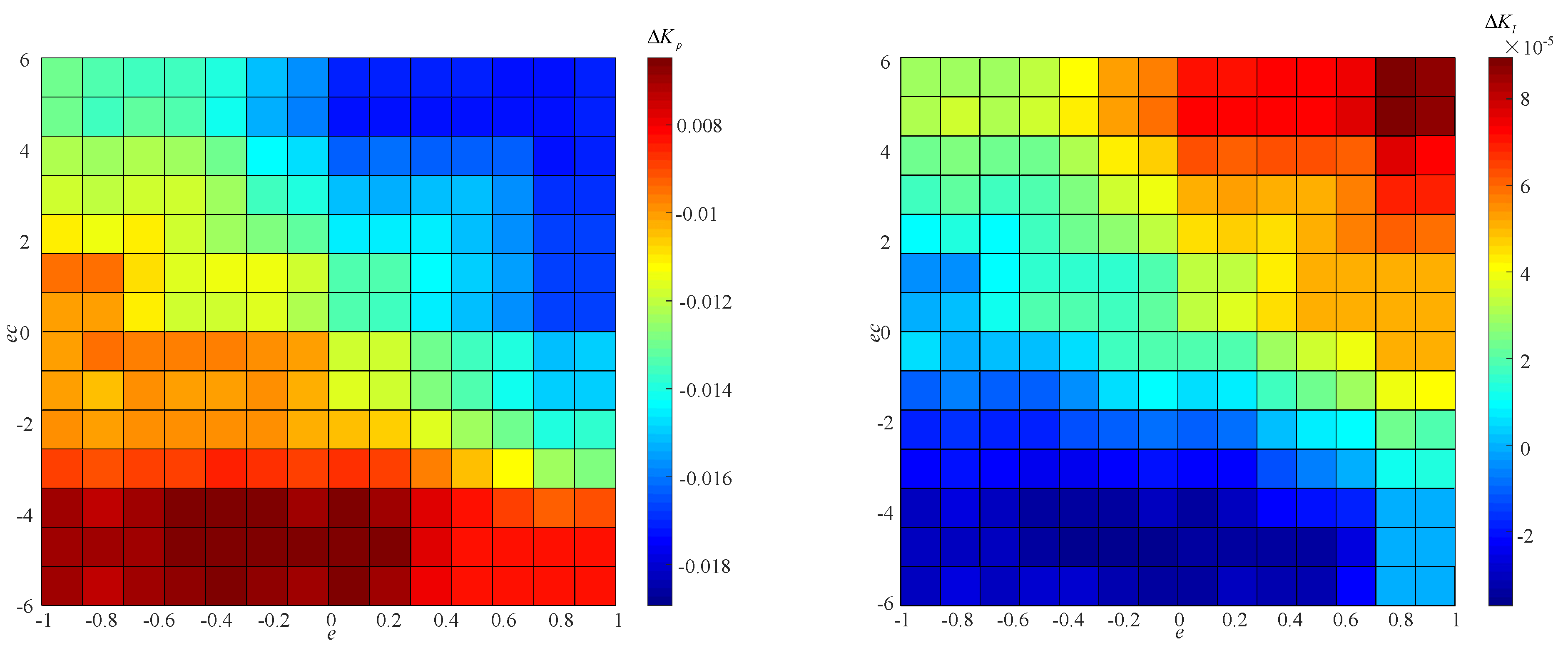
4.1. Fuzzy Adjustment of the Controller Parameters Based on Pole Configuration
4.2. Design of Disturbance Observer Based on the Nominal Model
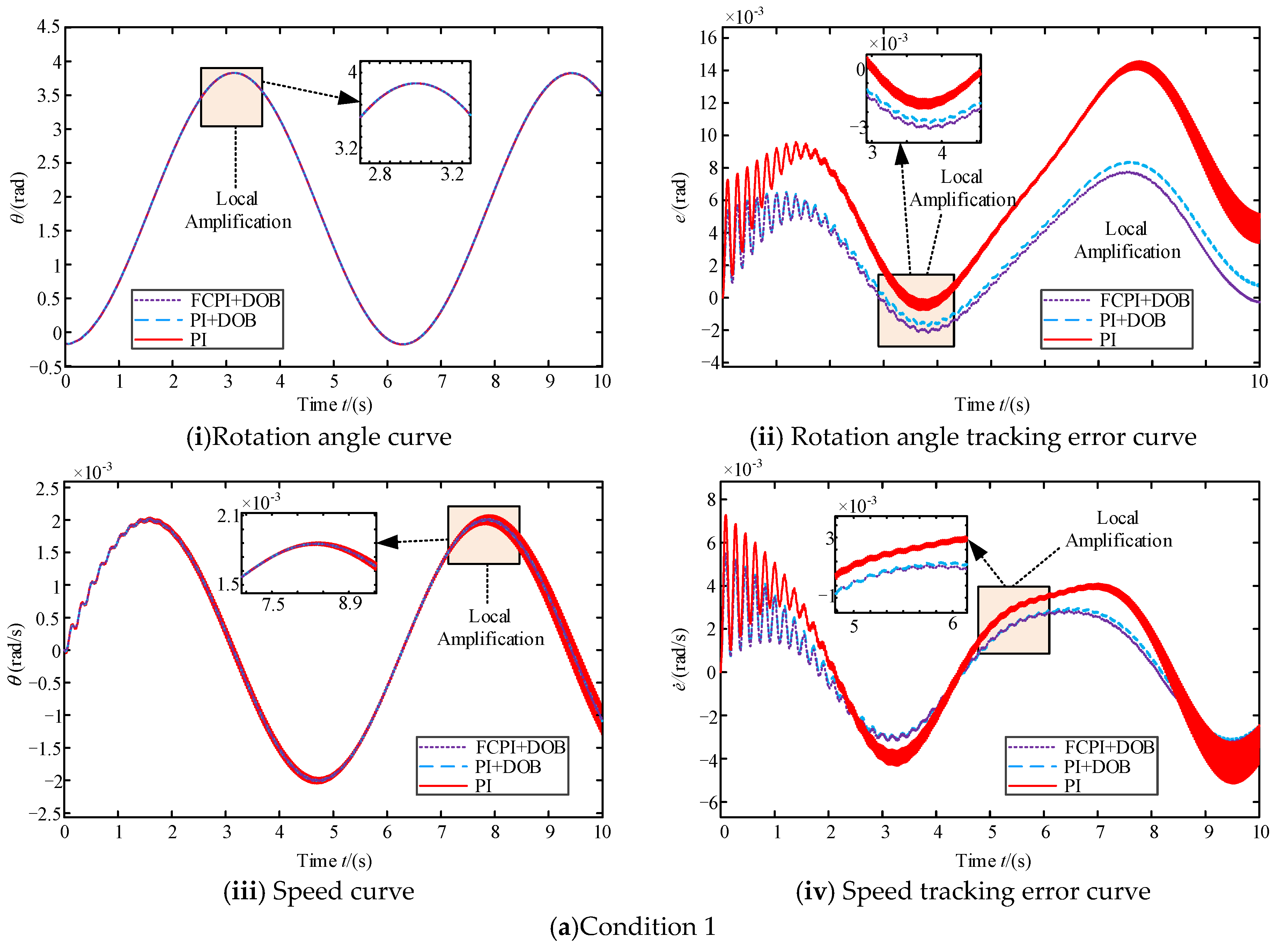
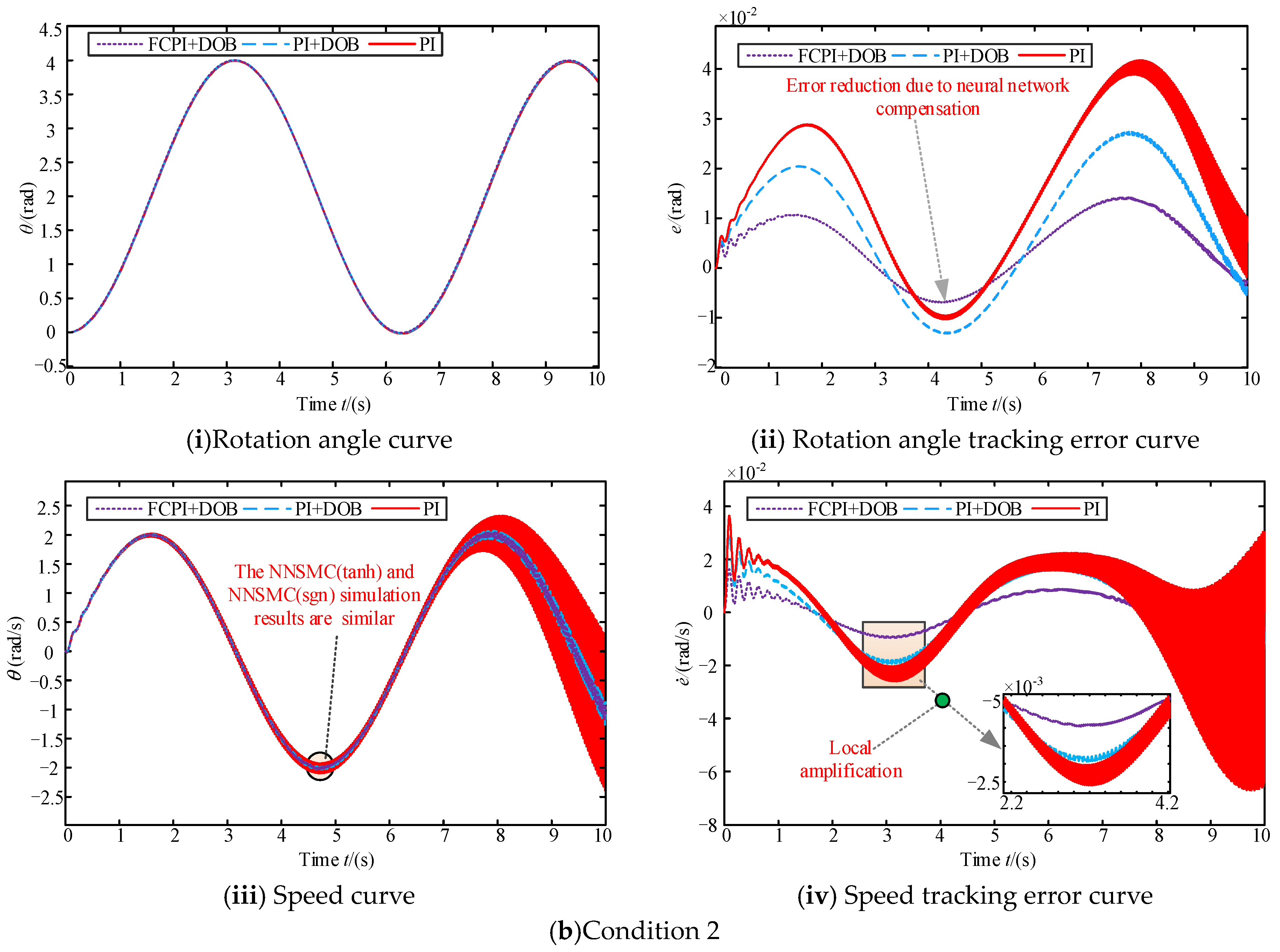
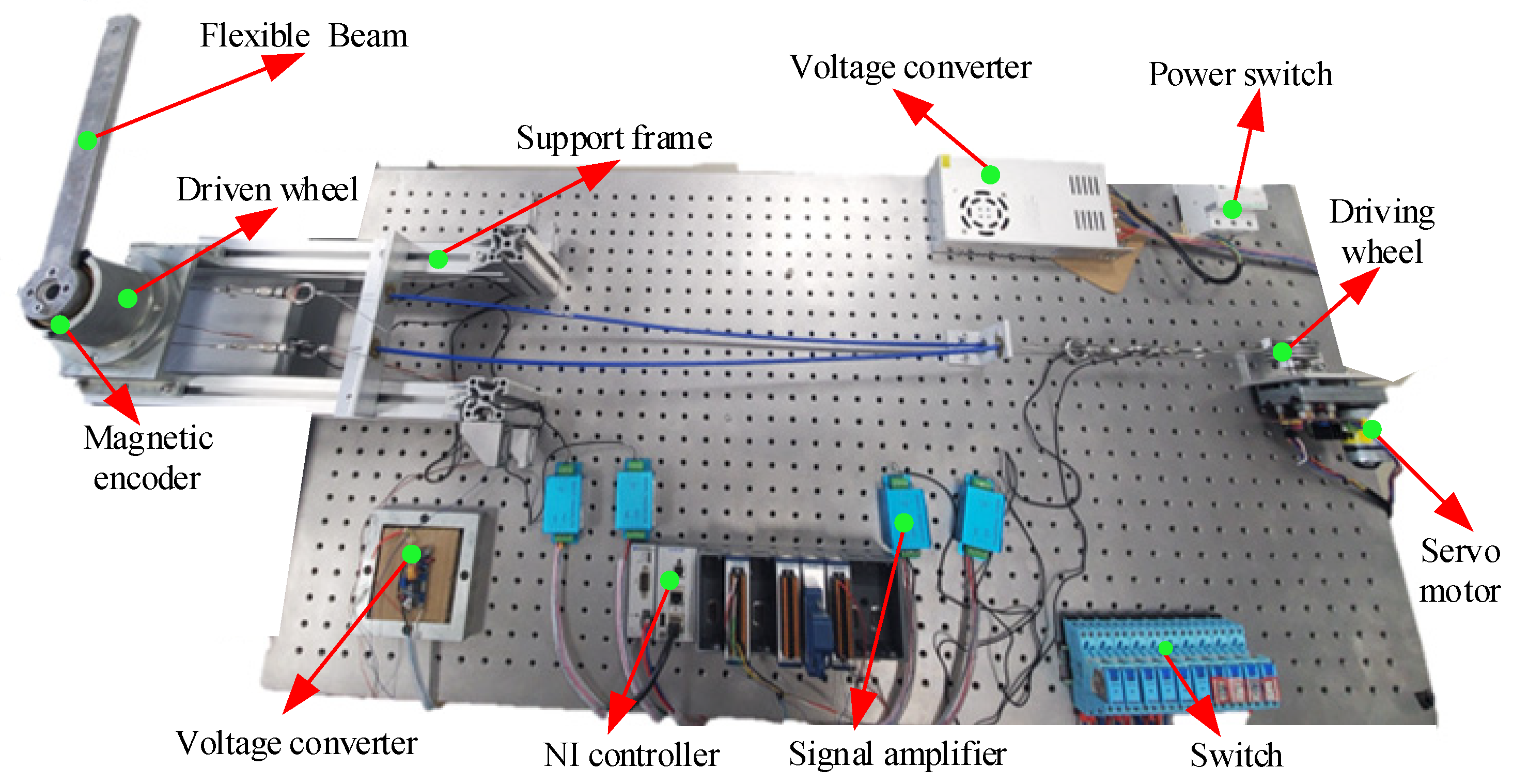
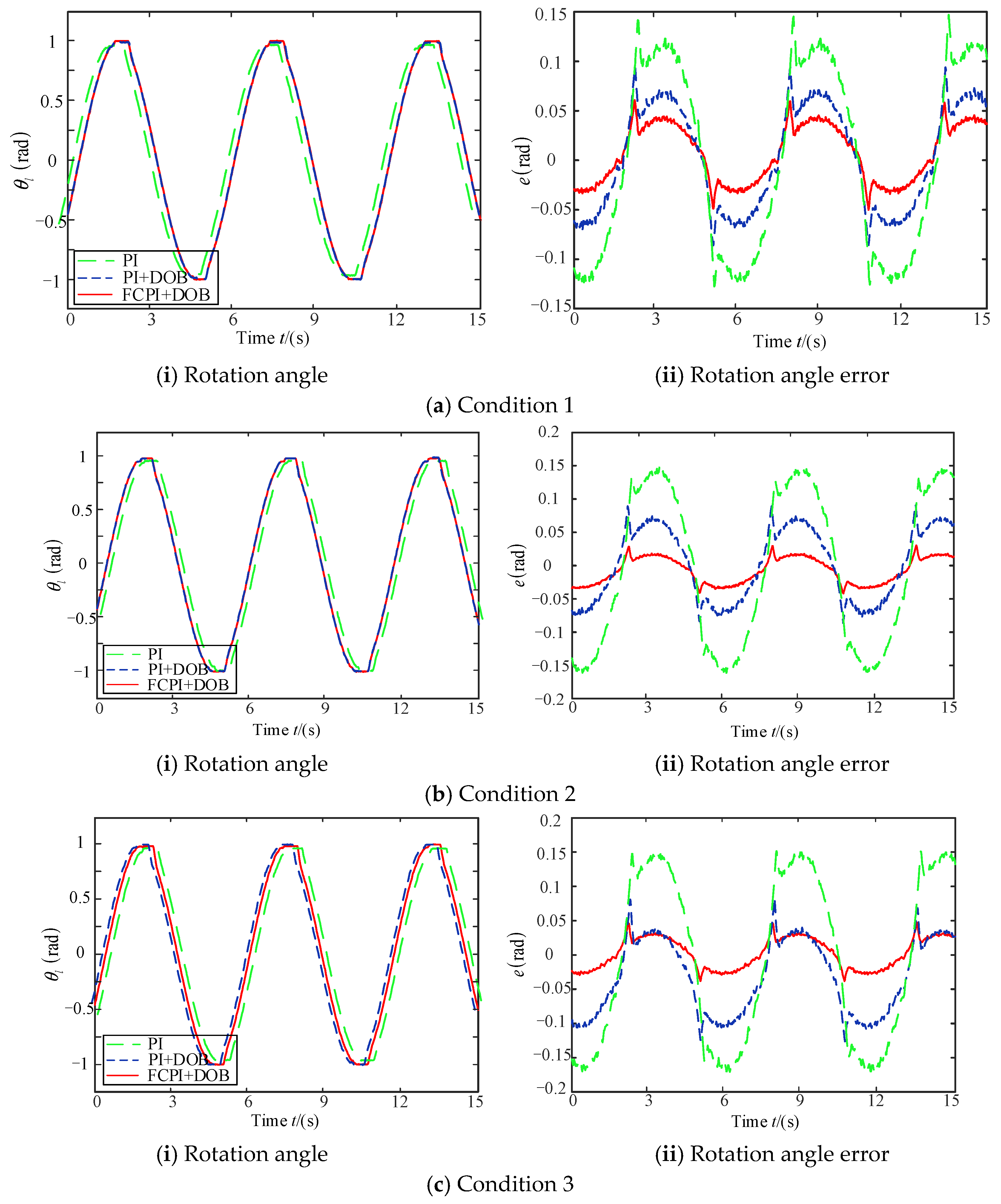
5. Simulation and Physical Prototype Control Experiments on Ground
5.1. Simulation Analysis
5.2. Ground Physical Prototype Control Experiment
6. Discussions
6.1. Comparison of Dynamic Modeling Methods
6.2. DOB Robust Stability
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moghaddam, B.M.; Chhabra, R. On the guidance, navigation and control of in-orbit space robotic missions: A survey and prospective vision. Acta Astronaut. 2021, 184, 70–100. [Google Scholar] [CrossRef]
- Li, Y.M.; Tong, S.C.; Li, T.S. Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping, Nonlinear Anal. Real World Appl. 2012, 14, 483–494. [Google Scholar] [CrossRef]
- Li, W.J.; Cheng, D.Y.; Liu, X.G.; Wang, Y.B.; Shi, W.H.; Tang, Z.X.; Gao, F.; Zeng, F.M.; Chai, H.Y.; Luo, W.B.; et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Prog. Aerosp. Sci. 2019, 108, 32–120. [Google Scholar] [CrossRef]
- Peng, J.Q.; Xu, W.F.; Liu, T.L.; Yuan, H.; Liang, B. End-effector pose and arm-shape synchronous planning methods of a hyper-redundant manipulator for spacecraft repairing. Mech. Mach. Theory 2021, 155, 104062. [Google Scholar] [CrossRef]
- Yang, S.J.; Zhang, Y.L.; Wen, H.; Jin, D.P. Coordinated control of dual-arm robot on space structure for capturing space targets. Adv. Space Res. 2023, 71, 2437–2448. [Google Scholar] [CrossRef]
- Gasbarri, P.; Pisculli, A. Dynamic/control interactions between flexible orbiting space-robot during grasping, docking and post-docking manoeuvres. Acta Astronaut. 2015, 110, 225–238. [Google Scholar] [CrossRef]
- Sabatini, M.; Gasbarri, P.; Monti, R.; Palmerini, G.B. Vibration control of a flexible space manipulator during on orbit operations. Acta Astronaut. 2012, 73, 109–121. [Google Scholar] [CrossRef]
- Mehrjooee, O.; Dehkordi, S.F.; Korayem, M.H. Dynamic modeling and extended bifurcation analysis of flexible-link manipulator. Mech. Based Des. Struct. Mach. 2019, 48, 87–110. [Google Scholar] [CrossRef]
- Chu, A.M.; Nguyen, C.D.; Duong, X.B.; Nguyen, A.V.; Nguyen, T.A.; Le, C.H.; Packianather, M. A novel mathematical approach for finite element formulation of flexible robot dynamics. Mech. Based Des. Struct. March. 2020, 50, 3747–3767. [Google Scholar] [CrossRef]
- Du, H.; Lim, M.K.; Liew, K.M. A nonlinear finite element model for dynamics of flexible manipulators. Mech. Mach. Theory 1996, 31, 1109–1119. [Google Scholar] [CrossRef]
- Hewit, J.R.; Morris, J.R.; Sato, K.; Ackermann, F. Active force control of a flexible manipulator by distal feedback. Mech. Mach. Theory 1997, 32, 583–596. [Google Scholar] [CrossRef]
- Xiao, W.; Hu, D.A.; Yang, G.; Jiang, C. Modeling and analysis of soft robotic surfaces actuated by pneumatic network bending actuators. Smart Mater. Struct. 2022, 31, 055001. [Google Scholar] [CrossRef]
- Zhang, X.S.; Zhang, D.G.; Chen, S.J.; Hong, J.Z. Modal characteristics of a rotating flexible beam with a concentrated mass based on the absolute nodal coordinate formulation. Nonlinear Dyn. 2017, 88, 61–77. [Google Scholar] [CrossRef]
- Kumar, P.; Pratiher, B. Influences of generic payload and constraint force on modal analysis and dynamic responses of flexible manipulator. Mech. Based Des. Struct. Mach. 2020, 50, 1968–1986. [Google Scholar] [CrossRef]
- Qiu, Z.C.; Li, C.; Zhang, X.M. Experimental study on active vibration control for a kind of two-link flexible manipulator. Mech. Syst. Signal Process. 2018, 118, 623–644. [Google Scholar] [CrossRef]
- Mukherjee, S.; Roy, H. Modeling of flexible damped coupling and its influence on rotor dynamics. Mech. Based Des. Struct. Mach. 2023, 52, 1377–1398. [Google Scholar] [CrossRef]
- Kumar, P.; Pratiher, B. Nonlinear dynamic analysis of a multi-link manipulator with flexible links-joints mounted on a mobile platform. Adv. Space Res. 2023, 71, 2095–2127. [Google Scholar] [CrossRef]
- Korayem, M.H.; Shafei, A.; Absalan, M.; Kadkhodaei, F.B.; Azimi, A. Kinematic and dynamic modeling of viscoelastic robotic manipulators using Timoshenko beam theory: Theory and experiment. Int. J. Adv. Manuf. Technol. 2014, 71, 1005–1018. [Google Scholar] [CrossRef]
- Mahto, S. Shape optimization of revolute-jointed single link flexible manipulator for vibration suppression. Mech. Mach. Theory 2014, 75, 150–160. [Google Scholar] [CrossRef]
- Guo, F.; Cheng, G.; Pang, Y.S. Explicit dynamic modeling with joint friction and coupling analysis of a 5-dof hybrid polishing robot. Mech. Mach. Theory 2022, 167, 104509. [Google Scholar] [CrossRef]
- He, J.; Zheng, H.C.; Gao, F.; Zhang, H.B. Dynamics and control of a 7-DOF hybrid manipulator for capturing a non-cooperative target in space. Mech. Mach. Theory 2019, 140, 83–103. [Google Scholar] [CrossRef]
- Cui, L.L.; Wang, H.S.; Chen, W.D. Trajectory Planning of a Spatial Flexible Manipulator for Vibration Suppression. Rob. Auton. Syst. 2019, 123, 103316. [Google Scholar] [CrossRef]
- Kim, H.K.; Choi, S.B.; Thompson, B.S. Compliant control of a two-link flexible manipulator featuring piezoelectric actuators. Mech. Mach. Theory 2001, 36, 411–424. [Google Scholar] [CrossRef]
- Malgaca, L.; Yavuz, A.; Akda, M.; Karagülle, H. Residual vibration control of a single-link flexible curved manipulator. Simul. Modell. Pract. Theory 2016, 67, 155–170. [Google Scholar] [CrossRef]
- Han, D.; Dong, G.Q.; Huang, P.F.; Ma, Z.Q. Capture and detumbling control for active debris removal by a dual-arm space robot. Chin. J. Aeronaut. 2022, 35, 342–353. [Google Scholar] [CrossRef]
- Ahmadizadeh, M.; Shafei, A.M.; Fooladi, M. Dynamic modeling of closed-chain robotic manipulators in the presence of frictional dynamic forces: A planar case. Mech. Based Des. Struct. Mach. 2021, 51, 4347–4367. [Google Scholar] [CrossRef]
- Huang, J.B.; Xie, Z.W.; Jin, M.H.; Jiang, Z.N.; Liu, H. Adaptive impedance-controlled manipulator based on collision detection. Chin. J. Aeronaut. 2009, 22, 105–112. [Google Scholar] [CrossRef]
- Feyzollahzadeh, M.; Bamdad, M. Efficient technique in computational dynamic modeling of a flexible manipulator with large deformation. J. Vib. Control 2023, 29, 2227–2241. [Google Scholar] [CrossRef]
- Bamdad, M.; Feyzollahzadeh, M. Computational efficient discrete time transfer matrix method for large deformation analysis of flexible manipulators. Mech. Based Des. Struct. Mach. 2020, 50, 4274–4296. [Google Scholar] [CrossRef]
- Liu, X.F.; Li, H.Q.; Chen, Y.J.; Cai, G.P. Dynamics and control of space robot considering joint friction. Acta Astronaut. 2015, 111, 1–18. [Google Scholar] [CrossRef]
- Zhai, G.; Zheng, H.M.; Zhang, B. Observer-based control for the platform of a tethered space robot. Chin. J. Aeronaut. 2018, 31, 1786–1796. [Google Scholar] [CrossRef]
- Ibrahim, K.; Sharkawy, A.B. A hybrid PID control scheme for flexible joint manipulators and a comparison with sliding mode control. Ain Shams Eng. J. 2019, 9, 3451–3457. [Google Scholar] [CrossRef]
- Lu, K.; Han, S.; Yang, J.; Yu, H. Inverse Optimal Adaptive Tracking Control of Robotic Manipulators Driven by Compliant Actuators. IEEE Trans. Ind. Electron. 2023, 71, 6139–6149. [Google Scholar] [CrossRef]
- Zhang, S.; Schmidt, R.; Qin, X.S. Active vibration control of piezoelectric bonded smart structures using PID algorithm. Chin. J. Aeronaut. 2015, 28, 305–313. [Google Scholar] [CrossRef]
- Ranjan, R.; Dwivedy, S.K. Dynamic analysis and control of a string-stiffened single-link flexible manipulator with flexible joint. Mech. Based Des. Struct. Mach. 2022, 51, 6329–6359. [Google Scholar] [CrossRef]
- Ravandi, A.K.; Khanmirza, E.; Daneshjou, K. Hybrid force/position control of robotic arms manipulating in uncertain environments based on adaptive fuzzy sliding mode control. Appl. Soft Comput. 2018, 70, 864–874. [Google Scholar] [CrossRef]
- Chen, J.H.; Huang, T.C. Applying neural networks to on-line updated pid controllers for nonlinear process control. J. Process Control 2004, 14, 211–230. [Google Scholar] [CrossRef]
- Wen, S.H.; Zheng, W.; Jia, S.D.; Ji, Z.X.; Hao, P.C.; Lam, H.K. Unactuated Force Control of 5-DOF Parallel Robot Based on Fuzzy PI. Int. J. Control Autom. Syst. 2020, 18, 1629–1641. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Lopes, A.M. Disturbance observer-based delayed robust feedback control design for a class of uncertain variable fractional-order systems: Order-dependent and delay-dependent stability. ISA Trans. 2023, 138, 20–36. [Google Scholar] [CrossRef]
- Jiang, T.T.; Liu, J.K.; He, W. Boundary control for a flexible manipulator based on infinite dimensional disturbance observer. J. Sound. Vib. 2015, 348, 1–14. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J. Speed control strategy of dual flexible servo system considering time-varying parameters for a flexible manipulator with an axially translating arm. Asian J. Control 2023, 25, 61975. [Google Scholar] [CrossRef]
- Yin, H.B.; Kobayashi, Y.; Hoshino, Y.; Emaru, T. Modeling and vibration analysis of flexible robotic arm under fast motion in consideration of nonlinearity. J. Syst. Des. Dyn. 2011, 5, 909–924. [Google Scholar] [CrossRef][Green Version]
- Hess, D.P.; Soom, A. Friction at a lubricated line contact operating at oscillating sliding velocities. J. Tribol. 1990, 112, 147–152. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J. Dynamic modeling and fuzzy adaptive control strategy for space flexible robotic arm considering joint flexibility based on improved sliding mode controller. Adv. Space Res. 2022, 70, 3520–3539. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J. Dynamic modeling and fuzzy compensation sliding mode control for flexible manipulator servo system. Appl. Math. Modell. 2022, 107, 530–556. [Google Scholar] [CrossRef]
- Feliu, V.; Pereira, E.; Diaz, I.M. Passivity-based control of single-link flexible manipulators using a linear strain feedback. Mech. Mach. Theory 2013, 71, 191–208. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J.; Wen, B.C. Rotation Angle Control Strategy for Telescopic Flexible Manipulator Based on a Combination of Fuzzy Adjustment and RBF Neural Network. Chin. J. Mech. Eng. 2022, 35, 53. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J. Speed control method for dual-flexible manipulator with a telescopic arm considering bearing friction based on adaptive PI controller with DOB. Alex. Eng. J. 2022, 61, 4741–4756. [Google Scholar] [CrossRef]
- Yun, J.N.; Su, J.B.; Kim, Y.I.; Kim, Y.C. Robust Disturbance Observer for Two-Inertia System. IEEE Trans. Ind. Electron. 2013, 60, 2700–2710. [Google Scholar] [CrossRef]
- Sun, C.; Gao, H.; He, W.; Yu, Y. Fuzzy Neural Network Control of a Flexible Robotic Manipulator Using Assumed Mode Method. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5214–5227. [Google Scholar] [CrossRef]
- Yang, X.; Liu, M.; Zhang, W.; Melnik, R.V. Invariant and energy analysis of an axially retracting beam. Chin. J. Aeronaut. 2016, 29, 952–961. [Google Scholar] [CrossRef]
- Chen, Y.-P.; Hsu, H.-T. Regulation and Vibration Control of an FEM-Based Single- Link Flexible Arm Using Sliding-Mode Theory. J. Vib. Control 2001, 7, 741–752. [Google Scholar] [CrossRef]
- Alandoli, E.A.; Lee, T.S.; Lin, Y.J.; Vijayakumar, V. Dynamic Model and Intelligent Optimal Controller of Flexible Link Manipulator System with Payload Uncertainty. Arab. J. Sci. Eng. 2021, 46, 7423–7433. [Google Scholar] [CrossRef]
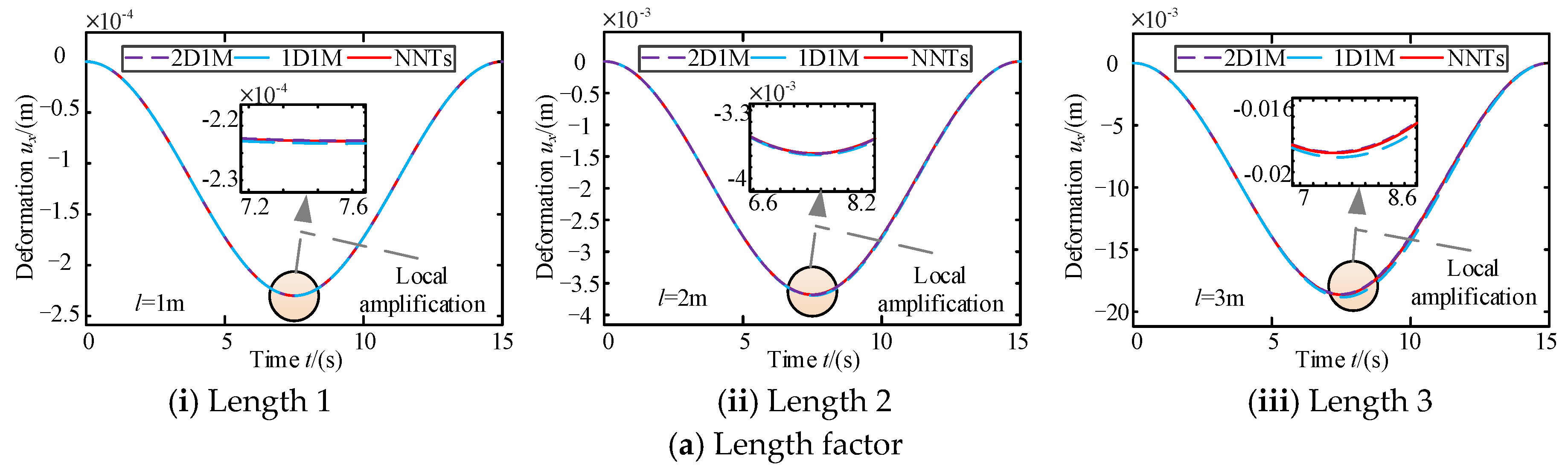
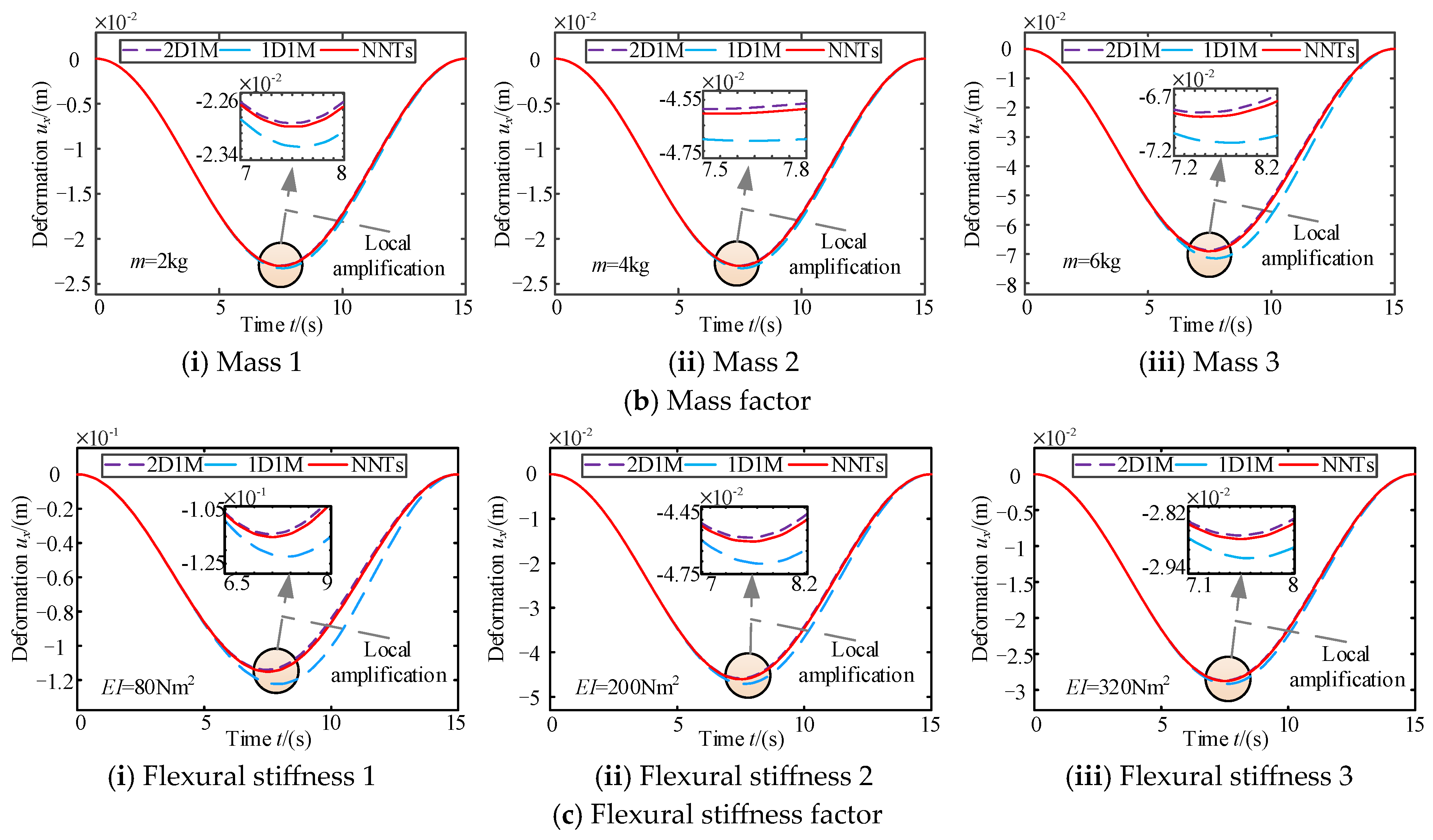


| Condition | l (m) | M (kg) | (rad/s) | EI (Nm2) |
|---|---|---|---|---|
| Length 1 (a-i) | 1 | 3 | 1 | 160 |
| Length 2 (a-ii) | 2 | 3 | 1 | 160 |
| Length 3 (a-iii) | 3 | 3 | 1 | 160 |
| Mass 1 (b-i) | 3.5 | 2 | 1 | 160 |
| Mass 2 (b-ii) | 3.5 | 4 | 1 | 160 |
| Mass 3 (b-iii) | 3.5 | 6 | 1 | 160 |
| Flexural stiffness 1 (d-i) | 3.5 | 5 | 1 | 80 |
| Flexural stiffness 2 (d-ii) | 3.5 | 5 | 1 | 200 |
| Flexural stiffness 3 (d-iii) | 3.5 | 5 | 1 | 320 |
| Parameters | Condition 1 | Condition 2 |
|---|---|---|
| Length l/m | 0.8 | 1 |
| Mass m/kg | 0.8 | 1.1 |
| Flexural rigidity EI/Nm2 | 400 | 400 |
| Coulomb friction torque Fc/Nm | 0.28 | 0.28 |
| Static friction torque Fs/Nm | 0.34 | 0.34 |
| Low-pass filter parameters α | 0.1 | 0.1 |
| Low-pass filter parameters β | 0.1 | 0.1 |
| Low-pass filter parameters γ | 0.1 | 0.1 |
| Controller parameters KP | 20 | 20 |
| Controller parameters KI | 5 | 5 |
| Parameters | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|
| Length l/m | 3 | 3.5 | 4 |
| Mass m/kg | 2 | 2 | 2 |
| Flexural rigidity EI/Nm2 | 50 | 50 | 50 |
| Low-pass filter parameters α | 0.1 | 0.1 | 0.1 |
| Low-pass filter parameters β | 0.1 | 0.1 | 0.1 |
| Low-pass filter parameters γ | 0.1 | 0.1 | 0.1 |
| Controller parameters KP | 10 | 10 | 10 |
| Controller parameters KI | 5 | 5 | 5 |
| Control Strategy | Means of Absolute Error | Variance of Error | Standard Deviation of Error | |
|---|---|---|---|---|
| Condition 1 | PI | 0.1587 | 0.0221 | 0.149 |
| PI + DOB | 0.1406 | 0.0145 | 0.121 | |
| FCPI + DOB | 0.1253 | 0.0133 | 0.115 | |
| Condition 2 | PI | 0.1626 | 0.0232 | 0.152 |
| PI + DOB | 0.1497 | 0.0195 | 0.139 | |
| FCPI + DOB | 0.1428 | 0.0152 | 0.123 | |
| Condition 2 | PI | 0.1706 | 0.0424 | 0.206 |
| PI + DOB | 0.1643 | 0.0308 | 0.175 | |
| FCPI + DOB | 0.1462 | 0.0267 | 0.166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, X.; Yin, M.; Wei, L.; Wang, H. Modeling and Rotation Control Strategy for Space Planar Flexible Robotic Arm Based on Fuzzy Adjustment and Disturbance Observer. Mathematics 2024, 12, 2513. https://doi.org/10.3390/math12162513
Liu J, Li X, Yin M, Wei L, Wang H. Modeling and Rotation Control Strategy for Space Planar Flexible Robotic Arm Based on Fuzzy Adjustment and Disturbance Observer. Mathematics. 2024; 12(16):2513. https://doi.org/10.3390/math12162513
Chicago/Turabian StyleLiu, Jiaqi, Xiaopeng Li, Meng Yin, Lai Wei, and Haozhe Wang. 2024. "Modeling and Rotation Control Strategy for Space Planar Flexible Robotic Arm Based on Fuzzy Adjustment and Disturbance Observer" Mathematics 12, no. 16: 2513. https://doi.org/10.3390/math12162513
APA StyleLiu, J., Li, X., Yin, M., Wei, L., & Wang, H. (2024). Modeling and Rotation Control Strategy for Space Planar Flexible Robotic Arm Based on Fuzzy Adjustment and Disturbance Observer. Mathematics, 12(16), 2513. https://doi.org/10.3390/math12162513






