A Novel Radial Basis and Sigmoid Neural Network Combination to Solve the Human Immunodeficiency Virus System in Cancer Patients
Abstract
1. Introduction
2. Materials and Methods
2.1. DNN Procedure
2.2. Radial Basis and Sigmoid Activation Functions
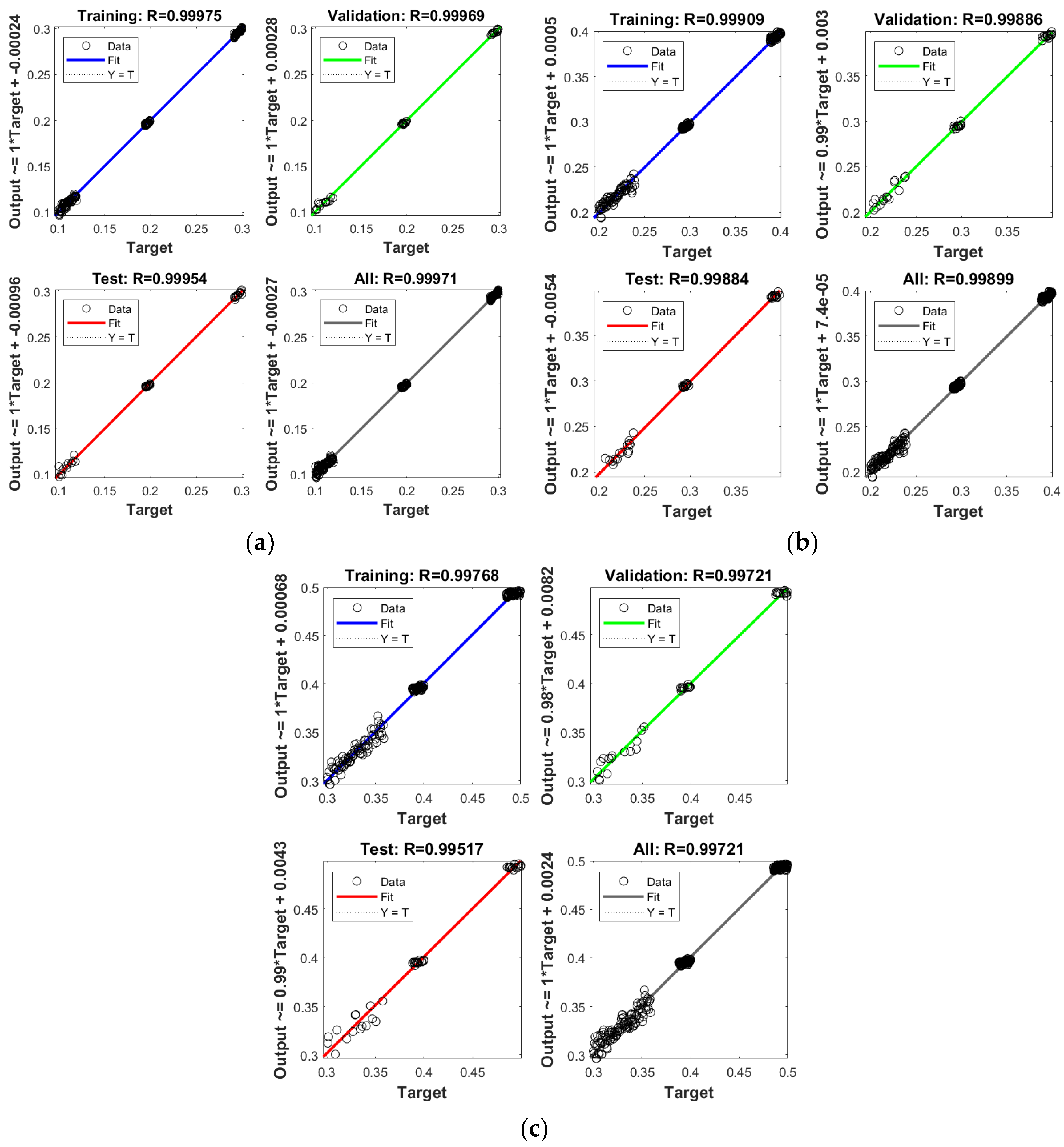
3. Results and Discussion
4. Conclusions
- The numerical representations of the dynamical HIV-1 infection system in cancer patients were proposed successfully by applying the proposed computational framework.
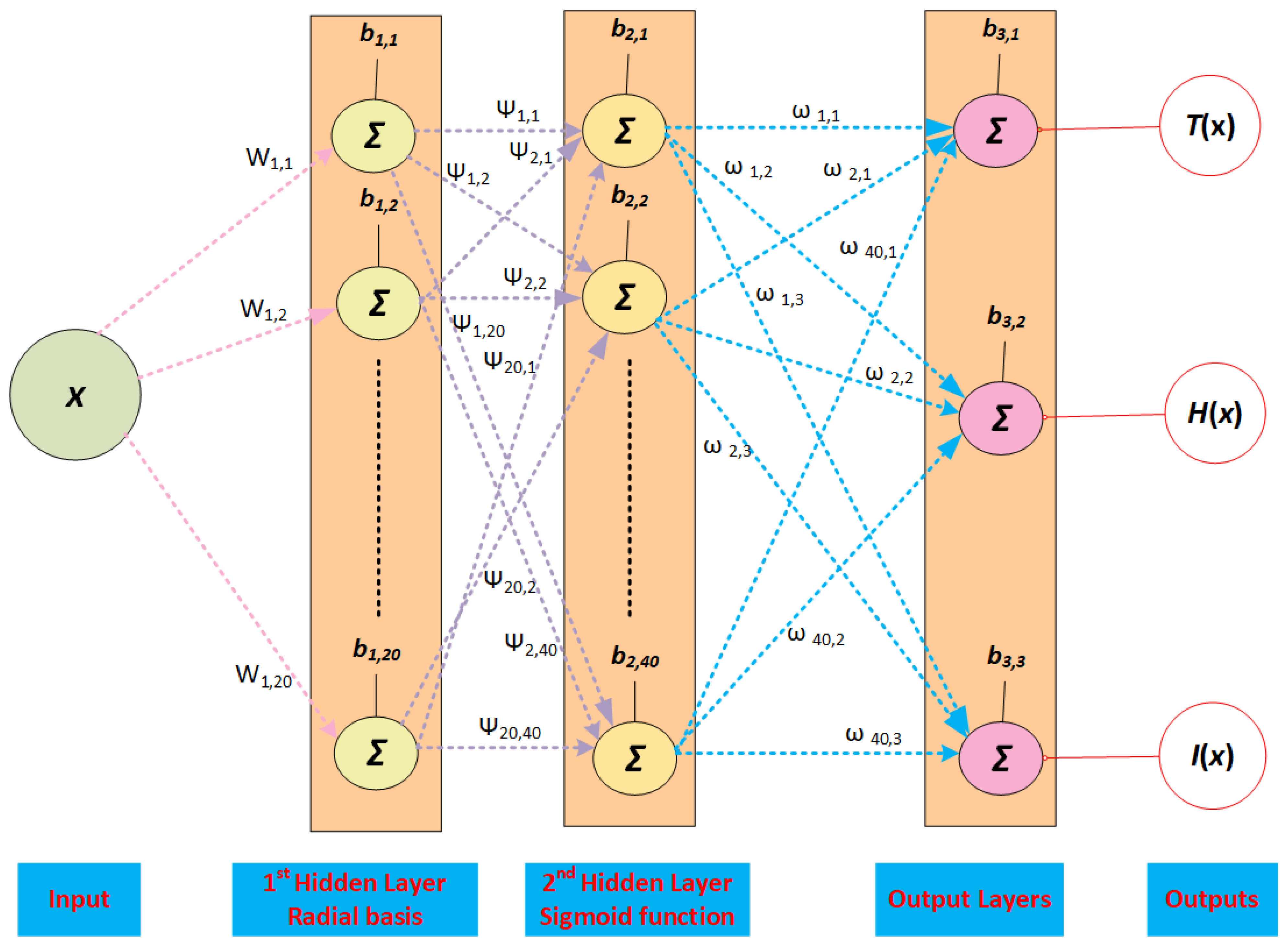
- A novel deep layer design was provided using the radial basis and sigmoid activation functions in the first and second hidden layers.
- The neural network is updated by taking twenty neurons in the first hidden layer and forty neurons in the second layer to solve the dynamical HIV-1 infection system in cancer patients.
- An optimization based on the competent scale conjugate gradient scheme was performed to present the solutions of the dynamical HIV-1 infection system in cancer patients.
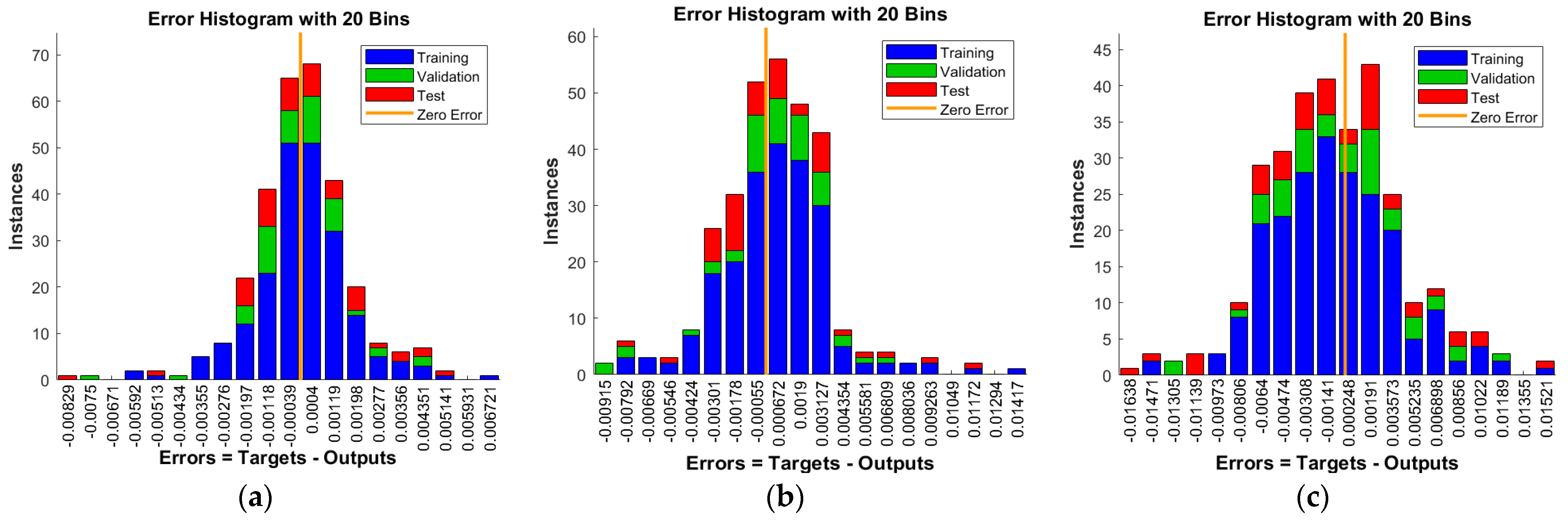
- The perfection of the proposed numerical scheme was observed through the overlapping with the reference results, the Runge–Kutta scheme, and the negligible values of the absolute error, which were found to range from 10−3 to 10−4.
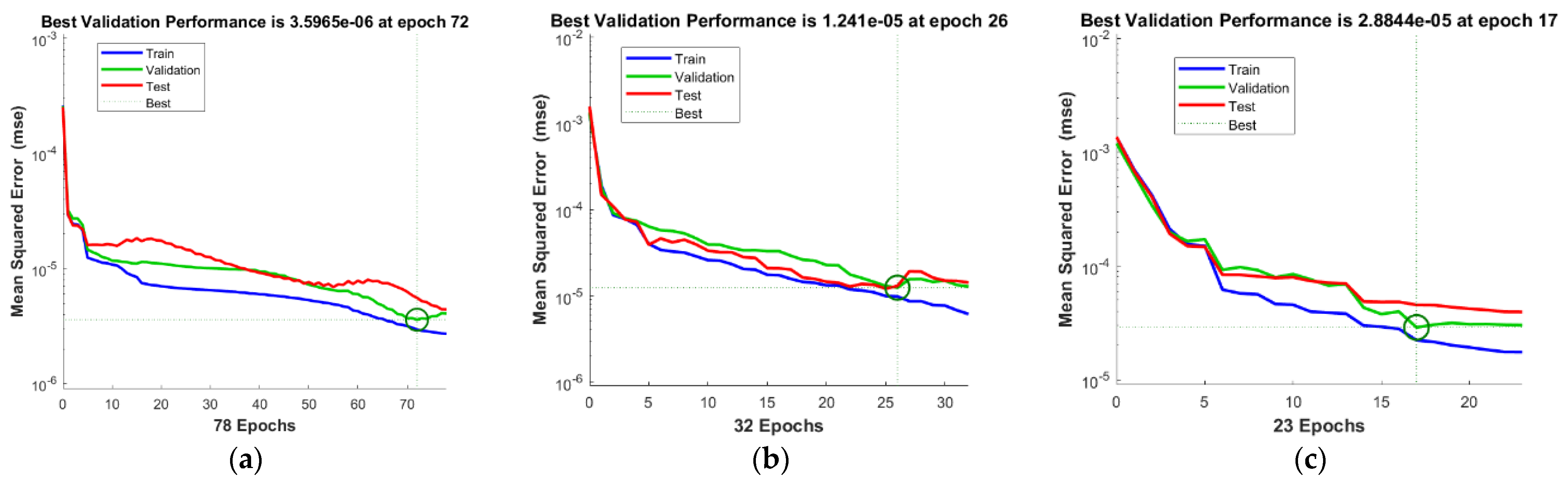
- The database solutions are used to lessen the MSE by taking 72%of the data for training, while 14%of the data was chosen for both authentication and testing.
- To credibility of the novel procedure is authenticated through the graphical plots based on different performances.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lou, J.; Ruggeri, T. A time delay model about AIDS-related cancer: Equilibria, cycles and chaotic behavior. Ric. Mat. 2007, 56, 195–208. [Google Scholar] [CrossRef]
- Leav, B.A.; Fanburg, B.; Hadley, S. Invasive pulmonary aspergillosis associated with high-dose inhaled fluticasone. N. Engl. J. Med. 2000, 343, 586. [Google Scholar] [CrossRef]
- Duarte, J.; Januário, C.; Martins, N.; Ramos, C.C.; Rodrigues, C.; Sardanyés, J. Optimal homotopy analysis of a chaotic HIV-1 model incorporating AIDS-related cancer cells. Numer. Algorithms 2018, 77, 261–288. [Google Scholar] [CrossRef]
- Lou, J.; Ruggeri, T.; Tebaldi, C. Modeling cancer in HIV-1 infected individuals: Equilibria, cycles and chaotic behavior. Math. Biosci. Eng. 2006, 3, 313. [Google Scholar]
- Boshoff, C.; Weiss, R. AIDS-related malignancies. Nat. Rev. Cancer 2002, 2, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Gross, L. Intradermal immunization of C3H mice against a sarcoma that originated in an animal of the same line. Cancer Res. 1943, 3, 326–333. [Google Scholar]
- Cranage, M.P.; Whatmore, A.M.; Sharpe, S.A.; Cook, N.; Polyanskaya, N.; Leech, S.; Smith, J.D.; Rud, E.W.; Dennis, M.J.; Hall, G.A. Macaques infected with live attenuated SIVmac are protected against superinfection via the rectal mucosa. Virology 1997, 229, 143–154. [Google Scholar] [CrossRef] [PubMed]
- Diegel, M.L.; Moran, P.A.; Gilliland, L.K.; Damle, N.K.; Hayden, M.S.; Zarling, J.M.; Ledbetter, J.A. Regulation of HIV production by blood mononuclear cells from HIV-infected donors: II. HIV-1 production depends on T cell-monocyte interaction. AIDS Res. Hum. Retrovir. 1993, 9, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Perelson, A.S. HIV-1 infection and low steady state viral loads. Bull. Math. Biol. 2002, 64, 29–64. [Google Scholar] [CrossRef] [PubMed]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Baskonus, H.M.; Yao, S.W.; Ilhan, E. A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells. Results Phys. 2021, 25, 104235. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S. A delay-differential equation model of HIV infection of CD4+ T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef] [PubMed]
- Lou, J.; Ma, Z.; Li, J.; Shao, Y.; Han, L. The impact of the CD8+ cell non-cytotoxic antiviral response (CNAR) and cytotoxic T lymphocyte (CTL) activity in a cell-to-cell spread model for HIV-1 with a time delay. J. Biol. Syst. 2004, 12, 73–90. [Google Scholar] [CrossRef]
- Sabir, Z.; Said, S.B.; Al-Mdallal, Q. Artificial intelligent solvers for the HIV-1 system including AIDS based on the cancer cells. Intell. Syst. Appl. 2024, 21, 200309. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Sidorov, D. Application of the stochastic arithmetic to validate the results of nonlinear fractional model of HIV infection for CD8+ T-cells. In Mathematical Analysis of Infectious Diseases; Agarwal, P., Nieto, J.J., Torres, D.F.M., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 259–285. [Google Scholar]
- Sabir, Z.; Arbi, A.; Hashem, A.F.; Abdelkawy, M.A. Morlet wavelet neural network investigations to present the numerical investigations of the prediction differential model. Mathematics 2023, 11, 4480. [Google Scholar] [CrossRef]
- Sabir, Z.; Hashem, A.F.; Arbi, A.; Abdelkawy, M.A. Designing a bayesian regularization approach to solve the fractional Layla and Majnun system. Mathematics 2023, 11, 3792. [Google Scholar] [CrossRef]



| Parameter | Details |
|---|---|
| Cancer cells | |
| HIV infected cells | |
| Healthy cells | |
| Rate of unrestrained proliferation cells of cancer | |
| Healthy cells based on inherent progression | |
| Rate of immune killing using the tumor cells | |
| Infection rate coefficient | |
| Active carrying capacity of the system | |
| Rate of losing cells of immune | |
| Total immune system killing infection effects | |
| Initial conditions | |
| Infection force | |
| Natural death rate per capita | |
| Time |
| Index | Settings |
|---|---|
| Dataset | Runge–Kutta |
| Hidden layer 1 | Radial basis |
| Hidden layer 2 | Sigmoid function |
| Neurons in the first hidden layer | 20 |
| Neurons in the second hidden layer | 40 |
| Hidden layers | 2 |
| Minimum gradient | 10−10 |
| Samples assortment | Random |
| Maximum verification failures | Inf |
| Performance goal | 0 |
| Training time | Inf |
| Training data | 0.72 |
| Testing data | 0.14 |
| Authentication data | 0.14 |
| Maximum epochs for training | 1200 |
| Training | SCG |
| Stoppage standards | Default |
| 0 | 0.10000016943 | 0.10868775969 | 0.20000008321 | 0.19777037341 | 0.29999785078 | 0.29666379600 |
| 0.1 | 0.10181070891 | 0.10054160977 | 0.20059785133 | 0.19910492158 | 0.29113385624 | 0.30027524875 |
| 0.2 | 0.10365435168 | 0.10475029814 | 0.20119756273 | 0.19752226400 | 0.28253192998 | 0.29733258735 |
| 0.3 | 0.10553010512 | 0.10906943671 | 0.20179884254 | 0.19730820783 | 0.27418555979 | 0.29725420585 |
| 0.4 | 0.10743964687 | 0.10964018943 | 0.20240186724 | 0.19709838780 | 0.26609013390 | 0.29603841816 |
| 0.5 | 0.10938490222 | 0.11115338137 | 0.20300721939 | 0.19706652181 | 0.25822556442 | 0.29569799059 |
| 0.6 | 0.11136543800 | 0.111435116972 | 0.20361440339 | 0.19605622218 | 0.25059632840 | 0.29477258299 |
| 0.7 | 0.11338115446 | 0.113757188816 | 0.20422330888 | 0.19604788037 | 0.24319377896 | 0.29440618652 |
| 0.8 | 0.11543283457 | 0.116365231945 | 0.20483395732 | 0.19585288523 | 0.23601153161 | 0.29264639065 |
| 0.9 | 0.11752328540 | 0.117294283045 | 0.20544696957 | 0.19487912232 | 0.22903667420 | 0.29127034342 |
| 1 | 0.11965051111 | 0.112513456419 | 0.20606160205 | 0.19659756280 | 0.22227046540 | 0.29487454521 |
| 0 | 0.2000017596 | 0.20672928236 | 0.3000004514 | 0.296868317750 | 0.39999350745 | 0.396895963115 |
| 0.1 | 0.2036203843 | 0.20274680488 | 0.3008950644 | 0.300453914746 | 0.38818162865 | 0.398755989912 |
| 0.2 | 0.2073055561 | 0.20889790587 | 0.3017927952 | 0.295910556060 | 0.37671481077 | 0.396283569317 |
| 0.3 | 0.2110571379 | 0.21285846167 | 0.3026933066 | 0.296958616589 | 0.36558757916 | 0.398265169235 |
| 0.4 | 0.2148764204 | 0.21182550649 | 0.3035966306 | 0.296177205247 | 0.35478949532 | 0.392529695129 |
| 0.5 | 0.2187649056 | 0.21786449577 | 0.3045028295 | 0.294783608812 | 0.34431028450 | 0.393938035846 |
| 0.6 | 0.2227239001 | 0.22232468833 | 0.3054119255 | 0.293705720489 | 0.33414021356 | 0.393138719155 |
| 0.7 | 0.2267548696 | 0.22959061858 | 0.3063239578 | 0.292720504741 | 0.32427001165 | 0.393024504442 |
| 0.8 | 0.2308587164 | 0.22967777474 | 0.3072388593 | 0.293132906098 | 0.31469109403 | 0.393240135109 |
| 0.9 | 0.2350371310 | 0.237549332324 | 0.30815669210 | 0.293286405664 | 0.30539499855 | 0.387324826792 |
| 1 | 0.2392908428 | 0.229888828815 | 0.30907735224 | 0.292377815516 | 0.29637375030 | 0.390382212614 |
| 0 | 0.3000007094 | 0.304066489582 | 0.4000001497 | 0.398591491498 | 0.4999983571 | 0.496011729745 |
| 0.1 | 0.3054288289 | 0.301837431541 | 0.4011911130 | 0.396402639620 | 0.4852308158 | 0.489933006182 |
| 0.2 | 0.3109548473 | 0.320782076340 | 0.4023858733 | 0.394418744477 | 0.4708992905 | 0.493583836983 |
| 0.3 | 0.3165810809 | 0.320448887260 | 0.4035844771 | 0.396575641205 | 0.4569926818 | 0.492421288975 |
| 0.4 | 0.3223083941 | 0.323445853659 | 0.4047868367 | 0.396774634204 | 0.4434960538 | 0.492704489205 |
| 0.5 | 0.3281401774 | 0.331885125197 | 0.4059931721 | 0.395747127372 | 0.4303983361 | 0.493284746323 |
| 0.6 | 0.3340769185 | 0.328464097378 | 0.4072032912 | 0.395481359892 | 0.4176872355 | 0.492734841347 |
| 0.7 | 0.3401217296 | 0.335523769646 | 0.4084173831 | 0.395444373642 | 0.4053510683 | 0.494042069547 |
| 0.8 | 0.3462761785 | 0.346878349148 | 0.4096353977 | 0.392797123047 | 0.3933786779 | 0.492964820021 |
| 0.9 | 0.3525416759 | 0.366959035239 | 0.4108572420 | 0.396150276041 | 0.3817601399 | 0.490824781744 |
| 1 | 0.3589201975 | 0.343832788774 | 0.4120829043 | 0.395519994541 | 0.3704852824 | 0.492857310554 |
| Case | MSE | Gradient | Performance | Epochs | Time | ||
|---|---|---|---|---|---|---|---|
| Training | Authorization | Testing | |||||
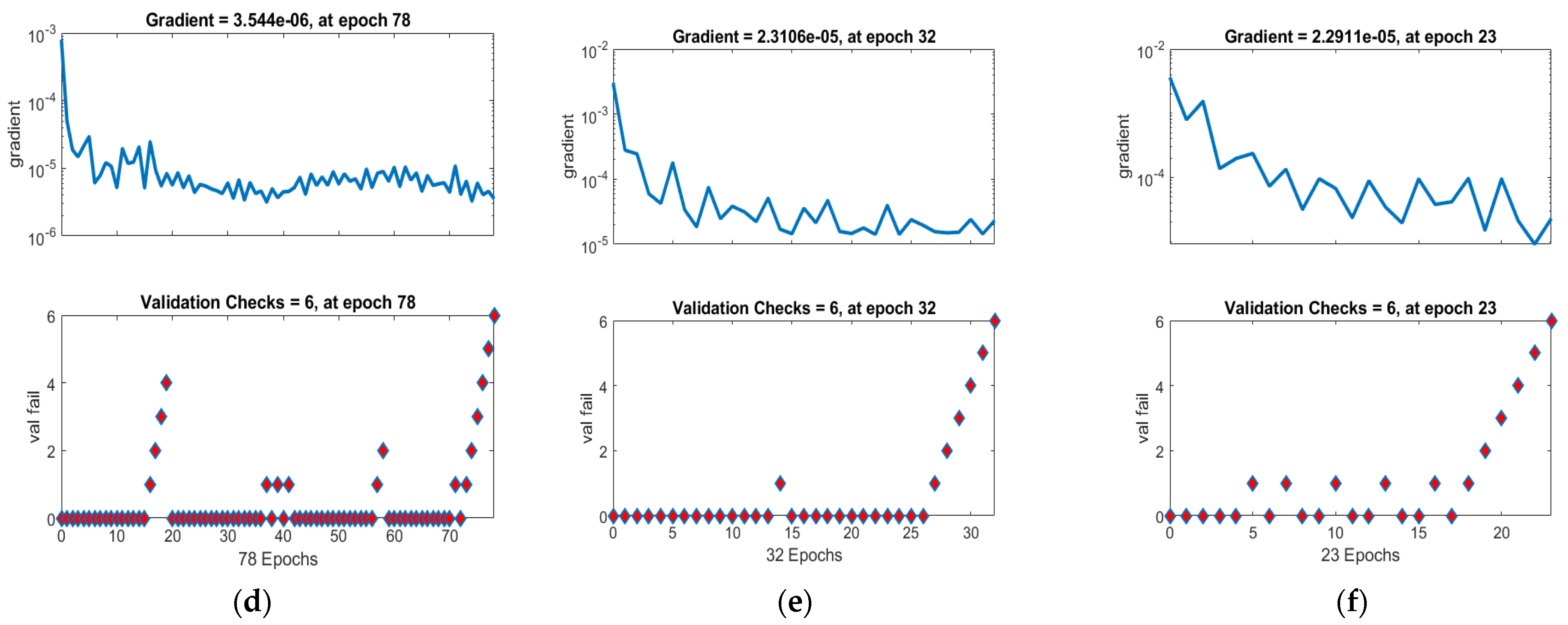
| I | 2.9456 × 10−6 | 3.5965 × 10−6 | 5.5755 × 10−6 | 3.54 × 10−6 | 2.72 × 10−6 | 78 | 01 |
| 2 | 9.8158 × 10−6 | 1.2410 × 10−5 | 1.2984 × 10−5 | 2.31 × 10−5 | 6.14 × 10−6 | 32 | 01 |
| 3 | 2.2233 × 10−5 | 2.8844 × 10−5 | 4.5467 × 10−5 | 2.29 × 10−5 | 1.75 × 10−5 | 23 | 04 |
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T(x) | 9 × 10−3 | 1 × 10−3 | 1 × 10−3 | 4 × 10−3 | 2 × 10−3 | 2 × 10−3 | 8 × 10−5 | 4 × 10−4 | 9 × 10−4 | 2 × 10−4 | 7 × 10−3 |
| 7 × 10−3 | 9 × 10−4 | 2 × 10−3 | 2 × 10−3 | 3 × 10−3 | 9 × 10−4 | 4 × 10−4 | 3 × 10−3 | 1 × 10−3 | 3 × 10−3 | 9 × 10−3 | |
| 4 × 10−3 | 4 × 10−3 | 1 × 10−2 | 4 × 10−3 | 1 × 10−3 | 4 × 10−3 | 6 × 10−3 | 5 × 10−3 | 7 × 10−4 | 1 × 10−2 | 1 × 10−2 | |
| H(x) | 2 × 10−3 | 3 × 10−4 | 1 × 10−3 | 9 × 10−4 | 5 × 10−4 | 7 × 10−5 | 3 × 10−4 | 2 × 10−4 | 6 × 10−4 | 2 × 10−4 | 3 × 10−3 |
| 3 × 10−3 | 1 × 10−3 | 2 × 10−3 | 3 × 10−4 | 2 × 10−4 | 7 × 10−4 | 9 × 10−4 | 1 × 10−3 | 3 × 10−4 | 1 × 10−3 | 1 × 10−3 | |
| 1 × 10−3 | 2 × 10−3 | 3 × 10−3 | 2 × 10−4 | 2 × 10−3 | 2 × 10−3 | 3 × 10−3 | 4 × 10−3 | 2 × 10−3 | 7 × 10−3 | 8 × 10−3 | |
| I(x) | 3 × 10−3 | 1 × 10−3 | 9 × 10−4 | 7 × 10−5 | 4 × 10−4 | 1 × 10−4 | 1 × 10−4 | 6 × 10−4 | 3 × 10−4 | 8 × 10−4 | 4 × 10−3 |
| 3 × 10−3 | 5 × 10−5 | 1 × 10−3 | 2 × 10−3 | 3 × 10−3 | 1 × 10−4 | 2 × 10−4 | 1 × 10−3 | 3 × 10−3 | 2 × 10−3 | 2 × 10−3 | |
| 4 × 10−3 | 9 × 10−3 | 3 × 10−3 | 3 × 10−3 | 1 × 10−3 | 7 × 10−4 | 2 × 10−3 | 4 × 10−3 | 5 × 10−3 | 4 × 10−3 | 8 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabir, Z.; Dirani, S.; Bou Saleh, S.; Mabsout, M.K.; Arbi, A. A Novel Radial Basis and Sigmoid Neural Network Combination to Solve the Human Immunodeficiency Virus System in Cancer Patients. Mathematics 2024, 12, 2490. https://doi.org/10.3390/math12162490
Sabir Z, Dirani S, Bou Saleh S, Mabsout MK, Arbi A. A Novel Radial Basis and Sigmoid Neural Network Combination to Solve the Human Immunodeficiency Virus System in Cancer Patients. Mathematics. 2024; 12(16):2490. https://doi.org/10.3390/math12162490
Chicago/Turabian StyleSabir, Zulqurnain, Sahar Dirani, Sara Bou Saleh, Mohamad Khaled Mabsout, and Adnène Arbi. 2024. "A Novel Radial Basis and Sigmoid Neural Network Combination to Solve the Human Immunodeficiency Virus System in Cancer Patients" Mathematics 12, no. 16: 2490. https://doi.org/10.3390/math12162490
APA StyleSabir, Z., Dirani, S., Bou Saleh, S., Mabsout, M. K., & Arbi, A. (2024). A Novel Radial Basis and Sigmoid Neural Network Combination to Solve the Human Immunodeficiency Virus System in Cancer Patients. Mathematics, 12(16), 2490. https://doi.org/10.3390/math12162490







