Strong Stability Preserving Two-Derivative Two-Step Runge-Kutta Methods
Abstract
1. Introduction
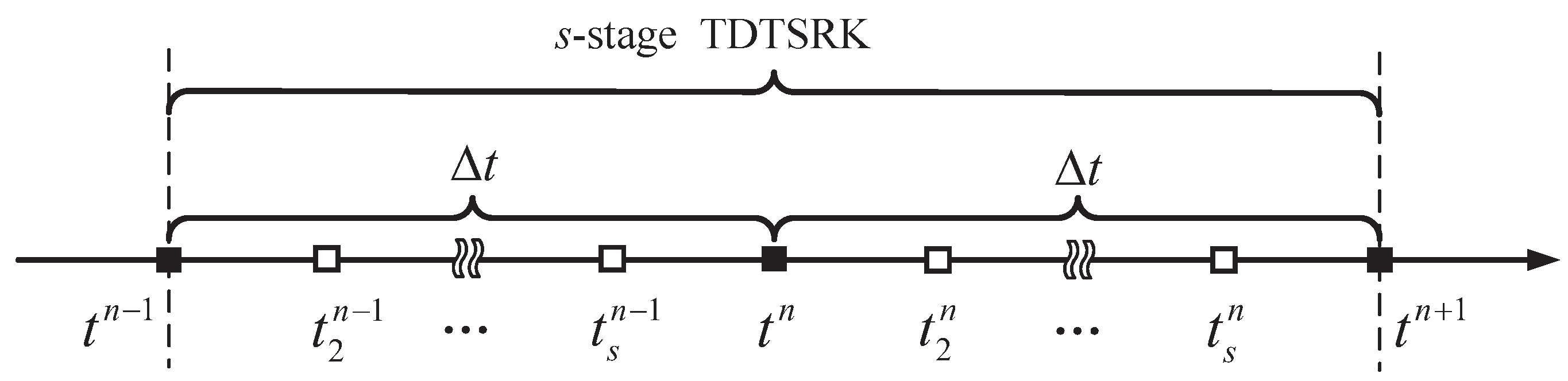
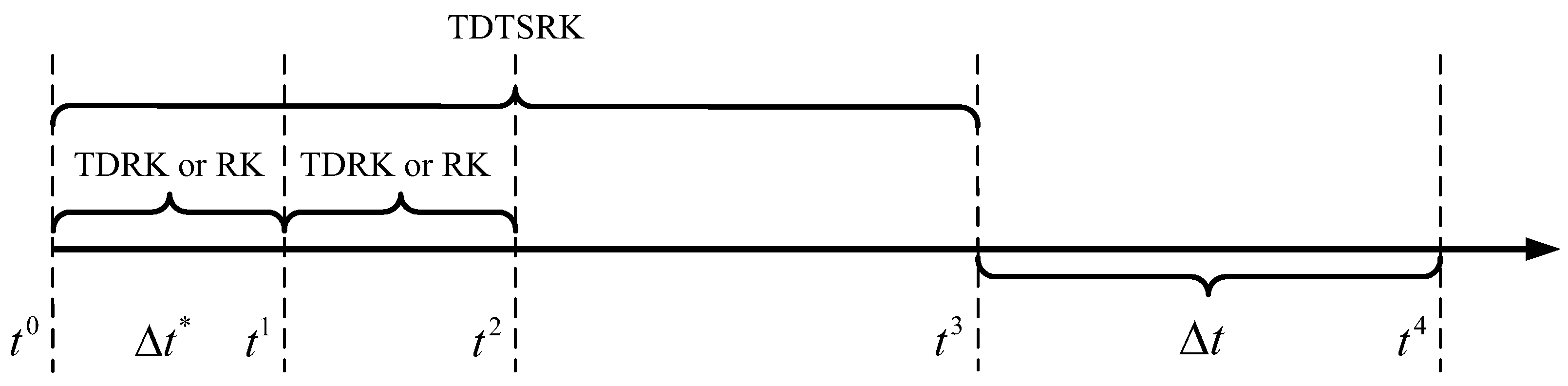
2. Structure of TDTSRK Methods
2.1. Derivation of TDTSRK Methods
2.2. Order Conditions of TDTSRK Methods
2.3. Some High-Order TDTSRK Methods
3. The SSP TDTSRK Methods
3.1. A Review of SSP Methods
3.2. SSP Condition for TDTSRK Methods
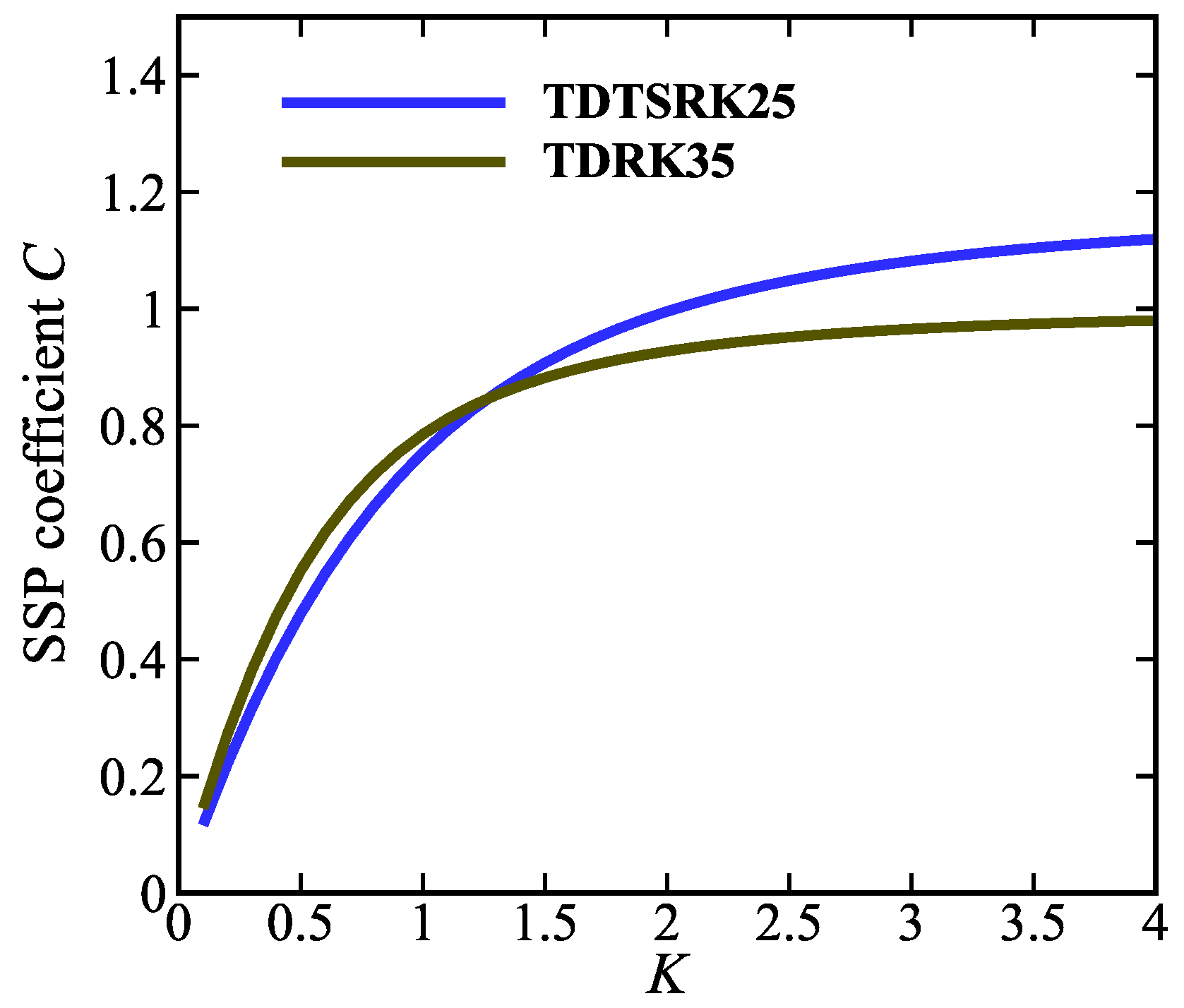
3.3. Optimal SSP TDTSRK Methods
4. Numerical Experiments
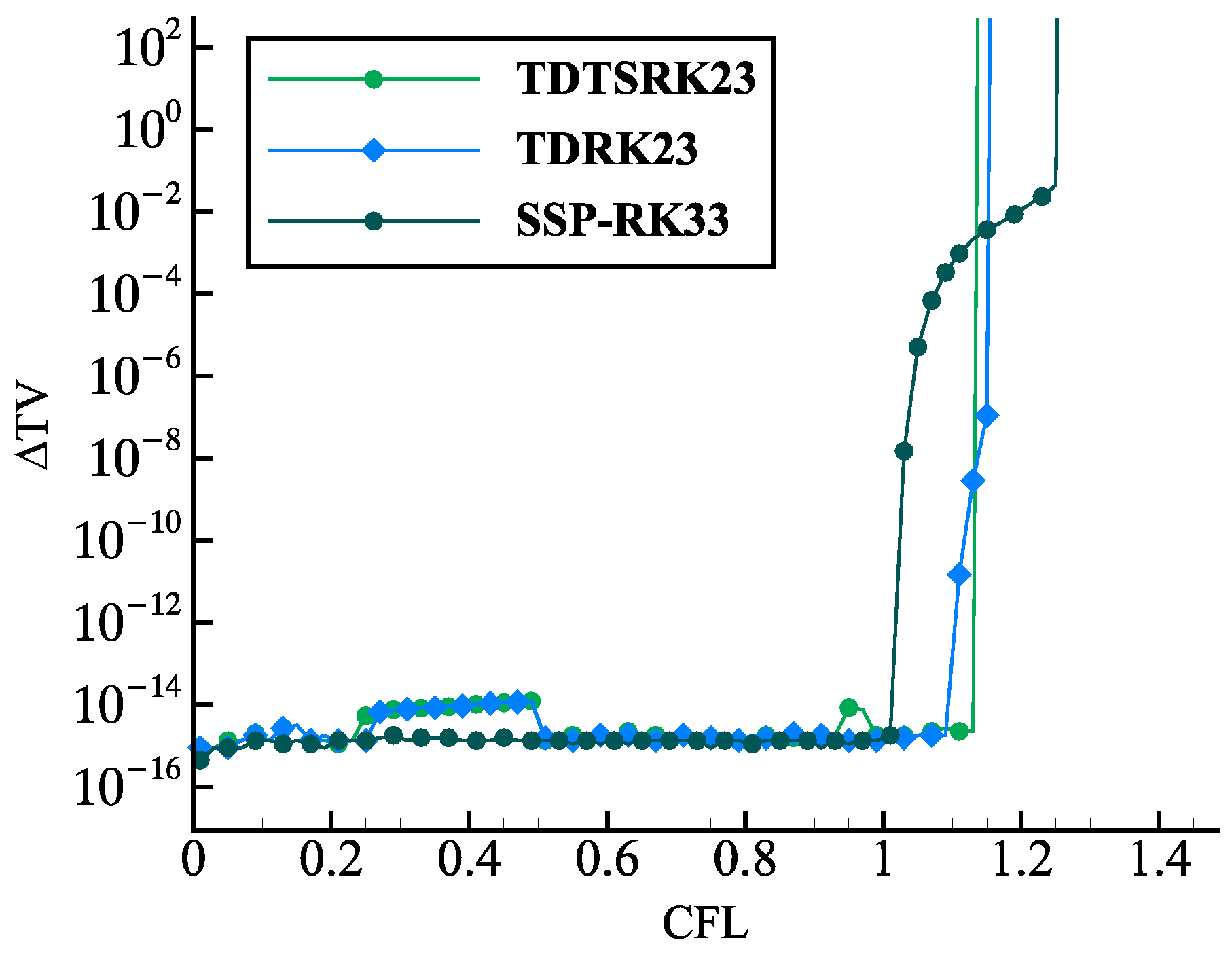
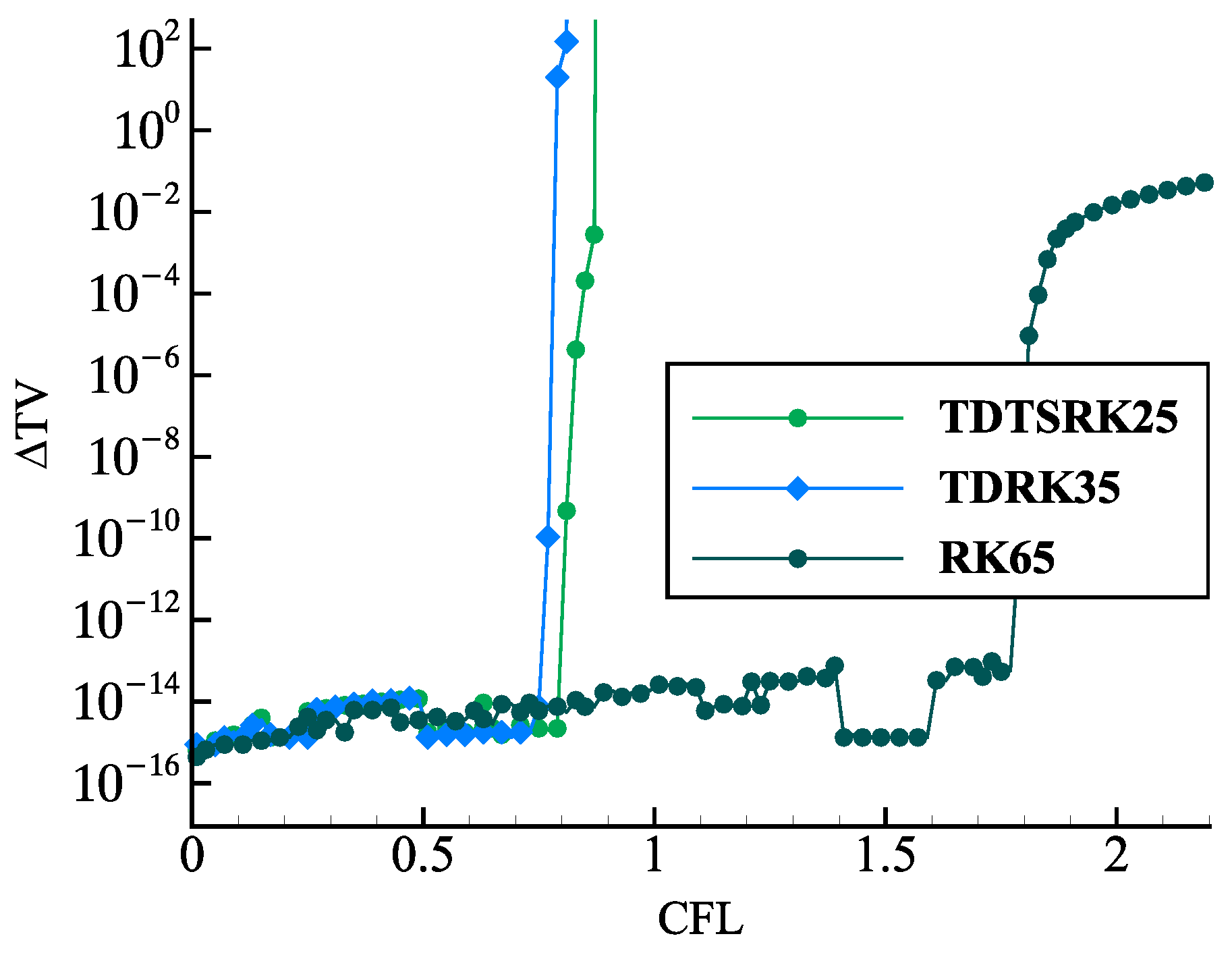
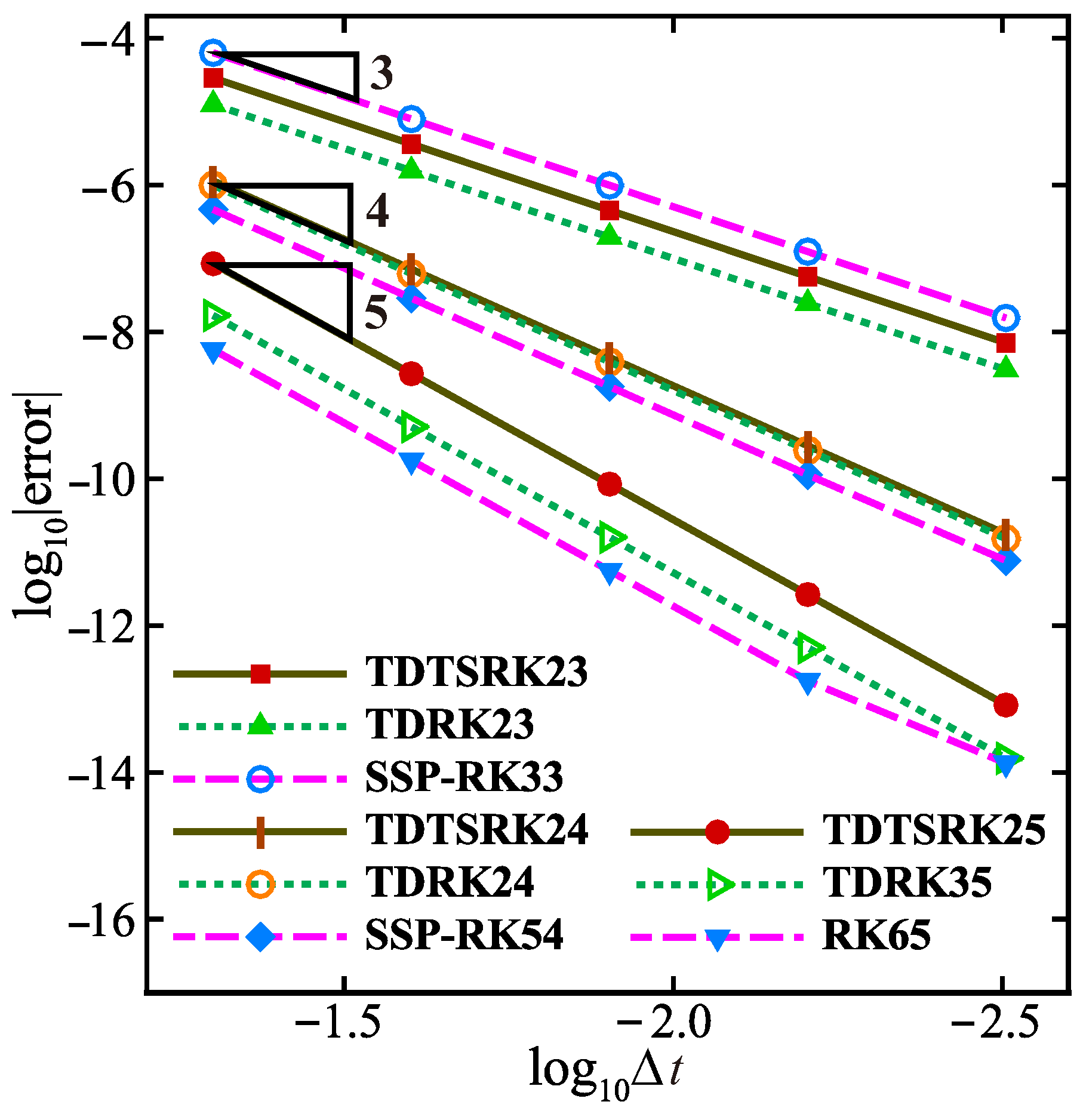
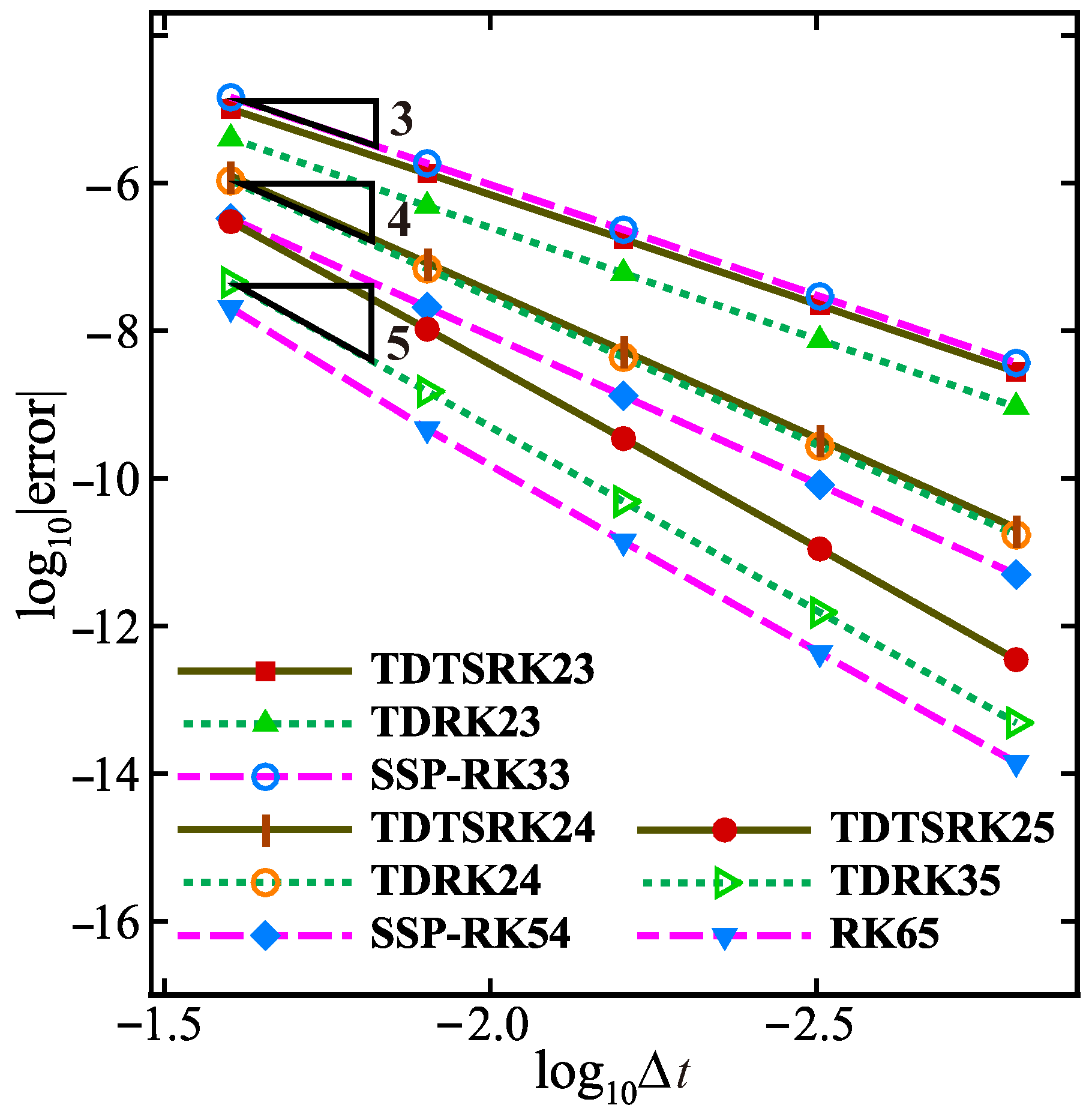
- TDTSRK23, TDTSRK24, TDTSRK25: the two-stage third-order, two-stage fourth-order, and two-stage fifth-order TDTSRK methods are shown in Appendix B.
- TDRK23, TDRK24, TDRK35: the two-stage third-order, two-stage fourth-order, and three-stage fifth-order TDRK methods are quoted from [27].
- SSP-RK33: the three-stage third-order SSP-RK method is the most popular explicit time scheme in Shu and Stanley [3].
- SSP-RK54: the five-stage fourth-order SSP-RK method is presented by Spiteri [33].
- RK65: the classical six-stage fifth-order RK method is given in Butcher [34].
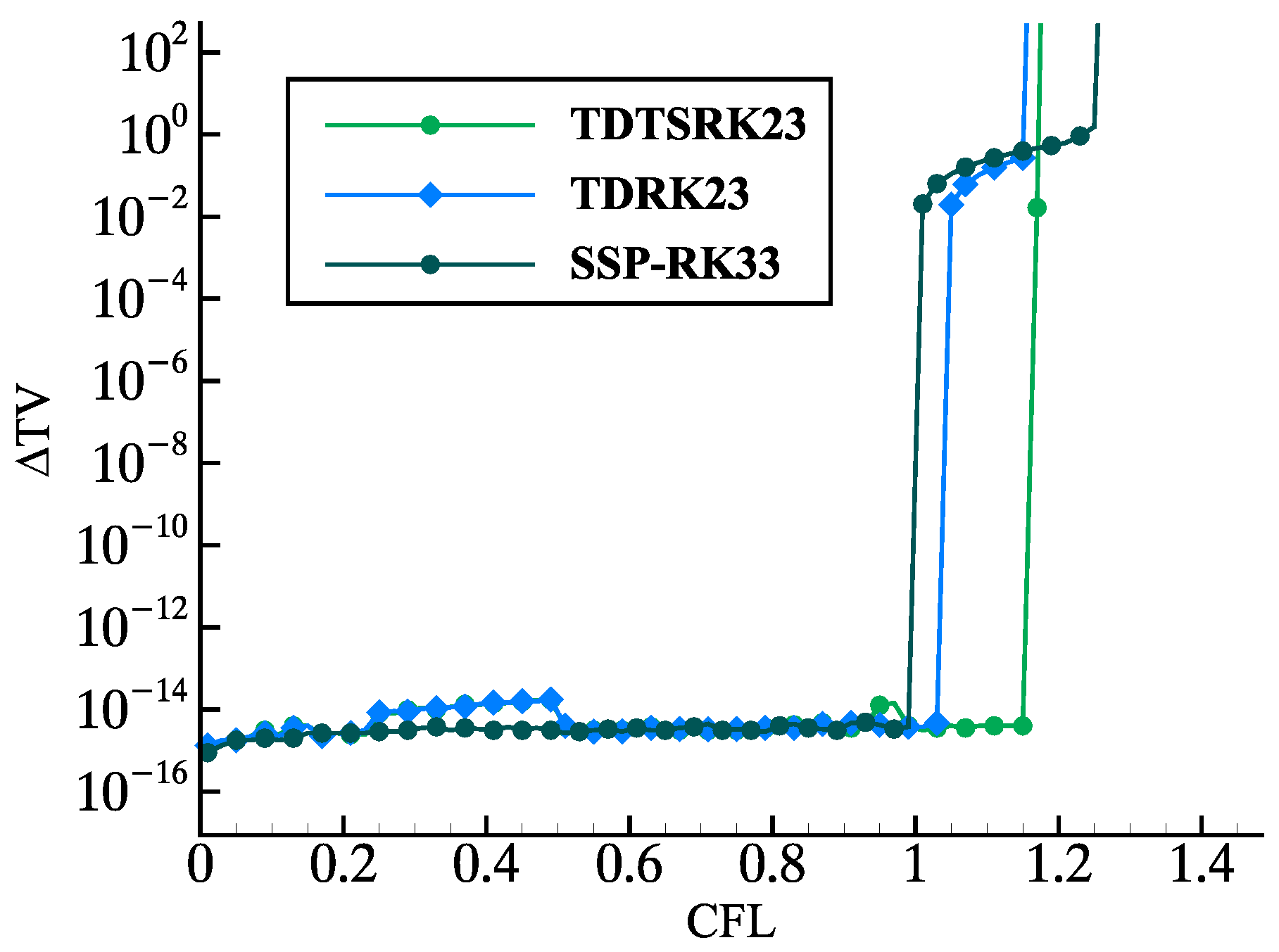
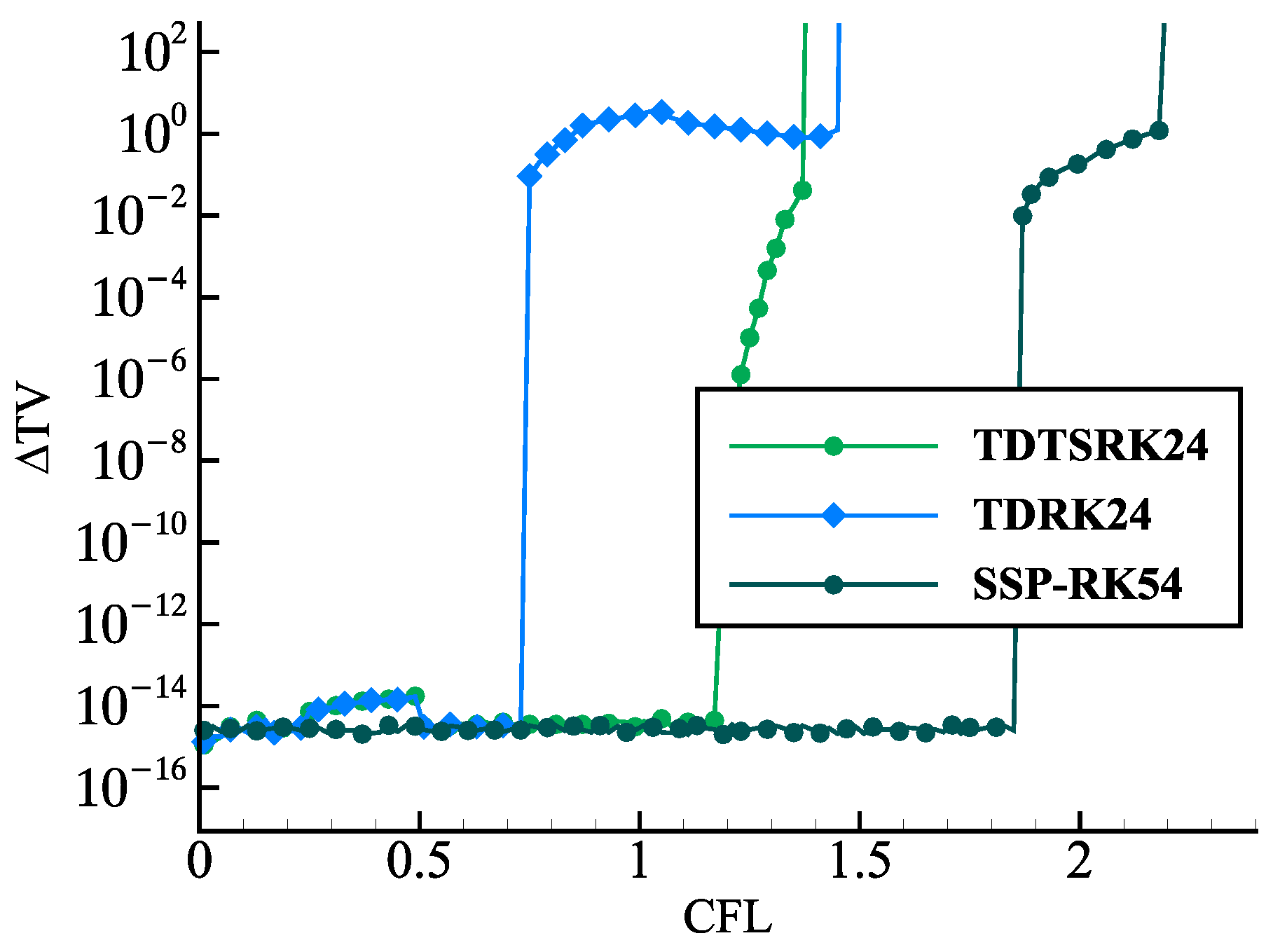
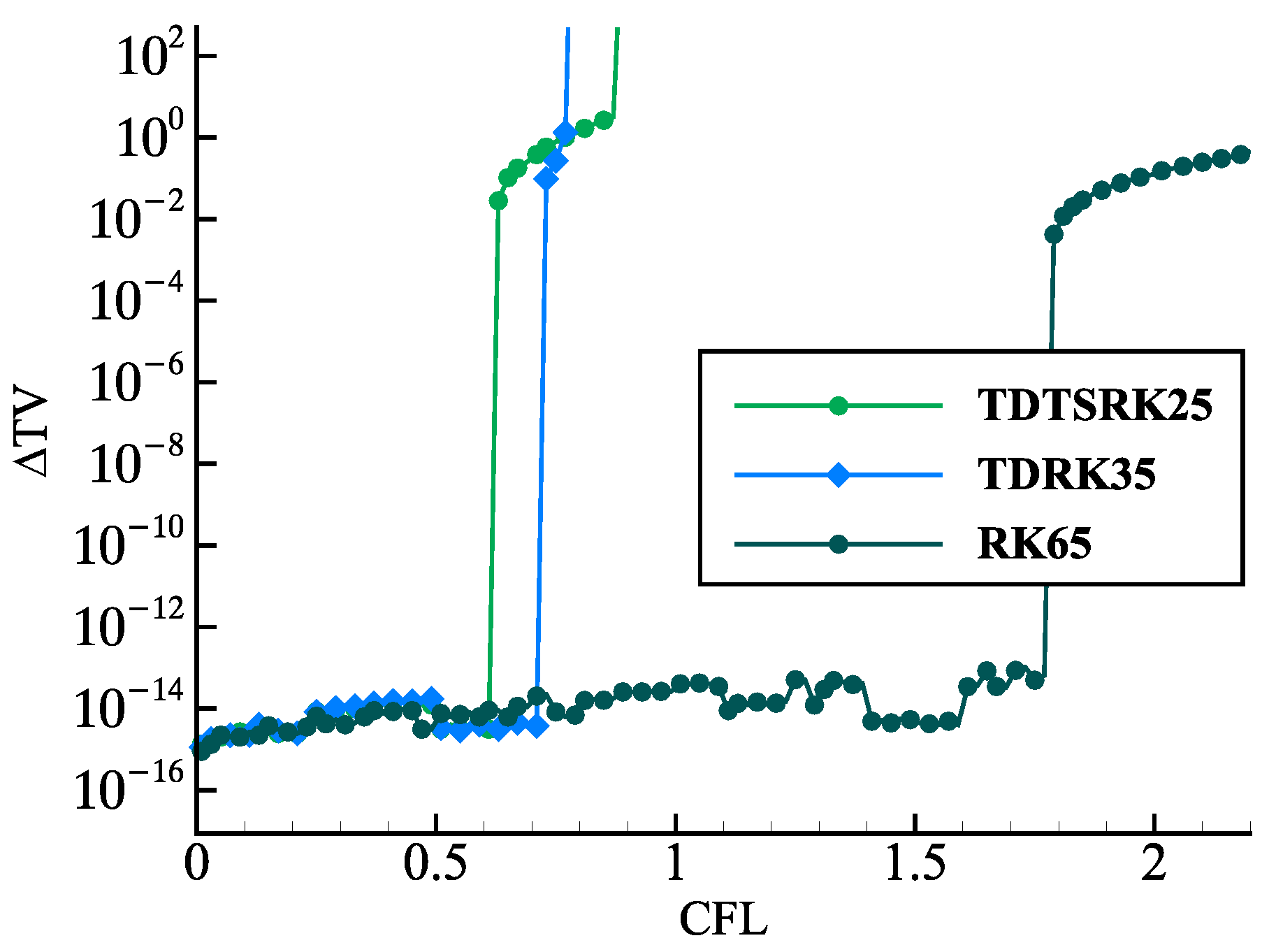
4.1. SSP Properties of the TDTSRK Methods on the Linear Advection
4.2. SSP Properties of the TDTSRK Methods on the Burgers’ Equation
4.3. Order Accuracy of the TDTSRK Methods on the Linear Advection
4.4. Order Accuracy of the TDTSRK Methods on the Burgers’ Equation
4.5. Efficiency for TDMSRK Schemes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Order Conditions for TDTSRK Schemes
| Condition: |
| Terms | ||
| Condition: | ||
| Terms | ||
| Condition: | ||
| Terms: | ||
| Condition: | ||
| Terms: (ignore ) | ||
| Condition: | ||
| Terms: (ignore ) | ||
| Condition: | ||
| Terms: (ignore ) | ||
| Condition: | ||
Appendix B. Coefficients of High-Order TDTSRK Schemes
References
- Jiang, G.-S.; Shu, C.-W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.-W. Runge-Kutta discontinuous galerkin methods for convection-dominated problems. J. Sci. Comput. 2001, 16, 173–261. [Google Scholar] [CrossRef]
- Shu, C.-W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing methods. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Askar, A.H.; Nagy, Á.; Barna, I.F.; Kovács, E. Analytical and Numerical Results for the Diffusion-Reaction Equation When the Reaction Coefficient Depends on Simultaneously the Space and Time Coordinates. Computation 2023, 11, 127. [Google Scholar] [CrossRef]
- Khayrullaev, H.; Omle, I.; Kovács, E. Systematic Investigation of the Explicit, Dynamically Consistent Methods for Fisher’s Equation. Computation 2024, 12, 49. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Y. A new difference scheme with high accuracy and absolute stability for solving convection-diffusion equations. J. Comput. Appl. Math. 2009, 230, 600–606. [Google Scholar] [CrossRef]
- Gottlieb, S.; Ketcheson, D.I.; Shu, C.-W. Strong Stability Preserving Runge-Kutta and Multistep Time Discretizations; World Scientific: Singapore, 2011. [Google Scholar]
- Qin, X.; Yu, J.; Yan, C. Derivation of Three-Derivative Two-Step Runge–Kutta Methods. Mathematics 2024, 12, 711. [Google Scholar] [CrossRef]
- Qin, X.; Yu, J.; Jiang, Z.; Huang, L.; Yan, C. Explicit strong stability preserving second derivative multistep methods for the Euler and Navier-Stokes equations. Comput. Fluids 2024, 268, 106089. [Google Scholar] [CrossRef]
- Afsaneh, M.; Jeremy, C.; Raffaele, D.; Jochen, S. Jacobian-free explicit multiderivative general linear methods for hyperbolic conservation laws. Numer. Algorithms 2024, 1572–9265. [Google Scholar]
- Kovalnogov, V.N.; Fedorov, R.V.; Karpukhina, T.V.; Simos, T.E.; Tsitouras, C. On Reusing the Stages of a Rejected Runge-Kutta Step. Mathematics 2023, 11, 2589. [Google Scholar] [CrossRef]
- Gottlieb, S.; Ketcheson, D.I. Time discretization techniques. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2016; Volume 17, pp. 549–583. [Google Scholar]
- Gottlieb, S.; Ketcheson, D.I.; Shu, C.-W. High order strong stability preserving time discretizations. J. Sci. Comput. 2009, 38, 251–289. [Google Scholar] [CrossRef]
- Seal, D.C.; Güçlü, Y.; Christlieb, A.J. High-order multiderivative time integrators for hyperbolic conservation laws. J. Sci. Comput. 2014, 60, 101–140. [Google Scholar] [CrossRef]
- Qin, X.; Jiang, Z.; Yu, J.; Huang, L.; Yan, C. Strong stability-preserving three-derivative Runge–Kutta methods. Comput. Appl. Math. 2023, 42, 171. [Google Scholar] [CrossRef]
- Butcher, J.C. An algebraic theory of integration methods. Math. Comput. 1972, 26, 79–106. [Google Scholar] [CrossRef]
- Butcher, J.C. Trees and numerical methods for ordinary differential equations. Numer. Algorithms 2010, 53, 153–170. [Google Scholar] [CrossRef]
- Albrecht, P. The Runge-Kutta theory in a nutshell. SIAM J. Numer. Anal. 1996, 33, 1712–1735. [Google Scholar] [CrossRef]
- Butcher, J.C.; Tracogna, S. Order conditions for two-step Runge-Kutta methods. Appl. Numer. Math. 1997, 24, 351–364. [Google Scholar] [CrossRef]
- Chan, R.P.; Tsai, A.Y. On explicit two-derivative Runge-Kutta methods. Numer. Algorithms 2010, 53, 171–194. [Google Scholar] [CrossRef]
- Turaci, M.Ö.; Öziş, T. On explicit two-derivative two-step Runge-Kutta methods. Comput. Appl. Math. 2018, 37, 6920–6954. [Google Scholar] [CrossRef]
- Ketcheson, D.I.; Gottlieb, S.; Macdonald, C.B. Strong stability preserving two-step Runge-Kutta methods. SIAM J. Numer. Anal. 2011, 49, 2618–2639. [Google Scholar] [CrossRef]
- Jackiewicz, Z.; Vermiglio, R. General linear methods with external stages of different orders. BIT Numer. Math. 1996, 36, 688–712. [Google Scholar] [CrossRef]
- Moradi, A.; Farzi, J.; Abdi, A. Order conditions for second derivative general linear methods. J. Comput. Appl. Math. 2021, 387, 112488. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Jackiewicz, Z. Continuous two-step Runge–Kutta methods for ordinary differential equations. Numer. Algorithms 2010, 54, 169–193. [Google Scholar] [CrossRef]
- Movahedinejad, A.; Hojjati, G.; Abdi, A. Second derivative general linear methods with inherent Runge–Kutta stability. Numer. Algorithms 2016, 73, 371–389. [Google Scholar] [CrossRef]
- Christlieb, A.J.; Gottlieb, S.; Grant, Z.; Seal, D.C. Explicit strong stability preserving multistage two-derivative time-stepping methods. J. Sci. Comput. 2016, 68, 914–942. [Google Scholar] [CrossRef]
- Grant, Z.; Gottlieb, S.; Seal, D.C. A strong stability preserving analysis for explicit multistage two-derivative time-stepping schemes based on taylor series conditions. Commun. Appl. Math. Comput. 2019, 1, 21–59. [Google Scholar] [CrossRef]
- Bresten, C.; Gottlieb, S.; Grant, Z.; Higgs, D.; Ketcheson, D.; Németh, A. Explicit strong stability preserving multistep Runge–Kutta methods. Math. Comput. 2017, 86, 747–769. [Google Scholar] [CrossRef]
- Izzo, G.; Jackiewicz, Z. Strong stability preserving general linear methods. J. Sci. Comput. 2015, 65, 271–298. [Google Scholar] [CrossRef]
- Moradi, A.; Farzi, J.; Abdi, A. Strong stability preserving second derivative general linear methods. J. Sci. Comput. 2019, 81, 392–435. [Google Scholar] [CrossRef]
- Qin, X. Explicit Two-Derivative Two-Step Runge-Kutta Methods Code. 2024. Available online: https://github.com/aerfa-buaa/Explicit_Two-Derivative_Two-Step_Runge-Kutta_Methods_TDTSRK (accessed on 23 May 2024).
- Spiteri, R.J.; Ruuth, S.J. A new class of optimal high-order strong-stability-preserving time discretization methods. SIAM J. Numer. Anal. 2002, 40, 469–491. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Don, W.-S.; Borges, R. Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes. J. Comput. Phys. 2013, 250, 347–372. [Google Scholar] [CrossRef]

| Order p | Conditions |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | ; |
| 6 | |
| 7 | |
| TDTSRK23 | TDTSRK24 | TDTSRK25 | |
|---|---|---|---|
| Values of parameters | |||
| Range of parameters | |||
| Range of and |
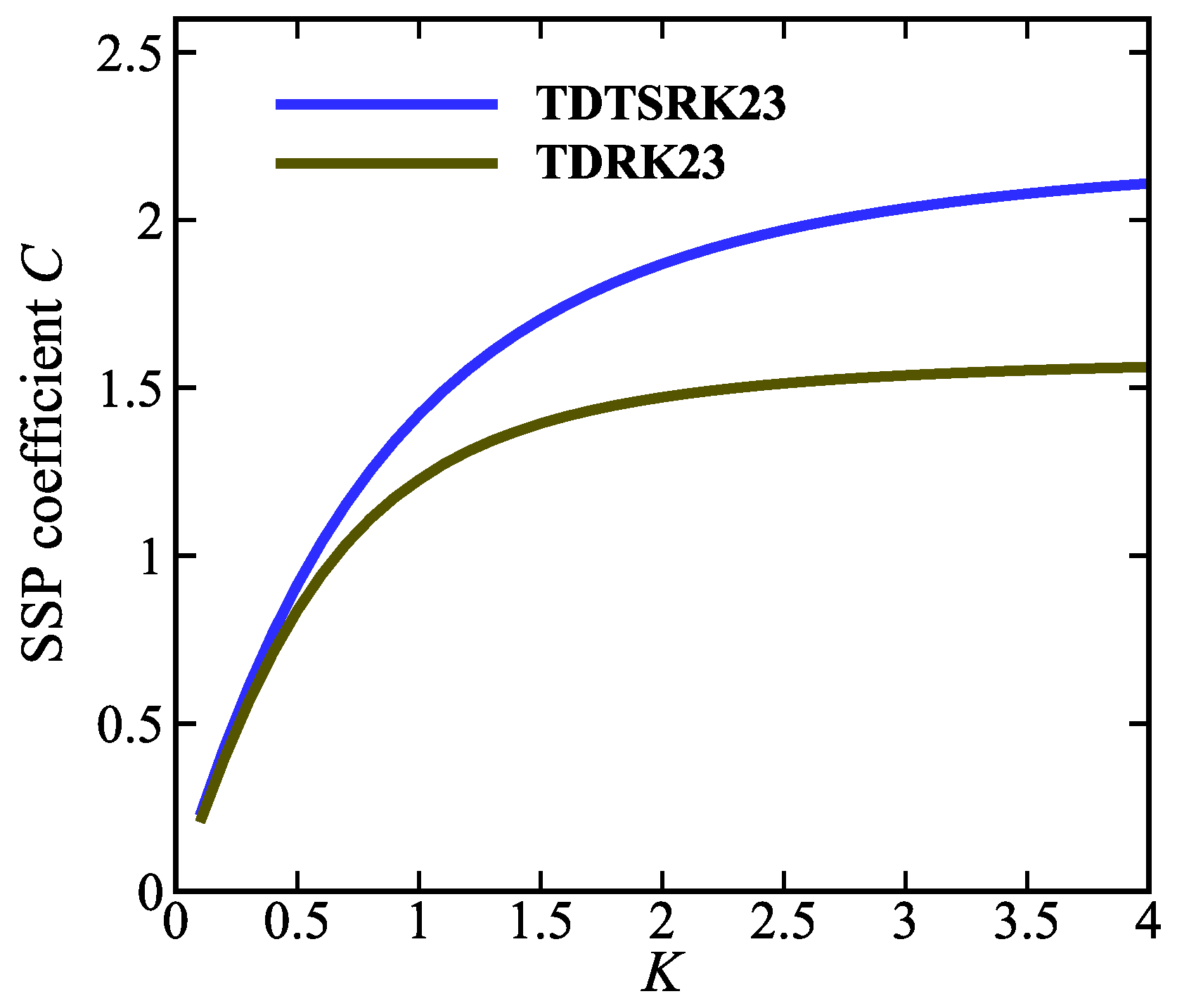
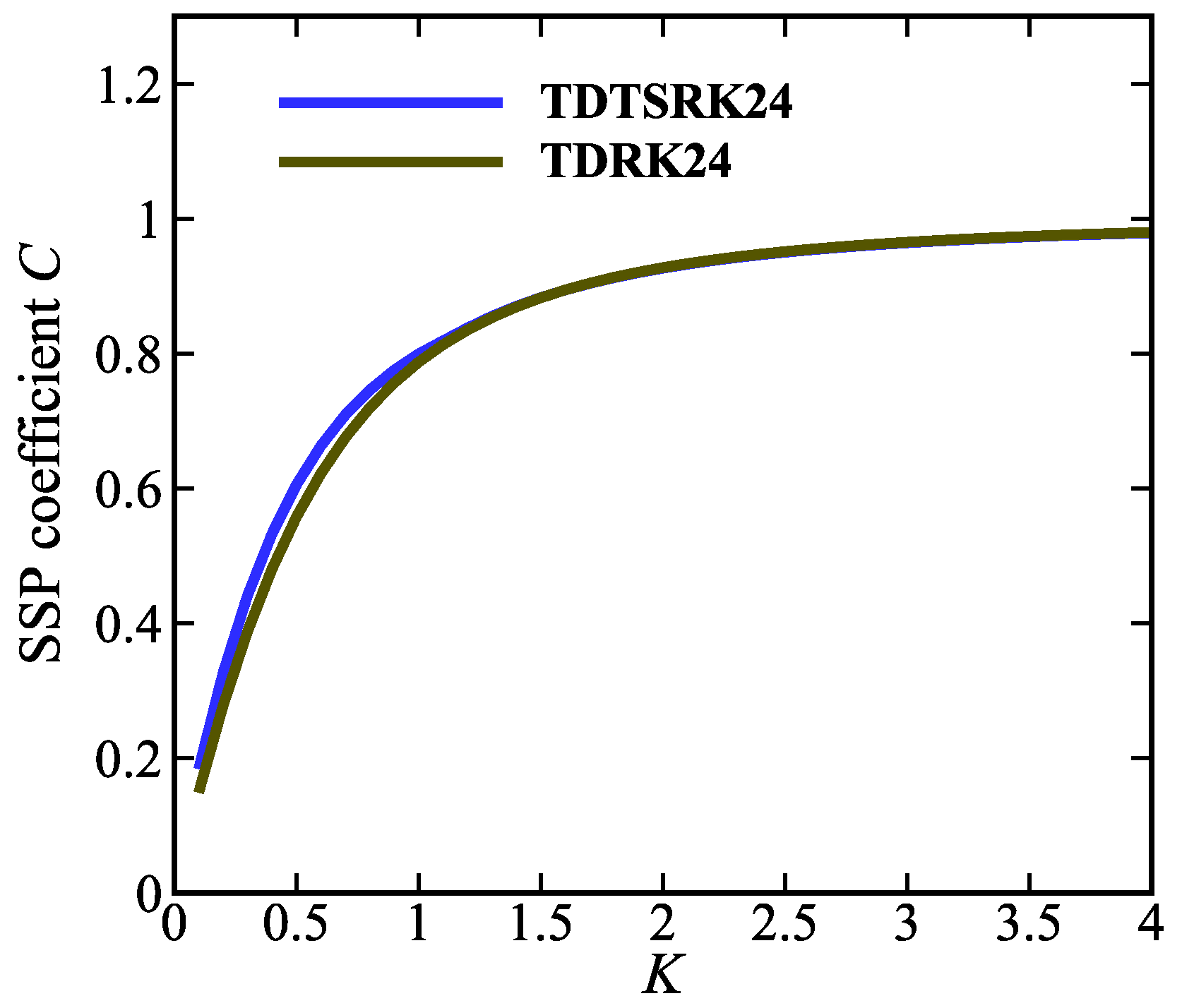
| K | TDTSRK23 | TDRK23 | TDTSRK24 | TDRK24 | TDTSRK25 | TDRK35 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.583 | 0.354 | 0.226 | 0.206 | 0.579 | 0.184 | 0.149 | 0.758 | 0.116 | 0.795 | 0.145 |
| 0.2 | 0.572 | 0.354 | 0.429 | 0.396 | 0.532 | 0.327 | 0.278 | 0.758 | 0.222 | 0.784 | 0.272 |
| 0.3 | 0.563 | 0.363 | 0.610 | 0.564 | 0.510 | 0.441 | 0.388 | 0.758 | 0.317 | 0.775 | 0.381 |
| 0.4 | 0.555 | 0.371 | 0.771 | 0.711 | 0.495 | 0.533 | 0.481 | 0.758 | 0.402 | 0.767 | 0.474 |
| 0.5 | 0.547 | 0.377 | 0.914 | 0.837 | 0.484 | 0.606 | 0.558 | 0.758 | 0.478 | 0.761 | 0.552 |
| 0.6 | 0.540 | 0.383 | 1.041 | 0.944 | 0.475 | 0.663 | 0.622 | 0.765 | 0.547 | 0.755 | 0.617 |
| 0.532 | 0.389 | 1.161 | 1.040 | 0.468 | 0.712 | 0.679 | 0.765 | 0.635 | 0.750 | 0.675 | |
| 0.8 | 0.527 | 0.393 | 1.253 | 1.110 | 0.464 | 0.746 | 0.720 | 0.765 | 0.662 | 0.747 | 0.716 |
| 1.0 | 0.515 | 0.401 | 1.420 | 1.226 | 0.457 | 0.800 | 0.787 | 0.765 | 0.754 | 0.741 | 0.785 |
| 1.5 | 0.494 | 0.416 | 1.704 | 1.394 | 0.954 | 0.883 | 0.883 | 0.765 | 0.907 | 0.733 | 0.882 |
| 2.0 | 0.481 | 0.426 | 1.869 | 1.472 | 0.970 | 0.927 | 0.928 | 0.765 | 0.995 | 0.728 | 0.927 |
| 3.0 | 0.467 | 0.437 | 2.035 | 1.537 | 0.985 | 0.964 | 0.965 | 0.765 | 1.082 | 0.277 | 0.965 |
| 4.0 | 0.460 | 0.442 | 2.109 | 1.562 | 0.990 | 0.979 | 0.980 | 0.765 | 1.119 | 0.270 | 0.980 |
| TDTS | TD | SSP- | TDTS | TD | SSP- | TDTS | TD | RK65 | |
|---|---|---|---|---|---|---|---|---|---|
| RK23 | RK23 | RK33 | RK24 | RK24 | RK54 | RK25 | RK35 | ||
| 1.161 | 1.040 | 1.000 | 0.712 | 0.679 | 1.508 | 0.635 | 0.675 | − | |
| 0.581 | 0.520 | 0.333 | 0.356 | 0.340 | 0.302 | 0.318 | 0.225 | − | |
| 111.6% | 100% | 64.1% | 104.9% | 100% | 88.8% | 141.1% | 100% | − | |
| 1.168 | 1.040 | 1.000 | 1.189 | 0.732 | 1.861 | 0.622 | 0.714 | 1.777 | |
| 0.585 | 0.520 | 0.333 | 0.595 | 0.366 | 0.372 | 0.311 | 0.238 | 0.296 | |
| 112.3% | 100% | 64.1% | 162.4% | 100% | 101.7% | 130.7% | 100% | 124.4% |
| TDTS | TD | SSP- | TDTS | TD | SSP- | TDTS | TD | RK65 | |
|---|---|---|---|---|---|---|---|---|---|
| RK23 | RK23 | RK33 | RK24 | RK24 | RK54 | RK25 | RK35 | ||
| 1.143 | 1.117 | 1.021 | 1.134 | 0.849 | 1.886 | 0.807 | 0.769 | 1.789 | |
| 0.572 | 0.559 | 0.340 | 0.567 | 0.425 | 0.377 | 0.404 | 0.256 | 0.298 | |
| 102.3% | 100% | 60.9% | 133.6% | 100% | 88.9% | 157.4% | 100% | 116.3% |
| Grid | TDTSRK23 | TDRK23 | SSP-RK33 | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 40 | ||||||
| 80 | 2.99 | 3.00 | 3.00 | |||
| 160 | 2.99 | 3.00 | 3.00 | |||
| 320 | 3.00 | 3.00 | 3.00 | |||
| 640 | 3.00 | 3.00 | 3.00 | |||
| Grid | TDTSRK24 | TDRK24 | SSP-RK54 | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 40 | ||||||
| 80 | 3.99 | 3.99 | 3.99 | |||
| 160 | 3.99 | 4.00 | 4.00 | |||
| 320 | 4.00 | 4.00 | 4.00 | |||
| 640 | 4.00 | 4.00 | 3.88 | |||
| Grid | TDTSRK25 | TDRK35 | RK65 | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 40 | ||||||
| 80 | 4.98 | 5.04 | 5.01 | |||
| 160 | 4.99 | 5.00 | 4.99 | |||
| 320 | 5.00 | 5.00 | 4.98 | |||
| 640 | 5.00 | 5.00 | 3.72 | |||
| Grid | TDTSRK23 | TDRK23 | SSP-RK33 | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 80 | ||||||
| 160 | 2.90 | 3.05 | 2.97 | |||
| 320 | 2.95 | 3.02 | 2.99 | |||
| 640 | 2.98 | 3.01 | 3.00 | |||
| 1280 | 2.99 | 3.00 | 3.00 | |||
| Grid | TDTSRK24 | TDRK24 | SSP-RK54 | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 80 | ||||||
| 160 | 3.91 | 3.96 | 3.99 | |||
| 320 | 3.96 | 3.98 | 3.99 | |||
| 640 | 3.98 | 3.99 | 4.00 | |||
| 1280 | 3.99 | 4.00 | 4.04 | |||
| Grid | TDTSRK25 | TDRK35 | RK65 | |||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 80 | ||||||
| 160 | 4.84 | 4.90 | 5.45 | |||
| 320 | 4.92 | 4.96 | 5.06 | |||
| 640 | 4.97 | 4.98 | 5.01 | |||
| 1280 | 4.98 | 4.97 | 4.94 | |||
| TDTS | TD | SSP- | TDTS | TD | SSP- | TDTS | TD | RK65 | |
|---|---|---|---|---|---|---|---|---|---|
| RK23 | RK23 | RK33 | RK24 | RK24 | RK54 | RK25 | RK35 | ||
| Stage s | 2 | 2 | 3 | 2 | 2 | 5 | 2 | 3 | 6 |
| CPU Time | 256.3 | 254.7 | 327.5 | 256.8 | 254.9 | 548.2 | 256.9 | 386.4 | 655.1 |
| Ratio | 2.35 | 2.33 | 3.00 | 2.35 | 2.33 | 5.02 | 2.35 | 3.54 | 6.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Jiang, Z.; Yan, C. Strong Stability Preserving Two-Derivative Two-Step Runge-Kutta Methods. Mathematics 2024, 12, 2465. https://doi.org/10.3390/math12162465
Qin X, Jiang Z, Yan C. Strong Stability Preserving Two-Derivative Two-Step Runge-Kutta Methods. Mathematics. 2024; 12(16):2465. https://doi.org/10.3390/math12162465
Chicago/Turabian StyleQin, Xueyu, Zhenhua Jiang, and Chao Yan. 2024. "Strong Stability Preserving Two-Derivative Two-Step Runge-Kutta Methods" Mathematics 12, no. 16: 2465. https://doi.org/10.3390/math12162465
APA StyleQin, X., Jiang, Z., & Yan, C. (2024). Strong Stability Preserving Two-Derivative Two-Step Runge-Kutta Methods. Mathematics, 12(16), 2465. https://doi.org/10.3390/math12162465






