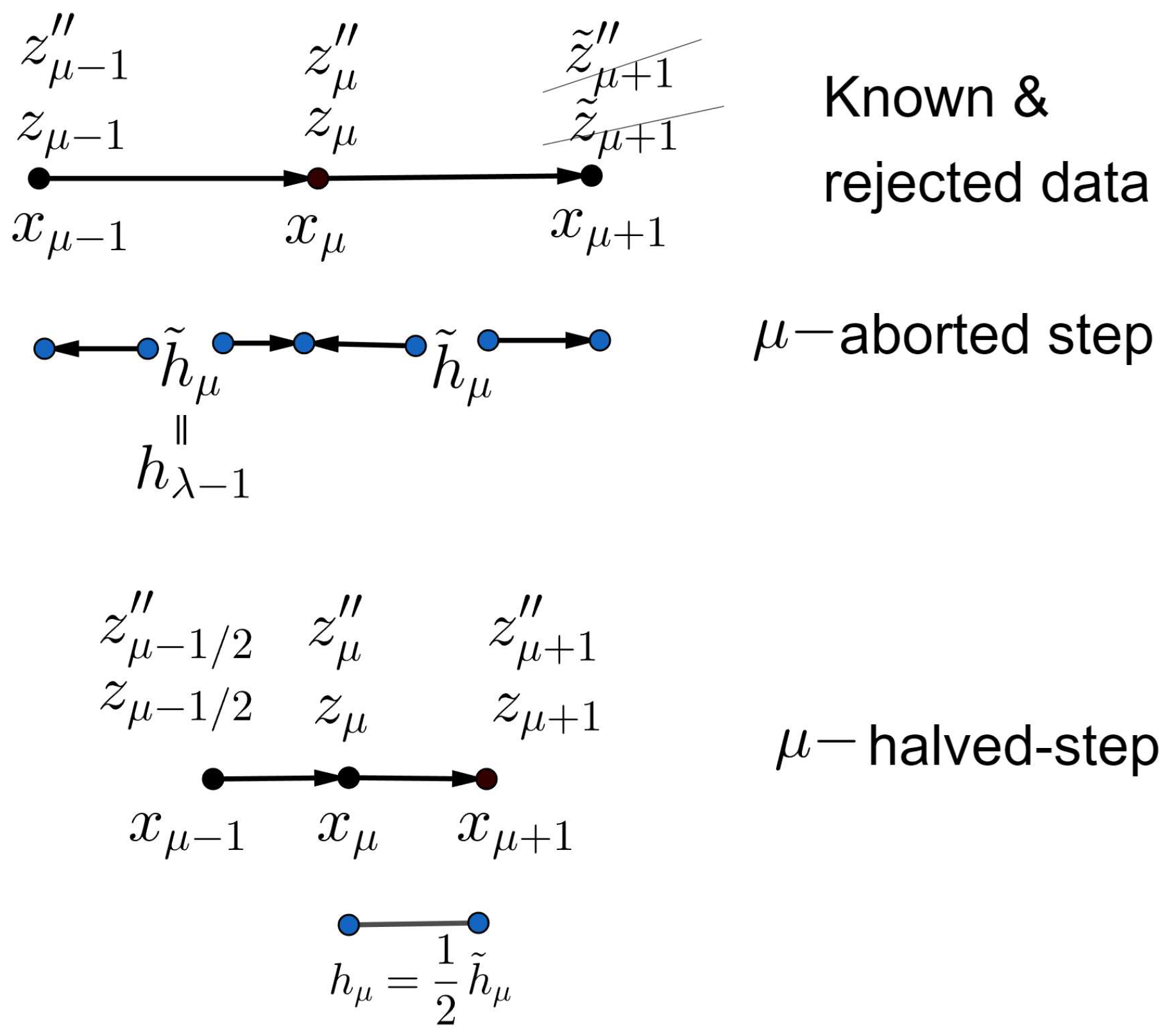
%----------------------------------------------------------------------------- function [xout,zout,ireject]=num8var(gcn,x0,xe,h,z0,dz0,tol); % Variable step Numerov 8th order (NEW8ph18 from MMAS2017 paper) d=[0,0,0,0,0,0,0,0,0,0; 0,0,0,0,0,0,0,0,0,0; 0.03514436477478967271695543856798,0.778985172673572292604174397326821, ... 0,0,0,0,0,0,0,0; -0.030756691100062805827044701849216,-0.07869613284023427590783998801148, ... 0.011929412323501202370387215214963,0,0,0,0,0,0,0; 0.031121796239394819774224147358071,0.147811428598972016085442546229843, ... -0.011362151424849423218299194192520,0.00048457570357029208773192112857, ... 0,0,0,0,0,0; 0.30141579735411936564090356179718,5.192050394473954713157163942448410, ... 0.32804602267391035193477393037790,-2.43624015403357970664126740503822, ... -2.20301905709547980011694371100782,0,0,0,0,0; -5.229446756260189e-02 -5.291660460847162e-01 7.710819781755138e-02 ... 5.832199643851225e-01 -5.323442275392505e-03 -8.234617732012934e-03 0 0 0 0; 9.778994089862780e-02 1.533163927607464e+00 1.592368698012818e-01 ... -3.268980182507659e-01 -4.666459166972902e-01 1.537296514463354e-05 ... 3.337823675537400e-03 0 0 0; 6.593020920369334e-01 3.620612536615338e+00 3.245537413836930e-02 ... -2.066275385333197e+00 -2.174528664209118e+00 -4.567750736985592e-01 ... -4.595125484205432e-01 7.204703432105997e-01 0 0; 7.000913567080177e-01 3.806666958489904e+00 3.499348837605611e-02 ... -2.164799272132436e+00 -2.291672103336968e+00 -4.819285087785059e-01 ... -4.879049142356707e-01 7.600995265565401e-01 -1.092548371386614e-04 0]; w=[8.147088962485628e-02 -3.128563096754995e-01 0 6.078286168553779e-01 ... 6.078286168553779e-01 -3.287135164248439e-02 -3.287135164248439e-02 ... 8.147088962485628e-02]; a=[-1 0 8.704959229770528e-01 -2.655790607338836e-01 ... 2.655790607338836e-01 1.116943414824975e+00 -1.116943414824975e+00 1 ... -5.386955899250456e-01 -5.295728527470133e-01]’; ws=[-9.098777438949393e-03 7.462144825335587e-03 0 ... -6.969481411423929e-02 -1.985097776074821e-03 -6.740601700302488e-05 ... 1.973900294814832e-03 1.284303505510030e-04 -1 9.462816198755651e-01]; e=[2.081470889624856e+00 1.088603394668112e+01 0 -6.206975601041206e+00 ... -6.206975601041206e+00 -1.317512261924209e+00 -1.317512261924209e+00 ... 2.081470889624856e+00 0 0]; g0=feval(gcn,x0,z0); % g0 [x1,z1]=rkn86(gcn,x0,x0+h,z0,dz0,tol/1000); % initial z1 z1=z1(end,:)’; x=x0+h; % advance x g1=feval(gcn,x,z1); % g1 xout = [x0 x0+h zeros(1,634998)]; % preallocate output for x m=length(z0); % dimension of system zout=zeros(m,635000); % preallocate output of z zout(:,1)=z0; zout(:,2)=z1; k=2;ireject=0;dipl=1; % The main loop while (x < xe-1e-9), za1=(d(3,1)*g0+d(3,2)*g1)*h^2-a(3)*z0+(1+a(3))*z1; ga1=feval(gcn,x+a(3)*h,za1); % 1st stage za2=(d(4,1)*g0+d(4,2)*g1+d(4,3)*ga1)*h^2-a(4)*z0+(1+a(4))*z1; ga2=feval(gcn,x+a(4)*h,za2); % 2nd stage za3=(d(5,1)*g0+d(5,2)*g1+d(5,3)*ga1+d(5,4)*ga2)*h^2-a(5)*z0+(1+a(5))*z1; ga3=feval(gcn,x+a(5)*h,za3); % 3rd stage za4=(d(6,1)*g0+d(6,2)*g1+d(6,3)*ga1+d(6,4)*ga2+d(6,5)*ga3)*h^2 ... -a(6)*z0+(1+a(6))*z1; ga4=feval(gcn,x+a(6)*h,za4); % 4th stage za5=(d(7,1)*g0+d(7,2)*g1+d(7,3)*ga1+d(7,4)*ga2+d(7,5)*ga3+ ... d(7,6)*ga4)*h^2-a(7)*z0+(1+a(7))*z1; ga5=feval(gcn,x+a(7)*h,za5); % 5th stage za6=(d(8,1)*g0+d(8,2)*g1+d(8,3)*ga1+d(8,4)*ga2+d(8,5)*ga3 ... +d(8,6)*ga4+d(8,7)*ga5)*h^2-a(8)*z0+(1+a(8))*z1; ga6=feval(gcn,x+a(8)*h,za6); % 6th stage % error estimation delta=1e2*max(abs(h^2*(e(1)*g0+e(2)*g1+e(3)*ga1+e(4)*ga2+e(5)*ga3 ... +e(6)*ga4+e(7)*ga5+e(8)*ga6))); % Update the solution only if the error is acceptable if delta <= tol*16, x = x + h; k=k+1; xout(k)=x; z2=2*z1-z0+h^2*(w(1)*g0+w(2)*g1+w(3)*ga1+w(4)*ga2+w(5)*ga3 ... +w(6)*ga4+w(7)*ga5+w(8)*ga6); zout(:,k)=z2; if (delta<tol/16) && (dipl==0), h=h+h;dipl=1; % Double the step else z0=z1;g0=g1;dipl=0; % Keep the same step end; z1=z2; g1=feval(gcn,x+h,z2); % 7th stage else ireject=ireject+1; % Halve the step za7=(d(9,1)*g0+d(9,2)*g1+d(9,3)*ga1+d(9,4)*ga2+d(9,5)*ga3 ... +d(9,6)*ga4+d(9,7)*ga5+d(9,8)*ga6)*h^2-a(9)*z0+(1+a(9))*z1; ga7=feval(gcn,x+a(9)*h,za7); % 1st extra stage za8=(d(10,1)*g0+d(10,2)*g1+d(10,3)*ga1+d(10,4)*ga2+d(10,5)*ga3 ... +d(10,6)*ga4+d(10,7)*ga5+d(10,8)*ga6+d(10,9)*ga7)*h^2-a(10)*z0+(1+a(10))*z1; ga8=feval(gcn,x+a(10)*h,za8); % 2nd extra stage z0=(ws(1)*g0+ws(2)*g1+ws(3)*ga1+ws(4)*ga2+ws(5)*ga3+ws(6)*ga4+ ... ws(7)*ga5+ws(8)*ga6+ws(9)*ga7+ws(10)*ga8)*h^2+z0/2+z1/2; g0=feval(gcn,x-1/2*h,z0); % 3rd extra stage h=h/2; dipl=1; end; end; xout=xout(1:k);zout=zout(:,1:k); return; %-----------------------------------------------------------------------------
|