Laplace-Logistic Unit Distribution with Application in Dynamic and Regression Analysis

Abstract

This manuscript presents a new two-parameter unit stochastic distribution, obtained by transforming the Laplace distribution, using a generalized logistic map, into a unit interval. The distribution thus obtained is named the Laplace-logistic unit (abbreviated LLU) distribution, and its basic stochastic properties are examined in detail. Also, the procedure for estimating parameters based on quantiles is provided, along with the asymptotic properties of the obtained estimates and the appropriate numerical simulation study. Finally, the application of the LLU distribution in dynamic and regression analysis of real-world data with accentuated “peaks” and “fat” tails is also discussed.

1. Introduction

Unit stochastic distributions, defined on the interval $(0,1)$, represent an important tool of contemporary probability theory. They are primarily used as stochastic models that can describe so-called proportional (percentage) variables and represent theoretical models that can successfully explain the behavior of some real-world phenomena (see, for more contemporary examples, e.g., [1,2,3,4]). On the other hand, modeling with unit distributions differs from common stochastic modeling procedures, primarily due to the limitation of data within the $(0,1)$ interval. Although the procedure for creating unit distributions can be given in a general form [5], the most common approach is based on continuous transformations of distributions defined on infinite intervals into a unit interval (for some recent results, see, e.g., [6,7,8,9,10]). Nevertheless, most of these distributions are limited by a unique form of (a)symmetry and modality, “vanishing” data at the ends of the unit interval, etc. This is often inappropriate for modeling real phenomena with different characteristics, especially where data with pronounced “peaks” and “fat tails” appear.

To this end, proceeding from similar considerations as in Stojanović et al. [11,12], a new unit distribution, named the Laplace-logistic unit (LLU) distribution, is described here. It is based on a general logistic mapping of the Laplace distribution to a unit interval and, as will be seen, has considerable flexibility and suitability for describing a variety of empirical distributions, from those with pronounced extremes to increasing, decreasing, or bathtub-shaped ones. The definition and the key stochastic properties of the LLU distribution, regarding its limit properties, (a)symmetry, and modality, are presented in Section 2. Thereafter, Section 3 considers the parameter estimation based on sample quantiles and the asymptotic properties of the thus obtained estimators, as well as a numerical Monte Carlo study of them. An application of the LLU distribution in fitting some real-world data, primarily from the aspect of dynamic and regression analysis, is presented in Section 4, while Section 5 contains some concluding remarks.

2. The LLU Distribution

2.1. Definition and Main Properties

Let us first consider a random variable (RV) Y with a symmetric Laplace distribution, whose probability density function (PDF) is

$$g(y;\theta )={\displaystyle \frac{\lambda }{2}}exp\left(-\lambda \left|y\right|\right),$$

(1)

where $y\in \mathbb{R}$ and $\lambda >0$ is the scale parameter. Further, for an arbitrary $\theta >0$, let us define the so-called general logistic map $x=\phi (y;\theta )={\left(1+exp\left(y\right)\right)}^{-1/\theta }$. Obviously, it is the bijective, continuous transformation $\phi :(-\infty ,+\infty )\times (0,+\infty )\to (0,1)$, with limits

$$\underset{y\to -\infty }{lim}\phi (y;\theta )=1^{-},\underset{y\to +\infty }{lim}\phi (y;\theta )=0^{+}.$$

Thus, by using Equation (1) and the inverse transformation $y={\phi }^{-1}(x;\theta )=ln(x^{-\theta }-1)$, the new RV $X=\phi (Y;\theta )$, defined on the unit interval $(0,1)$ is obtained. After some computation, for the PDF of the RV X one obtains

$$\begin{array}{cc}\hfill f(x;\lambda ,\theta )& =g\left({\phi }^{-1}(x;\theta );\lambda \right)·\left|{\displaystyle \frac{\partial {\phi }^{-1}(x;\theta )}{\partial x}}\right|={\displaystyle \frac{\theta \lambda }{2x(1-x^{\theta })}}exp\left(-\lambda |ln(x^{-\theta }-1\left)\right|\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}{\displaystyle \frac{\theta \lambda x^{\theta \lambda -1}}{2{\left(1-x^{\theta }\right)}^{\lambda +1}},}\hfill & x\le 2^{-1/\theta }\hfill \\ {\displaystyle \frac{\theta \lambda {\left(1-x^{\theta }\right)}^{\lambda -1}}{2x^{\theta \lambda +1}},}\hfill & x>2^{-1/\theta }\hfill \end{array}\right.,\hfill \end{array}$$

(2)

where $x\in (0,1)$ and ${\int }_0^{1}f(x;\lambda ,\theta )\mathrm{d}x=1$. Thus, we say that the RV X, whose PDF is given by Equation (2), has a Laplace-logistic unit (LLU) distribution, with the parameters $\lambda ,\theta >0$, or abbreviated, $X:\mathcal{L}(\lambda ,\theta )$. Obviously, the LLU distribution is a two-parameter distribution, where, in addition to the scale parameter $\lambda >0$, there is also a shape parameter $\theta >0$. Also, let us emphasize that symmetric Laplace density is expressed in terms of the absolute difference from the zero and it has pronounced “peaks” and tails more “fat” than, for instance, the Gaussian distribution. For these reasons, the RV $X:\mathcal{L}(\lambda ,\theta )$ will have similar properties, but it also has some other specificities. To describe them more completely, we first introduce some terms related to the limit behavior of the density at the ends of the unit interval.

Definition 1.

Let $X:\mathcal{L}(\lambda ,\theta )$ be the RV with the LLU distribution, whose PDF $f(x;\lambda ,\theta )$ is given by Equation (2). The PDF $f(x;\lambda ,\theta )$ is left- (right-) vanishing if the following is valid:

$$\underset{x\to 0^{+}}{lim}f(x;\lambda ,\theta )=0^{+}\left(\underset{x\to 1^{-}}{lim}f(x;\lambda ,\theta )=0^{+}\right).$$

Otherwise, the PDF $f(x;\lambda ,\theta )$ is left- (right-) tailed.

Now, some properties of the LLU distribution regarding its possible shapes and boundary characteristics can be given by the following proposition:

Theorem 1.

The PDF $f(x;\lambda ,\theta )$ of the RV $X:\mathcal{L}(\lambda ,\theta )$ is a continuous function, non-differentiable at the point $x_0=2^{-1/\theta }$, with the following properties:

(i)

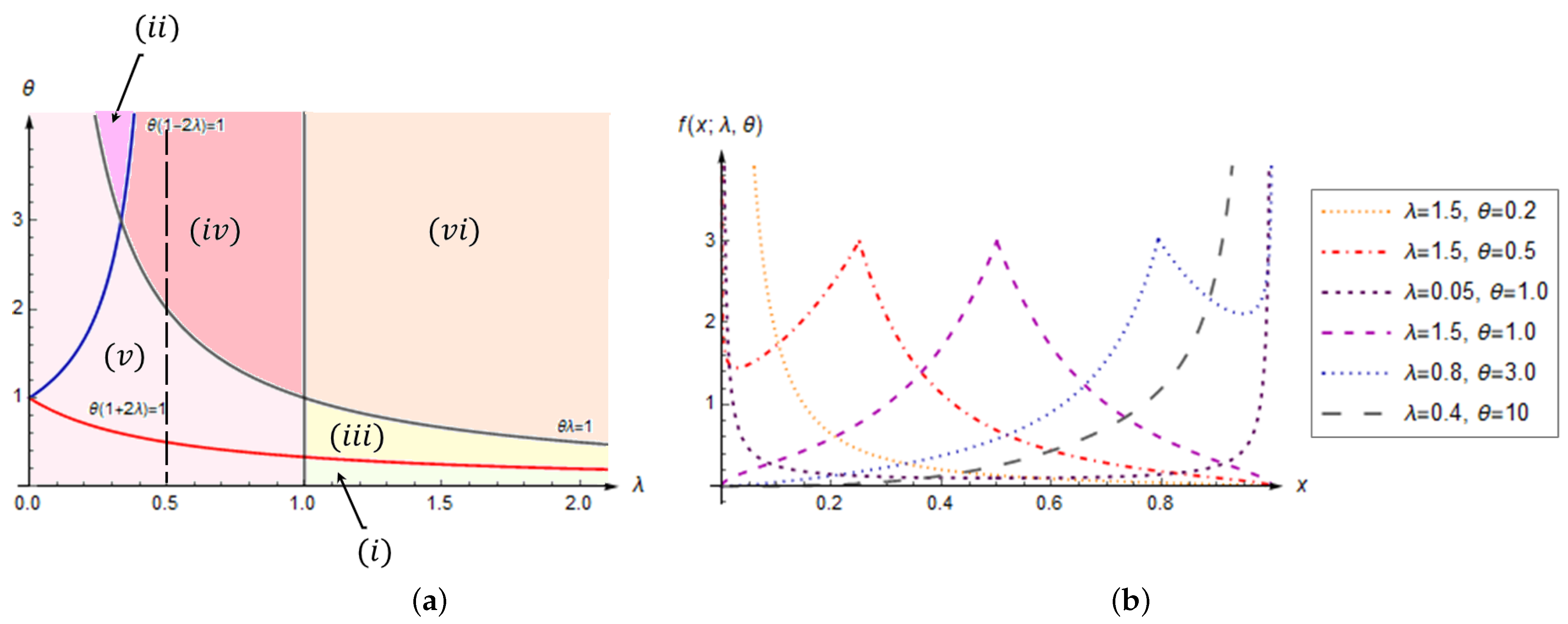
When $\theta (1+2\lambda )<1$ and $\lambda >1$, it is decreasing.

(ii)

When $\theta (1-2\lambda )>1$ and $\theta \lambda >1$, it is increasing.

(iii)

When $\theta (1+2\lambda )\ge 1$, $\theta \lambda \le 1$ and $\lambda >1$, it is left-tailed and right-vanishing.

(iv)

When $\theta (1-2\lambda )\le 1$, $\theta \lambda >1$ and $\lambda \le 1$, it is right-tailed and left-vanishing.

(v)

When $\theta \lambda \le 1$ and $\lambda \le 1$, it is (both sides) tailed.

(vi)

When $\theta \lambda >1$ and $\lambda >1$, it is (both sides) vanishing.

Proof. 

For simplicity, let us denote the left and right branches of the PDF $f(x;\lambda ,\theta )$, respectively, as follows:

$${\displaystyle f_1(x;\lambda ,\theta ):=\frac{\theta \lambda x^{\theta \lambda -1}}{2{\left(1-x^{\theta }\right)}^{\lambda +1}},f_2(x;\lambda ,\theta ):=\frac{\theta \lambda {\left(1-x^{\theta }\right)}^{\lambda -1}}{2x^{\theta \lambda +1}}.}$$

Accordingly, it is obtained that

$$\underset{x\to 2^{-1/\theta }}{\lim }{f}_1(x;\lambda ,\theta )=\underset{x\to 2^{-1/\theta }}{\lim }{f}_2(x;\lambda ,\theta )=\theta \lambda 2^{1/\theta },$$

so the PDF $f(x;\lambda ,\theta )$ is indeed continuous at $x_0=2^{-1/\theta }$. Furthermore, after some computation, one obtains

$$\underset{x\to 0^{+}}{\lim }{f}_1(x;\lambda ,\theta )=\left\{\begin{array}{cc}0,\hfill & \theta \lambda >1\hfill \\ 1/2,\hfill & \theta \lambda =1\hfill \\ +\infty ,\hfill & \theta \lambda <1\hfill \end{array}\right.,\underset{x\to 1^{-}}{\lim }{f}_2(x;\lambda ,\theta )=\left\{\begin{array}{cc}0,\hfill & \lambda >1\hfill \\ \theta /2,\hfill & \lambda =1\hfill \\ +\infty ,\hfill & \lambda <1\hfill \end{array}\right.,$$

(3)

as well as

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial f_1(x;\lambda ,\theta )}{\partial x}}& ={\displaystyle \frac{\theta \lambda x^{\theta \lambda -2}}{2{\left(1-x^{\theta }\right)}^{\lambda +2}}}\left((\theta +1)x^{\theta }+\theta \lambda -1\right),\hfill \\ \hfill {\displaystyle \frac{\partial f_2(x;\lambda ,\theta )}{\partial x}}& ={\displaystyle \frac{\theta \lambda {\left(1-x^{\theta }\right)}^{\lambda -2}}{2x^{\theta \lambda +2}}}\left((\theta +1)x^{\theta }-\theta \lambda -1\right).\hfill \end{array}$$

(4)

Thus, the sign of the partial derivatives in Equation (4) depends on the sign of the functions

$${\psi }_1(x;\lambda ,\theta )=(\theta +1)x^{\theta }+\theta \lambda -1,{\psi }_2(x;\lambda ,\theta )=(\theta +1)x^{\theta }-\theta \lambda -1.$$

Obviously, both of these functions are monotonically increasing on $x\in (0,1)$, and their values at the critical points $x\in \{0,2^{-1/\theta },1\}$ are, respectively,

$$\begin{array}{cc}\hfill & {\psi }_1(0;\lambda ,\theta )=\theta \lambda -1,{\psi }_1(2^{-1/\theta };\lambda ,\theta )={\displaystyle \frac{1}{2}}\left(\theta (2\lambda +1)-1\right),\hfill \\ \hfill & {\psi }_2(2^{-1/\theta };\lambda ,\theta )={\displaystyle \frac{1}{2}}\left(\theta (1-2\lambda )-1\right),{\psi }_2(1;\lambda ,\theta )=\theta (1-\lambda ).\hfill \end{array}$$

(5)

Then, by using Equations (3) and (5), all cases in the statement of the theorem are simply obtained. □

Remark 1.

The different conditions for the shape and boundary behavior of the LLU distribution can be seen in Figure 1a, where the six different areas mentioned in the previous theorem are shown. On the other hand, Figure 1b shows typical, different shapes of the PDFs of this distribution. As can be easily seen, the LLU distribution takes very different forms, where in addition to the typical one with a “peak”, which is similar to the Laplace distribution, it can have a decreasing, increasing, or bathtub-shaped PDF. In that way, it has significant flexibility, which is of particular importance in applications. Moreover, when $\lambda \approx 0$ one obtains

$${\psi }_1(x;\lambda ,\theta ){|}_{x=2^{-1/\theta }}\approx {\psi }_2(x;\lambda ,\theta ){|}_{x=2^{-1/\theta }}\approx 0,$$

so, in this asymptotic case the PDF $f(x;\lambda ,\theta )$ will be an approximately differentiable, with an extreme value (i.e., mode) at the point $x_0=2^{-1/\theta }$. In any case, the modality of the LLU distribution is explored in more detail in the next part of this section.

The PDF of the LLU distribution can also be used to obtain its moments and other moment-based features, as given below.

Theorem 2.

The $r^{th}$ moment of the LLU-distributed RV X can be expressed as

$$\begin{array}{cc}\hfill {\mu }_r(\lambda ,\theta ):=E\left(X^r\right)& ={\displaystyle \frac{\lambda }{2}}\left(B_{1/2}\left({\displaystyle \frac{r}{\theta }}+\lambda ,-\lambda \right)+B_{1/2}\left(\lambda ,{\displaystyle \frac{r}{\theta }}-\lambda \right)\right),\hfill \end{array}$$

(6)

where r is an integer and $B_z(a,b)={\int }_0^z{t}^{a-1}{(1-t)}^{b-1}\mathrm{d}t$ is an incomplete beta function. In addition, the following convergence holds:

$$\underset{\theta \to \infty }{lim}{\mu }_r(\lambda ,\theta )=1.$$

(7)

Proof. 

By definition of the LLU distribution, its $r^{th}$ moment can be computed as follows:

$${\mu }_r(\lambda ,\theta )={\int }_0^1{x}^{r}f(x;\lambda ,\theta )\mathrm{d}x={\mu }_r^{\left(1\right)}(\lambda ,\theta )+{\mu }_r^{\left(2\right)}(\lambda ,\theta ),$$

(8)

wherein

$$\begin{array}{cc}\hfill {\mu }_r^{\left(1\right)}(\lambda ,\theta )& :={\int }_0^{x_0}{x}^r{f}_1(x;\lambda ,\theta )\mathrm{d}x={\displaystyle \frac{\lambda \theta }{2}}{\int }_0^{x_0}{\displaystyle \frac{x^{r+\lambda \theta -1}\mathrm{d}x}{{(1-x^{\theta })}^{\lambda +1}}}={\displaystyle \frac{\lambda }{2}}{\int }_0^{1/2}{t}^{r/\theta +\lambda -1}{(1-t)}^{-\lambda -1}\mathrm{d}t\hfill \\ \hfill & ={\displaystyle \frac{\lambda }{2}}{B}_{1/2}\left({\displaystyle \frac{r}{\theta }}+\lambda ,-\lambda \right),\hfill \\ \hfill {\mu }_r^{\left(2\right)}(\lambda ,\theta )& :={\int }_{x_0}^1{x}^r{f}_2(x;\lambda ,\theta )\mathrm{d}x={\displaystyle \frac{\lambda \theta }{2}}{\int }_{x_0}^1{\displaystyle \frac{{(1-x^{\theta })}^{\lambda -1}\mathrm{d}x}{x^{\lambda \theta +1-r}}}={\displaystyle \frac{\lambda }{2}}{\int }_{1/2}^1{t}^{r/\theta -\lambda -1}{(1-t)}^{\lambda -1}\mathrm{d}t\hfill \\ \hfill & ={\int }_0^{1/2}{z}^{\lambda -1}{(1-z)}^{r/\theta -\lambda -1}\mathrm{d}z={\displaystyle \frac{\lambda }{2}}{B}_{1/2}\left(\lambda ,{\displaystyle \frac{r}{\theta }}-\lambda \right)),\hfill \end{array}$$

as well as $x_0=2^{-1/\theta }$, $t=x^{\theta }$, $z=1-t$, and $B_z(a,b)={\int }_0^z{t}^{a-1}{(1-t)}^{b-1}\mathrm{d}t$. According to this and Equation (8), the first part of the theorem, that is, Equation (6), is proven. Finally, Equation (7) follows from the equalities

$$B_{1/2}\left(\lambda ,-\lambda \right)={\int }_0^{1/2}{\displaystyle \frac{t^{\lambda -1}\mathrm{d}t}{{(1-t)}^{\lambda +1}}}={\int }_0^1{u}^{\lambda -1}\mathrm{d}u={\displaystyle \frac{1}{\lambda }},$$

where $u=t/(1-t)$. □

Remark 2.

By using Equation (6), for the mean and the variance of the RV $X:\mathcal{L}(\lambda ,\theta )$ one obtains, respectively,

$$\begin{array}{cc}\hfill \mathrm{E}\left(X\right)& ={\mu }_1(\lambda ,\theta )={\displaystyle \frac{\lambda }{2}}\left[B_{\frac{1}{2}}\left(\lambda ,{\displaystyle \frac{1}{\theta }}-\lambda \right)+B_{\frac{1}{2}}\left(\lambda +{\displaystyle \frac{1}{\theta }},-\lambda \right)\right],\hfill \\ \hfill \mathrm{Var}\left(X\right)& ={\mu }_2(\lambda ,\theta )-{\left({\mu }_1(\lambda ,\theta )\right)}^2={\displaystyle \frac{\lambda }{2}}[B_{\frac{1}{2}}\left(\lambda ,{\displaystyle \frac{2}{\theta }}-\lambda \right)+B_{\frac{1}{2}}\left(\lambda +{\displaystyle \frac{2}{\theta }},-\lambda \right)\hfill \\ \hfill & -{\displaystyle \frac{\lambda }{2}}{\left(B_{\frac{1}{2}}\left(\lambda ,{\displaystyle \frac{1}{\theta }}-\lambda \right)+B_{\frac{1}{2}}\left(\lambda +{\displaystyle \frac{1}{\theta }},-\lambda \right)\right)}^2].\hfill \end{array}$$

(9)

Additionally, according to Equation (7), it follows that

$$\underset{\theta \to \infty }{lim}\mathrm{E}\left(X\right)=1,\underset{\theta \to \infty }{lim}\mathrm{Var}\left(X\right)=0,$$

that is, in this limit case, $X\stackrel{as}{=}1$ holds, where “as” means “almost surely”. Therefore, the RV X is then reduced to a unit constant, obtained by transforming the Laplace distribution, whose PDF is given by Equation (1), using the trivial logistic map $\phi (y;\theta )\equiv 1$. This can also be seen in Figure 2 below, where 3D plots of the mean value and variance are shown, depending on the parameters $\lambda ,\theta >0$.

Similarly, the skewness coefficient and the kurtosis of the RV $X:\mathcal{L}(\lambda ,\theta )$ are, respectively,

$$\begin{array}{cc}\hfill S(\lambda ,\theta )& :={\displaystyle \frac{E{(X-{\mu }_1(\lambda ,\theta ))}^3}{{\left[\mathrm{Var}\left(X\right)\right]}^{3/2}}}={\displaystyle \frac{{\mu }_3(\lambda ,\theta )-3{\mu }_1(\lambda ,\theta )\mathrm{Var}\left(X\right)-{\left({\mu }_1(\lambda ,\theta )\right)}^3}{{\left[\mathrm{Var}\left(X\right)\right]}^{3/2}}},\hfill \\ \hfill K(\lambda ,\theta )& ={\displaystyle \frac{E{\left(X-{\mu }_1(\lambda ,\theta )\right)}^4}{{\left[\mathrm{Var}\left(X\right)\right]}^2}}\hfill \\ \hfill & ={\displaystyle \frac{{\mu }_4(\lambda ,\theta )-4{\mu }_3(\lambda ,\theta ){\mu }_1(\lambda ,\theta )+6{\mu }_2(\lambda ,\theta ){\left({\mu }_1(\lambda ,\theta )\right)}^2-3{\left({\mu }_1(\lambda ,\theta )\right)}^4}{{\left[\mathrm{Var}\left(X\right)\right]}^2}}.\hfill \end{array}$$

Nevertheless, because of the complexity a more detailed procedure for calculating these coefficients is omitted.

2.2. Cumulative, Hazard, and Quantile Functions

Using Equation (2), the cumulative distribution function (CDF) of the LLU distribution can be obtained as follows:

$$F(x;\lambda ,\theta )=P\{X<x\}={\int }_0^{x}f(t;\lambda ,\theta )\mathrm{d}t=\left\{\begin{array}{cc}{\displaystyle \frac{x^{\theta \lambda }}{2{\left(1-x^{\theta }\right)}^{\lambda }}},\hfill & x\le 2^{-1/\theta }\hfill \\ 1-{\displaystyle \frac{{\left(1-x^{\theta }\right)}^{\lambda }}{2x^{\theta \lambda }}},\hfill & x>2^{-1/\theta }\hfill \end{array}\right.,$$

(10)

where $x\in (0,1)$. Note that the function $F(x;\lambda ,\theta )$ is differentiable on $x\in (0,1)$, and well defined outside the unit interval, since the following is valid:

$$\underset{x\to 0^{+}}{lim}F(x;\lambda ,\theta )=0^{+},\underset{x\to 1^{-}}{lim}F(x;\lambda ,\theta )=1^{-}.$$

Furthermore, according to Equations (2) and (8), the hazard rate function (HRF) can be obtained as follows:

$$H(x;\lambda ,\theta ):={\displaystyle \frac{f(x;\lambda ,\theta )}{1-F(x;\lambda ,\theta )}}=\left\{\begin{array}{cc}{\displaystyle \frac{\theta \lambda x^{\theta \lambda -1}}{\left(1-x^{\theta }\right)\left(2{\left(1-x^{\theta }\right)}^{\lambda }-x^{\theta \lambda }\right)}},\hfill & x\le 2^{-1/\theta }\hfill \\ {\displaystyle \frac{\theta \lambda }{x(1-x^{\theta })}},\hfill & x>2^{-1/\theta }\hfill \end{array}\right..$$

(11)

The basic properties of the HRF $H(x;\lambda ,\theta )$ can be expressed by the following statement.

Theorem 3.

Let $X:\mathcal{L}(\lambda ,\theta )$ and $H(x;\lambda ,\theta )$ be the HRF of the RV X, defined by Equation (11). Then, $H(x;\lambda ,\theta )$ is a continuous function, non-differentiable at the point $x_0=2^{-1/\theta }$, with the following properties:

(i)

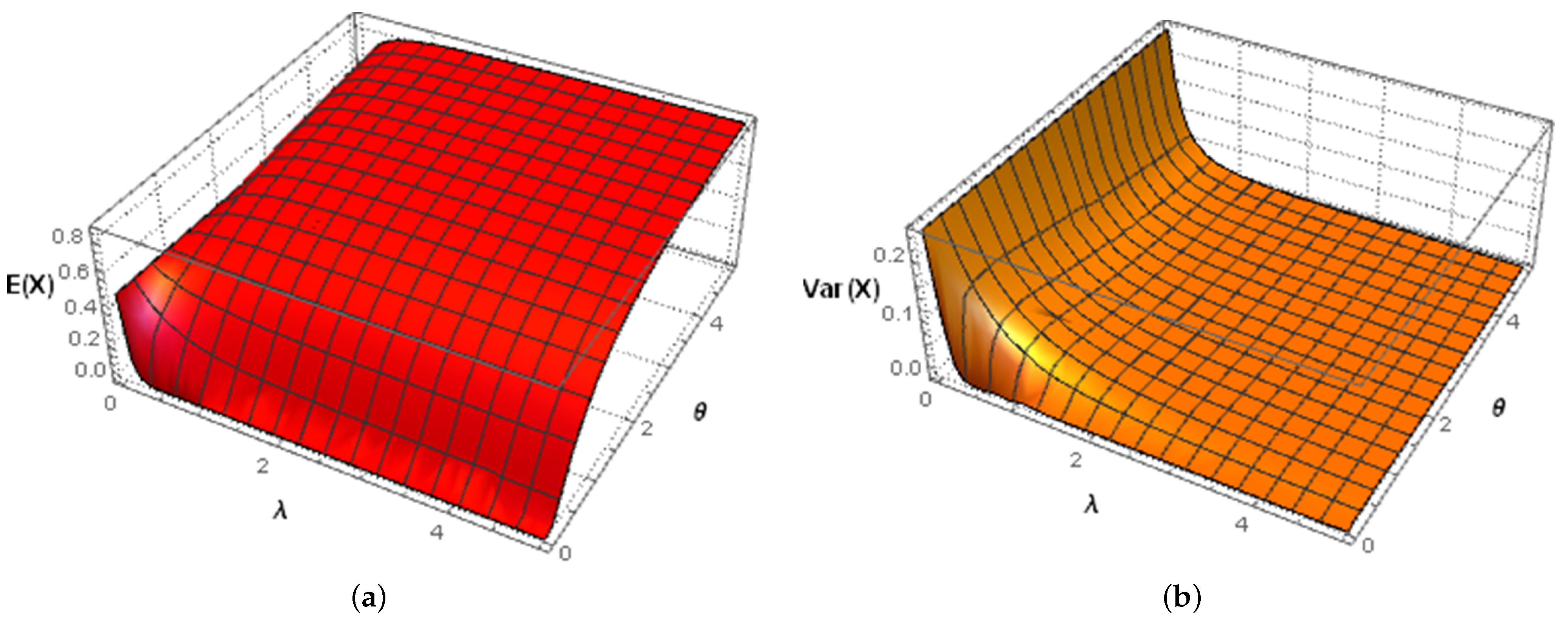
When $\theta \lambda \le 1$ and $\theta <1$, it is (both sides) tailed with a local maximum at $x_0=2^{-1/\theta }$.

(ii)

When $\theta \lambda \le 1$ and $\theta \ge 1$, it is (both sides) tailed without maxima, that is, bathtub-shaped.

(iii)

When $\theta \lambda >1$ and $\theta <1$, it is left-vanishing with a local maximum at $x_0=2^{-1/\theta }$.

(iv)

When $\theta \lambda >1$ and $\theta \ge 1$, it is increasing.

Proof. 

Similarly as in the proof of Theorem 1, let us denote

$$H_1(x;\lambda ,\theta ):={\displaystyle \frac{\theta \lambda x^{\theta \lambda -1}}{\left(1-x^{\theta }\right)\left(2{\left(1-x^{\theta }\right)}^{\lambda }-x^{\theta \lambda }\right)}},H_2(x;\lambda ,\theta ):={\displaystyle \frac{\theta \lambda }{x(1-x^{\theta })}},$$

according to which it follows that

$$\underset{x\to 0^{+}}{\lim }{H}_1(x;\lambda ,\theta )=\left\{\begin{array}{cc}0,\hfill & \theta \lambda >1\hfill \\ 1/2,\hfill & \theta \lambda =1\hfill \\ +\infty ,\hfill & \theta \lambda <1\hfill \end{array}\right.,\underset{x\to 1^{-}}{\lim }{H}_2(x;\lambda ,\theta )=+\infty ,$$

(12)

as well as

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial H_1(x;\lambda ,\theta )}{\partial x}}& ={\displaystyle \frac{\theta \lambda x^{\theta \lambda -2}\left(x^{\theta \lambda }\left(1-(\theta +1)x^{\theta }\right)+2(\theta +1)x^{\theta }{\left(1-x^{\theta }\right)}^{\lambda }+2(\theta \lambda -1){\left(1-x^{\theta }\right)}^{\lambda }\right)}{{\left(x^{\theta }-1\right)}^2{\left(x^{\theta \lambda }-2{\left(1-x^{\theta }\right)}^{\lambda }\right)}^2}},\hfill \\ \hfill {\displaystyle \frac{\partial H_2(x;\lambda ,\theta )}{\partial x}}& ={\displaystyle \frac{\theta \lambda \left((\theta +1)x^{\theta }-1\right)}{x^2{\left(x^{\theta }-1\right)}^2}}.\hfill \end{array}$$

(13)

Thus, Equations (12) and (13) give the statement of the theorem. □

Remark 3.

Plots of the CDF and HRF of the LLU distribution are given in Figure 3 below. It is known that the hazard (failure) rate represents the failure frequency of the designed system or component. Thus, the HRF usually increases, which means that the probability that the designed system or component will fail increases. In contrary, decreasing failure rate (DFR) describes the phenomenon where this probability decreases in some interval. As can be concluded from the previous theorem, both of these situations can be obtained from the LLU distribution, for certain values of its parameters. Moreover, in cases where the HRF has a local maximum at $x_0\in (0,1)$, the “peaked” value can then be interpreted as the critical point of the system. Therefore, these properties of the HRF give diverse possibilities of its practical application, which are discussed later.

In the last part of this section, the so-called quantile function (QF) of the LLU distribution is considered, obtained as the inverse function of its CDF:

$$Q(p;\lambda ,\theta ):=F^{-1}(p;\lambda ,\theta )=\left\{\begin{array}{cc}{\left(2p\right)}^{{\displaystyle \frac{1}{\theta \lambda }}}{\left({\left(2p\right)}^{1/\lambda }+1\right)}^{-{\displaystyle \frac{1}{\theta }}},\hfill & 0<p\le 1/2\hfill \\ {\left({\left(2(1-p)\right)}^{1/\lambda }+1\right)}^{-{\displaystyle \frac{1}{\theta }}},\hfill & 1/2<p<1\hfill \end{array}\right.,$$

(14)

where $p=F(x;\lambda ,\theta )$. The QF is a useful tool for obtaining some more properties of the LLU distribution, primarily related to its modality and (a)symmetry.

Theorem 4.

Let $X:\mathcal{L}(\lambda ,\theta )$ be the LLU-distributed RV, whose QF is given by Equation (14). Then, the following statements hold:

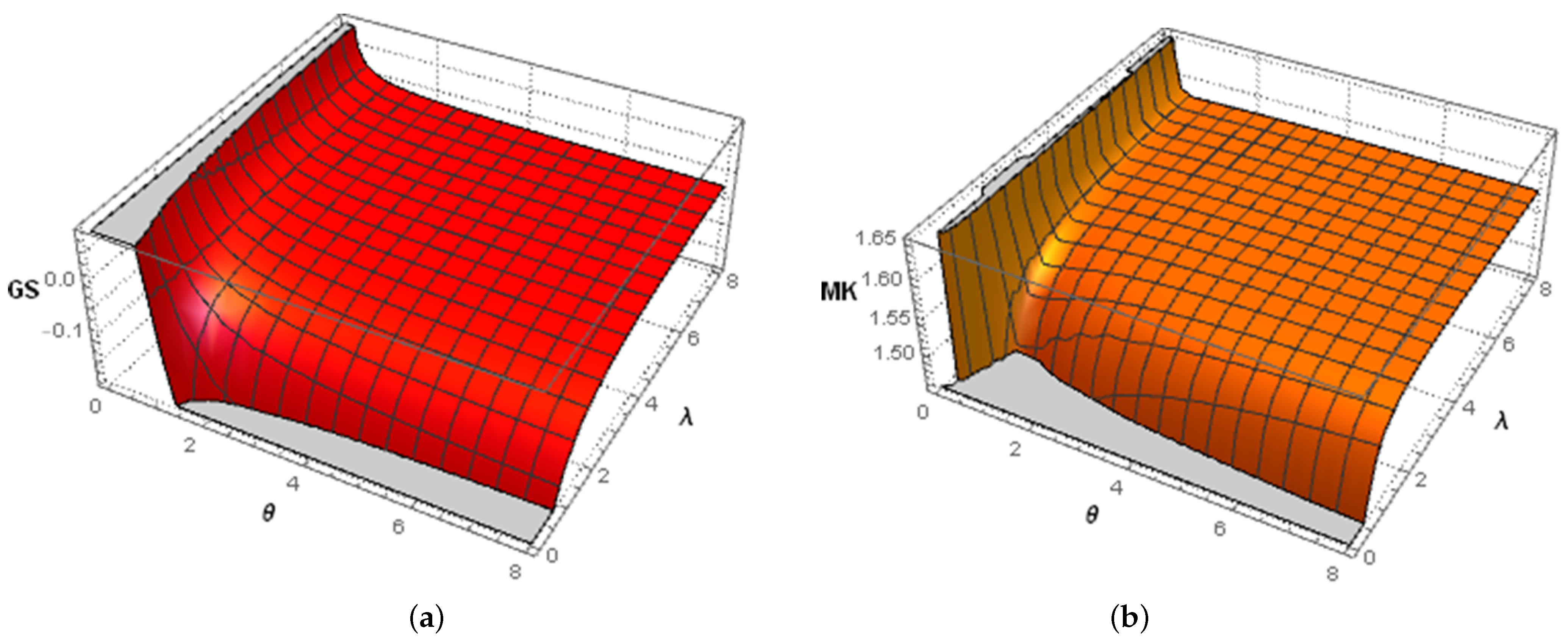
(i)

The RV X is symmetrically distributed if and only if $\theta =1$. Otherwise, X is positively asymmetric when $0<\theta <1$, and negatively asymmetric when $\theta >1$.

(ii)

The RV X is unimodal, with the mode $x_0=2^{-1/\theta }$, if and only if $\theta (1+2\lambda )\ge 1$ and $\theta (1-2\lambda )\le 1$.

Proof. 

$\left(i\right)$ By substituting the quantile $p=1/2$ into the QF $Q(p;\lambda ,\theta )$, the median $m=Q(1/2;\lambda ,\theta )=2^{-1/\theta }$ is obtained. Thus, the RV X is symmetrically distributed if and only if the median is equal to 1/2, that is, when $\theta =1$. The positive and negative asymmetry conditions are also easily obtained, by solving the inequalities $Q(1/2;\lambda ,\theta )<1/2$ and $Q(1/2;\lambda ,\theta )>1/2$, respectively.

$\left(ii\right)$ Using the rule for the derivative of the inverse function, for the derivatives up to the second order of the QF $Q(p;\lambda ,\theta )$ one obtains

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial Q(p;\lambda ,\theta )}{\partial p}}& ={\displaystyle \frac{1}{\partial F(x;\lambda ,\theta )/\partial x}}={\displaystyle \frac{1}{f(x;\lambda ,\theta )}},\hfill \\ \hfill {\displaystyle \frac{\partial Q^2(p;\lambda ,\theta )}{\partial p^2}}& =-{\displaystyle \frac{\partial f(x;\lambda ,\theta )/\partial x}{f^2(x;\lambda ,\theta )}}\hfill \end{array}.$$

(15)

where $p\ne 1/2$. Further, if we denote

$$Q_1(p;\lambda ,\theta ):={\left(2p\right)}^{{\displaystyle \frac{1}{\theta \lambda }}}{\left({\left(2p\right)}^{1/\lambda }+1\right)}^{-{\displaystyle \frac{1}{\theta }}},Q_2(p;\lambda ,\theta ):={\left({\left(2(1-p)\right)}^{1/\lambda }+1\right)}^{-{\displaystyle \frac{1}{\theta }}},$$

then, after some computation, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial Q_1^2(p;\lambda ,\theta )}{\partial p^2}}& =-{\displaystyle \frac{2^{\frac{1}{\theta \lambda }}{p}^{\frac{1}{\theta \lambda }-2}\left(\theta 2^{1/\lambda }(\lambda +1)p^{1/\lambda }+\theta \lambda -1\right)}{{\theta }^2{\lambda }^2{\left(2^{1/\lambda }{p}^{1/\lambda }+1\right)}^{2+\frac{1}{\theta }}}}\hfill \\ \hfill {\displaystyle \frac{\partial Q_2^2(p;\lambda ,\theta )}{\partial p^2}}& ={\displaystyle \frac{{(2-2p)}^{1/\lambda }\left((\theta \lambda +1){(2-2p)}^{1/\lambda }+\theta (\lambda -1)\right)}{{\theta }^2{\lambda }^2{(1-p)}^2{\left({(2-2p)}^{1/\lambda }+1\right)}^{2+\frac{1}{\theta }}}}.\hfill \end{array}$$

(16)

Obviously, the sign of derivatives in Equation (16) depends on the sign of the functions:

$$\begin{array}{cc}\hfill {\xi }_1(x;\lambda ,\theta )& =-\theta 2^{1/\lambda }(\lambda +1)p^{1/\lambda }-\theta \lambda +1,\hfill \\ \hfill {\xi }_2(x;\lambda ,\theta )& =(\theta \lambda +1){(2-2p)}^{1/\lambda }+\theta (\lambda -1),\hfill \end{array}$$

which are, respectively, monotonically decreasing and increasing on $p\in (0,1)$. Thus, according to the second part in Equations (15), the RV X has a local maximum at $x_0=2^{-1/\theta }$ if and only if the following inequalities hold:

$${\xi }_1(1/2;\lambda ,\theta )=1-\theta (1+2\lambda )\le 0,{\xi }_2(1/2;\lambda ,\theta )=1-\theta (1-2\lambda )\ge 0.$$

(17)

Therefore, Equation (17) obviously provides a statement of this part of the theorem. □

Remark 4.

Theorem 4, along with the previously proved Theorem 1, gives a complete insight into the variety of shapes of the LLU distribution (see again Figure 1a.) At the same time, note that its median and mode are equal, but that the true symmetry holds only for $\theta =1$. This can also be confirmed by the definition of the PDF of LLU distribution, given by Equation (2), based on which it follows that $f(x;\lambda ,1)=f(1-x;\lambda ,1)$ for each $x\in (0,1)$.

Remark 5.

In the symmetric case, when $\theta =1$, we can additionally analyze some Bayesian inferences of the LLU distribution. In this sense, suppose that the symmetric LLU distribution $\mathcal{L}(\lambda ,1)$ is the prior for some (binomial) parameter $p\in (0,1)$, i.e., $\pi \left(p\right)=f(p;\lambda ,1)$ and

$$h\left(x\right|p)=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{x}}\right)p^x{(1-p)}^{n-x},x=0,1,\dots ,n$$

(18)

is the sample (binomial) distribution. Then, the posterior distribution of the observed data point x is

$$h\left(p\right|x)={\displaystyle \frac{h\left(x\right|p\left)\pi \right(p)}{h\left(x\right)}},$$

where $h\left(x\right)={\int }_0^{1}h\left(x\right|p)\pi \left(p\right)\mathrm{d}p$ is a marginal distribution. Using some common notation (see, e.g., Rundel [13]), we can write

$$h\left(p\right|x)\propto h\left(x\right|p)\pi (p),$$

which is subjected to some normalization on the unit interval. Then, according to Equations (2) and (18), one obtains

$$h\left(p\right|x)\propto h\left(x\right|p)f(p;\lambda ,1)\propto \left\{\begin{array}{cc}{p}^{x+\lambda -1}{\left(1-p\right)}^{n-x-\lambda -1},\hfill & 0<p\le 1/2\hfill \\ {\left(1-p\right)}^{n-x+\lambda -1}{p}^{x-\lambda -1},\hfill & 1/2<p<1\hfill \end{array}\right..$$

Thus, the posterior distribution is determined as follows:

$$h\left(p\right|x)=\left\{\begin{array}{cc}{c}^{-1}{p}^{x+\lambda -1}{\left(1-p\right)}^{n-x-\lambda -1},\hfill & 0<p\le 1/2\hfill \\ c^{-1}{q}^{n-x+\lambda -1}{(1-q)}^{x-\lambda -1},\hfill & 0<q<1/2\hfill \end{array}\right.,$$

where $q=1-p$ and $c:=B_{1/2}(x+\lambda ,n-x-\lambda )+B_{1/2}(n-x+\lambda ,x-\lambda )$ is the normalizing constant. Note that the resulting posterior distribution has a similar (but not the same) form as the LLU distribution, and that similar Bayesian inferences can be made for some other stochastic distributions.

Remark 6.

Using the QF $Q(p;\lambda ,\theta )$, given by Equation (14), some more measures of shape of the CLU distribution can be studied. These are, for instance, Galton’s skewness (GS), which measures the degree of the long tail; and Moors kurtosis (MK), which measures the degree of weight of the tail of the distribution (see, e.g., [2]). In the case of the LLU distribution, these two measures, after some calculation, can be expressed as

$$\begin{array}{cc}\hfill GS(\lambda ,\theta )& ={\displaystyle \frac{Q\left(3/4;\lambda ,\theta \right)-2Q\left(1/2;\lambda ,\theta \right)+Q\left(1/4;\lambda ,\theta \right)}{Q\left(3/4;\lambda ,\theta \right)-Q\left(1/4;\lambda ,\theta \right)}}\hfill \\ \hfill & ={\displaystyle \frac{2^{-1/\theta }\left(-2^{\frac{1}{\theta \lambda }+1}{\left(2^{-1/\lambda }+1\right)}^{1/\theta }+2^{\frac{\lambda +1}{\theta \lambda }}+2^{1/\theta }\right)}{2^{\frac{1}{\theta \lambda }}-1}},\hfill \\ \hfill MK(\lambda ,\theta )& ={\displaystyle \frac{Q\left(7/8;\lambda ,\theta \right)-Q\left(5/8;\lambda ,\theta \right)+Q\left(3/8;\lambda ,\theta \right)-Q\left(1/8;\lambda ,\theta \right)}{Q\left(3/4;\lambda ,\theta \right)-Q\left(1/4;\lambda ,\theta \right)}}\hfill \\ \hfill & =2^{-\frac{1}{\theta \lambda }}{\left(2^{-1/\lambda }+1\right)}^{1/\theta }\left(\left(2^{\frac{1}{\theta \lambda }}+1\right){\left(4^{-1/\lambda }+1\right)}^{-1/\theta }+\frac{\left(3^{\frac{1}{\theta \lambda }}-4^{\frac{1}{\theta \lambda }}\right){\left({\left(\frac{3}{4}\right)}^{1/\lambda }+1\right)}^{-1/\theta }}{2^{\frac{1}{\theta \lambda }}-1}\right),\hfill \end{array}$$

and 3D plots of their dependence in relation to $(\lambda ,\theta )$ are given in Figure 4.

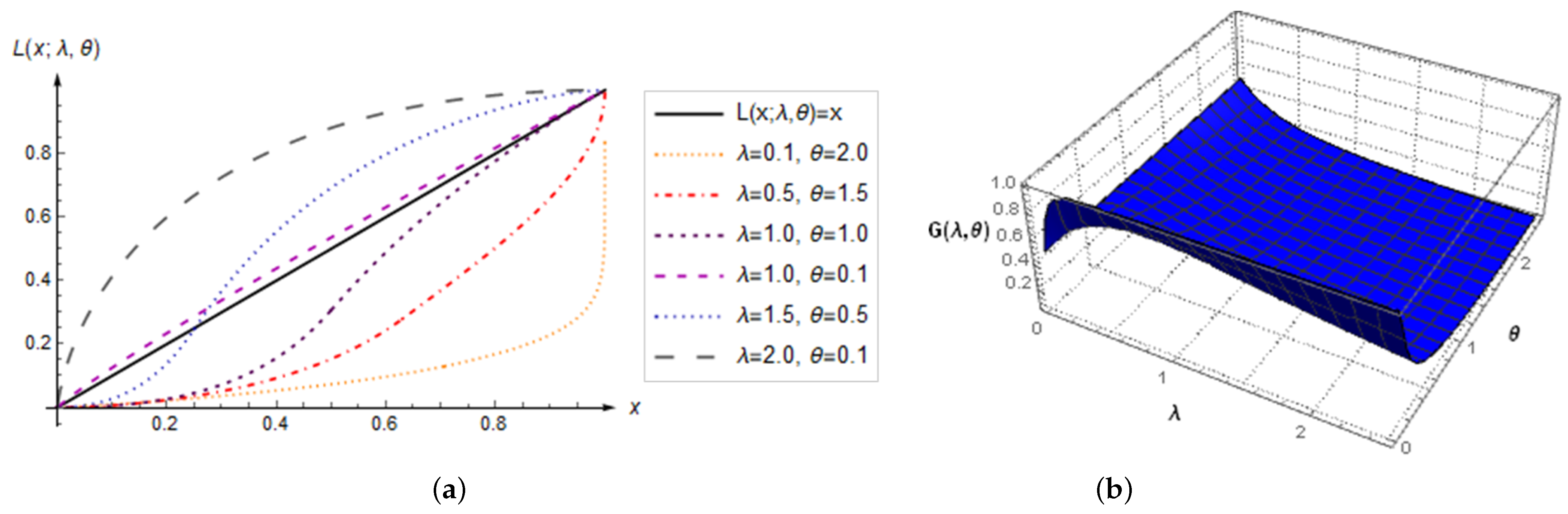
2.3. Income Distribution and Entropy

In economics, income distribution describes how a country’s total GDP is distributed among the population. Unequal distribution of income causes economic inequality and it is of interest to find a way to determine it quantitatively. One of the useful tools for stochastic measurement of inequality in income distribution is based on incomplete moments. For an RV X with the LLU distribution, the r-th incomplete moment is defined by

$$M_r(x;\lambda ,\theta ):={\int }_0^x{u}^{r}f(u;\lambda ,\theta )\mathrm{d}u,$$

where $r\in \mathbb{N}$ and $x\in (0,1)$. Explicit expressions for the r-th incomplete moments can be specified by the following statement.

Theorem 5.

The r-th incomplete moment of the LLU-distributed RV X can be expressed as

$$M_r(x;\lambda ,\theta )=\left\{\begin{array}{cc}{\displaystyle \frac{\lambda }{2}{B}_{x^{\theta }}\left(\frac{r}{\theta }+\lambda ,-\lambda \right),}\hfill & x\le 2^{-1/\theta }\hfill \\ \\ {\displaystyle \frac{\lambda }{2}}\left(B_{1/2}\left({\displaystyle \frac{r}{\theta }}+\lambda ,-\lambda \right)+B_{1/2}^{x^{\theta }}\left({\displaystyle \frac{r}{\theta }}-\lambda ,\lambda \right)\right),\hfill & x>2^{-1/\theta }\hfill \end{array}\right.,$$

(19)

where r is the integer, $B_z(a,b)={\int }_0^z{t}^{a-1}{(1-t)}^{b-1}\mathrm{d}t$ is the incomplete beta function, and $B_{z_1}^{z_2}(a,b)={\int }_{z_1}^{z_2}{t}^{a-1}{(1-t)}^{b-1}\mathrm{d}t$ is the generalized incomplete beta function.

Proof. 

Using a similar procedure and notation as in the proofs of Theorems 1 and 2, we consider the following two cases:

$\left(i\right)$ When $x\le 2^{-1/\theta }$, the r-th incomplete moment is given as follows:

$$\begin{array}{cc}\hfill M_r(x;\lambda ,\theta )& ={\int }_0^x{u}^r{f}_1(u;\lambda ,\theta )\mathrm{d}x={\displaystyle \frac{\lambda \theta }{2}}{\int }_0^x{\displaystyle \frac{u^{r+\lambda \theta -1}\mathrm{d}u}{{(1-u^{\theta })}^{\lambda +1}}}\hfill \\ \hfill & ={\displaystyle \frac{\lambda }{2}}{\int }_0^{x^{\theta }}{t}^{r/\theta +\lambda -1}{(1-t)}^{-\lambda -1}\mathrm{d}t\hfill \\ \hfill & {\displaystyle =\frac{\lambda }{2}{B}_{x^{\theta }}\left(\frac{r}{\theta }+\lambda ,-\lambda \right).}\hfill \end{array}$$

(20)

$\left(ii\right)$ When $x>2^{-1/\theta }$, by using previous Equation (20), for the r-th incomplete moment one obtains

$$\begin{array}{cc}\hfill M_r(x;\lambda ,\theta )& ={\int }_0^{2^{-1/\theta }}{u}^r{f}_1(u;\lambda ,\theta )\mathrm{d}u+{\int }_{2^{-1/\theta }}^x{u}^r{f}_2(u;\lambda ,\theta )\mathrm{d}u\hfill \\ \hfill & ={\displaystyle \frac{\lambda }{2}}{\int }_0^{1/2}{t}^{r/\theta +\lambda -1}{(1-t)}^{-\lambda -1}\mathrm{d}t+{\displaystyle \frac{\lambda }{2}}{\int }_{1/2}^{x^{\theta }}{t}^{r/\theta -\lambda -1}{(1-t)}^{\lambda -1}\mathrm{d}t\hfill \\ \hfill & ={\displaystyle \frac{\lambda }{2}}\left(B_{1/2}\left({\displaystyle \frac{r}{\theta }}+\lambda ,-\lambda \right)+B_{1/2}^{x^{\theta }}\left(\lambda ,{\displaystyle \frac{r}{\theta }}-\lambda \right)\right),\hfill \end{array}$$

(21)

where $t=u^{\theta }$. Thus, Equations (20) and (21) obviously imply Equation (19). □

As already mentioned, incomplete moments are very useful in studying measures of income inequality. For this purpose, the so-called Lorenz curve is most often used:

$$L(x;\lambda ,\theta ):={\displaystyle \frac{M_1(x;\lambda ,\theta )}{{\mu }_1(x;\lambda ,\theta )}}={\displaystyle \frac{1}{\mu }}{\int }_0^{x}uf(u;\lambda ,\theta )\mathrm{d}u,$$

(22)

where $\mu ={\mu }_1(x;\lambda ,\theta )=\mathrm{E}\left(X\right)$ and $M_1(x;\lambda ,\theta )$ is an incomplete first moment given as in Equation (19), when $r=1$. Figure 5a shows the Lorenz curve for some parameter values, where greater distance from the diagonal line indicates a greater level of inequality in income distribution. On the other hand, the Lorenz curve “approaching” to the diagonal indicates a uniform distribution of income. As can be seen, the LLU distribution in this sense (again) shows great flexibility in describing the behavior of these phenomena.

As a quantitative measure of income inequality closely related to the previous one, the so-called Gini index is widely used. The Gini index is basically defined using the Lorenz curve, showing the percentage of its deviation from the diagonal. Thus, a value of Gini index equal to 0 reflects perfect income equality, while a Gini index equal to 1 reflects maximum wealth inequality. As the income distribution can be represented by a continuous probability density function, the Gini coefficient can be calculated directly from the appropriate CDF by applying the equality (see, e.g., Giles [14]):

$$G(\lambda ,\theta ):={\displaystyle \frac{1}{\mu }}{\int }_0^{1}F(x;\lambda ,\theta )\left(1-F(x;\lambda ,\theta )\right)\mathrm{d}x.$$

In the case of the LLU distribution, by using Equation (10) and after some computation similar to in the proof of Theorem 5, one obtains

$$\begin{array}{cc}\hfill G(\lambda ,\theta )& =\frac{1}{\mu }\left[{\int }_0^{2^{-1/\theta }}\frac{x^{\theta \lambda }}{2{\left(1-x^{\theta }\right)}^{\lambda }}\left(1-\frac{x^{\theta \lambda }}{2{\left(1-x^{\theta }\right)}^{\lambda }}\right)\mathrm{d}x+{\int }_{2^{-1/\theta }}^1\frac{{\left(1-x^{\theta }\right)}^{\lambda }}{2x^{\theta \lambda }}\left(1-\frac{{\left(1-x^{\theta }\right)}^{\lambda }}{2x^{\theta \lambda }}\right)\mathrm{d}x\right]\hfill \\ & =\frac{1}{2\theta \mu }\left({\int }_0^{1/2}{t}^{\lambda +\frac{1}{\theta }-1}{(1-t)}^{-\lambda }\mathrm{d}t+{\int }_0^{1/2}{z}^{\lambda }{(1-z)}^{-\lambda +\frac{1}{\theta }-1}\mathrm{d}z\right)\hfill \\ & -\frac{1}{4\theta \mu }\left({\int }_0^{1/2}{t}^{2\lambda +\frac{1}{\theta }-1}{(1-t)}^{-2\lambda }\mathrm{d}t+{\int }_0^{1/2}{z}^{2\lambda }{(1-z)}^{-2\lambda +\frac{1}{\theta }-1}\mathrm{d}z\right)\hfill \\ & =\frac{1}{2\theta \mu }\left(B_{\frac{1}{2}}\left(\lambda +\frac{1}{\theta },1-\lambda \right)+B_{\frac{1}{2}}\left(\lambda +1,\frac{1}{\theta }-\lambda \right)\right)\hfill \\ & -\frac{1}{4\theta \mu }\left(B_{\frac{1}{2}}\left(2\lambda +\frac{1}{\theta },1-2\lambda \right)+B_{\frac{1}{2}}\left(2\lambda +1,\frac{1}{\theta }-2\lambda \right)\right),\hfill \end{array}$$

where $t=x^{\theta }$ and $z=-t$. A 3D plot of the dependence of the Gini index in relation to parameters $\lambda ,\theta >0$ is given in Figure 5b.

Further, the entropy of the LLU distribution is briefly described. As is well known, the entropy is defined as a measure of the uncertainty’s variation, where greater uncertainty is indicated by a high entropy value, and vice versa. One of the frequently used measures of entropy, which generalizes various other forms of entropy, and is also related to the Gini index mentioned above (see, e.g., Jurdana [15]), is the so-called Rényi entropy. For the RV X with LLU distribution, the Rényi entropy reads as follows:

$$H_{\alpha }\left(X\right):={\displaystyle \frac{1}{1-\alpha }}ln\left({\int }_0^1{f}^{\alpha }(x;\lambda ,\theta )\mathrm{d}x\right),$$

where $\alpha \in (0,+\infty )\backslash \left\{1\right\}$. According to the PDF of the RV X, given by Equation (2), as well as after some calculations similar to the previous one, we obtain

$$\begin{array}{cc}\hfill H_{\alpha }\left(X\right)& :={\displaystyle \frac{1}{1-\alpha }}\left[\alpha ln\left({\displaystyle \frac{\lambda }{2}}\right)+(\alpha -1)ln\theta +ln\left(B_{1/2}\left(\alpha \lambda +{\displaystyle \frac{1-\alpha }{\theta }},-\alpha \lambda +1-\alpha \right)+B_{1/2}\left(\alpha \lambda +1-\alpha ,-\alpha \lambda +{\displaystyle \frac{1-\alpha }{\theta }}\right)\right)\right].\hfill \end{array}$$

From here, in the limiting case when $\lambda \to 1$ and by applying L’Hôpital’s rule in the last equality, the well-known Shannon entropy is obtained as follows:

$$\begin{array}{cc}\hfill H\left(X\right)& :=\mathrm{E}\left(-lnf\left(X\right)\right)=\underset{\alpha \to 1}{lim}{H}_{\alpha }\left(X\right)=-ln\left({\displaystyle \frac{\lambda \theta }{2}}\right)-{\displaystyle \frac{\lambda }{2}}\underset{\alpha \to 1}{lim}\left[{\displaystyle \frac{\partial B_{1/2}}{\partial \alpha }}\left(\alpha \lambda +{\displaystyle \frac{1-\alpha }{\theta }},-\alpha \lambda +1-\alpha \right)\right.\hfill \\ & \left.+{\displaystyle \frac{\partial B_{1/2}}{\partial \alpha }}\left(\alpha \lambda +1-\alpha ,-\alpha \lambda +{\displaystyle \frac{1-\alpha }{\theta }}\right)\right].\hfill \end{array}$$

Thereby, note that the partial derivatives in the last expression exist (see, e.g., Özçag et al. [16]), but are omitted here due to their complexity.

3. Parameter Estimation and Simulation Study

In this section, the procedure for estimating the unknown parameters $\lambda ,\theta >0$ of the LLU-distributed RV X is presented. In this, note that according to the previously described properties of the LLU distribution, using some common procedures to estimate its parameters brings some difficulties. Thus, for instance, due to the fact that the moments of the LLU distribution, given by Equation (6), are expressed using the beta function, the method of moments requires certain complex calculations. On the other hand, since the PDF of the LLU distribution is not differentiable at $x_0=2^{-1/\theta }$, the usage of the maximum likelihood (ML) estimation method is very specific. Considering that the ML estimator of the scale parameter $\lambda$ in the case of the Laplace distribution is equal to the sample median (see for more detail Norton [17]), here we consider methods of parameter estimation based on the quantiles of the LLU distribution.

For that cause, let $X_1,X_2,\dots ,X_n$ be the random sample of length n, for which we define the corresponding order statistics $X_{\left(1\right)}\le X_{\left(2\right)}\le \dots X_{\left(n\right)}$. As is well known, the PDF of i-th order statistics $X_{\left(i\right)}$ is given as follows:

$$f_{X_{\left(i\right)}}(x;\lambda ,\theta )={\displaystyle \frac{n!}{(i-1)!(n-i)!}}f(x;\lambda ,\theta ){\left[F(x;\lambda ,\theta )\right]}^{i-1}{\left[F(x;\lambda ,\theta )\right]}^{n-i},$$

(23)

where $i=1,\dots ,n$. By substituting $p=j/4$, $j=1,2,3$ into the QF $Q_p:=Q(p;\lambda ,\theta )$, given by Equation (14), for the quartiles of the RV X one obtains

$$Q(1/4;\lambda ,\theta )=2^{-{\displaystyle \frac{1}{\theta \lambda }}}{\left(2^{-1/\lambda }+1\right)}^{-1/\theta },Q(3/4;\lambda ,\theta )={\left(2^{-1/\lambda }+1\right)}^{-1/\theta },$$

(24)

while the second quartile is the median $m=Q(1/2;\lambda ,\theta )=2^{-1/\theta }$. On the other hand, the sample quantiles are given by the equality

$${\widehat{Q}}_p:=X_{\left(i_p\right)},i_p=\left\{\begin{array}{cc}np,\hfill & np\mathrm{is}\mathrm{integer},\hfill \\ 1+\left[np\right],\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(25)

where $\left[np\right]$ is the integer part of $np$. In this way, the sample quantiles are in fact the order statistics, and their distribution can be obtained according to Equation (23).

Furthermore, the sample quartiles ${\widehat{Q}}_{j/4}$, $j=1,2,3$ can be used as the estimators of theoretical ones. Thus, by equating the median $m=2^{-1/\theta }$ of the RV X with the sample one $\widehat{m}={\widehat{Q}}_{1/2}$, the estimator of the shape parameter $\widehat{\theta }=-ln2/\ln \widehat{m}$ is easily obtained. In addition, according to Equation (24), it follows that

$${\left({\displaystyle \frac{Q\left(3/4,\lambda ,\theta \right)}{Q\left(1/4,\lambda ,\theta \right)}}\right)}^{\theta }=2^{1/\lambda },$$

and using the estimator $\widehat{\theta }$ for the estimator of the scale parameter $\lambda$, one obtains

$$\widehat{\lambda }={\displaystyle \frac{ln2}{\widehat{\theta }\left(ln{\widehat{Q}}_{3/4}-ln{\widehat{Q}}_{1/4}\right)}}.$$

(26)

In the following, we examine the asymptotic properties of the proposed estimators:

Theorem 6.

The statistics $(\widehat{\lambda },\widehat{\theta })$ are consistent and asymptotically normal (AN) estimators of the true parameters $(\lambda ,\theta )$, respectively.

Proof. 

First, by using some general asymptotic sample quantile theory [18], we prove the consistency of the proposed estimators. For that cause, let us notice that the CDF $p=F(x;\lambda ,\theta )$ is differentiable and increasing on $p\in (0,1)$. Thus, the quantiles $Q_p:=Q(p;\lambda ,\theta )$ are uniquely determined by Equation (14), and sample quantiles ${\widehat{Q}}_p$ are uniquely determined by Equation (25). Using Bahadur’s representation of sample quantiles (see, e.g., Theorem 1 in Dudek & Kuczmaszewska [18], or Serfling [19], pp. 91–92), one obtains

$${\widehat{Q}}_p=Q_p+{\displaystyle \frac{p-F_n\left(Q_p\right)}{f(Q_p;\lambda ,\theta )}}+\mathcal{O}\left[{\left({\displaystyle \frac{lnn}{n}}\right)}^{3/4}\right],$$

(27)

where $F_n\left(x\right):=n^{-1}{\sum }_{i=1}^{n}1(X_i<n)$ is the empirical CDF. As is known, for each $x\in \mathbb{R}$, the empirical CDF $F_n\left(x\right)$ almost surely and uniformly converges to the CDF $p=F(x;\lambda ,\theta )$ when $n\to \infty$. So, by applying this convergence on Equation (27), when $x=Q_p$, it follows that

$${\widehat{Q}}_p\stackrel{as}{⟶}{Q}_p,n\to \infty ,$$

i.e., the sample quantiles are consistent estimators of the theoretical ones. Finally, as estimators $(\widehat{\lambda },\widehat{\theta })$ are continuous functions of sample quartiles ${\widehat{Q}}_{j/4}$, $j=1,2,3$, by using the property of continuity of almost sure convergence (see, e.g., Serfling [19], p. 24), it is obtained that

$$(\widehat{\lambda },\widehat{\theta })\stackrel{as}{⟶}(\lambda ,\theta ),n\to \infty .$$

For the proof of the AN property, notice that under the same assumptions as above, Equation (27) gives the following convergence in distribution:

$$\sqrt{n}\left({\widehat{Q}}_p-Q_p\right)\stackrel{d}{⟶}\mathcal{N}\left(0,{\displaystyle \frac{p(1-p)}{{\left[f(Q_p,\lambda ,\theta )\right]}^2}}\right),n\to \infty .$$

(28)

According to Equation (28), for the sample median $\widehat{m}={\widehat{Q}}_{1/2}$ one obtains

$$\sqrt{n}\left(\widehat{m}-m\right)\stackrel{d}{⟶}\mathcal{N}\left(0,{\sigma }_m^2\right),n\to \infty ,$$

wherein

$${\sigma }_m^2={\displaystyle \frac{1}{4{\left[f(m;\lambda ,\theta )\right]}^2}}{|}_{m=2^{-1/\theta }}={\displaystyle \frac{4^{-\frac{1}{\theta }-1}}{{\lambda }^2{\theta }^2}}.$$

Now, using the continuity of convergence in distribution (see, e.g., Serfling [19], p. 118), for the estimator $\widehat{\theta }=-ln2/\ln \widehat{m}$ we obtain

$$\sqrt{n}\left(\widehat{\theta }-\theta \right)\stackrel{d}{\to }\mathcal{N}\left(0,{\sigma }_{\theta }^2\right),n\to \infty ,$$

(29)

wherein

$${\sigma }_{\theta }^2:=\mathrm{Var}\left(\widehat{\theta }\right)={\left[-{\displaystyle \frac{\partial }{\partial m}}\left({\displaystyle \frac{ln2}{lnm}}\right)\right]}^2{|}_{m=2^{-1/\theta }}·{\sigma }_m^2={\displaystyle \frac{{\theta }^2}{4{\lambda }^2{ln}^{2}2}}.$$

The AN property of the estimator $\widehat{\lambda }$, given by Equation (26), is similarly proven. For this purpose, let us first define a statistic,

$$\widehat{\eta }:=\widehat{\theta }\left(ln{\widehat{Q}}_{3/4}-ln{\widehat{Q}}_{1/4}\right),$$

which is a consistent estimator of $\eta :=\theta ln\left(Q_{3/4}/Q_{1/4}\right)$. Using Equation (28), as well as the continuity of convergence in distribution, it follows that

$$\sqrt{n}\left(\widehat{\eta }-\eta \right)\stackrel{d}{⟶}\mathcal{N}\left(0,{\sigma }_{\eta }^2\right),n\to \infty ,$$

where, after some computations, one obtains

$$\begin{array}{cc}\hfill {\sigma }_{\eta }^2& :=\mathrm{Var}\left(\widehat{\eta }\right)={\theta }^2\left({\displaystyle \frac{\mathrm{Var}\left({\widehat{Q}}_{1/4}\right)}{Q_{1/4}^2}}+{\displaystyle \frac{\mathrm{Var}\left({\widehat{Q}}_{3/4}\right)}{Q_{3/4}^2}}\right)={\displaystyle \frac{3{\theta }^2}{16}}\left({\displaystyle \frac{1}{Q_{1/4}^2{f}^2\left(Q_{1/4},\lambda ,\theta \right)}}+{\displaystyle \frac{1}{Q_{3/4}^2{f}^2\left(Q_{3/4},\lambda ,\theta \right)}}\right)\hfill \\ \hfill & ={\displaystyle \frac{3{\theta }^2}{16}}\left({\displaystyle \frac{2^{\frac{2}{\lambda }+4}}{{\theta }^2{\lambda }^2{\left(2^{1/\lambda }+1\right)}^2}}+{\displaystyle \frac{16}{{\theta }^2{\lambda }^2{\left(2^{1/\lambda }+1\right)}^2}}\right)={\displaystyle \frac{3\left(4^{1/\lambda }+1\right)}{{\lambda }^2{\left(2^{1/\lambda }+1\right)}^2}}.\hfill \end{array}$$

(30)

Finally, according to $\widehat{\lambda }=ln2/\widehat{\eta }$ and Equation (30), we obtain

$$\sqrt{n}\left(\widehat{\lambda }-\lambda \right)\stackrel{d}{⟶}\mathcal{N}\left(0,{\sigma }_{\lambda }^2\right),n\to \infty ,$$

(31)

wherein

$${\sigma }_{\lambda }^2:=\mathrm{Var}\left(\widehat{\lambda }\right)={\left[{\displaystyle \frac{\partial }{\partial \eta }}\left({\displaystyle \frac{ln2}{\eta }}\right)\right]}^2·{\sigma }_{\eta }^2={\displaystyle \frac{3{\lambda }^2\left(4^{1/\lambda }+1\right)}{{ln}^{2}2{\left(2^{1/\lambda }+1\right)}^2}}.$$

(32)

Thus, the proven convergences in Equations (29) and (31) confirm the AN properties of both proposed estimators $(\widehat{\theta },\widehat{\lambda })$. □

Remark 7.

It is worth noting that the variance of the estimator $\widehat{\lambda }$, given by Equation (32), does not depend on the parameter θ. This, among others, is one of the reasons that justifies the use of this estimator.

Figure 6. Left plots: Realizations of the different samples taken from the LLU distribution. Right plots: Empirical and fitted PDFs of the RV $X:\mathcal{L}(\lambda ,\theta )$.

Figure 6. Left plots: Realizations of the different samples taken from the LLU distribution. Right plots: Empirical and fitted PDFs of the RV $X:\mathcal{L}(\lambda ,\theta )$.

A numerical study of the effectiveness of the proposed estimators is presented below, based on Monte Carlo simulations of samples $x_1,\dots ,x_n$ taken from the LLU distribution. More precisely, for different samples and parameter values the proposed estimators were calculated and a statistical analysis was performed. To this end, three different types of samples are considered (see also Figure 6 above):

(i) Sample I was drawn from an increasing LLU distribution with parameters $\lambda =0.3$ and $\theta =3.5$.

(ii) Sample II was drawn from a symmetric, both-sides-tailed (i.e., bathtub-shaped) LLU distribution with parameters $\lambda =0.3$ and $\theta =1$.

(iii) Sample III was drawn from a symmetric, both-sides-vanishing, unimodal LLU distribution with parameters $\lambda =2$ and $\theta =1$.

The simulated values of all samples were generated by the R-package “distr” [20], according to which the estimates $\widehat{\theta }$ and $\widehat{\lambda }$ were easily obtained. In order to additionally check the effectiveness of the proposed estimators, the sample realizations of different lengths $n\in \{150,500,1500\}$ were observed. It is worth noting that the above sample sizes were chosen to be similar to some of the real-world data which will be further analyzed. Additionally, $S=200$ independent simulations were performed for each sample, and the results of a statistical analysis of them are presented in

Table 1. Summary statistics, estimation errors, and AN testing of parameter estimates of the LLU distribution: Sample I with the parameter values $\theta =3.5$ and $\lambda =0.3$.

Statistics	$\mathit{n}=150$		$\mathit{n}=500$		$\mathit{n}=1500$
	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$
Min.	1.770	0.1773	2.247	0.2190	2.676	0.2400
Mean	3.210	0.2850	3.378	0.2883	3.459	0.2928
Max.	5.907	0.4094	4.099	0.3660	3.650	0.3195
SD	0.0636	0.0448	0.0332	0.0260	0.0180	0.0150
MSEE	0.0790	0.0471	0.0722	0.0335	0.0712	0.0269
FEE (%)	8.286	15.715	3.486	11.029	1.171	8.959
$AD$	0.8939 ∗	1.6913 ∗∗	0.3090	0.6818	0.3796	0.1678
(p-value)	(0.0221)	(2.38 $\times {10}^{-4}$)	(0.5553)	(0.0739)	(0.4013)	(0.9359)
W	0.9823 ∗	0.9806 ∗∗	0.9919	0.9864	0.9952	0.9878
(p-value)	(0.0126)	(7.31 $\times {10}^{-3}$)	(0.3300)	(0.0523)	(0.7768)	(0.0851)

^∗ $0.01<p<0.05$, ^∗∗$p<0.01$.

,

Table 2. Summary statistics, estimation errors, and AN testing of parameters estimates of the LLU distribution: Sample II with the parameter values $\theta =1$ and $\lambda =0.3$.

Statistics	$\mathit{n}=150$		$\mathit{n}=500$		$\mathit{n}=1500$
	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$
Min.	0.5990	0.2161	0.7375	0.2369	0.8494	0.2602
Mean	1.0254	0.3054	1.0170	0.2987	1.0018	0.2968
Max.	1.8447	0.5394	1.4075	0.3824	1.2316	0.3477
SD	0.1907	0.0508	0.1224	0.0252	0.0698	0.0156
MSEE	0.0254	0.1169	0.0170	0.1019	0.0020	0.0981
FEE (%)	2.1346	34.453	0.5739	24.476	0.2030	21.908
$AD$	1.1064 ∗∗	1.481 ∗∗	0.6684	0.8172 ∗	0.5166	0.6030
(p-value)	(6.58 $\times {10}^{-3}$)	(7.83 $\times {10}^{-4}$)	(0.0798)	(0.0341)	(0.1879)	(0.1159)
W	0.9814 ∗∗	0.9797 ∗∗	0.9912	0.9844 ∗	0.9914	0.9931
(p-value)	(9.36 $\times {10}^{-3}$)	(5.38 $\times {10}^{-3}$)	(0.2641)	(0.0264)	(0.2808)	(0.4755)

^∗$0.01<p<0.05$, ^∗∗$p<0.01$.

and

Table 3. Summary statistics, estimation errors, and AN testing of parameters estimates of the LLU distribution: Sample III with the parameter values $\theta =1$ and $\lambda =2$.

Statistics	$\mathit{n}=150$		$\mathit{n}=500$		$\mathit{n}=1500$
	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\theta }}$	$\widehat{\mathit{\lambda }}$
Min.	0.9036	1.4760	0.9529	1.657	0.9698	1.860
Mean	1.0048	2.0360	1.0009	2.024	1.0003	2.016
Max.	2.6290	1.1179	1.0606	2.483	1.0262	2.243
SD	0.0305	0.2603	0.0166	0.1451	9.20 $\times {10}^{-3}$	0.0767
MSEE	4.78 $\times {10}^{-3}$	0.2621	8.88 $\times {10}^{-4}$	0.1466	2.71 $\times {10}^{-4}$	0.0782
FEE (%)	0.4783	13.106	0.0888	7.3314	0.0271	3.9117
$AD$	0.4960	0.8509 ∗	0.4029	0.2194	0.2951	0.3024
(p-value)	(0.2113)	(0.0282)	(0.3539)	(0.8346)	(0.5930)	(0.5726)
W	0.9885	0.9861 ∗	0.9942	0.9912	0.9945	0.9926
(p-value)	(0.1084)	(0.0471)	(0.6338)	(0.2678)	(0.6722)	(0.4160)

^∗$0.01<p<0.05$.

.

More precisely, Table 1, Table 2 and Table 3 contain the summary statistics of the obtained estimates, that is, their minimum (min.), mean (mean), and maximum (max.) values, and standard deviation (SD). Additionally, mean square estimation error (MSEE), fractional estimation error (FEE), and the results of the Anderson–Darling and Shapiro–Wilk normality tests are also provided. According to these, it can be observed that bias and sample range (max.–min.), as well as SD, MSEE, and FEE values decrease with increasing sample size; that is, the proposed estimators are efficient. Thereby, it can be easily noticed that estimates $\widehat{\theta }$ are more stable and efficient than $\widehat{\lambda }$. This is obviously a consequence of the fact that the estimate $\widehat{\lambda }$ is obtained by using a two-step procedure, that is, using the previously obtained estimate $\widehat{\theta }$, and then, applying Equation (26).

Similar conclusions can be confirmed based on the AN analysis of the obtained estimates. As previously stated, the examination was performed using the Anderson–Darling and Shapiro–Wilk normality tests, whose test statistics, denoted AD and W, respectively, as well as the corresponding p-values, are also shown in Table 1, Table 2 and Table 3. According to them, it can be observed that the estimates of $\widehat{\lambda }$ have a less pronounced AN feature than for $\widehat{\theta }$, especially for smaller samples. Nevertheless, the AN property is clearly confirmed in most simulation cases, especially for larger samples. Some confirmation of these facts can also be seen in Figure 6, where realizations of empirical and theoretical distributions of the observed samples are shown.

4. Applications of the LLU Distribution

This section discusses some possibilities of applying the LLU distribution in real-world data modeling, primarily in the domain of dynamic and regression analysis. Also, a comparison of the LLU distribution with some existing, well-known and frequently used unit distributions is made. For this purpose, three sets of data are considered, and a brief description of them is as follows:

(i) The first dataset, called series A, represents broadband usage in $n=153$ rural counties in the United States, based on Microsoft’s Air Belt initiative to help close the rural broadband gap and improve the performance and security of broadband software and services. More specifically, this dataset, taken from the GitHub, Inc. database [21], consists of the percentage of devices connected to the Internet at broadband speed by each zip code in October 2020.

(ii) The second dataset (series B), taken from the official website of the National Center for Environmental Information, contains historical data on the melting rate of the South Greenland ice sheet. The dataset itself was based on research and reconstruction of ice melting rates conducted by Kameda et al. [22] and the World Data Center for Paleoclimatology. In this way, a time series of annual percentage data was generated for the period from 1546 to 1989, the length of which is $n=444$.

(iii) Finally, the third dataset, series C, is obtained according to the official data from the National Association of Securities Dealers Automated Quotations (NASDAQ) Stock Market [23], and the so-called log-returns of daily changes in natural gas prices (in US dollars per cubic meter) from 1 January 2018 to 1 March 2023. It represents a time series of length $n=1302$, which was also considered in Stojanović et al. [24], where it was shown that it can be viewed as a series of independent realizations of RVs with Laplace distribution. Therefore, this series was transformed using the previously mentioned logistic function $x=\phi (y;\theta )$, and thus, a corresponding regression model with an output variable that can be seen as the realization of independent RVs with LLU distribution was obtained.

Realizations of the series mentioned above, along with the fitted PDFs obtained by the previously described estimation procedures, are shown in Figure 7. As can be seen, all series have pronounced and persistent fluctuations, which create “heavy tails” in their distributions. Specifically, series A has an increasing PDF, for series B the PDF is positively asymmetric and unimodal, while the PDF of series C indicates the symmetry of its distribution. In order to verify the effectiveness of the LLU distribution in fitting the dynamics and (empirical) distributions of the observed series, it is compared with the well-known beta distribution and the Kumaraswamy distribution, whose PDFs are, respectively,

$$\begin{array}{cc}\hfill g_1(x;a,b)& ={\displaystyle \frac{1}{B(a,b)}}{x}^{a-1}{(1-x)}^{b-1},\hfill \\ \hfill g_2(x;a,b)& =ab{x}^{a-1}{(1-x^a)}^{b-1}.\hfill \end{array}$$

Herein, $0<x<1$, while $a,b>0$ are the distribution parameters, and $B(a,b)$ is the beta function.

To obtain the estimated values of the parameters of the beta distribution, the method of moments (MM) is applied, according to which the estimates are as follows:

$$\begin{array}{cc}\hfill \widehat{a}& =\overline{x}\left({\displaystyle \frac{\overline{x}(1-\overline{x})}{\overline{v}}}-1\right),\hfill \\ \hfill \widehat{b}& =(1-\overline{x})\left({\displaystyle \frac{\overline{x}(1-\overline{x})}{\overline{v}}}-1\right).\hfill \end{array}$$

Here, $\overline{x}=n^{-1}{\sum }_{i=1}^n{x}_i$ and $\overline{v}={(n-1)}^{-1}{\sum }_{i=1}^n{(x_i-\overline{x})}^2$ are the sample mean and variance, respectively, wherein $\overline{v}<\overline{x}(1-\overline{x})$. As is known, both estimators, as functions of the unbiased estimators of the mean and variance, have the properties of stability and asymptotic normality (see, e.g., [25]). For the Kumaraswamy distribution, the percentile estimation method is used, based on the minimization of the objective function

$$P(a,b)=\sum _{i=1}^n{\left[x_{\left(i\right)}-Q(p_i;a,b)\right]}^2,$$

where $x_{\left(i\right)}$ is an i-th order statistic, $p_i=i/(n+1)$ and $Q(p;a,b)={(1-{(1-p)}^{1/b})}^{1/a}$ is a quantile function of the Kumaraswamy distribution. Note that the thus obtained estimators are somewhat related to the quantile estimators of the LLU distribution and, as shown in Dey et al. [26], they are among the more efficient estimators of the Kumaraswamy distribution.

The estimated parameter values for each series and for all competing models are shown in

Table 4. Estimated parameters of the LLU, beta, and Kumaraswamy distributions, along with the corresponding estimation errors and fit statistics.

Parameter/	Series A			Series B			Series C
Statistic	LLU	BETA	KUM	LLU	BETA	KUM	LLU	BETA	KUM
$\lambda /a$	0.2972	1.6572	4.1901	2.5106	1.9375	1.6443	35.459	1133.27	11.782
$\theta /b$	8.4338	0.3394	0.5469	0.3436	10.299	16.048	0.9999	1133.21	3421.22
MSEE	0.0091	0.0139	0.0342	0.0025	0.0039	0.0041	1.31 $\times {10}^{-4}$	2.28 $\times {10}^{-4}$	0.0200
AIC	−812.13	−398.61	−310.69	−2671.99	−891.80	−899.90	−17785.9	−8173.7	−4244.88
$KS$	0.0892	0.0797	0.1077	0.0541	0.0676	0.1216 ∗∗	0.0215	0.0760 ∗	0.4524 ∗∗
(p-value)	(0.2534)	(0.3818)	(0.0986)	(0.5354)	(0.2629)	(0.0028)	(0.9241)	(0.0108)	(0.00)

^∗$0.01<p<0.05$; ^∗∗$p<0.01$.

, according to which $S=1000$ independent Monte Carlo simulations of the thus obtained fitted models were conducted. Thereafter, the agreement of the distributions between the actual and fitted data was checked using the MSEE error statistic, the Akaike information criterion (AIC), and the Kolmogorov–Smirnov (KS) test of equivalence of the asymptotic distribution of two samples. Based on the results thus obtained, it is noticeable that the MSEE and AIC values are generally lower when the LLU distribution is applied. Also, only in this case does the KS test not reject, with a significant level $p>0.01$, the hypothesis of equivalence with the observed empirical distributions.

5. Conclusions

A new distribution, the so-called the LLU distribution, is presented here, along with the corresponding key properties and a procedure for estimating its parameters based on quantiles. The consistency and AN property of the estimators were also examined, and a Monte Carlo study of their efficiency was performed. A practical application of the LLU distribution in fitting real-world data is also presented, where it is compared with the beta and Kumaraswamy distributions. According to the thus obtained results, the LLU distribution provides a better fit to the observed data, which is a motivation for further research of some other new unit distributions, with slightly different characteristics. Thus, for instance, by applying the logistic map to some other probability distribution supported on the entire real line (such as, for example, the normal, Student, or Gumbel distributions), new unit distributions can be obtained. On the other hand, logistic regressions often occur in data science and machine learning, so it can also be a guideline for some potential further research regarding the application of unit distributions based on logistic maps.