A Political Radicalization Framework Based on Moral Foundations Theory

Abstract

Moral foundations theory proposes that individuals with conflicting political views base their behavior on different principles chosen from a small group of universal moral foundations. This study proposes using a set of widely accepted moral foundations (fairness, in-group loyalty, authority, and purity) as proxies to determine the degree of radicalization of online communities. A fifth principle, care, is generally surpassed by others that are higher in the radicalized groups’ moral hierarchy. Moreover, the presented data-driven methodological framework proposes an alternative way to measure whether a community complies with a certain moral principle or foundation: not evaluating its speech, but its behavior through the interactions of its individuals, establishing a bridge between the structural features of the interaction network and the intensity of communities’ radicalization regarding the considered moral foundations. Two foundations were assessed using the network’s structural characteristics: in-group loyalty measured by group-level modularity, and authority evaluated using group domination, for detecting potential hierarchical substructures within the network. By analyzing a set of Pareto-optimal groups regarding a multidimensional moral relevance scale, the most radicalized communities were identified among those considered extreme in some of their attitudes or views. An application of the proposed framework is illustrated using real-world datasets. The radicalized communities’ behavior exhibited increasing isolation, and their authorities and leaders showed growing domination over their audience. Differences were also detected between users’ behavior and speech, showing that individuals tended to share more “extreme” in-group content than they publish: extreme views get more likes on social media.

1. Introduction

According to the Cambridge Dictionary, morality is a set of standards for good or bad behavior; it is also the quality of being right, honest, or acceptable [1]. Moral norms help us answer the question, “How should we live?” at the individual level.

Politics, on the other hand, address the same question at the social level, establishing public policies and laws that reinforce some behaviors and discourage others. Despite the complexity and wealth of different political viewpoints, a single left–right (or liberal–conservative) continuum is generally used as a helpful approximation [2]. Liberals generally have an optimistic view of human nature and the possibility of human perfection. They hold what Sowell [3] refers to as an “unconstrained vision” according to which individuals should be given the greatest amount of freedom to follow their own paths in personal development. On the contrary, conservatives traditionally have a more pessimistic outlook on human nature, assuming humans are naturally flawed, imperfect, or limited in their aspirations. As a result, they adhere to a so-called “constrained vision”, according to which individuals must submit to the rules of institutions, authority, and tradition to coexist peacefully.

The connection between morality and politics is reflected in the fact that individuals with different political views base their behavior on different sets of primary moral principles or foundations [4]. In a seminal article, Graham, Haidt, and Nosek [2] investigated how political liberals and conservatives construct their moral systems. They showed that, in the U.S., liberals essentially have two psychological foundations (care and fairness), while political conservatives build their moral systems more evenly using five psychological foundations (the same ones as liberals, plus binding foundations: in-group loyalty, authority, and purity).

The existence of these five basic moral foundations (care, fairness, in-group loyalty, authority, and purity) was introduced in a widespread psychological framework called moral foundations theory (MFT) [5]. There is a vast literature applying MFT to moral psychology, bioethics, psychopathy, religion, and politics, and since its emergence, the central articles of MFT have been cited thousands of times.

Studies have shown that the positioning of individuals on the extremes of the left–right ideological spectrum is associated with their greater degree of radicalization [6]. Radicalization is also defined as the process of changing an individual’s beliefs and behaviors, which involves a growing acceptance of the use of offline or online violence to achieve their ideological goals [7,8]. Increasing societal polarization is directly related to the radicalization process of each individual’s views observed in various online communities.

The growing polarization and radicalization of individuals and groups is an increasingly relevant social threat [9]. The authors of the most recent Global Risks Report [10] published by the World Economic Forum (WEF) stated that the erosion of social cohesion and polarization ranked as the most significant societal risks among those pointed out by WEF 2023. Moreover, societal polarization was listed as the fifth-most severe global risk in the short term.

The goal of this article is to explore a novel characterization of radicalized online communities by positioning these groups on a multidimensional relevance scale of a set of primary moral foundations. Each moral principle or foundation corresponds to one dimension or axis of this scale, and the degree to which the individuals from certain communities comply with this principle corresponds to its location on the axis.

The following specific research questions will be answered in this study:

• Is there a way to measure whether an online community complies with a moral principle or foundation by evaluating not only individual’s speech but also their behavior?
• How can online communities’ radicalization be measured and compared, considering their different principles and moral foundations?

This study will explore whether two of the considered foundations—authority and in-group loyalty—can be measured objectively by evaluating a group’s behavior using the structural characteristics of the interaction network of individuals.

Regarding the measurement of communities’ radicalization, the assumption being made in this study is that radicalized communities will be positioned at the extremes of the relevance scale for all or some of the considered moral foundations. The more extreme the positioning of the community on a specific moral principle, the more radical this community will be, and the greater propensity it will have to act outside the legal norms to defend the principles it believes are absolute and unconditional.

In a previous study, Bliuc et al. [11] stated that radicalized online communities are ideologically driven groups; therefore, their collective beliefs, values, and norms are crucial to understanding their actions. Hahn et al. [12] applied the conceptual framework of moral foundations theory to discover the dominant motives and moral motivations of several specific terrorist groups. Radicalization has also been studied by identifying “warning” speech markers in online communities; however, this approach is not very generalizable, given the difficulty of establishing ad hoc an appropriate and general set of radicalization warning markers that would work for any group [13].

This article is organized as follows: Section 2 presents the methodology for defining the relevant set of primary moral foundations and establishing a data-driven relevance scale for them. It also proposes an approach for choosing the most radicalized communities using this multidimensional scale, based on the content they produce and their structural characteristics. The results that illustrate the practical application of the proposed framework are presented in Section 3. Conclusions are drawn in Section 4.

2. Methods

This section describes a data-driven methodology that defines the positioning of communities on the relevance scales of a set of primary moral foundations. This methodology is based on analyzing the individuals’ speech and their interaction networks in online platforms, where people generally are grouped in various communities of like-minded users.

For each moral foundation, a scale will be established that indicates the degree to which the group complies with this principle. Given a set of communities, an approach to choose the most radicalized ones using a multidimensional scale of several moral foundations is also described in this section.

2.1. Choosing Primary Moral Foundations for Measuring Radicalization

Moral foundations theory states that there are five widely accepted moral foundations [4]. The first two foundations, care and fairness, are called the individualizing foundations, because they emphasize the rights and welfare of individuals. The other three foundations, in-group loyalty, authority, and purity, are called the binding foundations because they emphasize group-binding loyalty, duty to the group, and self-correspondence to group ideals. Further studies sometimes included a sixth moral foundation: liberty/oppression [14], although there is no consensus regarding its “foundationhood” [15]. In this article, the existence of the five consensual moral foundations will be assumed.

However, since radicalization involves a growing acceptance of the use of violence [7,8], the care foundation will not be considered in our framework. Human behavior is driven by moral hierarchies, in which some motivations are deemed more important than others. Even though humans have compassion-driven psychological restraints against harming others, Bandura [16] showed that radicalized groups harm others, seeing their actions as an effort to uphold moral values they deem most important, i.e., committing violence and rejecting concerns of care in pursuit of “broader aims”. This means that the moral foundation of care is surpassed by other principles that are higher in their moral hierarchy.

Identifying the degree of relevance of the other four foundations (fairness, in-group loyalty, authority, and purity) to a certain community allows for measuring how extreme or radical this community is. It provides indicators of incentives the individuals of the community have to act outside social boundaries, the established social rules that most people in society agree are reasonable or should be respected. Thus, political radicalization is analyzed in more detail, outside the widely used binary left–right simplification, introducing several dimensions often evaluated simultaneously or implicitly.

Hereinafter, this study focuses on fairness, in-group loyalty, authority, and purity as proxies to determine the degree of a community’s radicalization.

2.2. Relevance of Moral Foundations Using Group Speech

One of the most traditional and direct ways to measure the relevance of each moral foundation to the individuals from a group or community is through the analysis of group speech. Different online communities use specific words to create “frames” that make attitudes or decisions seem morally good or bad [17].

Quantitative content analysis [18] of user posts can be used as an objective approach to examine online communities’ endorsement of specific moral principles. This involves creating categories of words and calculating the frequencies of words from each category in a corpus of text, as proposed in previous studies [2,19,20]. In this case, each category corresponds to one moral foundation. While there is some subjectivity when choosing the set of words in each category, the method proved efficient in identifying differences in the attention given to each moral principle across the different groups [2,19].

The Moral Foundations Dictionary (MFD), available at [15], is a widely used categorization of hundreds of keywords into moral categories based on the MFT. There are also non-English versions of the MFD. For example, MFD-BR is the Brazilian-Portuguese version of MFD created by Carvalho et al. [21].

For each online community and each moral foundation, the frequencies of words from the foundation-related category in the corpus of individuals’ publications may be used as a primary indicator of the positioning of this community in the foundation’s relevance scale.

2.3. Interaction Networks

The analysis of group speech is widely used to evaluate a moral foundation’s relevance to communities. An alternative way this study proposes to measure whether a community complies with a moral principle or foundation is to explore its behavior through the interactions of its individuals.

The behavior of individuals in a group is reflected in their interactions with other individuals from their own and other communities. Interaction networks are mathematical abstractions that represent the structure of social relations in a certain time period. An interaction network is modeled as a graph $G=(V,E)$, being V a set of n vertices (representing individuals) and E a set of m edges (representing interactions).

Two foundations were identified that can be measured through the analysis of the structure of an interaction network: in-group loyalty and authority. Next, it will be shown how we can evaluate the degree to which a community complies with these principles using the interaction network’s structure, establishing a bridge between the structural features of the interaction network of individuals and the intensity of community radicalization regarding the considered moral foundations.

Note that different platforms have different characteristics that shape user interactions. However, each platform has one or more categories of interactions that represent endorsement. Retweets on Twitter mostly represent endorsement, as do shares or likes on Facebook. Consequently, the same strategy as in this work may be applied to any social network or platform (e.g., YouTube) where users can interact through endorsements or recommendations. In all these platforms, it is possible to build a behavioral interaction network based on links that represent the support or endorsement of one user of content published by another.

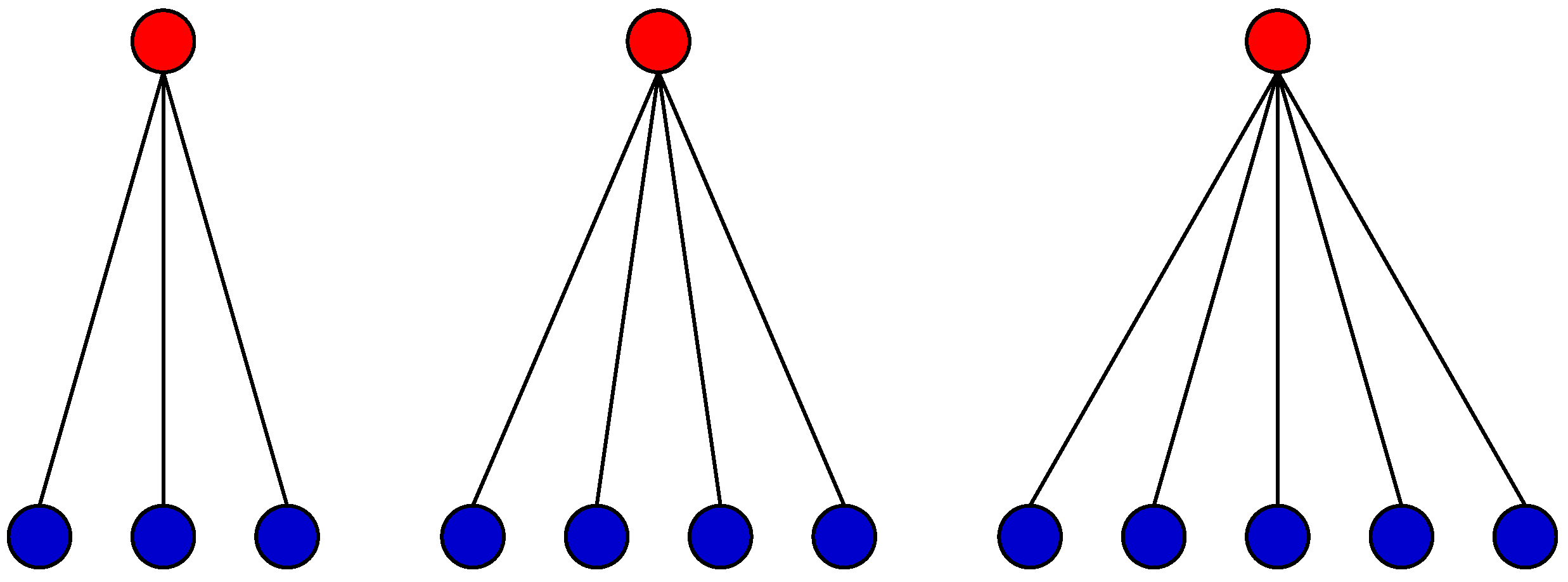
2.4. Group-Binding Loyalty and Isolation

According to Haidt, people always seek ways to create competing groups and cohesive coalitions: the in-group loyalty foundation is a part of our innate tendency to self-preserve and adapt [4].

In one of the four studies conducted by Graham et al. [2], the participants rated several moral judgment statements on a six-point scale (from strongly disagree to strongly agree), where each statement instantiated or violated a specific abstract principle. For example, the relevance of the in-group loyalty principle to participants was evaluated using statements like the following:

“When it comes to close friendships and romantic relationships, it is okay for people to seek out only members of their own ethnic or religious group.”

“Loyalty to one’s group is more important than one’s individual concerns.”

Group-binding loyalty reinforces the interactions with members of the same community and discourages interactions with other groups. At its limit, this leads to the isolation of individuals from people coming from any group except their own. Therefore, a structural indicator for the in-group loyalty foundation should measure the degree of group cohesion and its isolation from different groups.

Note that modularity [22] is a well-known network-level indicator of the internal cohesion and isolation of communities. Given a division of certain network vertices into a collection of groups, modularity reflects the concentration of edges within groups compared with a random distribution of edges between all vertices regardless of the groups. More formally, if a graph $G(V,E)$ with $\left|V\right|=n$ vertices and $\left|E\right|=m$ edges has its vertex set V partitioned into k disjoint groups $\{A_1,A_2,\dots ,A_k\}$, the modularity Q is defined as

$$Q=\frac{1}{2m}\sum _{u,v\in V}(a_{uv}-\frac{d\left(u\right)d\left(v\right)}{2m})·{\delta }_{g_u{g}_v},$$

(1)

where $d\left(v\right)$ is the degree of vertex $v\in V$; $g_v$ the index of v’s group; $a_{uv}=1$ if there is an edge between vertices u and v, 0 otherwise; and ${\delta }_{ij}$ is the Kronecker delta.

However, modularity is not designed to evaluate group-level cohesion or isolation. For example, if we evaluate the modularity of the subgraph induced by a group $A_i$ (i.e., a subgraph that contains all vertices in $A_i$ and all edges between vertices in $A_i$), then the modularity value Q for this single group will be equal to zero [23]. A previous study showed a lack of consolidated measures for evaluating the cohesion and isolation of network nodes at the group level [24].

To evaluate group cohesion and its isolation from other groups in the network, an approach that measures the relative contribution of a specific group $A_i$ to the overall modularity of the network was developed. Since ${\delta }_{g_u{g}_v}=1$ if and only if the vertices u and v are from the same group (and is zero otherwise), the Equation (1) that defines modularity Q can be rewritten as follows:

$$Q=\frac{1}{2m}\sum _{i=1}^k\sum _{u,v\in A_i}(a_{uv}-\frac{d\left(u\right)d\left(v\right)}{2m})$$

(2)

Suppose that a specific group $A_i$ is chosen. Consider an addend in Equation (2) corresponding to the group $A_i$. Note that this term ${\sum }_{u,v\in A_i}(a_{uv}-d\left(u\right)d\left(v\right)/2m)$ considers only pairs of vertices u and v that both belong to $A_i$, and $\sum a_{uv}$ represents the actual number of in-group edges. Moreover, $\sum d\left(u\right)d\left(v\right)/2m$ represents the expected number of $A_i$’s in-group edges after rewiring or randomizing the edges in the network, while preserving the degree of every vertex (randomization known as the configuration model). If group $A_i$ gives no more within-community edges than would be expected by random chance, then the whole term ${\sum }_{u,v\in A_i}(a_{uv}-d\left(u\right)d\left(v\right)/2m)$ will be nullified. On the other hand, if group $A_i$ gives significantly more within-community edges than would be expected by random chance, then the contribution of this group to network modularity will be large.

Therefore, the contribution $Q_i$ of the group $A_i$ to the overall network modularity Q can be measured in the following way:

$$Q_i=\frac{1}{2m}\sum _{u,v\in A_i}(a_{uv}-\frac{d\left(u\right)d\left(v\right)}{2m})$$

Note that ${\sum }_{i=1}^k{Q}_i=Q$, i.e., the sum of the contributions of all groups produces the overall network modularity.

However, a relative (not an absolute) contribution of the group $A_i$ to the network’s modularity is being sought. The d-modularity $d_i$ of G with respect to the group $A_i$ is defined as

$$d_i=\frac{Q_i}{Q},$$

Thus, $d_i$ reflects the relative contribution of a specific group $A_i$ to the overall modularity of the network.

Figure 1 shows an example of a graph with 12 vertices partitioned into three equally-sized groups, with four vertices each. Note that each red and each blue vertex has exactly two in-group adjacent vertices and one adjacent vertex from a different group. Each black vertex, however, has exactly three in-group neighbors and, at most, one adjacent vertex from a different group: the black group is more internally cohesive and isolated. The overall modularity of the graph is $0.402$, and the group $A_1$ composed of black vertices has a relative contribution to modularity of $d_1=44.8\%$ ($Q_1=0.180$). The relative contribution of the other two groups, $A_2$ and $A_3$, with red and blue vertices, respectively, is quite smaller: $d_2=d_3=27.6\%$ ($Q_2=Q_3=0.111$).

In summary, the d-modularity value $d_i$ defines the positioning of the community $A_i$ on the in-group loyalty foundation scale.

2.5. Authority and Hierarchy

The authority foundation is much concerned with respecting (or not respecting) hierarchical relationships [4]. These hierarchical relationships are generally bidirectional: up toward superiors and down toward subordinates. Authority should not be confused with raw power backed by the threat of force and the ability to inflict violence. Authorities in human societies are also about taking responsibility for maintaining order, justice, and representativeness in front of democratic institutions.

In a previously cited study by Graham et al. [2], participants evaluated the relevance of the authority principle by rating moral judgment statements like the following ones:

“If I were a soldier and disagreed with my commanding officer’s orders, I would obey anyway because that is my duty.”

“Respect for authority is something all children need to learn.”

In summary, individuals guided by the authority principle are more sensitive to a sense of duty to authorities and their group’s leaders. At its limit, this means that all members of a group or community follow, listen, or interact with a small set of authoritative voices and leaders. From a structural perspective, it means that the group shows a clear hierarchy among its members.

Therefore, a structural measure for the authority foundation should evaluate the degree to which a group shows a hierarchical structure. This may vary from the most disordered and chaotic (non-hierarchical) to a fully hierarchical structure of relations, as represented in Figure 2, which shows a network with 15 vertices, where three red vertices (the “authorities”) are able to reach all of the remaining 12 blue vertices. As we shall see, identifying substructures like the one represented in Figure 2 inside existing interaction networks is not always a computationally simple problem.

Now, the goal is to identify a relatively small set of individuals (called authorities) capable of reaching (dominating) the greatest number of individuals over an online interaction network. In short, the goal is to identify hierarchical substructures inside online interaction networks.

For this purpose, the concept of domination is used. The mathematical study of domination originated in the 1960s. It was applied, for example, to identifying coordinated communication in social networks by Campan et al. [25]. The reader is referred to Haynes et al. [26] for a more detailed review of domination in networks.

Since the degree to which a group shows a hierarchical structure is to be measured, it is more appropriate in this study to use partial domination. More formally, let $V=1,\dots ,n$ be the set of the n individuals in the group (here, the interactions inside only one community are considered). The goal is to find the smallest subset $S^{*}$ of V such that the number of individuals reached from $S^{*}$ is at least $\rho ·n$, where $\rho$ is a parameter that reflects the minimum proportion of individuals to be reached. The problem can be studied considering, for example, $\rho =$ 100%, $\rho =$ 75%, or $\rho =$ 50% of a given group.

Note that when $\rho =$ 100%, the abovementioned problem is identical to the classical dominating set problem (DS) [27]. The smallest subset $S^{*}\subseteq V$ that reaches each vertex represents a group of authorities that dominates the whole group. The dominating set problem is known to be NP-hard, i.e., there is no efficient algorithm for finding the optimum solution unless $P=NP$.

However, in the more general case, when $\rho \le$ 100%, the problem requires a specific formulation called the partial dominating set problem (PDS). An instance of the PDS problem comprises a graph $G(V,E)$ and a parameter $\rho$. The goal is to find a dominating set that reaches at least $\rho \left|V\right|=\rho n$ vertices. The PDS is also NP-hard, since it contains the DS problem as a special case ($\rho =1$).

Since the problem is NP-hard, heuristic algorithms can be used to solve it for large interaction networks. Possibly the most well-acknowledged algorithm for the DS problem is a greedy constructive heuristic has been shown to be the best in terms of the approximation ratio for the DS problem unless $P=NP$ (for a more detailed analysis of the algorithm, see Parekh [28]; for the approximation ratio proof, see Chlebík and Chlebíková [29]).

At the beginning of the algorithm, $S^{*}=\varnothing$. The greedy algorithm adds a new vertex to $S^{*}$ in each iteration until $S^{*}$ forms a solution. In each iteration, it puts into $S^{*}$ the vertex (individual) connected with the maximum number of yet uncovered vertices and stops when all vertices have been covered. Note that the algorithm can be easily adapted for the PDS problem simply by stopping when the solution $S^{*}$ covers $\rho \left|V\right|$ vertices.

The lower the number of authoritative individuals in $S^{*}$, the higher the degree to which the group shows a hierarchical structure. This number, the cardinality of the set $S^{*}$, defines the positioning of the community on the authority foundation scale. Note that groups with a non-hierarchical structure may need a very large number of individuals in $S^{*}$ to be dominated, a quantity of the magnitude of the size of the group itself.

Finally, it is necessary to define how the value of $\rho$ should be chosen in practice. For example, critical mass theory studies have found that reasonably large minority sizes (30% or 40% of the population) are often enough to trigger a collective behavior [30]. Nevertheless, in practice, the specific value chosen for $\rho$ generally affects the raw values, but does not significantly affect the relative positioning of communities on the authority foundation scale.

2.6. Integrating the Relevance Scales

Regardless of the type of relevance scales to be used (whether structural or speech-based), it is necessary to integrate them into a single decision-support framework that allows choosing the most radicalized communities.

The problem of finding the most radicalized groups can be seen as a multi-criteria optimization problem, where each moral foundation relevance is a criterion, and the goal is to find those groups that have the most extreme values across the multidimensional scale. In a situation where there are several entities (groups), each characterized by several variables (moral criteria), multiple-criteria decision analysis (MCDA) is a tool that can help find solutions [31].

For example, let us consider a structural relevance scale composed of only two criteria: in-group loyalty and authority. The criteria are evaluated in different ways. In-group loyalty is measured in a continuous $[0,1]$-based d-modularity scale, with greater (closer to one) values representing more isolation. Authority, on the other hand, is evaluated in a discrete integer scale representing the cardinalities of partial dominating sets, with smaller values representing better-defined hierarchical structures. Each criterion has an “increasing radicalization” direction: for in-group loyalty, more isolation (greater d-modularity) means greater radicalization risk, and for authority, smaller partial dominating sets represent an increased radicalization risk.

Note that there may be groups that are no more radicalized than others according to all criteria. More formally, group A is referred to as dominated by another group B if and only if B is as or more radicalized than A with respect to all criteria. The Pareto frontier, on the other hand, is a set of non-dominated groups. That is, there is no community in the Pareto frontier whose radicalization could be improved by another community without sacrificing at least one of the criteria. The Pareto frontier concept for MCDA is presented in detail, for example, by Luc [32].

The Pareto criterion is used when elements or solutions have several dimensions, and we try to find optimal elements following the assumption that all dimensions are significant and none may be neglected. It offers an alternative to another common multi-criteria approach of assigning (often) arbitrary or weakly justified weights to each criterion. In our structural relevance scale approach, the criteria can hardly be compared or combined using weights, since in-group loyalty and authority evaluation have very different natures.

In the same way, the Pareto criterion may also be used in a speech-based approach. In this case, there are four dimensions, among which the communities are evaluated (fairness, in-group loyalty, authority, and purity).

When using the Pareto criterion adapted specifically for our radicalization decision analysis based on MFT, the goal is to choose the most radicalized communities among those considered extreme in some of their attitudes or views. The set of communities on the Pareto frontier are the candidates to be analyzed in more detail due to their radicalization risk.

3. Results

This section illustrates the practical application of the proposed framework using several real-world datasets. It is shown how, using structural relevance scales, radicalized communities can be detected by analyzing sets of non-Pareto-dominated groups. The framework also shows that sometimes group behavior aligns with group speech. In other cases, however, group behavior is disconnected from group speech.

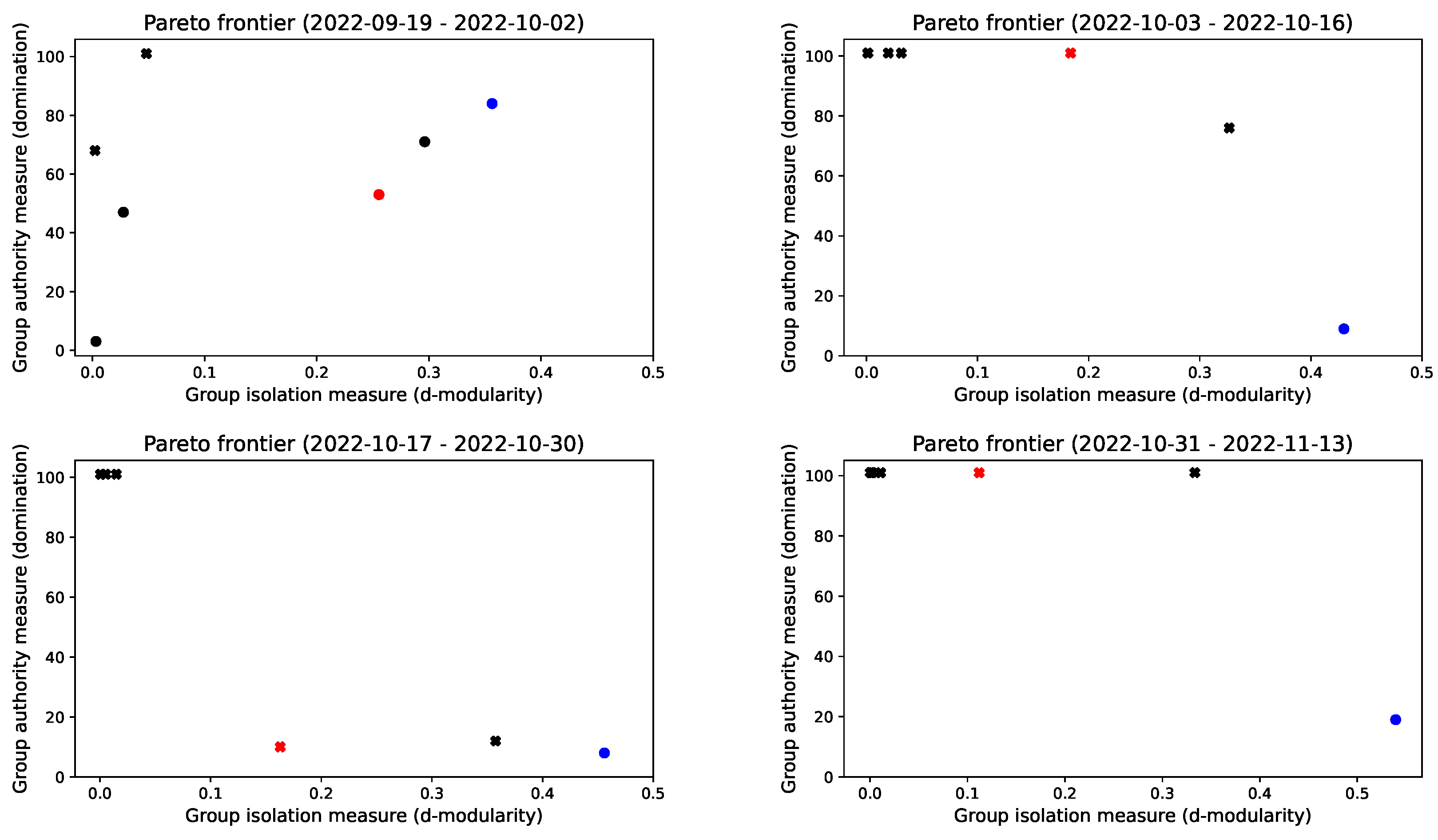
3.1. Datasets and Communities

The framework was evaluated using several datasets collected before, during, and after the 2022 Brazilian presidential election from the Twitter social network.

Majority rule with two electoral rounds is used in the Brazilian presidential election. If no candidate receives the majority of votes in the first round, the two candidates with the most votes proceed to a second round, excluding all others. In 2022, the first round of voting was held on 2 October. As no candidate for president received more than half of the valid votes, a runoff election was carried out on 30 October.

The data collection period was from 19 September to 13 November 2022, with eight weeks in total. This period started two weeks before the first round of voting and finished two weeks after the second round.

Each of the four created datasets covered two weeks of data and contained all tweets that mentioned certain election-related words in Portuguese (eleição OR eleições OR eleitoral OR eleitorais). Each dataset was very large, containing millions of tweets and interactions, enabling the use of structural and speech-based approaches.

Table 1. Datasets adopted for illustrating the use of the framework. Election days are marked in bold.

Dataset	Dates	Period	Number of Tweets	Number of Users
D1	19 September–2 October 2022	Before elections	4,087,911	934,870
D2	3 October–16 October 2022	During elections	4,193,174	808,428
D3	17 October–30 October 2022	During elections	8,131,875	1,126,346
D4	31 October–13 November 2022	After elections	6,264,584	1,025,486

shows the main features of the collected datasets, such as the number of tweets and the number of tweet authors. The table also indicates which data covered which period: before, during, and after the election.

The datasets contained a clearly radicalized right-leaning community that invaded the Supreme Federal Court, the National Congress building, and the Planalto Presidential Mansion in the Three Powers Plaza in Brasília on 8 January 2023. Several other communities were detected in the datasets.

The community detection method of Blondel et al. [33] was used for identifying the communities for all four datasets in one run, using the retweet network of interactions from 17 September to 29 October 2022, that is, approximately 75% of the data. It was verified that, starting from the election’s second round, 30 October 2022, the pattern of interactions was a very binary one. Therefore, nearly 25% of the data, starting from 30 October 2022, were excluded from community detection, so that binary voting decisions did not affect the communities formed during the whole period. The users who had not interacted before the election’s second round, i.e., those who only interacted after the electoral period, were not considered in the analysis of the fourth dataset.

Several online communities were identified. Two specific groups (left-leaning and right-leaning) could be easily positioned in the ideological spectrum by observing that many high-degree individuals in these groups corresponded to key political figures in the elections, such as the former president, Luiz Inácio Lula da Silva, and the president at the time, Jair Bolsonaro. There were several other communities, the largest of which corresponded to mainstream media and press followers. We did not emphasize the left–right political identifications within the theoretical formulation of the framework. Nevertheless, many researchers and the media widely use this left–right spectrum, and we used two specific communities of users that positioned themselves as adversarial groups traditionally placed on the extremes of this spectrum.

Due to resolution limits in community detection in such large datasets [34], only communities with at least 4000 individuals were considered, since communities smaller than $\sqrt{2L}$ users can result from an arbitrary merging of smaller structures, where L is the total number of links in the network. Seven communities satisfied this restriction.

3.2. Radicalization by Network Structural Features

First, the radicalization of communities was evaluated considering only two structural criteria: in-group loyalty and authority.

Figure 3 shows the positioning of online communities on the two-dimensional scale for the four analyzed datasets. Each point corresponds to one community. The further to the right and down the point’s position, the more radicalized that community is, indicating an “increasing radicalization” direction. The shape of the marker indicates Pareto-optimality (a circle O for Pareto-efficient and an X mark for non-Pareto-efficient), while the color of some groups indicates the group leaning (blue for right-leaning and red for left-leaning).

The first dataset, containing data collected before the election’s first round (2 October 2022), did not show one, but several, non-dominated communities. However, the right-leaning group already appeared on the Pareto frontier due to its relatively high in-group loyalty measure value. For the other three datasets, there was only one Pareto optimum. The right-leaning community dominated the rest of the groups, because its in-group isolation increased, while the dominating set sizes, which measure authority strength, decreased simultaneously. The community’s behavior exhibited increasing isolation, and its authorities and leaders showed a growing domination over their audience.

The results showed an increasing radicalization of the right-leaning community that invaded the three branches of government in Brasília on 8 January 2023. There were no other groups that exhibited this kind of behavior.

3.3. Radicalization by Group Speech Measurement

The relevance of moral principles to communities can also be measured using the more traditional speech-based method. However, in this case, the multi-criteria approach based on the moral foundations theory can also help indicate the most radicalized groups.

Four dimensions were evaluated using the group speech of each community: fairness, in-group loyalty, authority, and purity, as described in Section 2.2. The Brazilian-Portuguese version of MFD called MFD-BR created by Carvalho et al. [21] was used for the investigated datasets.

For each of the seven communities, there were four values that represented the frequencies of the words related to each foundation in the corpus of texts published by that community. Parallel coordinates were used for visualizing these four-dimensional data. In this visualization, communities were represented as connected line segments. Each vertical line or axis represented one moral foundation measure. Communities with similar measures tended to appear closer together. Any group whose line appeared on the top of a foundation’s axis belonged to the Pareto frontier, since no other group dominated it in this dimension.

Figure 4 shows the speech-based positioning of online communities for the four analyzed datasets. Looking at this visualization, it can be seen that the blue line greatly surpasses the rest on one axis, showing the extreme relevance of the authority foundation for the right-leaning community when compared to the rest of the groups. This replicates the results obtained using the authority structural feature in the previous section, showing that, in this case, group speech and behavior went hand in hand.

However, the speech-based in-group loyalty foundation measurement had a different behavior. The right-leaning community, more isolated and internally cohesive, did not beat the other groups, and not showing a greater use of in-group loyalty-related words. The degree of isolation of the analyzed communities did not seem to be correlated with the use of these words, and group behavior was disconnected from the speech-based in-group loyalty evaluation.

This mismatch between behavior and speech regarding the in-group loyalty foundation may be first explained by the specific circumstances in which the 2022 elections occurred in Brazil. Due to the existing polarization, the possible re-election of incumbent President Bolsonaro was interpreted by a significant part of the adversary electorate as a threat to the current political system. On the other side, for Bolsonaro’s followers, the possible election of former president Lula da Silva was also perceived as a nearly existential threat to their political group.

In that context, the behavior we measured using interactions with content published by political groups strongly reflected this threat perceived by both communities: users strongly reinforced (endorsed) messages published by their political groups. However, on average, the content published by the same users was much more neutral, with fewer in-group-related words; their speech had a larger diversity of content.

In summary, our discovery implied that users promoted more strongly, on average, in-group-oriented messages when compared to their average use of in-group-oriented speech, which was much more neutral. These differences between behavior and speech show that users tend to share more “extreme” in-group content than they publish: extreme views get more likes on social media [35].

In all four analyzed datasets, the other two moral foundations, fairness and purity, did not significantly differ in their frequency of foundation-related words across the groups. For fairness, the frequencies of foundation-related words were similar in all cases. For purity, they were very similar for all datasets, except for the last one, D4.

4. Conclusions

In this study, a political radicalization framework based on moral foundations theory was presented. A novel characterization of radicalized online communities was explored by positioning these groups on a multidimensional relevance scale of a set of primary moral foundations.

There are two ways to measure the degree to which individuals from a certain community comply with each moral foundation, i.e., the positioning of the community in the foundation’s relevance scale. A more traditional method is based on evaluating group speech by measuring the appearance of foundation-related words in the content produced by individuals in the group.

An alternative approach is evaluating group behavior in the network of interactions between individuals. Two foundations, in-group loyalty and authority, may be measured using the interaction network’s structural features. Using structural relevance scales, radicalized communities can be detected by analyzing sets of non-Pareto-dominated groups. An application of the proposed framework was illustrated using real-world datasets, with a radicalized right-leaning community that invaded the three branches of government in Brasília on 8 January 2023, being the only Pareto optimum for the last three (chronologically) of the four analyzed datasets.

Therefore, the following answers were found to the research questions posed in this study:

• Is there a way to measure whether an online community complies with a moral principle or foundation by evaluating not only individuals’ speech but also their behavior?

  -

  Yes, we found two network features that, conceptually, reflect the degree to which individual’s interactions are consistent with their respective moral principles.

• How can online communities’ radicalization be measured and compared, considering their different principles and moral foundations?

  -

  Given a set of moral foundation structural relevance scales, the set of communities on the Pareto frontier are candidates to have a greater radicalization risk. We illustrated the use of the framework by showing that, unlike before the elections, during and after the 2022 Brazilian electoral process, the right-leaning radicalized community was the only Pareto optimum.

Among the limitations of our study, the use of modularity-based community detection in interaction networks imposes resolution limits [34], such that small groups (in our case, smaller than 4000 vertices) may go undetected. The focus of the study on sufficiently large interaction groupings limited the potential for detecting smaller and more exclusive groups that are more easily radicalized and may lead to violence. We consider that, in future studies, using community detection methods focused on smaller groups, such as hierarchical clustering, could facilitate discovering these smaller groups embedded in larger communities.

In future works, we also intend to explore the idea of linking the moral foundations theory to levels of self-confidence and parenting styles, which may potentially lead to a predictive model.

In some cases, group behavior is in line with group speech. Regarding the authority foundation, evaluated by detecting hierarchical structures within the network, there was a match between the presence of these substructures in communities and the use of authority-related words.

In other cases, group behavior was disconnected from group speech. For the in-group loyalty foundation, the right-leaning community was more isolated and internally cohesive, despite its low use of in-group loyalty-related words when compared to other communities. The analyzed communities’ isolation did not seem to be correlated with their use of words related to the in-group loyalty foundation. These differences between behavior and speech show that users tend to share more “extreme” in-group content than that they publish: “Extreme views get more likes on social media” [35].

The behavior of radicalized communities detected through structural relevance scales indicates an increasing isolation and a growing domination of the authorities and leaders over their audience. The proposed framework can be used to identify those groups exhibiting risky behavior by analyzing the structural characteristics of social networks and other platforms of interacting users.