A Multistep Method for Integration of Perturbed and Damped Second-Order ODE Systems
Abstract
1. Introduction
2. Definition and Properties of the Ψ-Functions and the Ψ-Functions Series Method
3. Ψ-Multistep Methods
3.1. Explicit Ψ-Multistep Method of p Steps for Perturbed and Damped Systems
3.2. Implicit Ψ-Multistep Method of p Steps for Perturbed and Damped Systems
3.3. Predictor–Corrector Ψ-Multistep Method for Perturbed and Damped Systems
4. Recurrent Calculus of the Matrices and and a New Definition of the Multistep Methods
4.1. Recurrent Calculus and a New Definition of the Explicit Ψ-Multistep Method
4.2. Recurrent Calculus and New Definition of the Implicit Ψ-Multistep Method
4.3. New Predictor–Corrector Ψ-Multistep Method
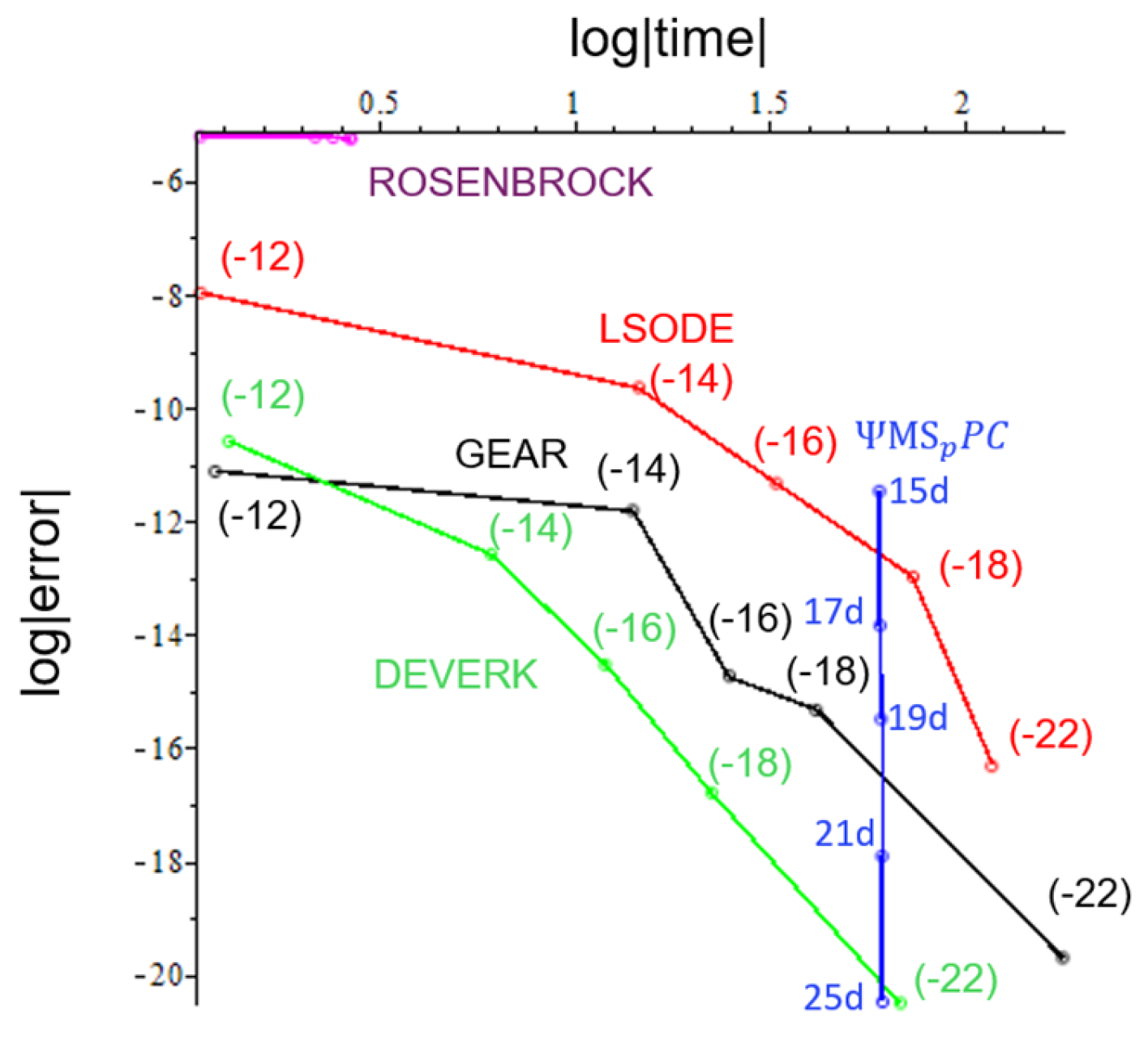
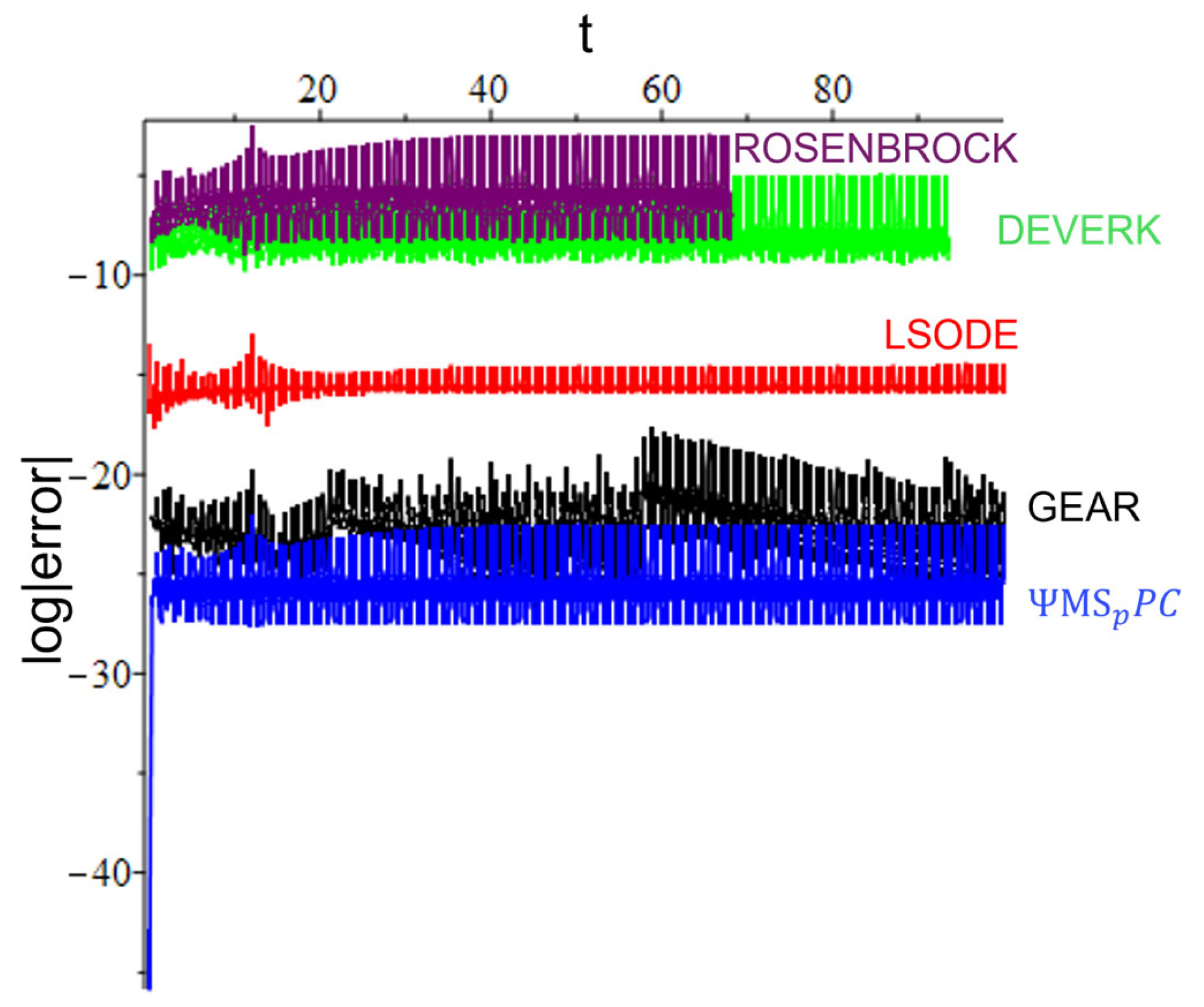
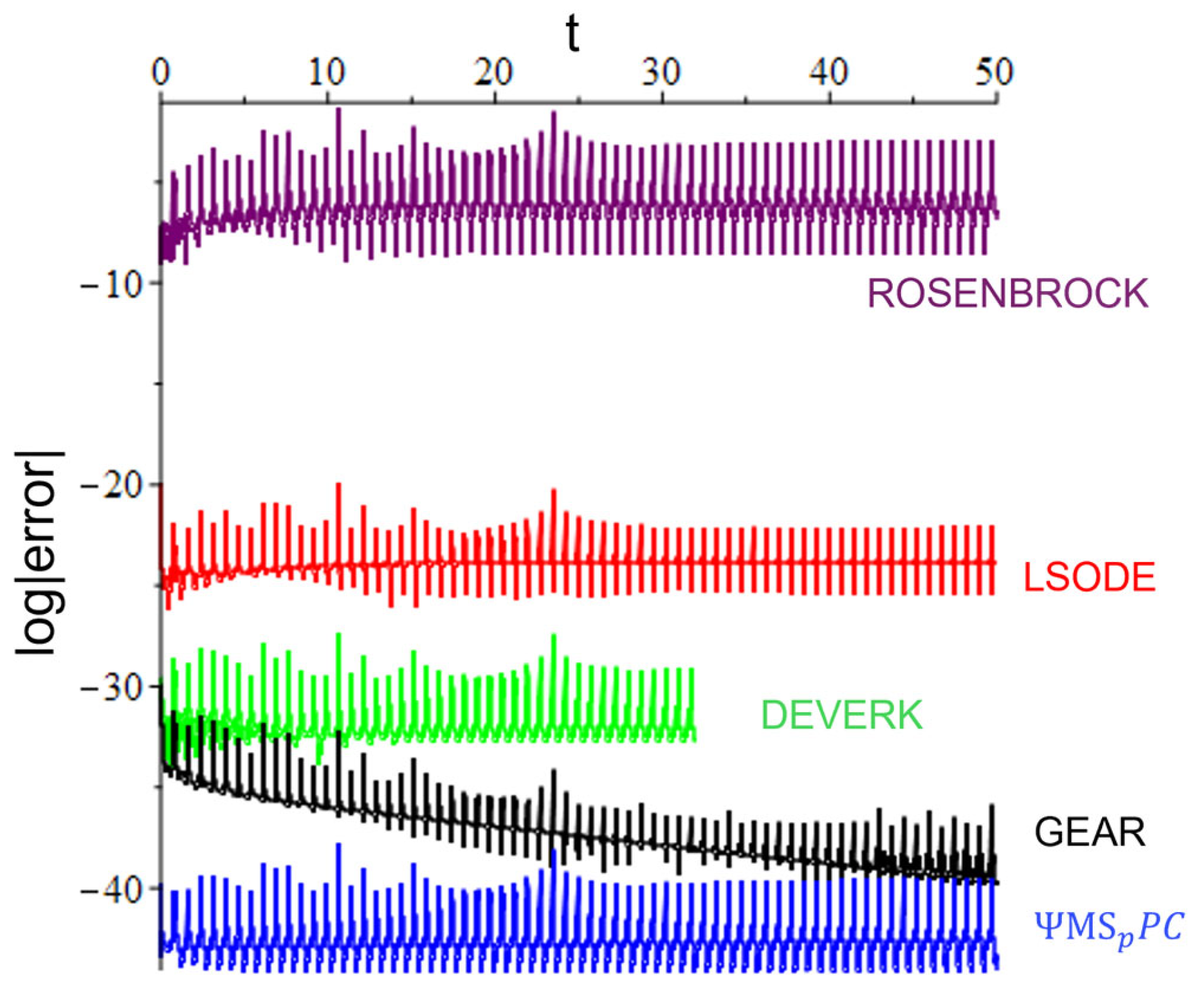
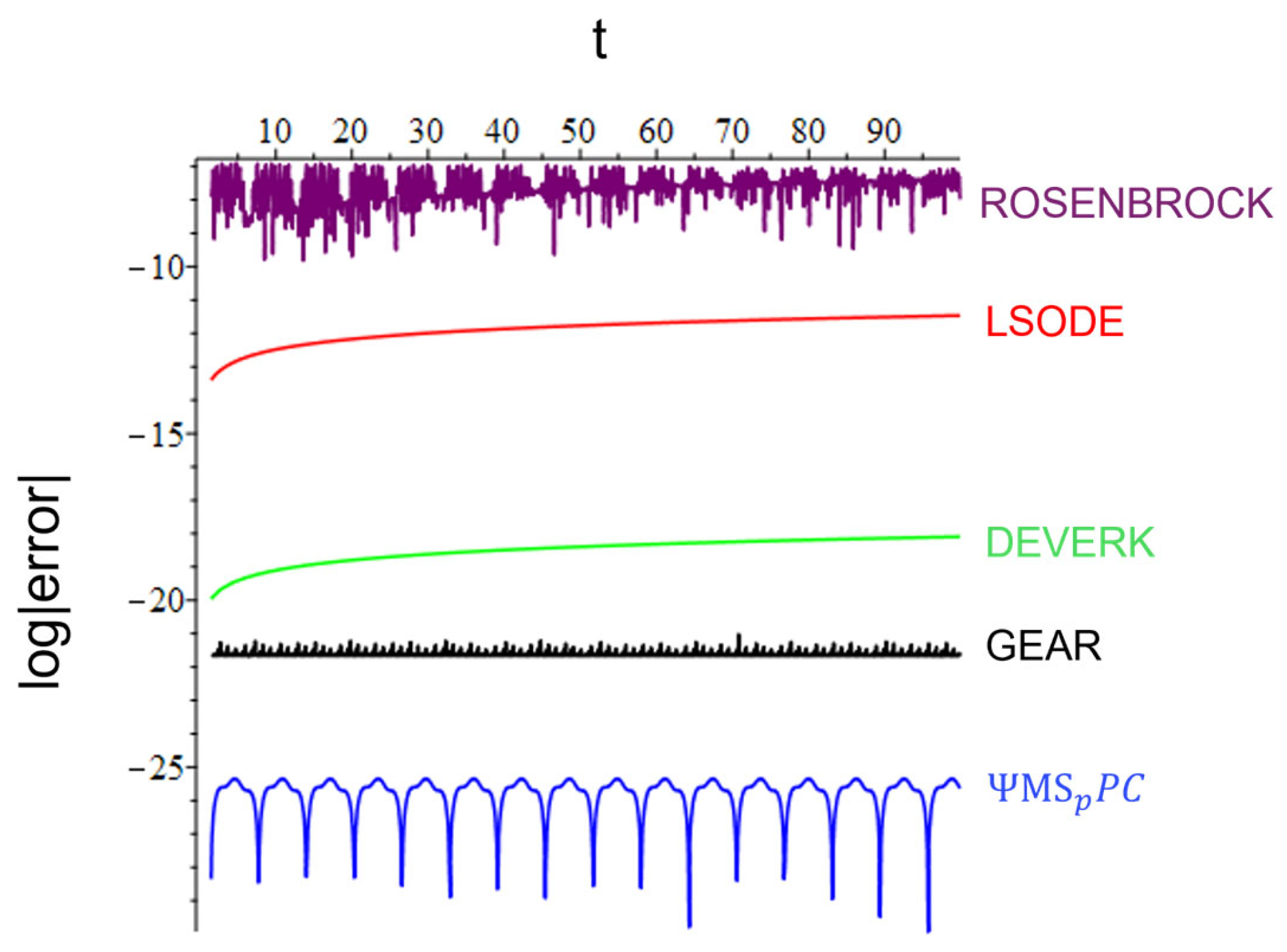
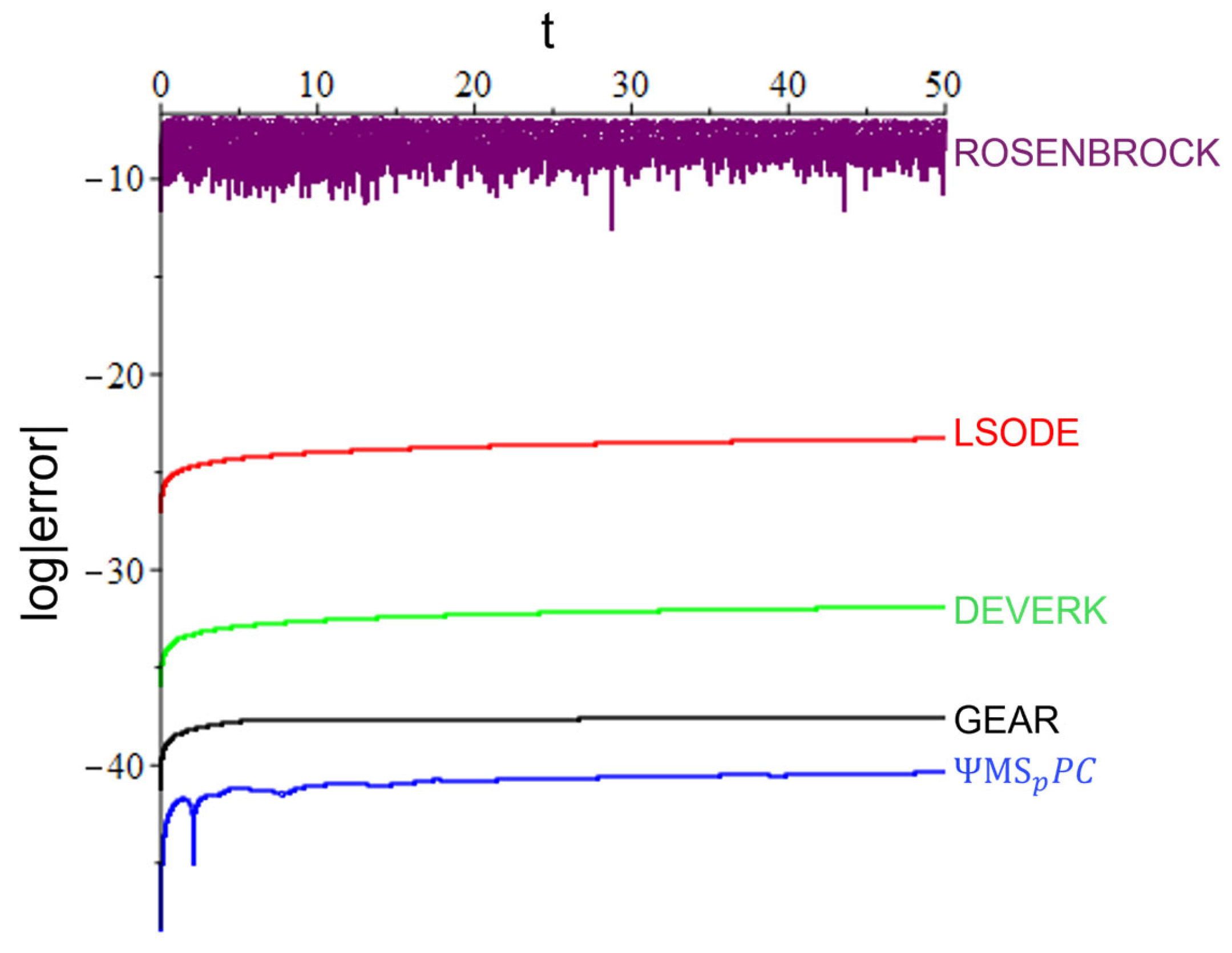
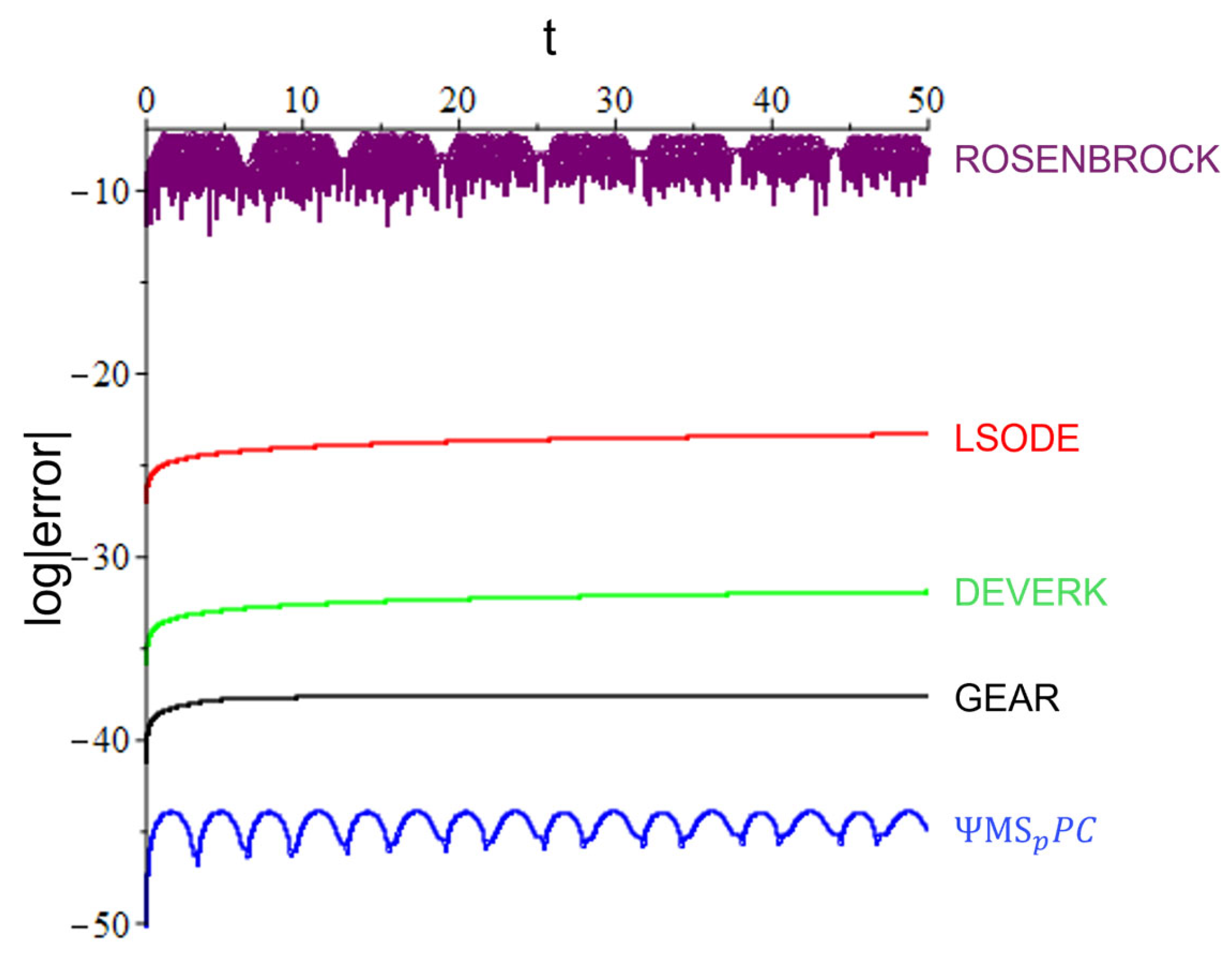
5. Numerical Experiments
- LSODE methods cause a numerical solution to be found using the Livermore Stiff ODE solver.
- GEAR finds a numerical solution using a Gear single-step extrapolation method.
- ROSENBROCK finds a numerical solution using an Implicit Rosenbrock third–fourth-order Runge–Kutta method with third-degree interpolant.
- DVERK78 finds a numerical solution using a seventh–eighth-order continuous Runge–Kutta method.
5.1. Problem 1
5.2. Problem 2
5.3. Problem 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kunstaanheimo, P.; Stiefel, E. Perturbation theory of Kepler motion based on spinor Regularization. J. Reine Angew. Math. 1965, 218, 204–219. [Google Scholar] [CrossRef]
- Burdet, C.A. Le mouvement Keplerian et les oscillateurs harmoniques. J. Reine Angew. Math. 1969, 238, 71–78. [Google Scholar] [CrossRef]
- Ferrándiz, J.M. A general canonical transformation increasing the number of variables with application to the two-body problem. Celes. Mech. 1988, 41, 343–357. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. ASCE J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A family of single-step Houbolt time integration algorithms for structural dynamics. Comput. Methods Appl. Mech. Eng. 1994, 118, 1–11. [Google Scholar] [CrossRef]
- Craig, R.R., Jr.; Kurdila, A.J. Fundamentals of Structural Dynamics; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Gholampour, A.; Ghassemieh, M. New implicit method for analysis of problems in nonlinear structural dynamics. Appl. Comput. Mech. 2011, 5, 15–20. [Google Scholar]
- Hart, G.C.; Wong, K. Structural Dynamics for Structural Engineers; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Bangash, M.Y.H. Analyses, Numerical Computations, Codified Methods; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Dormand, J.R. Numerical Methods for Differential Equations. A Computational Approach; CRC Press: Boca Ratón, FL, USA, 1996. [Google Scholar]
- Henrici, P. Discrete Variable Methods in Ordinary Differential Equations; John Wiley & Sons: New York, NY, USA, 1962. [Google Scholar]
- Herrick, S. Astrodynamics. Vol. 2: Orbit Correction, Perturbation Theory Integration; Van Nostrand Reinhold: London, UK, 1972. [Google Scholar]
- González, A.B.; Martín, P. A note concerning Gauss-Jackson method. Extr. Math. 1996, 11, 255–260. [Google Scholar]
- Scheifele, G. On Numerical Integration of Perturbed Linear Oscillating Systems. Z. Für Angew. Math. Phys. 1971, 22, 186–210. [Google Scholar] [CrossRef]
- Stiefel, E.L.; Scheifele, G. Linear and Regular Celestial Mechanics; Springer: New York, NY, USA, 1971. [Google Scholar]
- Stiefel, E.; Bettis, D.G. Stabilization of Cowell’s Method. Numer. Math. 1969, 13, 154–175. [Google Scholar] [CrossRef]
- Bettis, D.G. Stabilization of finite difference methods of numerical integration. Celest. Mech. 1970, 2, 282–295. [Google Scholar] [CrossRef]
- Bettis, D.G. Numerical integration of products of Fourier and ordinary polinomials. Numer. Math. 1970, 14, 421–434. [Google Scholar] [CrossRef]
- Martín, P.; Ferrándiz, J.M. Behaviour of the SMF method for the numerical integration of satellite orbits. Celest. Mech. Dyn. Astron. 1995, 63, 29–40. [Google Scholar] [CrossRef]
- Martín, P.; Ferrándiz, J.M. Multistep numerical methods based on Scheifele G-functions with application to satellite dynamics. SIAM J. Numer. Anal. 1997, 34, 359–375. [Google Scholar] [CrossRef]
- Martín, P.; Ferrándiz, J.M. Numerical integration of perturbed linear systems. Appl. Math. 1999, 31, 183–189. [Google Scholar] [CrossRef]
- Martín, P.; Farto, J.M. Increasing the order of the SMF method for a special type of problem. SIAM J. Numer. Anal. 1998, 35, 773–777. [Google Scholar] [CrossRef]
- You, X.; Zhang, Y.; Zhao, J. Trigonometrically-Fitted Scheifele Two-Step. Methods for Perturbed Oscillators. Comput. Phys. 2011, 182, 1481–1490. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ferrándiz, J.M. Higher-order variable-step algorithms adapted to the accurate numerical integration of perturbed oscillators. Comput. Phys. 1998, 12, 467–470. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ferrándiz, J.M. A general procedure for the adaptation of multistep algorithms to the integration of oscillatory problems. SIAM J. Numer. Anal. 1998, 35, 1684–1708. [Google Scholar] [CrossRef]
- Reyes, J.A.; García-Alonso, F.; Ferrándiz, J.M.; Vigo-Aguiar, J. Numeric multistep variable methods for perturbed linear system integration. Appl. Math. Comput. 2007, 190, 63–79. [Google Scholar] [CrossRef]
- García-Alonso, F.; Reyes, J.A. A new approach for exact integration of some perturbed stiff linear systems of oscillatory type. Appl. Math. Comput. 2009, 215, 2649–2662. [Google Scholar] [CrossRef]
- García-Alonso, F.; Reyes, J.A.; Villacampa, Y. A new approach for multistep numerical methods in several frequencies for perturbed oscillators. Adv. Eng. Softw. 2012, 45, 252–260. [Google Scholar] [CrossRef]
- Khalsaraei, M.M.; Shokri, A. An explicit six-step singularly P-stable Obrechkoff method for the numerical solution of second-order oscillatory value problems. Numer. Algorithms 2020, 84, 871–886. [Google Scholar] [CrossRef]
- Ramos, H.; Kalogiratou, Z.; Monovasilis, T.; Simos, T.E. An optimized two-step hybrid block method for solving general second order initial-value problems. Numer. Algorithms 2016, 72, 1089–1102. [Google Scholar] [CrossRef]
- Ramos, H.; Rufai, M.A. A new one-step method with three intermediate points in a variable step-size mode for stiff differential systems. J. Math. Chem. 2023, 61, 673–688. [Google Scholar] [CrossRef]
- Ramos, H.; Metha, S.; Vigo-Aguiar, J. A unified approach for the development of k-step block Falkner-type methods for saving general second-order initial-value problems in ODES. J. Comput. Appl. Math. 2017, 318, 550–564. [Google Scholar] [CrossRef]
- Abdulganiy, R.I.; Ramos, H.O.; Akinfenwa, A.; Okunuga, S.A. A functionally-fitted block Numerov method for solving second-order initial-value problems with oscillatory solutions. Mediterr. J. Math. 2021, 18, 259. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ramos, H. Variable stepsize implementation of multistep methods for y″ = f(x, y, y′). J. Comput. Appl. Math. 2006, 192, 114–131. [Google Scholar] [CrossRef]
- Papadopoulos, D.F.; Anastassi, Z.A.; Simos, T.E. A phase-fitted Runge-Kutta-Nyström methods for the numerical solution of initial value problems with oscillating solutions. Comput. Phys. Commun. 2009, 180, 1839–1846. [Google Scholar] [CrossRef]
- Yang, H.; Wu, X.; You, X.; Fang, Y. Extended RKN-type methods for numerical integration of perturbed oscillators. Comput. Phys. Commun. 2009, 180, 1777–1794. [Google Scholar] [CrossRef]
- Yang, H.; Zeng, X.; Wu, X.; Ru, Z. A Simplified Nystrom-Tree Theory for Extended Runge-Kutta-Nystrom Integrators Solving. Comput. Phys. Commun. 2014, 185, 2841–2850. [Google Scholar] [CrossRef]
- González, A.B.; Farto, J.M.; López, D.J. Reformulation of the RKGM Methods using Scheifele Expansions. Appl. Math. Lett. 2000, 13, 63–66. [Google Scholar] [CrossRef]
- Fang, Y.; Wu, X. A New Pair of Explicit ARKN Methods for the Numerical Integration of General Perturbed Oscillators. Appl. Numer. Math. 2007, 57, 166–175. [Google Scholar] [CrossRef]
- You, X.; Zhao, J.; Yang, H.; Fang, Y.; Wu, X. Order Conditions for RKN Methods Solving General Second-Order Oscillatory Systems. Numer. Algor. 2014, 66, 147–176. [Google Scholar] [CrossRef]
- Martín, P.; López, D.J.; García, A. Implementation of Falkner method for problems of the form y” = f(x,y). Appl. Math. Comput. 2000, 109, 183–187. [Google Scholar] [CrossRef]
- Franco, J.M. New Methods for Oscillatory Systems Based on ARKN Methods. Appl. Numer. Math. 2006, 56, 1040–1053. [Google Scholar] [CrossRef]
- García-Alonso, F.; Reyes, J.A.; Cortés-Molina, M. An algorithm for the numerical integration of perturbed and damped second-order ODE systems. Mathematics 2020, 8, 2028. [Google Scholar] [CrossRef]
- Simos, T.E.; Vigo-Aguiar, J. Exponentially fitted symplectic integrator. Phys. Rev. E 2003, 67, 016701. [Google Scholar] [CrossRef] [PubMed]
- Ramos, J.I. Piecewise-linearized methods for initial-value problems with oscillating solutions. Appl. Math. Comput. 2006, 181, 123–146. [Google Scholar] [CrossRef]
- Van de Vyver, H. Two-step hybrid methods adapted to the numerical integration of perturbed oscillators. arXiv 2007, arXiv:math/0612637v1. [Google Scholar]
- Janin, G. Accurate computation of highly eccentric satellite orbits. Celest. Mech. 1974, 10, 451–456. [Google Scholar] [CrossRef]
- Ferrándiz, J.M.; Sansaturio, M.E.; Pojman, J.R. Increased accuracy of computations in the main satellite problem through linearization methods. Celest. Mech. 1992, 53, 347–364. [Google Scholar] [CrossRef]
- MacDonald, I.G. Symmetric Functions and Hall Polynomials; Oxford University Press Inc.: New York, NY, USA, 1998. [Google Scholar]
- Vigo-Aguiar, J. An approach to variable coefficients methods for special differential equations. Int. J. Appl. Math. 1999, 8, 911–921. [Google Scholar]
- Steffensen, J.F. On the Differential Equations of Hill in the Theory of the Motion of the Moon. Acta Math. 1955, 93, 169–177. [Google Scholar] [CrossRef]
- Steffensen, J.F. On the Differential Equations of Hill in the Theory of the Motion of the Moon (II). Acta Math. 1956, 95, 25–37. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Alonso, F.; Reyes, J.A.; Cortés-Molina, M. A Multistep Method for Integration of Perturbed and Damped Second-Order ODE Systems. Mathematics 2024, 12, 2018. https://doi.org/10.3390/math12132018
García-Alonso F, Reyes JA, Cortés-Molina M. A Multistep Method for Integration of Perturbed and Damped Second-Order ODE Systems. Mathematics. 2024; 12(13):2018. https://doi.org/10.3390/math12132018
Chicago/Turabian StyleGarcía-Alonso, Fernando, José Antonio Reyes, and Mónica Cortés-Molina. 2024. "A Multistep Method for Integration of Perturbed and Damped Second-Order ODE Systems" Mathematics 12, no. 13: 2018. https://doi.org/10.3390/math12132018
APA StyleGarcía-Alonso, F., Reyes, J. A., & Cortés-Molina, M. (2024). A Multistep Method for Integration of Perturbed and Damped Second-Order ODE Systems. Mathematics, 12(13), 2018. https://doi.org/10.3390/math12132018





