Chaotic Phenomena, Sensitivity Analysis, Bifurcation Analysis, and New Abundant Solitary Wave Structures of The Two Nonlinear Dynamical Models in Industrial Optimization
Abstract
1. Introduction
2. Exposition of the Mentioned Method
3. Application of the LWE
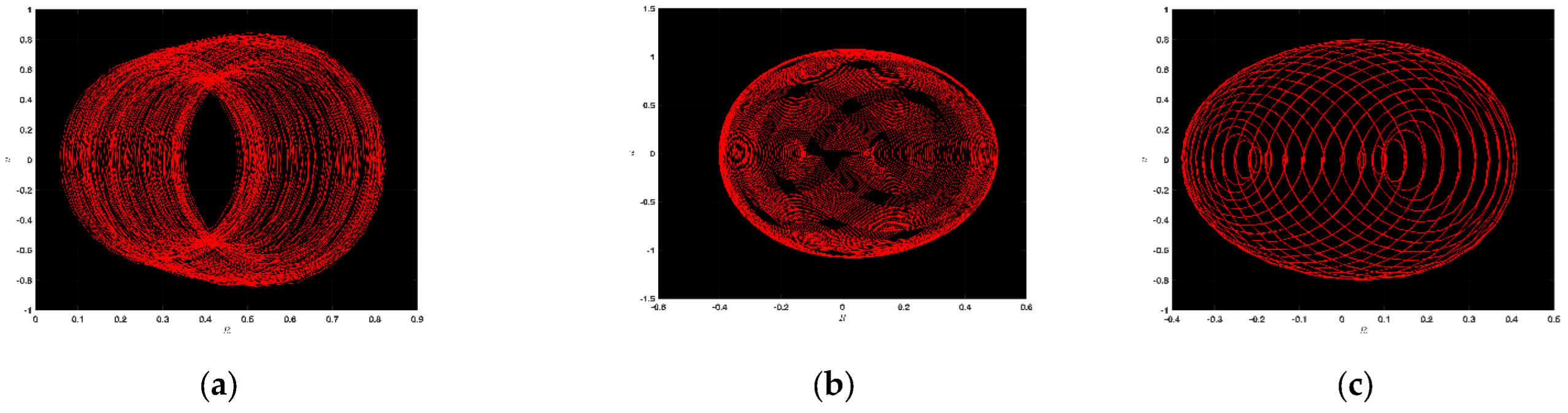
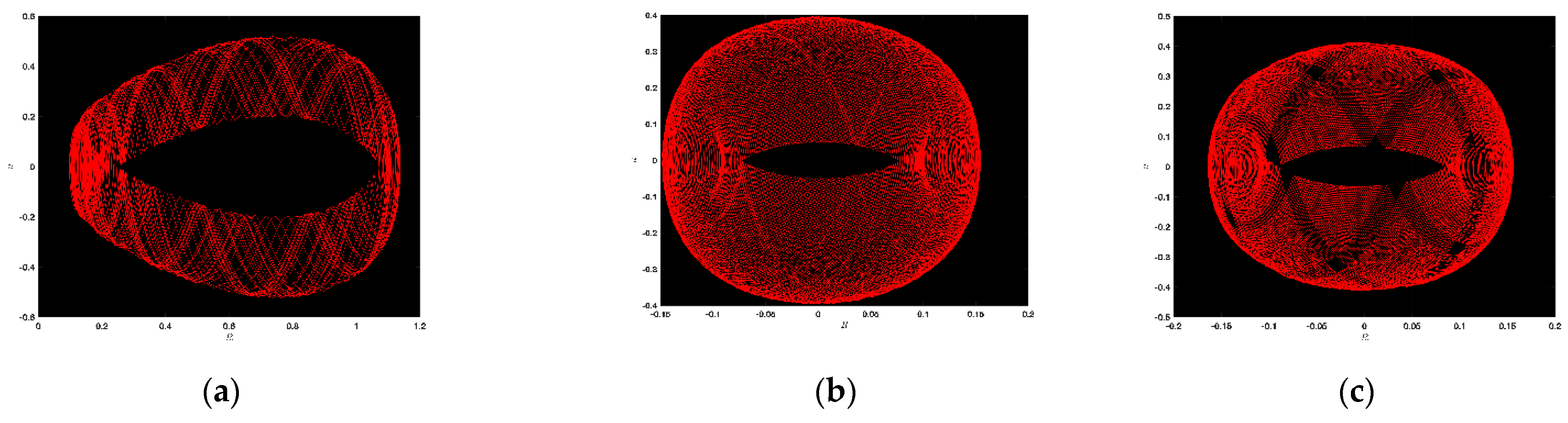
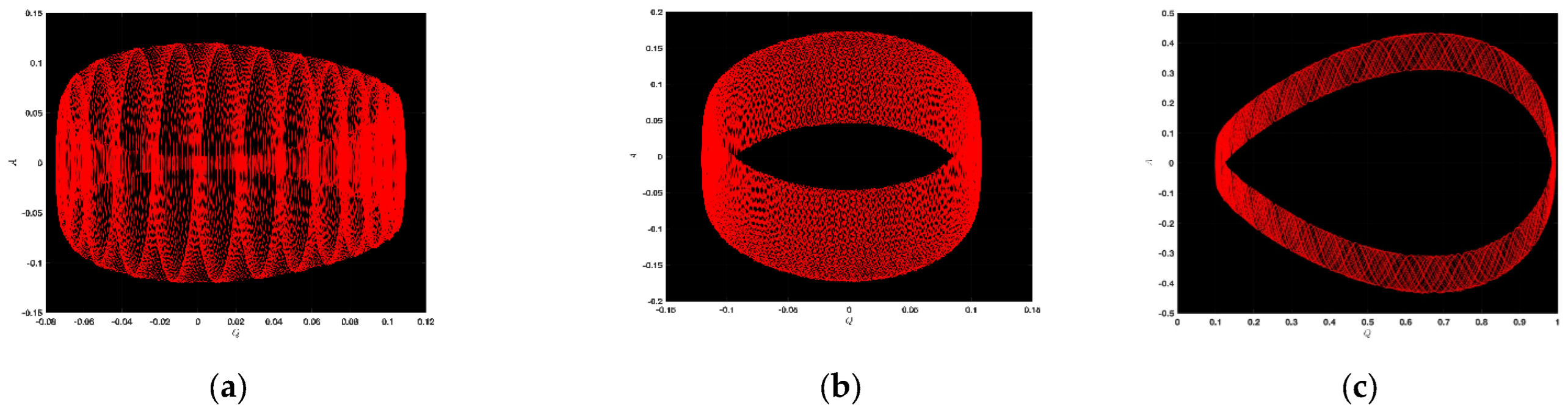
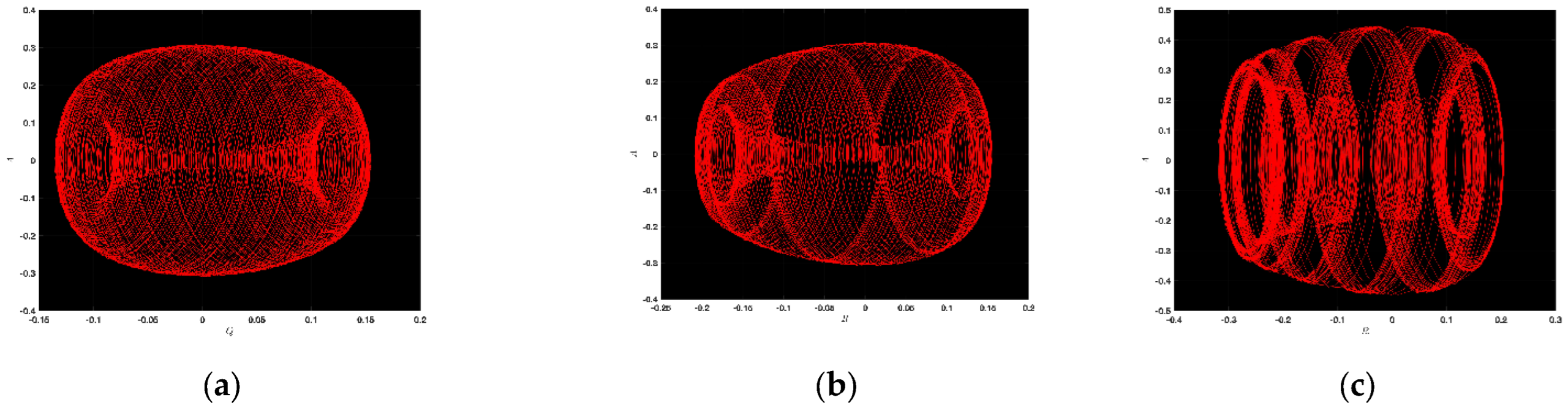
3.1. Chaotic Analysis of LWE
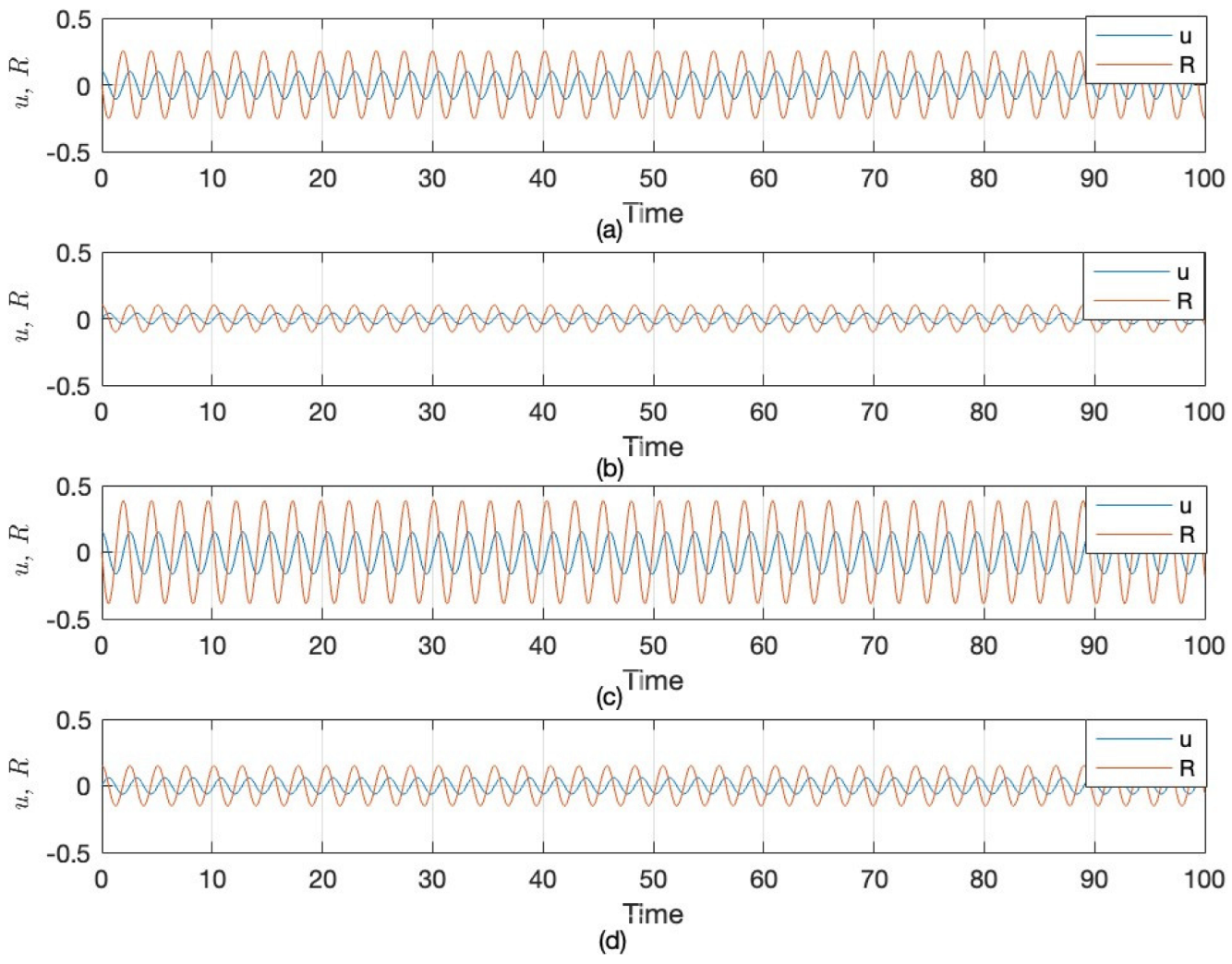
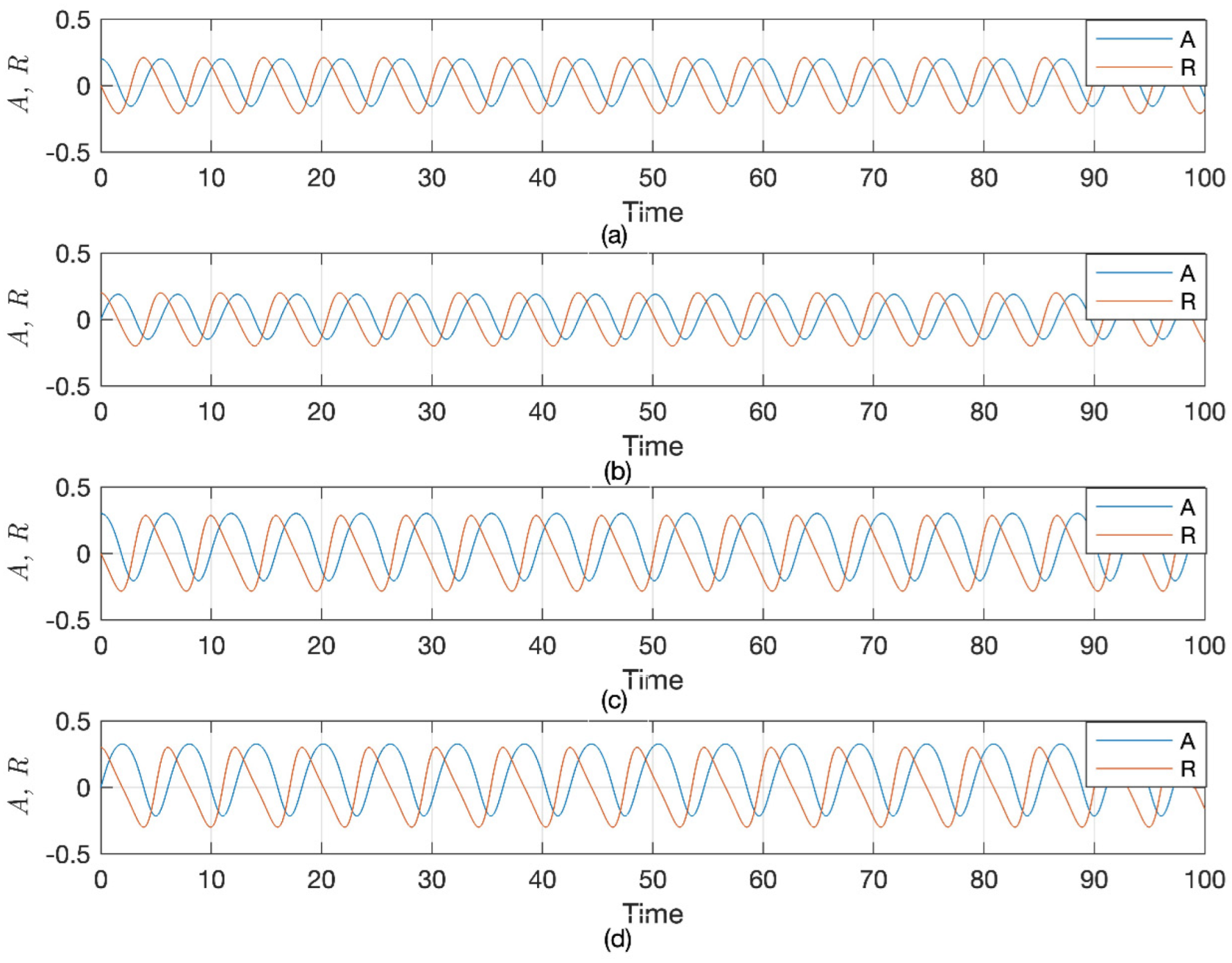
3.2. Sensitivity Analysis of LWE
- (i)
- and ;
- (ii)
- and ;
- (iii)
- and ;
- (iv)
- and
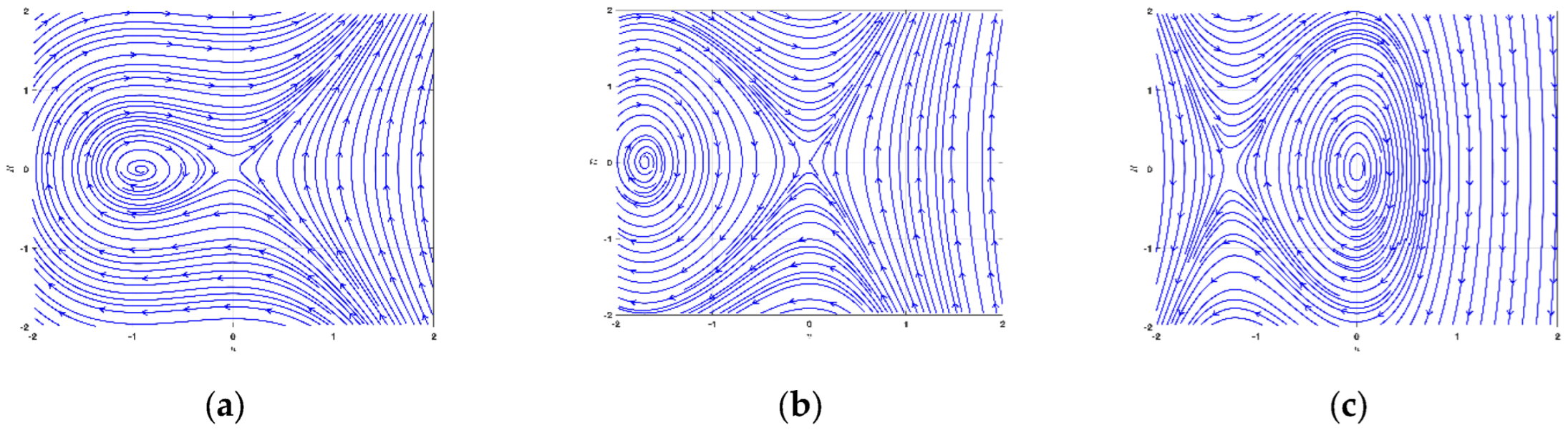
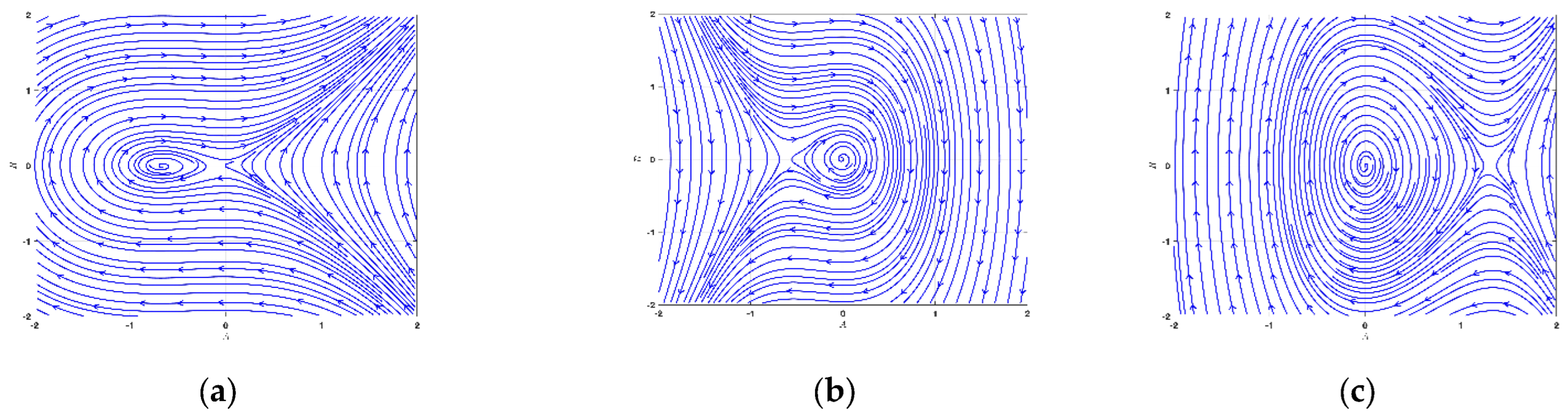
3.3. Bifurcation and Phase Portrait Analysis of LWE
- The equilibrium position denotes a saddle point, whereas ;
- The equilibrium position stands for a center point, whereas ;
- The equilibrium position characterizes a cuspid point, whereas .
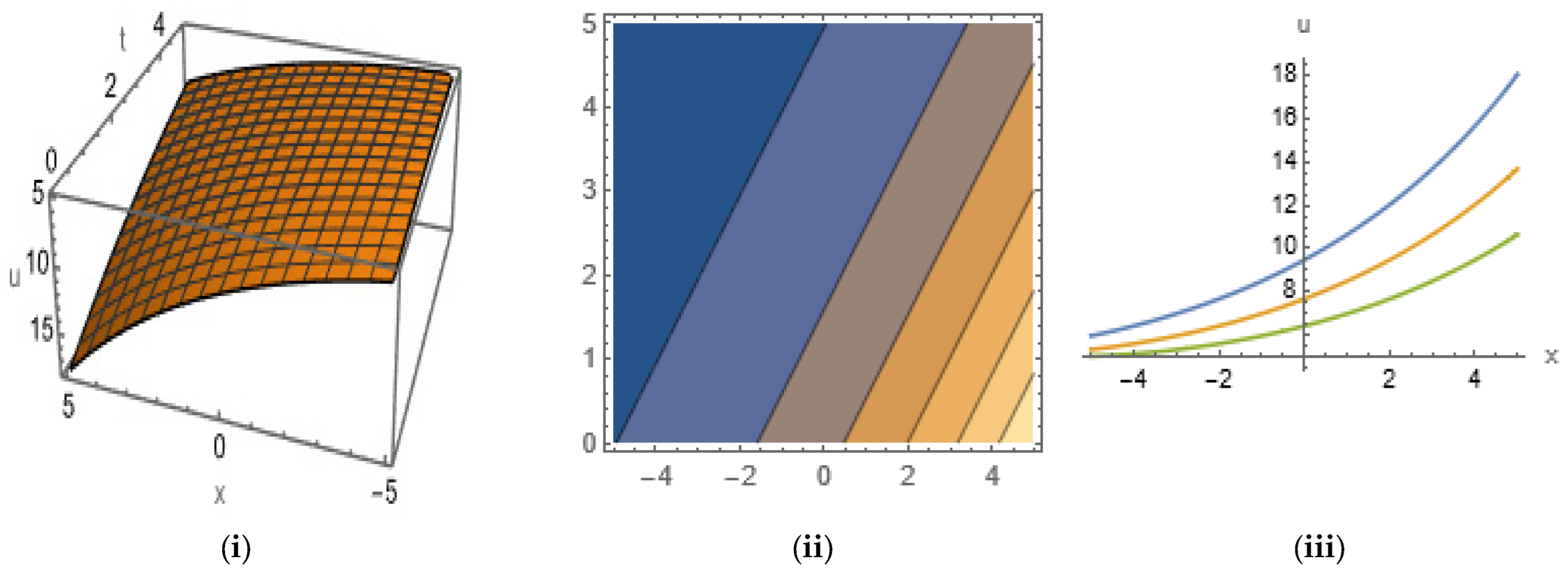
3.4. Soliton Solutions of LWE
4. Application of the SNNVS
4.1. Chaotic Analysis of SNNVS
4.2. Sensitivity Analysis of SNNVS
- (i)
- and ;
- (ii)
- and ;
- (iii)
- and ;
- (iv)
- and
4.3. Bifurcation and Phase Portrait Analysis of SNNVS
- The equilibrium standpoint refer to a saddle point, while ;
- The equilibrium standpoint means a center point, while ;
- The equilibrium standpoint implies a cuspid point, while .
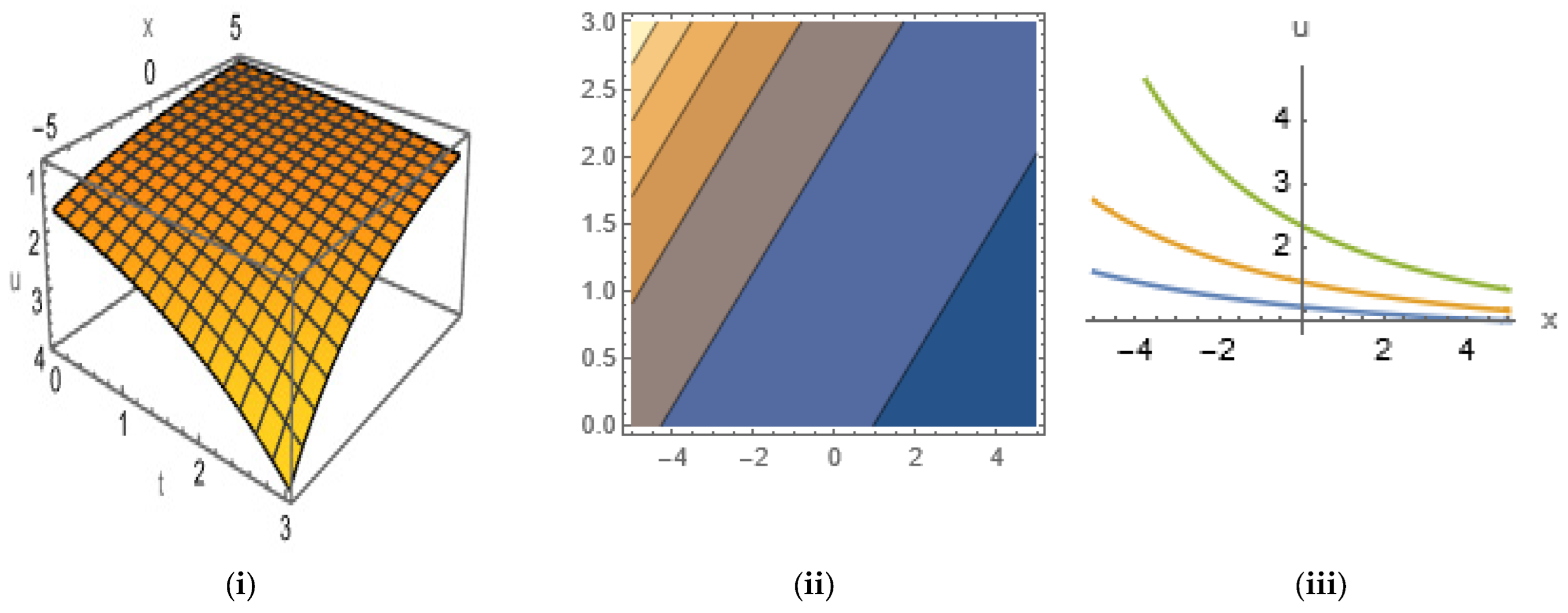
4.4. Soliton Solutions of SNNVS
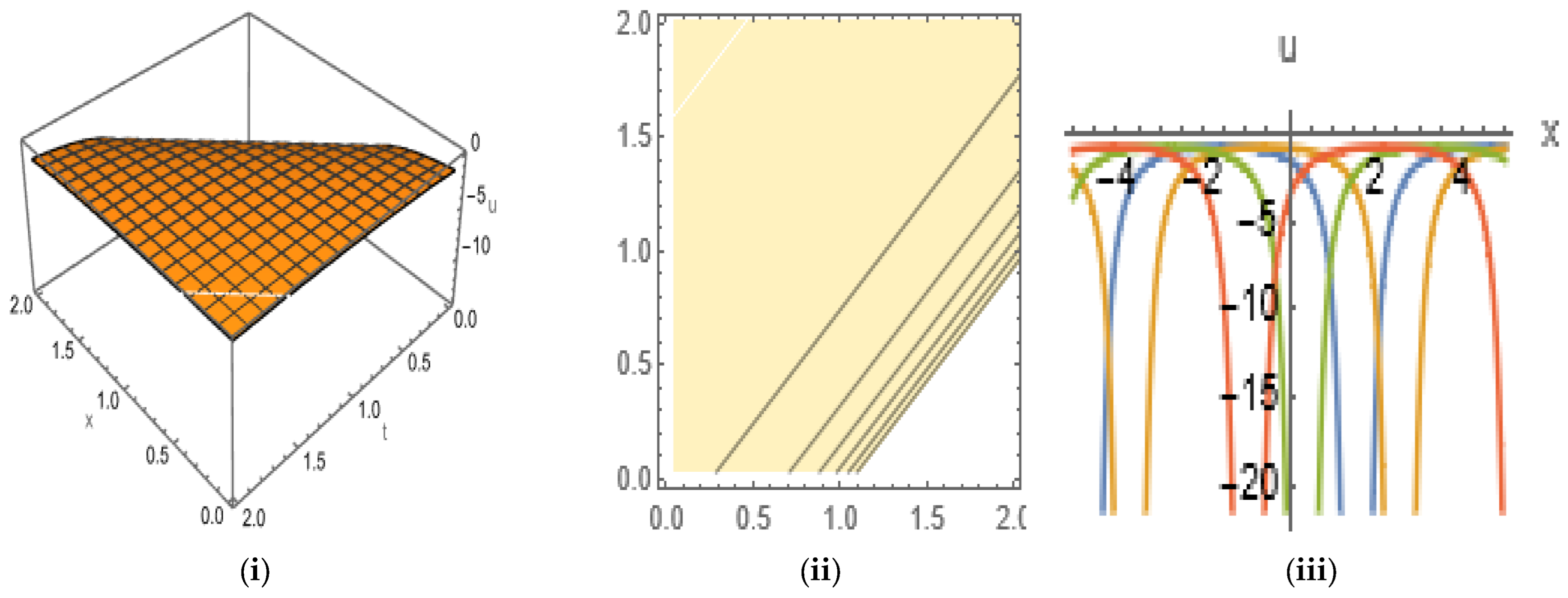
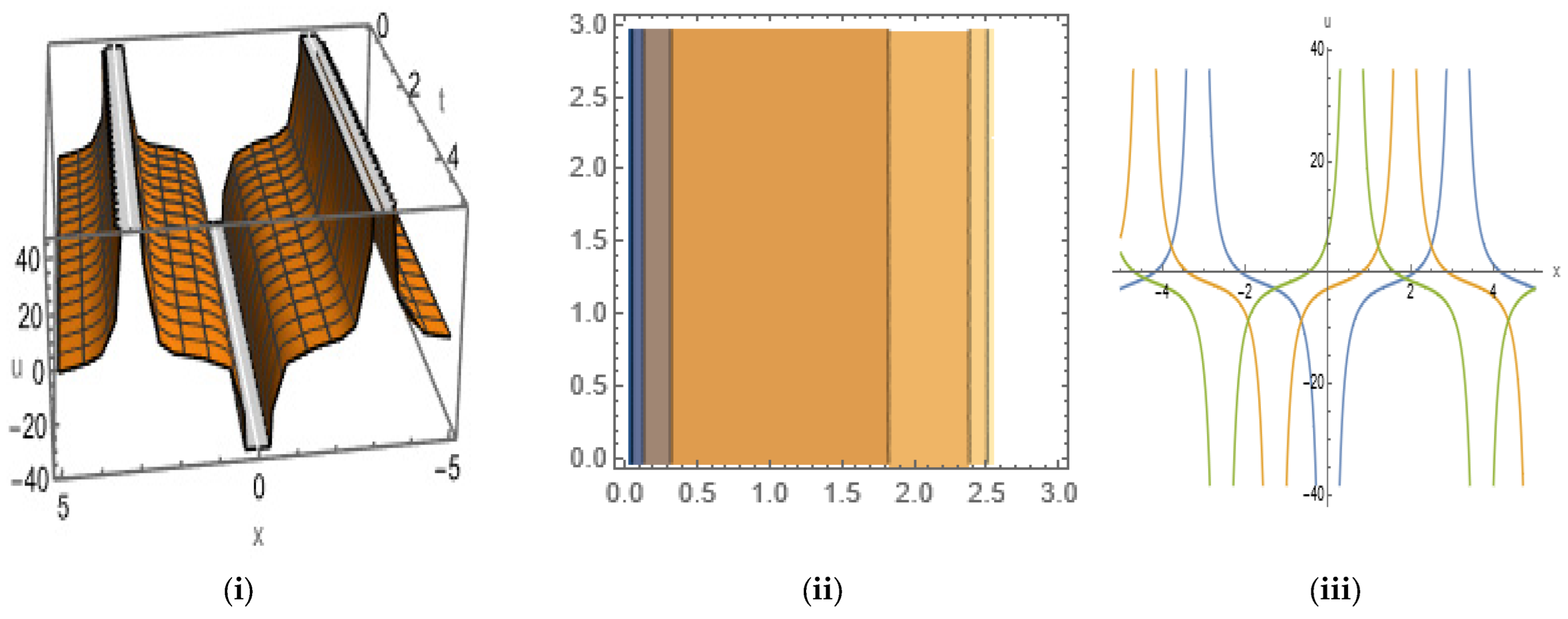
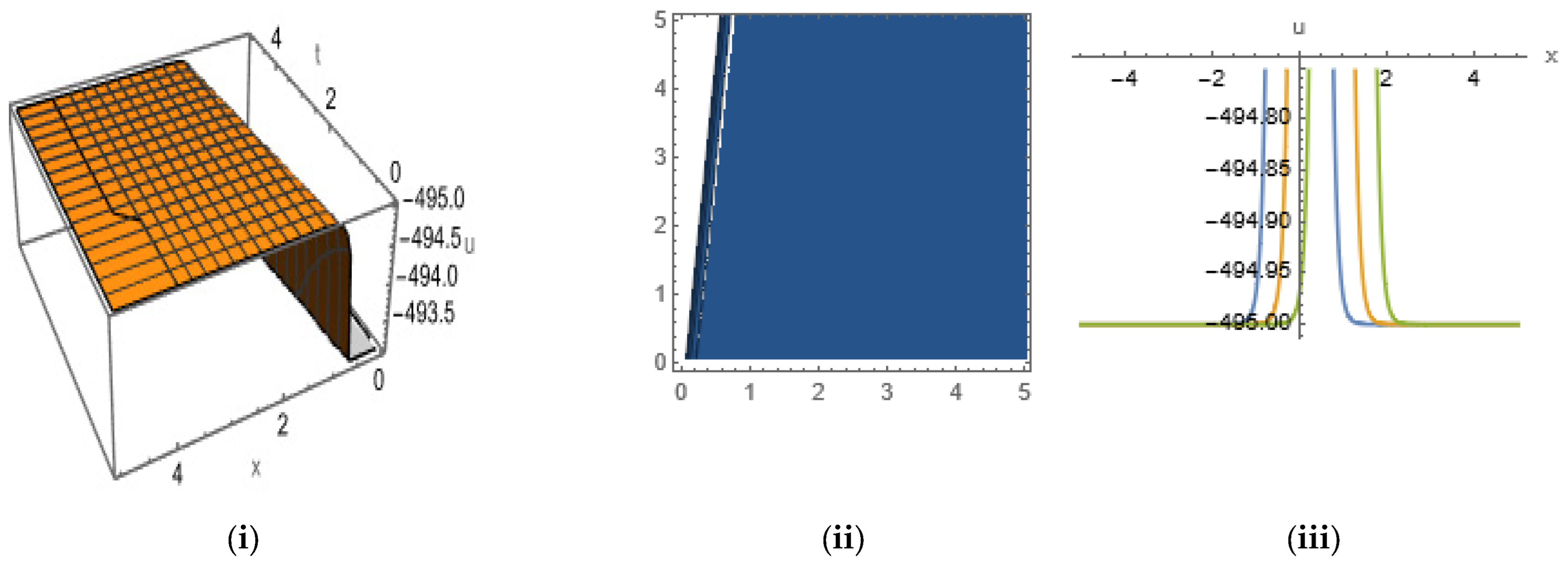
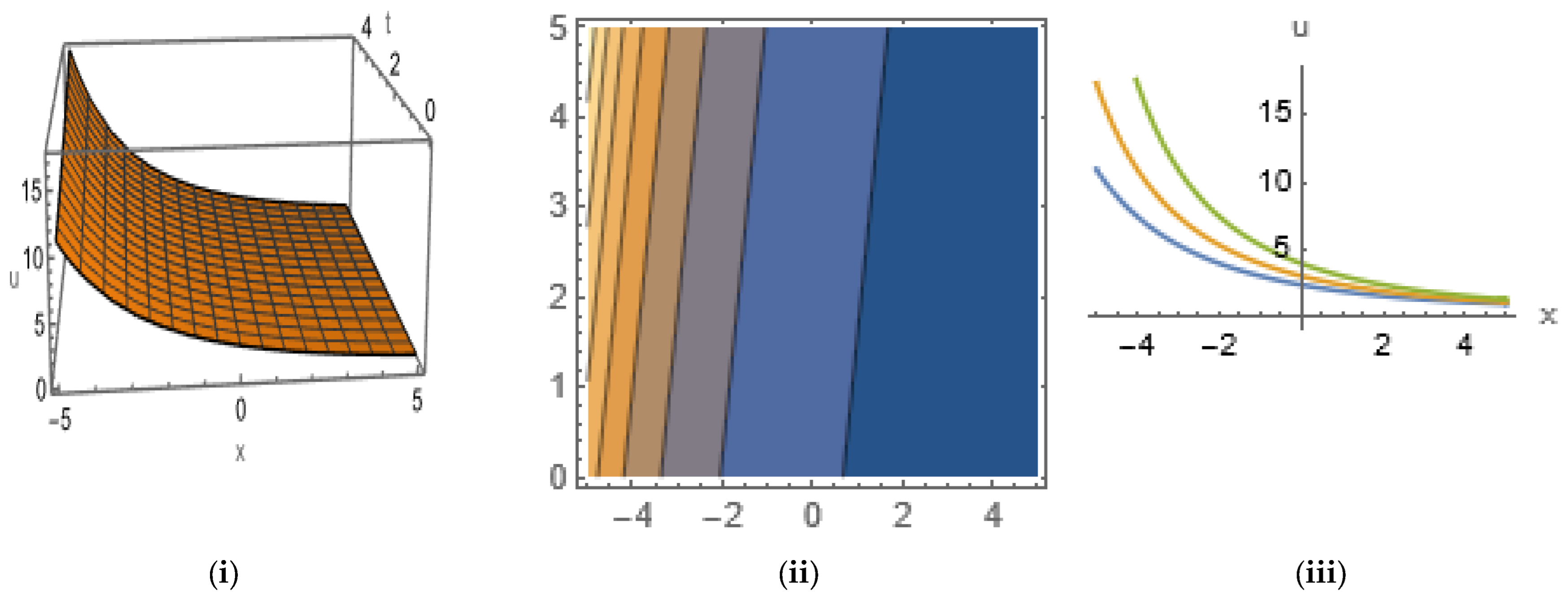
5. Graphical Representation of Soliton Solutions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Malwe, B.H.; Betchewe, G.; Doka, S.Y.; Kofane, T.C. Travelling wave solutions and soliton solutions for the nonlinear transmission line using the generalized Riccati equation mapping method. Nonlinear Dyn. 2016, 84, 171–177. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y. A new version of the generalized F-expansion method for the fractional Biswas-Arshed equation and Boussinesq equation with the beta-derivative. J. Funct. Spaces 2023, 3, 1–14. [Google Scholar] [CrossRef]
- Zhao, Y.M. F-expansion method and its application for finding new exact solutions to the Kudryashov-Sinelshchikov equation. J. Appl. Math. 2023, 2023, 895760. [Google Scholar] [CrossRef]
- Na, S. Auxiliary equation method and new solutions of Klein-Gordon equation. Chaos Solitons Fractals 2007, 31, 943–950. [Google Scholar]
- Liu, Y.; Wu, G. Using a new auxiliary equation to construct abundant solutions for nonlinear evolution equations. J. Appl. Math. Phys. 2021, 9, 12. [Google Scholar] [CrossRef]
- SLiu, K.; Fu, Z.T.; Liu, S.D.; Zhao, Q. Jacobi elliptic function method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar]
- Hussain, A.; Chahlaoui, Y.; Zaman, F.D.; Parveen, T.; Hassan, A.M. The Jacobi elliptic function method and its application for the stochastic NNV system. Alex. Eng. J. 2023, 81, 347–359. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rashidy, K.E. Travelling wave solution for some coupled nonlinear evolution equations. Math. Comput. Model. 2013, 57, 1371–1379. [Google Scholar] [CrossRef]
- Taghizadeh, N.; Neirameh, A.; Shokooh, S. New application of the direct algebraic method to Eckhaus equation. Trends Appl. Sci. Res. 2012, 7, 476–482. [Google Scholar] [CrossRef]
- Ohwada, T. Cole-Hopf transformation as a numerical tool for the Burgers equation. Appl. Comput. Math. 2009, 8, 107–113. [Google Scholar]
- Rong, F.; Li, Q.; Shi, B.; Chai, Z. A lattice Boltzmann model based on Cole-Hopf transformation for N-dimensional coupled Burgers’ equations. Comput. Math. Appl. 2023, 134, 101–111. [Google Scholar] [CrossRef]
- Mamun, A.A.; Ananna, S.N.; Gharami, P.P.; An, T.; Asaduzzaman, M. The improved modified extended tanh-function method to develop the exact travelling wave solutions of a family of 3D fractional WBBM equations. Results Phys. 2022, 41, 105969. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Wu, J.; Wang, Y.; Chen, C. Extended tanh-function method and its applications in nonlocal complex mKdV equations. Mathematics 2022, 10, 3250. [Google Scholar] [CrossRef]
- Carillo, S.; Schiebold, C. Soliton equations: Admitted solutions and invariances via Bäcklund transformations. Open Commun. Nonlinear Math. Phys. 2024, 1, 1–11. [Google Scholar] [CrossRef]
- Liu, J.G.; He, Y. New periodic solitary wave solutions for the (3+1)-dimensional generalized shallow water equation. Nonlinear Dyn. 2017, 90, 363–369. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The Hirota’s bilinear method and the tanh-coth method for multiple-soliton solutions of the Sawada-Kotera-Kadomstsev-Petviashvili equation. Appl. Math. Comput. 2008, 200, 160–166. [Google Scholar]
- Kumar, S.; Mohan, B. A novel and efficient method for obtaining Hirota’s bilinear form for the nonlinear evolution equation in (n+1)-dimensions. Partial. Differ. Equ. Appl. Math. 2022, 5, 100274. [Google Scholar] [CrossRef]
- Ghanbari, B. Employing Hirota’s bilinear form to find novel lump waves solutions to an important nonlinear model in fluid mechanics. Results Phys. 2021, 29, 104689. [Google Scholar] [CrossRef]
- Chadwick, E.; Hatam, A.; Kazem, S. Exponential function method for solving nonlinear ordinary differential equations with constant coefficients on a semi-infinite domain. Proc.-Indian Acad. Math. Sci. 2016, 126, 79–97. [Google Scholar] [CrossRef]
- Kadkhoda, N.; Jafari, H. Analytical solutions of the Gerdjikov-Ivanov equation by using exp(−Φ(ξ))-expansion method. Optic 2017, 139, 72–76. [Google Scholar] [CrossRef]
- Rahman, M.M.; Habib, M.A.; Ali, H.M.S.; Miah, M.M. The generalized Kudryashov method: A renewed mechanism for performing exact solitary wave solutions of some NLEEs. J. Mech. Contin. Math. Sci. 2019, 14, 323–339. [Google Scholar] [CrossRef]
- Ekici, M. Exact solutions to some nonlinear time-fractional evolution equations using the generalized Kudryashov method in mathematical physics. Symmetry 2023, 15, 1961. [Google Scholar] [CrossRef]
- Yousif, A.A.; AbdulKhaleq, F.A.; Mohsin, A.K.; Mohammed, O.H.; Malik, A.M. A developed technique of homotopy analysis method for solving nonlinear systems of Volterra integro-differential equations of fractional order. Partial. Differ. Equ. Appl. Math. 2023, 8, 100548. [Google Scholar] [CrossRef]
- Gusu, D.M.; Gudeta, W. Solving Nonlinear Partial Differential Equations of Special Kinds of 3rd Order Using Balance Method and Its Models. Int. J. Differ. Equ. 2023, 2023, 7663326. [Google Scholar] [CrossRef]
- Wang, M.; Li, X. Simplified homogeneous balance method and its applications to the Whitham-Broer-Kaup model equations. J. Appl. Math. Phys. 2014, 2, 8. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alurrfi, K.A.E. The homogeneous balance method and its applications for finding the exact solutions for nonlinear evolution equations. Ital. J. Pure Appl. Math. 2014, 33, 307–318. [Google Scholar]
- Neamaty, A.; Agheli, B.; Darzi, R. Variational iteration method and He’s polynomials for time-fractional partial differential equations. Prog. Fract. Differ. Appl. 2015, 1, 47–55. [Google Scholar]
- Pham, V.H.S.; Dang, N.T.N.; Nguyen, V.N. Enhancing engineering optimization using hybrid sine cosine algorithm with Roulette wheel selection and opposition-based learning. Sci. Rep. 2024, 14, 694. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.A.; Miah, M.M.; Ali, H.M.S.; Shahen, N.H.M.; Deifalla, A. New applications of the fractional derivative to extract abundant soliton solutions of the fractional order PDEs in mathematics physics. Partial. Differ. Equ. Appl. Math. 2024, 9, 100597. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Miah, M.M.; Rasid, M.M.; Alshehri, H.M.; Osman, M.S. An investigation of two integro-differential KP hierarchy equations to find out closed form solitons in mathematical physics. Arab. J. Basic Appl. Sci. 2023, 30, 535–545. [Google Scholar] [CrossRef]
- Ganie, A.H.; Sadek, L.H.; Tharwat, M.M.; Iqbal, M.A.; Miah, M.M.; Rasid, M.M.; Elazab, N.S.; Osman, M.S. New investigation of the analytical behaviors for some nonlinear PDEs in mathematical physics and modern engineering. Partial. Differ. Equ. Appl. Math. 2024, 9, 100608. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J. The (G’/G)-expansion method and travelling wave solutions of nonlinear evolution equation in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar]
- Khan, A.T.; Naher, H. Some New Non-Travelling Wave Solutions of the Fisher Equation with Nonlinear Auxiliary Equation. Orient. J. Phys. Sci. 2018, 3, 92–101. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A. New approach of (G’/G)-expansion method and new approach of generalized (G’/G)-expansionmethod for nonlinear evolution equation. AIP Adv. 2013, 3, 032116. [Google Scholar] [CrossRef]
- Zayed, E.M.E. The (G’/G)-expansion method and its applications to some nonlinear evolution equations in the mathematical physics. J. Appl. Math. Comput. 2009, 30, 89–103. [Google Scholar] [CrossRef]
- Shakeel, M.; Mohyud-Din, S.T. Modified (G’/G)-expansion method with generalized Riccati equation to the sixth-order Boussinesq equation. Ital. J. Pure Appl. Math. 2013, 30, 393–410. [Google Scholar]
- Saba, F.; Jabeen, S.; Akbar, H.; Mohyud-Din, S.T. Modified alternative (G’/G)-expansion method to general Sawada-Kotera equation of fifth-order. J. Egypt. Math. Soc. 2015, 23, 416–423. [Google Scholar] [CrossRef]
- Zhu, M. Solving the Burgers-Huxley equation by (G’/G)-expansion method. J. Appl. Math. Phys. 2016, 4, 7. [Google Scholar] [CrossRef][Green Version]
- Bin, Z. (G’/G)-expansion method for solving fractional partial differential equations in the theory of mathematical physics. Commun. Theor. Phys. 2012, 58, 623. [Google Scholar]
- Akçağıl, Ş.; Aydemir, T. Comparison between the (G’/G)-expansion method and the modified extended tanh method. Open Phys. 2016, 14, 88–94. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Baleanu, D.; Miah, M.M.; Ali, H.M.S.; Alshehri, H.M.; Osman, M.S. New soliton solutions of the mZK equation and the Gerdjikov-Ivanov equation by employing the double (G’/G, 1/G)-expansion method. Results Phys. 2023, 47, 106391. [Google Scholar] [CrossRef]
- Miah, M.M.; Seadawy, A.R.; Ali, H.M.S.; Akbar, M.A. Abundant closed form wave solutions to some nonlinear evolution equations in mathematical physic. J. Ocean. Eng. Sci. 2020, 5, 269–278. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Wang, Y.; Miah, M.M.; Osman, M.S. Study on Date-Jimbo-Kashiwara-Miwa equation with conformable derivative dependent on time parameter to find the exact dynamic wave solutions. Fractal Fract. 2022, 6, 4. [Google Scholar] [CrossRef]
- Inc, M.; Miah, M.M.; Chowdhury, A.; Ali, H.M.S.; Rezazadeh, H.; Akinlar, M.A.; Chu, Y.M. New exact solutions for Kaup-Kupershmidt equation. AIMS Math. 2020, 5, 6726–6738. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. Some applications of the (G’/G, 1/G)expansion method for finding exact traveling wave solutions of nonlinear fractional evolution equations. Symmetry 2019, 11, 952. [Google Scholar] [CrossRef]
- Hossain, M.N.; Alsharif, F.; Miah, M.M.; Kanan, M. Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization. Mathematics 2024, 12, 1585. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Miah, M.M.; Iqbal, M.A.; Alshehri, H.M.; Baleanu, D.; Osman, M.S. Advanced exact solutions to the nano-ionic currents equation through MTs and the soliton equation containing the RLC transmission line. Eur. Phys. J. Plus 2023, 138, 502. [Google Scholar] [CrossRef]
- Miah, M.M.; Iqbal, M.A.; Osman, M.S. A study on stochastic longitudinal wave equation in a magneto-electro-elastic annular bar to find the analytical solutions. Commun. Theor. Phys. 2023, 75, 085008. [Google Scholar] [CrossRef]
- Duran, S. Travelling wave solutions and simulation of the Lonngren wave equation for tunnel diode. Opt. Quantum Electron. 2021, 53, 8. [Google Scholar] [CrossRef]
- Roshid, M.M.; Rahman, M.M.; Bashar, M.H.; Hossain, M.M.; Mannaf, M.A.; Roshid, H.O. Dynamical simulation of wave solutions for the M-fractional Lonngren wave equation using two distinct methods. Alex. Eng. J. 2023, 81, 460–468. [Google Scholar] [CrossRef]
- Ahmad, J.; Mustafa, Z.; Rehman, S.U.; Turki, N.B.; Shah, N.A. Solitary wave structures for the stochastic Nizhnik-Novikov-Veselov system via modified generalized rational exponential function method. Results Phys. 2023, 52, 106776. [Google Scholar] [CrossRef]
- Shaikh, T.S.; Baber, M.Z.; Ahmed, N.; Iqbal, M.S.; Akgül, A.; Din, S.M.E. Investigation of solitary wave structures for the stochastic Nizhnik–Novikov–Veselov (SNNV) system. Results Phys. 2023, 48, 106389. [Google Scholar] [CrossRef]
- Jhangeer, A.; Almusawa, H.; Hussain, Z. Bifurcation study and pattern formation analysis of a nonlinear dynamical system for chaotic behavior in traveling wave solution. Results Phys. 2022, 37, 105492. [Google Scholar] [CrossRef]
- Li, Z.; Hu, H. Chaotic pattern, bifurcation, sensitivity and traveling wave solution of the coupled Kundu-Mukherjee-Naskar equation. Results Phys. 2023, 48, 106441. [Google Scholar] [CrossRef]
- Rafiq, M.H.; Raza, N.; Jhangeer, A. Dynamic study of bifurcation, chaotic behavior and multi-soliton profiles for the system of shallow water wave equations with their stability. Chaos Solitons Fractals 2023, 171, 113436. [Google Scholar] [CrossRef]
- Wang, P.; Yin, F.; Rahman, M.U.; Khan, M.A.; Baleanu, D. Unveiling complexity: Exploring chaos and solitons in modified nonlinear Schrödinger equation. Results Phys. 2024, 56, 107268. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miah, M.M.; Alsharif, F.; Iqbal, M.A.; Borhan, J.R.M.; Kanan, M. Chaotic Phenomena, Sensitivity Analysis, Bifurcation Analysis, and New Abundant Solitary Wave Structures of The Two Nonlinear Dynamical Models in Industrial Optimization. Mathematics 2024, 12, 1959. https://doi.org/10.3390/math12131959
Miah MM, Alsharif F, Iqbal MA, Borhan JRM, Kanan M. Chaotic Phenomena, Sensitivity Analysis, Bifurcation Analysis, and New Abundant Solitary Wave Structures of The Two Nonlinear Dynamical Models in Industrial Optimization. Mathematics. 2024; 12(13):1959. https://doi.org/10.3390/math12131959
Chicago/Turabian StyleMiah, M. Mamun, Faisal Alsharif, Md. Ashik Iqbal, J. R. M. Borhan, and Mohammad Kanan. 2024. "Chaotic Phenomena, Sensitivity Analysis, Bifurcation Analysis, and New Abundant Solitary Wave Structures of The Two Nonlinear Dynamical Models in Industrial Optimization" Mathematics 12, no. 13: 1959. https://doi.org/10.3390/math12131959
APA StyleMiah, M. M., Alsharif, F., Iqbal, M. A., Borhan, J. R. M., & Kanan, M. (2024). Chaotic Phenomena, Sensitivity Analysis, Bifurcation Analysis, and New Abundant Solitary Wave Structures of The Two Nonlinear Dynamical Models in Industrial Optimization. Mathematics, 12(13), 1959. https://doi.org/10.3390/math12131959




