Constructing Solutions to Multi-Term Cauchy–Euler Equations with Arbitrary Fractional Derivatives

Abstract

We further extend the results of other researchers on existence theory to homogeneous fractional Cauchy–Euler equations ${\displaystyle \sum _{i=1}^m}{d}_i{x}^{{\alpha }_i}{D}^{{\alpha }_i}u\left(x\right)+\mu u\left(x\right)=0,{\alpha }_i>0,$ with the derivatives in Caputo or Riemann–Liouville sense. Unlike the existing works, we consider multi-term equations without any restrictions on the order of fractional derivatives. The results are based on the characteristic equations which generate the solutions. Depending on the roots of the characteristic equations (real, multiple, or complex), we construct the corresponding solutions and prove their linear independence.

1. Introduction

We consider the following multi-term fractional Cauchy–Euler equation:

$$\sum _{i=1}^m{d}_i{x}^{{\alpha }_i}{D}^{{\alpha }_i}u\left(x\right)+\mu u\left(x\right)=0,\mu ,d_i\in \mathbb{R},$$

(1)

where $D^{{\alpha }_i}$ are fractional derivatives of order ${\alpha }_i>0$. Let us introduce $n_{\max }=\underset{1\le i\le m}{max}\lceil {\alpha }_i\rceil$. Thus, $n_{\max }$ is the lowest integer number above the highest ${\alpha }_i,i=1,\dots ,m$. The fractional derivatives considered here are understood either in Riemann–Liouville

$$D_R^{\alpha }u\left(x\right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}\frac{d^n}{d{x}^n}{\int }_0^x\frac{u\left(t\right)dt}{{(x-t)}^{\alpha +1-n}}$$

(2)

or Caputo sense

$$D_C^{\alpha }u\left(x\right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_0^x\frac{u^{\left(n\right)}\left(t\right)dt}{{(x-t)}^{\alpha +1-n}},$$

(3)

where $n-1<\alpha <n,n\in \mathbb{N}$, and $\mathrm{\Gamma }$ is the gamma function.

We use notation $D^{\alpha }u\left(t\right)$ for either derivative and demonstrate the differences in these two definitions of fractional derivatives where applicable.

Using integral Mellin transform, A.A. Kilbas and N.V. Zhukovskaya [1,2] constructed a mathematical theory for a three-term equation with subsequent derivatives:

$$x^{\alpha +2}\left(D^{\alpha +2}y\right)\left(x\right)+\mu x^{\alpha +1}\left(D^{\alpha +1}y\right)\left(x\right)+\lambda x^{\alpha }\left(D^{\alpha }y\right)\left(x\right)=f\left(x\right).$$

A multi-term equation with subsequent derivatives

$$\sum _{k=0}^m{a}_k{x}^{\alpha +k}{D}_R^{\alpha +k}u\left(x\right)=f\left(x\right)$$

was analyzed in [3], where the author represents solution in the form of a Riemann–Liouville fractional integral, which converts the equation into an equation with integer derivatives, then uses the Mellin transform. However, in view of the limitations caused by the integral transforms, the developed technique for subsequent derivatives [1,2,3] cannot be extended further to the derivatives of arbitrary orders because the Mellin transform will not end up as a polynomial.

The goal of this paper is to construct the solutions for fractional Cauchy–Euler equations without any restrictions on derivatives. To achieve this goal, we introduce an approach that is without the use of integral transforms.

2. Constructing Solutions

Similarly to the case with integer derivatives, we assume that the solution to Equation (1) can be represented as $x^{\gamma }$. The formula

$$D^{\alpha }{x}^{\gamma }=\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -\alpha )}{x}^{\gamma -\alpha }$$

(4)

holds if $\gamma >-1$ for Riemann–Liouville derivatives and if $\gamma >\lceil \alpha \rceil -1$ for Caputo derivatives. These restrictions are needed to ensure the existence of the corresponding derivatives. If we substitute (4) into Equation (1),

$$\begin{array}{c}\hfill x^{\gamma }\left(\sum _{i=1}^m{d}_i\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}+\mu \right)=0,\end{array}$$

then we arrive at the characteristic equation

$$\sum _{i=1}^m\frac{d_i·\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}+\mu =0.$$

(5)

If it has p simple roots ${\gamma }_i$, $1\le i\le p$, then

$$u\left(x\right)=\sum _{i=1}^p{c}_i{x}^{{\gamma }_i},c_i\in \mathbb{R},$$

(6)

is a solution. Taking into account the domain of existence of fractional derivatives, we pick only ${\gamma }_i>-1$ for Riemann–Liouville derivatives and ${\gamma }_i>n_{\max }-1$ for Caputo derivatives. Here, $n_{\max }={max}_{1\le i\le m}\lceil {\alpha }_i\rceil$.

Let us consider complex roots to the characteristic equation.

Lemma 1. 

If the root of Equation (5) is complex, then the conjugate of the root is also a root of characteristic Equation (5).

Proof. 

Let $\gamma$, which is the root of Equation (5), be a complex number. Based on the properties of the $\mathrm{\Gamma }$-function, we know that $\overline{\mathrm{\Gamma }\left(z\right)}=\mathrm{\Gamma }\left(\overline{z}\right)$; therefore,

$$\begin{array}{c}\hfill \sum _{i=1}^m\frac{d_i·\mathrm{\Gamma }\left(\overline{1+\gamma }\right)}{\mathrm{\Gamma }\left(\overline{1+\gamma -{\alpha }_i}\right)}=\sum _{i=1}^m\frac{d_i·\overline{\mathrm{\Gamma }(1+\gamma )}}{\overline{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}}.\end{array}$$

Using

$$\begin{array}{ccc}& & \frac{a\pm bi}{c\pm di}=\frac{ac+bd\pm i(bc-ad)}{c^2+d^2},\hfill \end{array}$$

(7)

we see that if $\gamma$ is the complex root of Equation (5) and $\mu \in \mathbb{R}$, then the imaginary part in the sum of (5) is zero. But the imaginary parts in (7) only differ by the sign. Hence, the real part under the sum in Equation (5) of the conjugate of the root $\overline{\gamma }$ is the same as for the root $\gamma$ and is the solution to Equation (5). □

Each root of (5) represents a solution $x^{\gamma }$ if the fractional derivative for that root exists. In the case of complex roots for (5), for each pair of conjugates we obtain

$$u\left(x\right)=x^{\Re \left(\gamma \right)}\left(Acos(\Im (\gamma )lnx)+Bsin(\Im (\gamma )lnx)\right),$$

(8)

where $\Re \left(\gamma \right)\ge n_{\max }-1$ for Caputo derivatives, and $\Re \left(\gamma \right)>-1$ for Riemann–Liouville derivatives. Thus, we can state the following result:

Theorem 1. 

For the simple real roots γ of characteristic Equation (5), the solutions are $x^{\gamma }$. For complex roots, the corresponding solutions are $x^{\Re \left(\gamma \right)}cos(\Im \left(\gamma \right)lnx)$ and $x^{\Re \left(\gamma \right)}sin(\Im \left(\gamma \right)lnx)$.

Let us consider real roots $\gamma$ with multiplicity greater than one.

Theorem 2. 

Let the multiplicity of a real root $\widehat{\gamma }$ to characteristic Equation (5) be $k>1$ and $\widehat{\gamma }$ belong to the admissible domain of the existence of fractional derivatives. Then, the corresponding solutions are $x^{\widehat{\gamma }},x^{\widehat{\gamma }}lnx,x^{\widehat{\gamma }}{ln}^{2}x,\dots ,x^{\widehat{\gamma }}{ln}^{k-1}x$.

Proof. 

Since $\widehat{\gamma }$ has multiplicity k, then $g_0\left(\widehat{\gamma }\right)=0$, where

$$g_0\left(\gamma \right)=\frac{1}{{(\gamma -\widehat{\gamma })}^{k-1}}\left(\sum _{i=1}^m\frac{d_i·\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}+\mu \right).$$

However, $\gamma =\widehat{\gamma }$ is not a root of function

$$g\left(\gamma \right)=\frac{1}{{(\gamma -\widehat{\gamma })}^k}\left(\sum _{i=1}^m\frac{d_i·\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}+\mu \right).$$

Therefore, let us consider the roots of function ${(\gamma -\widehat{\gamma })}^{k}g\left(\gamma \right)$.

We know that ([4] Table 9.1)

$$D^{\alpha }\left(x^{\gamma }{ln}^{j}x\right)=x^{\gamma -\alpha }\sum _{n=0}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){(lnx)}^{j-n}·\frac{{\partial }^n}{\partial {\gamma }^n}\left(\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -\alpha )}\right),n\in \mathbb{N}.$$

(9)

We substitute $u=x^{\widehat{\gamma }}{ln}^{j}x,1\le j\le k-1,$ in Equation (1) and obtain

$$\begin{array}{ccc}& & \sum _{i=1}^m{d}_i{x}^{{\alpha }_i}{D}^{{\alpha }_i}u\left(x\right)+\mu u\left(x\right)\hfill \\ & & =\sum _{i=1}^m{d}_i{x}^{{\alpha }_i}·x^{\widehat{\gamma }-{\alpha }_i}\sum _{n=0}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){(lnx)}^{j-n}·\frac{{\partial }^n}{\partial {\gamma }^n}\left(\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}\right){|}_{\gamma =\widehat{\gamma }}+\mu x^{\widehat{\gamma }}{ln}^{j}x\hfill \\ & & =x^{\widehat{\gamma }}\sum _{n=0}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){(lnx)}^{j-n}·\sum _{i=1}^m{d}_i\frac{{\partial }^n}{\partial {\gamma }^n}\left(\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}\right){|}_{\gamma =\widehat{\gamma }}+\mu x^{\widehat{\gamma }}{ln}^{j}x.\hfill \end{array}$$

Let us take out the term for $n=0$ in the above sum. This will give us

$$\begin{array}{c}\sum _{i=1}^m{d}_i{x}^{{\alpha }_i}{D}^{{\alpha }_i}u\left(x\right)+\mu u\left(x\right)=x^{\widehat{\gamma }}{ln}^{j}x\left(\sum _{i=1}^m{d}_i\frac{\mathrm{\Gamma }(1+\widehat{\gamma })}{\mathrm{\Gamma }(1+\widehat{\gamma }-{\alpha }_i)}+\mu \right)\hfill \\ +x^{\widehat{\gamma }}\sum _{n=1}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){(lnx)}^{j-n}·\sum _{i=1}^m{d}_i\frac{{\partial }^n}{\partial {\gamma }^n}\left(\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}\right){|}_{\gamma =\widehat{\gamma }}.\hfill \end{array}$$

(10)

The first term in expression (10) contains characteristic Equation (5) and, thus, is equal to zero. Hence,

$$\begin{array}{ccc}& & \sum _{i=1}^m{d}_i{x}^{{\alpha }_i}{D}^{{\alpha }_i}u\left(x\right)+\mu u\left(x\right)\hfill \\ & =& x^{\widehat{\gamma }}\sum _{n=1}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){(lnx)}^{j-n}·\frac{{\partial }^n}{\partial {\gamma }^n}\left(\sum _{i=1}^m{d}_i\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -{\alpha }_i)}+\mu \right){|}_{\gamma =\widehat{\gamma }}\hfill \\ & =& x^{\widehat{\gamma }}\sum _{n=1}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){(lnx)}^{j-n}·\frac{{\partial }^n}{\partial {\gamma }^n}\left({(\gamma -\widehat{\gamma })}^{k}g\left(\gamma \right)\right){|}_{\gamma =\widehat{\gamma }}.\hfill \end{array}$$

(11)

Expression (11) is equal to zero because $\widehat{\gamma }$, the solution of characteristic Equation (5), has multiplicity k and, therefore, all n-th derivatives of ${(\gamma -\widehat{\gamma })}^{k}g\left(\gamma \right)$ are zero for $0<n<k$. This proves Theorem 2. □

In the case of the Caputo derivative, all solutions that we considered have the form $x^{\gamma }·f\left(x\right)$, provided that $\gamma >n_{max}-1$. This condition is necessary for the existence of the Caputo derivative; therefore, all of its derivatives up to $n_{max}-1$ at zero are equal to zero. The correspondence between the Riemann–Liouville and Caputo derivative is [5]

$$D_R^{\alpha }(x^{\gamma }·f\left(x\right))=D_C^{\alpha }\left(x^{\gamma }·f\left(x\right)\right)+\sum _{k=0}^{n_{max}-1}\frac{{\left[x^{\gamma }·f\left(x\right)\right]}_{x=0}^{\left(k\right)}}{\mathrm{\Gamma }(1+k-\alpha )}·x^{k-\alpha }=D_C^{\alpha }\left(x^{\gamma }·f\left(x\right)\right).$$

(12)

The above formula is based on the Leibniz rule:

$${\left(x^{\gamma }·f\left(x\right)\right)}^{\left(j\right)}=\sum _{n=0}^j\left(\genfrac{}{}{0pt}{}{j}{n}\right){\left(x^{\gamma }\right)}^{(j-n)}·f^{\left(n\right)}\left(x\right),$$

and the equality ${\left(x^{\gamma }\right)}^{(j-n)}{|}_{x=0}=0$ for $\gamma >n_{max}-1$ and $0\le n\le j$ hinges on the boundedness of function $f\left(x\right)$ and its derivatives. For complex roots $\gamma$, such a boundedness holds in view of $f\left(x\right)=sin\left(x\right)$ or $cos\left(x\right)$. Consequently, the sum in (12) is equal to zero.

In the case of multiple roots, $f\left(x\right)={ln}^{j-k}\left(x\right)$, $k=1,\dots ,j-1$, and, in view of $\gamma >j$, we again obtain zero for the sum thanks to the fact that $\underset{x\to 0}{lim}{\left(x^{\gamma }\right)}^{(j-n)}{\left({ln}^{j-k}x\right)}^{\left(n\right)}=0$. Finally, we obtain the equality of the Riemann–Liouville and Caputo derivatives (12), which justifies the above proof of Theorem 2 for both types of fractional derivatives.

3. Linear Independence of Solutions

As we can see from Section 2, all solutions have forms $x^{\gamma },\gamma \in \mathbb{C}$, or $x^{\gamma }{ln}^{j}x$ in the case of roots $\gamma$ with multiplicity k, $j=1,\dots ,k-1$.

Lemma 2. 

Let ${\gamma }_i$ be simple roots of characteristic Equation (5) (i.e., the roots of multiplicity one). Then, solutions $x^{{\gamma }_i},i=1,\dots ,k$, are linearly independent.

Proof. 

The Wronskian for functions $x^{{\gamma }_i},i=1,\dots k$, at $x=1$ is as follows:

$$\begin{array}{ccc}\hfill W(x^{{\gamma }_1},\dots ,x^{{\gamma }_k}){|}_{x=1}& =& \left|\begin{array}{cccc}1& 1& \dots & 1\\ {\gamma }_1& {\gamma }_2& \dots & {\gamma }_k\\ \dots & \dots & \dots & \dots \\ \prod _{i=0}^{k-2}({\gamma }_1-i)& \prod _{i=0}^{k-2}({\gamma }_2-i)& \dots & \prod _{i=0}^{k-2}({\gamma }_k-i)\end{array}\right|\hfill \\ & =& \left|\begin{array}{cccc}\frac{\mathrm{\Gamma }(1+{\gamma }_1)}{\mathrm{\Gamma }(1+{\gamma }_1)}& \frac{\mathrm{\Gamma }(1+{\gamma }_2)}{\mathrm{\Gamma }(1+{\gamma }_2)}& \dots & \frac{\mathrm{\Gamma }(1+{\gamma }_k)}{\mathrm{\Gamma }(1+{\gamma }_k)}\\ \frac{\mathrm{\Gamma }(1+{\gamma }_1)}{\mathrm{\Gamma }\left({\gamma }_1\right)}& \frac{\mathrm{\Gamma }(1+{\gamma }_2)}{\mathrm{\Gamma }\left({\gamma }_2\right)}& \dots & \frac{\mathrm{\Gamma }(1+{\gamma }_k)}{\mathrm{\Gamma }\left({\gamma }_k\right)}\\ \dots & \dots & \dots & \dots \\ \frac{\mathrm{\Gamma }(1+{\gamma }_1)}{\mathrm{\Gamma }({\gamma }_1-i)}& \frac{\mathrm{\Gamma }(1+{\gamma }_2)}{\mathrm{\Gamma }({\gamma }_2-i)}& \dots & \frac{\mathrm{\Gamma }(1+{\gamma }_k)}{\mathrm{\Gamma }({\gamma }_k-i)}\\ \dots & \dots & \dots & \dots \\ \frac{\mathrm{\Gamma }(1+{\gamma }_1)}{\mathrm{\Gamma }({\gamma }_1-k+1)}& \frac{\mathrm{\Gamma }(1+{\gamma }_2)}{\mathrm{\Gamma }({\gamma }_2-k+1)}& \dots & \frac{\mathrm{\Gamma }(1+{\gamma }_k)}{\mathrm{\Gamma }({\gamma }_k-k+1)}\end{array}\right|\hfill \end{array}$$

$$\begin{array}{c}\hfill =\prod _{i=1}^k\mathrm{\Gamma }(1+{\gamma }_i)·\left|\begin{array}{cccc}\frac{1}{\mathrm{\Gamma }(1+{\gamma }_1)}& \frac{1}{\mathrm{\Gamma }(1+{\gamma }_2)}& \dots & \frac{1}{\mathrm{\Gamma }(1+{\gamma }_k)}\\ \frac{1}{\mathrm{\Gamma }\left({\gamma }_1\right)}& \frac{1}{\mathrm{\Gamma }\left({\gamma }_2\right)}& \dots & \frac{1}{\mathrm{\Gamma }\left({\gamma }_k\right)}\\ \dots & \dots & \dots & \dots \\ \frac{1}{\mathrm{\Gamma }({\gamma }_1-i)}& \frac{1}{\mathrm{\Gamma }({\gamma }_2-i)}& \dots & \frac{1}{\mathrm{\Gamma }({\gamma }_k-i)}\\ \dots & \dots & \dots & \dots \\ \frac{1}{\mathrm{\Gamma }({\gamma }_1-k+1)}& \frac{1}{\mathrm{\Gamma }({\gamma }_2-k+1)}& \dots & \frac{1}{\mathrm{\Gamma }({\gamma }_k-k+1)}\end{array}\right|\end{array}$$

(13)

From [6],

$$det{\left[\frac{1}{\mathrm{\Gamma }(z_j-i)}\right]}_{i,j=0,\dots ,n-1}=\frac{1}{{\prod }_{j=0}^{n-1}\mathrm{\Gamma }\left(z_j\right)}{\Delta }_n\left(\mathbf{z}\right),$$

(14)

where

$${\Delta }_n\left(\mathbf{z}\right)=\Delta (z_0,\dots ,z_{n-1})=\left\{\begin{array}{cc}1,\hfill & n=1\hfill \\ \prod _{0\le i<j\le n-1}(z_i-z_j),\hfill & n=2,3,\dots \hfill \end{array}\right.$$

(15)

Therefore, the Wronskian is nonzero:

$$\begin{array}{c}\hfill W(x^{{\gamma }_1},\dots ,x^{{\gamma }_k})=\frac{{\prod }_{i=1}^k\mathrm{\Gamma }(1+{\gamma }_i)}{{\prod }_{j=1}^k\mathrm{\Gamma }(1+{\gamma }_j)}{\Delta }_k(1+\gamma )=\prod _{1\le i<j\le k}({\gamma }_i-{\gamma }_j)\ne 0.\end{array}$$

(16)

This proves Lemma 2. □

Lemma 3. 

If root γ has multiplicity j, then functions $x^{\gamma },x^{\gamma }lnx,\dots ,x^{\gamma }{ln}^{j-1}x$ are linearly independent and their linear combinations are the solutions to Equation (1).

Proof. 

At $x=1$, the Wronskian for these functions is as follows

$$\begin{array}{ccc}& & W(x^{\gamma },x^{\gamma }lnx,\dots ,x^{\gamma }{ln}^{j}x){|}_{x=1}\hfill \\ & =& \left|\begin{array}{ccccccc}1& 0& 0& 0& \dots & 0& 0\\ \gamma & 1& 0& 0& \dots & 0& 0\\ \gamma (\gamma -1)& 2\gamma -1& 2& 0& \dots & 0& 0\\ \gamma (\gamma -1)(\gamma -2)& 3{\gamma }^2-6\gamma +2& 6\gamma -1& 6& \dots & 0& 0\\ \dots & \dots & \dots & \dots & \dots & \dots \\ \prod _{k=0}^{j-3}(\gamma -k)& P_{j-3}\left(\gamma \right)& P_{j-4}\left(\gamma \right)& \dots & \dots & (j-2)!& 0\\ \prod _{k=0}^{j-2}(\gamma -k)& P_{j-2}\left(\gamma \right)& P_{j-3}\left(\gamma \right)& \dots & \dots & P_1\left(\gamma \right)& (j-1)!\end{array}\right|\hfill \\ & \phantom{=}& \phantom{WWWWWWWWWWWWWWWWWWWWWW}=\prod _{k=1}^{j-1}k!\ne 0.\hfill \end{array}$$

(17)

Here, $P_k\left(\gamma \right)$ are polynomials of order k. This proves Lemma 3. □

Theorem 3. 

Functions

$$x^{{\gamma }_1},x^{{\gamma }_2},\dots ,x^{{\gamma }_k},x^{{\gamma }_{r_1}}lnx,\dots ,x^{{\gamma }_{r_1}}{ln}^{j_1-1}x,\dots ,x^{{\gamma }_{r_p}}lnx,\dots ,x^{{\gamma }_{r_p}}{ln}^{j_p-1}x$$

are linearly independent. Here $j_i,i=1,\dots ,p$ is the multiplicity of root ${\gamma }_{r_i}$.

Proof. 

The functions are linearly independent if the only solution for the set of coefficients ${\left\{c_i\right\}}_{i=1}^n$

$$\begin{array}{ccc}\hfill c_1{x}^{{\gamma }_1}+\dots +c_k{x}^{{\gamma }_k}+c_{k+1}{x}^{{\gamma }_{r_1}}lnx+\dots +c_{k+j_1}{x}^{{\gamma }_{r_1}}{ln}^{j_1-1}x& & \hfill \\ \hfill +\dots +c_{n-j_p+1}{x}^{{\gamma }_{r_p}}lnx+c_n{x}^{{\gamma }_{r_p}}{ln}^{j_p-1}x& =& 0,\hfill \end{array}$$

(18)

($j_{r_l}$ is the multiplicity of the root $x^{{\gamma }_{r_l}}$) is the trivial solution $c_1=c_2=\dots =c_n=0$.

Let us define operator $D=x\frac{d}{dx}$. Then,

$$\begin{array}{c}D\left(x^{{\gamma }_i}\right)={\gamma }_i{x}^{{\gamma }_i},\hfill \\ (D-{\gamma }_i)x^{{\gamma }_i}=0,\hfill \\ (D-{\gamma }_j)x^{{\gamma }_i}=({\gamma }_i-{\gamma }_j)x^{{\gamma }_i},\hfill \\ (D-{\gamma }_i)(x^{{\gamma }_i}lnx)=(D-{\gamma }_i)({\gamma }_i{x}^{{\gamma }_i}lnx+x^{{\gamma }_i})=x^{{\gamma }_i},\hfill \\ (D-{\gamma }_j)(x^{{\gamma }_i}lnx)=(D-{\gamma }_j)({\gamma }_i{x}^{{\gamma }_i}lnx+x^{{\gamma }_i})=({\gamma }_i-{\gamma }_j)x^{{\gamma }_i}lnx+x^{{\gamma }_i},\hfill \\ (D-{\gamma }_i)\left(x^{{\gamma }_i}{ln}^{k}x\right)=(D-{\gamma }_i)({\gamma }_i{x}_i^{\gamma }{ln}^{k}x+x^{{\gamma }_i}{ln}^{k-1}x)=x^{{\gamma }_i}{ln}^{k-1}x.\hfill \end{array}$$

(19)

From the formulas in (19), we can conclude that if we apply operator $(D-{\gamma }_1)·\dots ·(D-{\gamma }_k)$ to Equation (18), it will eliminate all $x^{{\gamma }_i}$. In order to eliminate term $x^{{\gamma }_l}ln{x}^{j_l-i}x$, operator $(D-{\gamma }_l)$ should be applied j times. Eventually, we will be left only with all terms of one root of multiplicity $j_m$. The case of functions that represent only one root of multiplicity $j>1$ was considered in Lemma 3. Therefore, all coefficients $c_{n-j_m+1},\dots ,c_n$ have to be equal to zero. Then, we can do the same for the next set of roots of multiplicity that are higher than one, proving that their coefficients are also zero. Finally, we are left with the following equation:

$$c_1{x}^{{\gamma }_1}+c_2{x}^{{\gamma }_2}+\dots +c_k{x}^{{\gamma }_k}=0.$$

(20)

From Lemma 2, we know that these functions are linearly independent, and therefore, $c_1=c_2=\dots =c_k=0$ is the only solution for Equation (20), which makes all coefficients in (18) equal to zero. This proves Theorem 3. □

4. Examples

Example 1. 

Characteristic equation with two simple real roots.

Let us consider the following equation:

$$x^{1.6}{D}^{1.6}u\left(x\right)-2x^{0.8}{D}^{0.8}u\left(x\right)+u\left(x\right)=0.$$

(21)

Characteristic Equation (5), in this case, is as follows:

$$\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -1.6)}-2\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -0.8)}+1=0.$$

It has two simple real roots: ${\gamma }_1=0.15430751$ and ${\gamma }_1=2.3742236$ (Figure 1).

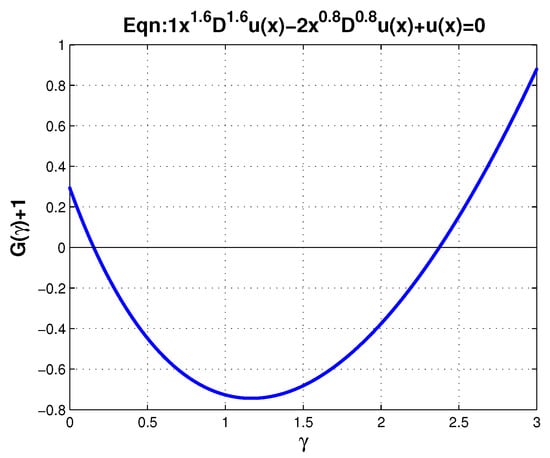
Figure 1. Graph of the left-hand side of the characteristic equation for (21), which has two simple real roots.

They correspond to two solutions in the case of Riemann–Liouville derivatives: $u_1\left(x\right)=x^{0.15430751}$ and $u_2\left(x\right)=x^{2.3742236}$. However, there is only one solution, $u_2$, for Caputo derivatives. Numerical method [7] confirms that solution $u_2$ is correct on interval $[0,3]$, with a precision of ${10}^{-3}$.

Example 2. 

Real root of multiplicity two.

Let us consider the following equation

$$0.277749678698444x^{1.6}{D}^{1.6}u\left(x\right)-0.895810258738965x^{0.8}{D}^{0.8}u\left(x\right)+u\left(x\right)=0.$$

(22)

Characteristic Equation (5), in this case, is as follows:

$$0.277749678698444\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -1.6)}-0.895810258738965\frac{\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -0.8)}+1=0.$$

It has one real root, ${\gamma }_1=2$, of multiplicity 2 (Figure 2).

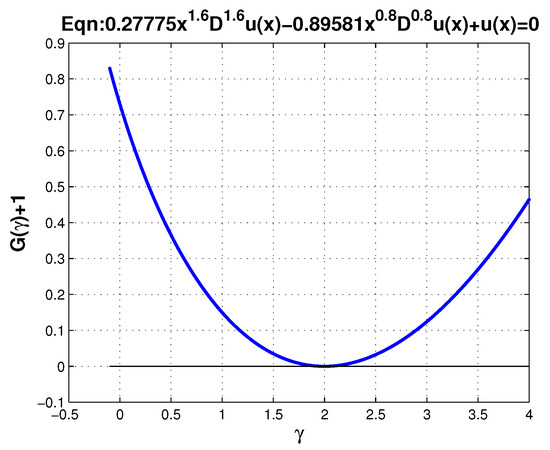
Figure 2. Characteristic equation for Equation (22) has one root, $\gamma =2$, of multiplicity 2.

The first solution, in this case, for both Riemann–Liouville and Caputo derivatives is $u_1\left(x\right)=x^2$, and the second solution is $u_2\left(x\right)=x^{2}lnx$. The substitution method of calculation for the Caputo derivative confirms that both solutions are correct, with a precision of ${10}^{-3}$ on the $[0,3]$ interval. The solutions are shown in Figure 3.

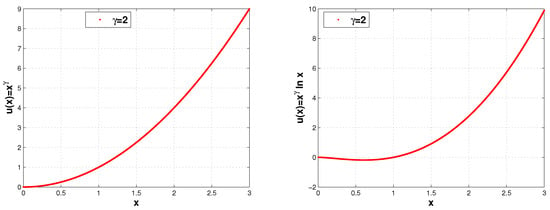
Figure 3. Solutions to Equation (22) with Caputo derivative. Both solutions correspond to the same multiple root $\gamma =2$ of the characteristic equatin.

Example 3. 

Two complex roots.

Let us consider the following equation:

$$0.3x^{1.6}{D}^{1.6}u\left(x\right)-0.8x^{0.8}{D}^{0.8}u\left(x\right)+u\left(x\right)=0.$$

(23)

Characteristic Equation (5), in this case, is as follows:

$$\frac{0.3·\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -1.6)}-\frac{0.8·\mathrm{\Gamma }(1+\gamma )}{\mathrm{\Gamma }(1+\gamma -0.8)}+1=0.$$

It has two complex roots, $\gamma =1.53663359\pm 1.13798709i$, and as we can see in Figure 4, since the graph of the left-hand side of the characteristic equation is in the upper half-plane, there are no real roots. We find complex roots computationally.

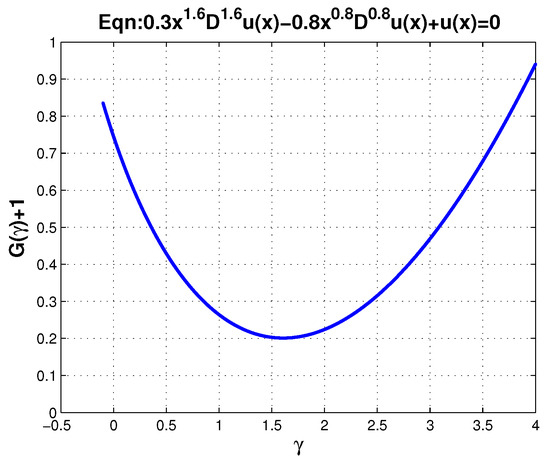
Figure 4. Solution of the characteristic equation to (23). It has no real roots.

The real part of the roots $\Re \left(\gamma \right)>1$, and therefore, we obtain two solutions for both Riemann–Liouville and Caputo derivatives: $u_1\left(x\right)=x^{1.53663359}sin(1.13798709lnx)$ and $u_2\left(x\right)=x^{1.53663359}cos(1.13798709lnx)$. The substitution method of calculation for the Caputo derivative [7] confirms that both solutions are correct, with a ${10}^{-3}$ precision on the interval $[0,3]$. The solutions are shown in Figure 5.

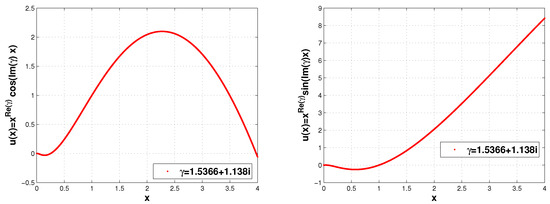
Figure 5. Two solutions for Equation (23). The characteristic equation has conjugate complex roots $\gamma =1.53663359\pm 1.13798709i$.

5. Conclusions

We have elaborated the existence theory for fractional multi-term Cauchy–Euler equations by directly constructing linearly independent solutions. Unlike more general quasi-Bessel fractional equations [8,9], here, we could avoid the restrictions on the derivatives. Numerical modeling confirms the analytic results. Previous results for ordinary and partial differential equations with fractional Cauchy–Euler operators and close Bessel-like operators can be found in [1,2,3,10,11]. It is worth also mentioning that the last steps in the development of the existence theory for linear fractional equations with constant coefficients were presented in [12].