A Parallel Optimization Method for Robustness Verification of Deep Neural Networks

Abstract

Deep neural networks (DNNs) have gained considerable attention for their expressive capabilities, but unfortunately they have serious robustness risks. Formal verification is an important technique to ensure network reliability. However, current verification techniques are unsatisfactory in time performance, which hinders the practical applications. To address this issue, we propose an efficient optimization method based on parallel acceleration with more computing resources. The method involves the speedup configuration of a partition-based verification aligned with the structures and robustness formal specifications of DNNs. A parallel verification framework is designed specifically for neural network verification systems, which integrates various auxiliary modules and accommodates diverse verification modes. The efficient parallel scheduling of verification queries within the framework enhances resource utilization and enables the system to process a substantial volume of verification tasks. We conduct extensive experiments on multiple commonly used verification benchmarks to demonstrate the rationality and effectiveness of the proposed method. The results show that higher efficiency is achieved after parallel optimization integration.

1. Introduction

While recent years have witnessed the superior performance of deep neural networks (DNNs) in real applications [1,2], they are vulnerable to adversarial attacks [3]. Recent studies [4,5] have shown that it is possible to mislead well-trained DNN classifiers by generating inputs with small perturbations (a.k.a. adversarial examples), making them restricted in the safety-critical systems [6]. The reason is that the robustness is an inherent defect of deep learning models [7,8], and this property may bring incalculable losses to human beings in the practical application of DNNs.

Robustness issue poses serious security threats to artificial intelligence models, it is necessary to provide formal guarantees for DNN behavior. Unfortunately, artificial reasoning of large neural networks is impossible because their complex structure makes them incomprehensible to humans. Therefore, there is an urgent need for automatic verification techniques to guarantee the robustness of DNN models. Formal verification provides a reliable security guarantee for the model through strict mathematical methods [9]. The verifiers can be broadly fall into exact or approximate [10,11]. Exact verifiers include methods such as Satisfiability Modulo Theories (SMT) [12,13,14] and Mixed Integer Linear Programming (MILP) [15,16,17], which return definite results by solving the problems as the constraints (a.k.a. complete verification). However, such methods have expensive computational costs and are not satisfactory in efficiency. Approximate verifiers have been improved in efficiency, represented by abstract interpretation, convex relaxation, interval boundary propagation, linear approximation and Lipschitz constant [18,19,20,21]. By approximating the internal behavior of the model and compute an over-approximation of the network output to determine whether the property holds, but may not yield a definitive answer (a.k.a. incomplete verification). Such methods are difficult to achieve a good balance between efficiency and accuracy when verifying large-scale neural networks.

Although formal verification is an important technique for the safety evaluation of deep learning models, the inefficiency caused by the exact encoding of complex structures of the models is inevitable, which has become the main limitation. Even state-of-the-art tools [22,23,24,25] in the neural network verification competition [26] face the lack of performance and scalability when handling complex networks and large quantities of tasks. In light of this, a feasible optimization scheme is parallelization [27,28,29,30]. Computational complexity is a long-standing problem in verification technologies, distributing tasks to multiple workers in parallel for simultaneous computation can improve the solving performance and the number of applicable input tasks. Most current neural network verifiers can support or extend to parallel mode [31,32]. Huang et al. [12] emphasized the importance of parallelization for the verification. Katz et al. [28] attempted to parallelize Reluplex [14], and achieved a obvious improvement in efficiency. Wu et al. [33] implemented a parallel method of split-and-conquer (SnC) within the Marabou framework, which uses a highly parallel preprocessing algorithm to simplify the verification problem of neural networks. However, there are few parallel optimization studies for DNN verification. Due to the particularity of deep learning models, encoding its complex nonlinear and large-scale structure will lead to high verification algorithm complexity and excessive resource occupation. In the conventional parallel verification, the time consumption and fluctuation of each processing unit are high, which limits the overall parallel efficiency. Thus, the existing parallel verification methods still have large room for improvement.

In order to improve the efficiency of DNN verification and promote its practical applications, this work focuses on an optimization approach for parallel computing. A efficient parallel solutions towards verification systems is designed. It fully analyzes the robustness verification process of neural networks, considers several commonly used verification modes, and extends them modularly in parallel. We consider a partition-based verification and design parallel optimization strategies. Based on the analysis of the split operation, it saves the computation cost in the verification by controlling the task length in the target selection; The timeout strategy is used to alleviate the excessive occupation of workers for difficult problems; And the result judgment, applicable scenarios, and different types of verification tool integration are discussed. We exploit the ease of parallelism of the verification problems to design an easily integrated parallel optimization framework. It considers different verification modes and main computing resources, and integrates several auxiliary optimization modules; The unified scheduling of a substantial amount of parallel inputs is realized based on the call among multiple modules, so as to give full play to the computing power of the system and overcome the impact of backward workers; And its distributed extension is also studied, the constructions at the single and multiple machine level are presented respectively. The framework can be adapted to any verification mode. In summary, our principal contributions are as delineated follows:

• We introduce optimization strategies for the partition verification. Based on the analysis and improvement of key processes in this mode, the running speed is optimized.
• We design a general parallel verification framework for large batch inputs accordance with the features of DNN verification system. The verification efficiency is improved by the collaborative work between the modules and parallel task scheduling strategy.
• We combine the parallel optimization method with verification tools and conduct experiments to evaluate the effectiveness of the proposed method. The empirical results demonstrate that it has a positive impact on the efficiency of the tools.

The rest of this paper is organized as follows. We begin with some background on neural networks, robustness analysis and formal verification in Section 2. Partition-based verification and related optimizations are described in Section 3. We present the parallel verification framework and workflow in Section 4. The effectiveness of proposed method is demonstrated through the experiments in Section 5. Finally, our findings and future studies are summarized in Section 6.

2. Background and Related Work

In this section, we introduce general concepts, mathematical symbols and research works related to robustness verification of neural network models, as well as analyze the parallelization and execution modes in verification.

2.1. Neural Networks and Robustness

An ℓ-layer deep feed-forward neural network $f:{\mathbb{R}}^{n_0}\to {\mathbb{R}}^{n_{\ell }}$ is composed of an input layer, an output layer and multiple hidden layers, and the layers are connected by multiple neuron nodes. The dimension of the input vector x depends on the number of features, the linear operation $h^k\left(x\right)=W^k{x}^k+b^k$ is performed on x by the weight parameter W and the bias parameter b, and backward propagation is controlled by the activation function $\sigma$. The output ${\widehat{h}}^k\left(x\right)$ of each layer of neurons as the input $x^{k+1}:{\widehat{h}}^k\left(x\right)=\sigma \left(h^k\left(x\right)\right)$ of the next layer of neurons, for $k=0,\dots ,\ell -1$. The output of the network is: $f\left(x\right)=W^{\ell }{\widehat{h}}^{\ell -1}\left(x\right)+b^{\ell }$, and the c-th output of the network can be expressed as $f_c\left(x\right)$, where the class $c\in L$ and L is the set of all classification labels. Moreover, a popular activation function is ReLU, defined as $\sigma \left(x\right)=max(0,x)$. The neuron is active when the $\sigma$ is positive, otherwise is inactive. Activation functions endow DNNs with powerful expression ability, but their nonlinear operation hinder formal coding in verification problems.

Unlike traditional software models, deep neural networks have complex structures and lack interpretability [34]. Their internal parameters are obtained through solving optimization problems with large amounts of data during training. The behavior of neural networks often lacks the guidance of formalized logic or rules, and it is difficult for people to understand their principles in use, so they are regarded as black-box models. The complexity of DNN models is reflected in their nonlinear and large-scale structure. The nonlinear structure refers to the activation functions, which leads to DNN models contain not only linear expressions but also more complex nonlinear expressions. Large-scale structure refers to deep hidden layers and massive neuron nodes, and neural networks that perform well in practical applications usually have a large scale.

Robustness is an important security property of DNNs, which reflects the anti-interference ability of the model, i.e., small norm-bounded perturbations will not cause abnormal function of the neural network. A robust neighborhood of the input (a.k.a. adversarial region) can be defined as an $L_p$-ball (a convex set) [35], taking the most widely used $L_{\infty }$ norm as an example, we have $B_{\infty }(x,\delta ):=\left\{x^{\prime }|{∥x^{\prime }-x∥}_{\infty }\le \delta \right\}$. The local robustness of the neural network means that for all $x^{\prime }$ in a certain input space $\eta =B_p(x,\delta )$, the result of the network is always unchanged [24], that is:

$$Robust(f,\eta )\triangleq \forall x^{\prime }\in \eta :f_c\left(x^{\prime }\right)>f_t\left(x^{\prime }\right),$$

(1)

where $\forall t\in L$, $t\ne c$, and $x^{\prime }$ can be regarded as the perturbed input. A neural network f is locally robust to condition $\eta$ and given c if it classifies all $x^{\prime }$ in $\eta$ as c.

While local robustness is easy to verify, the limitation is that it can only characterize the stability of neural network behavior within a given input neighborhood. Global robustness describes the stability of the neural network behavior over the full range of the input set. Given constants $\delta >0$ and $\epsilon >0$, the definition of the network f is globally robust on $D\subseteq {\mathbb{R}}^{n_0}$ is as follows [28]:

$$\forall x,\check{x}\in D.∥x-\check{x}∥\le \delta ,\left|f_c\left(x\right)-f_c\left(\check{x}\right)\right|<\epsilon .$$

(2)

Intuitively, the behavior of any two inputs that are close enough inside the input domain D of the neural network is nearly consistent. Since the global robustness is too strict on the network property, the existing verification tools focus on local robustness verification.

2.2. Formal Verification and Parallelization

Formal verification provides rigorous proof of security and reliability for models through theoretical descriptions of models and properties. The verification problem of the neural networks consists of model f and property $\psi$. A neural network f contains a set of linear constraints and nonlinear activation function constraints. The property $\psi$ is of the input-output form: ${\psi }_{in}\Rightarrow {\psi }_{out}$. ${\psi }_{in}$ is the input constraint of the network, which defines a set of input regions ${\eta }_i=\left\{l_i\le x_i\le u_i\right\}$ based on the robust radius $\delta$, where $u,l\in \mathbb{R}$ represent the upper and lower bounds of the range and the dimension $i\in \left\{1,\dots ,n\right\}$. The output constraint ${\psi }_{out}$ of the network defines that the classification result of the output layer is always unchanged. The verifier will typically give such a query $f\left(x^{\prime }\right)\subseteq {\psi }_{out}$ and try to find a counterexample, i.e., for any input point $x^{\prime }$ in ${\left\{{\eta }_i\right\}}_{i=1}^n$, whether the output of the network f is in a given range. The $\psi$ holds only if f classifies all $x^{\prime }$ in the same way.

The main challenge in formal verification of DNNs lies in accurately encoding the behavior of neural networks. Due to the complex nonlinear and large-scale structure of the models, it is difficult to fundamentally solve the efficiency problem. Complete verification based on SMT and LP has been proved to be NP-complete [14]. Existing verification algorithms use the construction and transformation of LP or MILP problems [15,17], use linear approximation to handle nonlinear activation functions [20], use abstract domains in abstract interpretation to analyze neural networks [31], or rely on some other approximation or abstraction operations [21,35]. Although approximate coding can help reduce the solution difficulty, it is bound to introduce some errors. Therefore, it is often impossible to simultaneously guarantee precision and efficiency at the DNN verification algorithm level. Even many state of the art verification tools [26] still have high running time while ensuring precision.

In conventional verification, a single solving is a process of serial computation with a single thread. The solver may hang on a solving for a long time, which makes the subsequent problem must wait for the previous solving to complete before continuing. Many high-precision tools take a long time to perform one verification, but verifying the local robustness of the model for one or few input points is not convincing, so a large number of inputs need to be considered. With the increase of the network scale and the amount of tasks to be verified, the serial computing has serious performance defects. How to enhance the efficiency of DNN robustness verification is a key scientific problem.

Parallelization is often used in complex programs and large-scale tasks. It extends the originally serial program into a multi-threaded mode, thus distribute the task $\left\{V_1,V_2,\dots ,V_M\right\}$ to multiple computing units to achieve speedup. In the execution of DNN verification tasks, multiple control flows are independent of each other, which is easy to be parallelized. Thus, using parallel computing to the solving process of verification tools is crucial for their practical application, the acceleration is obtained dramatically by investing more computing resources. However, current parallel verification methods do not consider the resource utilization of the system, load balancing of each computing unit, and efficient task allocation. We will propose parallel optimization methods specifically for DNN verification later.

2.3. Verification Mode

To design efficient parallel optimization method, we present an analysis of existing verification modes, which are divided into point-wise and partitioned verification. First, considering the general form of property specification (input-output), the verification process is point-wise, where one input corresponds to one output, and threads do not interfere with each other (i.e., independent). This allows us to create multiple workers $\left\{v_1,v_2,\dots ,v_m\right\}$ as the basic execution unit, and achieving speedup by assigning verification tasks to different workers. Thus, most verifiers can support or easily extend the parallel mode. Several studies have proposed partition-based verification [11,27,33,36], where a verification query $V:=〈f,\psi 〉$ is iteratively split into a number of sub-queries $\left\{{\tilde{V}}_j|V={\bigcup }_j{\tilde{V}}_j\right\}$ and $({\tilde{V}}_j\cap {\tilde{V}}_{\tilde{j}}=\varphi ,\forall j\ne \tilde{j})$. They are based on the idea of Branch and Bound (BaB) [14,37] and can be divided into input-based and ReLU-based partitions.

The essence of the input splitting is to partition the robust neighborhood $\eta =B_{\infty }$. Take an input containing two variables as an example, corresponding to two intervals $(l_1\le x_1\le u_1)$ and $(l_2\le x_2\le u_2)$ encoded by the property to be verified. If we split the first interval, we can get $(\frac{u_1+l_1}{2}\le x_1\le u_1)\wedge (l_2\le x_2\le u_2)$ and $(l_1\le x_1\le \frac{u_1+l_1}{2})\wedge (l_2\le x_2\le u_2)$. Anderson et al. [36] pointed out that splitting the input region into two partitions facilitates the search for adversarial counterexamples when the property is false. Even in the global case, the input domain D can be divided into multiple subdomains for separate testing. Considering the efficiency and solving ability of the verification tools, the main concern here is on local robustness. The splitting of The ReLU node ${\widehat{h}}_d^k=\sigma \left(h_d^k\right)$ is to divide the activation states of neurons [13,32], i.e., $\left\{{\widehat{h}}_d^k=0,h_d^k\le 0\right\}$ (inactive) and $\left\{{\widehat{h}}_d^k=h_d^k,h_d^k\ge 0\right\}$ (active), where ${\widehat{h}}_d^k$ is the output of the d-th neuron of the k-th layer. Palma et al. [38] proposed an improved Branch and Dual Network Bound (BaDNB) framework, which uses Filtered Smart Branching (FSB) strategy to select more reasonable branching options to reduce the size of the search tree and improve the quality of segmentation and approximation. It is obvious that a large number of subtasks will be generated under this mode, which has a higher dependence on parallelization. All split verification problems should cover the original query (i.e., exhaustive) and can be checked independently, which is conducive to parallel batch.

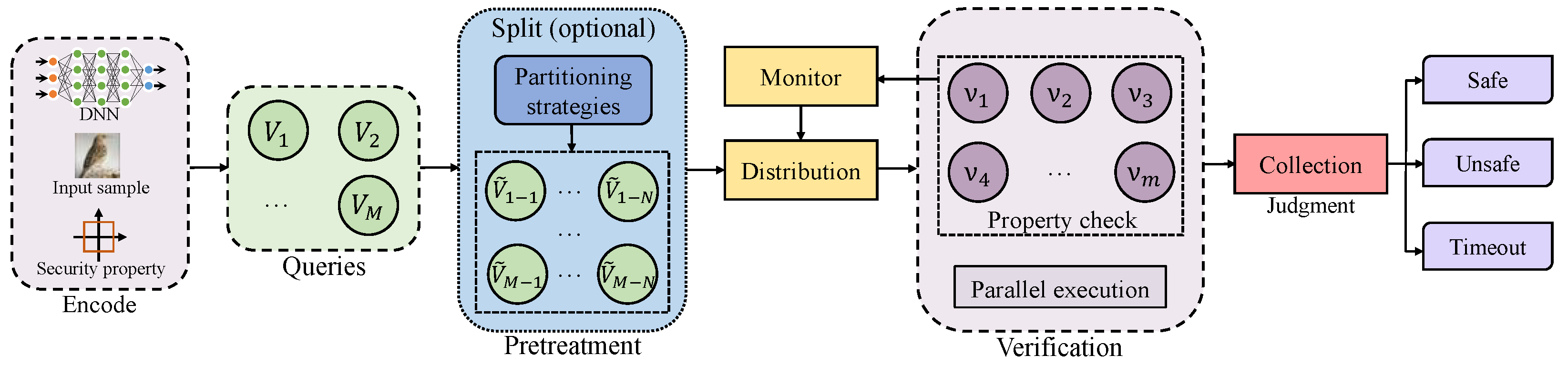
3. Parallel Optimization for Partition Verification

In addition to the conventional point-wise verification, partition verification should be considered in parallelization. In this section, we adopt targeted optimization strategies to boost the parallel efficiency of this model, and analyze the applicability to different types of network structures and verification tools.

3.1. Partition Mode

We first review the partition-based verification. The robustness of neural networks depicts that small changes in the input without large deviation in the output. Traditional point-by-point verification takes a verification query $V:=〈f,\psi 〉$ as input and obtains a corresponding result. Although it is easy to be parallelized, but is limited by the computational cost of the verification algorithm. Borrowing from the partition mode, the verification problem can be automatically divided into multiple simpler sub-problems, and thus obtain high-quality tighter upper and lower bounds, which has been proven to be sound and complete [39]. It can divide the input space or neuron activation phases, with each worker $v_q$ responsible for the independent processing of a specific sub-problem [40] ${\tilde{V}}_j:=〈f,{\tilde{\psi }}_j〉$, where $q\in \left\{1,\dots ,m\right\}$ and $j\in \left\{1,\dots ,N\right\}$. The two verification modes are shown in Figure 1.

Input partition. Considering the definition of robustness, given a query V, the input vector x is extended by the robustness radius $\delta$ to an input space $\eta$, that is, the input constraint ${\psi }_{in}$. Then, for each eigenvector corresponding to input x, we have $x_i\in \left[a_i-\delta ,a_i+\delta \right]$, which is measured by ${∥\delta ∥}_p$. The input to be verified is in the form of a multi-dimensional interval, the solution involves vast amounts of interval arithmetic, which is highly parallelizable [27]. In this case, the hyperplane can be used to split $\eta$ into N non-intersecting sub-spaces $\left\{{\tilde{\eta }}_1,\dots ,{\tilde{\eta }}_N\right\}$, $\tilde{\eta }\in \tilde{V}$. Additionally, the verification performance depends not only on the size of the network, but also on the perturbation radius; a larger $\delta$ leads to a larger $\eta$, which makes the property more difficult to verify. The dependency error of neural network computation generally decreases as the input interval shrinks, and this iterative splitting of input intervals to refine the output interval is similarly highly parallelizable.

ReLU partition. In fact, splitting the input is only suitable for the problems with low dimensional input spaces (such as the ACAS Xu benchmark [41]) and does not scale well to cases like high dimensional inputs. ReLU-based partitioning has already performed well. It divides the search space by repairing ReLU nodes to create two new subdomains, splits the activation unit $\sigma$ into positive and negative cases as $h\left(x\right)\ge 0$ and $h\left(x\right)<0$. The tighter global lower bound on model f with respect to constraint ${\psi }_{in}$ can be obtained by computing the sub-domains [39]. Here it only focuses on the unfixed objective that the upper and lower bounds satisfy $\left\{l_d^k\le 0\le u_d^k\right\}$. This splitting of activation nodes can avoid overestimation errors and improve subsequent bounds during verification, and outperforms input splitting on larger networks, which is of considerable importance for DNN verification.

The essence of the splitting is to reduce the search space to improve the verification accuracy [42], and the difficulty and time of solving the single sub-problem ${\tilde{V}}_j$ after the split are also lower than the original problem. For input splitting, it is universal and simple, but suffers from the curse of dimensionality of high-dimensional data. For ReLU splitting, it is also limited by the size of the neural network and has not been extended to activation function types other than ReLU. The input partitioning is for the input constraint ${\psi }_{in}$ in the verification query V, while the ReLU partitioning is for the encoding of model f, which affects the output constraint ${\psi }_{out}$. Naturally, both partitioning modes can be used simultaneously. However, different verification modes have their own application scenarios, which depend on factors such as network size, verification type, encoding method and hardware conditions.

3.2. Key Processes Analysis and Optimization

In fact, the splitting in DNN verification may perform well on tests with only a few tasks and relatively simple neural network benchmarks. With the increase of input dimension and network scale, it is difficult to achieve higher performance by only splitting a single input region or ReLU node. Therefore, compared with pointwise verification, partition verification has larger-scale tasks, which becomes its computational bottleneck. The optimization strategies are used for efficiency, and the key operations are modularized to better control the verification process.

3.2.1. Split Operation

Based on the specification of DNN robustness, we introduce the partition verification mode, which assigns a batch of generated sub-tasks ${\bigcup }_{j=1}^N{\tilde{V}}_j$ to different workers for parallel verification. On the one hand, the single computation time of each $v_q$ can be reduced by splitting the input encoded by the property to be verified under the sufficient computing resources, and the results are quickly given by parallel processing. On the other hand, a more exact output over-approximation range are obtained in each verification sub-query $V:=〈f,\psi 〉$. Although a single sub-problem is easier to solve, the processing a large batch size makes the overall efficiency suffer. Thus, this mode mainly improves the accuracy by partitioning strategy, and improves the efficiency by investing more computing resources.

The balanced split enables the verification system to perform well. More partitions can obtain higher precision, but improper splitting will incur additional computational cost, so the optimization strategy is more prone to improve the verification efficiency and take into account the balance between precision. The execution of partition verification can be regarded as a tree structure. It will continuously select the verification questions to branch and dynamically generate sub-queries, and give the decision after the tasks are completed. The partition mode can be parameterized as $S(N,\lambda )$, where N is the number of sub-problems and $\lambda$ is the partitioning operation on the target node, including the input and ReLU types. A split of the activation phase or input space creates two new sub-problems. The tailor of a specific partitioning strategy often needs to consider factors such as model structure, constraint coding, performance of verification tools and equipment. One possible approach is to dynamically adjust the splitting operator during the verification [33].

3.2.2. Target Selection

The DNN verification problem has a large search space and potential splitting options, and the shape of the search tree is determined by the branching step. The main challenge is to select high-quality leaves for splitting, which can obtain more accurate results and significantly reduce the number of branches and running time, so effective splitting target selection is important. We summarize relevant methods [27,33,42], including input range size, gradient information, and some heuristics to guide the partitioning. For example, the gradients explain the impact of input features and ReLU nodes on the model decisions. A heuristic method BaBSR determines the splitting priority by estimating the improvement of each ReLU node on the tightness of the lower bound, and FSB version improves its splitting quality and reduces the total number of branches in the search tree with fast dual bounding [38]. Another heuristic is based on the symmetry of the polarity metric the ReLU boundary with respect to zero $\left[l_d^k,0\right]$ and $\left[0,u_d^k\right]$ to find sub-problems with more balanced partitions, that is, active and inactive ranges are as close as possible. These methods actually set a score $S_{TS}$ for the split target, and prioritize split the node with the highest score, which has a good effect in target selection. Based on the above method, we designed the corresponding component specifically for the target selection as a flexible unified evaluation step under this mode to better control this process.

Actual DNN models are usually of a large scale. The branching strategy in the partition mode has a significant impact on the DNN verification problem, which directly affects the performance. While more partitions are better for improving precision, it also takes less time to solve fewer partitions. To balance the efficiency and precision after splitting, we set a threshold $H_{TL}$ to limit the sub-task length $T=\left\{{\tilde{V}}_1,{\tilde{V}}_2,\dots ,{\tilde{V}}_N\right\}$ such that its maximum length satisfies $N\le H_{TL}$. The setting of this parameter depends on the actual verification requirements, and is only suitable for relatively small batch splits under CPU and serial conditions. We then embed this strategy into the target selection component to avoid over-segmentation, and when the length reaches the threshold, all the child nodes can be pruned to reduce branches. This process is guided by the target selection score to choose the best candidates and control the number of sub-problems, thus reducing the overall running time without compromising the completeness of the verification. Additionally, generating a large number of sub-tasks incurs substantial communication overhead, which can also be alleviated by limiting the task length in target selection.

3.2.3. Timeout Strategy

Point-by-point mode tends to cause a single worker to be occupied for a long time. While reasonable partitioning can alleviate this phenomenon, its running time cannot be effectively estimated for many high-precision tools. For the high time consumption and high fluctuation of DNN verification methods, we set a timeout threshold $H_{TO}$ to prevent verification queries from hanging dead. If the execution time ${\mathcal{T}}_j>H_{TO}$ of a worker $v_q$ in a query V or $\tilde{V}$, then it will be terminated. The priority will be given to problems that are verifiable within the given time budget. At this point, we can collect the original verification problem to which the timeout sub-problem belongs, and then further refine the timeout input by adjusting the splitting parameter $S(N,\lambda )$. Note that $H_{TO}$ needs to consider the specific solver performance in different modes. Although it is possible to perform repeated splits of tasks with frequent timeout, each call to solve the timeout problem is actually a waste of time and resources, and sometimes even incurring additional consumption beyond the cost of the problem itself. Because each additional time includes the maximum timeout of j corresponding sub-problems, and the cost of re-splitting and processing. We want to avoid this efficiency loss by appropriate splitting strategy and timeout setting.

3.2.4. Result Judgment

In essence, partition verification builds a search tree where each leaf is a sub-domain, and the property $\psi$ can only be proved if it holds on all leaves, but not if there are branches that violate the constraint. In this mode, the sub-queries ${\left\{{\tilde{V}}_j\right\}}_{j=1}^N$ are handled separately, and then the original problem is analyzed by the verification results of each sub-query. Once a violation counterexample is found (unsafe), or all sub-queries are verified (safe), or a timeout occurs, the verification is terminated. Each worker works independently and only interacts at termination. When the property does not hold or cannot be successfully verified, the processing of the corresponding remaining sub-problem is omitted. Additionally, when calculating the global minimum [42] $minf\left(x^{\prime }\right),\forall x^{\prime }\in \eta$ of the output difference of the network, any sub-problem whose lower bound is greater than the current global upper bound can be removed.

3.3. Integration Discussion

We discusses integrated extensions of partition mode and related optimizations. Neural network verification has high time consumption and fluctuation under the premise of ensuring precision. Both this mode and the optimizations are not conducive to performance improvement without appropriate scenarios and configurations. In general, the complete verification methods have exact results and can generate concrete counterexamples when the verification fails, but there are the lack of efficiency and scalability. Incomplete methods have higher efficiency, the precision of verifying complex neural networks is not satisfactory. The specific partitioning for different verification methods is guided by the target selection and without excessive splitting, because it will reduce the original efficiency. In practical applications, the types and performance of verification tools should be combined.

Some complete methods are strict in encoding the verification problem, which is difficult to solve. The verification difficulty and time are positively related to robustness radius $\delta$. We consider that there is a large difference in the time cost of verifying different input points, which needs to set the timeout factor according to the scale of the network to be verified and the perturbation radius $\delta$ to balance the working time of $v_q$. The computation and time consumption of such tools are large, so the number of partitions N should be far less than that of approximate methods, and parallelization and the partition optimization are useful for the efficiency. The incomplete methods approximate the encoding of the verification problem, but cannot further determine whether the property holds when the verification fails. This requires the modification of the judgment condition in the verification algorithm, that is, the “unknown” result is directly given when the sub-problem is unverifiable or timeout. These tools are generally efficient, while the overhead caused by the partition mode are shared by parallel workers. Another drawback is that the number of verifiable points decreases rapidly as the robustness radius increases. Current research has demonstrated that the partition can obtain tighter output bounds, which reduces the number of run timeouts and the corresponding waiting time. Therefore, this approach is also useful for balancing the verification precision and efficiency of such tools.

This paper aims to propose a general parallel verification optimization. The core process involved in DNN verification is basically the same, so these optimization methods are suitable for different split versions, and can improve the efficiency of partition verification. Note that since split operation does not necessarily have the same effect on different verification methods, we have the flexibility to turn it on or off.

4. Parallel Verification Optimization Design

Most verification methods are computationally expensive and cannot take full advantage of parallel hardware resources. In this section, a parallel optimization framework is designed to improve the adaptability of the verification system when dealing with large-scale input data.

4.1. Parallel Framework

Considering the lack of representative of the local specification, it is not convincing to verify the local robustness of a neural network only for a single input point, so it is necessary to verify a large number of input samples (especially for unobserved samples). However, as the number of inputs to be verified increases, the efficiency issue becomes more prominent. The verification program based on the partition mode consists of a number of disjoint sub-queries ${\left\{{\tilde{V}}_j\right\}}_{j=1}^N$. For example, a split of M verification queries yields a task of size $M\times N$. In order to further improve the performance and fully leverage the advantages of parallelization technology, we propose a general parallel verification framework, which is applicable to any verification mode, as shown in Figure 2. The framework for our parallel optimization is very modular. For the uneven task distribution and low resource utilization in neural network verification, we design and integrate multiple auxiliary modules to maximize the efficiency of parallel verification through the collaborative work between each module, mainly including:

Splitting module: It integrates partition-based verification. By preprocessing the corresponding input space and ReLU nodes in the robustness query $V:=〈f,\psi 〉$ to obtain $V:={\tilde{V}}_1\wedge \dots \wedge {\tilde{V}}_N$ and submit to the task distribution module. This operation is lightweight and this module can be enabled or disabled according to the actual verification requirements, default is point-wise when closed. We integrate the parallel optimizations for the partition mode. In principle, it is advisable to control the number of sub-tasks to reduce the overall verification time to exploit the best effect.

Monitoring module: It collects the real-time load status of workers $v_q$ by monitoring the resource pool. Current verification techniques can be divided into CPU-based and GPU-based. Most tools support and adopt CPU verification mode [26], which can be parallelized in a multi-core environment and involves plenty of calculations and logical judgment operations. In this context, we can classify verification queries as CPU-intensive tasks that are processed asynchronously by multicore CPUs. The queue ${\mathcal{Q}}_q$ can reflect the load condition of $v_q$ in the next period. Thus for the load factor $\mathcal{L}$ of v, we use the utilization $\mathcal{C}$ of each core in each CPU to which the basic execution unit belongs and the queue factor $\mathcal{Q}$, as follows: $\mathcal{L}=\alpha \mathcal{C}+\beta \mathcal{Q}$, where $\alpha$, $\beta$ are rational constants and $\mathcal{Q}$ is bounded. We also take into account active status, queue saturation and blocking time of the workers to make the allocation of subsequent tasks more reasonable. When the performance of the computing system is high, there is a higher processing efficiency for V, and the declining rate of $\mathcal{L}$ will be faster. Furthermore, the metric in verification tools using GPU should be replaced with GPU usage $\mathcal{G}$, where the blocks in CUDA corresponds to the concept of CPU cores.

The verification on GPU is more efficient, with more threads and higher parallelism than the CPU, which can make full use of the hardware resources and reduce the CPU burden. Owing to the substantial interval and matrix operations involved in the verification, this approach applies to massive parallel batch processing in partition mode. Although the parallel mechanism on GPU is suitable for the development of scalable verification, it is not fully competent for the some complex operations, so that numerous verification methods are still dominated by CPU mode.

Task distribution module: In view of the unbalanced load of workers caused by large-scale verification tasks (especially after splitting), we implement a task scheduling strategy towards the verification system based on this module. When processing a large batch of verification queries, it needs to pre-create as many workers (with hyper-threading) as possible within a reasonable range based on the actually available computing resources, and assign priorities to processing units $v_q$ based on ${\mathcal{L}}_q$. We mainly employ the master-worker model to allocate the verification tasks according to the activity status of each $v_q$, and then establish effective mappings of them to relatively idle workers.

Verification module: This module contains the core components of the integrated verification tool. It encodes the neural network model f and the security property $\psi$ into a set of constraints. For $\psi$ it is usually necessary to consider the concealment principle of the disturbance and the robustness difference of the models to make parameter $\delta$ within a reasonable range. We extend the traditional verification to parallel mode, execute multiple received verification queries or sub-queries simultaneously, and then it submits each result to the collection module. Since the verification tasks are independent of each other, no preemption occurs.

Collection module: Regardless of point-wise or partition mode, each verification corresponds to a result, which typically includes “safe, unsafe or unknown, and timeout” cases. As the number of inputs increases, it marks the verification query V, makes synchronous judgments according to the input and output constraints $\psi$ in the model properties, and collects the results. If V or all the corresponding sub-queries ${\tilde{V}}_1\wedge \dots \wedge {\tilde{V}}_N$ are successfully verified to be true, then network f is locally robust to input x; On the contrary, if any case that does not satisfy the property is found, then f is not robust and the counterexample can be collected. If the timeout occurs, it is also summarized by this module, and then the splitting operator $S(N,\lambda )$ can be adjusted actively in the partition mode to further refine the timeout target and re-verify. In addition, incomplete tools may not be able to give a certain unsafe if the property has not been successfully verified, so we tend to consider the input point as relatively unsafe in this case. Note that most verification methods [14,24,32] adopt the form of negative encoding for the property, that is, if the verification tool is unsatisfiable (UNSAT) for all calls, then the network f is safe for the property $\psi$.

The framework is relatively loosely coupled. Each module has clear function and is easy to integrate, and is applicable for both single and multiple machine levels. The modules are configured with corresponding interfaces to interact and call each other, and can be flexibly enabled or not. Relying on this, when there are available computing resources, all tasks are executed continuously, and different tasks can be processed simultaneously, which reduces the idle time of the workers. It fully considers the characteristics of the verification scenario to better exert the computing power of the system and improve the overall verification efficiency.

4.2. Acceleration Strategies

The verification problem for neural networks is well suited for parallelization, and calls to the verifier can be run on different threads. The complex structure of the model in verification can make its encoding more difficult. Under the premise of ensuring precision, it often requires high computational overhead to execute a verification query. In addition, there is often a large number of tasks involved in verification (especially in partition mode). Uneven task allocation among workers in parallel computing is not conducive to performance optimization, which may lead to empty or lock of threads, resulting in lower resource utilization. Therefore, it is necessary to ensure that the verification task is properly assigned. We propose a unified scheduling strategy to balance the load and working time of each work unit $v_q$.

First, ensure that verification tasks are given priority to the idle $v_q$, and that all requests are run continuously whenever possible. Then, we sort the scheduling priorities of $v_q$ to adaptively allocate the tasks according to the load metrics ${\mathcal{L}}_q$ dynamically feedback by the monitoring module. This avoids the high occupation of the computing resources affecting the execution of other tasks and the overall efficiency degradation. Since the verification tool has a large fluctuation in the time of each verification query, it cannot process the subsequent tasks in time, which affects the scheduling strategy and the overall performance. If the task submission rate per unit time is higher than the resolution rate, the blocked queue will accumulate too long. For the possible load skew in the thread pool, it requires to adjust the subsequent task distribution in real time. We further set the threshold $H_{load}$ such that if ${\mathcal{L}}_q>H_{load}$, the distribution to the worker is stopped. The purpose is to control the task queue length to alleviate the saturation state of each $v_q$ adaptively, and continue the allocation after ${\mathcal{L}}_q$ satisfies the condition. In the verification process, once the violation of the sub-problem is found, it can immediately terminate and give a determination. Additionally, verification tasks can be migrated between cores of the same CPU to the run-queue of low ${\mathcal{L}}_q$ workers because they share cache.

When partitioning is enabled, the verification problem is split into smaller independent sub-problems. We introduce a pre-analysis procedure for the split target before verification. The target selection strategy is combined to control the number of generated branches, to save the high computation and transmission costs in large number sub-tasks. Considering the difference of solving time between verification problems, we use the time-out strategy to terminate the solving process of this and the remaining sub-problems and turn to the subsequent problems when the results cannot be obtained within a given time. The formulation of related parallel optimization strategies needs to consider the actual efficiency of the verification tool, and has different settings for different modes. At the level of multiple machines, sub-problems with the same ownership are preferentially assigned to the same physical CPU or GPU to reduce cache misses and facilitate data communication. In addition, the use of split mode affects the type, quantity and solving time of the tasks in scheduling.

Due to the long running time of a single verification, there is enough time to implement scheduling during the execution. Note that we can choose to distribute the tasks individually or in batches depending on the available resources and the efficiency of the tool. We control the concurrent number and the submission rate of tasks, the frequency of real-time monitoring and updating the load, and avoid the termination of a program triggered by memory exhaustion during verification. We show the detailed parallel verification algorithm in the next section.

4.3. Verification Algorithm

In the local robustness verification of neural networks, it is often requires to consider a lot of input points to improve its persuasiveness. For partition-based verification, splitting multiple verification queries separately creates more sub-problems and require more worker threads. In order to better cope with the concurrent verification of a large number of inputs and make full use of server resources and parallel advantages, we show the parallel verification algorithm based on the execution process of the optimization framework, the pseudo-code is shown in Algorithm 1.

Algorithm 1 shows the basic workflow of the parallel verification framework, which is mainly divided into three stages. The setting of relevant parameters should consider the actual verification scenario. Note that, the main loop of the algorithm is naturally suitable for parallelization, since the solve calls to each input are independent of each other, which facilitates asynchronous batching of multiple workers. All verification tasks can be queued and dequeued asynchronously.

Algorithm 1 Parallel Verification
Input: query $V:〈f,\psi 〉$, partition parameter $S(N,\lambda )$, length threshold $H_{TL}$, timeout threshold $H_{TO}$, load threshold $H_{load}$
1: Initialization
2: if split=true then	▹ Stage 1: Splitting
3:     for $\left\{V\right\}$ do
4:         pick out split targets by $S_{TS}$
5:         $\left\{{\tilde{V}}_1,\dots ,{\tilde{V}}_N\right\}$← split V and $N\le H_{TL}$
6:         add $\left\{\tilde{V}\right\}$ to verification queue Q
7: while Q is not empty do	▹ Stage 2: Scheduling
8:     calculate ${\mathcal{L}}_q$ for each $v_q$
9:     sort $\left\{{\mathcal{L}}_q\right\}$ from low to high
10:     distribute ${\tilde{V}}_j$ to $v_q$ in order of $\left\{{\mathcal{L}}_q\right\}$
11:     if ${\mathcal{L}}_q>H_{load}$ then
12:         stop distribution to $v_q$
13: result ← solve $\left\{\tilde{V}\right\}$	▹ Stage 3: Determination
14: if $\forall {\tilde{V}}_j$ := UNSAT then
19:     return safe
16: else if $\exists {\tilde{V}}_j$ := SAT then
17:     return unsafe
18: else if ${\mathcal{T}}_j>H_{TO}$ then
19:     return timeout

Stage 1 shows the partitioning process, where query V is preprocessed by the splitting module. In general, the split sub-query ${\tilde{V}}_j$ is easier to verify. During this operation, the target selection score and length limit $H_{TL}$ are used to guide the order and total number of branches (lines 4–5). Then, the resulting sub-queries are put into the task queue, and the distribution module is responsible for receiving and assigning them to different available computing units $v_q$ (line 6).

Stage 2 shows the parallel scheduling strategy. Upon receiving the verification request, it computes and sorts the load status ${\mathcal{L}}_q$ for each $v_q$ based on the collection from the monitoring module (lines 8–9). Then, the verification tasks are mapped to the appropriate workers in the thread pool and processed by calling the verification algorithm (line 10). The states of V and $v_q$ change dynamically during verification, which requires the load condition ${\mathcal{L}}_q$ of each $v_q$ to be updated and reordered before the next round of distribution. If the current load of a worker exceeds the threshold $H_{load}$, the subsequent distribution to is suspended (lines 11–12). Thus achieving efficient scheduling.

Stage 3 corresponds to the result judgement. The property constraint $\psi$ is usually the same for each input point in a set of verifications. The results are presented directly for pointwise mode. In partitioned mode, if all sub-problems are UNSAT, the return network is safe for the input (lines 14–15); If any sub-query violates the property constraint, unsafe is returned and the verification of subsequent sub-queries corresponding to the original query is stopped (lines 16–17); If the execution time of a query V or ${\tilde{V}}_j$ exceeds the threshold $H_{TO}$, then timeout is returned and the next verification is executed directly (lines 18–19).

4.4. Distributed Extension

The current verification uses the DNN itself as the verification model. As the structure of neural networks becomes more complex, the performance bottleneck will be more prominent. The parallel mode of a single machine may not meet real demand. When the problem cannot be solved completely, using more computational resources obviously helps to improve the efficiency. To further improve the ability of the verification tool to handle larger-scale tasks, we present a construction idea in the multi-node environment, which extends the parallel architecture in the distributed manner to transform multi-threading into cooperative work among multiple nodes.

In the parallel verification framework, each module can be easily implemented at the node level. Post-deployment calls to the core verification component can be made on different nodes $\left\{n_1,n_2,\dots ,n_m\right\}$, and the optimization in this paper apply as well. Based on cross-node information sharing [43], we add a layer of inter-node scheduling while maintaining the worker thread v as the basic execution unit of parallelization. On the basis of the original architecture, the special nodes are responsible for the function of each module, and the verification process involves multiple communications and calls of multiple different function nodes. First, the load of each node ${\left\{n_p\right\}}_{p=1}^m$ is uniformly monitored, including the main resource utilization and the queue factor. The metric $\mathcal{L}$ is extended at the node level to establish a mapping from task V to $n_p$ and then to the multicore level. Multi-threaded parallel can not run across nodes. When split is true, the closely related $\left\{\tilde{V}\right\}$ in the same V will be packaged and sent to the same $n_p$ to facilitate the result judgment and statistics. We can choose a single or multiple parallel optimization framework based on the actual verification requirements. In addition, distributed-based verification can handle larger scale application scenarios, such as the verification of multiple or deeper neural network models.

5. Experiments

In this section, we evaluate the effectiveness of the parallel optimization method, testing the efficiency impact of this method by integrating the verification framework with representative verification tools.

5.1. Experimental Setups

We integrated the proposed method with two advanced verification tools, Marabou [22] and $\alpha$-$\beta$-Crown [25], to highlight its applicability. For Marabou, it only supports running in CPU mode, which is a complete verification tool; $\alpha$-$\beta$-Crown supports CPU and GPU modes, and provides complete and incomplete verification. All experiments were run on Ubuntu 22.04.2 LTS server with Intel Xeon Silver 4216@2.10 GHz 16 cores CPU, 128 GB memory and nvidia tesla v100 32 GB GPU. Both tools have built-in partition mode (running in parallel), and we extend and integrate the optimization framework and method on top of that. The configuration information in each verification instance combines the specific tools, network size and hardware conditions. The verification benchmarks involved in this paper are shown in

Table 1. Experimental benchmarks.

Tool	Model	Dataset	$\mathit{\delta }$	Device	S Mode
Marabou	FCN	MNIST	0.003	CPU	SnC
			0.006
$\alpha$-$\beta$-Crown	CNN	CIFAR10	0.0059	CPU, GPU	FSB
			0.0078

.

Benchmarks: We used popular verification benchmarks and followed the basic configuration of the tools. For Marabou, it supports small scale networks based on ReLU activation functions in the version tested.Considering the insufficient efficiency of complete verification, we used the MNIST [44] dataset to train a 9 × 20 fully connected neural network (FCN) for testing. For $\alpha$-$\beta$-Crown, it can achieve more advanced performance on larger scale networks. We chose two convolutional neural networks (CNN) with 4852 and 62,464 hidden nodes trained on CIFAR10 [45] dataset in [23] (denoted as CNN1 and CNN2) for testing on CPU and GPU.

We considered the efficiency of the verification tools in the test, and selected 150 and 1000 images for Marabou and $\alpha$-$\beta$-Crown, respectively. The purpose is to prove the effectiveness of our parallel optimization by comparing the efficiency changes of each benchmark after integrating the parallel framework under the given number of verification tasks and computing resources. Note that the total running time of all the tools is heavily affected by timeouts.

Robustness property: Here we consider local robustness based on the $L_{\infty }$ norm metric, where the size of the robust neighborhood depends on the robustness radius $\delta$, which represents the maximum acceptable perturbation range ${∥r∥}_{\infty }\le \delta$ for the input. Since different models are known to differ in the reliability of against $L_p$-norm perturbation attacks, there are different settings for $\delta$ for the test benchmarks. The verification of DNN robustness only focuses on the original input samples that can be correctly classified in the model.

5.2. Experimental Results

We compare the efficiency improvement of the neural network parallel verification optimization under the specified benchmarks, which is intuitively reflected in the completion time variation of all tasks (including timeout). For Marabou, we compared the parallel optimizations for pointwise and partition (denoted as Sch and Spo) with the conventional serial, the common parallel between pointwise, and the initialized SnC partition parallel mode [22,33] (denoted as Seq, Par and Spar). For $\alpha$-$\beta$-Crown, splitting is enabled by default, we compared Spo with Spar on CPU and GPU, where the partitioning mode is FSB version [25,38]. All of these modes can be implemented in the configuration file of the corresponding tool. Next, we further explain these baselines for speed comparison. Improvement methods: (1) Sch is optimized pointwise parallel mode (mainly including the scheduling strategy); (2) Spo is optimized partition mode; both are integrated within the proposed parallel verification framework. Original methods: (3) Seq is pointwise serial mode; (4) Par is pointwise parallel mode; (5) Spar is partition mode.

The essence of parallel optimization is to shorten the verification time by using more computing resources for simultaneous computation. Figure 3 and Figure 4 show the comparison of completion time as the task scale increases, indicating the adaptability of the proposed framework to a large amount of inputs. The specific execution times of all tasks are shown in

Table 2. Execution time (min) of Marabou.

Bench.	Device	$\mathit{\delta }$	Seq	Par	Sch	Spar	Spo
M-FCN	CPU	0.003	1937.07	417.65	368.15	1229.90	1061.80
		0.006	2192.99	486.24	402.99	1409.23	1130.03

and

Table 3. Execution time (min) of $\alpha$-$\beta$-Crown.

Bench.	Device	$\mathit{\delta }$	Spar	Spo
$\alpha$$\beta$C-CNN1	CPU	0.0059	91.50	77.46
		0.0078	118.26	97.77
$\alpha$$\beta$C-CNN2	CPU	0.0059	732.95	630.96
		0.0078	1028.22	869.77
$\alpha$$\beta$C-CNN1	GPU	0.0059	41.23	36.91
		0.0078	54.02	46.62
$\alpha$$\beta$C-CNN2	GPU	0.0059	80.74	70.32
		0.0078	120.59	103.46

. It can be seen that the optimized parallel verification has higher operational efficiency in each comparison mode. For more precise tools, the split problems are usually easier to solve. Our timeout and task scheduling strategies can avoid excessive occupation and idle of the parallel unit. Moreover, by limiting the task length after splitting in the partition mode, the resource consumption of excessive branches is alleviated while the computational efficiency is guaranteed. For Marabou, it takes a long time to perform a full verification query in a worker, which makes the high computational resource occupation, and then affects other workers in the same core. For $\alpha$-$\beta$-Crown, we observed the limited parallel acceleration on multi-core CPU, its partition mode applies more to run on GPU and is able to accommodate more branches. Compared with the original parallel mode of these tools, using the scheduling strategy will also be faster, and the average utilization of the main computing resources is higher and more balanced through more rationalized task assignment, especially as the increase of the number of tasks. The above aspects show that the parallel optimization is effective, and it has advantages in efficiency for the verification tools. In addition, these optimizations do not rely on a specific verification method, and have strong generality and universality.

The evaluation of verification performance should consider both efficiency and precision factors. The partition mode has been shown to reduce the accumulation of dependency errors in neural network verification, resulting in a more precise output over approximation range. This is reflected in the increased number of successfully verified points within a given time, alleviating the overhead caused by timeout. How to improve efficiency without losing precision in neural network verification has always been a challenge. The parallel extension of the traditional point-by-point mode is naturally helpful for speed sharply. The partition mode is mainly optimized for verification precision, which may affect the efficiency. Optimization from the perspective of parallelization is a feasible route, so our method plays an key role in this.

In the case of being unable to completely solve the problem of low time performance of complex neural network verification, effectively utilizing more computational resources is the key to its use in reality. Figure 5 shows the comparison of the time consumption of the verification tools on a randomly sampled set of samples in a single-machine serial, parallel, and simulated distributed environment (denoted as S, P, D in the figure). The above three cases respectively represent a single worker, a single machine multi-core environment with restrictions on resource allocation, and a multi-machine environment with more shared resources. The lightweight virtualization technology docker container is used to build and simulate, and the corresponding modes of the tools in the specific environments are run under the default configurations and CPU conditions. Obviously, the overall running time is significantly reduced (275.0~759.4%) with the increase of computing resources. Therefore, building a distributed parallel optimization framework and expanding the rational utilization of GPU resources with higher parallel computing power on the basis of existing work are the key research directions in the future.

6. Conclusions

In this work, we propose an optimization method for DNN robustness parallel verification by leveraging the ease parallelism of verification problems. The partition mode can be used to reduce the complexity of problem coding and improve verification accuracy, but the multitude of tasks may not be processed efficiently. For this mode, we use appropriate strategies to optimize the key steps to reduce the verification overhead and improve the parallel efficiency. We design a parallel verification framework based on the extension of the verification system. Targeted task scheduling is implemented through multiple auxiliary modules, which further improves the resource utilization of the parallel system and the ability to handle large-scale tasks. These optimization strategies fully consider the actual DNN verification scenarios and can be easily integrated into current verification technologies. The experimental results show that our framework is more efficient compared with popular benchmarks in typical verification tools when processing high-volume verification queries. We believe that effectively utilizing more computational resources for parallel computing is of great significance for the practical application of this important technology for DNN reliability guarantee.

Possible future work includes:

(i) To further improve the ability of verification tools to solve multiple neural network models and larger scale tasks, we intend to implement the distributed framework expansion from multi-thread to multi-node, using more computing resources to improve the performance. This requires consideration of the module and communication overhead in a distributed environment, as well as the need for large batch management. Additionally, the local robustness verification of a single input point is often lack of convincing and representative, and the computational cost of global robustness verification is too expensive. Thus, we can integrate the parallel verification with the GPU mode [30] to explore some more complex security properties.

(ii) Based on the definition of DNN verification problem, partition mode is beneficial to improve the accuracy. However, this mode is not yet widely used, and we can integrate the optimized partition parallel verification into more types of the tools. In addition, the splitting strategy often relies on human experience, which may not achieve the optimal effect. In the future, we can try to use the training of neural network to guide the setting of key parameters in the strategy.

(iii) Most of the existing DNN robustness verification techniques focus on image classification. The use of different types of network structures, activation functions, and input data is still limited. We are also interested in encoding higher-level abstractions for neural network verification problems, and exploring the application of verification techniques to safety-critical systems [46] that typically employ more complex model structures and discrete inputs data.