Abstract
The pinning control of complex networks is a hot topic of research in network science. However, most studies on pinning control ignore the impact of external interference on actual control strategies. To more comprehensively evaluate network synchronizability via pinning control in the attack–defense confrontation scenario, the paper constructs an attacker-defender game model. In the model, the attacker needs to control nodes in the network as much as possible. The defender will do their best to interfere with the attacker’s control of the network. Through a series of experiments, we find that the random attack strategy is always the dominant strategy of the attacker in various equilibriums. On the other hand, the defender needs to constantly change dominant strategy in equilibrium according to the set of defense strategies and cost constraints. In addition, scale-free networks with different network metrics can also influence the payoff matrix of the game. In particular, the average degree of the network has an obvious impact on the attacker’s payoff. Moreover, we further verify the correctness of the proposed attacker-defender game through a simulation based on the specific network synchronization dynamics. Finally, we conduct a sensitivity analysis in different network structures, such as the WS small-world network, the ER random network, and the Google network, to comprehensively evaluate the performance of the model.
MSC:
91A10
1. Introduction
The rapid development of network science has led more and more researchers to analyze the structure and dynamic processes in various complex systems from the perspective of network science [,,,,,,,]. In particular, the synchronization of complex networks has attracted many scholars to undertake in-depth research [,,,,,]. There are two key issues that have attracted widespread interest in this field: (1) how to analyze the stability of network synchronization dynamics; (2) how network structure affects synchronization dynamics. Around these issues, numerous research results have been achieved in the research field of network synchronization. For example, Mahmoud, G. M. et al. [] used Lyapunov exponents to study the basic dynamic properties of unforced oscillators and their stability and chaotic behavior. Rossa, F. D. et al. [] analyzed the stability of cluster synchronization in multi-layer networks through master stability functions. In addition, synchronization dynamics on small-world networks and scale-free networks have been intensively studied [,,]. It is worth noting that previous research also found that some network structures cannot achieve self-synchronization, but synchronization can be achieved by adding some controllers to these networks [].
In many realistic scenarios, it is almost unrealistic to control all nodes of a network, especially in a large-scale network with a large number of nodes and complex connections. To save control costs, some local feedback injections can be applied to only some nodes of the network to control the entire network, i.e., pinning control [,]. This research direction has received widespread attention and has made much progress [,,,,,]. Wang et al. [] studied the pinning control of scale-free networks and found that they need fewer nodes with a large degree than randomly selected nodes for control. Yu et al. [] discovered that, for the pinning control of linear feedback, the network can achieve synchronization by adaptively adjusting the coupling strength. Liu et al. [] determined the minimum eigenvalue of the Laplacian matrix after deleting the controlled nodes, which can reflect the network synchronization capability after pinning control.
Previous research on pinning control in complex networks has mostly assumed that all nodes in the network belong to the decision space of the pinning scheme [,,,]. These studies focus on how to efficiently improve network synchronizability via pinning control, ignoring the possibility of external interference or confrontation in the pinning scheme. Taking the reaching consensus of group views as an example, it may be evident that there is one party who wants to achieve consensus through control opinion dynamics, and there are also some people who want to interfere with the achievement of the corresponding consensus []. Game theory provides a suitable modeling framework for describing the above attack–defense confrontation scenario [,,,]. Many scholars use the attacker-defender game to model various attack and defense confrontations in complex networks. For instance, Li et al. [] considered the topology of the infrastructure system and modeled the attack–defense confrontation of critical infrastructure as a game to analyze. Liu et al. [] constructed an adversarial dynamic game to deeply analyze the dynamics of information dissemination on social networks. Wang et al. [] modeled network security investment behavior on the Internet through interdependent security games (IDS), and studied the dynamics of social payoffs and the average social investment from various attack scenarios.
In summary, the paper analyzes network synchronization via pinning control from the perspective of an attacker-defender game. In this game, the attacker wants to control specific nodes to maximize the network synchronization capability, while the defender needs to establish defenses to interfere with the attacker’s control of the network. Our work and its contributions can be summarized as:
- We propose an attacker-defender game to analyse network synchronization via pinning control in the confrontation scenario.
- Through a series of experiments, the payoff matrix of the game and equilibrium are explored.
- The correctness of the proposed attacker-defender game is verified by simulation based on the specific network synchronization dynamics.
- The performance of the proposed attacker-defender game on different network structures is analyzed.
2. Model
First, we introduce the network structure of the model. The paper conducts experiments on an undirected graph with N nodes. Let represent the undirected graph, where is the set of nodes and is the set of edges. The degree of the node is , and the average degree of the network is <k> = . is the Laplacian matrix of graph G. The specific definition of the matrix is as follows: if node and node have a connecting edge (), , otherwise, ; . Since scale-free networks can more accurately simulate the structural characteristics of real-world networks [], we prefer scale-free networks in our modeling. Furthermore, to comprehensively evaluate the performance of the model, we also conduct analysis of the model in WS small-world networks, ER random networks, and a real-world network. In the real-world network, the nodes represent web pages and directed edges represent hyperlinks between them []. We call this network the Google network in this paper.
2.1. Strategy
To explore pinning control in the adversarial scenario, we propose a two-player zero-sum static game with complete information. In this game, one player is the attacker who wants to control the nodes in the network as much as possible to improve the network synchronization capabilities. The other player is the defender who aims to interfere with the attacker’s control of the network nodes as much as possible. and represent the set of nodes that the attacker chooses to control and the set of nodes that the defender chooses to defend, respectively. Obviously, even for a network with , the number of strategies for both the attacker and defender is very large (). However, due to limited decision-making information and computing power, decision-makers usually only follow certain heuristic criteria to determine specific attack(defense) targets. Albert et al. [] first proposed typical attack strategies (target attack and random attack) and defense strategies (target defense and random defense), which were widely used in subsequent research.
In summary, the attacker can adopt the following strategies in the game: target attack strategy (TAS) and random attack strategy (RAS). TAS indicates that the attacker prioritizes the nodes based on a certain kind of metric (e.g., degree) and determines the nodes controlled in order according to the priority. Obviously, different evaluation methods have different impacts on TAS. In the Results section, we will introduce in detail the TAS under different evaluation indicators. RAS denotes that the attacker randomly selects the nodes to be controlled. Similarly, the defenders have two alternative strategies: target defense strategy (TDS) and random defense strategy (RDS).
In addition, attack(defense) behaviors should consume a certain amount of resources in reality. Therefore, the model considers the influence of both sides’ available resources on the execution effect of their strategies. and denote the resources spent on attack and defense of node , respectively. and are incremental functions of an attribute of node , i.e., the costs of attack(defense) increase as increases. and are defined as follows:
and () are cost-sensitive parameters for attack and defense, respectively. Obviously, for both sides of the game, when , each target’s attack(defense) cost is the same. When , the larger the attribute of the attack(defense) node, the more resources it consumes. The parameters and can be set to various values in different systems depending on the cost difference between attack and defense. To facilitate analysis, the paper only discusses the attacker-defender confrontation scenario with . The available resources of the attacker and defender are defined as and , which are obtained from Equation (1):
and are the cost constraints of attack(defense), which determine the total amount of resources for the attacker/defender (, ). According to the defined attack(defense) strategy and the constraints of the available resources, all nodes are traversed to determine the attack(defense) nodes, and the sets of the final attack node and defense node are obtained. Taking RAS as an example, firstly, randomly generate the sequence of all nodes, and traverse the nodes sequentially according to this sequence. If , then the traversed node j () is added to . For the sake of generality [,,,], let be the degree of the node. Therefore, the above equation is updated to .
2.2. Payoff Matrix
When node i is attacked by the attacker and is not defended, it implies that the attack against node i is successful and the attacker is able to control node i. All other situations (e.g., the defender defended node i, or the attacker does not attack node i, and so on) mean that the attacker does not successfully control node i. Let denote the set of all nodes successfully controlled by the attacker, which is described by
At this time, represents the nodes that can actually be controlled. Our goal is to conduct an in-depth analysis of network synchronization via pinning control in a confrontation scenario. For the attacker, the higher the payoff, the stronger the network synchronization capability after controlling the nodes in . For the defender, it is necessary to prevent the attacker from efficiently achieving network synchronization as much as possible. Therefore, we use a zero-sum game to describe the payoff relationship between attacker and defender in the attacker-defender game, and the payoffs of each party are strongly correlated with the network synchronization capability after pinning control to the set of nodes . Recently, Liu et al. [] demonstrated that the effectiveness of the pinning control scheme can be measured by the minimum eigenvalue of the sub-Laplacian matrix, which is obtained by deleting the rows and columns corresponding to the controlled nodes from the original Laplacian matrix. The larger the minimum eigenvalue, the better the network synchronization capability is demonstrated. Therefore, we define the attacker’s payoff and the defender’s payoff based on the findings of Liu et al.:
where X and Y represent specific attack strategies and defensive strategies, respectively. represents the minimum eigenvalue of the Laplacian matrix . represents the sub-Laplacian matrix obtained by deleting the rows and columns corresponding to the controlled node from the Laplacian matrix of the network. In particular, the attacker’s payoff essentially reflects the network synchronization capability under the final pinning control scheme . To sum up, the payoff matrix of the game model is shown in Equation (5), where is the attacker’s payoff when the attacker chooses strategy i and the defender chooses strategy j. For example, represents the attacker’s payoff when the attacker chooses TAS and the defender chooses TDS.
3. Experimental Results and Analysis
In this paper, we simulate the experiment on a scale-free network with 1000 nodes. The degree distribution of the network follows , where is the degree exponent. Unless otherwise specified, the degree exponent of the network is 3 []. To reduce the uncertainty caused by random strategies (RAS and RDS), the payoffs are averaged from 1000 experiments.
As shown in Figure 1, we first analyze the impact of various attack strategies on the network synchronization capability when there is no interference from the defender (i.e., pinning control). Among them, LDP-TAS (low degree priority-TAS) denotes the priority control of nodes with small degrees in the network. HDP-TAS means the priority control of nodes with large degree in the network. HEP-TAS (high eigenvalue priority-TAS) denotes the priority control of nodes with large value of . represents the minimum eigenvalue of the Laplacian matrix after removing the row and column of node i. The y-axis in the figure is consistent with the payoff’s definition in Equation (4), which reflects the network synchronization capability after controlling the corresponding node. In Figure 1, it shows that the impact of LDP-TAS and HDP-TAS on the network synchronization capabilities is also consistent with the conclusions obtained from previous studies. When the number of control nodes is large, LDP-TAS can significantly improve the network synchronization capabilities. When the number of control nodes is small, HDP-TAS and HEP-TAS can improve the network synchronization capabilities better than other strategies, and the impact of these two strategies on the network synchronization capabilities is very similar.

Figure 1.
The payoffs as a function of the number of controlled nodes for different strategies on a scale-free network. Parameters: , <k> = 10, .
In reality, it is common for defenders to interfere with attackers’ control of nodes. To deeply analyze the Nash equilibrium between the attacker and the defender in various cases, the attacker’s payoffs under combinations of different parameters are plotted in Figure 2. Since it is a zero-sum game, the defender’s payoff is the negative of the attacker’s payoff, so its payoff is not drawn here. In Figure 2, and represent the two thresholds of q, corresponding to and , respectively. Take in Figure 2a as an example. When , for the attacker, and , so the dominant strategy of the attacker is RAS. Since , the defender definitely takes RDS. Therefore, it can be determined that the Nash equilibrium of both the attacker and defender at this time is (RAS, RDS). To sum up, we can identify the Nash equilibria corresponding to different intervals and label them in Figure 2. If there is no Nash equilibrium between the attacker and the defender in an interval, we label this interval as ‘mixed’. That is, neither the attacker nor the defender has a dominant strategy, and both parties can only choose strategies randomly.

Figure 2.
Payoffs of the attacker in the payoff matrix as a function of q with different strategies and on a scale-free network. The TAS and TDS correspond with a low-degree priority strategy, i.e., LDP-TAS and LDP-TDS (a–c). The TAS and TDS correspond with a high-eigenvalue priority strategy, i.e., HEP-TAS and HEP-TDS (d–f). The TAS and TDS correspond with a high-degree priority strategy, i.e., HDP-TAS and HDP-TDS (g–i). Parameters: , <k> = 10, .
By comparing the results of different values of in Figure 2, it is shown that changes in the value of have little impact on the payoff’s trends of the three strategies. However, as increases, the range of the mixed strategy decreases significantly. This is because the higher attack(defense) resource allows both decision-makers to choose more nodes for attack(defense), which, in turn, easily leads to the Nash equilibrium in various scenarios. In addition, the payoff’s curves of and nearly overlap when is very large (e.g., ). The reason for this phenomenon is that the defender adopts the RDS strategy at this time, which can nearly saturate the defense of most nodes in the network, which makes the attacker effectively interfere with its control of the nodes in the network, regardless of the attack strategy it uses.
Next, we further analyze the impact of parameter q on the payoff matrix of the attacker-defender game. The larger the cost-sensitive parameter q of attack(defense), the more cost the attacker/defender needs to pay in the node selected. Interestingly, the attacker’s dominant strategy is RAS, regardless of the value of q. However, the defender constantly changes its dominant strategy based on the optional strategies and the value of q. In cases where the defender’s optional strategies are LDP-TDS and RDS, the defender’s dominant strategy is RDS when q is small. As the value of q increases, the defender’s dominant strategy becomes LDP-TDS to ensure that it can choose to defend as many nodes as possible when the defense cost is high. In particular, in the situation where the defender’s TDS corresponds with high-eigenvalue priority or high-degree priority, as the value of q increases, the evolution of the defender’s dominant strategy changes from HDP-TDS (HEP-TDS) to RDS.
In addition, by comparing the results of Figure 2d–f and Figure 2g–i, we can see that target strategies based on high-degree priority or high-eigenvalue priority have a consistent impact on the payoff matrix. In Figure 3, we further analyze the relationship between and the degree of node i. It is easy to find that there exists an obvious positive correlation between and . Therefore, the priority selection of target nodes based on these two weights leads to almost the same set of selected nodes, which further causes no significant difference in the impact on the network synchronization capability.

Figure 3.
The relationship of and the degree of node i on a scale-free network. Parameters: , <k> = 10, .
Subsequently, we further analyze the impact of different network structures on the attacker-defender game. As shown in Figure 4, the payoff matrix of attackers and defenders in various situations under different average degrees is analyzed. We find that the attacker’s payoff increases significantly as the average degree of the network increases. This is because for networks with higher average degree, controlling the same scale of nodes can effectively improve the network synchronization capability []. As a result, the differences between the attack and defense strategy pairs in the payoff matrix become more pronounced as the average degree increases. In addition, we also analyze the impact of different power-law exponents on the attacker’s payoff in Figure 5. We can see that the degree exponent has limited influence on the payoff matrix. It also means that, controlling nodes with large degree has a limited impact on improving the network synchronization capability, when considering applying pinning control to the network in the attacker-defender confrontation scenario. Therefore, maximizing the number of nodes that can ultimately control the network is more effective in improving the network synchronization capability.
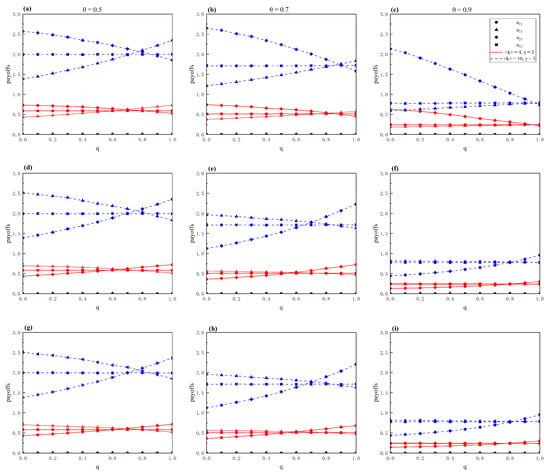
Figure 4.
For scale-free networks with different average degrees, different strategy and , payoffs of the attacker in the payoff matrix as a function of q with different strategies and . The TAS and TDS correspond with a low-degree priority strategy, i.e., LDP-TAS and LDP-TDS (a–c). The TAS and TDS correspond with a high-eigenvalue priority strategy, i.e., HEP-TAS and HEP-TDS (d–f). The TAS and TDS correspond with a high-degree priority strategy, i.e., HDP-TAS and HDP-TDS (g–i). Parameters: , .

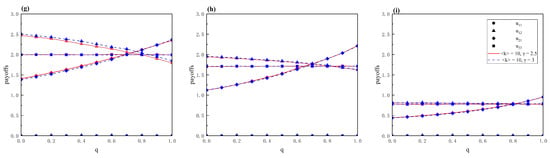
Figure 5.
For scale-free networks with degree exponents , different strategies and , payoffs of the attacker in the payoff matrix as a function of q with different strategies and . The TAS and TDS correspond with a low-degree priority strategy, i.e., LDP-TAS and LDP-TDS (a–c). The TAS and TDS correspond with a high-eigenvalue priority strategy, i.e., HEP-TAS and HEP-TDS (d–f). The TAS and TDS correspond with a high-degree priority strategy, i.e., HDP-TAS and HDP-TDS (g–i). Parameters: , <k> = 10.
Finally, to verify the correctness and effectiveness of the above payoff matrix, we also conduct simulation experiments combined with synchronous dynamics on the network in Figure 6. We first determine the actual controlled node based on the attacker and defender strategies. Then, the evolution process of the node state is obtained based on the specific synchronization dynamics. Among them, the target states of nodes are Chen’s chaotic system, and the pinning control scheme is performed using an adaptive controller to control the nodes that are successfully attacked. A detailed description of the network synchronization dynamics is provided in Appendix A. The parameter settings of Figure 6 correspond to Figure 2d. When in Figure 2d, . In Figure 6, we can clearly see that the network can achieve synchronization faster when the attacker-defender strategy pair is (HEP-TAS, RDS). The network synchronization results of the attacker-defender strategy pair (RAS, RDS) are also better than the results of the attacker-defender strategy pair (RAS, HEP-TDS). In summary, the above results verify the rationality of the attacker-defender game model proposed in this paper.

Figure 6.
Error states of Chen systems with different attacker-defender strategy pairs on a scale-free network. Each color line represents the error state of one node, and there is a total of N node error states. The TAS and TDS correspond with a high-eigenvalue priority strategy. (a1–a3) shows the error state evolution using the attacker-defender strategy pair is (HEP-TAS, RDS). (b1–b3) shows the error state evolution using the attacker-defender strategy pair is (RAS, HEP-TDS). (c1–c3) shows the error state evolution using the attacker-defender strategy pair is (RAS, RDS). Parameters: , <k> = 10, , , .
Sensitivity Analysis on Different Network Structures
To fully evaluate the experimental results, we conduct experiments on different networks, i.e., the ER network (Figure 7), the WS small-world network (Figure 8), and the Google network (Figure 9). As shown in Figure 7, in the ER network, we find that the parameter has a relatively limited effect on the payoffs of the three strategies, which is similar to the previous observations on the scale-free network. In addition, as the value of q increases, the attacker always sticks to the strategy of RAS, while the evolution of the defender’s dominant strategy changes from HDP-TDS (HEP-TDS) to RDS. It is worth noting that there is no mixed strategy region in the ER network. For all values of , the strategies of both the attacker and the defender show a clear equilibrium state. In the WS small-world network (Figure 8), we observe that the difference in the payoff matrix is not significant regardless of how q is changed, and the variation in the target strategy using LDP or HDP is also not obvious. This is mainly because the heterogeneity of small-world networks is low, which makes the differences in the degrees of all nodes small.

Figure 7.
Payoffs of the attacker in the payoff matrix as a function of q with different strategies and on the ER random network. The TAS and TDS correspond with a low-degree priority strategy, i.e., LDP-TAS and LDP-TDS (a–c). The TAS and TDS correspond with a high-eigenvalue priority strategy, i.e., HEP-TAS and HEP-TDS (d–f). The TAS and TDS correspond with a high-degree priority strategy, i.e., HDP-TAS and HDP-TDS (g–i). Parameters: , <k> = 10.

Figure 8.
Payoffs of the attacker in the payoff matrix as a function of q with different strategies and on the WS small-world network. The TAS and TDS correspond with a low-degree priority strategy, i.e., LDP-TAS and LDP-TDS (a–c). The TAS and TDS correspond with a high-eigenvalue priority strategy, i.e., HEP-TAS and HEP-TDS (d–f). The TAS and TDS correspond with a high-degree priority strategy, i.e., HDP-TAS and HDP-TDS (g–i). Parameters: , <k> = 10.

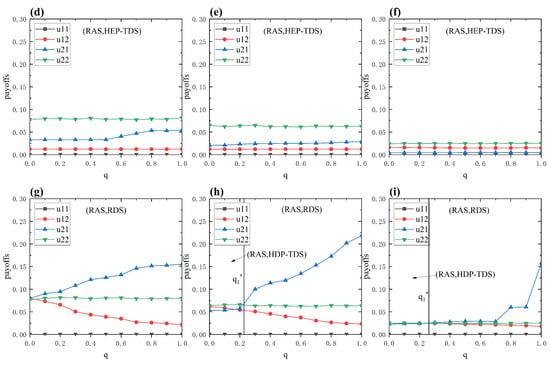
Figure 9.
Payoffs of the attacker in the payoff matrix as a function of q with different strategies and on the Google network. The TAS and TDS correspond with a low-degree priority strategy, i.e., LDP-TAS and LDP-TDS (a–c). The TAS and TDS correspond with a high-eigenvalue priority strategy, i.e., HEP-TAS and HEP-TDS (d–f). The TAS and TDS correspond with a high-degree priority strategy, i.e., HDP-TAS and HDP-TDS (g–i). Parameters: , <k> = 4.3.
In addition, in the Google network (Figure 9), the payoff trends of LDP and HDP show a clear contrast, which highlights the heterogeneous characteristics of the network; that is, there are large differences in the degrees of each node. However, it is worth noting that the payoff trends of HEP-TDS and HDP-TDS are not identical, which indicates that there is no linear relationship between nodes with high degrees and their corresponding feature values after deleting the nodes. In particular, if the target strategy corresponds with HEP, exceeds in terms of payoff when the value of is large (), showing a significant advantage. In this scenario, the impact of changes in the value of q on the payoff matrix is almost negligible.
Next, we report simulation experiments on ER networks, WS small-world networks, and the Google network in combination with synchronization dynamics. During the synchronization evolution of the ER network (Figure 10), we find that the synchronization results under different strategy pairs are consistent with the phenomenon in Figure 7. Specifically, the network is able to reach the synchronization state more rapidly when the attacker-defender strategy pairs are (HEP-TAS, RDS) and (RAS, RDS), respectively, demonstrating a higher synchronization efficiency. However, when the attacker-defender strategy pair is (RAS, HEP-TDS), the synchronization effect of the network is significantly worse, and even fails to achieve synchronization in some states (Figure 10(b3)). In Figure 11 (WS small-world network), we compare the synchronization effects under different strategies and find that the attacker-defender strategy pair (HDP-TAS, RDS) performs better in promoting network synchronization, and its effect exceeds the attacker-defender strategy pair (RAS, RDS). At the same time, whether it is (HDP-TAS, RDS) or (RAS, RDS), their synchronization effects are significantly better than the attacker-defender strategy pair (RAS, HDP-TDS).

Figure 10.
Error states of Chen systems with different attacker-defender strategy pairs on the ER random network. Each color line represents the error state of one node, and there is a total of N node error states. The TAS and TDS correspond with a high-eigenvalue priority strategy. (a1–a3) shows the error state evolution using the attacker-defender strategy pair is (HEP-TAS, RDS). (b1–b3) shows the error state evolution using the attacker-defender strategy pair is (RAS, HEP-TDS). (c1–c3) shows the error state evolution using the attacker-defender strategy pair is (RAS, RDS). Parameters: , <k> = 10, , .
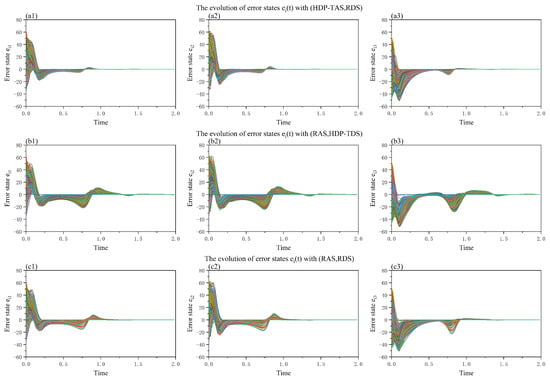
Figure 11.
Error states of Chen systems with different attacker-defender strategy pairs on the WS small-world network. Each color line represents the error state of one node, and there is a total of N node error states. The TAS and TDS correspond with a high-degree priority strategy. (a1–a3) shows the error state evolution using the attacker-defender strategy pair is (HDP-TAS, RDS). (b1–b3) shows the error state evolution using the attacker-defender strategy pair is (RAS, HDP-TDS). (c1–c3) shows the error state evolution using the attacker-defender strategy pair is (RAS, RDS). Parameters: , <k> = 10, , .
In the Google network (Figure 12), we find that the attacker-defender strategy pair (RAS, HDP-TDS) performs the best in promoting network synchronization. Its synchronization effect is significantly ahead of other strategies. It is followed by (RAS, RDS). However, under the same conditions, the attacker-defender strategy pair (HDP-TAS, RDS) does not achieve complete synchronization within the simulation time.

Figure 12.
Error states of Chen systems with different attacker-defender strategy pairs on the Google network. Each color line represents the error state of one node, and there is a total of N node error states. The TAS and TDS correspond with a high-degree priority strategy. (a1–a3) shows the error state evolution using the attacker-defender strategy pair is (HDP-TAS, RDS). (b1–b3) shows the error state evolution using the attacker-defender strategy pair is (RAS, HDP-TDS). (c1–c3) shows the error state evolution using the attacker-defender strategy pair is (RAS, RDS). Parameters: , <k> = 4.3, , .
In summary, we find that the results of the game model can be consistent with the simulation results of synchronization simulation on different network structures. Regardless of the network’s topology, attackers almost universally prefer random attack strategies, while defenders’ strategies are more susceptible to changes in different parameters.
4. Conclusions
In reality, there are always a variety of confrontational scenarios. In recent years, many scholars have begun to focus on attacker-defender confrontation issues in complex networks. However, pinning control of a complex network has hardly been explored under attacker-defender confrontation scenarios. In fact, network synchronization via pinning control also naturally exists in attacker-defender confrontations. For example, when someone tries to make the group reach a consensus on a certain view, there may also be others who want to interfere with the consensus. Therefore, the paper constructs an attacker-defender game model to explore pinning control in complex networks under confrontation scenarios. There are two parties involved in the game. On one side, the attacker wants to improve network synchronization capabilities through control nodes as much as possible; on the other side, the defender interferes with the attacker’s control of the network. We firstly analyze the impact of different attack strategies on network synchronization capabilities when there is no defender. Then, we analyze the payoff matrix and equilibrium of the attack–defense game in various scenarios on the scale-free network. Through experiments, we find that the random attack strategy is always the dominant strategy of the attacker under various equilibria. For the defender, it is necessary to determine its own dominant strategy based on the set of defense strategies and cost constraints. In addition, the network metrics of scale-free networks can also have an impact on the payoff matrix. The higher the average degree of the network, the more the attacker’s payoffs can obtain. Moreover, we further validate the correctness of the game model’s results by simulating specific network synchronization dynamics. Finally, to comprehensively evaluate the performance of the model, we conduct a sensitivity analysis in different network structures, such as the WS small-world network, the ER random network, and the Google network. We find that the model has good applicability in analyzing the impact of network synchronization through pinning control in a confrontation scenario.
We hope that this work can provide some inspiration for network synchronization via pinning control from the perspective of attacker-defender games. In addition, this work can be extended much further. In future work, a more complex attacker-defender game model should be constructed to more realistically describe complex systems in reality, such as a more complex strategy set, dynamic game model, and with limited information available to the attacker and defender.
Author Contributions
Conceptualization, T.A.; Methodology, P.P.; Software, H.Z. (Haihan Zhang) and C.Y.; Validation, P.P. and H.Z. (Haihan Zhang); Formal analysis, P.P., H.Z. (Huizhen Zhang) and C.Y.; Investigation, H.Z. (Haihan Zhang); Resources, H.Z. (Huizhen Zhang); Data curation, H.Z. (Haihan Zhang); Writing—original draft, P.P.; Visualization, H.Z. (Huizhen Zhang); Supervision, C.Y. and T.A.; Project administration, T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Jilin Provincial Department of Science and Technology (YDZJ202301ZYTS496, YDZJ202303CGZH010, 20240305048YY, YDZJ202201ZYTS549), the Education Department of Jilin Province (JJKH20230673KJ, JJKH20220597KJ), and Xinjiang University Scientific Research Program (XJEDU2024P080).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Synchronizing to a chaotic orbit is generally more difficult []. Therefore, to validate the effectiveness of our model, we conduct simulations by synchronizing with a chaotic orbit of Chen’s chaotic system. Specifically, the chaotic system discovered by Chen et al. in 1999 is widely used in the study of synchronization dynamics [], described as follows:
which is chaotic when . In addition, we use the synchronous dynamics mentioned by Liu et al. []. These dynamics are described by:
where . Vector is the state of node i, where represents the dimension of Chen’s chaotic system’s state. The function represents a complex dynamical network, which is composed of the self-dynamics of N identical to Chen’s chaotic systems. The positive constant c is the coupling strength, and is the inner coupling matrix. Matrix is the Laplacian matrix of the topological structure of the network. are the pinning controllers, defined as follows: if node is under control, then is active; otherwise, .
Consider the target state of the network is , satisfying:
We aim to select a part of the nodes from the network to control, such that all nodes in the network converge to the target state . From the network state and the target state dynamics, the error system is described by:
where . Here, can be a scalar or a vector, which depends on the state dimension n of the node i. For example, represents the error between node ’s state 1 and the target node s’s state 1. Similarly, and are also defined in this way.
In this article, the description of the adaptive controller used is as follows:
In the simulation described in Section 3 of this article, we set the node states to follow Chen’s chaotic system, the inner coupling matrix , the coupling strength , and the parameters of the adaptive controller are set as .
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Gross, T.; Blasius, B. Adaptive coevolutionary networks: A review. J. R. Soc. Interface 2008, 5, 259–271. [Google Scholar] [CrossRef] [PubMed]
- Cimini, G.; Squartini, T.; Saracco, F.; Garlaschelli, D.; Gabrielli, A.; Caldarelli, G. The statistical physics of real-world networks. Nat. Rev. Phys. 2019, 1, 58–71. [Google Scholar] [CrossRef]
- De Domenico, M. More is different in real-world multilayer networks. Nat. Phys. 2023, 19, 1247–1262. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; An, T.; Jin, X.; Wang, C.; Zhao, J.; Wang, Z. Effect of vaccine efficacy on vaccination behavior with adaptive perception. Appl. Math. Comput. 2024, 469, 128543. [Google Scholar] [CrossRef]
- Ying, X.; Wang, J.; Jin, X.; Wang, C.; Zhang, Z.; Wang, Z. Temporal-spatial perception adjustment to fitness enhances the cooperation in the spatial prisoner’s dilemma game. Front. Phys. 2023, 11, 1200506. [Google Scholar] [CrossRef]
- Chen, J.; Luo, K.; Tang, C.; Zhang, Z.; Li, X. Optimizing polynomial-time solutions to a network weighted vertex cover game. IEEE/CAA J. Autom. Sin. 2022, 10, 512–523. [Google Scholar] [CrossRef]
- Tang, C.; Yang, B.; Xie, X.; Chen, G.; Al-Qaness, M.A.; Liu, Y. An Incentive Mechanism for Federated Learning: A Continuous Zero-Determinant Strategy Approach. IEEE/CAA J. Autom. Sin. 2024, 11, 88–102. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Jin, X.; Ma, L.; Chen, Y.; Wang, C.; Zhao, J.; An, T. Subsidy policy with punishment mechanism can promote voluntary vaccination behaviors in structured populations. Chaos Solitons Fractals 2023, 174, 113863. [Google Scholar] [CrossRef]
- Zhang, H.; An, T.; Yan, P.; Hu, K.; An, J.; Shi, L.; Zhao, J.; Wang, J. Exploring cooperative evolution with tunable payoff’s loners using reinforcement learning. Chaos Solitons Fractals 2024, 178, 114358. [Google Scholar] [CrossRef]
- Klinshov, V.V.; Kovalchuk, A.V.; Soloviev, I.A.; Maslennikov, O.V.; Franović, I.; Perc, M. Extending dynamic memory of spiking neuron networks. Chaos Solitons Fractals 2024, 182, 114850. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Wang, J.; Lv, H. An optical flow estimation method based on multiscale anisotropic convolution. Appl. Intell. 2024, 54, 398–413. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Farghaly, A.A.; Abed-Elhameed, T.M.; Aly, S.A.; Arafa, A.A. Dynamics of distributed-order hyperchaotic complex van der Pol oscillators and their synchronization and control. Eur. Phys. J. Plus 2020, 135, 32. [Google Scholar] [CrossRef]
- Della Rossa, F.; Pecora, L.; Blaha, K.; Shirin, A.; Klickstein, I.; Sorrentino, F. Symmetries and cluster synchronization in multilayer networks. Nat. Commun. 2020, 11, 3179. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.F.; Chen, G. Pinning control of scale-free dynamical networks. Phys. A Stat. Mech. Its Appl. 2002, 310, 521–531. [Google Scholar] [CrossRef]
- Hong, H.; Choi, M.Y.; Kim, B.J. Synchronization on small-world networks. Phys. Rev. E 2002, 65, 026139. [Google Scholar] [CrossRef] [PubMed]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Chen, G. Pinning a complex dynamical network to its equilibrium. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 2074–2087. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, J.a.; Lü, J. Pinning adaptive synchronization of a general complex dynamical network. Automatica 2008, 44, 996–1003. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Lu, J.; Kurths, J. Synchronization via pinning control on general complex networks. SIAM J. Control Optim. 2013, 51, 1395–1416. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.; Wang, Y.; Fan, H.; Wang, X. Pinning control of cluster synchronization in regular networks. Phys. Rev. Res. 2020, 2, 023084. [Google Scholar] [CrossRef]
- Liu, H.; Xu, X.; Lu, J.A.; Chen, G.; Zeng, Z. Optimizing pinning control of complex dynamical networks based on spectral properties of grounded Laplacian matrices. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 786–796. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Lü, J. On pinning synchronization of complex dynamical networks. Automatica 2009, 45, 429–435. [Google Scholar] [CrossRef]
- Hassani, H.; Razavi-Far, R.; Saif, M.; Chiclana, F.; Krejcar, O.; Herrera-Viedma, E. Classical dynamic consensus and opinion dynamics models: A survey of recent trends and methodologies. Inf. Fusion 2022, 88, 22–40. [Google Scholar] [CrossRef]
- Lin, J.C.; Chen, J.M.; Chen, C.C.; Chien, Y.S. A game theoretic approach to decision and analysis in strategies of attack and defense. In Proceedings of the 2009 Third IEEE International Conference on Secure Software Integration and Reliability Improvement, Shanghai, China, 8–10 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 75–81. [Google Scholar]
- La, Q.D.; Quek, T.Q.; Lee, J.; Jin, S.; Zhu, H. Deceptive attack and defense game in honeypot-enabled networks for the internet of things. IEEE Internet Things J. 2016, 3, 1025–1035. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, Y.; Li, Y.; Wu, J. Which targets to protect in critical infrastructures-a game-theoretic solution from a network science perspective. IEEE Access 2018, 6, 56214–56221. [Google Scholar] [CrossRef]
- Li, Y.P.; Tan, S.Y.; Deng, Y.; Wu, J. Attacker-defender game from a network science perspective. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, R.; Chen, L.; Wang, Z.; Hu, L. An Adversarial Dynamic Game to Controlling Information Diffusion under Typical Strategies on Online Social Networks. Front. Phys. 2022, 10, 934741. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Jin, X.; Ding, H.; Cui, G.; Yu, L. Evolutionary dynamics of the interdependent security games on complex network. Appl. Math. Comput. 2021, 399, 126051. [Google Scholar] [CrossRef]
- Leskovec, J.; Lang, K.J.; Dasgupta, A.; Mahoney, M.W. Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters. Internet Math. 2009, 6, 29–123. [Google Scholar] [CrossRef]
- Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zhou, C.; Small, M.; Wang, B. Hub nodes inhibit the outbreak of epidemic under voluntary vaccination. New J. Phys. 2010, 12, 023015. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).