EDiffuRec: An Enhanced Diffusion Model for Sequential Recommendation

Abstract

Sequential recommender models should capture evolving user preferences over time, but there is a risk of obtaining biased results such as false positives and false negatives due to noisy interactions. Generative models effectively learn the underlying distribution and uncertainty of the given data to generate new data, and they exhibit robustness against noise. In particular, utilizing the Diffusion model, which generates data through a multi-step process of adding and removing noise, enables stable and effective recommendations. The Diffusion model typically leverages a Gaussian distribution with a mean fixed at zero, but there is potential for performance improvement in generative models by employing distributions with higher degrees of freedom. Therefore, we propose a Diffusion model-based sequential recommender model that uses a new noise distribution. The proposed model improves performance through a Weibull distribution with two parameters determining shape and scale, a modified Transformer architecture based on Macaron Net, normalized loss, and a learning rate warmup strategy. Experimental results on four types of real-world e-commerce data show that the proposed model achieved performance gains ranging from a minimum of $2.53\%$ to a maximum of $13.52\%$ across HR@K and NDCG@K metrics compared to the existing Diffusion model-based sequential recommender model.

1. Introduction

In the realm of recommendation systems, sequential recommendation plays a pivotal role in deducing user preferences from historical interactions such as clicks, reviews, and purchases. Its primary objective is to predict the next item that a user might find appealing, therefore enhancing user engagement and satisfaction. For example, if an online shopping mall recommends popular products based solely on overall purchase data, it might suggest items that are not relevant to the user’s recent searches or purchase history. On the other hand, by considering sequential purchase history and recent searches, it can make more effective recommendations, such as suggesting suitable phone accessories to a user who has just purchased a smartphone. Therefore, sequential recommendations that can reflect the evolving preferences and current interests of users over time can provide personalized recommendations that enhance user satisfaction.

Since the introduction of the Transformer [1], a groundbreaking architecture for natural language processing, Transformer-based recommender models such as Bert4Rec [2] and SASRec [3] have garnered attention in a sequential recommendation. However, in the face of noisy interactions stemming from random events or sparse data scenarios, these models can yield biased outcomes, including false positives and false negatives [4]. Put differently, recommender systems that overlook noise may have adverse effects and could impede the accurate learning of user preferences [5]. Furthermore, drawing inferences from highly sparse user behavioral data can limit the representation capacity of sequential pattern encoding and pose a risk of inherent popularity bias [6].

To address these issues, there has been a surge in research on generative recommender models that can learn the underlying data distributions and uncertainties [7]. Generative models can infer the underlying distribution of the data through learning and generate probabilities based on this inferred distribution. This allows them to produce reliable data even in noisy scenarios, as they are less affected by noise. Therefore, generative models can be effectively used in recommendation tasks where there is a lack of user–item interaction information or in cases where noise, such as incorrect clicks unrelated to user preferences, is present. Specifically, generative recommendation models can generate probabilities for items with no interactions in situations where interaction information is lacking and can derive useful information by learning latent features in noisy data scenarios. They are broadly categorized into two types: those leveraging Generative Adversarial Networks (GAN) [8] and those based on Variational AutoEncoders (VAE) [9]. However, GAN-based models often grapple with optimization instability, leading to degraded performance, while VAE-based models face issues such as posterior collapse [10].

Recently, the Diffusion model (DM) has garnered acclaim across diverse domains [11,12]. By operating via forward and reverse processes, the DM gradually introduces noise into the original data during the forward process and then reconstructs the original input by iteratively removing noise in the reverse process. This multi-step generation approach offers stable and efficient optimization, addressing challenges such as posterior collapse. In other words, generative models infer the underlying distribution of data through learning and generate new data. In recommendation systems, they can learn the latent distribution of data and handle noise, therefore deriving useful information for personalized recommendations. Specifically, diffusion models, which progressively add and remove noise, can model the sequential interaction process of users and predict preference changes over time, making them effectively applicable to sequential recommendations. Consequently, there is growing interest in leveraging the DM to more accurately model complex interaction generation in recommendation systems [13,14]. Although most DM-based sequential recommendation models have employed Gaussian distribution noise, there is potential for performance enhancement by exploring distributions with higher degrees of freedom [15].

In this paper, we present a novel approach to address these challenges. We introduce a new noise distribution based on the Weibull distribution, which can derive various distributions with just two parameters. Additionally, we suggest a modified Transformer structure based on Macaron Net [16], along with normalized loss and a warmup strategy [17]. Ultimately, we propose a new Diffusion model-based sequential recommender model that integrates these approaches. Our research focuses on four datasets from life-related online commerce [18], closely associated with real-world recommendation scenarios. Through experiments, we validate that the proposed model outperforms the existing Diffusion model-based sequential recommender model [19] and provides insights into the effectiveness of methodologies for enhancing sequential recommender systems.

2. Related Work

Recommendation systems have evolved from traditional methods, such as collaborative filtering, to approaches using deep learning. However, they often struggle with limited generalization performance in scenarios with weak collaborative signals, inappropriate latent representations, and noisy data. To address these challenges, methods utilizing generative models such as VAEs [20] and GANs [21] have emerged. However, VAEs often fail to effectively capture personalized user preferences, and GANs suffer from training instability. To overcome these limitations, Walker et al. [22] were the first to apply the DM to recommender systems, offering superior representational capabilities and training stability. Through the DM, they leveraged robust collaborative signals and latent representations of user–item interactions, resulting in improved performance compared to previous VAE-based models. However, their approach still had limitations in handling sequential scenarios due to a lack of consideration for temporal information.

Considering the temporal changes in user preferences, Wang et al. [13] proposed DiffRec, which integrates the DM into recommender systems, and introduced its extensions, L-DiffRec and T-DiffRec. L-DiffRec clusters items and compresses interactions, then performs diffusion processes in the latent space to generate top-K recommendations. T-DiffRec employs a time-aware reweighting mechanism, assuming that recent interactions can better capture user preferences. By giving more weight to recent interactions compared to earlier ones, it enhances the model’s adaptability and performance regarding user behavior. These results demonstrate the impact of considering temporal information on improving recommendation performance.

Recently, Li et al. [19] proposed a new DM for sequential recommendation. They defined sequences in the preprocessing stage of the dataset, organizing interactions in chronological order and treating the most recent interaction as the target data for training. This preprocessing allows for the direct reflection of users’ temporal information. Moreover, they utilized the DM’s ability to generate distributions to represent the latent features of items and the multi-level interests of users. The introduction of noise in the DM acted as a factor inducing a more robust learning process. Instead of the Mean Squared Error (MSE) used in the previous DDPM, they employed cross-entropy loss for relevance calculation in the reverse process due to the static nature of item embeddings. Additionally, they used transformers as an approximation for reconstructing item representations.

The characteristics of the aforementioned representative DM-based recommender systems are summarized in

Table 1. The literature review of DM-based recommender systems.

Reference	Model	Merit	Demerit
Walker et al. [22] (2022)	CODIGEM: The pioneer study in applying DM to recommendation systems	Achieves enhanced performance compared to VAE-based models by leveraging strong collaborative signals	Exhibits limited capability in handling sequential scenarios due to inadequate consideration of temporal information
Wang et al. [13] (2023)	DiffRec: A DM-based recommender model along with its extensions, L-DiffRec and T-DiffRec	Reduces resource costs through clustering and facilitates time-sensitive modeling by integrating weights	Falls short in fully capturing sequential interaction information
Li et al. [19] (2023)	DiffuRec: A DM-based recommender model tailored for sequential recommendations	Offers direct reflection of user interaction sequence information	Utilization of Gaussian noise distribution and basic Transformer structure may leave room for performance enhancement

.

3. Methodology

In sequential recommendation, the set of users is denoted as U, and the set of items as I. User–item interactions are sorted in chronological order according to timestamp t to construct a sequence $S_u=\{i_1,i_2,\dots ,i_t\}$, where $i_t\in I$ and $u\in U$. The goal is to predict the next item of interest for the user based on previous interactions. In other words, based on sequence S, we can summarize it as $p\left(i_{t+1}\right|i_1,i_2,\dots ,i_t)$. Each item $i_t\in I$ is also transformed into its corresponding embedding vector e. Consequently, the interaction sequence $S_u$ can be represented as $S_u=\{e_1,e_2,\dots ,e_t\}$.

3.1. Model Architecture

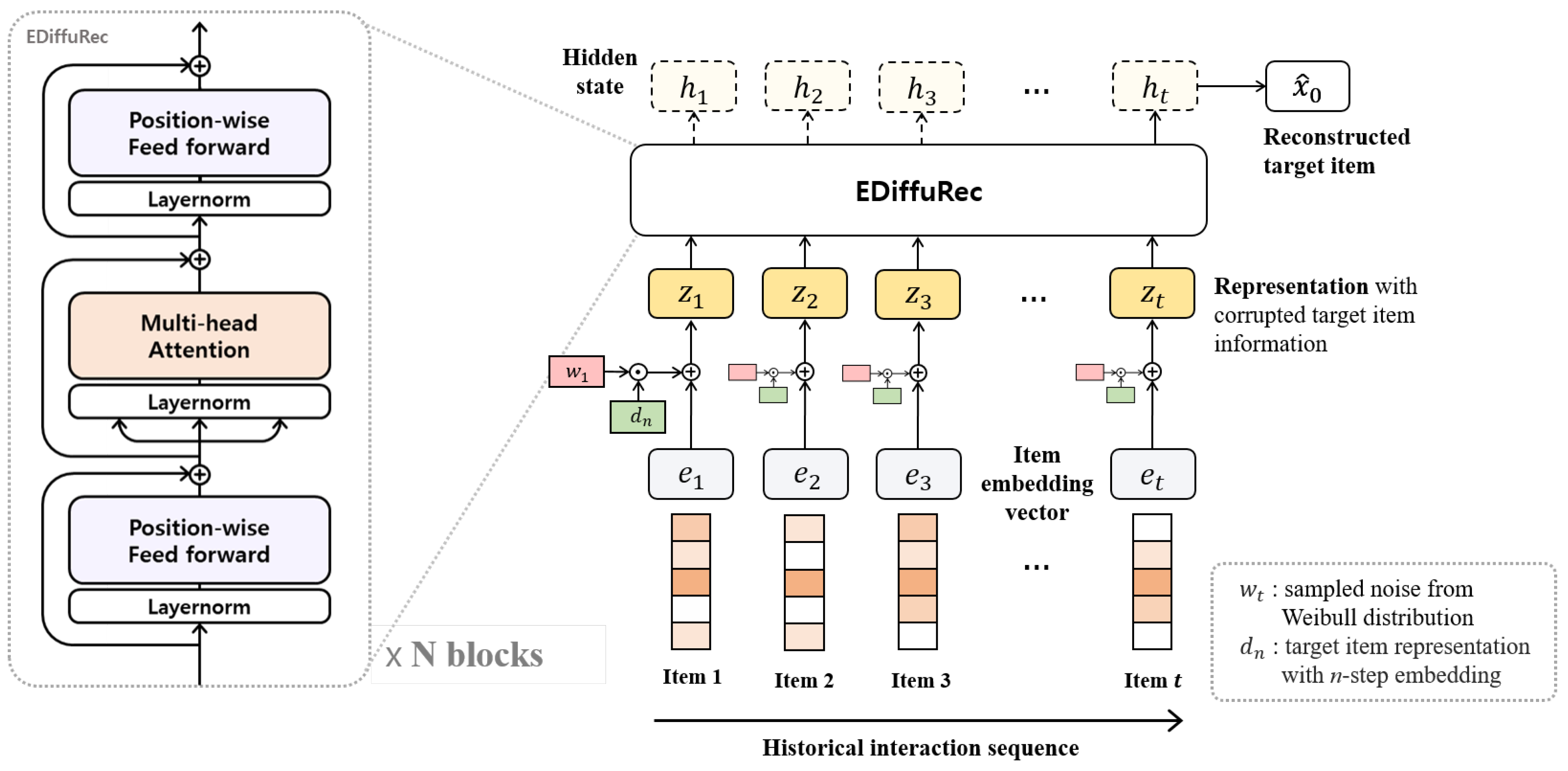
We utilize a model inspired by the Macaron Net [16], a Transformer-based model, as the approximator for the proposed EDiffuRec. Unlike the basic Transformer, which consists of a multi-head attention block and an FFN block, the existing Macaron Net positions two FFN layers before and after the multi-head attention block and multiplies the FFN outputs by 0.5. The proposed model uses the Macaron Net structure but uses the FFN outputs without multiplying by 0.5, thus enhancing the model’s representation capability. EDiffuRec is illustrated in Figure 1. The right side of the figure illustrates the training process of the approximator, where $e_t$ represents the embedded item vector and $w_t$ denotes the noise sampled from the Weibull distribution. $d_n$ indicates the value obtained by adding positional embeddings to $x_n$ at step n. By element-wise multiplying $w_t$ and $d_n$ and adding them to $e_t$, a representation $z_t$ is created, which serves as the input to the approximator. The output of the approximator yields the reconstructed target item representation ${\widehat{x}}_0$ through training. In the training process, a sampled step n is used, while the test process involves a reverse process over the total step T.

3.2. Diffusion Model

The DM, as established by the DDPM [23] framework, has demonstrated considerable effectiveness in various domains such as image generation [11], text generation [24], and audio generation [12]. As a likelihood-based generative model, the DM shares similarities and differences with VAEs. One of the main differences is that while VAEs utilize a single latent variable, the DM utilizes multiple latent variables for degradation and restoration. In terms of the learning objectives of the model, both models are similar in optimizing the Evidence Lower Bound (ELBO) by minimizing negative log-likelihood. Generally, the DM consists of a forward process and a reverse process. In the forward process, noise is gradually added to the original data to corrupt the sample, and in the reverse process, the model learns to recover the corrupted data.

• In the forward process, given a data sample $x_0\sim q\left(x_0\right)$, Gaussian noise is incrementally added at each step according to a Markov chain, corrupting the original data. The scale of the noise added at each step is determined by the variance schedule ${\beta }_t$. This is formalized as follows:

  $$q\left(x_{1:T}\right|x_0)=\prod _{t=1}^{T}q\left(x_t\right|x_{t-1}),q\left(x_t\right|x_{t-1})=N(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I),$$

  (1)

  where t in ${\left\{{\beta }_t\right\}}_{t=1}^T$ represents the diffusion step to add noise, and I denotes the identity matrix. Furthermore, according to the reparameterization trick [23], $x_t$ can be directly derived from $x_0$. This is formalized as follows:

  $$q\left(x_t\right|x_0)=N(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)I),{\alpha }_t=1-{\beta }_t,{\overline{\alpha }}_t=\prod _{s=1}^t{\alpha }_s.$$

  (2)

• In the reverse process, the DM learns to remove the added noise from $x_t$ to restore $x_{t-1}$ in the reverse direction, iteratively approximating the original $x_0$. Since $x_0$ cannot be directly estimated, it is commonly approximated using an approximator such as Transformer [1] or U-Net [25]. This process is formalized as follows:

  $$p_{\theta }\left(x_{0:T}\right)=p_{\theta }\left(x_T\right)\prod _{t=1}^T{p}_{\theta }\left(x_{t-1}\right|x_t),$$

  (3)

  $$p_{\theta }\left(x_{t-1}\right|x_t)=N(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t)),$$

  (4)

  where $\mu (x_t,t)$ and ${\Sigma }_{\theta }(x_t,t)$ represent the mean and variance parameterized by $\theta$, respectively. Through parameterization [23], ${\Sigma }_{\theta }(x_t,t)$ can be set as a constant.
  Additionally, $p_{\theta }\left(x_{t-1}\right|x_t)$ can be approximated by the tractable distribution $p_{\theta }\left(x_{t-1}\right|x_t,x_0)$, and rewritten as follows using Bayes’ rule [26]:

  $$\begin{array}{c}{p}_{\theta }(x_{t-1}|x_t,x_0)=N(x_{t-1};{\tilde{\mu }}_t(x_t,x_0),{\tilde{\beta }}_{t}I),\\ {\tilde{\mu }}_t(x_t,x_0)=\frac{\sqrt{{\overline{\alpha }}_{t-1}}(1-{\alpha }_t)}{1-{\overline{\alpha }}_t}{x}_0+\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{x}_t,\\ {\tilde{\beta }}_t=\frac{(1-{\alpha }_t)(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}.\end{array}$$

  (5)

• The optimization process minimizes the KL divergence between the posterior distribution in the forward process and the prior distribution in the reverse process to optimize the parameter $\theta$. Therefore, the objective function is formalized as follows through simplification [23]:

  $$L_{simple}={\mathbb{E}}_{t,x_0,ϵ}\left[{∥ϵ-{ϵ}_{\theta }(\sqrt{\overline{{\alpha }_t}}{x}_0+\sqrt{1-{\overline{a}}_t}ϵ,t)∥}^2\right],$$

  (6)

  where $ϵ$ represents the noise sampled from the Gaussian distribution $N(0,I)$, and ${ϵ}_{\theta }$ denotes the approximator.

In this paper, based on the DM structure in [19] for sequential recommendation, the forward process initially adds noise to each item in the sequence, which is transformed into embedding vectors, to obtain the distribution representation $Z_{x_n}=[z_1,z_2,\dots ,z_n]$, where n is determined through step sampling. The added noise is sampled from the specified noise distribution. Subsequently, the obtained $Z_{x_n}=[z_1,z_2,\dots ,z_n]$ serves as the input to the approximator, which is trained to predict $x_0$. In the reverse process, the approximator trained through the forward process is utilized to predict the target item. The reverse process is performed through the T step without step sampling. In summary, the process can be described as follows:

Forward process:

$$\begin{array}{cc}\hfill x_n& \leftarrow q\left(x_n\right|x_0,n),\hfill \\ \hfill {\widehat{x}}_0& =Approximator\left(Z_{x_n}\right).\hfill \end{array}$$

(7)

According to Equation (2), $x_n$ can be expressed as $x_n=\sqrt{{\overline{\alpha }}_n}{x}_0+\sqrt{1-{\overline{\alpha }}_n}ϵ$.

Reverse process:

$$\begin{array}{cc}\hfill & \widehat{x_0}=Approximator\left(Z_{x_t}\right),\hfill \\ & x_{t-1}\leftarrow p_{\theta }\left(x_{t-1}\right|\widehat{x_0},x_t).\hfill \end{array}$$

(8)

According to Equation (5), $x_{t-1}$ can be expressed as $x_{t-1}={\tilde{\mu }}_t(x_t,{\widehat{x}}_0)+\widetilde{{\beta }_t}ϵ$.

3.3. Noise Distribution

The DM essentially adds Gaussian noise, based on the Gaussian distribution $N(0,1)$, to data samples in the forward process. In the reverse process, it removes noise from data samples containing Gaussian noise, generating data samples during the inference process. The Gaussian distribution has a fixed mean of 0 and a degree of freedom of 1. Using distributions with more degrees of freedom can potentially improve the performance of generative models [15].

We propose using the Weibull distribution with shape and scale parameters as a new noise distribution. The Weibull distribution can derive various distributions, including asymmetric shapes, by using two parameters. Examples of the Weibull distribution and Gaussian distribution are shown in Figure 2. To define the DM process using the Weibull distribution, we can rewrite the equation obtained when using the Gaussian distribution, as shown in Equation (1), as follows:

$$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{ϵ}_t,$$

(9)

where ${ϵ}_t$ represents the noise from the Gaussian distribution at step t. We define the Weibull distribution as $Weibull(k,\lambda )$, with k as the shape parameter and $\lambda$ as the scale parameter. Taking this into account, Equation (9) can be rewritten as follows:

$$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{w}_t,$$

(10)

where $w_t\sim Weibull(k_t,{\lambda }_t)+c$, and since the typical Weibull distribution only takes non-negative values to reflect noise across various ranges, we introduce a location parameter c allowing for variation across different ranges. Therefore, the probability density function of the proposed distribution is as follows:

$$\begin{array}{c}\hfill f\left(x\right)=\left\{\begin{array}{cc}\frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{-{\left(x/\lambda \right)}^k}+c,\hfill & x\ge c,\hfill \\ 0,\hfill & x<c.\hfill \end{array}\right.\end{array}$$

(11)

To summarize, the Weibull distribution can derive various distributions using two parameters that determine shape and scale, enabling more precise modeling by accounting for different types of noise. Additionally, while the traditional Gaussian distribution is affected by extreme values or outliers that influence the mean, the Weibull distribution, being asymmetric, can mitigate the impact of noise or outliers. Therefore, utilizing the Weibull distribution allows for more accurate modeling of user behavior characteristics, providing personalized recommendations, and proving useful in real-world data that is noisy or asymmetric.

3.4. Normalized Loss

The loss function commonly used to train the approximator of the DM is MSE. However, this is more suitable for continuous distribution problems and is not suitable for sequential recommendation mapping in a discrete item space. Furthermore, sequential recommendation, inferring the target item from multiple items, can be viewed as a multi-class classification problem, and the goal is to minimize the difference between the predicted distribution and the actual distribution. Hence, we utilize cross-entropy loss as follows:

$$\widehat{y}=\frac{exp(\parallel {\widehat{x}}_0\parallel ·e_{t+1})}{{\Sigma }_{i\in I}exp(\parallel {\widehat{x}}_0\parallel ·e_i)},{\mathcal{L}}_{CE}=\frac{1}{\left|U\right|}\sum _{i\in U}-log{\widehat{y}}_i,$$

(12)

where I denotes a set of items, and U denotes a set of users. The symbol · represents the inner product, and ${\widehat{x}}_0$ denotes the target item representation reconstructed through the approximator. In this scenario, by applying L2 normalization to ${\widehat{x}}_0$, denoted as $\parallel {\widehat{x}}_0\parallel$, the vectors have the same range, making the comparison easier as the recommendation scores reflect a more consistent comparison based on the directionality of the embedding values. This approach enhances the stability and performance of the model.

3.5. Learning Rate Warmup

Typically, at the beginning of training, all parameters are initialized with random values. However, using a learning rate (LR) that is too large in such a state can potentially lead to numerical instability. To prevent this, LR warmup [17] is a strategy that starts with a small LR initially and transitions to the initially set LR value when the training process achieves stability. LR warmup involves slowly increasing the LR, and adjusting the LR during this process is referred to as LR scheduling. This strategy can also contribute to improving the performance of deep learning models [27].

The initial LR for warmup is set to ${10}^{-5}$ with a duration of 20 epochs, gradually increasing the LR during the first 20 epochs of training. Subsequently, the LR transitions to the model’s initial LR value of ${10}^{-3}$, allowing for stable LR maintenance and continued optimization.

3.6. Experimental Datasets

In this paper, we conduct experiments on publicly available product review datasets [18] for Beauty, Toys, Tools, and Video sourced from Amazon, one of the real-life-oriented online commerce platforms. The dataset consists of user review data for products in each category collected from May 1996 to July 2014.

We preprocess the dataset in accordance with the prior research [3]. We treat all interactions as implicit feedback and exclude users and items associated with interactions of fewer than five. Subsequently, we arrange interactions following the chronological order of timestamps. Given a sequence of interactions, $S_u=\{i_1,i_2,\dots ,i_t\}$, we designate the most recent interaction $i_t$ as the test item. The preceding interaction, $i_{t-1}$ is assigned as the validation item. All interactions prior to these two, excluding $i_t$ and $i_{t-1}$, are considered to be training items. In summary, all datasets are divided into train, validation, and test items based on the order of interaction sequences.

Table 2. Statistics of datasets. Average Interaction represents the average number of interactions per user, calculated by dividing interactions by users.

Dataset	Users	Items	Interactions	Average Interaction
Beauty	22,363	12,101	198,502	8.88
Toys	19,412	11,924	167,597	8.63
Tools	16,638	10,217	134,476	8.08
Video	24,303	10,672	231,780	9.54

below presents the statistics of the dataset.

3.7. Evaluation Metrics

We evaluate the performance of our sequential recommender using commonly employed metrics: Hit Rate (HR@K) and Normalized Discounted Cumulative Gain (NDCG@K), following the top-K protocol as established in related research [28]. We consider $K=\{5,10,20\}$, where HR@K denotes the proportion of correctly recommended items within the top-K list. NDCG@K assesses recommendations by factoring in the order of recommended items and assigning weights accordingly. NDCG@K is calculated as follows:

$$NDCG@K=\frac{DCG}{IDCG},DCG@K=\sum _{i=1}^K\frac{r_i}{{log}_2(i+1)},IDCG@K=\sum _{i=1}^K\frac{r_i^{ideal}}{{log}_2(i+1)},$$

(13)

where DCG@K represents the sum of relevance scores $r_i$ considered up to rank K, and $r_i$ denotes the relevance scores between users and items. Additionally, Ideal DCG@K (IDCG@K) signifies the ideal recommendation ranking, indicating the maximum value of DCG@K. To sum up, the Hit Rate represents the proportion of recommendations that contain the actual correct answer, while NDCG measures how good the model’s recommendations are compared to the ideal recommendations, with values ranging from 0 to 1. For both metrics, higher values indicate better performance. Scores are computed by calculating the inner product between the sequence representation and candidate items, with all items in the dataset serving as candidate items. To mitigate potential biases resulting from a small number of negative items [29], we rank all candidate items to predict the target item.

3.8. Compared Methods

We conduct comparative experiments between the proposed EDiffuRec and the previous DM-based sequential recommendation model. Additionally, to comprehensively analyze the efficacy of EDiffuRec, we evaluate its performance by partially integrating it into the model.

• DiffuRec [19] is a pioneering work that applies the DM to a sequential recommendation. It utilizes the diffusion distribution to adaptively reflect users’ multiple interests. A Transformer backbone model is employed as an approximator for reconstructing the target item representation.
• Ablation 1 is a comparative model that applies a proposed structure, a variation of Macaron Net, to the approximator.
• Ablation 2 is a comparative model that applies L2 normalization to ${\widehat{x}}_0$ reconstructed through the approximator in cross-entropy during training.
• Ablation 3 is a comparative model that utilizes noise sampled from the Weibull distribution in the DM process.
• EDiffuRec denotes our proposed model, which uses a modified Transformer structure based on Macaron Net, normalization, Weibull distribution, and LR warmup.

3.9. Implementation Details

All experiments are conducted on a single Nvidia GeForce RTX 4070 Ti GPU, using Python 3.8.11 and PyTorch 1.8.0. We utilize Adam [30] for optimization, with a batch size of 512, a dropout rate of $0.1$, and dimensions of embeddings and hidden layers set to 128. We limit the maximum sequence length to 50. The initial LR for warmup is set to ${10}^{-5}$, and after a duration of 20, it is set to ${10}^{-3}$. Additionally, the parameters k and $\lambda$ for the Weibull distribution are set to 2 and $0.5$, respectively.

4. Results

We present the overall performance of our model and the contributions of each component in

Table 3. The overall results (%) for each component of EDiffuRec and DiffuRec. %Improve represents the extent of performance enhancement between EDiffuRec and DiffuRec.

Dataset	Methods	HR@5	HR@10	HR@20	NDCG@5	NDCG@10	NDCG@20
Beauty	DiffuRec	5.5758	7.9068	11.1098	4.0047	4.7494	5.5566
	Ablation 1	5.5130	7.5954	10.4358	4.0143	4.6839	5.3960
	Ablation 2	5.6308	8.0594	11.4899	3.9311	4.7133	5.5776
	Ablation 3	5.7345	7.8307	10.9876	4.0988	4.7737	5.5653
	EDiffuRec	6.0357	8.2166	11.3907	4.2564	4.9593	5.7602
	%Improve	8.25%	3.92%	2.53%	6.29%	4.42%	3.66%
Toys	DiffuRec	5.5650	7.4587	9.8417	4.1667	4.7724	5.3684
	Ablation 1	5.6768	7.3887	9.6234	4.2639	4.8154	5.3784
	Ablation 2	5.4446	7.8043	10.7206	3.8560	4.6170	5.3484
	Ablation 3	5.5613	7.4381	10.0595	4.1124	4.7141	5.3748
	EDiffuRec	6.1183	8.3079	11.1723	4.5110	5.2220	5.9420
	%Improve	9.94%	11.39%	13.52%	8.26%	9.42%	10.68%
Tools	DiffuRec	3.0149	4.1825	6.0558	2.1968	2.5728	3.0415
	Ablation 1	2.7905	3.8689	5.3445	2.0957	2.4382	2.8088
	Ablation 2	3.2469	4.6449	6.9201	2.2697	2.7183	3.2935
	Ablation 3	3.0508	4.3963	6.1087	2.2121	2.6433	3.0759
	EDiffuRec	3.2993	4.6271	6.7898	2.3888	2.8196	3.3616
	%Improve	9.43%	10.63%	12.12%	8.74%	9.59%	10.52%
Video	DiffuRec	7.7025	11.9674	17.4797	5.1225	6.4908	7.8789
	Ablation 1	7.5462	11.7058	17.4733	5.0522	6.3929	7.8427
	Ablation 2	8.1972	12.8096	18.9724	5.3300	6.8166	8.3687
	Ablation 3	7.5532	11.8064	17.6128	5.1127	6.4832	7.9443
	EDiffuRec	8.1420	12.5603	18.7079	5.3618	6.7782	8.3231
	%Improve	5.71%	4.95%	7.03%	4.67%	4.43%	5.64%

The highest score for each metric is indicated in bold.

. When using the modified Transformer structure based on the Macaron Net alone, we observe slightly improved performance in the NDCG metric for the Toys dataset. However, it degrades performance in other metrics. Utilizing normalization in the loss generally leads to improvements, notably enhancing performance across all metrics for the Tools and Video datasets. The model using noise sampled from the Weibull distribution shows enhanced improvements in the NDCG metric for the Beauty dataset and all metrics for the Tools dataset. Additionally, it exhibits particular performance improvements at $K=20$ in the Toys and Video datasets. EDiffuRec, combining these components, outperforms across all datasets and metrics.

Specifically, it achieves performance improvements ranging from $2.53\%$ to $8.25\%$ for the Beauty dataset, from $8.26\%$ to 13.52% for the Toys dataset, from $8.74\%$ to $12.12\%$ for the Tools dataset, and from $4.43\%$ to $7.03\%$ for the Video dataset.

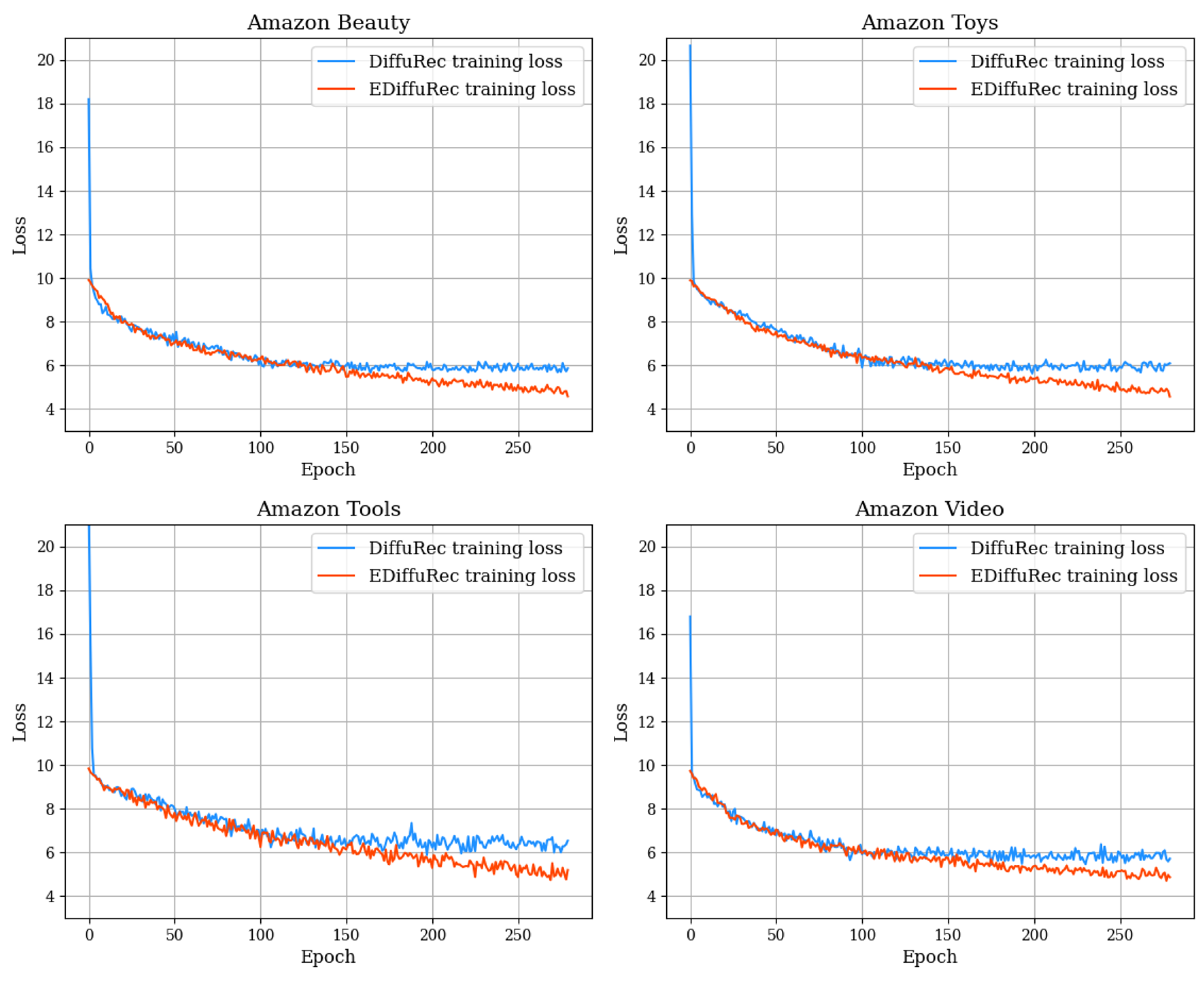
We illustrate the comparison of training losses between EDiffuRec and the baseline in Figure 3. Our proposed model, incorporating the L2 norm in the loss, starts with a significantly lower loss from the beginning of training. Moreover, using a warmup strategy to enhance the stability of the model, we observe even lower loss after 150 epochs.

We compare our proposed Weibull distribution with different noise assumptions in

Table 4. Performance comparison according to various noise distributions applied to EDiffuRec.

Dataset	Noise Distribution	HR@5	HR@10	HR@20	NDCG@5	NDCG@10	NDCG@20
Beauty	Gaussian	5.9745	8.2230	11.3753	4.2358	4.9638	5.7591
	Log-normal	5.9136	8.1501	11.3645	4.1779	4.8939	5.7027
	Gaussian mixture	5.8749	8.1323	11.3030	4.1885	4.9188	5.7198
	Weibull	6.0357	8.2166	11.3907	4.2564	4.9593	5.7602
Toys	Gaussian	6.0165	8.1248	10.8627	4.4485	5.1297	5.8186
	Log-normal	6.1773	8.2014	10.9231	4.5251	5.1770	5.8630
	Gaussian mixture	6.1207	8.2112	10.8441	4.5343	5.2127	5.8757
	Weibull	6.1183	8.3079	11.1723	4.5110	5.2220	5.9420
Tools	Gaussian	3.2762	4.5446	6.6126	2.3589	2.7667	3.2827
	Log-normal	3.1875	4.4967	6.3988	2.3092	2.7323	3.2089
	Gaussian mixture	3.1874	4.5802	6.6186	2.2987	2.7451	3.2587
	Weibull	3.2993	4.6271	6.7898	2.3888	2.8196	3.3616
Video	Gaussian	7.9176	12.3784	18.4179	5.3068	6.7475	8.2662
	Log-normal	7.9473	12.4371	18.4638	5.2760	6.7173	8.2338
	Gaussian mixture	7.8060	12.2237	18.4783	5.1961	6.6105	8.1834
	Weibull	8.1420	12.5603	18.7079	5.3618	6.7782	8.3231

The highest score for each metric is indicated in bold.

. In the Gaussian distribution as in DDPM [23], the mean is set to 0 and the variance to 1. The log-normal distribution utilizes parameters that determine the shape and scale, similar to the Weibull distribution. In this comparison experiment, we set the shape to 0 and the scale to $0.5$. The Gaussian mixture distribution combines two Gaussian distributions, both with a mean of 0 and variances of $0.8$ and $0.5$, respectively, with a weight of $0.5$. Comparing the results, the performance of the Gaussian distribution is superior in terms of HR@10 and NDCG@10 on the Beauty dataset, while on the Toys dataset, the log-normal distribution in HR@5 performs better than other methods, and the Gaussian mixture outperforms in NDCG@5. However, in all other metrics, our proposed Weibull distribution achieves the most superior performance. It proves that using a distribution with higher degrees of freedom, such as the noise distribution, could be helpful for performance improvement. In this sense, there is still the possibility of deriving a more suitable distribution for both the log-normal and Gaussian mixture distributions through parameter adjustments.

To further investigate the impact of warmup duration settings, we conducted performance comparison experiments on all datasets. The results are depicted in Figure 4. In the case of the Beauty dataset, there is not a significant difference in performance according to the HR metric, while a longer duration correlates with improved performance in the NDCG metric. In the Toys dataset, similarly, there is no significant performance difference in terms of HR metrics. However, in contrast to the Beauty dataset, performance improves with shorter durations. This difference is most pronounced in the Tools dataset, where it is evident that as the duration increases, performance remains notably low. For the Video dataset, a relatively shorter duration yields higher performance in both HR and NDCG at $K=10$ and $K=20$. These findings indicate that performance could fluctuate based on the duration, emphasizing the importance of selecting an appropriate duration that suits the characteristics of the data.

5. Discussion and Limitations

This study aimed to propose a model that better reflects personalized preferences through an improved Diffusion model in sequential recommendation systems. As shown in Table 3, EDiffuRec demonstrates enhanced performance compared to the existing Diffusion model-based sequential recommender model. We hypothesize that the addition of an extra FFN layer, unlike the traditional Transformer encoder structure, significantly contributes to the comprehensive learning of user behavior patterns embedded in sequential information.

Furthermore, the results presented in Table 4 align with previous research [15], which suggested that using distributions with higher degrees of freedom can positively impact the performance of generative models. This underscores the meaningful application of such distributions in generative recommendation models. The strategy of applying warmup, as demonstrated in Figure 3, enhances both performance and stability, corroborating the proposal of [17]. By starting with a sufficiently low learning rate during the initial stages of training, the numerical instability of the training weights is mitigated, allowing the model to avoid local optima and converge towards a global optimum, therefore achieving a lower loss.

As shown in

Table 5. Comparison of EDiffuRec and DiffuRec in terms of process time.

Dataset	Methods	Training Time per Sample (ms)	Convergence Epochs	Total Training Time (s)	Testing Time per Sample (ms)
Beauty	EDiffuRec	0.244	280	8960	3.091
	DiffuRec	0.137	440	7920	1.881
Toys	EDiffuRec	0.247	340	9180	3.914
	DiffuRec	0.137	480	7200	2.560
Tools	EDiffuRec	0.248	240	5040	4.137
	DiffuRec	0.142	380	4560	1.893
Video	EDiffuRec	0.245	220	8580	4.115
	DiffuRec	0.138	280	6160	1.876

, adding an additional FFN layer increased both the training and testing time compared to DiffuRec due to the increase in parameters. Nonetheless, EDiffuRec converges in fewer epochs due to stable learning, resulting in a comparable total training time and improved final performance. However, considering time efficiency, it is necessary to explore strategies to reduce the number of parameters or decrease training time in future work. Additionally, since this study did not separately investigate learning rate scheduling from learning rate warmup, there remains potential for more efficient and stable learning and consequent performance improvements.

6. Conclusions

In this paper, we have introduced a novel diffusion sequential recommendation model tailored for real-life-oriented online commerce. Our proposed model, EDiffuRec, integrates several key enhancements, including a modified Transformer structure inspired by the Macaron Net, a normalized loss function, a novel noise assumption following the Weibull distribution, and the incorporation of warmup techniques.

Specifically, we leverage a modified Transformer structure based on the Macaron Net to bolster the model’s information representation capacity. Furthermore, we introduce a Weibull distribution for generating noise tailored to the generative model’s requirements. Additionally, the adoption of a normalized loss function and warmup strategy contributes to the model’s overall stability. Extensive experiments, including ablation studies, were conducted to assess the effectiveness of each major design component.

Comparative experiments were carried out on four datasets, consistent with prior research in the field of diffusion sequential recommender models. Our experimental results demonstrate performance enhancements ranging from a minimum of $2.53\%$ to a maximum of $13.52\%$ across all evaluation metrics. Based on these findings, we anticipate that our EDiffuRec model will significantly elevate user satisfaction and marketing efficiency within the online commerce domain through enhanced personalization.

In today’s digital landscape, characterized by ubiquitous online and streaming services, personalized recommendations play a pivotal role in enhancing user satisfaction. Advancements in this research domain, focused on modeling human preferences, facilitate profound insights into human behavior from a machine-learning perspective.