Coupons versus Rebates: An Economic–Mathematical Comparative Analysis with Policy Implications

Abstract

It is very important to understand how promotions offered by sellers to consumers influence consumer and seller behaviors because it helps us study how consumers make their purchase decisions and how sellers determine their sale strategies. Unlike past studies which utilized the classical price discrimination dilemma and focused on sellers’ aspect to divide consumers into two types (higher/lower reservation prices), we focused on the consumers’ perspective and applied neoclassical consumer choice theory to develop a two-period mathematical utility-maximization model to study how different promotions influence consumer and seller behaviors. This mathematical study uncovered several key findings: (1) coupons offer consumers a greater discount compared to rebates with identical discount rates; (2) impatient consumers exhibit a preference for coupons over rebates; (3) coupons generate higher sales than rebates; and (4) sellers may adopt the coupon policy for low-ticket products and the rebate policy for high-ticket products.

1. Introduction

Promotional offers, such as coupons and rebates, make consumers more willing to purchase products at a lower price (the promotion price), rendering their consumer surplus positive. This practice in most cases increases sellers’ sales. In the summers of 2022 and 2023, we informally interviewed (i.e., free chatting conversation) about 33 restaurant and retail store managers/owners who had previously issued coupons/rebates to consumers in Indiana while we shopped at these stores or dined at these restaurants. Our question was the following: what was your main purpose in issuing coupons/rebates to consumers? All of them had a similar answer, such as “to increase sales”. We then further asked the following question: did you significantly increase sales during the promotion period? Most of them had a certain, positive answer, while some of them did not. Roehrig [1] has pointed out that rebates and coupons are the mechanisms that manufacturers often use to boost their sales. Lake [2] has further indicated that “94% of people use coupons and 38% buy more than they intended because they have a coupon. Among frequent coupon shoppers, 83% had coupons affect their purchasing behavior”. Moreover, according to the report by PYMNTS [3], “...rebates make consumers 75% more likely to make a purchase…”. In addition, statistical data provided in Statista [4] show that coupons saved shoppers up to USD4 billion in 2023. Further, over 90% of households reported that they had used at least one coupon in the year of 2023. The data mentioned above [1,2,3,4] all demonstrate that promotional vehicles, such as coupons and rebates, increase the number of consumer purchases and, hence, enlarge the amount of sellers’ sales.

Although both coupons and rebates are used as promotional tools, they exert different economic effects on consumer behavior. Coupons are viewed as a certificate that offers consumers an instant price discount on a purchase, while rebates are a refund provided post purchase [5]. Since coupons can be redeemed with a purchase while rebates are redeemed after a purchase, consumers with coupons can pay a lower price (i.e., the promotional price), but consumers with rebates pay the regular price and, therefore, only benefit from the promotion once they submit and receive the rebate [6,7]. In addition, when consumers use coupons, uncertainty can be resolved before a purchase, whereas uncertainty can be resolved only after a purchase with rebates. Therefore, rebates may carry more risks than coupons. Clearly, coupons and rebates do not have the same impact on consumers, even though their redemption costs are not different [8]. Moreover, taking an economic perspective, coupons have both substitution and income effects. The substitution effect refers to when the price of a good changes, say decreases, making other goods’ prices relatively more expensive. To keep the same level of consumer satisfaction, the consumer substitutes more units of the good for other goods. The income effect refers to when the price of a good changes, say decreases, increasing the consumer’s real income. Therefore, the consumer has more purchasing power and, hence, purchases more units of both the good and other goods. Coupons have both substitution and income effects due to a price deduction, while rebates only create an income effect when used as payment for a future purchase at the same store.

Variations in economic effects on consumer behavior have different impacts on seller behavior due to the prospect of additional/increased sales. That is, given the same production cost and discount rate for both coupons and rebates, additional sales due to the use of either will result in different seller behaviors. As observed by Lu and Moorthy [8], from the sellers’ point of view, they incur the promotional cost upfront when coupons successfully motivate consumers to purchase products; otherwise, sellers incur decreases in their sale rates. On the other hand, sellers offering rebates receive the regular price upfront and only incur the promotional cost when consumers redeem the rebates. If consumers do not redeem the rebates, sellers gain at the expense of consumers. For that reason, sellers and consumers may prefer different promotion policies. For example, consumers may prefer coupons to rebates, while sellers may prefer rebates to coupons. For instance, Menards (Menards is an American home improvement retail company headquartered in Eau Claire, Wisconsin) only offers rebates rather than coupons to consumers.

Discussions about coupons or rebates have occurred often during the past several decades (e.g., [6,7,8,9,10,11,12,13,14,15,16,17], etc.). Several of the researchers cited above (except for [8]) have focused their work on either coupons or rebates, while Lu and Moorthy [8] have focused on both. In the past, researchers (e.g., [8]) who studied the issue of coupons vs. rebates normally used the classical price discrimination dilemma and focused on the sellers’ perspective, dividing consumers into two types (consumers with a higher reservation price and those with a lower reservation price). This allowed researchers to study how promotions could be designed such that sellers could charge each type of consumer their reservation price to prevent consumers with a high reservation price from using a lower price. Consumers with a high reservation price are those who are willing to pay the higher price charged by sellers. Therefore, these consumers’ consumer surplus is positive. Instead, consumers with a low reservation price are those who are not willing to pay the higher price charged by sellers. Thus, their consumer surplus is negative. In addition, regarding rebates, researchers (e.g., [18,19,20,21]) have pointed out that some consumers may misperceive the benefit–cost algorithm of rebates when they make a purchase. Moreover, researchers (e.g., [22,23,24], etc.) have focused on sellers’ position in dealing with supply chains with the rebate strategy.

As mentioned above, Lu and Moorthy [8] employed the classical price discrimination dilemma and were absorbed with the sellers’ point of view. Yet, no researcher has investigated the issue of coupons vs. rebates by concentrating on the consumer standpoint and applying consumer theory. In fact, the issue of coupons vs. rebates can also be investigated from the consumers’ perspective rather than the sellers’ perspective. For this reason, in this research, we attempted to address the absence in the consumer point of view and did not examine the issue of design promotion. Instead, we focused on the consumer perspective and how these two promotions (coupons and rebates) influence consumer behavior (including consumer utility and product demand) and, in turn, affect seller behavior (including additional sales and promotion policy decisions).

Here, we adopted the theory of consumer choice (neoclassical consumer choice theory) and developed a two-period mathematical utility-maximization model for both coupons and rebates. In this framework, consumers can apply coupons to pay a lower price in the first period but need to incur a cost to obtain the rebate in the second period. The rebate amount expands consumers’ disposable income in the second period. Consumers incur a cost to obtain the rebates but no costs for using coupons. Impatient consumers discount the rebate that they receive in the second period. Under the neoclassical consumer choice theory, every consumer, no matter which type (high reservation price or low reservation price), maximizes their utility (wellbeing), subject to their budget constraints, which include all their costs, and makes optimal choices when faced with these promotions (coupons or rebates). That is, the equilibrium in this study was each consumer’s optimal choice.

As a result, based on our model and analysis, we developed three research questions. First, given the same discount rate for both coupons and rebates, do consumers receive a greater discount under the coupon promotion or the rebate promotion? Second, do patient or impatient consumers prefer coupons or rebates? Third, given the same production cost for sellers and the same discount rate for both coupons and rebates, are a seller’s additional sales greater under the coupon or the rebate promotion? Moreover, according to the results of the above research questions, we further discussed policy implications focusing on sellers’ point of view when evaluating which policy would most benefit them. Therefore, we developed a fourth research question: should sellers adopt the coupon or the rebate policy for low- or high-ticket products?

This paper offers several substantive contributions to the literature. For example, unlike past studies using the classical price discrimination dilemma and focusing on sellers’ point of view, we applied the neoclassical consumer choice theory to study the ways in which different promotions (coupons and rebates) influence consumer behavior (utility and product demand) and affect seller behavior (additional sales and policy adoption). In addition, we constructed a two-period mathematical utility-maximization model to study this issue and offered intricate insights into the dynamics between coupons and rebates. Moreover, we offered exploratory results about the possible dominance of coupons over rebates and suggested ways in which firms should use one versus the other. Furthermore, our comparative analysis of coupons and rebates has practical relevance and can contribute to the theoretical understanding of consumer behavior in the context of widely utilized marketing strategies, which is practically relevant and theoretically important.

2. The Mathematical Model

2.1. The Utility Function

We assume that every consumer maximizes their utility while they are consuming products in a store. In the first period, suppose that a representative consumer, say, Consumer A, needs to purchase two goods (denoted by X and Y) at a retail store (say retail Store B). We assume that these two goods (X and Y) are normal goods. The consumer can be satisfied by shopping for these two goods at a retail store. When the consumer shops at a retail store, the consumer not only enjoys purchasing goods but also the seller’s service (denoted by S) and the store’s environment (denoted by E). The quantity of goods X and Y is a factor that can be determined by the consumer; thus, these two factors are variables. However, the seller’s service (S) and the store’s environment (E) are factors that cannot be determined by the consumer, so these factors are constant terms. We let $K=S^a{E}^b$, where a and b are constant parameters and shares of the seller’s service (S) and the store’s environment (E), and $0<a,b<1$, $a+b\ge 1$. Moreover, we assume that the consumer’s utility function exhibits the Cobb–Douglas form, which can be shown as follows:

$$U=\left(S^a{E}^b\right)X^{\alpha }{Y}^{\beta }=K{X}^{\alpha }{Y}^{\beta }$$

(1)

where $\alpha$ and $\beta$ are constant parameters ($0<\alpha ,\beta <1$ and $\alpha +\beta \ge 1$) and shares of goods X and Y, respectively; $U_X,U_Y>0$; $U_{XX},U_{YY}<0$; and $U_{XY}=U_{YX}>0$.

In the second period, Consumer A may come back to the same retail store (retail store B) to shop for two other different goods (say, W and Z). The consumer’s utility function still displays the Cobb–Douglas form, but the consumer can now be satisfied by shopping for W and Z goods at the retail store in addition to enjoying the seller’s service (S) and the store’s environment (E). For this reason, the consumer’s utility function in the second period can be exhibited as follows:

$$U=\left(S^a{E}^b\right)W^{\gamma }{Z}^{\delta }=K{W}^{\gamma }{Z}^{\delta }$$

(2)

where $\gamma$ and $\delta$ are constant parameters ($0<\gamma ,\delta <1$ and $\gamma +\delta \ge 1$) and shares of goods W and Z, respectively; $U_W,U_Z>0$; $U_{WW},U_{ZZ}<0$; and $U_{WZ}=U_{ZW}>0$.

It should be noted that goods ([X and Y] or [W and Z]) being included in the consumer’s utility function means that these goods are the consumer’s preferences; otherwise, they would not be in the consumer’s utility function and the consumer would not even be in the market of these goods. In addition, a consumer’s previous shopping experiences can be influenced by the seller’s service quality (S) and the store’s environment quality (E). That is, a consumer’s previous shopping experiences can be reflected by both the seller’s service quality and the store’s environment quality (e.g., [25,26]). Moreover, brand loyalty belongs to the consumer’s preferences. If the consumer is loyal to the good’s brand, this good must be the consumer’s preference, and it must be in the consumer’s utility function; otherwise, it is not in the utility function. Consequently, we do not need to particularly create factors to identify individual consumer preferences, previous shopping experiences, or brand loyalty. Furthermore, and more importantly, this is a theoretical study rather than an empirical study. For the theoretical model, only two endogenous variables ([X and Y] or [W and Z]) can be included in the utility function, and all other factors need to be counted as exogenous variables; otherwise, we would not be able to solve the problem.

2.2. The Budget Constraint Line

Assume that Consumer A’s total budget in the first period for these X and Y goods is M and the sales tax rate is t ($0<t<1$). The price of good X is $P_X$, while the price of good Y is $P_Y$. Without coupons and rebates, the consumer pays not only the prices of goods X and Y but also the sale taxes for both goods. To simplify the model, we assume that the consumer’s total expenditures on these two goods (X and Y) are equal to the consumer’s total budget (M). Therefore, Consumer A’s total budget constraint line for shopping X and Y can be displayed as follows:

$$\left(1+t\right)P_{X}X+\left(1+t\right)P_{Y}Y=M$$

(3)

Similarly, in the second period, we assume that Consumer A’s total budget for shopping W and Z goods becomes I and the sales tax rate is still t ($0<t<1$), and W and Z are also normal goods. The price of good W is $P_W$, while the price of good Z is $P_Z$. Again, the consumer pays not only the prices of goods W and Z but also the sale taxes for both goods. We also assume that the consumer’s total expenditures on these two goods (W and Z) are equal to the consumer’s total budget (I). Therefore, Consumer A’s total budget constraint line for shopping for W and Z can be shown as follows:

$$\left(1+t\right)P_{W}W+\left(1+t\right)P_{Z}Z=I$$

(4)

3. Equilibriums

3.1. Coupons

The First Period

Suppose that retail store B issues a coupon for good X with a discount rate (${\rho }_c=\rho$ and $0<\rho <1$) to consumers. Consumer A receives the coupon and thus shops at retail store B and purchases goods X and Y. The coupon cannot be redeemed for cash. Due to the coupon being used for good X, the price of good X for the consumer drops to $\left(1-\rho \right)P_X$. Therefore, Consumer A’s total budget constraint line for shopping for X and Y in the first period becomes the following:

$$\left(1+t\right)\left(1-\rho \right)P_{X}X+\left(1+t\right)P_{Y}Y=M$$

(5)

To solve the consumer’s optimization problem, we maximize $U=K{X}^{\alpha }{Y}^{\beta }$ subject to $\left(1+t\right)\left(1-\rho \right)P_{X}X+\left(1+t\right)P_{Y}Y=M$ and choose X and Y. The first-order conditions for the constrained maximum can be displayed as shown below:

$$\frac{\alpha K{X}^{\alpha -1}{Y}^{\beta }}{\left(1+t\right)\left(1-\rho \right)P_X}=\frac{\beta K{X}^{\alpha }{Y}^{\beta -1}}{\left(1+t\right)P_Y} \mathrm{and}$$

(6)

$$M=\left(1+t\right)\left(1-\rho \right)P_{X}X+\left(1+t\right)P_{Y}Y.$$

(7)

Based upon Equations (6) and (7), we can solve the equilibriums of X and Y:

$$X_{1,C}^{\ast }=\frac{\alpha M}{\left(1+t\right)\left(1-\rho \right)P_X\left(\alpha +\beta \right)} \mathrm{and}$$

(8)

$$Y_{1,C}^{\ast }=\frac{\beta M}{\left(1+t\right)P_Y\left(\alpha +\beta \right)},$$

(9)

where $X_{1,C}^{\ast }$ and $Y_{1,C}^{\ast }$ mean the equilibriums of X and Y, respectively, in the first period under the coupon promotion policy. Plugging $X_{1,C}^{\ast }$ and $Y_{1,C}^{\ast }$ into the utility function (U), we can then solve $U_{1,C}^{\ast }$, the equilibrium of the consumer’s utility with a coupon in the first period:

$$U_{1,C}^{\ast }=\left(S^a{E}^b\right){\left(\frac{M}{\left(1+t\right)\left(\alpha +\beta \right)}\right)}^{\alpha +\beta }{\alpha }^{\alpha }{\beta }^{\beta }{\left(\frac{1}{\left(1-\rho \right)P_X}\right)}^{\alpha }{\left(\frac{1}{P_Y}\right)}^{\beta }.$$

(10)

It should be noted that, if the consumer does not use the coupon, then the consumer will pay the original price without discount, and, hence, the coupon will not influence the consumer’s behavior. For this reason, the consumer’s optimal choice (i.e., equilibriums of X and Y) and utility will be the same as the consumer’s optimal choice and utility in the first period under the rebate policy (i.e., Equations (18)–(20)). (For details, please refer to the model in the first period under the rebate policy shown in the following Subsection on “Rebates”) Thus, the difference between the equilibriums of using coupons and the equilibriums of not using coupons contains two effects: the substitution effect and the income effect. However, the mathematical model would not be able to directly show each of these effects. 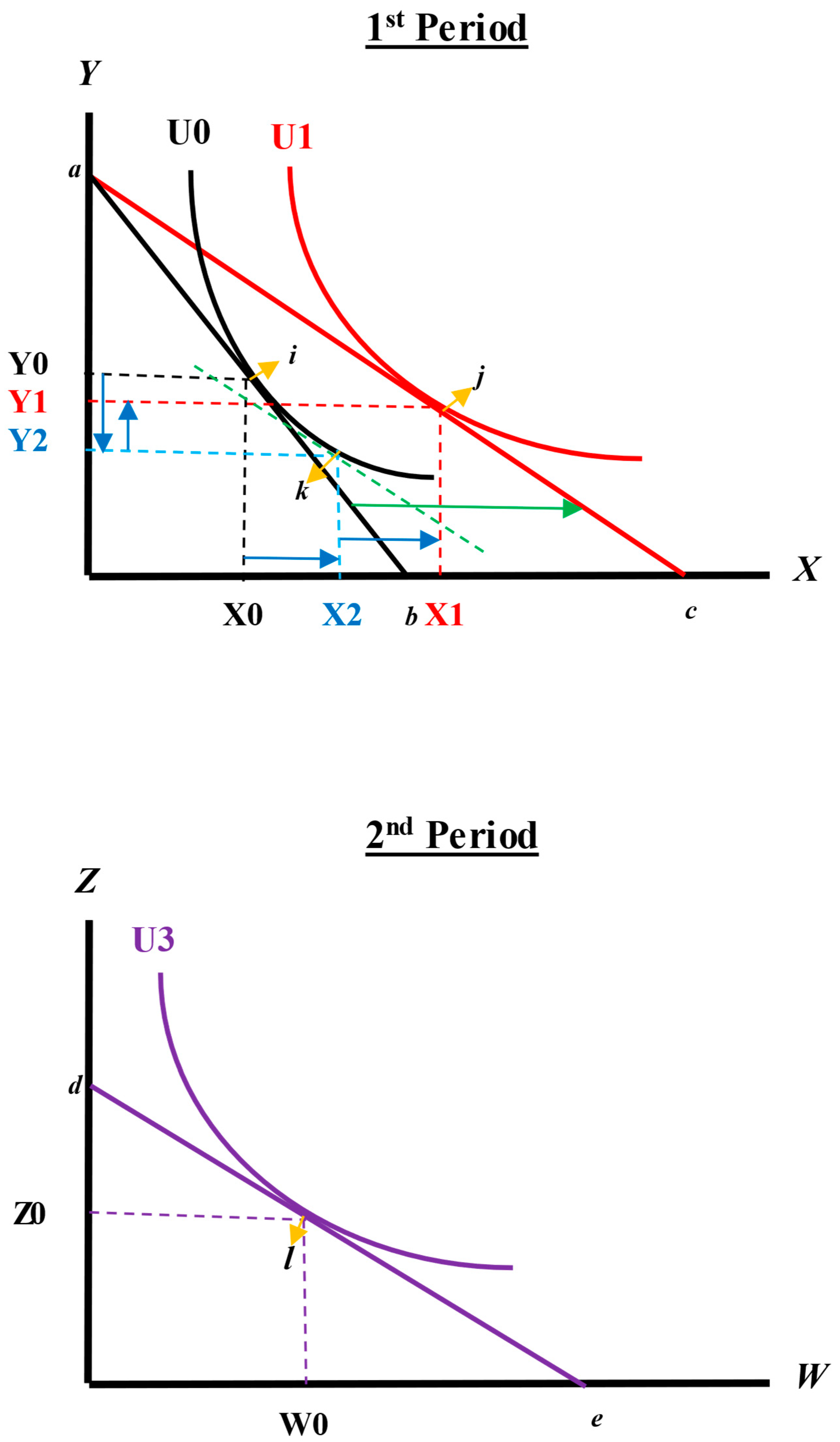For this reason, we will rely on a graphical analysis, which is displayed in Figure 1 in the following Section—“Comparative Static Analysis”. Figure 1 shows graphically the decomposition of the change in the consumer’s decision into the substitution effect and the income effect. Figure 1 shows changes in consumer behavior before and after the use of coupons, including substitution and income effects.

The Second Period

Consumer A returns to the retail store in the second period to shop for two other different goods (W and Z) without any coupons for these two goods. Similarly, we maximize $U=K{W}^{\gamma }{Z}^{\delta }$ subject to $\left(1+t\right)P_{W}W+\left(1+t\right)P_{Z}Z=I$ and choose W and Z to solve the consumer’s optimization problem. The first-order conditions for the constrained maximum can be shown as follows:

$$\frac{\gamma K{W}^{\gamma -1}{Z}^{\delta }}{\left(1+t\right)P_W}=\frac{\delta K{W}^{\gamma }{Z}^{\delta -1}}{\left(1+t\right)P_Z} \mathrm{and}$$

(11)

$$I=\left(1+t\right)P_{W}W+\left(1+t\right)P_{Z}Z.$$

(12)

Based upon Equations (11) and (12), we can solve the equilibriums for W and Z:

$$W_{2,C}^{\ast }=\frac{\gamma I}{\left(1+t\right)P_W\left(\gamma +\delta \right)} \mathrm{and}$$

(13)

$$Z_{2,C}^{\ast }=\frac{\delta I}{\left(1+t\right)P_Z\left(\gamma +\delta \right)},$$

(14)

where $W_{2,C}^{\ast }$ and $Z_{2,C}^{\ast }$ are the equilibriums for W and Z, respectively, in the second period under the coupon promotion policy in the first period. Plugging $W_{2,C}^{\ast }$ and $Z_{2,C}^{\ast }$ into the utility function (U), we can then solve $U_{2,C}^{\ast }$, the equilibrium of the consumer’s utility in the second period under the coupon promotion policy in the first period:

$$U_{2,C}^{\ast }=\left(S^a{E}^b\right){\left(\frac{I}{\left(1+t\right)\left(\gamma +\delta \right)}\right)}^{\gamma +\delta }{\gamma }^{\gamma }{\delta }^{\delta }{\left(\frac{1}{P_W}\right)}^{\gamma }{\left(\frac{1}{P_Z}\right)}^{\delta }.$$

(15)

3.2. Rebates

The First Period

In this case, we assume that the retail store issues consumers a rebate for good X rather than a coupon with a discount rate ${\rho }_r=\rho$ ($0<\rho <1$), which is the same discount rate as the coupon. However, with rebates, consumers cannot instantly receive a discount for good X but must file a rebate form and mail it in to the retail store. The process takes 8–10 weeks. These rebates cannot be redeemed for cash. That is, the rebate credit check is not redeemable for cash, gift cards, or kiosk purchases, and no cash can be refunded for an unused balance.

Consequently, Consumer A shops for goods X and Y at the retail store without any discount on X in the first period. Thus, we choose X and Y to solve the consumer’s optimization problem, which maximizes $U=K{X}^{\alpha }{Y}^{\beta }$ subject to $\left(1+t\right)P_{X}X+\left(1+t\right)P_{Y}Y=M$. The first-order conditions for the constrained maximum can be shown as follows:

$$\frac{\alpha K{X}^{\alpha -1}{Y}^{\beta }}{\left(1+t\right)P_X}=\frac{\beta K{X}^{\alpha }{Y}^{\beta -1}}{\left(1+t\right)P_Y} \mathrm{and}$$

(16)

$$M=\left(1+t\right)P_{X}X+\left(1+t\right)P_{Y}Y.$$

(17)

According to Equations (16) and (17), we can solve the equilibriums of X and Y:

$$X_{1,R}^{\ast }=\frac{\alpha M}{\left(1+t\right)P_X\left(\alpha +\beta \right)} \mathrm{and}$$

(18)

$$Y_{1,R}^{\ast }=\frac{\beta M}{\left(1+t\right)P_Y\left(\alpha +\beta \right)},$$

(19)

where $X_{1,R}^{\ast }$ and $Y_{1,R}^{\ast }$ are that equilibriums of X and Y, respectively, in the first period under the rebate promotion policy. Plugging $X_{1,R}^{\ast }$ and $Y_{1,R}^{\ast }$ into the utility function (U), we can then solve $U_{1,R}^{\ast }$, the equilibrium for the consumer’s utility in the first period under the rebate promotion policy:

$$U_{1,R}^{\ast }=\left(S^a{E}^b\right){\left(\frac{M}{\left(1+t\right)\left(\alpha +\beta \right)}\right)}^{\alpha +\beta }{\alpha }^{\alpha }{\beta }^{\beta }{\left(\frac{1}{P_X}\right)}^{\alpha }{\left(\frac{1}{P_Y}\right)}^{\beta }.$$

(20)

The Second Period

Case 1: Filing the Rebate Form

Suppose that the consumer takes the time to fill in the rebate form and mail it back to the retail store. The consumer is patient and waits 8–10 weeks to receive the discount certificate (i.e., rebate credit check) that can be used when shopping for other goods in the second period, when the consumer revisits the retail store. The discount amount from the rebate will be based upon the price and quantity of X purchased in the first period, which is equal to the following:

$$R={\rho }_R{P}_X{X}_{1,R}^{\ast }=\rho P_X\left(\frac{\alpha M}{\left(1+t\right)P_X\left(\alpha +\beta \right)}\right)=\frac{\alpha \rho M}{\left(1+t\right)\left(\alpha +\beta \right)}$$

(21)

To receive the discount amount (R) in the second period, the consumer must pay some process costs (denoted by $\Omega$), including a fill-in form cost, a postage cost, a transportation cost, a waiting cost, and an opportunity cost (invisible cost), among others. The process costs ($\Omega$) may be significant for some consumers and trivial for others. For example, some consumers who are not patient may not wish to wait 8–10 weeks to receive the discount. They would prefer an instant discount. Thus, these consumers’ process costs may be significant. As a result, Consumer A’s total budget for goods W and Z becomes $I+R-\Omega$. Note that Consumer A is patient and will wait for 8–10 weeks to receive the discount certificate, implying that the rebate discount amount (R) must be larger than the process costs ($\Omega$) for the consumer (i.e., $R>\Omega$). Therefore, the consumer’s budget constraint line for shopping goods W and Z becomes $\left(1+t\right)P_{W}W+\left(1+t\right)P_{Z}Z=I+R-\Omega$.

Consequently, we maximize $U=K{W}^{\gamma }{Z}^{\delta }$ subject to $\left(1+t\right)P_{W}W+\left(1+t\right)P_{Z}Z=I+R-\Omega$ and choose W and Z to solve the consumer’s optimization problem. The first-order conditions for the constrained maximum can be shown as follows:

$$\frac{\gamma K{W}^{\gamma -1}{Z}^{\delta }}{\left(1+t\right)P_W}=\frac{\delta K{W}^{\gamma }{Z}^{\delta -1}}{\left(1+t\right)P_Z} \mathrm{and}$$

(22)

$$I+R-\Omega =\left(1+t\right)P_{W}W+\left(1+t\right)P_{Z}Z.$$

(23)

Based upon Equations (22) and (23), we can solve the equilibriums for W and Z:

$$W_{2,R}^{\ast }=\frac{\gamma \left(I+R-\Omega \right)}{\left(1+t\right)P_W\left(\gamma +\delta \right)} \mathrm{and}$$

(24)

$$Z_{2,R}^{\ast }=\frac{\delta \left(I+R-\Omega \right)}{\left(1+t\right)P_Z\left(\gamma +\delta \right)},$$

(25)

where $W_{2,R}^{\ast }$ and $Z_{2,R}^{\ast }$ are the equilibriums for W and Z, respectively, in the second period under the rebate promotion policy. Plugging $W_{2,R}^{\ast }$ and $Z_{2,R}^{\ast }$ into the utility function (U), we can then solve $U_{2,R}^{\ast }$, the equilibrium for consumer utility in the second period under the rebate promotion policy:

$$U_{2,R}^{\ast }=\left(S^a{E}^b\right){\left(\frac{I+R-\Omega }{\left(1+t\right)\left(\gamma +\delta \right)}\right)}^{\gamma +\delta }{\gamma }^{\gamma }{\delta }^{\delta }{\left(\frac{1}{P_W}\right)}^{\gamma }{\left(\frac{1}{P_Z}\right)}^{\delta }.$$

(26)

Case 2: Electing not to File a Rebate Form

If the consumer is not patient and does not want to wait 8–10 weeks to receive the discount certificate, then the rebate discount amount (R) must be less than or equal to the process costs ($\Omega$) for the consumer (i.e., $R\le \Omega$). These consumers will not file rebate forms and will not be able to use the rebate promotion when revisiting the retail store to shop for other goods, W and Z. In this case, the consumer’s equilibriums for two goods (W and Z) and the consumer’s utility (U) in the second period will be the same as the equilibriums under the coupon promotion policy in the second period, which are the following:

$$W_{2,R}^{\ast }=W_{2,C}^{\ast }=\frac{\gamma I}{\left(1+t\right)P_W\left(\gamma +\delta \right)},$$

$$Z_{2,R}^{\ast }=Z_{2,C}^{\ast }=\frac{\delta I}{\left(1+t\right)P_Z\left(\gamma +\delta \right)}, \mathrm{and}$$

$$U_{2,R}^{\ast }=U_{2,C}^{\ast }=\left(S^a{E}^b\right){\left(\frac{I}{\left(1+t\right)\left(\gamma +\delta \right)}\right)}^{\gamma +\delta }{\gamma }^{\gamma }{\delta }^{\delta }{\left(\frac{1}{P_W}\right)}^{\gamma }{\left(\frac{1}{P_Z}\right)}^{\delta }.$$

In addition,

Table A1. Summary of equilibriums for goods and utility.

Goods and Utility	Coupons	Rebates
1st Period
X	$\frac{\alpha M}{\left(1+t\right)\left(1-\rho \right)P_X\left(\alpha +\beta \right)}$	$\frac{\alpha M}{\left(1+t\right)P_X\left(\alpha +\beta \right)}$
Y	$\frac{\beta M}{\left(1+t\right)P_Y\left(\alpha +\beta \right)}$	$\frac{\beta M}{\left(1+t\right)P_Y\left(\alpha +\beta \right)}$
U	$\left(S^a{E}^b\right){\left(\frac{M}{\left(1+t\right)\left(\alpha +\beta \right)}\right)}^{\alpha +\beta }{\alpha }^{\alpha }{\beta }^{\beta }{\left(\frac{1}{\left(1-\rho \right)P_X}\right)}^{\alpha }{\left(\frac{1}{P_Y}\right)}^{\beta }$	$\left(S^a{E}^b\right){\left(\frac{M}{\left(1+t\right)\left(\alpha +\beta \right)}\right)}^{\alpha +\beta }{\alpha }^{\alpha }{\beta }^{\beta }{\left(\frac{1}{P_X}\right)}^{\alpha }{\left(\frac{1}{P_Y}\right)}^{\beta }$
2nd Period
W	$\frac{\gamma I}{\left(1+t\right)P_W\left(\gamma +\delta \right)}$	Yes $\frac{\gamma \left(I+R-\Omega \right)}{\left(1+t\right)P_W\left(\gamma +\delta \right)}$ No $\frac{\gamma I}{\left(1+t\right)P_W\left(\gamma +\delta \right)}$
Z	$\frac{\delta I}{\left(1+t\right)P_Z\left(\gamma +\delta \right)}$	Yes $\frac{\delta \left(I+R-\Omega \right)}{\left(1+t\right)P_Z\left(\gamma +\delta \right)}$ No $\frac{\delta I}{\left(1+t\right)P_Z\left(\gamma +\delta \right)}$
U	$\left(S^a{E}^b\right){\left(\frac{I}{\left(1+t\right)\left(\gamma +\delta \right)}\right)}^{\gamma +\delta }{\gamma }^{\gamma }{\delta }^{\delta }{\left(\frac{1}{P_W}\right)}^{\gamma }{\left(\frac{1}{P_Z}\right)}^{\delta }$	Yes $\left(S^a{E}^b\right){\left(\frac{I+R-\Omega }{\left(1+t\right)\left(\gamma +\delta \right)}\right)}^{\gamma +\delta }{\gamma }^{\gamma }{\delta }^{\delta }{\left(\frac{1}{P_W}\right)}^{\gamma }{\left(\frac{1}{P_Z}\right)}^{\delta }$ No $\left(S^a{E}^b\right){\left(\frac{I}{\left(1+t\right)\left(\gamma +\delta \right)}\right)}^{\gamma +\delta }{\gamma }^{\gamma }{\delta }^{\delta }{\left(\frac{1}{P_W}\right)}^{\gamma }{\left(\frac{1}{P_Z}\right)}^{\delta }$

Note: “Yes” means that the consumer filed the rebate form and redeemed the rebate, while “No” means that the consumer did not file the rebate form and, thus, did not redeem the rebate.

(Appendix A.1) offers a summary of the equilibriums for the goods (X, Y, W, and Z) and the consumer’s utility in the first and second periods under the coupon and rebate promotion policies.

4. Comparative Static Analysis

Our mathematical demonstrations for comparative static analysis are provided in Appendix A.2. Here, we briefly express the results for the comparative static analysis.

Intuitively, as Equations (A2) and (A3) show, an increase in the consumer’s total budget raises demands for both goods X and Y. Moreover, as displayed in Equations (A4) and (A5), an increase in the price of good X decreases consumer demand for good X but does not provide a certain effect for good Y. Similarly, as reported in Equations (A6) and (A7), an increase in the price of good Y discourages consumer demand for good Y but offers uncertainty about good X. In addition, as shown in Equations (A8) and (A9), an increase in the sale tax rate deters consumer demand for both goods X and Y. Finally, as demonstrated in Equations (A10) and (A11), an increase in the coupon rate promotes consumer demand for good X but has an uncertain effect on good Y.

The comparative static analysis for goods W and Z is the same as the comparative static analysis for goods X and Y. A repetition of the process is, therefore, unnecessary. In addition, the effect of rebates on consumer demand for goods W and Z goes directly to the consumer’s total budget, which is $I+R-\Omega$ = $I+\frac{\alpha \rho M}{\left(1+t\right)\left(\alpha +\beta \right)}-\Omega$. Let $\Phi =I+\frac{\alpha \rho M}{\left(1+t\right)\left(\alpha +\beta \right)}-\Omega$; thus, $\frac{d\Phi }{d\rho }>0$. Moreover, $\frac{dW}{d\Phi }>0$ and $\frac{dZ}{d\Phi }>0$. Therefore, $\frac{dW}{d{\rho }_r}=\frac{dW}{d\Phi }\frac{d\Phi }{d{\rho }_r}>0$ and $\frac{dZ}{d{\rho }_r}=\frac{dZ}{d\Phi }\frac{d\Phi }{d{\rho }_r}>0$. (Note: ${\rho }_r=\rho$ = rebate rate). Intuitively, an increase in the rebate rate enhances consumer demand for both goods W and Z. The effect of rebates differs somewhat from that for coupons because coupons actually drop a good’s price while rebates do not influence the price—instead, they are a refund used as part of a future payment for merchandise purchases at the same store. For this reason, rebates only exert an income effect, while coupons result in both substitution and income effects. 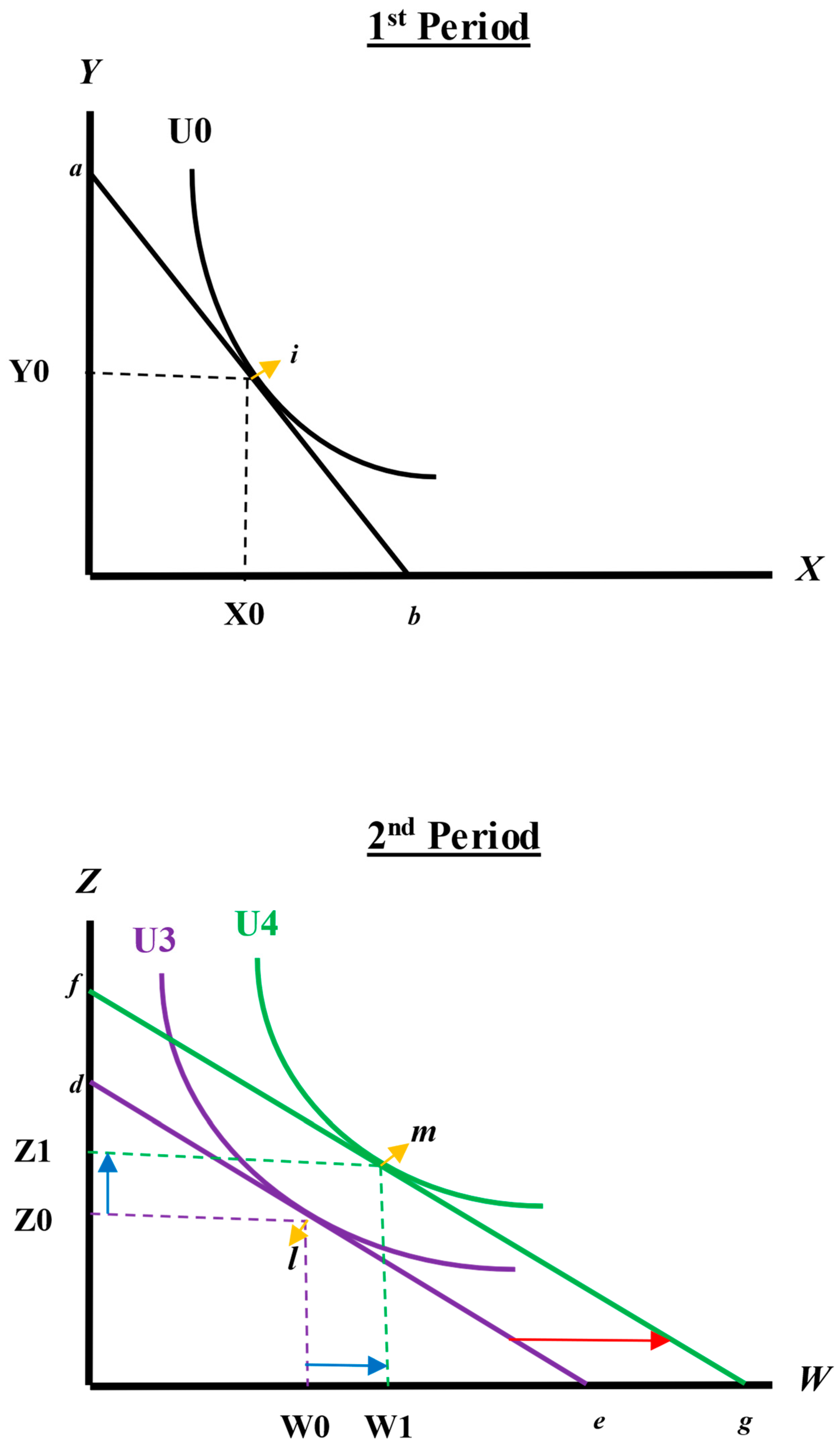Figure 1 and Figure 2 show how substitution and income effects can occur through coupons and rebates.

Figure 1 shows the case for coupons. In the first period, if the consumer does not have a coupon for good X, the consumer’s optimal choice will be (X0, Y0), and their utility will reach U0 under the initial budget constraint line ab. However, when the consumer uses a coupon (i.e., the price of X drops), then the consumer’s budget constraint line will switch (by rotating) to line ac, the optimal choice will move to (X1, Y1), and their utility will increase to U1. This is because, to maintain the same level of utility, the consumer will be more willing to substitute more units of X for Y. Consequently, the consumer will purchase more units of X (from X0 to X2) but fewer units of Y (from Y0 to Y2), which is referred to as a substitution effect. On the other hand, since the relative price between these two goods (X and Y) drops, the consumer’s real income is actually enhanced. Because these two goods (X and Y) are normal goods, when the real income increases, the consumer will purchase more units of both X (from X2 to X1) and Y (from Y2 to Y1)—an income effect. Both substitution and income effects occur in the first period under the coupon promotion policy. In Figure 1, although the consumer never actually chooses point k, this hypothetical point is useful to clarify the two effects that determine the consumer’s decision. The change from point i to point k represents a pure change in the marginal rate of substitution without any change in the consumer’s utility. Similarly, the change from point k to point j represents a pure change in utility without any changes in the marginal rate of substitution. Therefore, the movement from point i to point k shows the substitution effect, and the movement from point k to point j shows the income effect. In the second period, due to a lack of coupons for both goods (W and Z), the prices for both goods do not change. There are neither substitution nor income effects. The consumer’s optimal choice will stay (W0, Z0), and their utility will stay at the level of U3 under the budget constraint line de.

Figure 2 shows the case for rebates. In the first period, without promotions (such as rebates), the consumer’s optimal choice will be (X0, Y0), and their utility will reach U0 under the initial budget constraint line ab. Neither substitution nor income effects occur in the first period under the rebate promotion policy. After purchasing good X, the consumer receives a rebate form. Suppose that the consumer fills in the rebate form and mails it to the store and then, within 8–10 weeks, receives a rebate credit check (i.e., refund) to use on a future purchase at the same store. The consumer uses the refund at the same store in the second period. Because the prices of both goods W and Z do not change, the consumer’s initial budget constraint line de will shift in parallel to line fg, the consumer’s optimal choice will move from (W0, Z0) to (W1, Z1), and their utility will lift from a lower level of U3 to a higher level of U4. Although the relative price between these two goods (W and Z) does not change, the consumer’s income is enhanced by adding the refund. Since these two goods (W and Z) are normal goods, when the income increases, the consumer will purchase more units for both W (from W0 to W1) and Z (from Z0 to Z1)—an income effect. Consequently, only an income effect (no substitution effect) occurs in the second period under the rebate promotion policy.

5. Propositions

In this section, we demonstrate three propositions. The mathematical proofs for these three propositions are displayed in the Appendix A.

Proposition 1.

Given the same discount rate for both the coupon and the rebate (${\rho }_c={\rho }_r=\rho$), consumers actually receive a greater discount under the coupon policy than under the rebate policy. In addition, regardless of the redemption costs, when the retail store offers a higher discount rate, consumers can benefit more from coupons than from rebates.

(See the mathematical proof for Proposition 1 in Appendix A.3.)

To explain Proposition 1, we can use a simple numerical example. Suppose that the discount rate is 20% (for both coupon and rebate) and the price of X is USD10. Without the coupon, the consumer purchases one unit of X and spends USD10. However, with the coupon, the lower price (USD8) induces the consumer to purchase one more unit of X and thus spend USD16 rather than USD20 (=USD10 × 2) for two units of X if there is no coupon. In other words, the consumer indeed gains a USD4 (=USD20 − USD16) discount because of the coupon. On the other hand, when the consumer shops for X with a rebate, the consumer still needs to pay the regular price without receiving a discount (USD10, the higher price) when paying for the item. For this reason, unlike a coupon, the regular price (USD10) does not serve to encourage the consumer to purchase one more unit of X, even though the consumer realizes that they may receive a refund for a future purchase if they file the rebate form and re-visit the store. Therefore, the consumer has no incentive to purchase one more unit of X and, hence, only gains a USD2 (=USD10 × 20%) discount as a refund for a future purchase. Obviously, the benefit of coupons is that there are immediate discounts and, hence, encouragement for additional purchases, while rebates lack such a benefit. Instead, rebates lead to a delayed discount and, thus, no incentive for additional purchases.

Certainly, if the discount rate increases to, say, 30%, repeating the same process as above, the higher discount rate can induce the consumer to purchase even more units of X with a coupon and therefore acquire a greater discount than with a rebate. This is because coupons create both substitution and income effects when the consumer makes a purchase in the first period, while rebates do not create any effect when the consumer makes a purchase in the first period. Note that the discount rate is regarded as a marketing strategy. For this reason, Proposition 1 also shows how changes in marketing strategy (the discount rate) affect consumer behavior and benefit.

Proposition 2.

Patient consumers do not necessarily prefer coupons or rebates (perhaps indifferent to either), because their wellbeing (i.e., utility) may not be higher under the coupon policy than under the rebate policy (could be equal). Impatient consumers definitely prefer coupons to rebates because their wellbeing is greater under the coupon policy than under the rebate policy.

(See the mathematical proof for Proposition 2 in Appendix A.4.)

To explain Proposition 2, we need to realize that patient consumers are more willing to face uncertainty/take risks and wait 8–10 weeks for the rebate credit check. For this reason, patient consumers’ process costs ($\Omega$) are relatively smaller than impatient consumers’ process costs. Thus, patient consumers are much more likely to file their rebate forms and receive rebate credit checks that can be used as a refund for a future purchase in the second period. These rebates result in an income effect for consumers while making a future purchase in the second period and enhance their utility (wellbeing) in the second period. Although coupons result in both substitution and income effects for consumers in the first period and improve their utility (wellbeing) in the first period, there is no effect (neither substitution nor income) for consumers in the second period. As a result, there are no significant differences in the total utility (summation of the first and second periods) for patient consumers between coupons and rebates. Accordingly, patient consumers may be indifferent to either.

Nevertheless, impatient consumers are more reluctant to face uncertainty/take risks and wait 8–10 weeks for the rebate credit check. Consequently, impatient consumers’ process costs ($\Omega$) are relatively larger than patient consumers’ process costs. As a result, impatient consumers are not likely to file their rebate forms and do not gain rebate credit checks that can be used as a refund for a future purchase in the second period. Without the refund, there is no effect (neither substitution nor income) for consumers in the second period, and consumers’ utility (wellbeing) is not able to improve. Unlike rebates, coupons can advance consumers’ utility in the first period. For this reason, the total utility (summation of the first and second periods) for impatient consumers is higher with coupons than with rebates. Consequently, impatient consumers definitely prefer coupons to rebates.

Proposition 3.

Given the same production costs, the seller’s additional sales under the coupon policy are greater than under the rebate policy. The higher the discount rate is, the larger the seller’s additional sales will be from an individual consumer under the coupon policy. In addition, the higher the probability that a consumer is patient, the larger the seller’s additional sales will be from an individual consumer under the rebate policy.

(See the mathematical proof for Proposition 3 in Appendix A.5.)

Previously, we expressed in Proposition 1 that, due to both substitution and income effects, coupons induce consumers to make additional purchases and, thus, gain additional discounts than would be the case with rebates. For this reason, the higher the discount rate is, the greater the likelihood of additional purchases by consumers with coupons than with rebates. Additional purchases by consumers imply additional sales for sellers. Consequently, a seller’s additional sales due to their decision to distribute coupons are greater than would be the case with rebates, and, hence, the higher the discount rate is, the greater will be the seller’s additional sales from an individual consumer under the coupon policy.

Moreover, Proposition 2 indicates that patient consumers are more likely to file rebate forms and, hence, gain refunds that could induce them to make more purchases in the second period at the same store; meanwhile, impatient consumers are less likely to file rebate forms, thus not receiving refunds, and, therefore, may not make additional purchases in the second period at the same store. Therefore, under the rebate policy, if the percentage of patient consumers increases, additional purchases will be made by these consumers, which means more additional sales for the seller.

6. Discussion

In this section, we discuss two important issues stemming from the propositions discussed in the previous section. First, we proved that consumers actually receive greater discounts with coupons than with rebates, which leads us to ask the following: why do all consumers not prefer coupons to rebates? The mathematical evidence shows that patient consumers may not necessarily prefer one of either coupons or rebates (indifferent to either of them), while impatient consumers definitely prefer coupons to rebates. Second, we demonstrated that a consumer’s additional purchases from a seller are greater under a coupon policy than a rebate policy, but why do some retail stores (e.g., Menards) still offer rebate promotions rather than coupon promotions to consumers?

In discussing Issue 1, we recall Equation (A14) (see Appendix A.4). The result for this equation is uncertain (can be positive, negative, or equal to zero). Patient consumers can wait and may not significantly reveal their preferences for coupons or rebates. However, there must be a condition for them to identify whether they prefer coupons to rebates. That is, if the condition is satisfied, patient consumers would prefer coupons to rebates.

Condition 1.

As long as the discount rate ($\rho$) is higher than $1-{\left(1+\frac{R-\Omega }{I}\right)}^{-\left(\frac{\gamma +\delta }{\alpha }\right)}$, patient consumers would prefer coupons to rebates.

(See the mathematical proof for Condition 1 in Appendix A.6.)

Let us use one example for Condition 1. Suppose that $\gamma +\delta =1$, $\alpha =0.5$, and $\frac{R-\Omega }{I}=0.05$. According to Equation (A17), displayed in the Appendix A, the discount rate ($\rho$) has to be higher than 0.093 (9.3%) to satisfy Condition 1. That is, if the discount rate is at or above 9.3%, in this example, then patient consumers would prefer coupons to rebates.

Above all, when Condition 1 is satisfied, patient consumers prefer coupons to rebates, implying that all consumers prefer coupons to rebates because impatient consumers definitely prefer coupons to rebates no matter whether Condition 1 is satisfied or not. When Condition 1 is satisfied, Proposition 2 does not conflict with Proposition 1, and their results are consistent—consumers receive a greater discount under the coupon policy than under the rebate policy, and, hence, consumers prefer coupons to rebates Although time-inconsistent preferences could exist with some consumers, consumers also can exert self-control and overcome desire through willpower [27]. Here, we focus on the math equation and derive the condition to explain how it can be satisfied. “Time-inconsistent preferences” can refer to situations where someone’s choices can change over time due to factors like impatience. On the other hand, if Condition 1 is not satisfied, this infers that not all consumers prefer coupons to rebates.

Furthermore, although consumers can instantly receive a discount under the coupon policy, not every consumer receives coupons from sellers and/or remembers to use coupons during the effective promotion period. Rebates are a different matter. As long as consumers shop at stores during their rebate promotion period, all consumers can receive the rebate form. For this reason, if we consider the overall rather than the individual effect, the result for the overall effect may differ from that for the individual effect reported in Proposition 3.

To discuss Issue 2, we recall Equation (A16) exhibited in Appendix A.5. Let N be the number of all consumers who shop at the retail store during the effective promotion period, n be the number of consumers who receive and use the coupons and shop at the retail store during the effective promotion period, and $0<n\le N$. After considering the overall effect, Equation (A16), shown in Appendix A.5, can be rewritten as follows:

$${\displaystyle \sum \left({\Pi }_C-{\Pi }_{NC}\right)}-{\displaystyle \sum \left({\Pi }_R-{\Pi }_{NR}\right)}=n\left(\frac{1}{1-\rho }\right)R-N\lambda \left(\frac{R-\Omega }{1+t}\right)> or <or=0$$

(27)

As displayed in Equation (27), the result becomes uncertain (can be positive, negative, or equal to zero), implying that the consumer’s overall purchases from the seller may not necessarily be greater under the coupon policy than under the rebate policy. This may be why some retail stores (e.g., Menards) still offer rebate promotions rather than coupon promotions to consumers—because they do not need to worry about incomplete mailing lists or consumers missing opportunities to receive coupons through their mail or email. In addition, many consumers (especially impatient consumers) do not redeem their rebates because they do not file the form, while sellers increase their sales due to consumers’ purchases. Therefore, there must be a condition for the seller to distinguish between whether their overall additional sales to consumers are greater with coupons or with rebates.

Condition 2.

As long as the proportion of consumers who receive and use coupons is larger than $\left(\frac{\lambda \left(1-\rho \right)}{\left(1+t\right)}\right)\left(1-\frac{\Omega }{R}\right)$, the seller’s overall additional sales to consumers are greater under the coupon policy than under the rebate policy.

(See the mathematical proof for Condition 2 in Appendix A.7.)

Again, let us use one example for Condition 2. Suppose that $\lambda =0.8$, $\rho =0.1$, $t=0.1$, and $\frac{\Omega }{R}=0.1$, based upon Equation (A18), shown in Appendix A.7, the proportion of consumers who receive and use coupons ($\phi$) has to be higher than 0.59 (59%) to satisfy Condition 2 in this example. That is, if the proportion of consumers who receive and use coupons is at or above 59%, then the seller’s overall additional sales to consumers are larger with coupons than with rebates. In conclusion, when Condition 2 is satisfied, the seller’s overall number of additional sales to consumers is greater under the coupon policy than under the rebate policy. If this were not the case, then sellers would offer rebate promotions rather than coupon promotions to consumers, which may be a reason why some retail stores (e.g., Menards) still offer rebate promotions rather than coupon promotions to consumers.

7. Policy Implications

In this discussion of policy implications, we focus on the sellers’ perspective when evaluating which policy (coupons or rebates) most benefits sellers—that is, the sale strategy which provides sellers with both more sales and greater profits.

Given the same discount rate for both coupons and rebates, the main advantage of coupons for consumers is the immediate discount (i.e., redemption) at the time of purchase (no time delay). For this reason, coupons are more likely to draw consumers (both patient and impatient) to sellers’ stores and thereby increase sellers’ revenues. However, as mentioned earlier, not every consumer receives coupons issued from sellers and/or remembers to use coupons during the effective promotion period; especially, forgetful consumers may be easily excluded from the promotion program. On those occasions when many consumers use coupons, the effects on sales could adversely affect sellers’ revenues. In other words, sellers must instantly incur 100% of the redemption costs, limiting their profits.

Nevertheless, given the same discount rate for both coupons and rebates, the main advantage of rebates for consumers is that consumers do not need to worry about forgetting to follow through on a promotion or that they will be missed by the sellers. Rebates are redeemed post purchase—it normally takes 8–10 weeks to process a rebate [28,29]. Further, consumers incur some costs during the process of redeeming rebates. Also, rebates carry some uncertainty and risk for consumers, who may not be sure about whether their rebates can be redeemed or know when they can receive their promotions. For this reason, many consumers (especially impatient consumers) may not be attracted by a rebate promotion and, hence, may not shop at stores that offer rebates. Even if consumers elect to shop at rebate-oriented stores, if they are impatient consumers, they may not redeem rebates due to risk aversion and time delays.

On the other hand, according to a report by Dempsey [30], Edgar Dworsky (founder and editor of ConsumerWorld.org) indicated that “between 40% and 60% of rebates are never redeemed”. She then further added that “companies ensure that the redemption rate stays low by making it as difficult as possible for consumers to claim their rebates”. This is good news for sellers, who can save their redemption costs and increase their profits. The greater the number of consumers who do not redeem their rebates, the larger the profit margin will be for sellers. In addition, since it takes 8–10 weeks for sellers to process consumers’ rebates, sellers can hold onto the funds and earn interest on them [29]. The longer the sellers hold onto funds due to rebate-submitting consumers, the more interest the sellers can earn. For these reasons, numerous sellers may prefer a rebate policy to a coupon policy. Thus, the delay between rebate redemption and rebate payment actually benefits sellers.

As mentioned earlier, we informally interviewed around thirty-three restaurant and retail store managers/owners who had previously issued coupons/rebates to consumers. Based on these interviews, we found that restaurants (e.g., Oliver Garden) likely offered coupons to consumers, while home improvement retail companies (e.g., Menards) likely offered rebates to consumers. The spending for one restaurant meal per person normally would not exceed thirty USD, making it a low-ticket product. Yet, the spending for one kitchen appliance, say, a refrigerator, would usually be several hundred USD or even more than one thousand USD, making it a high-ticket product.

Corollary 1.

For low-ticket products (e.g., restaurant meals), sellers may offer coupons instead of rebates to consumers. For high-ticket products (e.g., kitchen appliance, say, a refrigerator), sellers may offer rebates instead of coupons to consumers.

To discuss Corollary 1, we recall Proposition 2 (i.e., impatient consumers would definitely prefer coupons to rebates) and Condition 1 (i.e., as long as the discount rate ($\rho$) is higher than $1-{\left(1+\frac{R-\Omega }{I}\right)}^{-\left(\frac{\gamma +\delta }{\alpha }\right)}$, patient consumers would prefer coupons to rebates). Since impatient consumers would definitely prefer coupons to rebates, we do not need to discuss impatient consumers, but we need to further explore patient consumers’ preferences, which would be the key factor for sellers adopting a policy.

Given the discount rate ($\rho$) set by the seller, the total budget (I), the process cost ($\Omega$), and all the other parameters ($\alpha$, $\gamma$, $\delta$), the only difference for consumers between low-ticket products and high-ticket products is the discount amount (R). We let $R_H$ be the discount amount for purchasing a high-ticket product, while $R_L$ is the discount amount for purchasing a low-ticket product, and $R_H>R_L$. We also let $\nu =\frac{R-\Omega }{I}$ (proportion of the net discount amount to the total budget); thus, ${\nu }_H=\frac{R_H-\Omega }{I}$ and ${\nu }_L=\frac{R_L-\Omega }{I}$ (Note: H = high-ticket product; L = low-ticket product). In addition, we let a consumer’s desired discount rate (${\rho }_d$) be $1-{\left(1+\nu \right)}^{-\left(\frac{\gamma +\delta }{\alpha }\right)}$; therefore,

$$\frac{d{\rho }_d}{d\nu }=\left(\frac{\gamma +\delta }{\alpha }\right){\left(1+\nu \right)}^{-\left(\frac{\gamma +\delta }{\alpha }\right)-1}>0.$$

(28)

Equation (28) implies that the larger the proportion of the net discount amount to the total budget is, the greater is the desired discount rate sought by the consumer. For example, suppose that the discount rate ($\rho$) set by the seller is 0.1 (i.e., 10%) and $\gamma +\delta =1$, $\alpha =0.5$, ${\nu }_L=\frac{R_L-\Omega }{I}=0.04$, and ${\nu }_H=\frac{R_H-\Omega }{I}=0.08$. As a result, a patient consumer’s desired discount rate for a low-ticket product (${\rho }_d^L$) is equal to 0.075 (i.e., 7.5%), which is lower than the 10% set by the seller, while the consumer’s desired discount rate for a high-ticket product (${\rho }_d^H$) is equal to 0.1426 (i.e., 14.26%), which is higher than the 10% set by the seller.

In short, ${\rho }_d^L=7.5\%<\rho =10\%$, while ${\rho }_d^H=14.26\%>\rho =10\%$. The results shown above imply that the patient consumer wishes that the desired discount rate for a low-ticket product would be at least 7.5%. Fortunately, the seller provides a 10% discount rate, which is higher than their desired discount rate. For this reason, according to Condition 1, this patient consumer would prefer coupons to rebates. On the other hand, the patient consumer wishes that the desired discount rate for a high-ticket product would be at least 14.26%. Unfortunately, the seller only provides a 10% discount rate, which is lower than their desired discount rate. Therefore, based on Condition 1, this patient consumer would prefer rebates to coupons or, at least, this patient consumer would be okay to accept a rebate offer.

For low-ticket products, due to lower spendings, rebates could be costly to redeem for a low-ticket product due to lower discount amounts. For this reason, consumers would prefer coupons to rebates when they are shopping for low-ticket products, because consumers can instantly receive the discount without uncertainty and risk, even though it is worth just a few USD. The more consumers visit the store due to the availability of coupons, the greater the amount of revenues that the seller will earn. Therefore, restaurant owners/managers usually offer coupons rather than rebates to consumers. Regarding how to determine an optimal coupon discount rate, Lin [31] provided a simple algorithm of coupon discount rates. In the following year, Lin [32] continued deriving an optimal coupon discount rate using the model of third-degree price discrimination. However, for high-ticket products, higher spendings will lead to larger discount amounts. Thus, compared with the discount amount, the cost to redeem rebates would become relatively smaller. Hence, consumers would be willing to wait for the rebate credit checks, even though it will take 8–10 weeks for the sellers to process the rebates, when the choice is only rebates. This may explain why home improvement retail companies (e.g., Menards) are more likely to offer rebates rather than coupons to consumers.

We hereby offer sellers two suggestions for determining whether to offer coupons or rebates to consumers. First, for low-ticket products (e.g., restaurant meals), we suggest that sellers offer coupons rather than rebates to consumers. For high-ticket products (e.g., kitchen appliances, say, a refrigerator), we suggest that sellers offer rebates rather than coupons to consumers. Second, in addition to the first suggestion, we suggest that sellers conduct a marketing survey to gather more information about consumers’ preferences in their local region. For instance, if most consumers prefer coupons to rebates for a certain seller’s products, offering coupons to consumers may be a better choice because performing so may attract more consumers to a store. More purchases will result in a greater volume of sales, which is the main purpose of offering coupons/rebates to consumers.

In summary, both coupons and rebates have advantages and disadvantages for sellers. Sellers may benefit from offering coupons, or rebates, or both. We believe that the answer may depend on various markets, locations, consumer types, local income levels, etc. To determine the best course of action, sellers should consider conducting a marketing survey, investigations, and research to collect more information prior to deciding which policy to adopt.

8. Conclusions

In this study, we adopted the theory of consumer choice and developed a two-period mathematical utility-maximization model. This research examined the impact of coupons and rebates on consumer and seller behaviors, investigating the differential effects of these promotional tools. Our assumptions imply that rebates and coupons with the same discount rate affect consumers’ utilities, budget constraints, and purchase amounts differently. Overall, coupons are more convenient, and the value of a coupon is realized sooner, which makes it more favorable to consumers than rebates.

Based upon our mathematical study, we verified three important propositions. First, consumers received a greater discount from coupons than from rebates with identical discount rates, and if the discount rate increased, consumers benefitted more from coupons regardless of the redemption costs. Second, patient consumers were indifferent in terms of their preference for coupons and rebates, while impatient consumers preferred coupons to rebates. Third, sellers’ additional sales were greater with coupons than with rebates given the same cost and discount rate, but if the probability of consumer patience increased, sellers’ additional sales were greater with rebates than with coupons.

We also discussed two implied issues: why do all consumers not prefer coupons to rebates, and why do many retail stores still offer rebates rather than coupons to consumers? Our theoretical analysis suggested that the answers depend on two conditions. If these conditions can be satisfied, all consumers would prefer coupons to rebates, and sellers’ overall additional sales to consumers would be larger under the coupon policy than under the rebate policy.

Furthermore, in looking at the policy implications of our findings, we showed that both coupons and rebates have advantages and disadvantages for sellers. We hereby suggest that sellers may offer coupons to consumers for low-ticket products (e.g., restaurant meals) and rebates for high-ticket products (e.g., kitchen appliances, say, a refrigerator). Meanwhile, we encourage sellers to conduct a marketing survey to assemble more information on markets, locations, consumer types, local income levels, etc. Further investigation is needed in the future to provide a complete picture of the policy implications of this research question.

Finally, this theoretical study has one limitation: only two endogenous variables could be included in the model (which is, in this case, the utility function), and all other factors needed to be counted as exogenous variables. For this reason, it may be necessary to rely on an empirical study to catch the effects of these exogenous variables. Therefore, based upon our current theoretical study, our future study regarding the extension of this topic will consider constructing an empirical study. Moreover, our future possible explorations regarding this issue may include a forward-looking examination of consumers’ dynamic decisions about purchases, stockpiling, and rebate redemptions, given their need to incur a cost to redeem a rebate. Consumers may exhibit time-inconsistent preferences when making these dynamic decisions.