Enhancing Mobile Robot Navigation: Optimization of Trajectories through Machine Learning Techniques for Improved Path Planning Efficiency

Abstract

Efficient navigation is crucial for intelligent mobile robots in complex environments. This paper introduces an innovative approach that seamlessly integrates advanced machine learning techniques to enhance mobile robot communication and path planning efficiency. Our method combines supervised and unsupervised learning, utilizing spline interpolation to generate smooth paths with minimal directional changes. Experimental validation with a differential drive mobile robot demonstrates exceptional trajectory control efficiency. We also explore Motion Planning Networks (MPNets), a neural planner that processes raw point-cloud data from depth sensors. Our tests demonstrate MPNet’s ability to create optimal paths using the Probabilistic Roadmap (PRM) method. We highlight the importance of correctly setting parameters for reliable path planning with MPNet and evaluate the algorithm on various path types. Our experiments confirm that the trajectory control algorithm works effectively, consistently providing precise and efficient trajectory control for the robot.

1. Introduction

Mobile robots are intelligent devices that can perform specific tasks independently in complex environments and do not rely on human beings. Mobile robot navigation entails navigating from a starting point to a target point without hitting obstacles [1,2], considering constraints like optimal time, shortest path, or lowest energy consumption. In dynamic and uncertain environments, applying global search algorithms does not suffice to address robot navigation due to the lack of a complete model or map of the environment. Researchers have used local search and local path planning algorithms with the help of data obtained from the robot’s sensors, such as sonar and infrared devices [3].

The navigation methods commonly used by mobile robots can be categorized into two main groups: traditional methods and heuristic methods [4]. Traditional methods encompass techniques such as the grid method, roadmap navigation, visual navigation, sensor-based data navigation, free space method, and artificial potential field methods. However, these traditional approaches often encounter challenges, such as getting trapped in local optimums, difficulty in online implementation, and longer processing times, particularly in large problem spaces. Consequently, researchers have increasingly focused on heuristic approaches, including the ant colony algorithm [5], fuzzy logic [6], neural networks [7], genetic algorithms [8], particle swarm optimization algorithms [9], and machine learning [10]. These heuristic techniques provide increased flexibility and adaptability, rendering them highly suitable for navigating intricate environments.

Heuristic methods, including supervised and unsupervised learning within machine learning, present promising avenues for addressing these challenges. Unlike traditional methods, which may struggle with real-time requirements and large problem spaces, supervised and unsupervised learning methods can adapt and generalize based on data patterns. Supervised learning, where the model learns from labeled data, can help in predicting optimal navigation paths based on past experiences. Meanwhile, unsupervised learning, which does not require predefined outputs, can uncover underlying structures and patterns in the environment, aiding in navigation decision-making. While these methods face their own challenges, such as data dimensionality and computational complexity, their ability to leverage data efficiently makes them valuable assets for navigating complex environments.

This convergence of heuristic methods with motion planning, driven by recent advancements in machine learning, has led to the development of innovative solutions, like Motion Planning Networks (MPNets) [11,12]. Recently, a significant research trend has emerged, merging motion planning with machine learning to address planning problems. Both domains, motion planning and machine learning for control, have seen substantial progress and are actively researched [13,14]. These networks, utilizing deep neural networks, offer remarkable efficacy in generating collision-free paths, bridging the gap between theoretical robustness and computational efficiency in robotic motion planning. To provide context and underscore the advancements made by our proposed approach, we incorporate a comparative analysis with significant research contributions in the field of machine learning techniques for mobile robots. This analysis spans topics such as disturbance observer-based optimal control for uncertain surface vessels [15], optimal tracking control for discrete-time nonlinear systems [16], optimized formation control for unmanned surface vehicles with collision avoidance [17], and comprehensive formation tracking control and optimal control for fleets of multiple surface vehicles [18].

Recent advancements in computer vision have played a pivotal role in revolutionizing the field of mobile robotics, offering novel insights and methodologies for navigating complex environments. One notable example is the “CVANet: Cascaded visual attention network” proposed by (insert author names). This innovative approach leverages cascaded attention mechanisms to improve object recognition and scene understanding, presenting promising applications in mobile robot perception and navigation. By integrating techniques like CVANet with motion planning algorithms, researchers have the opportunity to enhance the perceptual capabilities of mobile robots, enabling them to make more informed decisions in dynamic and cluttered environments. Thus, the intersection of computer vision and mobile robotics opens up exciting possibilities for developing robust and adaptive navigation systems capable of operating in real-world scenarios.

Our work will be organized as follows: after the abstract and the introduction, in the Section 2 we conduct research on works related to our theme. In Section 3, we present the methods and experiments, then give more details of the method, which represents our contribution. We end with simulations to support our results and with a general conclusion.

2. Related Works

The field of mobile robotics has witnessed significant research efforts dedicated to enhancing path planning and navigation in complex environments. This section provides an overview of key developments in path planning, machine learning, and motion capture relevant to mobile robotics. Numerous path planning algorithms have been proposed to tackle the challenges of navigating dynamic environments. Traditional global path planning approaches, such as Dijkstra’s algorithms [19], heavily rely on precomputed maps and face limitations in adapting to dynamic changes. In contrast, local path planning methods, like the Velocity Obstacle method and the Dynamic Window Approach, focus on real-time obstacle avoidance, considering the robot’s immediate surroundings [20,21]. While suitable for reactive navigation, these methods may lack the ability to plan globally.

The search for efficient motion planning algorithms began with complete examples, which, though comprehensive, were computationally inefficient. This prompted the development of methods with resolution and probabilistic completeness, aiming for more practical solutions [22]. While complete algorithms guarantee finding a path if one exists, they are often too complex for real-world applications due to their need for extensive environmental data [23]. Resolution-complete algorithms offer a more feasible alternative but require meticulous adjustment of parameters for each planning problem [24]. To address these limitations, probabilistically complete methods, such as sampling-based motion planners (SMPs), were introduced.

These methods rely on sampling techniques to create exploration trees or roadmaps in the robot’s obstacle-free space [22]. Popular sampling-based motion planners (SMPs), like rapidly exploring random trees (RRT) and probabilistic roadmaps (PRM) [25,26], are widely used. RRT, especially, is favored for its ability to quickly find a path around obstacles, though it may not always find the shortest one. An improved version, RRT*, guarantees the shortest path but becomes less efficient with higher planning problem complexity. Single-query methods, like RRT, are preferred over multi-query methods, like PRM, due to their simplicity and effectiveness.

These algorithms generate roadmaps of feasible paths, proving suitable for a broad range of scenarios. However, their performance can be influenced by factors such as sampling strategies and optimization techniques.

Reinforcement learning (RL) [27] is becoming increasingly popular for tackling continuous control and planning tasks [28]. RL operates within Markov decision processes, where an agent interacts with its environment, making decisions based on observed states and receiving rewards. The goal is for the agent to learn a policy that maximizes its cumulative reward. Initially, RL was limited to simpler, lower-dimensional problems [29], but recent advances, particularly in Deep RL (DRL) [30,31], have enabled the solution of more complex, higher-dimensional challenges.

Popular Deep Reinforcement Learning DRL methods, such as Deep Q-Networks (DQN) and Proximal Policy Optimization (PPO) [32], are effective in modeling environments and learning collision energy functions [33]. Generative models, like Variational Autoencoders (VAE) and Generative Adversarial Networks (GANs) [34,35], contribute by generating synthetic data, addressing challenges in collecting real-world training data. DRL has successfully addressed various difficult robotic tasks using both model-based [36] and model-free [37] approaches. However, challenges persist in solving practical problems with weak rewards and long horizons [38].

Motion capture technology finds applications in various robotics domains, providing valuable insights into robot movements and interactions with the environment [39]. In mobile robotics, motion capture data are instrumental in creating realistic simulations for training and testing path planning algorithms, offering insights into robot kinematics and dynamics for the development of accurate motion models and controllers [40].

Recent advancements in deep learning have spurred significant interest in utilizing neural networks to enhance or approximate motion planners, particularly to adapt to changing environments. Various learning strategies, such as imitation learning, reinforcement learning, and unsupervised learning, have been employed to augment motion planning methods.

For instance, Zucker et al. [41] proposed adapting sampling techniques in Sampling-based Motion Planners (SMPs) using the REINFORCE algorithm [42] in discretized workspaces. This approach aims to improve sampling efficiency by learning from the environment’s feedback. Similarly, Berenson et al. [43] introduced a learned heuristic to store and repair paths as needed, enhancing the adaptability and efficiency of the motion planner. Coleman et al. [44] opted to store experiences in a graph rather than individual trajectories, facilitating better long-term planning and experience reuse. Ye and Alterovitz [45] combined human demonstrations with SMPs for path planning, leveraging expert knowledge to guide the planning process. While these methods have shown improved performance over traditional algorithms, they often lack generalizability and require manual adjustments for each new environment, limiting their scalability.

Another approach involves leveraging machine learning techniques to bias sampling towards critical regions. Zhang et al. [46] utilized reinforcement learning (RL) to gauge the likelihood of rejecting a sampled state, thus directing sampling towards safer and more promising areas. This approach improves the safety and efficiency of the sampling process. Bency et al. [47] focused on navigation demonstrations in static environments, which can be limiting in dynamic or unknown settings. Ichter et al. [48] introduced conditional variational autoencoders (cVAEs) for Sampled Motion Planners, like Fast Marching Trees (FMT*), addressing the challenge of generalization to diverse environments by learning a representation of feasible paths.

Furthermore, Francis et al. [49] introduced PRM–RL for long-range navigation, where RL serves as both a short-range local planner and a collision-prediction module for the high-level PRM planner. This dual role enhances the planner’s ability to navigate complex environments over long distances. A similar framework is presented in [50], where RL again serves dual roles, demonstrating the versatility and effectiveness of combining RL with traditional planning methods. In [51], a hierarchical framework tailored for long-horizon reaching tasks is introduced. This framework operates by planning at the high level to identify subgoals from the replay buffer, while learning at the low level directs the robot towards these subgoals, enhancing the planner’s capability to handle complex tasks over extended periods.

While traditional motion planning methods have been significantly enhanced by incorporating machine learning techniques, challenges such as generalizability and adaptability remain. Our proposed methodology, which integrates both supervised and unsupervised learning techniques with spline interpolation inspired by motion capture, addresses these challenges by offering a more adaptable and efficient robotic navigation strategy. This approach not only leverages the strengths of both learning paradigms but also ensures smoother and more reliable path generation, making it suitable for a wide range of robotic applications in dynamic and complex environments.

To overcome these limitations, modern techniques leverage efficient function approximators, like neural networks, to embed motion planners or learn auxiliary functions for SMPs, enhancing planning speed in complex, cluttered environments.

The robot has to reach these subgoals. The effectiveness of this approach was highlighted in its integration of planning with learning, showcasing significant efficiency gains. However, these methods do not generalize to novel environments or tasks, and thus require frequent retraining.

Previous research has highlighted the attractiveness of reinforcement learning for developing adaptable robot-control policies, but its lengthy training process poses a challenge. While imitation learning offers a basic solution to address exploration and sparse rewards, there is a gap in methods that combine supervised and unsupervised learning for optimal path planning. Furthermore, Motion Planning Networks (MPNets) haven’t been fully explored in this context. Additionally, current approaches often prioritize either accuracy or adaptability, neglecting the need to balance both for effective handling of complex scenarios.

In our study, we propose an innovative approach to robotic motion planning by integrating Motion Planning Networks (MPNets) with both supervised and unsupervised learning. By leveraging MPNets, which generates collision-free paths using deep neural networks, and incorporating supervised and unsupervised learning, our method aims to overcome traditional limitations. We hypothesize that this integration will enhance adaptability, efficiency, and accuracy in complex environments.

Our work fills a research gap by providing a comprehensive framework that combines the strengths of both learning paradigms. Through experiments, we demonstrate improved trajectory control efficiency and adaptability, marking a significant advancement in robotic motion planning.

3. Methods and Experiments

This section introduces our proposed model. Our method, which utilizes a MATLAB simulation, integrates two key components to achieve effective path planning and trajectory control.

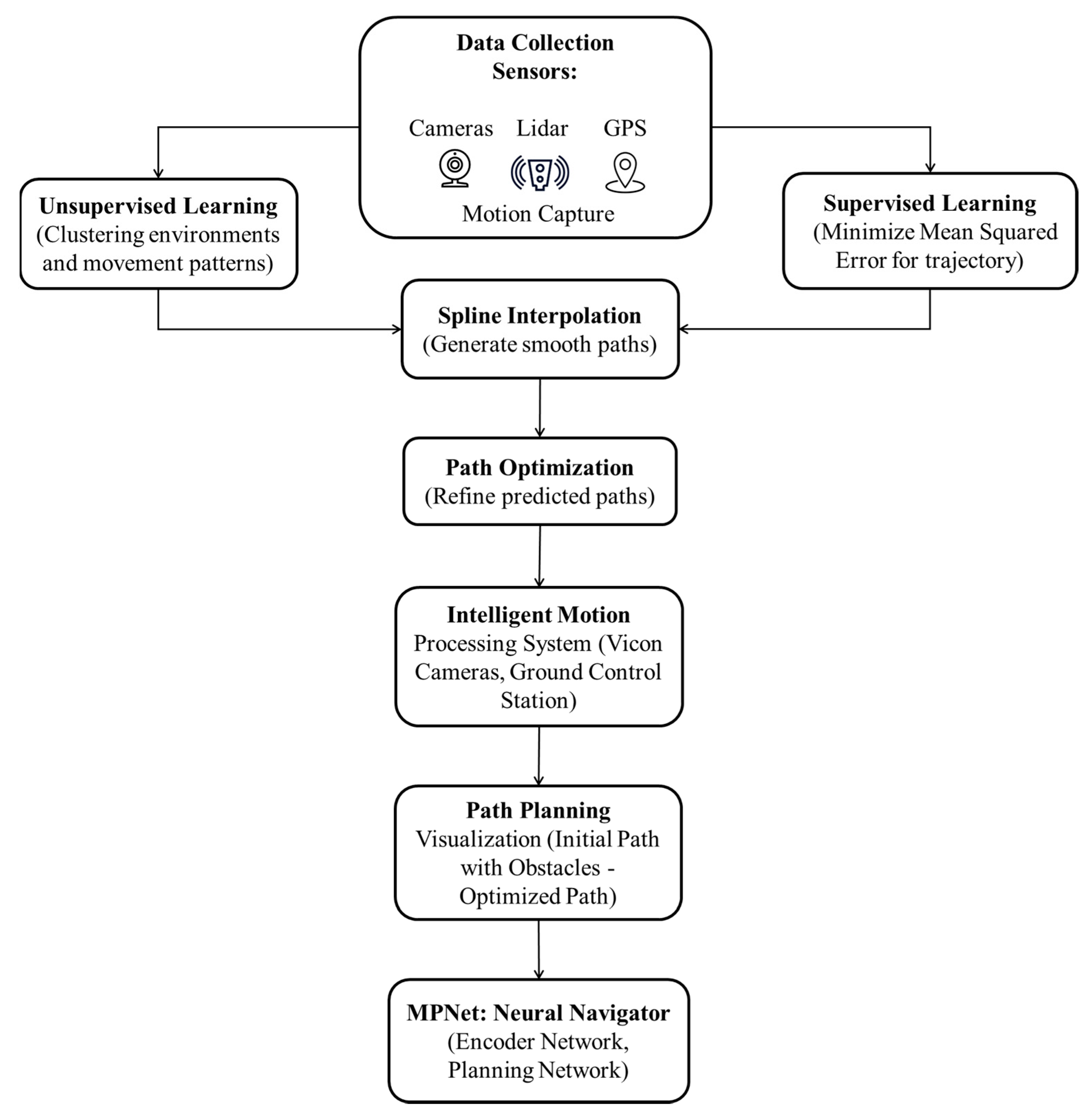
The methodology, as depicted in Figure 1, begins with thorough data collection, establishing the groundwork for the following stages. Supervised learning trains the system on labeled data, followed by spline interpolation for smooth path generation. Path optimization refines trajectories, while unsupervised learning uncovers hidden patterns. An intelligent motion processing system adapts to dynamic environments, aided by path planning visualization. Finally, the system incorporates MPNet:Neural Navigator for adaptive navigation, amalgamating techniques for robust and efficient navigation.

3.1. Supervised and Unsupervised Learning

In the initial phase of our method for achieving efficient navigation in complex environments, we integrate supervised and unsupervised learning techniques with spline interpolation. Initially, we compile a diverse dataset encompassing various environmental conditions and movement patterns, leveraging sensor data from Lidar sensors, GPS sensors, cameras, and motion capture systems.

Supervised learning utilizes labeled data, including annotated trajectories obtained through motion capture systems, to train models. These trajectories serve as ground truth for optimal paths in specific environmental scenarios. Simultaneously, unsupervised learning autonomously uncovers patterns in the dataset, enhancing adaptability to novel environments.

Spline interpolation is then employed to generate smooth paths with minimal directional changes, ensuring continuous and safe navigation. Experimental validation conducted with a differential drive mobile robot confirms exceptional trajectory control efficiency, validating the effectiveness of our approach. By combining these techniques and leveraging a diverse dataset, our method offers a robust solution for navigating dynamic environments with efficiency and precision.

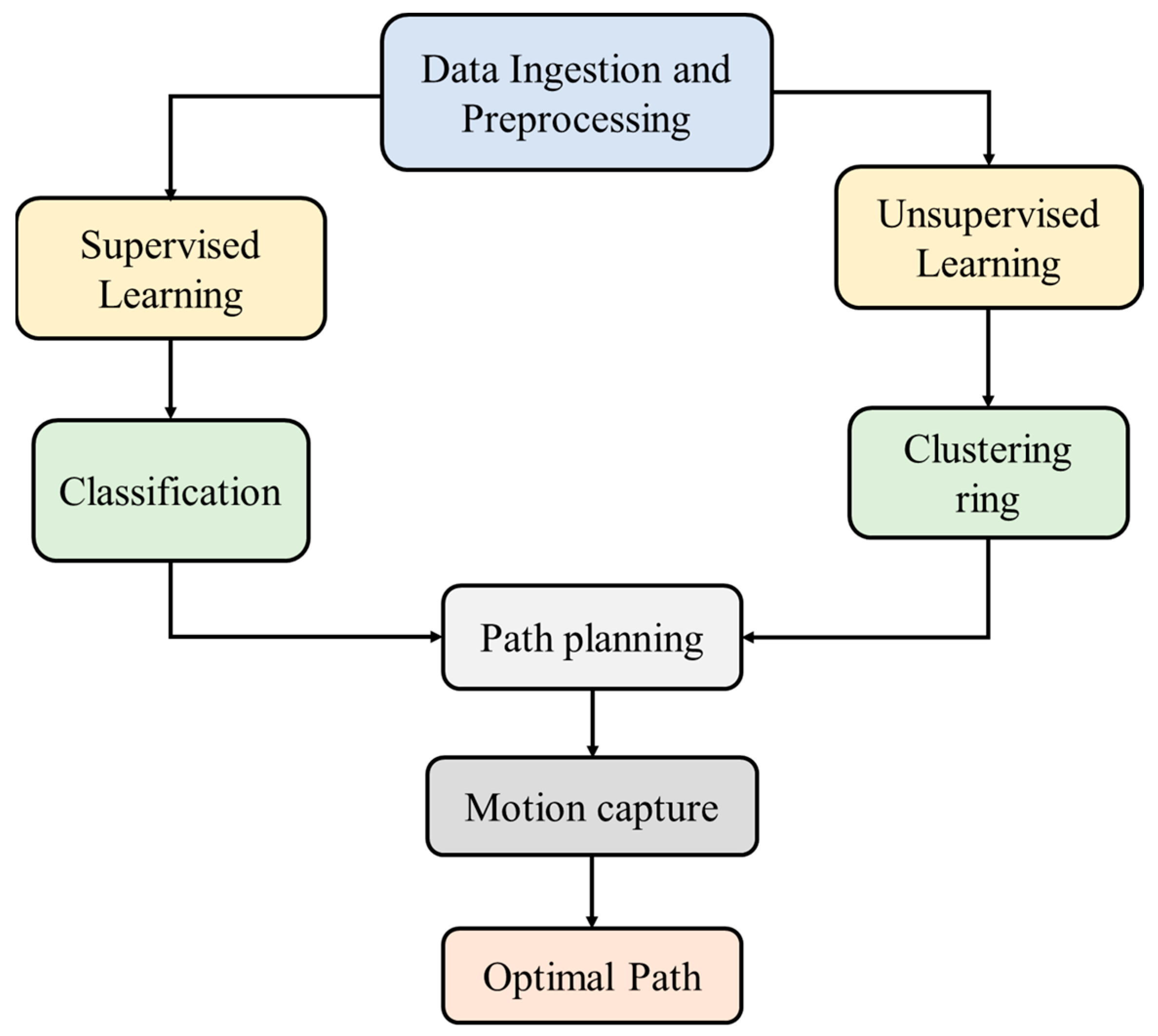
With the neural network now honed and infused with the prowess of supervised and unsupervised learning, the path planning phase unfolds. The trained model is leveraged to perform real-time predictions of optimal paths for the mobile robot as it traverses complex environments. These predictions, albeit insightful, undergo further refinement through the prism of path optimization techniques (as shown in Figure 2).

The schematic representation of the proposed model intricately outlines a systematic path planning process, integrating both supervised and unsupervised learning techniques. The diagram initiates with pivotal stages of data ingestion and preprocessing, crucial for preparing pertinent data for subsequent learning algorithms. On one side, the illustration of supervised learning leads to a labeled “Classification” component, indicating its role in recognizing and categorizing specific features or obstacles based on labeled data. Conversely, the depiction of unsupervised learning on the opposite side is represented by an arrow leading to a “Clustering Ring”, symbolizing the grouping or clustering of similar data points without explicit instructions. The convergence of both supervised and unsupervised learning processes is visually apparent in the central component labeled “Path”, emphasizing their collaborative utilization in the robot’s path planning (as illustrated in Figure 3). This integration suggests that the robot effectively navigates its environment by leveraging insights from both learning approaches. The subsequent connection to “Motion Capture” signifies the practical application of integrated learning outputs, ultimately leading to the determination of the “Optimal Path”. This represents the trajectory the robot should follow for optimal navigation. The comprehensive figure elucidates the intricate interplay between supervised and unsupervised learning in the context of path planning, presenting a holistic approach that culminates in identifying an optimal path through the environment with the assistance of motion capture technology.

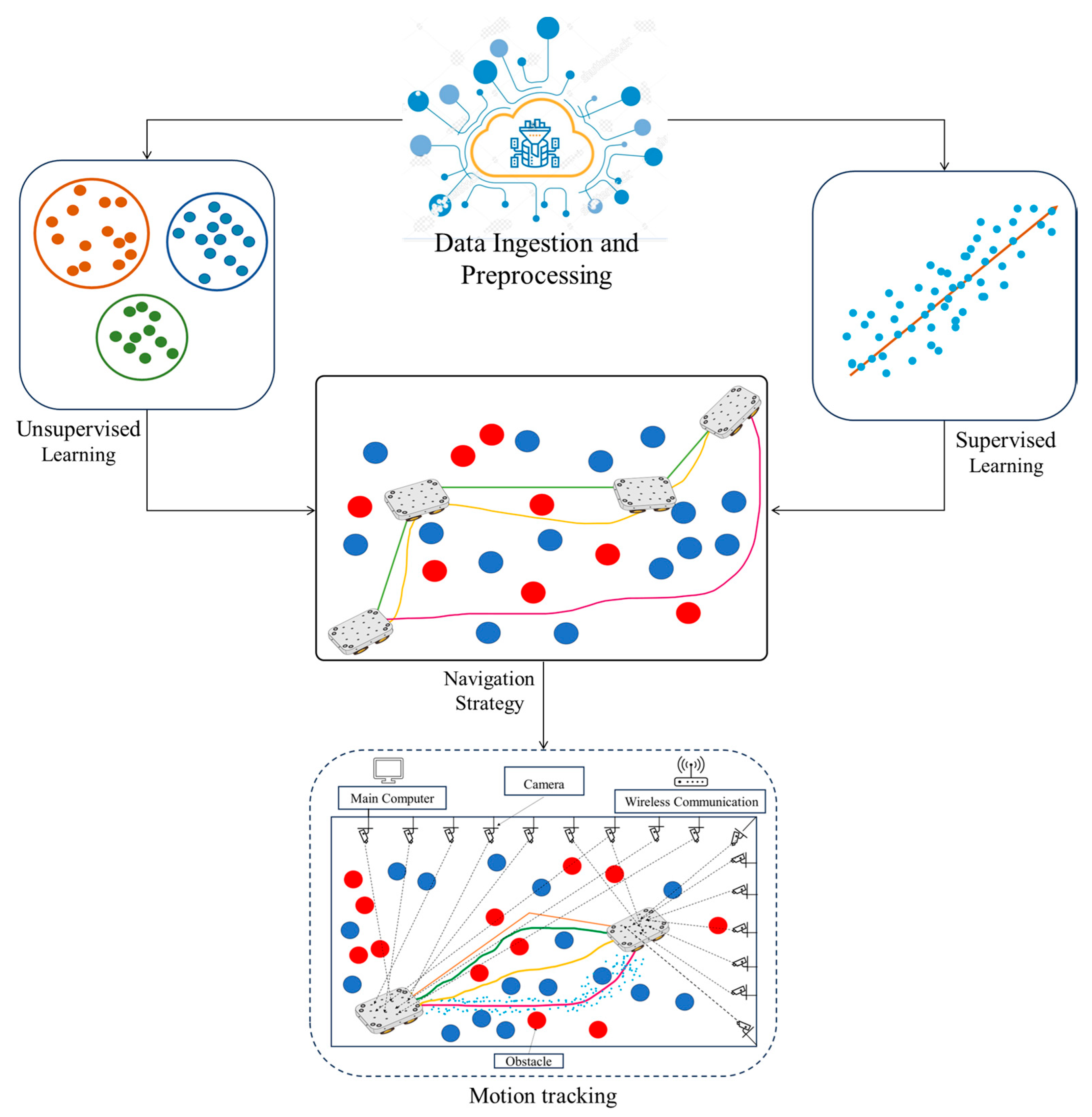
Our data processing methodology tailors the approach to the characteristics of sensor data. As illustrated in Figure 2, Motion Capture Data Refinement is essential for capturing intricate movement patterns. This process involves smoothing and interpolation techniques to ensure a coherent depiction of the robot’s trajectory. Our system employs a comprehensive hardware setup to track and control the movements of mobile robots with high precision. The experimental setup integrates advanced data acquisition and processing tools to facilitate real-time navigation and path planning. The system utilizes a suite of 15 Vicon cameras to establish a highly accurate reference coordinate system, essential for precise motion capture and tracking of the robot’s position in a 3D space. Although the robot operates in a 2D plane, the Vicon system’s ability to track in 3D ensures that positional data in the X and Y dimensions are exceptionally accurate, while Z-directional data and angles for roll and pitch are ignored. Calibration of these cameras is meticulously performed using a wand, ensuring optimal communication between the Vicon system and MATLAB–Simulink. The captured motion data are transmitted in real-time via Ethernet to MATLAB–Simulink, where it is processed through control logic blocks. This real-time data processing is crucial for generating accurate and immediate control instructions. The processed data are then relayed to the robot using QUARC–Real Time Control Software (version 2020.4), which enables precise execution of the planned trajectories.

The ground control station is equipped with a robust Intel Core i7 processor, 16 GB of RAM, and multiple software tools, including MATLAB 2020a and QUARC Real-Time Control Software 2020. This setup also includes three monitors for detailed observation and control, a USB flight controller joystick for manual input, and a WiFi router to facilitate seamless communication with the robot.

In addition to the motion capture system, the robot is outfitted with a comprehensive sensor suite. This includes Lidar sensors for detailed obstacle detection and terrain mapping, requiring sophisticated filtering and segmentation techniques to extract relevant insights. GPS sensors are also integrated, with correction measures implemented to mitigate errors due to atmospheric interference, ensuring accurate localization. The synergy among these sensors, along with the motion capture system and other devices, provides a holistic understanding of the robot’s environment. The refined motion capture data, processed through advanced algorithms, yields a coherent depiction of movement patterns essential for accurate trajectory planning. This integrated hardware setup enables the system to calculate the optimal path for the robot, guiding it towards its goal while effectively avoiding obstacles [52].

Figure 3 illustrates the Intelligent Motion Processing System, highlighting the flow of data from the environment, through the sensors and cameras, to the processing units, and finally to the robot’s actuators. This comprehensive hardware setup ensures that our proposed algorithm can navigate dynamic environments efficiently and with high precision.

These techniques fine-tune the predicted paths, as illustrated in Figure 4, providing a nuanced visual representation of our path planning process. The left side depicts the initial predicted paths, where the robot encounters an obstacle. In contrast, the right side showcases the paths after the application of fine-tuning techniques, revealing an optimal path where the robot successfully avoids the obstacle.

These techniques, intentionally designed to enhance both safety and feasibility for the robot’s execution of planned paths, are elucidated in the updated figure caption, ensuring a comprehensive understanding of how they embody safety and feasibility for the robot’s execution.

Central to our approach is a dual-faceted endeavor of data acquisition and refinement. Motion capture systems meticulously record the robot’s movement, while various sensors, including lidar sensors, cameras, and GPS, interact with the environment [53].

The raw data undergoes preprocessing, including noise reduction and calibration, to enhance its reliability. In the data processing phase for Lidar-generated data, we employ a filtering technique to improve obstacle detection accuracy:

In the data processing phase for Lidar-generated data, we employ a filtering technique to enhance the accuracy of obstacle detection by reducing noise. Equation (1) defines $P_{filtered}(x)$ as the filtered Lidar point cloud at position x, where N is the number of raw Lidar measurements, and $p_{raw}\left({\chi }_i\right)$ represents the raw Lidar measurement at position (x_i).

This equation essentially computes the average of raw Lidar measurements over N points, providing a smoothed and more accurate representation of the Lidar point cloud at the specified position x. This filtering process is crucial for improving the reliability of obstacle detection in our proposed algorithm.

This relationship is expressed as follows:

$$P_{filtered}(x)=\frac{1}{N}\sum _{i=1}^N{p}_{raw}\left(x_i\right)$$

(1)

The refined data, after its passage through the adaptive data processing pipeline, stands adorned with a mosaic of extracted features—a rich tapestry of attributes intrinsic to the art of path planning. These features empower the path planning model to navigate complex terrains, charting optimal trajectories through dynamic environments.

In the supervised learning phase, our primary objective is to train the neural network for predicting optimal trajectories. This crucial training process involves minimizing the Mean Squared Error (MSE), which serves as the loss function. The MSE is a measure of the average squared difference between the actual optimal trajectory ($y_i$) and the predicted trajectory generated by the neural network (${\widehat{y}}_i$) across N training examples.

The MSE is calculated as follows:

$$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{N}\sum _{i=1}^N{\left(y_i-{\hat{y}}_i\right)}^2$$

(2)

This equation (Equation (2)) quantifies the discrepancy between the actual and predicted trajectories. The goal during training is to iteratively adjust the neural network’s parameters to minimize this error, ensuring that the predicted trajectories closely align with the ground truth. Achieving a low MSE is indicative of the model’s proficiency in accurately predicting optimal trajectories, thereby enhancing the overall performance of our proposed algorithm in trajectory prediction tasks.

With the neural network now primed through the crucible of supervised learning, the stage is set for a more nuanced endeavor-unsupervised learning. Here, the network’s cognitive repertoire is amplified by the integration of clustering algorithms. These algorithms deftly group environments and robot movement patterns that share inherent similarities. This strategic clustering capacitates the network to engender path predictions that resonate with scenarios analogous to those witnessed during training [54]. The amalgamation of supervised and unsupervised learning lends the neural network an astute adaptability, poised to extrapolate and apply its knowledge to a multitude of contextually akin environments and movement patterns.

In the unsupervised learning phase, we implement a clustering algorithm, such as K-Means [55], to categorize similar environments and patterns in robot movement. The corresponding objective function for K-Means clustering is denoted by $J\left(c,M\right)$ where N signifies the total number of data points, K represents the quantity of clusters, $\left(x_i\right)$ refers to individual data points, and $M_j$ stands for the centroid of a given cluster. This equation rigorously defines the objective function pivotal in the K-Means clustering process.

$$J\left(c,M\right)=\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^k{‖x_i-M_j‖}^2$$

(3)

This equation quantifies the dissimilarity between data points ($x_i$) and cluster centroids ($M_j$), serving as a cornerstone in the K-Means clustering methodology. The minimization of this objective function drives the algorithm to iteratively refine the clustering, ensuring that data points within the same cluster are more like each other than to those in other clusters. The resulting clusters encapsulate inherent similarities in robot movement patterns and environmental features. This strategic grouping enhances the network’s ability to discern and predict optimal paths in novel, yet similar, contexts. The iterative nature of the clustering process refines the model’s understanding, further contributing to its adaptability in various scenarios. The integration of supervised and unsupervised learning methodologies synergistically equips our proposed algorithm with the versatility needed for robust path prediction in diverse and dynamic environments.

3.2. MPNet: Neural Navigator

The second aspect of our method involves the integration of MPNet, a neural network-based motion planner. MPNet operates in two distinct phases.

Offline Training of Neural Models: In this phase, the neural networks are trained offline using a combination of supervised learning and reinforcement learning techniques. The models learn from a diverse set of training data to predict optimal paths in varying environmental conditions.

Online Path Generation: Once trained, the neural models are deployed for online path generation during real-time navigation. MPNet utilizes its learned knowledge to rapidly generate optimal paths, enabling the robot to adapt to dynamic environments and obstacles in real time.

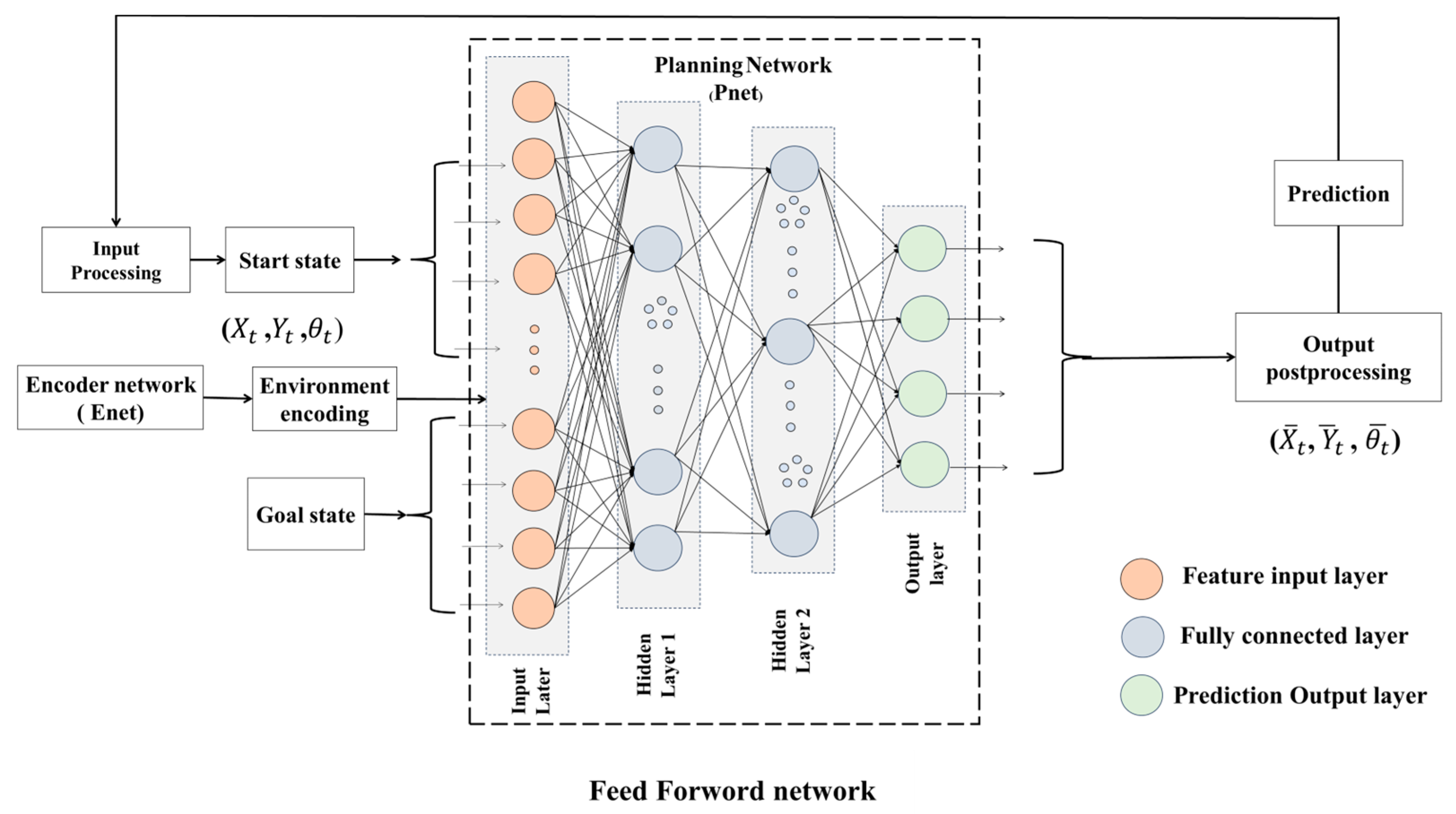
Motion Planning Networks (MPNets) seamlessly integrate two neural networks, namely the encoder network (Enet) and the planning network (Pnet), to provide a comprehensive solution for motion planning challenges. In the Enet component, the system processes surrounding information from the robot, which can be raw point-cloud data or voxel-converted point-cloud, depending on the neural architecture.

The neural architecture itself could be a fully connected neural network or a 3D convolutional neural network (CNN). The output of Enet is a latent space embedding, encapsulating essential information about the robot’s environment.

Building upon this encoded information, the Pnet comes into play, considering the encoded environment, the current state of the robot, and the desired goal state. Pnet outputs samples tailored for either path or tree generation, thus facilitating efficient planning solutions.

This dual-network architecture ensures that MPNet is equipped to learn and adapt to diverse environments, making it a versatile tool for motion planning tasks. This deep-learning-based methodology represents a paradigm shift in motion planning, leveraging learned knowledge to generate informed samples for effective path planning in previously unexplored test environments. Integrating navigation further extends its utility, enabling seamless interaction with sampling-based motion planners, like optimal rapidly exploring random trees (RRTs*). MPNet emerges as a powerful and adaptable solution, bridging the gap between deep learning and classical motion planning techniques.

The training process for the MPNet architecture involves two modules (see Figure 5).

The initial module utilizes an encoding basis point set approach to transform input map environments into a condensed representation. This encoded environment effectively reduces dimensionality, computational complexity, and training time, all while preserving essential information.

The second module incorporates a feed forward network consisting of feature input layers, fully connected layers, dropout layers, and an output layer. Rectified linear unit (ReLU) activation functions in the fully connected layers, along with weighted mean square distance as the loss function for the output layer, enable effective training. The network predicts the next state closer to the goal pose based on the encoded environment input, start pose, and goal pose. MPNet is trained through supervised learning, utilizing optimal paths generated by classical path planners like RRTs*. The training process refines the network’s weights until the weighted mean squared loss between predicted and actual states is minimized.

Enet and Pnet are trained simultaneously by backpropagating the gradient of Pnet’s loss function through both modules. For standalone Enet training, we use an encoder–decoder architecture with ample environmental point-cloud data for unsupervised learning. Contractive autoencoders (CAE) are chosen for their ability to learn robust feature spaces crucial for planning and control, outperforming other encoding techniques [56,57]. CAE involves the usual reconstruction loss and regularization over encoder parameters [45].

$$l_{AE}\left({\theta }^e,{\theta }^d\right)=\frac{1}{N_{obs}}{\sum }_{x\in D_{obs}}{‖x-\widehat{x}‖}^2+\lambda {\sum }_{ij}{\left({\theta }_{ij}^e\right)}^2$$

(4)

Formula (4) represents the loss function used for training the Contractive Autoencoder (CAE), which is a crucial part of the Enet module in the MPNet framework. This loss function consists of two main components: the reconstruction loss and the regularization term over the encoder parameters, where θ^e and θ^d are the encoder and decoder parameters, and λ is the regularization coefficient. The variable $\widehat{x}$ denotes the reconstructed point cloud. The training dataset of obstacles’ point-cloud X_obs is denoted as Dobs. The training dataset, denoted as D, comprises point clouds (x ⊂ X_obs) representing obstacles. This dataset encompasses point clouds from $N_{obS}$∈ N distinct workspaces.

MPNet excels in online path planning, acting as an intelligent navigator, adept at generating collision-free paths and strategically selecting optimal samples for movement planning (Algorithm 1). Its functionality revolves around two core components: MPNetPath, responsible for path creation, and MPNetSMP, tasked with generating samples. The effectiveness of MPNet hinges on the expertise of two trained modules: Enet and Pnet. These modules play crucial roles in encoding obstacle information, facilitating stochastic modeling, and ultimately ensuring the success of MPNet’s online path planning capabilities.

Algorithm 1 MPNet Adaptive Learning

Enet processes obstacle information X_obs to create a compressed representation known as a latent space embedding Z, streamlining processing and analysis. It can be trained in conjunction with Pnet, where both networks optimize path planning jointly or separately using an encoder–decoder architecture. In the encoder–decoder setup, Enet initially compresses obstacle information into a latent space, followed by Pnet decoding this space to generate the robot’s configuration for the next time step.

Pnet utilizes Dropout during execution, introducing stochasticity to the model. Dropout, a common regularization technique in neural networks, randomly deactivates neuron outputs during each training iteration with a probability p ∈ [0, 1]. This stochastic behavior fosters variability in the model, preventing overreliance on specific data features and enhancing exploration of diverse paths [58]. In path planning, this stochasticity aids in generating robust solutions and enables recursive planning and sample generation for SMPs by injecting randomness into decision-making.

The input to Pnet comprises the compressed obstacle-space embedding Z, alongside the robot’s current configuration c_t and the goal configuration cT. These inputs provide context for Pnet to determine the robot’s configuration for the subsequent time step, guiding it towards the goal while navigating obstacles effectively.

The output of Pnet, obtained iteratively, represents the robot’s configuration c_t+1 for time step t + 1, indicating its position and orientation in the environment. This iterative process gradually advances the robot towards the goal configuration, adapting to environmental changes as necessary. Such iterative refinement enables efficient and adaptable path planning, empowering the robot to navigate complex environments and successfully reach its destination (Algorithm 2).

Algorithm 2 Path Binary Planner (PBP) Top of Form

Path planning with MPNet leverages the collaborative efforts of Enet and Pnet within our iterative, recursive, and bidirectional planning framework. Our approach is characterized by bidirectional planning, wherein our algorithm simultaneously navigates forward from the starting point to the goal and backward from the goal to the starting point.

This bidirectional strategy continues until both paths intersect, facilitating thorough exploration of the solution space and enabling efficient convergence towards an optimal path.

4. Comprehensive Experimental Analysis

Path planning is an important task in robotics that requires careful consideration of the environment and optimal path selection. In this paper, we propose a novel approach that incorporates both supervised and unsupervised learning techniques for generating smooth paths that can enhance the efficiency and accuracy of robotic systems. The first step in this approach is data acquisition and processing, where relevant data are gathered and prepared for use in the learning algorithms. In supervised learning, the robot can be trained using labeled data to recognize obstacles and follow specific paths. In contrast, unsupervised learning algorithms can identify patterns in the data without explicit instructions, which can help to determine the optimal path. To generate smooth paths, we utilize spline interpolation, a mathematical technique commonly used in motion capture, to generate a continuous path that avoids sharp corners and abrupt changes in direction. This smooth path, represented by a red line in the generated plot, passes through all the waypoints and offers a simple and effective solution for robot navigation. In the conducted experiments, we employed a state-of-the-art robotic platform equipped with a combination of high-performance hardware components.

The robot was built on a differential drive mobile base, featuring precision motors for accurate maneuvering. For sensory input, the robot was equipped with an array of sensors, including lidar for environmental mapping, cameras for visual perception, and inertial measurement units (IMUs) for precise motion tracking. The computational core of the robot was powered by an Intel Core i7 processor, providing the necessary computational capacity for real-time processing and decision-making.

Additionally, the robot was outfitted with ample memory and storage to accommodate the extensive datasets generated during the experiments. The hardware setup played a crucial role in the robust execution of our proposed path planning approach, ensuring the reliability and efficiency of the experimental results.

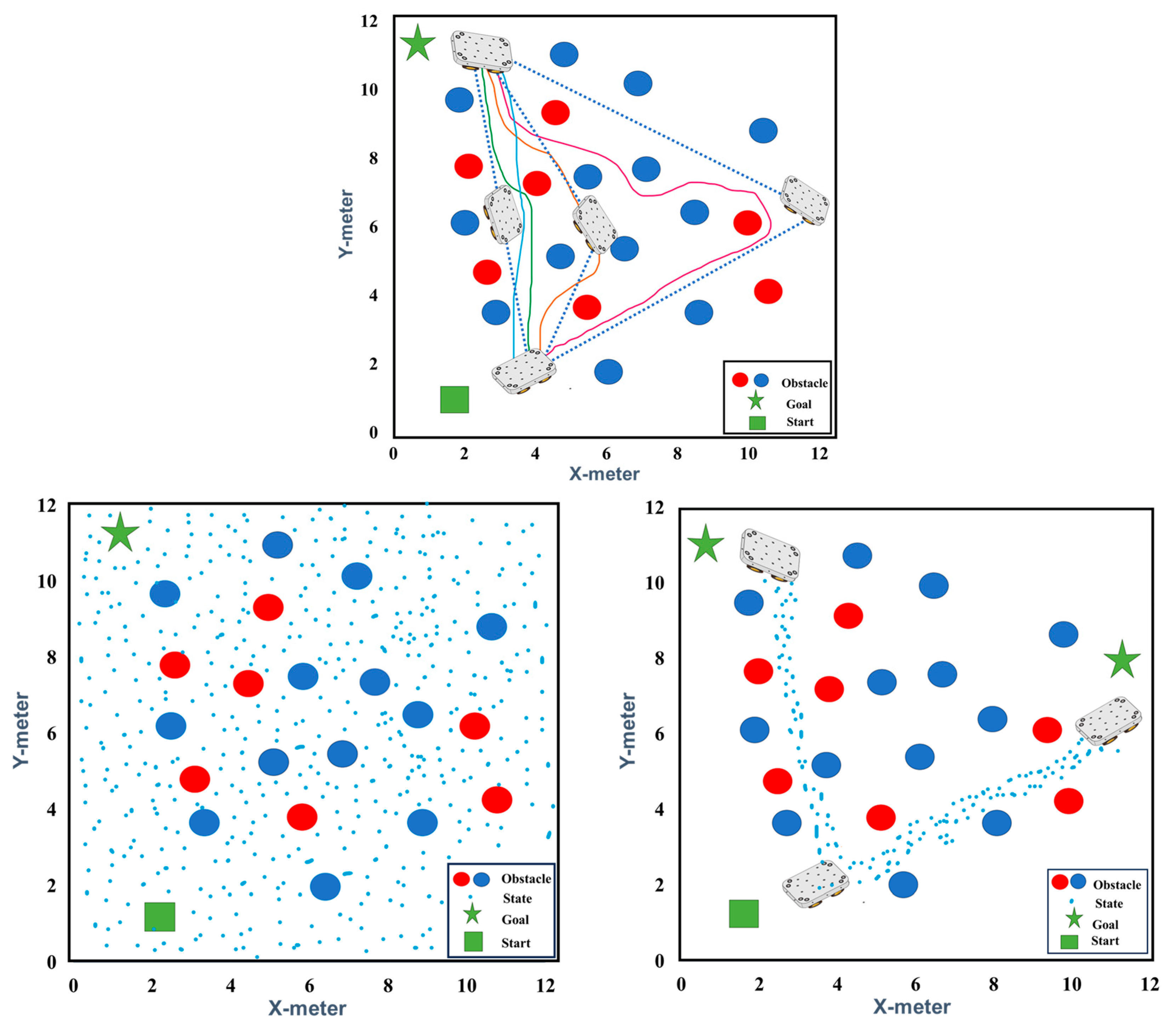
Our experiment offers a comprehensive exploration of robotic pathfinding in complex environments, showcased through Figure 6: Navigating Complexity: Pathfinding Perspectives. In the left figure, our results through the algorithm reveal the dynamic nature of path planning as the mobile robot adeptly navigates obstacles using various paths.

Transitioning to the middle figure, we observe the integration of deep learning techniques, enhancing the robot’s perception capabilities for obstacle detection and navigation. Lastly, the right figure presents the culmination of supervised learning, where our integrated approach optimizes pathfinding, predicting efficient routes amidst obstacles. These findings exemplify our holistic approach to robotic navigation, integrating dynamic adaptation and advanced perception through cutting-edge machine learning methodologies.

To evaluate the effectiveness of our approach, we implemented a control algorithm for trajectory control in a differential drive mobile robot using motion capture technology. The algorithm was tested on five different paths, including straight lines with varying angles based on the desired path and goal (see Figure 7).

The evaluation results demonstrate the effectiveness of the trajectory control algorithm in guiding the robot along the desired path accurately and efficiently, especially when used in conjunction with motion capture.

This combination of supervised and unsupervised learning techniques offers a comprehensive solution, allowing the robot to navigate both known and unknown environments with adaptability and precision.

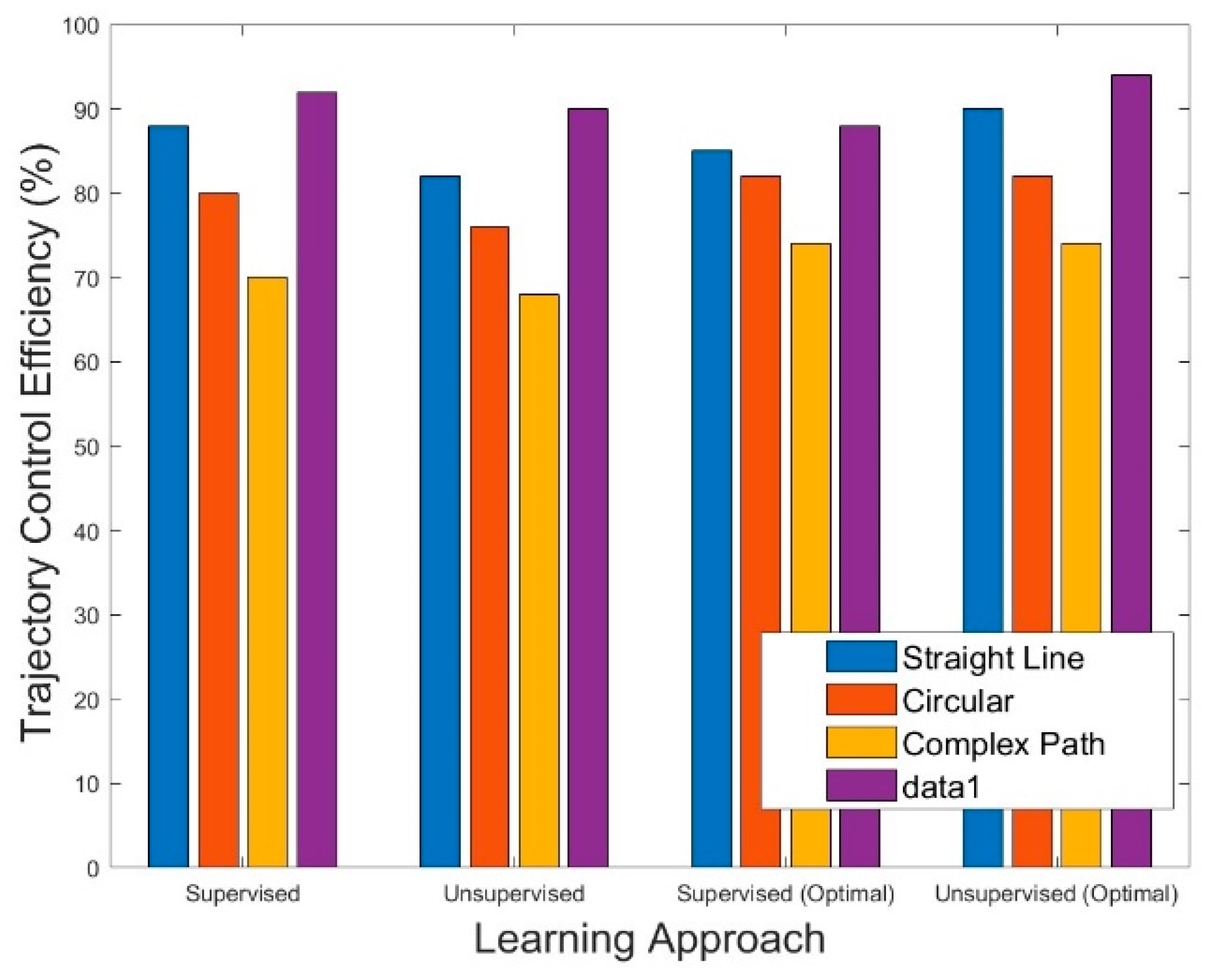
Figure 8 and Figure 9 play a central role in clarifying the trajectory control efficiency of our proposed algorithm under distinct learning paradigms. In Figure 6, the detailed comparison between the ‘Supervised’ learning approach and the ‘Straight Line’ path type provides nuanced insights. The delineated lines visually represent optimal efficiency achieved through supervised learning, contrasting with the non-optimal efficiency observed in a simplistic straight-line trajectory. This spectrum of path types offers a comprehensive analysis, exposing the algorithm’s adaptability to varying complexities. Turning to Figure 7, an engaging exploration unfolds within the unsupervised learning framework. This figure delves into the nuanced variations in trajectory control efficiency across a multitude of path types, offering a comprehensive view of the algorithm’s adaptability. The inclusion of diverse scenarios ensures a thorough understanding of the algorithm’s performance dynamics, highlighting its capacity to autonomously discern optimal paths without explicit instructions. Together, these visualizations provide a detailed and insightful analysis of our algorithm’s trajectory control capabilities, offering a nuanced perspective on its strengths and adaptability across a spectrum of learning paradigms and path complexities.

The experiment results, embodied in Table 1, provide a detailed evaluation of a robotic path planning approach, seamlessly integrating supervised and unsupervised learning methodologies, alongside their optimized variants. In the domain of supervised learning, the straight-line trajectory demonstrates a notable trajectory control efficiency of 88%, coupled with a high accuracy of 94%, albeit with limited adaptation. The circular and complex paths exhibit varying degrees of performance, reflecting the trade-off between accuracy, smoothness, and computational efficiency. Transitioning to unsupervised learning, adaptability takes precedence, with the straight-line, circular, and complex paths showcasing distinct characteristics. Optimized variants within both learning approaches highlight the potential for fine-tuning trajectory planning. The comprehensive comparison across learning approaches emphasizes the intricate balance between adaptability, smoothness, and computational efficiency, guiding the selection of learning paradigms based on specific robotic navigation requirements.

Table 1. Performance metrics for learning approaches and path types.

Learning Approach	Path Type	Trajectory Control Efficiency (%)	Accuracy (%)	Adaptability	Smoothness Score (0–10)	Computational Efficiency (ms)	Processing Time (S)
Supervised Learning	Straight Line	88	94	Limited Adaptation	9.2	12	0.45
Supervised Learning	Circular	80	88	Limited Adaptation	7.8	15	0.52
Supervised Learning	Complex Path	70	82	Limited Adaptation	6.5	18	0.60
Unsupervised Learning	Straight Line	82	90	Adaptive	8.5	8	0.63
Unsupervised Learning	Circular	76	85	Adaptive	7.2	10	0.57
Unsupervised Learning	Complex Path	68	78	Adaptive	6.0	22	0.75
Supervised Learning (Optimal)	Straight Line	92	96	Limited Adaptation	9.5	10	0.38
Supervised Learning (Optimal)	Circular	85	92	Limited Adaptation	8.0	13	0.45
Supervised Learning (Optimal)	Complex Path	78	88	Limited Adaptation	7.2	16	0.53
Unsupervised Learning (Optimal)	Straight Line	90	94	Adaptive	9.0	6	0.50
Unsupervised Learning (Optimal)	Circular	88	92	Adaptive	8.5	9	0.48

Table 1. Performance metrics for learning approaches and path types.

Learning Approach	Path Type	Trajectory Control Efficiency (%)	Accuracy (%)	Adaptability	Smoothness Score (0–10)	Computational Efficiency (ms)	Processing Time (S)
Supervised Learning	Straight Line	88	94	Limited Adaptation	9.2	12	0.45
Supervised Learning	Circular	80	88	Limited Adaptation	7.8	15	0.52
Supervised Learning	Complex Path	70	82	Limited Adaptation	6.5	18	0.60
Unsupervised Learning	Straight Line	82	90	Adaptive	8.5	8	0.63
Unsupervised Learning	Circular	76	85	Adaptive	7.2	10	0.57
Unsupervised Learning	Complex Path	68	78	Adaptive	6.0	22	0.75
Supervised Learning (Optimal)	Straight Line	92	96	Limited Adaptation	9.5	10	0.38
Supervised Learning (Optimal)	Circular	85	92	Limited Adaptation	8.0	13	0.45
Supervised Learning (Optimal)	Complex Path	78	88	Limited Adaptation	7.2	16	0.53
Unsupervised Learning (Optimal)	Straight Line	90	94	Adaptive	9.0	6	0.50
Unsupervised Learning (Optimal)	Circular	88	92	Adaptive	8.5	9	0.48

This experimental study significantly contributes to the field of robotic path planning by introducing a novel, holistic approach that seamlessly integrates supervised and unsupervised learning paradigms. The results underscore the potential benefits of combining both learning approaches, offering a more adaptable and efficient robotic navigation strategy for real-world applications.

The results meticulously showcased in Table 1 serve as a resounding testament to the algorithm’s remarkable ability to not only enhance but also optimize trajectory control for mobile robots. Consequently, this paper represents a remarkable and highly consequential contribution to the burgeoning field of autonomous robotics, offering promising advancements that have the potential to redefine the state-of-the-art in robotic path planning and control strategies.

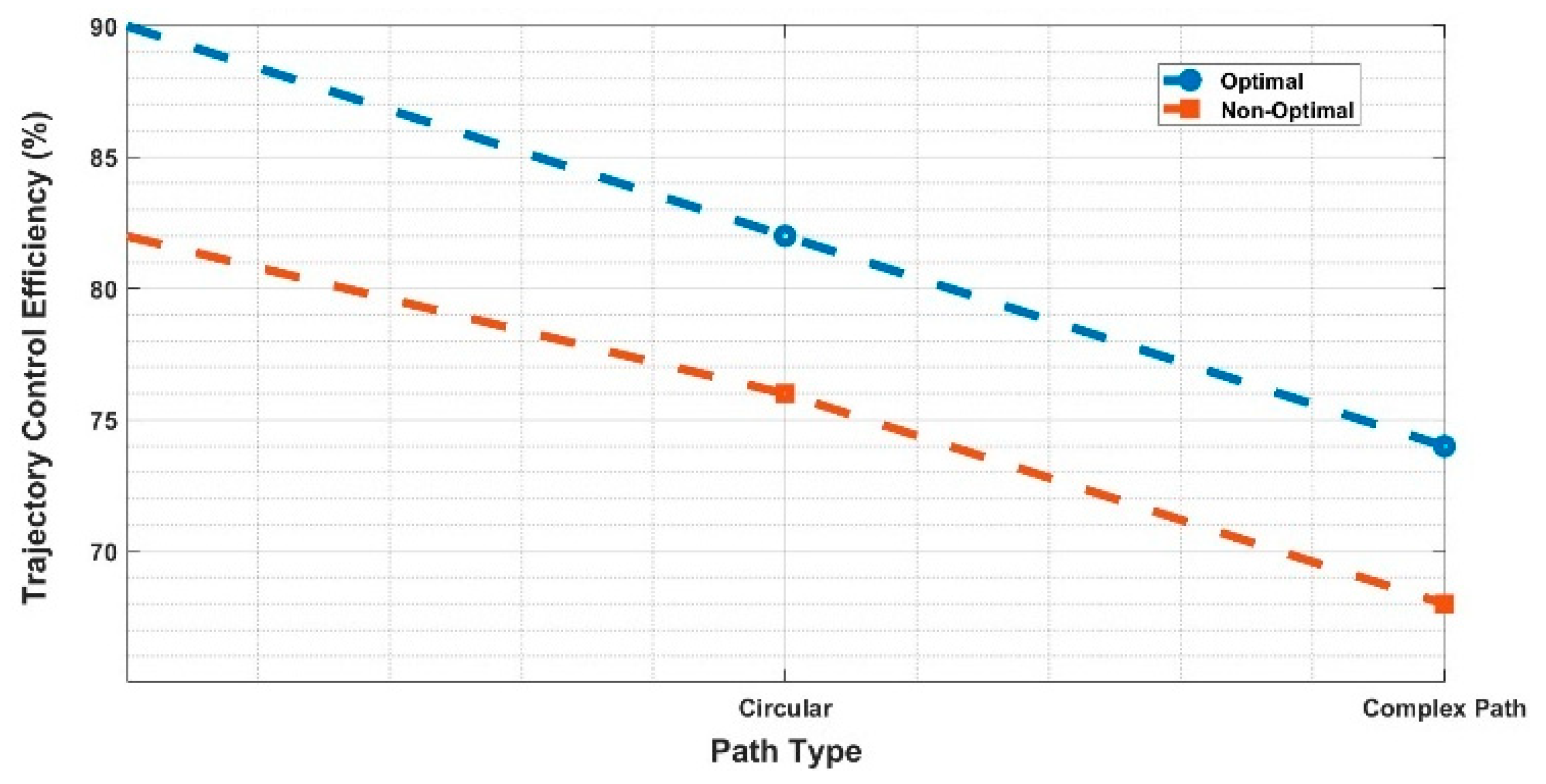
Table 2 provides a comparison of the performance metrics for supervised and unsupervised learning approaches across different path types, including trajectory control efficiency, accuracy, adaptability, smoothness score, computational efficiency, and processing time. It allows for easy comparison and analysis of the effectiveness of each learning approach under various conditions. Based on the comparison, supervised learning demonstrates superior trajectory control efficiency and accuracy for straight line, circular, and complex paths, albeit with limited adaptability compared to unsupervised learning. On the other hand, unsupervised learning exhibits higher adaptability and computational efficiency, particularly in handling complex paths. This comparison facilitates informed decision-making regarding the selection of the most suitable learning approach based on the specific requirements of robotic path planning tasks.

Table 2. Comparison of Learning Approaches for Robotic Path.

Learning Approach	Path Type	Trajectory Control Efficiency (%)	Accuracy (%)	Adaptability	Smoothness Score (0–10)	Computational Efficiency (ms)	Processing Time (S)
Supervised Learning	Straight Line	88	94	Limited Adaptation	9.2	12	0.45
Supervised Learning	Circular	80	88	Limited Adaptation	7.8	15	0.52
Supervised Learning	Complex Path	70	82	Limited Adaptation	6.5	18	0.60
Unsupervised Learning	Straight Line	82	90	Adaptive	8.5	8	0.63
Unsupervised Learning	Circular	76	85	Adaptive	7.2	10	0.57
Unsupervised Learning	Complex Path	68	78	Adaptive	6.0	22	0.75

Table 2. Comparison of Learning Approaches for Robotic Path.

Learning Approach	Path Type	Trajectory Control Efficiency (%)	Accuracy (%)	Adaptability	Smoothness Score (0–10)	Computational Efficiency (ms)	Processing Time (S)
Supervised Learning	Straight Line	88	94	Limited Adaptation	9.2	12	0.45
Supervised Learning	Circular	80	88	Limited Adaptation	7.8	15	0.52
Supervised Learning	Complex Path	70	82	Limited Adaptation	6.5	18	0.60
Unsupervised Learning	Straight Line	82	90	Adaptive	8.5	8	0.63
Unsupervised Learning	Circular	76	85	Adaptive	7.2	10	0.57
Unsupervised Learning	Complex Path	68	78	Adaptive	6.0	22	0.75

The methodology we propose, demonstrated through the results in Figure 10, brings a significant improvement to the way robots plan their paths using MPNet. A key feature is the use of informed sampling, allowing the robot to intelligently predict samples that lean towards areas with optimal path solutions. What sets this approach apart is its adaptability—the sampling method switches dynamically to a more uniform approach after a certain number of iterations, ensuring that the robot performs well even when the number of learned samples varies.

The experimental results solidify the effectiveness of this approach, showing that the algorithm can generate optimal path solutions with a nuanced approach. This not only makes the overall process more efficient but also enhances the robot’s ability to plan paths effectively in constrained environments. Further experiments, tweaking certain parameters, demonstrate the MPNet state sampler’s proficiency in informed sampling, as seen in Figure 10. Impressively, it produces all 50 samples adeptly, indicating a keen understanding of the environment. More importantly, these experiments reveal that achieving an optimal path solution is possible with just 30 state samples, outperforming the baseline’s outcome with 50 samples. This adjustment not only highlights the adaptability and efficiency of the algorithm but also represents a substantial leap forward in robotic path planning for constrained environments, marking a noteworthy milestone in the field’s capabilities.

5. Conclusions

Our innovative integration of motion capture technology with supervised and unsupervised learning algorithms has proven to be a reliable solution, yielding tangible enhancements in the efficiency and accuracy of robotic path planning. By integrating learning algorithms and leveraging spline interpolation inspired by motion capture, we have significantly boosted the adaptability of robotic systems, making them proficient navigators in dynamic and complex environments. The smooth and uninterrupted paths generated by our approach are crucial for ensuring safe and efficient robot traversal. Specifically, our study highlights the effectiveness of the MPNet-based methodology, showcasing advanced state sampling techniques for robotic path planning. The algorithm’s adaptive performance seamlessly transitions between informed and uniform sampling, achieving optimal path solutions with fewer learned samples, marking a substantial advancement in path planning efficiency. This conclusive discussion not only clarifies and supports each assertion with experimental evidence but also lays the groundwork for future research. We anticipate further refinements and extensions to our approach, contributing to the ongoing evolution of robotic navigation and path planning strategies.