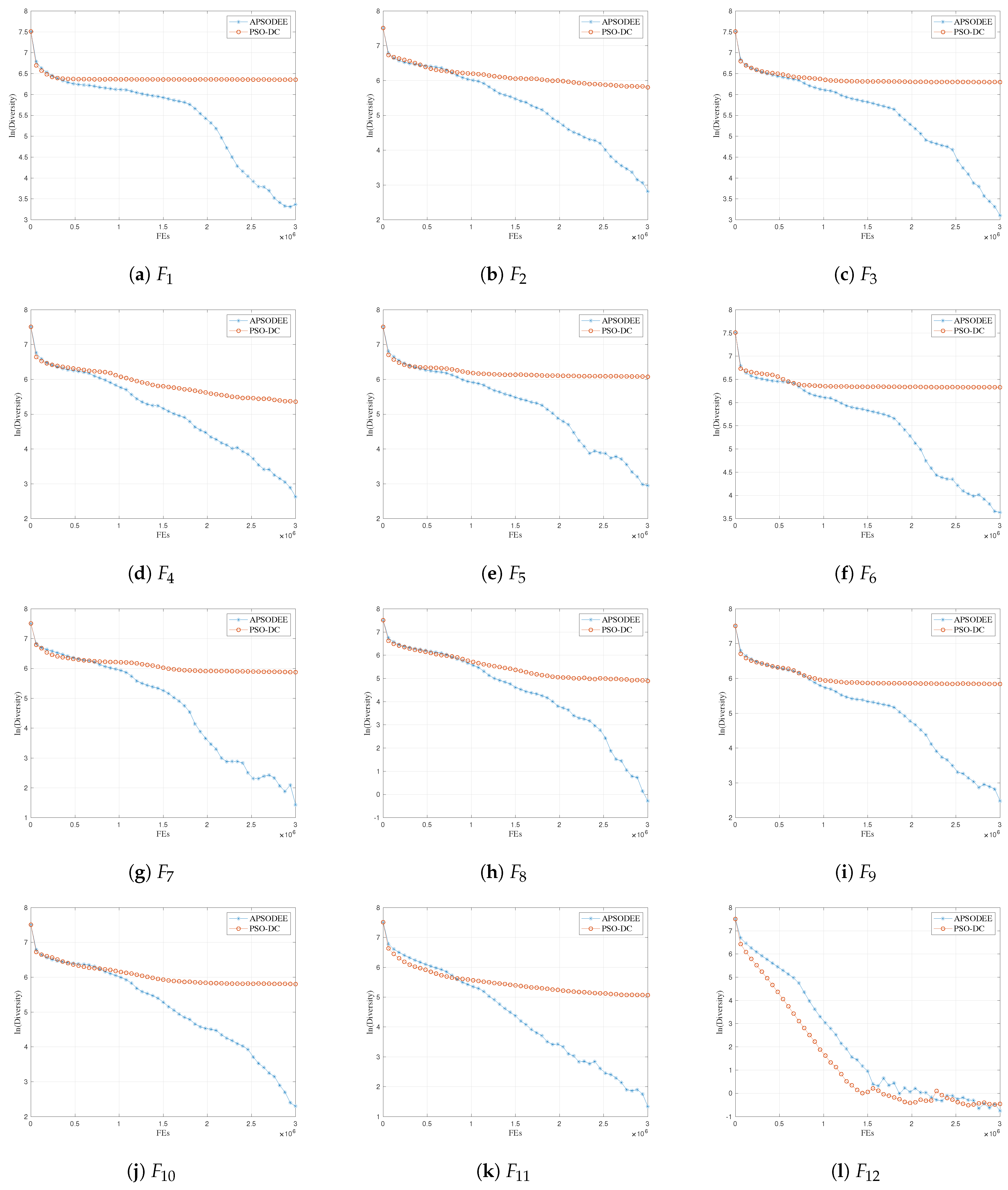1. Introduction
Particle swarm optimization (PSO) has been widely applied in engineering optimization in past decades due to their simplicity and efficiency [
1,
2,
3,
4,
5]. On the one hand, PSO shows better robustness and computational efficiency in comparison to gradient-based algorithms [
6]. On the other hand, in comparison to many existing evolutionary algorithms (e.g., genetic algorithms [
7], ant colony optimizer [
8], teaching–learning-based optimization [
9], and brain storm optimization [
10]), PSO has the advantages of easy implementation, efficient parameter tuning, and flexible manners of hybridization with other optimization methods [
11].
However, PSO has been found to be inefficient in solving large-scale optimization problems (LSOPs). Without losing generality, the LSOP mentioned in this paper aims to minimize a given function, which can be formulated by (
1).
where
D is the dimensionality of the considered optimization function, and
denotes the
dimension of the decision vector. Note that (i)
is a continuous black box function with boundary constraints on the decision variables, and (ii) the dimensionality considered in this paper is up to 1000, which is a common setting in relevant research. The main reason for this is that PSO cannot effectively conduct swarm diversity preservation when solving LSOPs and is thus easily trapped in local optima. To be specific, this is caused by PSO’s exemplar selection mechanism: the
and
in PSO are of poor diversity during the optimization process [
12], since it is difficult to locate more promising solutions based on the current swarm. Therefore, the swarm tends to converge to the local optimum, resulting in premature convergence. On the other hand, limited computing resources only allow PSO to search part of the search spaces [
13].
Targeting these two issues, a large body of research has been put forward to improve PSO for LSOPs. The mainstream of the current work can be roughly divided into three categories: exemplar diversification, decoupled learning, and hybridization of PSO and other techniques.
The methods in the first category propose to enhance the diversity of the exemplars for the updated particles [
12,
13,
14,
15,
16,
17,
18,
19], thereby improving PSO’s balance between exploration and exploitation. For instance, the competitive swarm optimizer (CSO) assigns each updated particle a distinguishing exemplar [
12], the social learning particle swarm optimizer (SLPSO) allows the updated particles to learn all of the particles that are better than the specific updated particles [
14], and the level-based learning swarm optimizer (LLSO) randomly selects two exemplars for each updated particle [
13]. Through these means, the exemplars of the updated particles can be hugely diversified in comparison to the basic PSO, which leads to benefits in diversity preservation.
The approaches in the second category focus on decoupling the convergence learning component and the diversity learning component in the velocity update structure for the basic PSO [
1,
20,
21]. Afterwards, such algorithms adjust the parameters in the diversity learning component to control swarm diversity. Consequently, an important design factor in such methods is the study of the local diversity measurements to be adopted as the basis of the diversity learning component, such as the local sparseness degree [
1].
For hybrid PSO, the main idea is to utilize other optimization techniques to enhance PSO in diversity preservation. For instance, chaotic local search [
22] and the memetic algorithm [
23] can be adopted to promote PSO in local search for diversity preservation. One possible solution that can be employed to help diversity preservation is to update the rules of the simulated annealing algorithm [
24] and the genetic algorithm [
25].
However, these methods still show room for further improvement. First, for the methods with exemplar diversification strategies, the early attempts, such as CSO and SLPSO, fail at simultaneously diversifying the two exemplars for the updated particles [
13]. Recent methods, such as LLSO, are ineffective in preserving promising particles, consequently resulting in adverse impacts on diversity preservation. Furthermore, recent methods often introduce additional operators for exemplar selection, leading to extra parameter tuning tasks and computational complexity. Second, the approaches with decoupled learning mechanisms show poor ability in preserving promising particles; on the other hand, they are computationally complex in evaluating the local diversity information, which should impose constraints on their performance if the computation resources are limited. In summary, one can find that both the recent methods in the two categories fail at effectively protecting promising particles from being updated for diversity preservation and simplifying the complexity of the algorithm. Third, for the hybrid PSO variants, extra parameter tuning tasks will be required due to the introduction of other optimization operators [
12]. Therefore, diversity preservation for PSO in LSOPs is still challenging.
To address this issue, this paper aims to design novel learning mechanisms for both diversity preservation and efficient exemplar selection to improve PSO in both performance and efficiency. To this end, a novel variant of PSO is proposed, and the main contributions of this paper are listed as follows:
To enhance the diversity preservation ability of PSO, this paper puts forward an efficient dual-competition-based learning mechanism, which is able to efficiently help diversify the exemplars of the updated particles and preserve promising particles. Therefore, the proposed mechanism can significantly enhance PSO in diversity preservation.
Based on the proposed dual-competition-based learning mechanism, a novel variant of PSO for LSOPs is proposed, referred to as the dual-competition-based particle swarm optimizer (PSO-DC).
Comprehensive theoretical analysis and experiments are conducted, which demonstrate the competitiveness of the proposed algorithm from both theoretical and experimental perspectives.
The subsequent sections of this work are structured as follows:
Section 2 provides a review of the current improvements in PSO for LSOPs.
Section 3 presents the details of the proposed dual-competition-based learning mechanism.
Section 4 provides a theoretical analysis of the computational complexity and the searching characteristics of the proposed algorithm.
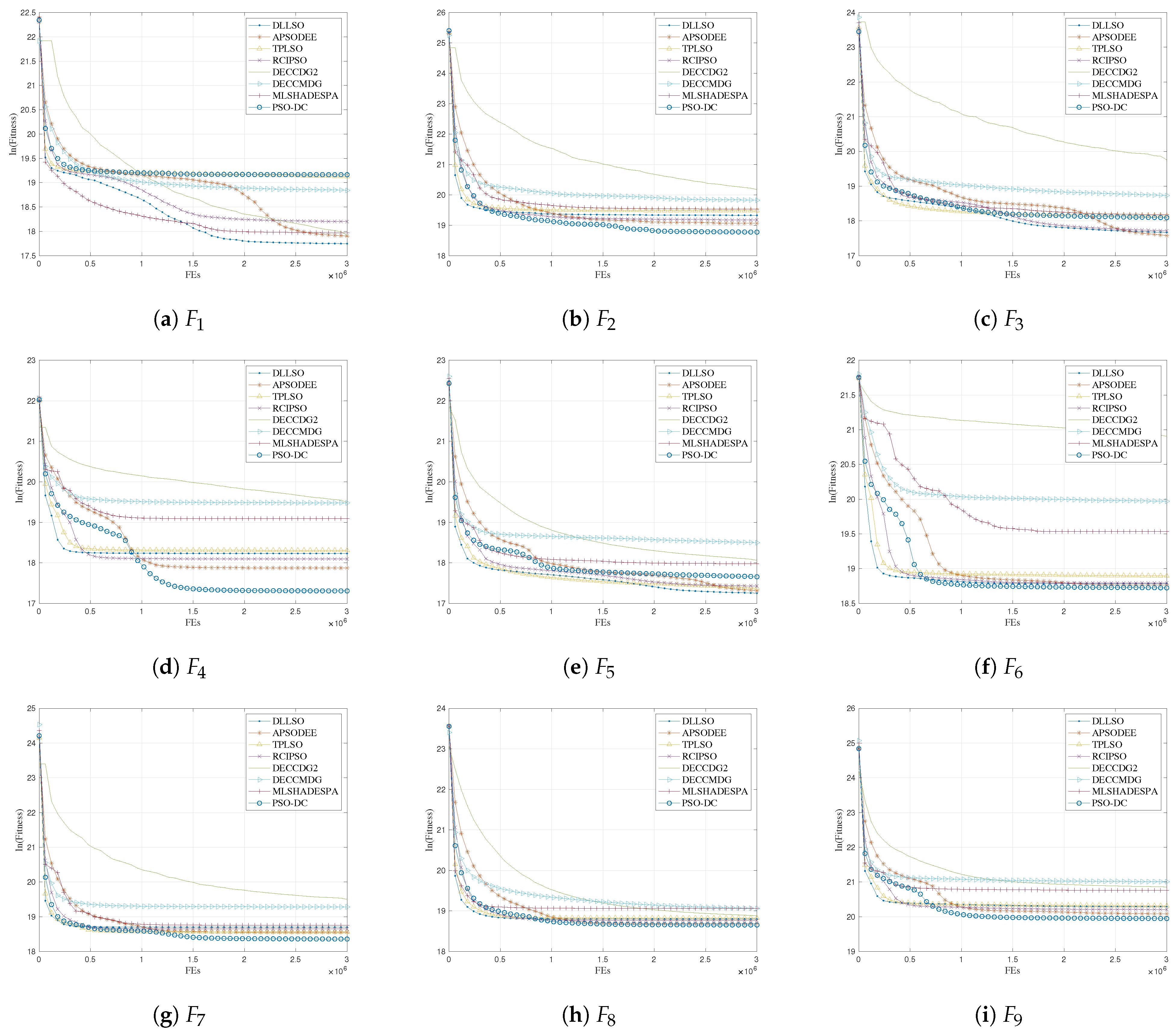
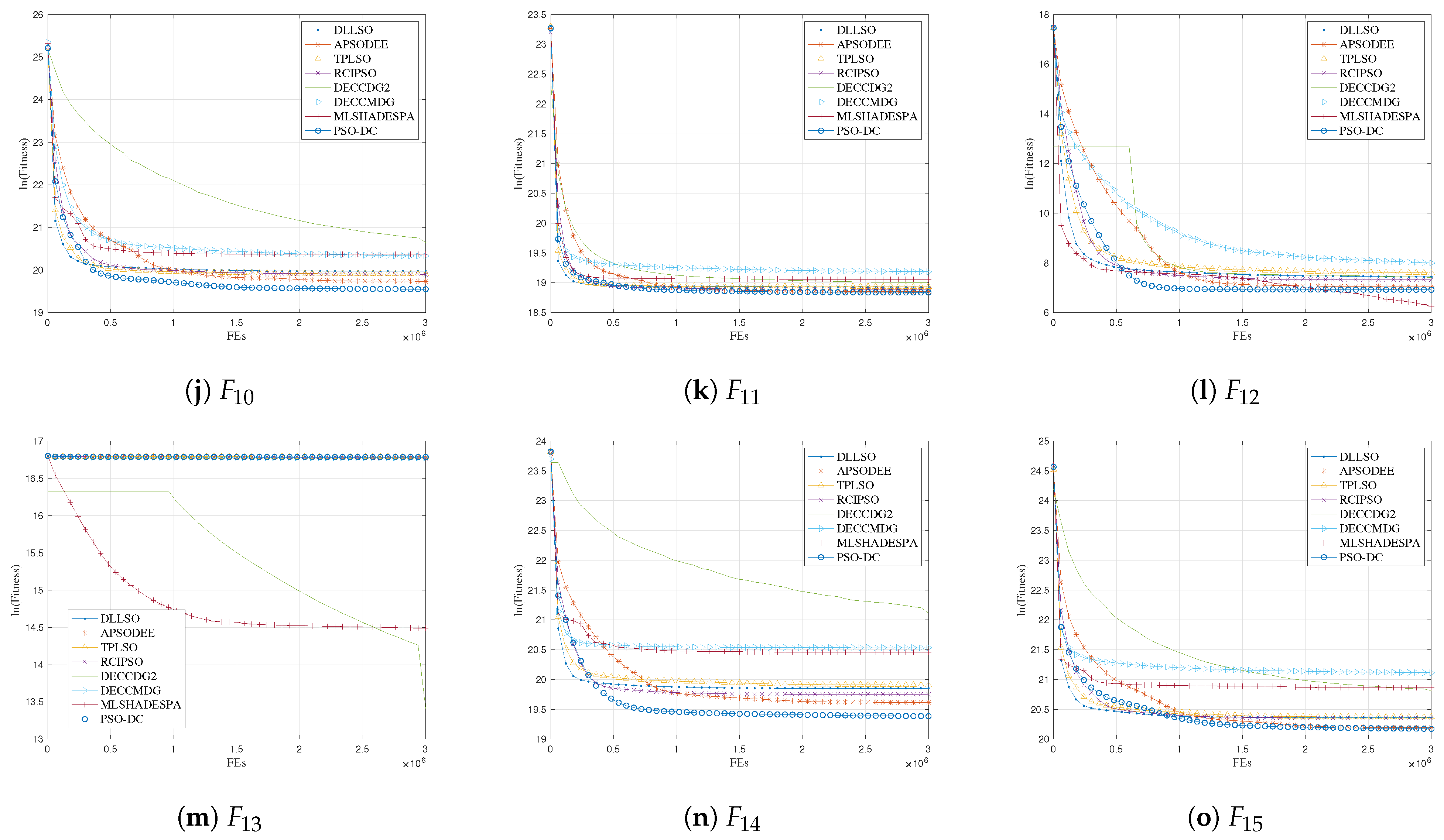
Section 5 experimentally tests the performance of the proposed algorithm. Finally, we conclude this paper and highlight directions for future work in
Section 6.
3. Proposed Method
In this section, this paper proposes a novel variant of particle swarm optimizer which can diversify the exemplars for the updated particles, protect the promising particles, and is of low computational cost.
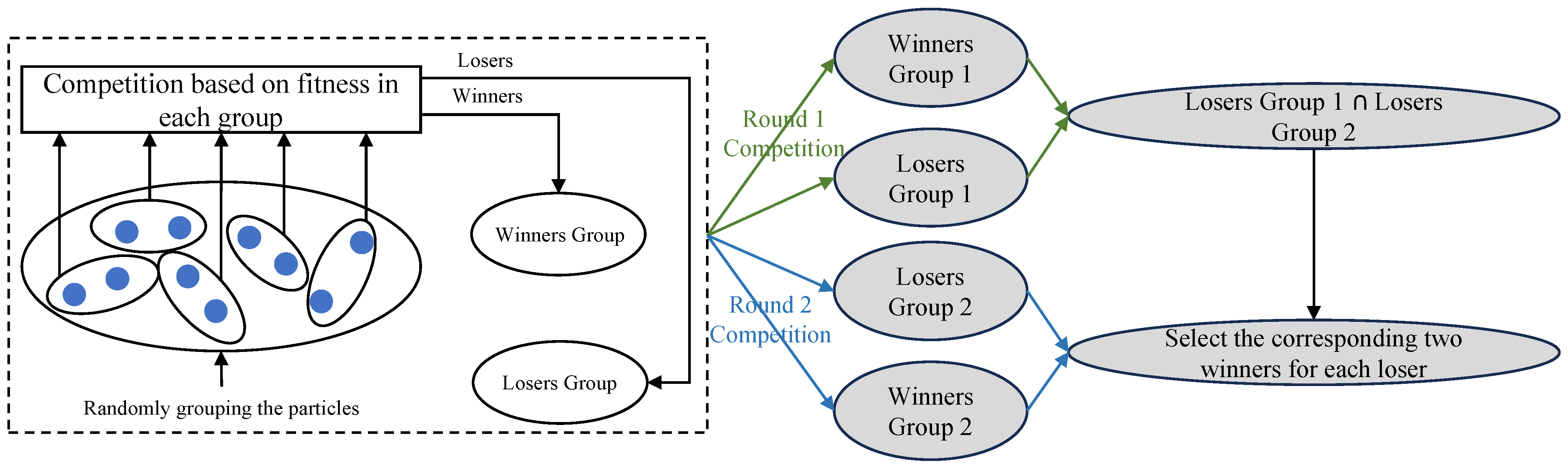
First, the proposed exemplar and updated particle selection method (referred to as the dual-competition-based strategy, DCS) can be illustrated in
Figure 1. To be specific, the competition mechanism [
12] is independently executed for twice at each generation, leading to two winners groups and two losers groups. Afterwards, the particles to be updated at each generation can be obtained by taking the intersection of the two loser groups, namely, “Losers Group 1” and “Losers Group 2” in
Figure 1. Consequently, the exemplars for the obtained particles to be updated are the corresponding winners in “Winners Group 1” and “Winners Group 2”. Here, a brief of the competition mechanism is presented to ensure the integrity of the proposed mechanism: first, a swarm with size
is randomly divided into
sub-swarms and second, in each sub-swarm, the particle with the better fitness is regarded as the winner and put into the winners group while the other one is put into the losers group.
Second, in order to distinguish the exploitation and exploration exemplars, the two exemplars for each particle are sorted based on their fitness: the better exemplar is adopted as the exploitation exemplar, and the other exemplar is employed as the exploration exemplar. This is inspired by [
13]: learning from a more promising exemplar shows advantages in exploitation, while learning from a relatively inferior exemplar tends to explore more regions of the decision space.
Finally, the velocity and position of the particles to be updated are iterated according to (2) and (3), leading to the proposed dual-competition-based particle swarm optimizer (PSO-DC).
where
is the
dimension of the
updated particle’s velocity at generation
t;
and
are the position of the exploitation exemplar and the exploration exemplar, respectively;
,
, and
are randomly generated numbers within
; and
is the parameter set by users for balance the exploration and exploitation. The pseudo code of the proposed algorithm is presented in Algorithm 1.
One can find that the proposed PSO-DC mainly differs from the current PSO variants via the following: (i) PSO-DC shows advantages over CSO and SLPSO, since it can select two different exemplars for the updated particles. (ii) PSO-DC has an improved ability to preserve promising particles at each generation, since it is able to keep allowing more than half of the particles to be retained to the next generation with DCS. This can significantly help PSO-DC with diversity preservation. (iii) PSO-DC does not introduce any extra parameters in comparison to APSODEE [
1], DLLSO [
13], and RCIPSO [
18], etc. In summary, PSO-DC exhibits advantages in both diversity preservation and simplicity.
| Algorithm 1 The pseudo code of PSO-DC. |
| Input: Swarm size , terminal criterion , variable boundary.
|
| Output: The best particle searched during the optimization.
|
| 1: Randomly generate a swarm with respect to and variable boundary;
|
| 2: ;
|
| 3: while if is not met do |
| 4: Evaluate the swarm;
|
| 5: Conduct DCS to obtain the particles to be update , the exploitation exemplar set , and the exploration exemplar set ;
|
| 6: for in do |
| 7: Update according to (2) and (3);
|
| 8: end for |
| 9: Update with |
| 10: ;
|
| 11: end while |
4. Theoretical Analysis
4.1. Computational Complexity
In this section, the computational complexity of PSO-DC is analyzed by comparing it with the basic PSO and APSODEE in terms of the learning structure, computational cost, and the requirements for memory.
First, for the update structure, all these methods adopt three components to form the velocity update structure.
Second, for the complexity analysis of the computational cost at each generation, taking the basic PSO as the baseline method, we mainly evaluate the extra computational cost introduced by PSO-DC and APSODEE at each generation. For the analysis of PSO-DC, the extra computational cost is manly brought by line 5 in Algorithm 1, which is
for two rounds of competition and
for obtaining the intersection of the two losers groups. Consequently, in comparison to the basic PSO, the extra computational complexity of PSO-DC at each generation is
. According to the analysis in [
1], in comparison to the basic PSO, the extra computational complexity of APSODEE is
.
Finally, for the memory cost, both PSO-DC and APSODEE do not need to store and in comparison to the basic PSO.
In summary, PSO-DC is simple for learning structure, more computationally efficient than APSODEE, and more memory efficient than the basic PSO.
4.2. Convergence Stability Analysis
Convergence stability analysis is crucial to EAs [
41,
42]. Considering that the exemplar selection mechanism of PSO-DC builds on randomness, this paper analyzes the convergence of
for the proposed algorithm with the method proposed by [
41], where
is the expectation of an arbitrary particle at generation
t. The details of the analysis are shown as follows. Note that convergence stability in 1-D search space is analyzed as follows, since each dimension of the particles is independently updated in PSO-DC.
For simplicity, the velocity update strategy of PSO-DC is rewritten as (4) and (5).
Consequently,
can be transformed to (
6), where
.
Then,
can be obtained as (
7), where
,
,
,
, and
are the expectations of the corresponding variables, respectively.
With (
7) and (
8), the following can be obtained:
For simplicity, we introduce (
9).
Based on the analysis in [
41], the necessary and sufficient condition for ensuring the convergence of
is as follows: the magnitude of the eigenvalues of
M (
) must be smaller than 1. Considering
,
, and
as random numbers within
,
,
, and
should be
. Afterwards, the necessary and sufficient condition for the convergence of
is shown by (
10).
By analyzing (
10), the necessary and sufficient condition for the convergence of
can be obtained as shown in (
11).
4.3. Diversity Preservation Characteristics
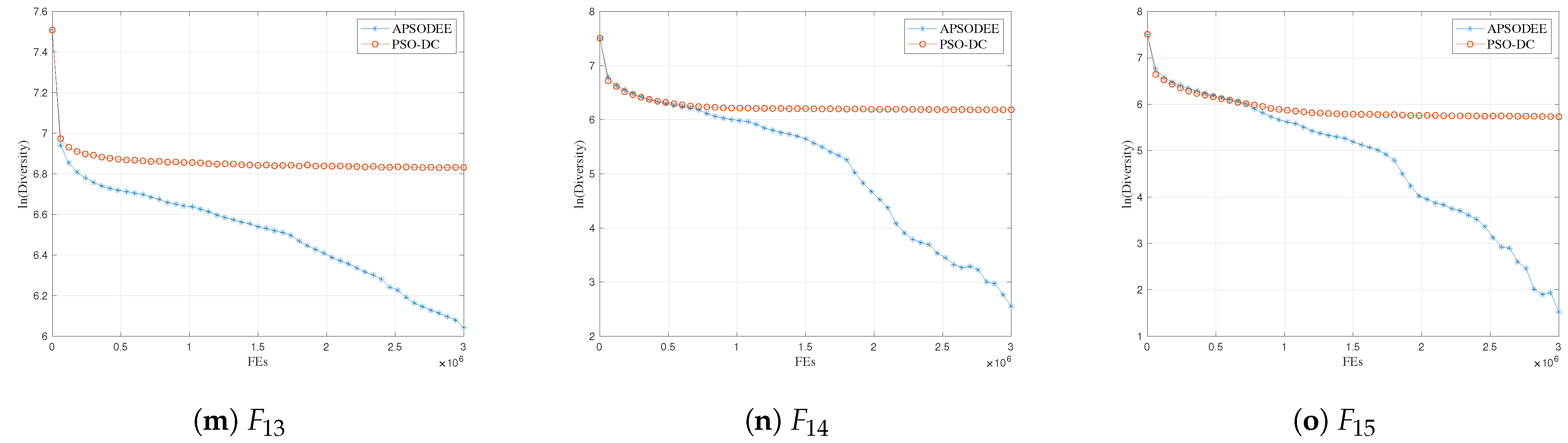
For the analysis of the diversity preservation characteristics of the proposed PSO-DC, this paper compares PSO-DC with APSO-DEE, which is a recently proposed PSO variant for LSOPs [
1] based on the analysis method presented in [
13].
In PSO-DC’s velocity update strategy, (
2) can be rewritten as (12)–(14).
Similarly, the velocity update strategy of APSO-DEE can be rewritten as (15)–(17):
where
and
are exemplars in APSO-DEE for convergence and diversity, respectively.
Consequently, the exploration ability of PSO-DC and APSO-DEE is mainly influenced by the diversity of and . In APSO-DEE, is the best particle of the sub-swarm that the particle is in, and it is shared by all the updated particles in this sub-swarm. In PSO-DC, and are both randomly selected with the proposed dual-competition strategy. Therefore, the diversity of should be better than that of . Furthermore, thanks to the dual-competition strategy, more than half of the particles can be preserved at each generation. In summary, the diversity preservation ability of PSO-DC is believed to be better than that of APSO-DEE, leading to a better exploration ability in PSO-DC.