Design of Secure and Privacy-Preserving Data Sharing Scheme Based on Key Aggregation and Private Set Intersection in Medical Information System
Abstract
1. Introduction
- We propose a privacy-preserving medical data sharing scheme. To maintain a balance between privacy and data sharing, we leverage PSI between the data owner and the data user before access requests. This facilitates interaction and data sharing while protecting sensitive information.
- The proposed scheme ensures secure data sharing and access control through KAE. Since KAE enables secure and flexible access control with a single aggregate key, the integration of KAE in the proposed scheme enhances data security by reducing the risk of data breaches and unauthorized disclosures.
- We perform security analysis using the Scyther tool [12] and mathematical analysis methods such as Burrows–Abadi–Needham (BAN) logic [13] and indistinguishability against the chosen plaintext attack (IND-CPA). In addition, we conduct performance analyses using the multiprecision integer and rational arithmetic cryptographic library (MIRACL) [14] and compare the obtained results with those of previous studies.
2. Related Works
3. Preliminaries
3.1. Elliptic Curve Cryptography
- Elliptic curve discrete logarithm problem (ECDLP): Given two points P and Q on , determining the scalar such that is considered computationally difficult.
- Elliptic curve computational Diffie–Hellman problem (ECCDHP): Given two points and , it is hard to calculate .
- Elliptic curve decisional Diffie–Hellman problem (ECDDHP): Given three points , , and , it is difficult to determine whether , where .
3.2. Bilinear Pairing
- Bilinearity: For , and , .
- Non-degeneracy: for some .
- Efficiency: can be calculated in polynomial time for .
3.3. Decisional Bilinear Diffie–Hellman (DBDH) Assumption
3.4. Key Aggregate Encryption
- (1)
- KAE.Setup (): Generate a random number , compute for , and publish . Then, discard
- (2)
- KAE.KeyGen (): Generate and compute . Then, output public and private key pair .
- (3)
- KAE.Encrypt (): For data in , choose a random number and compute , , . Then, output .
- (4)
- KAE.Extrac t (): For the subset of data class indices S, output the aggregate key .
- (5)
- KAE.Decrypt (): If , output ⊥. Otherwise, calculate , , and output .
3.5. Brakerski–Gentry–Vaikuntanathan
- (1)
- BGV.Setup (): Select a ring , where l is a power of 2. Given a security parameter , set the ciphertext modulus q, plaintext modulus t, and the noise distribution . Output .
- (2)
- BGV.KeyGen (): Generate the secret key , a random polynomial , and a random error polynomial . Calculate the public key .
- (3)
- BGV.Enc (): Generate , random polynomial u, and compute .
- (4)
- BGV.Dec (): Calculate using s.
3.6. Private Set Intersection
- (1)
- PSI.Setup (): Sender and receiver each generate a public–private key pair using the BGV.KeyGen procedure.
- (2)
- PSI.Enc (): Receiver encrypts each element using BGV.Enc and transmits the ciphertext to the sender.
- (3)
- PSI.Intersection (): Sender chooses a random number for , and computes . Then, the sender returns to the receiver.
- (4)
- PSI.Ext (): Receiver computes using BGV secret key s, and obtains where BGV.Dec().
4. System Models
4.1. Network Model
- : is a trusted authority that initiates the system by generating parameters for data sharing. undertakes the task of registering both and , issuing them with the necessary credentials.
- Data owner (): is hospitals, clinics, or research institutions. encrypts medical data and sends them to . When requests a common keyword identification query, computes an intersection set result, decryptable only by after legitimacy verification. also provides the aggregate key and relevant data class set upon ’s data access request.
- Data user (): is a doctor, nurse, researcher, patient, etc., within a medical institution. To access data, initiates a common keyword identification query. After receiving the results, requests access to data related to the matched keyword results and then uses the aggregate key to decrypt the data obtained from CS.
- Cloud server (): is an entity that stores the medical data and returns the data search results. When data are uploaded by , stores the data if has the necessary legal permissions. facilitates data access to following a verification process to ascertain the legal status of .
- (1)
- initializes the system parameters for authentication, intersection calculation, and data sharing.
- (2)
- registers and , storing the identity information to prevent duplicate registrations. Then, issues credentials for secure data sharing through authentication.
- (3)
- encrypts the medical data and uploads them to . then verifies the ’s legitimacy prior to storing the data.
- (4)
- submits the common keyword identification query for owned information. generates and transmits the encrypted intersection results after confirming ’s legitimacy with . verifies the received message and stores the intersection.
- (5)
- transmits a query for data access permission to using the intersection results. Then, generates and sends the aggregate key and corresponding data class set based on the intersected keywords.
- (6)
- requests the data from using a data class set and decrypts them using the aggregate key obtained from .
4.2. Adversary Model
4.3. Security Model
- Init. selects a specific set from the available set , which it aims to exploit.
- Setup. The simulator provides the system parameters to .
- Phase 1. For , submits an aggregate key request query to . Subsequently, generates and transmits the aggregate key to .
- Challenge. selects two plaintexts, and , of equal length from a set of possible plaintexts associated with class . These plaintexts are then forwarded to . Thereafter, obtains a random bit via a coin flip. Following this, encrypts the selected plaintext and transmits the resulting ciphertext to .
- Phase 2. iterates through Phase 1 for , encompassing classes that do not belong to .
- Guess. produces an estimate of the true value of ϰ and communicates it to . If the estimate aligns with the true value ϰ, is deemed successful in the game.
5. Proposed Scheme
5.1. Setup Phase
5.2. Registration Phase
- Step 1:
- selects and sends to .
- Step 2:
- checks whether is registered by computing . generates , , , and and computes , , . Then, stores , and sends to .
- Step 3:
- stores securely.
5.3. Data Upload Phase
- Step 1:
- generates a random nonce , and computes , , . also computes , , , , for document . Then, sends to .
- Step 2:
- Upon the uploaded message, computes and checks whether is equal to . If it it correct, computes and stores .
5.4. Common Keyword Identification Phase
- Step 1:
- generates , , and computes , , , . Then, sends .
- Step 2:
- After receiving the message, checks and by computing . If it is correct, generates and and computes , , . also generates for and computes . Then, transmits .
- Step 3:
- checks and computes . If is equated to , computes using , and inputs y in where .
5.5. Aggregate Key Issuance Phase
- Step 1:
- generates , and computes , , , . Then, sends .
- Step 2:
- checks , and computes , . If , generates , and computes , , , , . Then, transmits .
- Step 3:
- checks and computes for checking . If accurate, computes .
5.6. Data Request and Download Phase
- Step 1:
- generates , , computes , , , and sends .
- Step 2:
- According to the received message, checks and computes , . For S, generates and computes , , . Then, sends .
- Step 3:
- checks and obtains data by computing . To verify the data, checks whether is equal to .
- Correctness:
6. Security Analysis
6.1. Informal Security Analysis
6.1.1. Impersonation Attack
6.1.2. Replay and Man-in-the-Middle (MITM) Attack
6.1.3. Denial of Services (DoS) Attack
6.1.4. Mutual Authentication
6.1.5. Data Verification
6.2. Semantic Security
6.3. Formal Security Analysis Using BAN Logic
6.3.1. Rules
- Message mearning rule (MMR):
- Freshness rule (FR):
- Nonce verification rule (NVR):
- Jurisdiction rule (JR):
- Belief rule (BR):
6.3.2. Goals
- Goal 1:
- Goal 2:
- Goal 3:
- Goal 4:
6.3.3. Assumptions
- :
- :
- :
- :
- :
- :
6.3.4. Idealized Forms
- :
- :
6.3.5. Proof
- Step 1:
- can be obtained from .
- Step 2:
- can be obtained by applying the MMR with .
- Step 3:
- can be obtained by applying the FR with and .
- Step 4:
- can be obtained by applying the NVR with and .
- Step 5:
- can be obtained by applying the BR with .
- Step 6:
- can be obtained by applying the JR with and .
- Step 7:
- can be obtained from .
- Step 8:
- can be obtained by applying the MMR with .
- Step 9:
- can be obtained by applying the FR with and .
- Step 10:
- can be obtained by applying the NVR with and .
- Step 11:
- can be obtained by applying the BR with .
- Step 12:
- can be obtained by applying the JR with and .
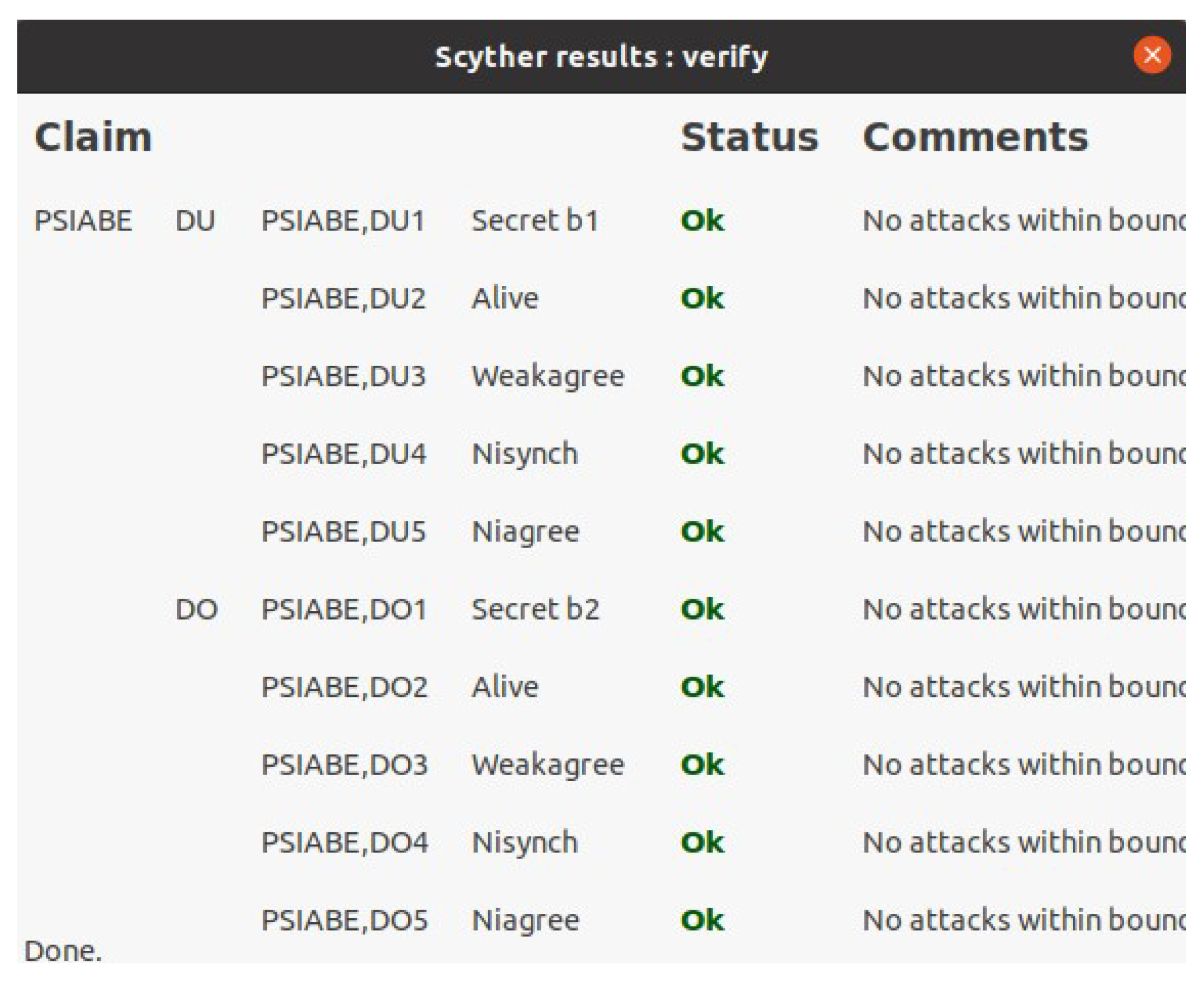
6.4. Scyther Tool
7. Comparative Analysis
7.1. Security Features
7.2. Computational Costs
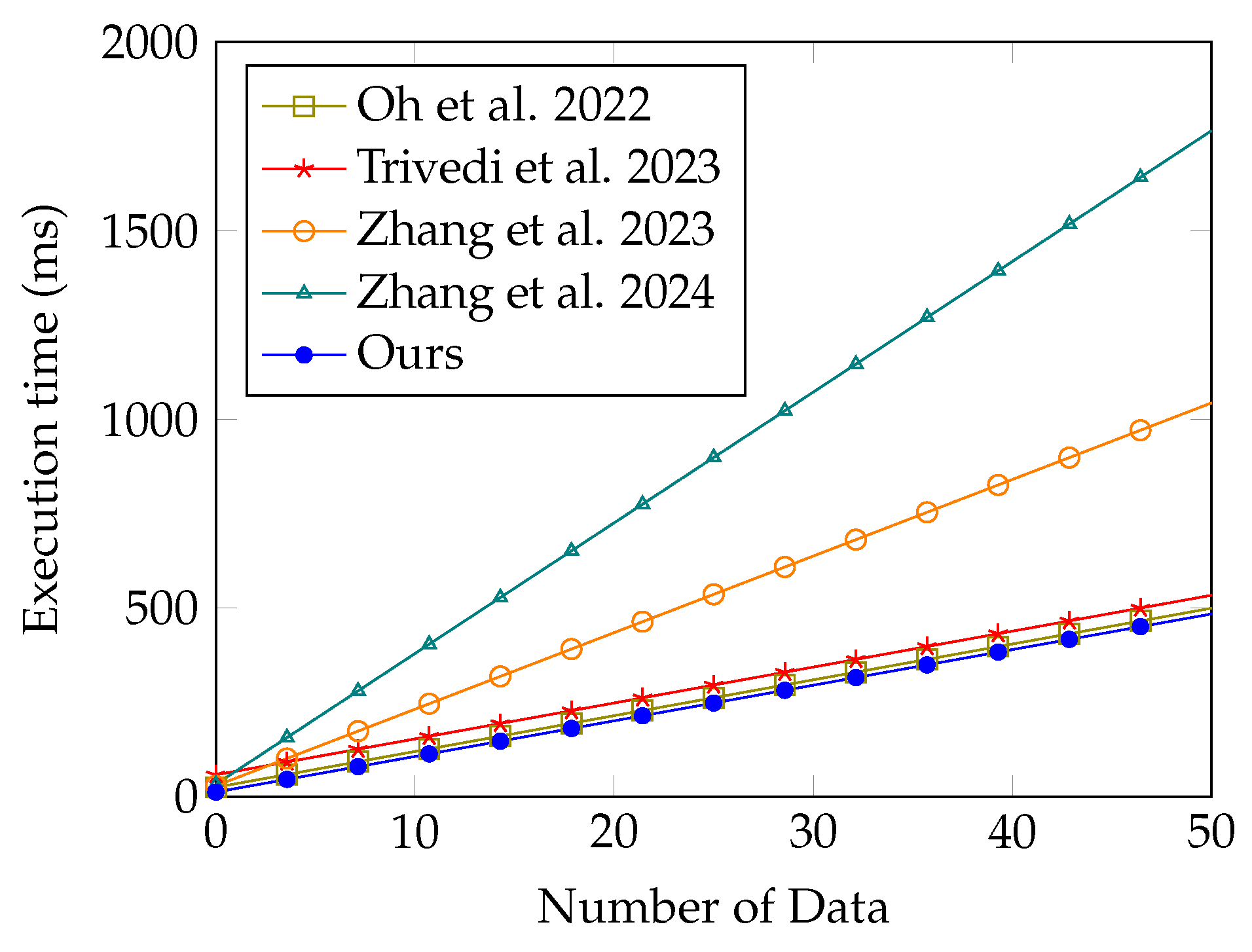
7.3. Time Complexity Comparison
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arunprasath, S.; Annamalai, S. Improving patient centric data retrieval and cyber security in healthcare: Privacy preserving solutions for a secure future. Multimed. Tools Appl. 2024, 1–31. [Google Scholar] [CrossRef]
- Wang, T.; Wu, Q.; Chen, J.; Chen, F.; Xie, D.; Shen, H. Health data security sharing method based on hybrid blockchain. Future Gener. Comp. Syst. 2024, 153, 251–261. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Liu, X.; Ma, J. An efficient blockchain-based hierarchical data sharing for Healthcare Internet of Things. IEEE Trans. Ind. Inform. 2022, 18, 7139–7150. [Google Scholar] [CrossRef]
- Khan, M.A.; Alhakami, H.; Alhakami, W.; Shvetsov, A.V.; Ullah, I. A smart card-based two-factor mutual authentication scheme for efficient deployment of an IoT-based telecare medical information system. Sensors 2023, 23, 5419. [Google Scholar] [CrossRef]
- Lee, J.; Oh, J.; Kwon, D.; Kim, M.; Kim, K.; Park, Y. Blockchain-enabled key aggregate searchable encryption scheme for personal health record sharing with multi-delegation. IEEE Internet Things J. 2024, 11, 17482–17494. [Google Scholar] [CrossRef]
- Sahai, A.; Waters, B. Fuzzy identity-based encryption. In Proceedings of the Advances in Cryptology–EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Volume 24, pp. 457–473. [Google Scholar] [CrossRef]
- Chu, C.K.; Chow, S.S.; Tzeng, W.G.; Zhou, J.; Deng, R.H. Key-aggregate cryptosystem for scalable data sharing in cloud storage. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 468–477. [Google Scholar] [CrossRef]
- Yang, L.; Li, C.; Cheng, Y.; Yu, S.; Ma, J. Achieving privacy-preserving sensitive attributes for large universe based on private set intersection. Inf. Sci. 2022, 582, 529–546. [Google Scholar] [CrossRef]
- Sucasas, V.; Mantas, G.; Papaioannou, M.; Rodriguez, J. Attribute-based pseudonymity for privacy-preserving authentication in cloud services. IEEE Trans. Cloud Comput. 2023, 11, 168–184. [Google Scholar] [CrossRef]
- Wang, H.; Liang, J.; Ding, Y.; Tang, S.; Wang, Y. Ciphertext-policy attribute-based encryption supporting policy-hiding and cloud auditing in smart health. Comput. Stand. Interfaces 2023, 84, 103696. [Google Scholar] [CrossRef]
- Oh, J.; Lee, J.; Kim, M.; Park, Y.; Park, K.; Noh, S. A secure data sharing based on key aggregate searchable encryption in fog-enabled IoT environment. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4468–4481. [Google Scholar] [CrossRef]
- Cremers, C.J. The Scyther Tool: Verification, Falsification, and Analysis of Security Protocols: Tool Paper. In Proceedings of the International Conference on Computer Aided Verification, Princeton, NJ, USA, 7–14 July 2008; pp. 414–418. [Google Scholar] [CrossRef]
- Burrows, M.; Abadi, M.; Needham, R. A logic of authentication. ACM Trans. Comput. Syst. 1990, 8, 18–36. [Google Scholar] [CrossRef]
- MIRACL Cryptographic SDK. Available online: https://github.com/miracl/MIRACL (accessed on 2 April 2024).
- Bao, Y.; Qiu, W.; Cheng, X. Secure and lightweight fine-grained searchable data sharing for IoT-oriented and cloud-assisted smart healthcare system. IEEE Internet Things J. 2022, 9, 2513–2526. [Google Scholar] [CrossRef]
- Mamta; Gupta, B.B.; Lytras, M.D. Fog-enabled secure and efficient fine-grained searchable data sharing and management scheme for IoT-based healthcare systems. In IEEE Transactions on Engineering Management; IEEE: New York, NY, USA, 2022; pp. 1–13. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, A.; Zhang, P.; Qu, Y.; Yu, S. Security-aware and privacy-preserving personal health record sharing using consortium blockchain. IEEE Internet Things J. 2022, 9, 12014–12028. [Google Scholar] [CrossRef]
- Oh, J.; Lee, J.; Kim, M.; Park, Y.; Park, K.; Noh, S. A secure personal health record sharing system with key aggregate dynamic searchable encryption. Electronics 2022, 11, 3199. [Google Scholar] [CrossRef]
- Trivedi, H.S.; Patel, S.J. Key-aggregate searchable encryption with multi-user authorization and keyword untraceability for distributed IoT healthcare systems. Trans. Emerg. Telecommun. Technol. 2023, 34, e4734. [Google Scholar] [CrossRef]
- Xu, G.; Qi, C.; Dong, W.; Gong, L.; Liu, S.; Chen, S.; Liu, J.; Zheng, X. A privacy-preserving medical data sharing scheme based on blockchain. IEEE J. Biomed. Health Inform. 2023, 27, 698–709. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Luo, X.; Fan, Q.; Wu, T.; Zhu, L. Enabling privacy-preserving multi-server collaborative search in smart healthcare. Future Gener. Comp. Syst. 2023, 143, 265–276. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, F.; Susilo, W.; Yang, G. Balancing privacy and flexibility of cloud-based personal health records sharing system. IEEE Trans. Cloud Comput. 2023, 11, 2420–2430. [Google Scholar] [CrossRef]
- Peng, G.; Zhang, A.; Lin, X. Patient-centric fine-grained access control for electronic medical record sharing with security via dual-blockchain. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2908–3921. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Li, Y.; Liu, X.; Lu, L. A blockchain-based anonymous attribute-based searchable encryption scheme for data sharing. IEEE Internet Things J. 2024, 11, 1685–1697. [Google Scholar] [CrossRef]
- Jastaniah, K.; Zhang, N.; Mustafa, M.A. Efficient user-centric privacy-friendly and flexible wearable data aggregation and sharing. In IEEE Transactions on Cloud Computing; IEEE: New York, NY, USA, 2024. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, Y.; Zhang, L.; Qiao, B.; Chen, W.; Wang, H. Attribute-based searchable encryption with decentralized key management for healthcare data sharing. J. Syst. Architect. 2024, 148, 103081. [Google Scholar] [CrossRef]
- Lai, C.; Zhang, H.; Lu, R.; Zheng, D. Privacy-preserving medical data sharing scheme based on two-party cloud-assisted PSI. IEEE Internet Things J. 2024, 11, 15855–15868. [Google Scholar] [CrossRef]
- Lax, G.; Nardone, R.; Russo, A. Enabling secure health information sharing among healthcare organizations by public blockchain. Multimed. Tools Appl. 2024, 1–17. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Patranabis, S.; Shrivastava, Y.; Mukhopadhyay, D. Dynamic key-aggregate cryptosystem on elliptic curves for online data sharing. In Progress in Cryptology, Proceedings of the INDOCRYPT 2015: 16th International Conference on Cryptology in India, Bangalore, India, 6–9 December 2015; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory (TOCT) 2014, 6, 13. [Google Scholar] [CrossRef]
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Trans. Inf. Theory 1983, 29, 198–208. [Google Scholar] [CrossRef]
- Son, S.; Lee, J.; Park, Y.; Park, Y.; Das, A.K. Design of blockchain-based lightweight V2I handover authentication protocol for VANET. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1346–1358. [Google Scholar] [CrossRef]
- Attir, A.; Naït-Abdesselam, F.; Faraoun, K.M. Lightweight anonymous and mutual authentication scheme for wireless body area networks. Comput. Netw. 2023, 224, 109625. [Google Scholar] [CrossRef]






| Notation | Description |
|---|---|
| Identity of and | |
| ’s public-master key based on ECC | |
| , | ’s public-private key pairs based on ECC and BGV |
| , | ’s public-private key pairs based on ECC and BGV |
| ’s public–private key pair based on ECC | |
| n | Maximum number of document |
| S | Dataset index of |
| Random number | |
| Random error | |
| Random nonce | |
| Timestamp | |
| Maximum transmission delay | |
| Aggregate key | |
| Additive group and multiplicative group | |
| Bilinear map | |
| h | One-way hash function |
| ⊕ | Bitwise exclusive-or operator |
| Concatenation operator |
| Notation | Description |
|---|---|
| believes statement | |
| Statement is fresh | |
| receives statement | |
| once said | |
| controls statement | |
| Statement is combined with secret statement | |
| is a secret known only to and |
| Claim Event | Description |
|---|---|
| Secrecy | Confirms that sensitive information remains confidential during communication |
| Alive | Verifies active participation of communicating parties |
| Weakagree | Checks whether the communicating participant is active user or not |
| Niagree | Ensures an implicit agreement between communicating participants |
| Nisynch | Ensures messages are exchanged in the proper order from authorized participants |
| Security Features | [18] | [19] | [22] | [24] | Ours |
|---|---|---|---|---|---|
| Replay attack | ∘ | ∘ | − | ∘ | ∘ |
| MITM attack | ∘ | ∘ | − | ∘ | ∘ |
| Impersonation attack | ∘ | ∘ | ∘ | ∘ | ∘ |
| DoS attack | ∘ | × | − | × | ∘ |
| Mutual authentication | ∘ | ∘ | × | × | ∘ |
| Data verification | ∘ | × | × | × | ∘ |
| Data Privacy | × | × | × | × | ∘ |
| Notation | Description | Execution Time |
|---|---|---|
| Bilinear pairing (: multiplicative group) | ms | |
| Exponentiation in | ms | |
| Multiplication/Division in | ms | |
| Multiplication in | ms | |
| Point addition in | ms | |
| Bilinear pairing (: additive group) | ms | |
| Exponentiation in | ms | |
| Multiplication/Division in | ms | |
| Multiplication in | ms | |
| Point addition in | ms | |
| Multiplication in | ms | |
| Addition in | ms | |
| Modular exponentiation | ms | |
| Symmetric key encryption/decryption | ms | |
| SHA-256 hash function | ms |
| Computation Cost | Communication Cost | |||||
|---|---|---|---|---|---|---|
| Scheme | Encryption | Request | Verification | Access Key | Request | Ciphertext |
| [18] | ||||||
| [19] | ||||||
| [22] | ||||||
| [24] | ||||||
| Ours | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, J.; Son, S.; Kwon, D.; Kim, M.; Park, Y.; Park, Y. Design of Secure and Privacy-Preserving Data Sharing Scheme Based on Key Aggregation and Private Set Intersection in Medical Information System. Mathematics 2024, 12, 1717. https://doi.org/10.3390/math12111717
Oh J, Son S, Kwon D, Kim M, Park Y, Park Y. Design of Secure and Privacy-Preserving Data Sharing Scheme Based on Key Aggregation and Private Set Intersection in Medical Information System. Mathematics. 2024; 12(11):1717. https://doi.org/10.3390/math12111717
Chicago/Turabian StyleOh, Jihyeon, Seunghwan Son, DeokKyu Kwon, Myeonghyun Kim, Yohan Park, and Youngho Park. 2024. "Design of Secure and Privacy-Preserving Data Sharing Scheme Based on Key Aggregation and Private Set Intersection in Medical Information System" Mathematics 12, no. 11: 1717. https://doi.org/10.3390/math12111717
APA StyleOh, J., Son, S., Kwon, D., Kim, M., Park, Y., & Park, Y. (2024). Design of Secure and Privacy-Preserving Data Sharing Scheme Based on Key Aggregation and Private Set Intersection in Medical Information System. Mathematics, 12(11), 1717. https://doi.org/10.3390/math12111717