Investigating the Dynamic Behavior of Integer and Noninteger Order System of Predation with Holling’s Response
Abstract
1. Introduction
2. Main Model and Its Mathematical Analysis
2.1. Boundness
2.2. Existence and Stability of Equilibria
- (a)
- in the case of the system of predation (4) has two nontrivial points;
- (b)
- in the case the dynamic model has a unique interior state;
- (c)
- for condition the predator–prey model has no interior steady state;
2.3. Local Bifurcation Analysis
2.3.1. Transcritical Bifurcation
2.3.2. Saddle-Node Bifurcation
2.3.3. Hopf Bifurcation
3. Fractional Predator–Prey Model of Reaction–Diffusion Type and Its Method of Approximation
Numerical Approximation Method
- given , compute with the aid of definition (55);
- define to be ;
- compute (that is, the derivative of function ) on the grid by applying (56).
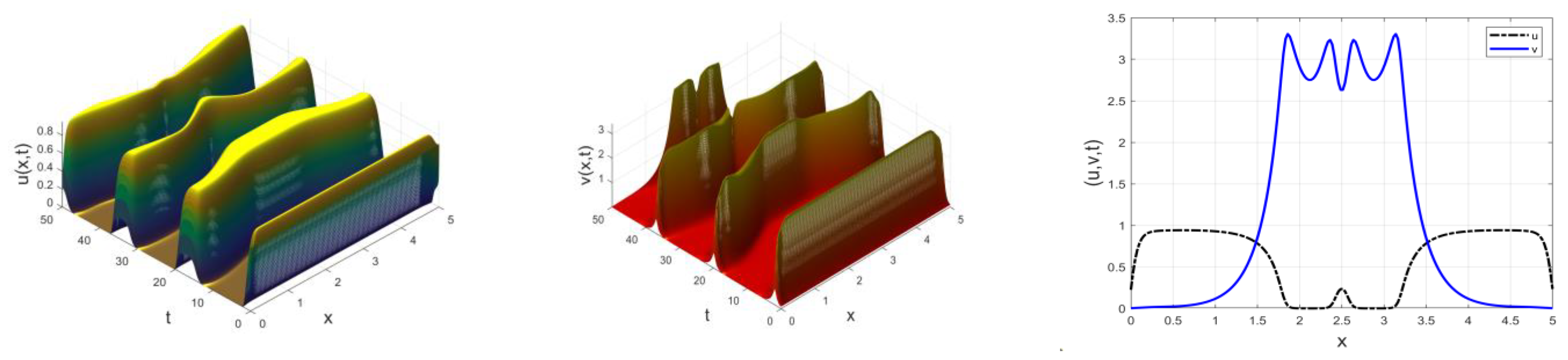
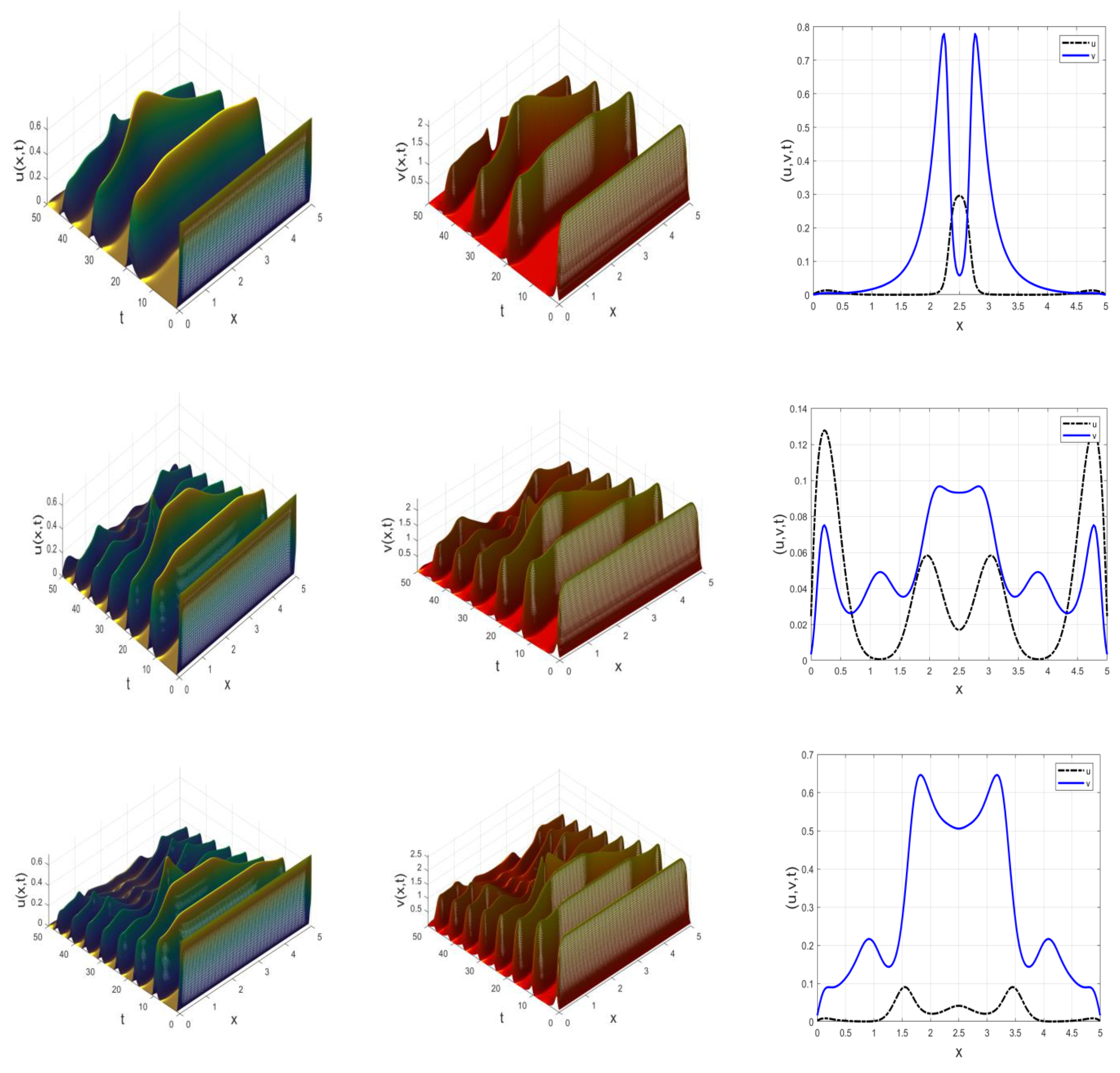
4. Numerical Experiment and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deacon, R. Fishery management by harvester cooperatives. Rev. Environ. Econ. Policy 2012, 6, 258–277. [Google Scholar] [CrossRef]
- Idels, L.; Wang, M. Harvesting fisheries management strategies with modified effort function. Int. J. Model. Identif. Control 2008, 3, 83–87. [Google Scholar] [CrossRef]
- Holling, C. The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 1965, 97, 5–60. [Google Scholar] [CrossRef]
- Freedman, H.; Wolkowicz, G. Predator-prey systems with group defence: The paradox of enrichment revisited. Bull. Math. Biol. 1968, 48, 493–508. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Xiao, D. Analyses of bifurcations and stability in a predator-prey system with Holling type-IV functional response. Acta Math. Appl. Sin. 2004, 20, 167–178. [Google Scholar] [CrossRef]
- Srinivasu, P.; Ismail, S.; Naidu, A.R. Global dynamics and controllability of a harvested prey-predator system. J. Biol. Syst. 2001, 9, 67–69. [Google Scholar] [CrossRef]
- Liu, X.; Huang, Q. The dynamics of a harvested predator-prey system with Holling type IV functional response. BioSystems 2018, 169–170, 26–39. [Google Scholar] [CrossRef] [PubMed]
- Andrews, J. A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates. Biotechnol. Bioeng. 1968, 10, 707–723. [Google Scholar] [CrossRef]
- Agrawal, O.P. Response of a diffusion-wave system subjected to deterministic and stochastic fields. J. Appl. Math. Mech. 2003, 83, 265–274. [Google Scholar] [CrossRef]
- Jain, S. Numerical analysis for the fractional diffusion and fractional Buckmaster equation by the two-step Laplace Adam-Bashforth method. Eur. Phys. J. Plus 2018, 133, 19. [Google Scholar] [CrossRef]
- Chakraborty, K.; Das, S. Biological conservation of a prey-predator system incorporating constant prey refuge through provision of alternative food to predators: A theoretical study. Acta Biotheor. 2014, 62, 183–205. [Google Scholar] [CrossRef] [PubMed]
- Zuo, W.; Jiang, D. Stationary distribution and periodic solution for stochastic predator-prey systems with nonlinear predator harvesting. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 65–80. [Google Scholar] [CrossRef]
- Upadhyaya, R.K.; Kumaria, N.; Raib, V. Wave of Chaos and Pattern Formation in Spatial Predator-Prey Systems with Holling Type IV Predator Response. Math. Model. Nat. Phenom. 2008, 3, 71–95. [Google Scholar] [CrossRef]
- Bandyopadhyay, M.; Bhattacharya, R.; Chakrabarti, C. A nonlinear two-species oscillatory system: Bifurcation and stability analysis. Int. J. Math. Math. Sci. 2003, 2003, 617217. [Google Scholar] [CrossRef]
- Barman, D.; Upadhyay, R.K. Modelling predator-prey interactions: A trade-off between seasonality and wind speed. Mathematics 2023, 11, 4863. [Google Scholar] [CrossRef]
- Guo, H.; Han, J.; Zhang, G. Hopf Bifurcation and Control for the Bioeconomic Predator-Prey Model with Square Root Functional Response and Nonlinear Prey Harvesting. Mathematics 2023, 11, 4958. [Google Scholar] [CrossRef]
- Hasibuan, A.; Supriatna, A.K.; Rusyaman, E.; Biswas, M.H.A. Predator–Prey Model Considering Implicit Marine Reserved Area and Linear Function of Critical Biomass Level. Mathematics 2023, 11, 4015. [Google Scholar] [CrossRef]
- Lv, Y.; Zhang, Z.; Yuan, R.; Pei, Y. Effect of harvesting and prey refuge in a prey-predator system. J. Biol. Syst. 2014, 22, 133–150. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, J. Qualitative analysis of a harvested predator-prey system with Holling-type III functional response. Adv. Differ. Equ. 2013, 2013, 249. [Google Scholar] [CrossRef][Green Version]
- Perko, L. Differential Equations and Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Alikhanov, A.A.; Huang, C. A high-order L2 type difference scheme for the time-fractional diffusion equation. Appl. Math. Comput. 2021, 411, 126545. [Google Scholar] [CrossRef]
- Liao, H.-L.; Tang, T.; Zhou, T. A second-order and nonuniform time-stepping maximum-principle preserving scheme for time-fractional Allen-Cahn equations. J. Comput. Phys. 2020, 414, 109473. [Google Scholar] [CrossRef]
- Liao, H.-L.; Li, D.; Zhang, J. Sharp error estimate of nonuniform L1 formula for time-fractional reaction-subdiffusion equations. SIAM J. Numer. Anal. 2018, 56, 1112–1133. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Jain, S. Spatial patterns through diffusion-driven instability in modified predator-prey models with chaotic behaviors. Chaos Solitons Fractals 2023, 174, 113839. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Agarwal, R.P.; Pindza, E.; Bernstein, S.; Osman, M.S. Complex Turing patterns in chaotic dynamics of autocatalytic reactions with the Caputo fractional derivative. Neural Comput. Appl. 2023, 35, 11309–11335. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Ren, L. A high-order l2-compact difference method for Caputo-type time-fractional sub-diffusion equations with variable coefficients. Appl. Math. Comput. 2019, 342, 71–93. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Generalized exponential time differencing methods for fractional order problems. Comput. Math. Appl. 2011, 62, 876–890. [Google Scholar] [CrossRef]
- Owolabi, K.M. Robust and adaptive techniques for numerical simulation of nonlinear partial differential equations of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 304–317. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 2014, 54, 937–954. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equation; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Dimitrov, Y. Three-point approximation for Caputo fractional derivative. Commun. Appl. Math. Comput. 2017, 31, 413–442. Available online: https://www.researchgate.net/publication/282606336 (accessed on 1 November 2023).
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Trefethen, L.N.; Embere, M. Spectral and Pseudospectra: The Behavior of Nonnormal Matrices and Operators; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owolabi, K.M.; Jain, S.; Pindza, E. Investigating the Dynamic Behavior of Integer and Noninteger Order System of Predation with Holling’s Response. Mathematics 2024, 12, 1530. https://doi.org/10.3390/math12101530
Owolabi KM, Jain S, Pindza E. Investigating the Dynamic Behavior of Integer and Noninteger Order System of Predation with Holling’s Response. Mathematics. 2024; 12(10):1530. https://doi.org/10.3390/math12101530
Chicago/Turabian StyleOwolabi, Kolade M., Sonal Jain, and Edson Pindza. 2024. "Investigating the Dynamic Behavior of Integer and Noninteger Order System of Predation with Holling’s Response" Mathematics 12, no. 10: 1530. https://doi.org/10.3390/math12101530
APA StyleOwolabi, K. M., Jain, S., & Pindza, E. (2024). Investigating the Dynamic Behavior of Integer and Noninteger Order System of Predation with Holling’s Response. Mathematics, 12(10), 1530. https://doi.org/10.3390/math12101530







