Dupin Cyclides Passing through a Fixed Circle

Abstract

Dupin cyclides are classical algebraic surfaces of low degree. Recently, they have gained popularity in computer-aided geometric design (CAGD) and architecture owing to the fact that they contain many circles. We derive algebraic conditions that fully characterize the Dupin cyclides passing through a fixed circle. The results are applied to the basic problem in CAGD of the blending of Dupin cyclides along circles.

1. Introduction

Dupin and Darboux cyclides are remarkable algebraic surfaces of degree four or three that contain many circles. They were discovered, respectively, by Charles Dupin [1] and Gaston Darboux [2] in the 19th century. Over the past few decades, they have gained popularity in computer-aided geometric design (CAGD) and architecture, making them interesting and important subjects for investigation. Dupin cyclides are used predominantly for blending surfaces along circles to model elaborate CAGD surfaces [3,4,5,6,7,8,9,10] or smoothly blending Dupin cyclides with natural quadrics and canal surfaces along the circles [11,12,13,14,15,16].

The prototypical example of a Dupin cyclide is a torus of revolution with major radius R and minor radius r. A canonical implicit equation of a torus is

$${\left(x^2+y^2+z^2+R^2-r^2\right)}^2-4R^2(x^2+y^2)=0.$$

(1)

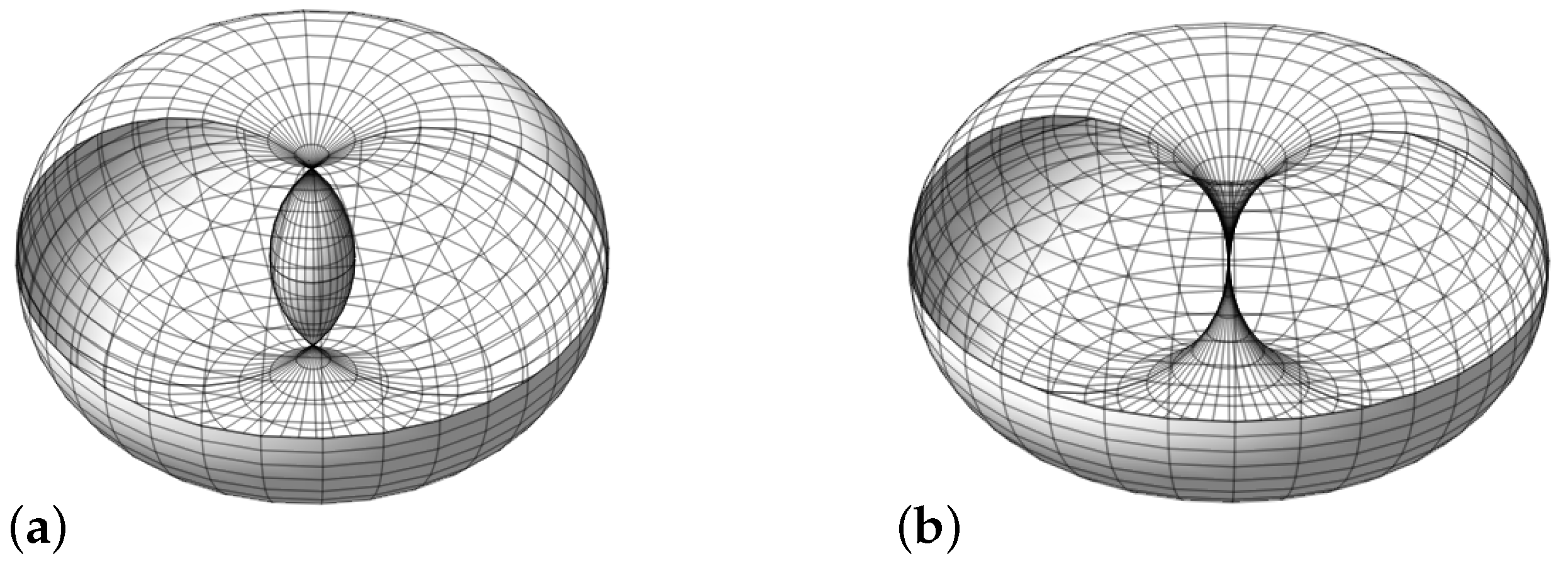
We must have $r<R$ for a smooth torus surface. A torus contains two orthogonal circles through each point. These circles are curvature lines of the torus and are called principal circles. A smooth torus has two additional circles through each point on a bitangent plane to the torus; see Figure 1a. They are called Villarceau circles [17].

A Dupin cyclide is the image of a torus under a Möbius transformation: for example, an inversion with respect to a sphere. These transformations preserve the angles and the set of circles and lines on the surfaces [18,19]. Accordingly, smooth Dupin cyclides inherit the property of having two principal circles and two Villarceau circles through each point; see Figure 1b. Some of these circles may degenerate to straight lines.

The implicit equation for a Dupin cyclide is of degree four or three and can be written in the form

$$\begin{array}{cc}\hfill a_0{\left(x^2+y^2+z^2\right)}^2& +2(b_{1}x+b_{2}y+b_{3}z)\left(x^2+y^2+z^2\right)\hfill \\ \hfill & +c_1{x}^2+c_2{y}^2+c_3{z}^2+2d_{1}yz+2d_{2}xz+2d_{3}xy\hfill \\ \hfill & +2e_{1}x+2e_{2}y+2e_{3}z+f_0=0,\hfill \end{array}$$

(2)

with some $a_0,b_1,\dots ,f_0\in \mathbb{R}$. For general values of the coefficients, this implicit equation defines a more general surface called a Darboux cyclide [20]. These cyclides typically have six circles through each point, and they are more challenging to use in geometric modeling [21]. The practical problem of distinguishing Dupin cyclides among Darboux cyclides is considered in [18].

The basic problem considered in this paper is the smooth blending of two Dupin cyclides along a fixed circle. Our approach is to match implicit equations (2) for the two Dupin cyclides we blend. To solve the basic problem algebraically, we first consider the general linear family of Darboux cyclides passing through a fixed circle. Then, we use the results in [18] to characterize the smaller family of Dupin cyclides in terms of the algebraic relations for the free coefficients of the general family of Darboux cyclides. This is considered in Section 3 together with the formulation of the main results of the paper. We prove them separately for quartic and cubic equations in Section 4 and Section 5. The smooth blending between two implicit equations of Dupin cyclides along a fixed circle is investigated in Section 6. In the last section, we express the Möbius invariant from [18] of Dupin cyclides as applied to our particular families of Dupin cyclides.

2. Preliminaries

First off, let us recall the salient results in [18] on distinguishing Dupin cyclides among Darboux cyclides. They are formulated using the following abbreviations of algebraic expressions in the coefficients in (2):

$$\begin{array}{cc}\hfill B_0=& b_1^2+b_2^2+b_3^2,\hfill \\ \hfill C_0=& c_1+c_2+c_3,\hfill \\ \hfill E_0=& e_1^2+e_2^2+e_3^2,\hfill \\ \hfill W_1=& c_1{c}_2+c_1{c}_3+c_2{c}_3-d_1^2-d_2^2-d_3^2,\hfill \\ \hfill W_2=& c_1{c}_2{c}_3+2d_1{d}_2{d}_3-c_1{d}_1^2-c_2{d}_2^2-c_3{d}_3^2,\hfill \\ \hfill W_3=& b_1^2{c}_1+b_2^2{c}_2+b_3^2{c}_3+2b_2{b}_3{d}_1+2b_1{b}_3{d}_2+2b_1{b}_2{d}_3,\hfill \\ \hfill W_4=& c_1{e}_1^2+c_2{e}_2^2+c_3{e}_3^2+2d_1{e}_2{e}_3+2d_2{e}_1{e}_3+2d_3{e}_1{e}_2.\hfill \end{array}$$

Let ${\sigma }_{12}, {\sigma }_{13}$ denote the permutations of the variables $b_1,b_2,b_3; c_1,c_2,c_3; d_1,d_2,d_3$; and $e_1,e_2,e_3$ that permute the indices $1,2$ or $1,3$, respectively.

To recognize quartic Dupin cyclides among the form (2), we can assume $a_0=1$ by dividing all coefficients by $a_0$. Then, we apply the shift

$$(x,y,z)\mapsto (x,y,z)-\frac{1}{2}(b_1,b_2,b_3)$$

(3)

to remove the cubic terms and reduce the equation to an intermediate Darboux form:

$$\begin{array}{cc}\hfill {\left(x^2+y^2+z^2\right)}^2& +c_1{x}^2+c_2{y}^2+c_3{z}^2+2d_{1}yz+2d_{2}xz+2d_{3}xy\hfill \\ \hfill & +2e_{1}x+2e_{2}y+2e_{3}z+f_0=0.\hfill \end{array}$$

(4)

Theorem 1.

The surface in ${\mathbb{R}}^3$ defined by (4) is a Dupin cyclide only if the 12 equations

$$\begin{array}{cccc}\hfill K_1=0,{\sigma }_{12}{K}_1=0,{\sigma }_{13}{K}_1& =0,\hfill & \hfill \hspace{1em}{L}_1& =0,{\sigma }_{12}{L}_1=0,{\sigma }_{13}{L}_1=0,\hfill \\ \hfill M_1=0,{\sigma }_{12}{M}_1=0,{\sigma }_{13}{M}_1& =0,\hfill & \hfill \hspace{1em}{N}_1& =0,N_2=0,N_3=0,\hfill \end{array}$$

are satisfied, where

$$\begin{array}{cc}\hfill K_1=& (c_3-c_2)e_2{e}_3+d_1(e_2^2-e_3^2)+(d_2{e}_2-d_3{e}_3)e_1,\hfill \\ \hfill L_1=& \left(W_1+4f_0-{(c_2+c_3)}^2-d_2^2-d_3^2\right)e_1\hfill \\ \hfill & +\left(C_0{d}_3+c_3{d}_3-d_1{d}_2\right)e_2+\left(C_0{d}_2+c_2{d}_2-d_1{d}_3\right)e_3,\hfill \\ \hfill M_1=& 2(c_1{e}_1+d_3{e}_2+d_2{e}_3)(W_1+4f_0)+e_1(W_2-C_0{W}_1-4E_0),\hfill \\ \hfill N_1=& \left(4W_1+12f_0-3C_0^2\right)(W_1+4f_0)-2C_0(W_2-C_0{W}_1-6E_0)-4W_4,\hfill \\ \hfill N_2=& 4(W_2-C_0{W}_1-2E_0)(W_1+4f_0)+\left(C_0^2-4f_0\right)\left(W_2+C_0{W}_1+8C_0{f}_0-4E_0\right),\hfill \\ \hfill N_3=& {\left(W_2+C_0{W}_1+8C_0{f}_0-4E_0\right)}^2-4{(W_1+4f_0)}^3.\hfill \end{array}$$

Proof. 

This result is covered by [18] (Proposition 3.6). We consider and use only the formulated necessity in the proof of the main new Theorem 3. □

Theorem 2.

The surface in ${\mathbb{R}}^3$ defined by (2) is a cubic Dupin cyclide only if the following equations are satisfied:

$$\begin{array}{cc}\hfill a_0=& 0,e_1=\frac{1}{4}{E}_1,e_2=\frac{1}{4}{\sigma }_{12}{E}_1,e_3=\frac{1}{4}{\sigma }_{13}{E}_1,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill f_0=& \frac{W_3}{4B_0^2}{\left(\frac{W_3}{B_0}-C_0\right)}^2+\frac{W_3{W}_1}{4B_0^2}+\frac{W_2-C_0{W}_1}{4B_0},\hfill \end{array}$$

(6)

where

$$\begin{array}{cc}\hfill E_1=& -\frac{b_1}{B_0}{\left(\frac{W_3}{B_0}-c_2-c_3\right)}^2+\frac{2b_1^2}{B_0^2}(b_3{c}_3{d}_2+b_2{c}_2{d}_3)-\frac{4b_1}{B_0^2}{(b_3{d}_2+b_2{d}_3)}^2\hfill \\ \hfill & +\frac{2(b_3{d}_2+b_2{d}_3)}{B_0^2}(b_2^2{c}_1+b_3^2{c}_1-2b_2{b}_3{d}_1)-\frac{2b_2{b}_3}{B_0^2}(c_2-c_3)(b_2{d}_2-b_3{d}_3)\hfill \\ \hfill & +\frac{b_1}{B_0}\left((c_1-c_2)(c_1-c_3)-d_1^2+d_2^2+d_3^2\right)+\frac{2d_1}{B_0}(b_2{d}_2+b_3{d}_3).\hfill \end{array}$$

Proof. 

This is covered by [18] (Theorem 2.4). □

3. Main Results

Without loss of generality, we assume that a fixed circle $\Gamma \subset {\mathbb{R}}^3$ with radius $r>0$ is given by the equations

$$x=0,y^2+z^2=r^2.$$

(7)

The Darboux cyclides passing through the circle $\Gamma$ form a linear subspace of the space of coefficients in (2), as we formulate in Lemma 1. Computing the variety of Dupin cyclides passing through the circle $\Gamma$ is less trivial. The defining equations are obtained by restricting the coefficients of (2) to cyclides passing through $\Gamma$ and by considering the effects on the equations in Theorems 1 and 2.

Lemma 1.

A Darboux cyclide passing through the circle Γ has an implicit equation of the form

$$\begin{array}{c}{u}_0{(x^2+y^2+z^2-r^2)}^2+2(x^2+y^2+z^2-r^2)(u_{1}x+u_{2}y+u_{3}z+u_4)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +2x\left(v_{1}x+v_{2}y+v_{3}z+v_4\right)=0,\hfill \end{array}$$

(8)

where $u_0,u_1,u_2,u_3,u_4,v_1,v_2,v_3,v_4$ are real coefficients.

Proof. 

The equation of a Darboux cyclide passing through the circle $\Gamma$ will be in the ideal generated by x and $y^2+z^2-r^2$ of the polynomial ring $\mathbb{R}\left(r\right)[x,y,z]$ over the field $\mathbb{R}\left(r\right)$. The terms of degree four and three should match the Darboux form (2). Therefore, we expand the generator $y^2+z^2-r^2$ to $x^2+y^2+z^2-r^2$ so that the quartic and cubic terms

$$u_0{(x^2+y^2+z^2-r^2)}^2+2(x^2+y^2+z^2-r^2)(u_{1}x+u_{2}y+u_{3}z),$$

are contained in the ideal of the circle $\Gamma$. The remaining terms of degree ≤2 should be in the same ideal; hence, they have the shape

$$2u_4(x^2+y^2+z^2-r^2)+2x\left(v_{1}x+v_{2}y+v_{3}z+v_4\right).$$

□

Following this lemma, the ambient-space of Darboux cyclides passing through the circle $\Gamma$ are identified as ${\mathbb{P}}^8$, with the coordinates $(u_0:\dots :u_4:v_1:\dots :v_4)$. The Dupin cyclides defined over $\mathbb{R}$ are represented by real points on an algebraic variety ${\mathcal{D}}_{\Gamma }$ in this projective space. If we consider the radius r as a variable, the variety ${\mathcal{D}}_{\Gamma }$ should be invariant under the scaling of $(x,y,z)\in {\mathbb{R}}^3$. Accordingly, the obtained equations can be checked to also be weighted-homogeneous, with weight 1 for r and the respective weights $0,1,1,1,2,2,2,2,3$ of the coordinates of ${\mathbb{P}}^8$. We assume r to be a parameter $r\ne 0$ in our proofs and computations.

We define the variety ${\mathcal{D}}_{\Gamma }$ of Dupin cyclides as a specialized image of the variety ${\mathcal{D}}_0$ in [18] (Figure 1) that represents the whole variety of Dupin cyclides within the projective family (2) of Darboux cyclides. The specialization is identified by the projective subfamily (8). The variety ${\mathcal{D}}_{\Gamma }$ turns out to be reducible and to have several components with a maximum dimension of four. Section 4 provides a brief description distinguishing those components. We are interested in the components that generically correspond to irreducible cyclide surfaces defined over $\mathbb{R}$. There are two components fulfilling this interest, which reflects the fact that the circle $\Gamma$ could be either a principal or a Villarceau circle on a Dupin cyclide; see Section 4. Accordingly, we split the main result into two Theorems as follows.

Theorem 3.

The surface in ${\mathbb{R}}^3$ defined by (8) is an irreducible Dupin cyclide containing Γ as a Villarceau circle if and only if the equations

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} v_4-2r^2{u}_1=0,& \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} v_1+2u_4-2r^2{u}_0=0,\end{array}$$

(9)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}{u}_2{v}_2+u_3{v}_3-2u_1{u}_4=0,& \hfill \hspace{1em}4r^2(u_1^2+u_2^2+u_3^2)-4u_4^2-v_2^2-v_3^2=0,\end{array}$$

(10)

and the inequality

$$u_4^2<r^2(u_2^2+u_3^2)$$

(11)

are satisfied.

Theorem 4.

The surface in ${\mathbb{R}}^3$ defined by (8) is an irreducible Dupin cyclide containing Γ as a principal circle only if the ranks of the following two matrices are equal to 1:

$$\begin{array}{cc}\hfill \mathcal{N}=& \left(\begin{array}{cc}{u}_2& v_2\\ u_3& v_3\\ u_4& v_4\end{array}\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \mathcal{M}=& \left(\begin{array}{cc}{u}_2& v_2(v_4-2r^2{u}_1)\\ u_3& v_3(v_4-2r^2{u}_1)\\ u_4& v_4(v_4-2r^2{u}_1)\\ 2u_0& v_2^2+v_3^2-4r^2{u}_1^2\\ u_1& 4r^2{u}_0{v}_4-2r^2(u_2{v}_2+u_3{v}_3)-4r^2{u}_1(v_1+u_4)\\ v_1& 4r^4(u_2^2+u_3^2+2u_0{v}_1)-4r^2{(v_1+u_4)}^2-{(v_4-2r^2{u}_1)}^2\\ v_2& -8r^4{u}_1{u}_2-4r^2{v}_2(v_1+u_4-2r^2{u}_0)\\ v_3& -8r^4{u}_1{u}_3-4r^2{v}_3(v_1+u_4-2r^2{u}_0)\\ v_4& -8r^4{u}_1{u}_4-4r^2{v}_4(v_1+u_4-2r^2{u}_0)\end{array}\right).\hfill \end{array}$$

(13)

Remark 1.

The rank conditions mean vanishing of the $2\times 2$ minors of the matrices $\mathcal{N}$ and $\mathcal{M}$. The $2\times 2$ minors from the first three rows of $\mathcal{M}$ differ from the minors of $\mathcal{N}$ by the common factor $v_4-2r^2{u}_1$. Incidentally, this factor appears as an equation for the Villarceau case. Localizing with ${(v_4-2r^2{u}_1)}^{-1}$ leads to the ideal for the principal circle case. But the Villarceau case equations of Theorem 3 do not imply a lesser rank of $\mathcal{M}$, as the second column does not necessarily vanish fully, particularly in the fourth row. Rather similarly, the $2\times 2$ minors from the last three rows of $\mathcal{M}$ differ from the minors of $\mathcal{N}$ by the common factor $-8r^4{u}_1$, as the terms $-4r^2{v}_i(v_1+u_4-2r^2{u}_0)$ are proportional to the first column. Therefore, the $2\times 2$ minors formed only by the first three rows or only by the last three rows of $\mathcal{M}$ can be ignored.

Remark 2.

The Hilbert series of the two algebraic varieties described by Theorems 3 and 4 can be computed using computer algebra systems Maple or Singular. The principal circle component of ${\mathcal{D}}_{\Gamma }$ has the Hilbert series $H_p\left(t\right)/{(1-t)}^4$, where

$$H_p\left(t\right)=1+4t+7t^2-10t^3+10t^4-5t^5+t^6.$$

(14)

Hence, the dimension of the variety equals 4, and the degree equals $H_p\left(1\right)=8$. The Zariski closure of the Villarceau circle component is a complete intersection. The Hilbert series of this component is $(1+2t+t^2)/{(1-t)}^4$. Hence, the dimension of this variety equals 4, and the degree equals 4.

4. Distinguishing Principal and Villarceau Circles

As we will analyze in Section 5, the specialized variety ${\mathcal{D}}_{\Gamma }$ of Dupin cyclides turns out to be reducible. We discard some of the components because they:

• Either represent only reducible cyclide surfaces: namely, a pair of touching spheres (where one of the spheres could be a plane or degenerates to a point); see Remark 4;
• Or generically represent cyclide surfaces with complex (rather than real) coefficients in (8); real surfaces appear only in lower-dimensional intersections with the two main families described in Theorems 3 and 4.

We claim that the two main families are distinguished by the homotopy class of $\Gamma$ as either a principal circle or a Villarceau circle. These two homotopical types can be discerned by inspecting the type of $\Gamma$ on representative surfaces under Möbius transformations (which are finite compositions of inversions). Indeed, principal circles are preserved [19] (Theorem 3.14) by Möbius transformations. The components of ${\mathcal{D}}_{\Gamma }$ are invariant under the continuous action of Möbius transformations that fix the circle $\Gamma$. As mentioned in the introduction, any Dupin cyclide can be obtained from a torus by a Möbius transformation. Further, the torus can be chosen to pass through the circle $\Gamma$ (by Euclidean similarity), and that circle can be considered as fixed. Therefore, it is enough to check the homotopy types for the toruses on both main components. Furthermore, the “vertical” principal circles (around the tube) and the “horizontal” principal circles (around the hole) can be interchanged by a Möbius transformation centered inside the torus tube; see [18] (§6.1). Hence, we consider only a fixed “vertical” principal circle in a moment.

Under Euclidean similarities, we can move the torus (1) so that the circle $\Gamma$ is a principal circle (with radius r) or a Villarceau circle (with radius R). The principal circles on the vertical plane $x=0$ are given by ${(y\pm R)}^2+z^2=r^2$. Identifying one of those circles with $\Gamma$ by the shift $y\mapsto y+R$, we obtain an equation of the form (8) with

$$\begin{array}{c}\hfill (u_0:u_1:u_2:u_3:u_4:v_1:v_2:v_3:v_4)=(1:0:-2R:0:2R^2:-2R^2:0:0:0)\end{array}$$

(15)

for the representative (under the Möbius transformations) tori with $\Gamma$ as a principal circle. It is straightforward to check that the second columns of $\mathcal{N}$ and $\mathcal{M}$ consist of zeroes for the representative tori (15), while the second and fourth equations of Theorem 3 are not satisfied generically. Hence, Theorem 4 covers the cases where $\Gamma$ is a principal circle.

Now consider a Villarceau circle of the torus (1) on the plane $z=\alpha x+\beta y$, where $\alpha =r/\varrho ,\beta =0$, $\varrho =\sqrt{R^2-r^2}$. It is moved onto $\Gamma$ by the Euclidean transformation

$$(x,y,z)\mapsto \left(\frac{rx+\varrho z}{R},r-y,\frac{rz-\varrho x}{R}\right).$$

(16)

Then the torus equation becomes

$${\left(x^2+y^2+z^2-2ry+R^2\right)}^2-4\left({(rx+\varrho z)}^2+R^2{(y-r)}^2\right)=0.$$

(17)

This identifies (8) with

$$\begin{array}{c}\hfill (u_0:u_1:u_2:u_3:u_4:v_1:v_2:v_3:v_4)=(1:0:-2r:0:2r^2:2R^2-4r^2:0:-4r\varrho :0)\end{array}$$

(18)

as an implicit equation for the representative tori with $\Gamma$ as a Villarceau circle. The representative tori (18) satisfy the equations of Theorem 3, while the rows with $u_2$ and $u_0$ in the first column form a lower-triangular matrix with non-zero determinant generically. Hence, Theorem 3 describes the cases with $\Gamma$ as a Villarceau circle.

Remark 3.

We must have $u_4^2\le r^2(u_2^2+u_3^2)$ for real points on the Villarceau circle component. Indeed, eliminating $v_3$ in (10) gives a quadratic equation for $v_2$ with the discriminant

$$16u_3^2(u_1^2+u_2^2+u_3^2)\left(r^2{u}_2^2+r^2{u}_3^2-u_4^2\right),$$

(19)

which has to be non-negative. The strict inequality (11) throws away horn cyclides; see the case $J_0=0$ in Section 7. Villarceau circles on horn cyclides coincide with “vertical" principal circles (that is, those around the tube). The Villarceau and principle circle components intersect exactly at the locus of horn Dupin cyclides on ${\mathcal{D}}_{\Gamma }$. In fact, Equations (9) and (10) together with rank $\mathcal{N}<2$ imply the equation $r^2(u_2^2+u_3^2)=u_4^2$ for horn cyclides already; then, the second column of $\mathcal{M}$ reduces to zero entries.

Remark 4.

The variety ${\mathcal{D}}_{\Gamma }$ contains a component of dimension 4 (and degree 10) that represents reducible surfaces (8) of two touching spheres (or a sphere and a tangent plane). This component is defined by the $2\times 2$ minors of the matrix

$$\begin{array}{cc}\hfill \mathcal{L}=& \left(\begin{array}{cc}{u}_2& v_2\\ u_3& v_3\\ u_4& v_4\\ u_0{v}_2& 2(u_1{v}_2-u_2{v}_1)\\ u_0{v}_3& 2(u_1{v}_3-u_3{v}_1)\\ u_0{v}_4& 2(u_1{v}_4-u_4{v}_1)\end{array}\right),\hfill \end{array}$$

(20)

and the additional equation

$$\begin{array}{c}\hfill 4r^2(u_1^2+u_2^2+u_3^2)+v_2^2+v_3^2-8v_1(r^2{u}_0-u_4)-4v_4{u}_1-4u_4^2=0.\end{array}$$

(21)

The condition rank $\mathcal{L}\le 1$ alone gives a reducible surface (8) . Its spherical (or plane) components are defined by

$$\begin{array}{c}{x}^2+y^2+z^2+sx-r^2=0,\hfill \end{array}$$

(22)

$$\begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} u_0(x^2+y^2+z^2)+(2u_1-s{u}_0)x+2u_{2}y+2u_{3}z+2u_4-r^2{u}_0=0,\hfill \end{array}$$

(23)

where $s=v_i/u_i$ for some or (usually) all $i\in \{1,2,3\}$. Equation (21) is the touching condition. The touching point is

$$(x,y,z)=-\frac{\left(s(u_2^2+u_3^2-2u_0{u}_4)+2u_1{u}_4,u_2(s{u}_1-2v_1+2u_4),u_3(s{u}_1-2v_1+2u_4)\right)}{2\left(u_1^2+u_2^2+u_3^2-2u_0{v}_1\right)}.$$

Further, we have surface degeneration to the circle Γ when $\mathrm{rank}\left(\mathcal{L}\right)=0$ and $u_1=0$, $v_1=2r^2{u}_0$. If we restrict the principal circle component to $\mathrm{rank}\left(\mathcal{L}\right)=0$, we have degeneration to a double sphere. The intersection of this degenerate component with the principal circle component represents the cases when the touching point is on Γ. The intersection with the Villarceau component represents a sphere through Γ and a point on Γ; this intersection has a lower dimension of two and is contained in the principal circle component as well.

5. Proving Theorems 3 and 4

Let us define the ring

$${\mathcal{R}}_{\Gamma }=\mathbb{R}\left(r\right)[u_1,u_2,u_3,u_4,v_1,v_2,v_3,v_4],$$

(24)

and let us denote the $2\times 2$ minors $\mathcal{N}$ as

$$\begin{array}{cc}\hfill T_2=& u_3{v}_4-u_4{v}_3,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill T_3=& u_2{v}_4-u_4{v}_2,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill T_4=& u_2{v}_3-u_3{v}_2.\hfill \end{array}$$

(27)

Let us also denote

$$\begin{array}{c}\hfill U_0=u_1^2+u_2^2+u_3^2.\end{array}$$

(28)

We define the variety ${\mathcal{D}}_{\Gamma }$ in Section 3 as the specialized image of the variety ${\mathcal{D}}_0$ in [18] (Figure 1). The variety ${\mathcal{D}}_0$, including the cubic part of Theorem 2, can be obtained from the 12 equations of Theorem 1 by applying the shift (3) backwards and homogenizing with $a_0$, as explained in [18] (§5). By straightforward Euclidean equivalence of cyclide surfaces, it is enough to consider (8) separately as a quartic equation that can be simplified by translating to (4) or as a cubic equation. Accordingly, we split the proofs into two cases and use Theorems 1 and 2 in a parallel way. We arrive at parallel options to simplify the reducible variety ${\mathcal{D}}_{\Gamma }$ from the full consideration of equations in those Theorems. Most of the particular equations or factors considered by us appear naturally in examined Gröbner bases. Even if an equation like (31) appears as an arbitrary choice, a formal proof does not have to justify the consideration.

5.1. Proof for Quartic Cyclides

Without loss of generality, we may assume $u_0=1$ while considering quartic cyclides. To apply Theorem 1, it is necessary to apply the shift (3) with $(b_1,b_2,b_3)=(u_1,u_2,u_3)$ so as to bring the cyclide equation (8) to the form (4). The obtained expression is

$$\begin{array}{cc}\hfill & {\left(x^2+y^2+z^2\right)}^2+\left(2(u_4+v_1-r^2)-u_1^2-\frac{U_0}{2}\right)x^2\hfill \\ \hfill & +\left(2(u_4-r^2)-u_2^2-\frac{U_0}{2}\right)y^2+\left(2(u_4-r^2)-u_3^2-\frac{U_0}{2}\right)z^2\hfill \\ \hfill & -2u_2{u}_{3}yz+2(v_3-u_1{u}_3)xz+2(v_2-u_1{u}_2)xy\hfill \\ \hfill & -\left(2u_1{v}_1+u_2{v}_2+u_3{v}_3-2v_4-u_1(U_0-2u_4)\right)x\hfill \\ \hfill & -\left(u_1{v}_2-u_2(U_0-2u_4)\right)y-\left(u_1{v}_3-u_3(U_0-2u_4)\right)z\hfill \\ \hfill & -\frac{3U_0^2}{16}+\frac{U_0(u_4+r^2)+u_1(u_1{v}_1+u_2{v}_2+u_3{v}_3-2v_4)}{2}-2r^2{u}_4+r^4=0.\hfill \end{array}$$

(29)

Identification with the coefficients $c_1,c_2,\dots ,f_0$ in (4) defines the ring homomorphism

$$\rho :\mathbb{R}[c_1,c_2,c_3,d_1,d_2,d_3,e_1,e_2,e_3,f_0]\to {\mathcal{R}}_{\Gamma }.$$

Let ${\mathcal{I}}_{\Gamma }\subset {\mathcal{R}}_{\Gamma }$ denote the ideal generated by the $\rho$-images of the 12 polynomials in Theorem 1. The polynomials in this ideal have to vanish when (8) is a Dupin cyclide. The polynomial $\rho \left(K_1\right)$ factors in ${\mathcal{R}}_{\Gamma }$: namely, $\rho \left(K_1\right)=-\frac{1}{4}{T}_4{V}_0$, where

$$\begin{array}{cc}\hfill V_0=& u_1^2(2u_1{u}_4-u_2{v}_2-u_3{v}_3)+(u_2^2+u_3^2-2u_4)(2u_1{u}_4+2u_1{v}_1+u_2{v}_2+u_3{v}_3-2v_4).\hfill \end{array}$$

This shows that the variety defined by ${\mathcal{I}}_{\Gamma }$ is reducible. To investigate real points of the variety, we consider three possible options: $T_4\ne 0$, $V_0\ne 0$, and $T_4=V_0=0$.

First, assume that $T_4\ne 0$. Elimination of $v_2,v_3,v_4$ gives the product $V_1{V}_2\in {\mathcal{I}}_{\Gamma }$ in the remaining variables, where

$$\begin{array}{c}\hfill V_1=v_1+2u_4-2r^2,V_2={(u_1^2+u_2^2+u_3^2-2u_4)}^2+4r^2{u}_1^2.\end{array}$$

(30)

If $V_2=0$, then $U_0-2u_4=0$, $u_1=0$ as we look only for real components. The augmented ideal contains this sum of squares: $v_4^2+r^2{V}_1^2=0$. Therefore, $V_1=0$ is inevitable for the real components with $T_4\ne 0$. The ideal ${\mathcal{I}}_{\Gamma }+\left(V_1\right)$ in ${\mathcal{R}}_{\Gamma }\left[T_4^{-1}\right]$ contains several multiples of the polynomial $V_3=v_4-2r^2{u}_1$. Localizing $V_3\ne 0$ gives the trivial ideal of ${\mathcal{R}}_{\Gamma }[T_4^{-1},V_3^{-1}]$, which is, hence, an empty variety. With $V_3=0$, we obtain the equations of Theorem 3 in the homogenized form with $u_0$. The points on the corresponding variety describe cases when $\Gamma$ is a Villarceau circle, as analyzed in Section 4.

Secondly, assume that $V_0\ne 0$. Localization of ${\mathcal{I}}_{\Gamma }$ in the ring ${\mathcal{R}}_{\Gamma }\left[V_0^{-1}\right]$ gives an ideal generated by the $2\times 2$ minors of the matrix $\mathcal{L}$ in (20) and the additional equation (21) with $u_0=1$. Here, we obtain the reducible Dupin cyclides of Remark 4.

The last option is $T_4=V_0=0$. We notice polynomial multiples of $T_2^2+T_3^2$ in the Gröbner basis of $({\mathcal{I}}_{\Gamma },T_4,V_0)$. Localization at $T_2^2+T_3^2\ne 0$ gives an ideal that contains the four polynomials of Theorem 3. Hence, it describes some points in the Villarceau circle component (of the option $T_4\ne 0$). We assume further that $T_2=T_3=0$. Consideration of the following polynomial allows further progress:

$$\begin{array}{cc}\hfill V_4=& (2r^2{u}_1+v_4)(U_0-2u_4-2v_1)-u_1(4r^2{u}_4+v_2^2+v_3^2)\hfill \\ \hfill & +(v_1-4r^2)(u_2{v}_2+u_3{v}_3)+8r^2{v}_4.\hfill \end{array}$$

(31)

The localization $V_4\ne 0$ leads to a subcase (describing touching spheres) of the option $V_0\ne 0$. Hence, we assume that $V_4=0$. Elimination of $v_2,v_3,v_4$ in the ideal $({\mathcal{I}}_{\Gamma },T_2,T_3,T_4,V_0,V_4)$ leads to some generators that factor with

$$V_5=u_1^2(u_2^2+u_3^2)+{(u_2^2+u_3^2-2u_4)}^2.$$

(32)

The further localization $V_5\ne 0$ leads to the principal circle component in Theorem 4. The remaining case $V_5=0$ splits into these two subcases, as we are interested in the real points only:

(i)

$u_1\ne 0$, so that $u_2=u_3=0$, and eventually $u_4=0$. The obtained ideal is reducible, with the prominent factor $V_6=u_1^2(v_2^2+v_3^2)+4v_4^2$ after elimination of $v_1$. The localization $V_7\ne 0$ belongs to the principal circle component. The case $V_6=0$ simplifies to $v_2=v_3=v_4=2v_1-u_1^2=0$, and the cyclide degenerates to a double-sphere case.

(ii)

$u_1=0$, $u_2^2+u_3^2-2u_4=0$. Elimination of the variables $u_1$, $u_2$, $u_3$, $u_4$ gives us a principal ideal, and the generator factors with

$$V_7={(v_2^2+v_3^2)}^3+{(v_1{v}_2^2+v_1{v}_3^2+2v_4^2)}^2.$$

(33)

The localization $V_7\ne 0$ belongs to the principal circle component. With $V_7=0$ we get $v_2=v_3=v_4=0$, and the resulting ideal contains the product ${(u_2^2+u_3^2+2v_1)}^2(u_2^2+u_3^2+2v_1-4r^2)$. Either of the factors leads to points on the principal circle component.

5.2. Proof for Cubic Cyclides

We use Theorem 2 to recognize cubic Dupin cyclides in the form (8) with $u_0=0$. The equation is first transformed to the form (2)

$$\begin{array}{c}\hfill 2(u_{1}x+u_{2}y+u_{3}z)(x^2+y^2+z^2)+2(u_4+v_1)x^2+2u_4{y}^2+2u_4{z}^2\\ \hfill +2v_{2}xy+2v_{3}xz+2(v_4-r^2{u}_1)x-2r^2{u}_{2}y-2r^2{u}_{3}z-2r^2{u}_4& =0.\hfill \end{array}$$

(34)

Let

$${\rho }_0:\mathbb{R}[b_1,b_2,b_3,c_1,c_2,c_3,d_1,d_2,d_3,e_1,e_2,e_3,f_0]\to {\mathcal{R}}_{\Gamma }.$$

be the ring homomorphism defined by the coefficient identification. Since ${\rho }_0\left(B_0\right)=U_0$, all remaining computations are considered over the localized ring ${\mathcal{R}}_{\Gamma }\left[U_0^{-1}\right]$. Let us denote by ${\mathcal{I}}_{\Gamma }^{\ast }$ the ideal generated by the numerators of the ${\rho }_0$-images of the four equations in Theorem 2. This ideal contains the product $T_4{V}_0^{\ast }$, where

$$\begin{array}{c}\hfill V_0^{\ast }=2u_1{u}_4{U}_0+2u_1{v}_1(u_2^2+u_3^2)+(u_2{v}_2+u_3{v}_3)(u_2^2+u_3^2-u_1^2).\end{array}$$

(35)

Like in the quartic case, we consider the three options: $T_4\ne 0$, $V_0^{\ast }\ne 0$, and $T_4=V_0^{\ast }=0$.

The localization $T_4\ne 0$ gives us directly the $u_0=0$ part of the Villarceau circle component in Theorem 3.

Localizing $V_0^{\ast }\ne 0$ gives an ideal containing the $2\times 2$ minors of the matrix $\mathcal{L}$ and Equation (21). This case describes only reducible cyclides of Remark 4.

With $T_4=V_0^{\ast }=0$, the ideal $({\mathcal{I}}_{\Gamma }^{\ast },T_4,V_0^{\ast })$ contains the sum of squares $T_2^2+T_3^2$. Hence, $T_2=T_3=0$ since we are looking only for real points of the variety ${\mathcal{D}}_{\Gamma }$. The further candidate for localization to consider is

$$V_1^{\ast }=4r^2{u}_1^2+v_2^2+v_3^2-4u_1{v}_4.$$

(36)

By comparing Gröebner bases, the localization of $({\mathcal{I}}_{\Gamma }^{\ast },T_2,T_3,T_4,V_0^{\ast })$ at $V_1^{\ast }\ne 0$ indeed coincides with the ideal of the principal circle defined by the $2\times 2$ minors of $\mathcal{N}$ and $\mathcal{M}$. The remaining case $V_1^{\ast }=0$ can be localized further at $V_2^{\ast }=u_2^2+u_3^2+u_4^2$. The localization $V_2^{\ast }\ne 0$ defines points on the principal circle component. The case $V_2^{\ast }=0$ simplifies to $u_2=u_3=u_4=0$, and the cyclide equation degenerates to a subcase of a touching sphere + plane case.

6. Smooth Blending of Cyclides

Here, we apply the main results to the practical problem of blending smoothly two Dupin cyclides along a common circle. Smooth blending in this context means that the cyclides share tangent planes along their common circle.

Lemma 2.

Consider two cyclide equations of the form (8) with possibly different coefficients $u_0,\dots ,u_4,v_1,\dots ,v_4$. Then they are joined smoothly along the circle Γ if and only if the rational function

$$\mathcal{F}(y,z)=\frac{v_{2}y+v_{3}z+v_4}{u_{2}y+u_{3}z+u_4}$$

(37)

is the same function on the circle Γ for both cyclides.

Proof. 

The normal vector of cyclides (8) along the circle Γ is defined by the gradient of the defining polynomial. The gradient is computed as

$$\left(v_{2}y+v_{3}z+v_4,2y(u_{2}y+u_{3}z+u_4),2z(u_{2}y+u_{3}z+u_4)\right).$$

On the two given cyclides, the paired gradient vectors should be proportional along the circle in order to obtain smooth blending. After the division by $u_{2}y+u_{3}z+u_4$, the gradient vectors are rescaled to $\left(\mathcal{F}(y,z),2y,2z\right)$ for direct comparison. □

A special case is when the rational function (37) is a constant on $\Gamma$. This is equivalent to $\mathrm{rank}\left(\mathcal{N}\right)=1$. Therefore, the rational function $\mathcal{F}$ is constant when $\Gamma$ is a principal circle case of a Dupin cyclide. As the following Lemma implies, the envelope surface of tangent planes of any cyclide equation satisfying $\mathrm{rank}\left(\mathcal{N}\right)=1$ along $\Gamma$ is a circular cone or cylinder. It is known [7] that the envelope appearing as a cone or cylinder occurs in the case of Dupin cyclides if the circle is principal. This is due to the representation of Dupin cyclides as canal surfaces, where they are considered as conics in the four-dimensional Minkowski space, and the tangent lines to those conics represent circular cones or cylinders; see [7] for details.

Lemma 3.

If the function $\mathcal{F}(y,z)\equiv \lambda$ on the circle Γ for some constant λ, then the envelope surface of tangent planes of the cyclide (8) along Γ is given by the equation

$$\begin{array}{c}\hfill y^2+z^2={\left(r-\frac{\lambda x}{2r}\right)}^2.\end{array}$$

(38)

It is a circular cone if $\lambda \ne 0$ or a cylinder if $\lambda =0$.

Proof. 

We parametrize the circle by $(0,rcos\phi ,rsin\phi )$. The envelope line passing through such a point is orthogonal to the rescaled gradient vector $\left(\lambda ,2rcos\varphi ,2rsin\varphi \right)$ and to the tangent vector $(0,-sin\varphi ,cos\varphi )$ to the circle. The line therefore follows the direction of the cross-product vector $(2r,-\lambda cos\varphi ,-\lambda sin\varphi )$. The envelope of tangent planes is parametrized therefore as

$$\begin{array}{c}\hfill (x,y,z)=(0,rcos\phi ,rsin\phi )+t(2r,-\lambda cos\phi ,-\lambda sin\phi ).\end{array}$$

(39)

Hence, $x=2rt$, $y^2+z^2={(r-\lambda t)}^2$. Elimination of t gives (38). □

Remark 5.

The envelope of tangent planes degenerates to the plane $x=0$ of the circle Γ when $\lambda =\infty$. If the circle is a Villarceau circle, then the envelope of tangent planes is a more complicated surface of degree four. As mentioned in Remark 3, the condition $\mathrm{rank}\left(\mathcal{N}\right)=1$ combined with the equations of the Villarceau component leads to singular horn cyclides. On the other hand, the cone envelope occurs also in the degenerate case of Remark 4.

6.1. Smooth Blending along Principal Circles

In this section, we focus on smooth blending between Dupin cyclides having $\Gamma$ as a principal circle. The main case to investigate is by fixing a tangent cone along the circle $\Gamma$ and finding Dupin cyclides that fit the blending conditions along the circle; see Figure 2a.

Proposition 1.

Let us fix the parameter $\lambda \ne 0$ and the cone (38) containing the circle Γ. The Dupin cyclides that join the fixed cone smoothly along Γ as a principle circle are fully characterized by the five equations

$$\begin{array}{cc}\hfill & v_2=\lambda u_2,v_3=\lambda u_3,v_4=\lambda u_4,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & 4r^2{u}_1(\lambda u_0-u_1)+{\lambda }^2(u_2^2+u_3^2)-2\lambda u_0{u}_4=0,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & 16r^4{(\lambda u_0-u_1)}^2+4{\lambda }^2{r}^2{u}_1^2-{\lambda }^2({\lambda }^2+4r^2)(u_2^2+u_3^2)-8{\lambda }^2{r}^2{u}_0{v}_1=0.\hfill \end{array}$$

(42)

Proof. 

From Lemmas 2 and 3, the tangency conditions along the circle are given by $v_i=\lambda u_i$ for $i\in \{2,3,4\}$. We specialize $u_0,v_2,v_3,v_4$ in the ideal generated by the $2\times 2$ minors of $\mathcal{N}$ and $\mathcal{M}$ and obtain an ideal ${\mathcal{I}}_{\lambda }$ in ${\mathcal{R}}_{\lambda }=\mathbb{R}\left(r\right)[u_1,u_2,u_3,u_4,v_1,\lambda ,{\lambda }^{-1}]$. We notice many multiples of $u_2,u_3,u_4$ in a Gröbner basis of ${\mathcal{I}}_{\lambda }$. If $u_2{u}_3{u}_4\ne 0$, we obtain an ideal ${\mathcal{I}}_{\lambda }^{\ast }\subset {\mathcal{R}}_{\lambda }\left[{\left(u_2{u}_3{u}_4\right)}^{-1}\right]$ generated by the five equations of the proposition. The points with $u_2{u}_3{u}_4=0$ satisfy the equations of ${\mathcal{I}}_{\lambda }^{\ast }\cup {\mathcal{R}}_{\lambda }$ by checking the cases $u_2=u_3=u_4=0$, $u_i=0,u_j{u}_k\ne 0$ or $u_i=u_j=0,u_k\ne 0$ with $i,j,k\in \{2,3,4\}$ being pairwise distinct. Each of the resulting ideals ${\mathcal{R}}_{\Gamma }[\lambda ,{\lambda }^{-1}]$ contains ${\mathcal{I}}_{\lambda }^{\ast }\cup {\mathcal{R}}_{\lambda }$. □

Remark 6.

The five equations of Proposition 1 are linear in the five variables $u_4$, $v_1$, $v_2$, $v_3$, $v_4$. Hence, we can easily solve the equations for those variables and obtain a parametrization of the family of Dupin cyclides touching the cone along the circle Γ. Apart from the first three equations, the variables $u_2,u_3$ appear only within the expression $u_2^2+u_3^2$, representing a rotational degree of freedom: rotating the two Dupin cyclide patches independently around the x-axis preserves the smooth blending along the circle Γ.

The limit cases $\lambda =0$ and $\lambda =\infty$ contain interesting families of Dupin cyclides as well. The family with $\lambda =0$ allows us to blend two toruses or a torus with a Dupin cyclide; see Figure 2b–d. The family in the case $\lambda =\infty$ allows us to blend a Dupin cyclide with a plane; see Figure 2e.

Proposition 2.

Let us fix the cylinder defined by the parameter $\lambda =0$ in (38). The only Dupin cyclides that join this cylinder smoothly along Γ are characterized by the equations

$$\begin{array}{cc}\hfill & u_1=v_2=v_3=v_4=0,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & 2r^2{u}_0{v}_1+r^2(u_2^2+u_3^2)-{(v_1+u_4)}^2=0.\hfill \end{array}$$

(44)

Those Dupin cyclides are symmetric with respect to plane $x=0$ of the circle Γ.

Proof. 

The equations $v_2=v_3=v_4=0$ follow from the condition $\lambda =0$ and the tangent conditions in Lemma 2. With those constraints, the ideal of the principal circle component reduces to the other two equations $u_1=0$ and (44). The symmetry property with the plane $x=0$ follows from Equation (43). □

Proposition 3.

Let us fix the plane $x=0$ (of the circle Γ) defined by the parameter $\lambda =\infty$ in (38). The only Dupin cyclides that join this plane smoothly along the circle Γ are characterized by the equations

$$\begin{array}{cc}\hfill & u_2=u_3=u_4=0,v_4=2r^2{u}_1,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & 16r^4{u}_0^2+4r^2{u}_1^2-(v_2^2+v_3^2)-8r^2{u}_0{v}_1=0.\hfill \end{array}$$

(46)

This family of Dupin cyclides is preserved by the reflection with respect to the plane of the circle.

Proof. 

Similar to the proof of Proposition 2. The equations $u_2=u_3=u_4=0$ follow from the tangent condition $\lambda =\infty$, and the ideal of the principal circle component reduces to the other two equations of the proposition. The reflection $(x,y,z)\mapsto (-x,y,z)$ with respect to the plane $x=0$ preserves the coefficients $u_0,u_2,u_3,u_4,v_1$ and symmetries $u_1,v_2,v_3,v_4$ to $-u_1,-v_2,-v_3,-v_4$ in (8). This transformation preserves Equations (45) and (46). □

Remark 7.

The cubic cyclides with $u_0=0$ in the family of Proposition 3 degenerate to reducible surfaces: namely, the cases of touching sphere + plane.

It is interesting to distinguish torus surfaces in the principal circle component. We get two cases depending on the position of the circle $\Gamma$ (wrapping around the torus hole or around the torus tube). Figure 2c,d illustrate two different configurations of torus blending using those two kinds of principal circles. The circle wraps around the torus tube of both toruses in Figure 2c. The circle wraps around the torus tube for one torus and around the torus hole for the other torus in Figure 2d. The examples satisfy the pertinent algebraic conditions exactly; this article does not consider the issue of numerical stability.

Proposition 4.

Equation (8) defines a torus having Γ as the principal circle if and only if one of the following applies:

(i) 

$u_0=1,u_2^2+u_3^2=2u_0{u}_4,v_1=-u_4,v_2=v_3=v_4=0$;

(ii) 

$u_0=1,u_2=u_3=v_2=v_3=0$, ${\displaystyle u_4=\frac{2r^2{u}_1(\lambda -u_1)}{{\lambda }^2}}$,

${\displaystyle v_1=\frac{{\lambda }^2{u}_1^2+4r^2{(\lambda -u_1)}^2}{2{\lambda }^2}}$, ${\displaystyle v_4=\lambda u_4=\frac{2r^2{u}_1(\lambda -u_1)}{\lambda }}$.

Proof. 

Assume that the circle $\Gamma$ is wrapping around the torus tube. Then we have a tangent cylinder along the circle, defined by $v_2=v_3=v_4=0$ as in Proposition 2. The cross section of (8) with the plane $x=0$ is a pair of circles with the same radius $(\Gamma ,{\Gamma }^{\prime })$:

$${\Gamma }^{\prime }:x={\left(y+\frac{u_2}{u_0}\right)}^2+{\left(z+\frac{u_3}{u_0}\right)}^2-\frac{r^2{u}_0^2-2u_0{u}_4+u_2^2+u_3^2}{u_0^2}=0.$$

We need $u_2^2+u_3^2=2u_0{u}_4$ for the equality of radii. Equation (44) then factors into $(v_1+u_4)(v_1+u_4-2r^2{u}_0)$. Due to the rotations in the $yz$-plane that preserve the circle $\Gamma$, we can assume that the revolution axis of the torus is parallel to the z-axis. Then $u_3=0$, and we say $u_2=\sqrt{2u_0{u}_4}$. Note that $u_0{u}_4>0$ by the derived equation $u_2^2+u_3^2=2u_0{u}_4$. The rotated cyclide equation must be

$$u_0{\left(x^2+{\left(y-\sqrt{\frac{u_4}{2u_0}}\right)}^2+z^2-r^2+\frac{u_4}{2u_0}\right)}^2-2u_4{\left(y-\sqrt{\frac{u_4}{2u_0}}\right)}^2+2v_1{x}^2=0.$$

(47)

Comparing with (1), we recognize a torus equation (with shifted y) when $v_1=-u_4$. The other option $v_1=2r^2{u}_0-u_4$ gives a surface that is not symmetric around the revolution axis; hence, that is not a torus. This shows possibility (i).

Assume now that the circle $\Gamma$ is wrapping around the torus hole. Then we have a tangent cone along the circle, i.e., $v_2=\lambda u_2$, $v_3=\lambda u_3$, $v_4=\lambda u_4$ as in Proposition 1. The section with $x=0$ should be a pair of concentric circles. Hence, $u_2=u_3=0$. Again, with $u_0=1$ and the parametrization in Proposition 1, the cyclide equation reduces to

$$\begin{array}{c}\hfill {\left({\left(x+\frac{u_1}{2}\right)}^2+y^2+z^2+\frac{r^2{(\lambda -u_1)}^2}{{\lambda }^2}-\frac{u_1^2({\lambda }^2+4r^2)}{4{\lambda }^2}\right)}^2-\frac{4r^2{(\lambda -u_1)}^2}{{\lambda }^2}(y^2+z^2)=0.\end{array}$$

This is a torus equation, comparable to (1). □

6.2. Smooth Blending along Villarceau Circles

By Remarks 3 and 5, it is not possible to smoothly blend a Dupin cyclide that has $\Gamma$ as a principle circle with a Dupin cyclide that has $\Gamma$ as a Villarceau circle. It is left to investigate blending between cyclides in the Villarceau circle component. The following result is illustrated in Figure 2f.

Proposition 5.

Let D denote a Dupin cyclide (8) that has Γ as a Villarceau circle. The only Dupin cyclides that join D smoothly along Γ are obtained by perturbing the equation of D by

$${(x^2+y^2+z^2-r^2)}^2+4r^2{x}^2.$$

Those cyclides have Γ as a Villarceau circle.

Proof. 

Let $D^{\prime }=(u_0:u_1^{\prime }:\dots :u_4^{\prime }:v_1^{\prime }:\dots :v_4^{\prime })$ be a Dupin cyclide that has $\Gamma$ as a Villarceau circle and assume that $D^{\prime }$ and D are smoothly blending along the circle $\Gamma$. We obtain the matrix equation:

$$\left(\begin{array}{cccccccc}0& 0& 0& 2& 1& 0& 0& 0\\ -2r^2& 0& 0& 0& 0& 0& 0& 1\\ 0& r^2{v}_2& 0& v_4& 0& -r^2{u}_2& 0& -u_4\\ 0& 0& r^2{v}_3& v_4& 0& 0& -r^2{u}_3& -u_4\\ 0& v_3& v_2& 0& 0& -u_3& -u_2& 0\\ 0& v_4& 0& v_2& 0& -u_4& 0& -u_2\\ 0& 0& v_4& v_3& 0& 0& -u_4& -u_3\end{array}\right)\left(\begin{array}{c}{u}_1^{\prime }\\ u_2^{\prime }\\ u_3^{\prime }\\ u_4^{\prime }\\ v_1^{\prime }\\ v_2^{\prime }\\ v_3^{\prime }\\ v_4^{\prime }\end{array}\right)=\left(\begin{array}{c}2r^2{u}_0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right).$$

The first two rows of the matrix are linear equations obtained from $D^{\prime }$ being in the Villarceau circle component. The last five rows are the tangency conditions for the given Dupin cyclide D from Lemma 2. Note that the $7\times 8$ matrix has the full rank seven symbolically. We must have $v_i\ne 0$ for some $i\in \{2,3,4\}$ to avoid rank $\mathcal{N}<2$ and degeneracy to a horn cyclide. Then, by setting $s=u_i^{\prime }/v_i$, we can solve

$$\begin{array}{cc}\hfill u_j^{\prime }& =s{u}_j,v_j^{\prime }=s{v}_j,\mathrm{for} j\in \{2,3,4\},\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill u_1^{\prime }& =s\frac{v_4}{2r^2}=s{u}_1,v_1^{\prime }=2r^2{u}_0-2s{u}_4.\hfill \end{array}$$

(49)

After dividing the equation of $D^{\prime }$ by s, all coefficients are fixed except $v_1^{\prime }=2r^2{u}_0/s-2u_4$, and $u_0$ becomes $u_0/s$. Hence, with $t=u_0/s-u_0$, $u_0$ and $v_1^{\prime }$ become $u_0+t$ and $2r^2{u}_0-2u_4+2r^{2}t=v_1+2r^{2}t$, respectively. This is exactly a perturbation by amount t. □

7. The Möbius Invariant ${\mathit{J}}_{\mathbf{0}}$

In this section, we compute a Möbius invariant denoted by $J_0$ [18] (Section 6) for Dupin cyclides in the Villarceau and principal circle components described by Theorems 3 and 4, respectively. This invariant extends the Möbius invariant

$$J_0=\frac{r^2}{R^2}\left(1-\frac{r^2}{R^2}\right)$$

(50)

for toruses to the Dupin cyclides. The smooth Dupin cyclides are characterized by $0<J_0\le 1/4$, and the singular Dupin cyclides are characterized by $J_0\le 0$. A singular Dupin cyclide can be obtained from a spindle or a horn torus (see Figure 3) by Möbius transformations.

We use [18] ((6.15) and (6.17)) to compute $J_0$ for, respectively, the quartic equation (8) with $u_0\ne 0$ and the cubic equation (8) with $u_0=0$. The obtained expression gives the Möbius invariant when the equation defines a Dupin cyclide. It is convenient to subtract $1/4$ from $J_0$ and obtain a perfect square expression frequently. Let us denote by ${\widehat{J}}_0$ the remainder $1/4-J_0$. The goal is to have a compact equivalent formula for $J_0$ in each of the two components.

Obtaining a $J_0$-expression for quartic Dupin cyclides in the principal circle case is not straightforward. Consider the ideal ${\mathcal{I}}_{\lambda }$ generated by the five equations of Proposition 1. By incorporating separately the numerator and the denominator of ${\widehat{J}}_0$ in the ideal ${\mathcal{I}}_{\lambda }$ and by eliminating the linear variables $u_4,v_1,\dots ,v_4$, we obtain a representative numerator and a representative denominator with a common factor. This gives a new expression of ${\widehat{J}}_0$ up to a constant multiplier. It is easy to find this constant by solving it from the difference of the two expressions of ${\widehat{J}}_0$ modulo ${\mathcal{I}}_{\lambda }$. The resulting $J_0$ expression is

$$\begin{array}{c}\hfill J_0=\frac{1}{4}-\frac{{\left(8r^4{(\lambda u_0-u_1)}^2-4r^2({\lambda }^2+4r^2)u_1^2+{\lambda }^2({\lambda }^2+2r^2)(u_2^2+u_3^2)\right)}^2}{16r^4{\left(4r^2{(\lambda u_0-u_1)}^2-{\lambda }^2(u_2^2+u_3^2)\right)}^2}.\end{array}$$

(51)

By further elimination of $u_2^2+u_3^2$ using (41)–(42), we obtain the more compact form

$$\begin{array}{c}\hfill J_0=\frac{1}{4}-\frac{{\left(4r^4\lambda u_0-2r^2({\lambda }^2+6r^2)u_1+\lambda ({\lambda }^2+2r^2)u_4\right)}^2}{16r^4{\left(2r^2\lambda u_0-2r^2{u}_1-\lambda u_4\right)}^2}.\end{array}$$

(52)

It is interesting that this compact form (52) also covers the $J_0$ expression of the family of cubic Dupin cyclides $u_0=0$ in Proposition 1.

Since the majority of Dupin cyclides in the principal circle component belong to the family of Dupin cyclides in Proposition 1, three equivalent expressions for $J_0$ in the principal circle component are obtained by substituting $\lambda =v_i/u_i$ into (52) for each $i=2,3,4$. The equality of two different $J_0$ expressions can be checked by reducing the numerator of the difference between them modulo the ideal of the principal circle component.

In the two limiting cases of Propositions 2 and 3 of the principal circle component, we use the same method and obtain the expression

$$\begin{array}{c}\hfill J_0=\frac{1}{4}-\frac{{(4r^2{u}_0-4u_4-3v_1)}^2}{4v_1^2}\end{array}$$

(53)

for the family $\lambda =0$ of Proposition 2, and

$$\begin{array}{c}\hfill J_0=\frac{1}{4}-\frac{{(3r^2{u}_0-v_1)}^2}{4r^4{u}_0^2}\end{array}$$

(54)

for the family $\lambda =\infty$ of Proposition 3. Note that the latter formula is always well-defined because the family of Proposition 3 does not contain irreducible cubic Dupin cyclides by Remark 7.

In the Villarceau circle case, the simplification of $J_0$ in [18] (6.15) modulo the equations (9) and (10) is straightforward. Elimination of $v_2$, $v_3$, and $v_4$ gives a common factor of the numerator and the denominator and leads to the expression

$$\begin{array}{c}\hfill J_0=\frac{r^2{u}_2^2+r^2{u}_3^2-u_4^2}{16(r^2{u}_2^2+r^2{u}_3^2-u_4^2)+4v_1^2}.\end{array}$$

(55)

Alternative eliminations give

$$\begin{array}{cc}\hfill J_0& =\frac{1}{4}-\frac{r^2{v}_1^2}{4\left(r^2(v_1^2+v_2^2+v_3^2)-v_4^2\right)},\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill & =\frac{1}{4}-\frac{v_1^2}{16r^2\left(u_2^2+u_3^2+u_0{v}_1-r^2{u}_0^2\right)}.\hfill \end{array}$$

(57)

These expressions are applicable to cubic Dupin cyclides as well. The invariant values should be positive because singular cyclides have no real Villarceau circles. Indeed, the numerator in (55) is positive by the inequality $u_4^2<r^2{u}_2^2+r^2{u}_3^2$ in (11). The denominator is positive as well from the same condition. The limiting case $u_4^2=r^2{u}_2^2+r^2{u}_3^2$ of Theorem 3 represents horn cyclides since $J_0=0$ from (55), as mentioned in Remark 3.

8. Conclusions

This paper derives the algebraic conditions that fully characterize the general family of Dupin cyclides passing through the fixed circle (7). The algebraic conditions restrict the coefficients of the general family (8) of Darboux cyclides passing through the circle. The main results are divided to Theorems 3 and 4, which reflect the position of the circle as either a Villarceau circle or a principal circle of the Dupin cyclides. The two obtained general families are four-dimensional; see Remark 2. The main results can be applied to check whether a particular surface (8) is a Dupin cyclide or to generate parametric families of Dupin cyclides (by considering subvarieties of ${\mathcal{D}}_{\Gamma }$).

The found algebraic conditions are used in Section 6 to characterize and exemplify pairs of Dupin cyclides that blend smoothly along circles. The construction of smooth blending constitutes the basic application of Dupin cyclides in CAGD. The focal case of smooth blending requires fixing a tangent cone along the circle (7), which reduces the dimension of general families of smoothly matching Dupin cyclides to three; see Proposition 1. Even if we would like to join two Dupin cyclides continuously along a circle at a constant angle [9], the straightforward way of modeling is to fix the tangent cones meeting at the desired angle. This leads to choosing within two distinct families of Dupin cyclides in the context of Section 6. The $J_0$-invariant of Section 7 determines (up to Möbius transformations) the proportions of a whole Dupin cyclide.

Using implicit equations like (8) rather than parametrizations amounts to an alternative technique of blending cyclides. Like in [18], the algebraic conditions on implicit equations for Dupin cyclides are quite non-linear. Their derivation and concise presentation required particular earnestness and attention. The derivation in Section 5 was facilitated by the computer algebra systems Maple 2018 and Singular 4.2.1, employment of a Gröbner basis, elimination and localization techniques, and syzygy computations [22].

Future work may establish blending routines of using implicit equations for Dupin cyclides and compare their practicability, efficiency, and accuracy to existing parametrization techniques [3,4,5,6,7,8]. The results could be applied to uniformize investigation of blending Dupin cyclides at two fixed circles or on fixed spheres, cones, or cylinders [11,12,13,14,15,16].