On V-Geometric Ergodicity Markov Chains of the Two-Inertia Systems

Abstract

This study employs the diffusion process to construct Markov chains for analyzing the common two-inertia systems used in industry. Two-inertia systems are prevalent in commonly used equipment, where the load is influenced by the coupling of external force and the drive shaft, leading to variations in the associated output states. Traditionally, the control of such systems is often guided by empirical rules. This paper examines the equilibrium distribution and convergence rate of the two-inertia system and develops a predictive model for its long-term operation. We explore the qualitative behavior of the load end at discrete time intervals. Our findings are applicable not only in control engineering, but also provide insights for small-scale models incorporating dual-system variables.

1. Introduction

Two-inertia systems [1,2,3], as shown in Figure 1, have always been an important model for the miniaturization or simplification of rotating systems, especially the coupling of two-inertia systems involving nonlinear models [2]. For example, the common quarter car model of automotive suspension systems is used to construct active or semi-active suspension systems. Similarly, when satellites perform solar charging or communication, they require attitude control. In these cases, the two-inertia model is often adopted for modeling, analysis, and compensation. In vibration control of robot systems [4], or for vibration suppression control between floors in buildings, two-inertia systems are also frequently used for diagnosis and analysis. Therefore, a large number of industrial applications and research involving interactions with large servo motor-driven load systems can be conducted within the framework of relevant two-inertia system applications and theories. For instance, Wang et al. [5] proposed an improved adaptive neural control algorithm for a nonlinear two-inertia servo mechanism with rotational backlash, which has been validated through experiments. Yokokura & Ohnishi [6] introduced a load-side acceleration control method for two-inertia systems, utilizing torque sensors to suppress resonance vibrations. This method has been proven effective for controlling load-side acceleration through both theoretical analysis and experiments. Kawai et al. [7] suggested a high-robustness force control method for changes in environmental stiffness, based on the duality of two-inertia systems. Traditional force control methods do not consider variations in environmental stiffness, leading to instability when stiffness changes. To achieve higher robust stability, Kawai et al. [7] proposed a high-robustness force control method based on the duality of two-inertia systems, validated by numerical simulations and experiments for their robustness against environmental stiffness changes. Jung et al. [8] proposed a new iterative feedback tuning method for cascade control in two-inertia systems. This method included position and speed errors in the cost function, and has been proven effective under various conditions through experiments.

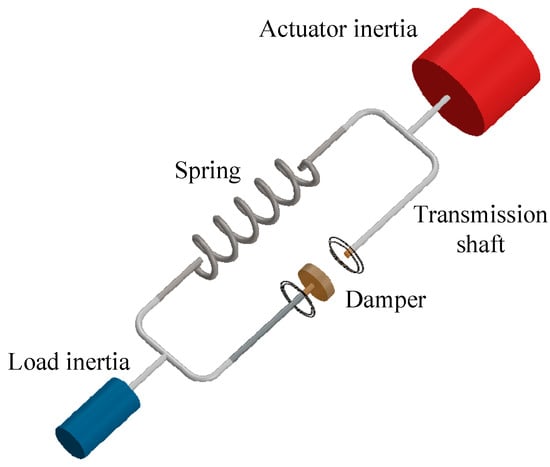
Figure 1. Two-inertia system.

Ideally, two-inertia systems represent a linear, time-invariant model and a causal system. Therefore, the system’s response can easily be predicted, whether dynamically or in a steady state, through the solutions of governing equations. However, real physical systems, especially mass-produced products, often have issues such as defect rates or early failure. Hence, employing probabilistic statistical models to provide these types of two-inertia systems with an additional “anomaly prediction” warning has become an important function and contribution of stochastic control, extending into LTI (linear time-invariant) systems in recent years. In stochastic process [9,10,11,12], Markov chains can be used to model issues such as system performance degradation, stability, and system aging [13,14]. Krishnamoorthy & Kozyrev [15] conducted a novel analysis of the system by simulating the dwell time in states using semi-Markov rules and exponential distributions, through the transformation of the product space of three Markov chains. Wang et al. [16] established a joint optimization model for emergency engineering equipment maintenance and spare parts inventory strategy considering demand priority. They derived system performance indicators using Markov process embedding methods.

As a result, stochastic modeling has received considerable attention in industrial applications in recent years. In this study, a Markov chain is constructed to describe a two-inertia system using diffusion processes. This paper refers to the theory of [17] to study the equilibrium distribution and convergence speed of the two-inertia system. The two-inertia system can be applied to many common large or small facilities in daily life. As the load will be subjected to external forces and the nonlinearity of the drive shaft, there will be a gap between the output speed state and the actuator speed state. In practice, such nonlinear drops are often compensated by rules of thumb. This study uses probabilistic modeling to explore the qualitative behavior of the load at each discrete time and describes it from the perspective of stochastic control.

2. Existence of Invariant Measure

In this study, suppose that a diffusion ${\left\{S_t\right\}}_{t\ge 0}$ on $(0,\infty )$ drives the rotational speed of a motor in a two-inertia system with a generator [18]:

$$L=\frac{1}{2}\sigma {\left(x\right)}^2\frac{d^2}{d{x}^2}+b\left(x\right)\frac{d}{dx},$$

where $\sigma (x)$ and $b(x)$ are both continuous, and $\sigma (x)>0$ for all $x\in \left(0,\infty \right)$; and ${\rho }^{\pm }(x)$ denotes the limitation of a load with ${\rho }^{-}(x)<x<{\rho }^{+}(x)$. In general, the expression of operators L often adopts the approach of $Lf=\frac{1}{2}\sigma {\left(x\right)}^2\frac{d^{2}f}{d{x}^2}+b\left(x\right)\frac{df}{dx}$, where the function $f\left(x\right)$ belongs to a proper function space. However, in the field of stochastic processes, the $L=\frac{1}{2}\sigma {\left(x\right)}^2\frac{d^2}{d{x}^2}+b\left(x\right)\frac{d}{dx}$ approach is predominantly used. The operator L, along with initial conditions, determines the solution of ${\left\{S_t\right\}}_{t\ge 0}$ diffusion. Herein, the coefficient variation of $\sigma (x)$ represents the variability of motor speed, while the drift term of $b(x)$ represents the drift of motor speed. We then construct a homogeneous Markov chain ${\left\{X_n\right\}}_{n=0}^{\infty }$ with state space $(0,\infty )$ as follows. The transition probability $p\left(x,dy\right)$ of ${\left\{X_n\right\}}_{n=0}^{\infty }$ is defined by:

$$p\left(x,dy\right)=P_x\left(S_{1\wedge {\tau }^{+}\wedge {\tau }^{-}}\in dy\right), {\tau }^{+}=\inf \left\{t\ge 0:S_t={\rho }^{+}(x)\right\}, {\tau }^{-}=\inf \left\{t\ge 0:S_t={\rho }^{-}(x)\right\},$$

where $S_0=x$. We use ${\left\{X_n\right\}}_{n=0}^{\infty }$ to express the rotational speed of a load. Referring to [14], we obtain that ${\left\{X_n\right\}}_{n=0}^{\infty }$ is irreducible. Let

$$s(x)={\displaystyle {\int }_1^x\exp \left\{-I(y)\right\}}dy,$$

(1)

where

$$I\left(y\right)={\displaystyle {\int }_1^y\frac{2b(z)}{\sigma {(z)}^2}dz}.$$

Then $s(x)$ is increasing on $(0,\infty )$. Let $s^{-1}(x)$ be the inverse function of $s(x)$.

Assumption 1.

Assume that $\sigma (x)$ and $b(x)$ fulfill the following

$$\underset{x\to \infty }{\lim }s(x)=\infty and \underset{x\to -\infty }{\lim }s(x)=-\infty .$$

Substituting ${\left\{S_t\right\}}_{t\ge 0}$ into $s(x)$, we obtain the diffusion ${\left\{s\left(S_t\right)\right\}}_{t\ge 0}$, which takes value on $(-\infty ,\infty )$, and its generator becomes $\frac{d^2}{m(x)d{x}^2}$, where

$$m(x)=\frac{2}{\sigma {\left(s^{-1}(x)\right)}^2}\exp \left\{2I\left(s^{-1}(x)\right)\right\}.$$

(2)

In addition, ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ also takes value on $(-\infty ,\infty ).$

In order to clarify the asymptotic behavior of the whole process, firstly, we present the following definitions.

Definition 1

([10]). ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ is said to possess an invariant finite measure $\pi \left(\cdot \right)$, if, and only if, for any positive integer $n$ and any Borel set $A$ of $(-\infty ,\infty )$,

$${\displaystyle {\int }_{-\infty }^{\infty }{P}_y\left(X_n\in A\right)\pi \left(dy\right)}=\pi \left(A\right).$$

Assume that ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ possesses the invariant measure $\pi \left(\cdot \right)$. Given a twice differentiable function $V:R\to [1,\infty )$ with $\underset{x\to \pm \infty }{\lim }V\left(x\right)=\infty$, set ${‖f‖}_V=\underset{x\in R}{\sup }\frac{\left|f\left(x\right)\right|}{V\left(x\right)}$:

$$C_V=\left\{f:f \mathrm{is} \mathrm{a} \mathrm{continuous} \mathrm{function} \mathrm{with} \mathrm{domain} R \mathrm{and} {‖f‖}_V<\infty \right\}$$

Define the operator $T$ as follows:

$$Tf\left(x\right)=E_{x}f\left(s\left(X_1\right)\right) \mathrm{and} {‖T^n-\pi ‖}_V=\underset{f\in C_V}{\sup }\underset{x\in R}{\sup }\frac{\left|T^{n}f\left(x\right)-\pi \left(f\right)\right|}{V\left(x\right)}.$$

Definition 2

([17]). We call ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ a “V -geometrical ergodicity Markov chain”, if, and only if, there exists the $\rho$ such that

$${‖T^n-\pi ‖}_V=O\left({\rho }^n\right) \mathit{as} n\to \infty .$$

Assumption 2.

Assume that $s\left({\rho }^{+}(x)\right)=2x$ and $s\left({\rho }^{-}(x)\right)=0.5x$ for $x>0$. On the other hand, $s\left({\rho }^{+}(x)\right)=0.5x$ and $s\left({\rho }^{-}(x)\right)=2x$ for $x<0$, where $s\left(x\right)$ is defined in Equation (1).

Assumption 3.

Assume that $\alpha >2$ and $m(x)$ defined in Equation (2) satisfies

$$c_1{\left|x\right|}^{-\alpha }\le m(x)\le c_2{\left|x\right|}^{-\alpha }, \mathit{for} \left|x\right|\ge M,$$

where $c_1$, $c_2$, and $M$ are all positive constants and $M>1$.

Result 1.

Assume that Assumptions 2 and 3 hold. For the same $M$ in Assumption 2, if a twice differentiable function $V\left(x\right)$ on $R$ satisfies $V\left(x\right)=\sqrt{x}$ for $\left|x\right|>M$ and $V\left(x\right)=1$ for $\left|x\right|\le M$, and if ${\rho }^{+}(x)$ and ${\rho }^{-}(x)$ satisfy Assumption 2, then there exist positive constants $H$ and $\lambda$ such that $TV\left(x\right)\le H+\lambda V\left(x\right)$ for all $x\in R$.

Proof. 

Let $\psi \left(x\right)=V\left(x\right)-1$. It is easy to see $\underset{x\to \infty }{\lim }\psi \left(x\right)=\infty$ and for $x>M>1$,

$$\frac{d^2\psi \left(x\right)}{m(x)d{x}^2}=-\frac{1}{4}\times x^{-1.5}\times \frac{1}{m\left(x\right)}\le -\frac{1}{4}\times x^{0.5}\times x^{\alpha -2}\times \frac{1}{c_1}\le -\frac{1}{4c_1}\times x^{0.5}=-\frac{1}{4c_1}\psi \left(x\right),$$

given that $x>1$ and $-x^{\alpha -2}\le -1$. Taking $C=1$ and $\theta =\frac{1}{4c_1}$, we obtain

$$\frac{d^2\psi \left(x\right)}{m(x)d{x}^2}\le C-\theta \psi \left(x\right) \mathrm{for} x>M.$$

On the other hand, since $-\psi \left(x\right)=-\sqrt{x}$ is a convex function on $x>M$, we have

$$\frac{0.5}{1.5}\times 2^{0.5}+\frac{1}{1.5}\times {0.5}^{0.5}<{\left(\frac{0.5}{1.5}\times 2+\frac{1}{1.5}\times 0.5\right)}^{0.5}=1,$$

which implies

$$\begin{array}{l}\frac{\psi \left({\rho }^{+}(x)\right)}{\psi (x)}{Q}^{+}\left(1,x\right)+\frac{\psi \left({\rho }^{-}(x)\right)}{\psi (x)}{Q}^{-}\left(1,x\right)\\ =2^{0.5}{Q}^{+}\left(1,x\right)+{0.5}^{0.5}{Q}^{-}\left(1,x\right)\le 2^{0.5}\times \left(1-e^{-\theta }\right)\times \frac{0.5}{1.5}+{0.5}^{0.5}\times \left(1-e^{-\theta }\right)\times \frac{1}{1.5}\\ =\left(1-e^{-\theta }\right)\left(\frac{0.5}{1.5}\times 2^{0.5}+\frac{1}{1.5}\times {0.5}^{0.5}\right)<1-e^{-\theta },\end{array}$$

where

$$Q^{+}\left(1,x\right)=E_x\left\{1-e^{-(1-{\tau }^{+})\theta }:{\tau }^{+}\le {\tau }^{-},{\tau }^{+}\le 1\right\},$$

$$Q^{-}\left(1,x\right)=E_x\left\{1-e^{-(1-{\tau }^{-})\theta }:{\tau }^{-}\le {\tau }^{+},{\tau }^{-}\le 1\right\}.$$

In consequence, the conditions of Lemma 4.3 of [13] (Appendix A) are satisfied. This reveals that there exist positive constants $H$ and $\lambda$ such that $TV\left(x\right)\le H+\lambda V\left(x\right)$ for all $x\in R$. This completes the proof. □

Result 2.

Under Assumptions 1 and 3, ${\left\{s\left(S_t\right)\right\}}_{t\ge 0}$ possess the invariant finite measure $m\left(x\right)dx$. Namely, for any $t\ge 0$ and any Borel set $A$ of $(-\infty ,\infty )$, we have

$${\displaystyle {\int }_{-\infty }^{\infty }{P}_y\left(S_t\in A\right)m\left(y\right)dy}={\displaystyle {\int }_{A}m(y)dy}.$$

Proof. 

The reader can refer to Elliott’s theorem in [18] for the existence of the invariant measure. Herein, we can apply Theorem 12.2 of [10] (Appendix D), and the desired result is immediately obtained. This completes the proof. □

Result 3.

Let $\Xi =[-1,1]$ and

$\nu \left(A\right)=\underset{x\in \Xi }{\inf }{P}_x\left(s\left(S_1\right)\in A,\tau >1\right)$, then $\nu \left(\cdot \right)$ is a positive measure such that $\nu \left(1_{\Xi }\right)>0$ and

$$P_x\left(s\left(X_1\right)\in A\right)\ge 1_{\Xi }\left(x\right)\nu \left(A\right),$$

for any Borel subset $A$ of $R$ and $x\in R$, where $\tau ={\tau }^{+}\wedge {\tau }^{-}$.

Proof. 

Since $P_x\left(s\left(X_1\right)\in A\right)=P_x\left(s\left(S_{1\wedge {\tau }^{+}\wedge {\tau }^{-}}\right)\in A\right)$, it is clear that

$$P_x\left(s\left(X_1\right)\in A\right)=P_x\left(s\left(S_1\right)\in A,\tau >1\right)+p_d\left(x,A\right),$$

where

$$p_d\left(x,A\right)=P_x\left({\tau }^{+}\le {\tau }^{-},{\tau }^{+}\le 1\right)1_{\left\{s\left({\rho }^{+}(x)\right)\right\}}\left(A\right)+P_x\left({\tau }^{-}\le {\tau }^{+},{\tau }^{-}\le 1\right)1_{\left\{s\left({\rho }^{-}(x)\right)\right\}}\left(A\right).$$

Denote $u(x,A)=P_x\left(s\left(S_1\right)\in A,\tau >1\right)$ with fixed $A$, and view $u\left(x,A\right)$ as a function of $x$. It is clear that $u\left(x,A\right)$ is continuous on $\Xi$ because ${\left\{s\left(S_t\right)\right\}}_{t\ge 0}$ is a diffusion. Analogously, with fixed $x$, view $u\left(x,A\right)$ as a measure of $A$. It is clear that $u\left(x,A\right)$ is a positive measure. Since $\Xi$ is a compact set, we obtain that $\nu \left(\cdot \right)$ is a positive measure. Moreover, we have

$$\begin{array}{ll}{P}_x\left(s\left(X_1\right)\in A\right)& =P_x\left(s\left(S_1\right)\in A,\tau >1\right)+p_d\left(x,A\right)\\ & \ge P_x\left(s\left(S_1\right)\in A,\tau >1\right)\ge \nu \left(A\right),\end{array}$$

for $x\in \Xi$. Finally, view $P_x\left(s\left(S_1\right)\in \Xi ,\tau >1\right)$ as a function of $x$. It is well-known that $P_x\left(s\left(S_1\right)\in \Xi ,\tau >1\right)$ is continuous and

$$P_x\left(s\left(S_1\right)\in \Xi ,\tau >1\right)>0,$$

for $x\in R$. Since $\Xi =[-1,1]$ is a closed subset of $R$, this completes the proof. □

3. Main Findings

3.1. Conditions in Which ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ Possesses an Invariant Measure $\pi$

Regarding seeking conditions of ${\rho }^{+}(x)$ and ${\rho }^{-}(x)$ such that ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ possesses an invariant measure, we obtained the following result.

Result 4.

Under Assumptions 1 and 3, if ${\rho }^{+}(x)$ and ${\rho }^{-}(x)$ satisfy Assumption 2, then ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ possesses a unique invariant probability measure $\pi \left(\cdot \right)$ and $\pi \left(V\right)<\infty$, where $V\left(x\right)$ is defined in Result 1.

Proof. 

Since ${\rho }^{+}(x)$ and ${\rho }^{-}(x)$ satisfy Assumption 2, we have

$$-\infty =\underset{x\to -\infty }{\lim \sup } {\rho }^{+}(x)<\underset{x\to \infty }{\lim \inf } {\rho }^{-}(x)=\infty .$$

Moreover, we obtain

$$\begin{gathered} \underset{x\to \infty }{\lim \inf } x^{-s}\left\{{\rho }^{+}(x)-x\right\}=\underset{x\to \infty }{\lim \inf } 2x^{1-s}>0, \\ \underset{x\to \infty }{\lim \inf } x^{-s}\left\{x-{\rho }^{-}(x)\right\}=\underset{x\to \infty }{\lim \inf } 0.5x^{1-s}>0, \end{gathered}$$

$\underset{x\to -\infty }{\lim \inf } {\left|x\right|}^{-s}\left\{{\rho }^{+}(x)-x\right\}=\underset{x\to -\infty }{\lim \inf } 0.5{\left|x\right|}^{1-s}>0$, $\underset{x\to -\infty }{\lim \inf } {\left|x\right|}^{-s}\left\{x-{\rho }^{-}(x)\right\}=\underset{x\to -\infty }{\lim \inf } 2{\left|x\right|}^{1-s}>0$, for $s\in \left(0.5,1\right)$. By means of Theorem 3.3 in [13] (Appendix B), we obtain that ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ is a positive recurrent whose definition is defined in [13]. It yields that ${\left\{s\left(X_n\right)\right\}}_{n=0}^{\infty }$ possesses a unique invariant measure $\pi \left(\cdot \right)$. Furthermore, combining this with Assumptions 1 and 3, we get that all conditions of Theorem 3.5 hold in [13] (Appendix C). This yields $\pi \left(V\right)<\infty$, which implies

$$\begin{array}{ll}\infty >\pi \left(V\right)& ={\displaystyle {\int }_R{E}_{x}V\left(s\left(X_n\right)\right)}\pi \left(dx\right)\\ & ={\displaystyle {\int }_R{\displaystyle {\int }_{R}V\left(y\right)P_x\left(s\left(X_1\right)\in dy\right)}}\pi \left(dx\right)\\ & \ge {\displaystyle {\int }_R{\displaystyle {\int }_{R}V\left(y\right)v\left(dy\right)}}\pi \left(dx\right)=v\left(V\right).\end{array}$$

in terms of Result 3. This completes the proof. □

3.2. Approximation of $\pi$ by Utilizing Finite-Rank Operator

In order to approximate $\pi$, we refer to [17] and utilize the positive finite-rank operators combined with the Krein-Rutman theorem [19] to complete it.

Result 5.

Under Assumptions 1 and 3, if ${\rho }^{+}(x)$ and ${\rho }^{-}(x)$ satisfy Assumption 2, then $\pi \left(\cdot \right)$ in Result 4 has the following representation

$$\pi \left(\cdot \right)=\pi \left(1_{\Xi }\right){\displaystyle \sum _{k=1}^{\infty }{\beta }_k}\left(\cdot \right),$$

where ${\beta }_1\left(\cdot \right)=\nu \left(\cdot \right)$ and $k\ge 2$,

$${\beta }_k\left(f\right)=\nu \left(T^{k-1}f\right)-{\displaystyle \sum _{i=1}^{k-1}\nu \left(T^{k-i-1}{1}_{\Xi }\right)}{\beta }_i\left(f\right),$$

for any $f\in C_V$.

Proof. 

By Results 1 and 3, we see that Assumption (D) and (M) in [17] (Appendix E) hold. Therefore, the representation of $\pi \left(\cdot \right)$ is immediately obtained from [17]. This completes the proof. □

4. Evaluation of $\mathit{\rho }$

By means of Definition 2, to evaluate $\rho$, it suffices to compute $\underset{n\to \infty }{\lim }{\left\{{‖T^n-\pi ‖}_V\right\}}^{\frac{1}{n}}$.

Result 6.

Under Assumptions 1 and 3, if ${\rho }^{+}(x)$ and ${\rho }^{-}(x)$ satisfy Assumption 2, then

$$0<\underset{n\to \infty }{\lim }{\left\{{‖T^n-\pi ‖}_V\right\}}^{\frac{1}{n}}\le \min \left\{\ln \sqrt{2},\frac{\lambda v\left(1_R\right)+\tau }{v\left(1_R\right)+\tau }\right\},$$

where $\lambda$ and $H$ are defined in Result 1, $v(\cdot )$ is defined in Result 3, $\tau =\max \left\{0,H-v\left(V\right)\right\}$.

Proof. 

Since ${\rho }^{+}(x)$, ${\rho }^{-}(x)$ and $m(x)$ satisfy Assumptions 2 and 3, respectively, we obtain that $\beta =0.5$, $c_{-}=0.5$, and $d_{+}=0.5$, and the conditions of Theorem 2.4 in [14] (Appendix F) hold. This immediately leads to:

$$\underset{n\to \infty }{\lim }{\left\{{‖T^n-\pi ‖}_V\right\}}^{\frac{1}{n}}\le \ln \sqrt{2}.$$

(3)

This completes the proof. □

5. Simulations

In this section, we verify the most important result, Result 6, through a numerical simulation. We wish to compare $\underset{n\to \infty }{\lim }{\left\{{‖T^n-\pi ‖}_V\right\}}^{\frac{1}{n}}$ with $\ln \sqrt{2}$. Suppose that ${\left\{s\left(S_t\right)\right\}}_{t\ge 0}$ is the Ornstein–Uhlenbeck process, which satisfies $s\left(S_t\right)=e^{-t}s\left(S_0\right)+{\displaystyle {\int }_0^t{e}^{-\left(t-s\right)}d{B}_s}$, where ${\left\{B_t\right\}}_{t\ge 0}$ is a standard Brownian motion. Set $X_0=100$, ${\rho }^{+}(x)=2x$, ${\rho }^{-}(x)=0.5x$ for $x>0$. Take $V(x)=\sqrt{1+\left|x\right|}$. By means of Theorem 3.5 in [13] (Appendix C), we can use $\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(X_i\right)}$ to represent $T^{n}f$ and $\pi \left(f\right)$ due to

$$\underset{n\to \infty }{\lim }\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(X_i\right)}=\underset{n\to \infty }{\lim }{T}^{n}f \mathrm{and} \underset{n\to \infty }{\lim }\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(X_i\right)}=\pi \left(f\right).$$

Note that $f\left(x\right)=\sqrt{\left|x\right|}$. In the following, the simulation result is based on 1000 iterations. Figure 2 shows the main simulation result. In this figure, the x-axis represents the number of interactions, and the y-axis represents the error value of $\left|T^{n}f-\pi \left(f\right)\right|$. The red dashed line represents $y=\ln \sqrt{2}\doteq 0.347$, while the blue solid line represents $\left|T^{n}f-\pi \left(f\right)\right|$. Figure 2 demonstrates that the estimation of $\mathrm{Error}={\left\{{‖T^n-\pi ‖}_V\right\}}^{\frac{1}{n}}$ for $n=1000$ using the upper bound $\ln \sqrt{2}\doteq 0.347$ is valid, i.e., Equation (3) holds.

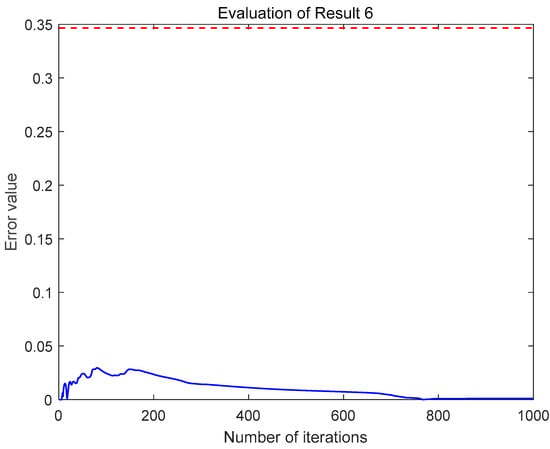
Figure 2. Numerical simulation.

6. Conclusions

Generally speaking, two-inertia systems can be applied in many common processes in daily life. Because the load will be affected by the external force and the transmission shaft, there exists a gap between the speed of the load and the actuator. In practice, rules of thumb are usually employed for compensation. However, these are not clear for user guidance. Therefore, this paper intended to discuss the qualitative behavior of the inherent state in the form of probabilistic modeling from a cross-domain perspective, so as to provide a control reference for relevant applications of such systems.

Essentially, this study constructs discrete-time Markov chains ${\left\{X_n\right\}}_{n=0}^{\infty }$ from a continuous-time diffusion process ${\left\{S_t\right\}}_{t\ge 0}$ by incorporating load constraints of ${\rho }^{-}(x)<x<{\rho }^{+}(x)$, resulting in two-inertia systems. This study first investigates the conditions for Markov chains ${\left\{X_n\right\}}_{n=0}^{\infty }$ with limiting distributions $\pi \left(\cdot \right)$. Subsequently, it explores the rate at which Markov chains ${\left\{X_n\right\}}_{n=0}^{\infty }$ converge to the limiting distribution $\pi \left(\cdot \right)$, which involves estimating the value of $\rho$.

Using the approach outlined in Herve & Ledoux, this study expresses the mathematical form of the limiting distribution $\pi \left(\cdot \right)$. The most noteworthy aspect is the estimation of the value of $\rho$, which outperforms the results of previous studies. Through numerical simulation, the effectiveness of this study has been confirmed. In the future, the discrete-time Markov chains constructed in this study ${\left\{X_n\right\}}_{n=0}^{\infty }$ can be utilized to integrate relevant control applications for more two-inertia systems, thereby facilitating the development of new technologies.