Optimal Control for an Epidemic Model of COVID-19 with Time-Varying Parameters
Abstract
1. Introduction
- (i)
- Undetected infections are considered.
- (ii)
- The parameter identification method to estimate the time-varying transmission rate functions in the epidemic model is employed.
- (iii)
- The optimal control measures for different infection peaks are shown.
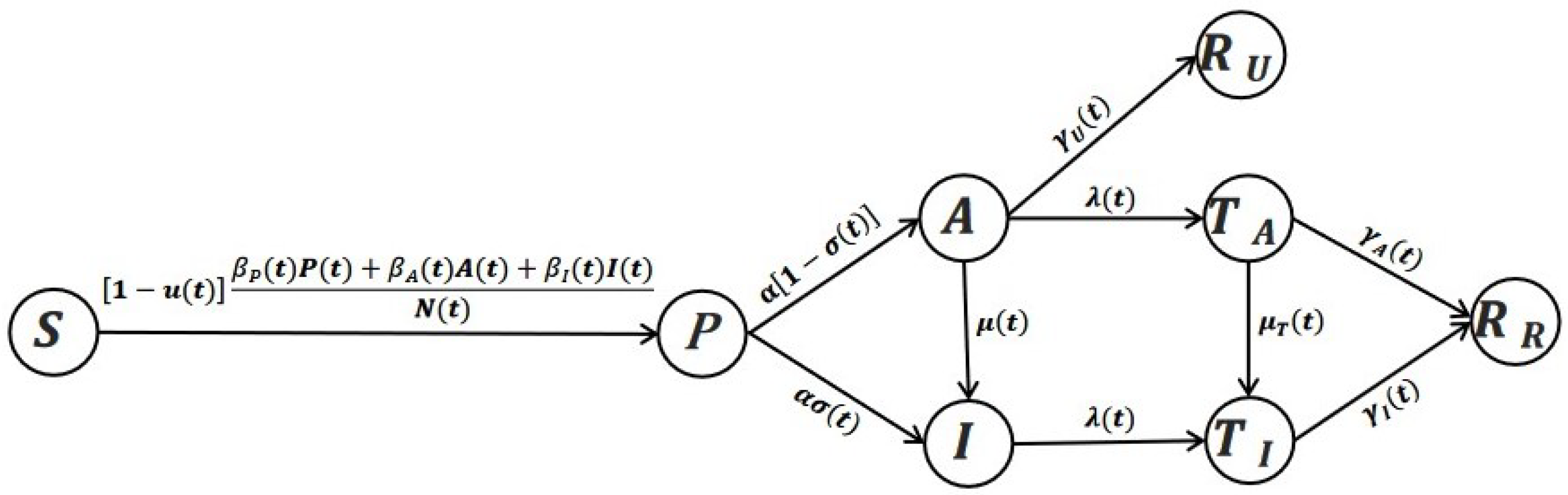
2. COVID-19 Control System
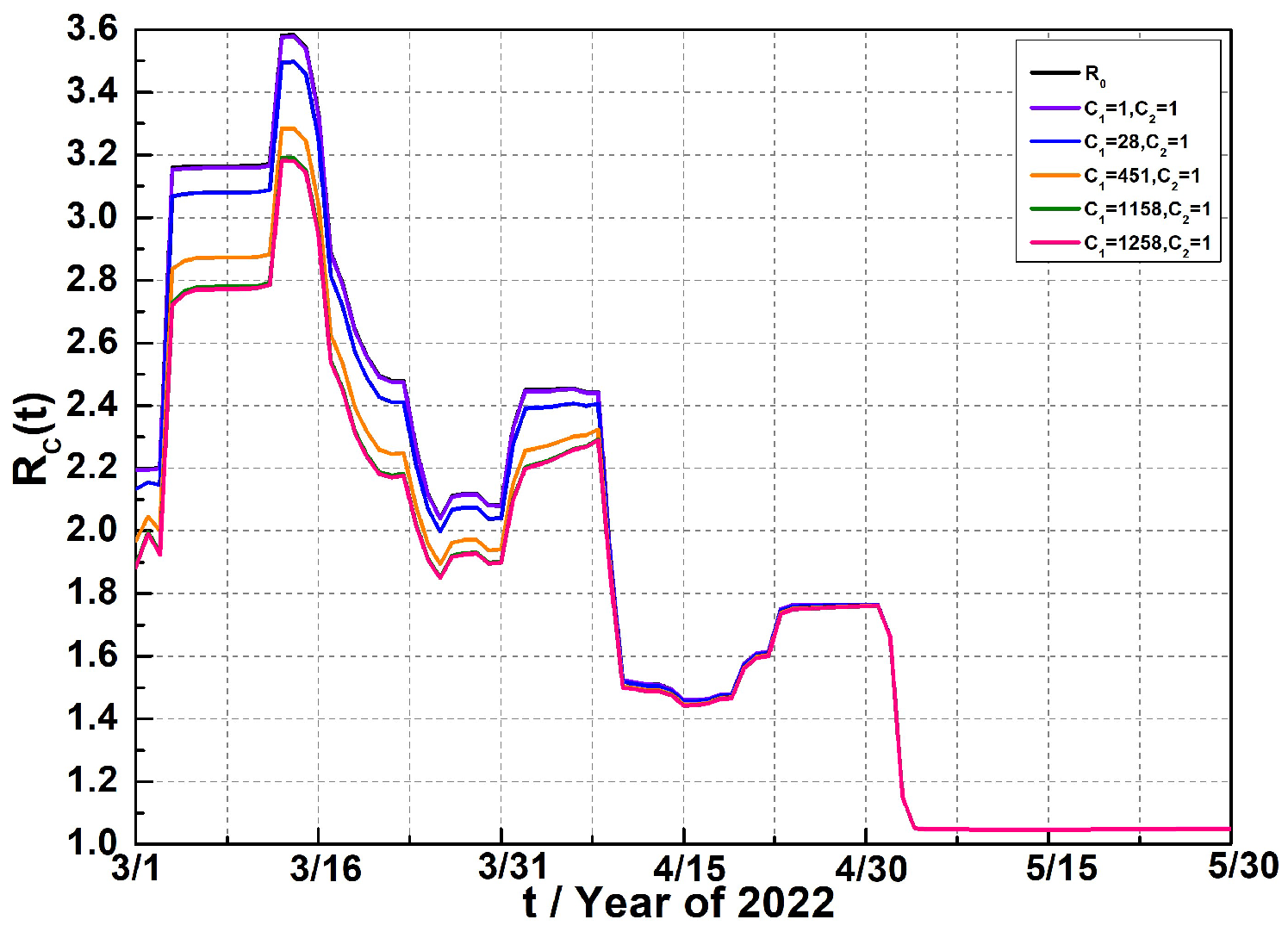
2.1. Control Reproduction Number
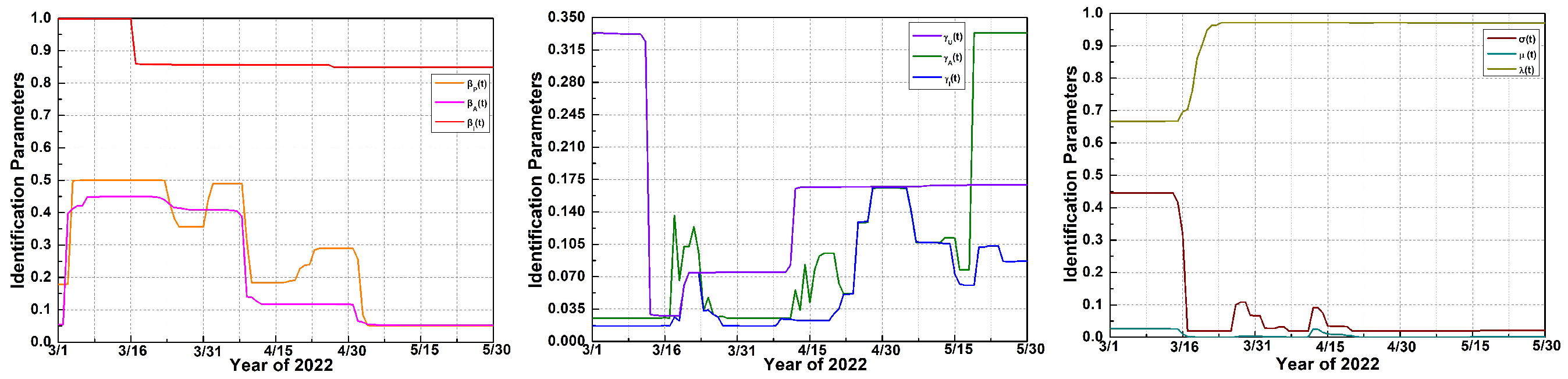
2.2. Parameter Identification
- Step 1°.
- Guess
- Step 2°.
- Divide the interval into m segments: Introduce the following objective functional:
- Step 3°.
- Randomly generate groups of initial valuesLet denote the kth iteration identification variable by the ith initial value Set .
- Step 4°.
- For every use the interior algorithm to solve the problem (NIP), and obtain
- Step 5°.
- From the groups of choose groups which satisfy the constraint conditions and take them as the initial population. Letbe the lth iteration identification variable. Set
- Step 6°.
- Use the genetic algorithm to solve the problem (NIP), and find Judge whether the stop condition is satisfied: if output the optimal solution otherwise, set
3. Optimal Control Problem
4. Numerical Results
4.1. Data Description and Parameter Value
4.2. Parameter Identification
4.3. Optimal Control
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pei, S.; Yamana, T.K.; Kandula, S.; Galanti, M.; Shaman, J. Burden and characteristics of COVID-19 in the United States during 2020. Nature 2021, 598, 338–341. [Google Scholar] [CrossRef] [PubMed]
- Walker, P.G.T.; Whittaker, C.; Watson, O.J.; Baguelin, M.; Winskill, P.; Hamlet, A.; Djafaara, B.A.; Cucunuba, Z.; Mesa, D.; Green, W. The impact of COVID-19 and strategies for mitigation and suppression in low-and middle-income countries. Science 2020, 369, 413–422. [Google Scholar] [CrossRef]
- Khan, Y.; Verhaeghe, N.; Devleesschauwer, B.; Cavillot, L.; Gadeyne, S.; NPauwels, S.; Van den Borre, L.; De Smedt, D. Impact of the COVID-19 pandemic on delayed care of cardiovascular diseases in Europe: A systematic review. Lancet 2023, 402, S61. [Google Scholar] [CrossRef] [PubMed]
- Opel, D.J.; Brewer, N.T.; Buttenheim, A.M.; Callaghan, T.; Carpiano, R.M.; Clinton, C.; Elharake, J.A.; Flowers, L.C.; Galvani, A.P.; Hotez, P.J.; et al. The legacy of the COVID-19 pandemic for childhood vaccination in the USA. Lancet 2023, 401, 75–78. [Google Scholar] [CrossRef] [PubMed]
- Ziauddeen, N.; Pantelic, M.; O’Hara, M.E.; Hastie, C.; Alwan, N.A. Impact of long COVID-19 on work: A co-produced survey. Lancet 2023, 402, S98. [Google Scholar] [CrossRef] [PubMed]
- Ogbuoji, O.; Mao, W.; Aryeetey, G. The long-term impact of COVID-19 on development assistance for health is still uncertain. Lancet 2021, 398, 1280–1281. [Google Scholar] [CrossRef] [PubMed]
- Cooper, B.S.; Evans, S.; Jafari, Y.; Pham, T.M.; Mo, Y.; Lim, C.; Pritchard, M.G.; Pople, D.; Hall, V.; Stimson, J.; et al. The burden and dynamics of hospital-acquired SARS-CoV-2 in England. Nature 2023, 623, 132–138. [Google Scholar] [CrossRef]
- Jassat, W.; Reyes, L.F.; Munblit, D.; Caoili, J.; Bozza, F.; Hashmi, M.; Edelstein, M.; Cohen, C.; Alvarez-Moreno, C.A.; Cao, B. Long COVID in low-income and middle-income countries: The hidden public health crisis. Lancet 2023, 402, 1115–1117. [Google Scholar] [CrossRef]
- Du, Z.; Pandey, A.; Bai, Y.; Fitzpatrick, M.C.; Chinazzi, M.; Piontti, A.P.Y.; Lachmann, M.; Vespignani, A.; Cowling, B.J.; Galvani, A.P.; et al. Comparative cost-effectiveness of SARS-CoV-2 testing strategies in the USA: A modeling study. Lancet Public Health 2021, 6, e184–e191. [Google Scholar] [CrossRef]
- Tang, B.; Zhou, W.; Wang, X.; Wu, H.; Xiao, Y. Controlling multiple COVID-19 epidemic waves: An insight from a multi-scale model linking the behaviour change dynamics to the disease transmission dynamics. Bull. Math. Biol. 2022, 84, 106. [Google Scholar] [CrossRef]
- Al-Darabsah, I.; Liao, K.; Portet, S. A simple in-host model for COVID-19 with treatments: Model prediction and calibration. J. Math. Biol. 2023, 86, 20. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Deng, X.; Yang, J.; Sun, K.; Liu, H.; Chen, Z.; Peng, C.; Chen, X.; Wu, Q.; Zou, J. Modeling transmission of SARS-CoV-2 Omicron in China. Nat. Med. 2022, 28, 1468–1475. [Google Scholar] [CrossRef] [PubMed]
- Albani, V.V.L.; Zubelli, J.P. Stochastic transmission in epidemiological models. J. Math. Biol. 2024, 88, 25. [Google Scholar] [CrossRef] [PubMed]
- Leung, K.; Wu, J.T.; Liu, D.; Leung, G.M. First-wave COVID-19 transmissibility and severity in China outside Hubei after control measures, and second-wave scenario planning: A modeling impact assessment. Lancet 2020, 395, 1382–1393. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Cheng, S.; Wu, D.; Wu, T.; Lin, X.; Wang, C. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 2020, 584, 420–424. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Zhu, F.; Ling, Y. Analyzing COVID-19 vaccination behavior using an SEIRM/V epidemic model with awareness decay. Front. Public Health 2022, 10, 817749. [Google Scholar] [CrossRef] [PubMed]
- Moneim, I.A.; El-Latif, E.I.A. Modelling the fourth wave of COVID-19 pandemic in Egypt. J. Math. Comput. Sci. 2023, 29, 52–59. [Google Scholar] [CrossRef]
- Xu, W.; Shu, H.; Wang, L.; Wang, X.; Watmough, J. The importance of quarantine: Modelling the COVID-19 testing process. J. Math. Biol. 2023, 86, 81. [Google Scholar] [CrossRef]
- Bai, J.; Wang, J. Modeling long COVID dynamics: Impact of underlying health conditions. J. Theor. Biol. 2024, 576, 111669. [Google Scholar] [CrossRef]
- Matrajt, L.; Eaton, J.; Leung, T.; Brown, E.R. Vaccine optimization for COVID-19: Who to vaccinate first? Sci. Adv. 2021, 7, eabf1374. [Google Scholar] [CrossRef] [PubMed]
- Kifle, Z.S.; Obsu, L.L. Co-dynamics of COVID-19 and TB with COVID-19 vaccination and exogenous reinfection for TB: An optimal control application. Infect. Dis. Model. 2023, 8, 574–602. [Google Scholar] [CrossRef] [PubMed]
- Mutesa, L.; Ndishimye, P.; Butera, Y.; Souopgui, J.; Uwineza, A.; Rutayisire, R.; Larissa Ndoricimpaye, E.; Musoni, E.; Rujeni, N.; Nyatanyi, T.; et al. A pooled testing strategy for identifying SARS-CoV-2 at low prevalence. Nature 2021, 289, 276–280. [Google Scholar] [CrossRef] [PubMed]
- Hubert, E.; Mastrolia, T.; Possamaï, D.; Warin, X. Incentives, lockdown, and testing: From Thucydides’ analysis to the COVID-19 pandemic. J. Math. Biol. 2022, 84, 37. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Khan, M.A. Modeling the impact of non-pharmaceutical interventions on the dynamics of novel coronavirus with optimal control analysis with a case study. Chaos Soliton. Fract. 2020, 139, 110075. [Google Scholar] [CrossRef] [PubMed]
- Worby, C.J.; Chang, H. Face mask use in the general population and optimal resource allocation during the COVID-19 pandemic. Nat. Commun. 2020, 11, 4049. [Google Scholar] [CrossRef] [PubMed]
- Mandal, M.; Jana, S.; Nandi, S.K.; Khatua, A.; Adak, S.; Kar, T.K. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Soliton. Fract. 2020, 136, 109889. [Google Scholar] [CrossRef] [PubMed]
- Kovacevic, R.M.; Stilianakis, N.I.; Veliov, V.M. A distributed optimal control model applied to COVID-19 pandemic. SIAM J. Control Optim. 2022, 60, S221–S245. [Google Scholar] [CrossRef]
- Grundel, S.; Heyder, S.; Hotz, T.; Ritschel, T.K.S.; Sauerteig, P.; Worthmann, K. How much testing and social distancing is required to control COVID-19? Some insight based on an age-differentiated compartmental model. SIAM J. Control Optim. 2022, 60, S145–S169. [Google Scholar] [CrossRef]
- d’Onofrio, A.; Iannelli, M.; Manfredi, P.; Marinoschi, G. Optimal epidemic control by social distancing and vaccination of an infection structured by time since infection: The COVID-19 case study. SIAM J. Appl. Math. 2023, S199–S224. [Google Scholar] [CrossRef]
- Albi, G.; Pareschi, L.; Zanella, M. Control with uncertain data of socially structured compartmental epidemic models. J. Math. Biol. 2021, 82, 63. [Google Scholar] [CrossRef] [PubMed]
- Sereno, J.; Anderson, A.; Ferramosca, A.; Hernandez-Vargas, E.A.; González, A.H. Minimizing the epidemic final size while containing the infected peak prevalence in SIR systems. Automatica 2022, 144, 110496. [Google Scholar] [CrossRef] [PubMed]
- Kuddus, M.A.; Paul, A.K.; Theparod, T. Cost-effectiveness analysis of COVID-19 intervention policies using a mathematical model: An optimal control approach. Sci. Rep. 2024, 14, 494. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Lia, Z.; Dinc, A.; Chen, T. Dynamic analysis and optimal control of a stochastic COVID-19 model. Math. Comput. Simul. 2024, 215, 498–517. [Google Scholar] [CrossRef]
- Reza, S.; Maboubeh, M.; Omid, N. Numerical analysis of COVID-19 model with Caputo fractional order derivative. AIP Adv. 2024, 14, 035202. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, Y.; Li, C. The Method of Qualitative Theory and Stability Theory of Ordinary Differential Equations, 2nd ed.; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Clarke, F.H.; Ledyaev, Y.S.; Stem, R.J. Nonsmooth Analysis and Control Theory; Springer: New York, NY, USA, 1998. [Google Scholar]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Comput. Simul. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Loxton, R.; Lin, Q.; Teo, K.L. Minimizing control variation in nonlinear optimal control. Automatica 2013, 49, 2652–2664. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, C.; Wang, Y. Optimal control of switched systems with multiple time-delays and a cost on changing control. J. Ind. Manag. Optim. 2018, 14, 183–198. [Google Scholar] [CrossRef]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1975. [Google Scholar]
- Shanghai Municipal Health Commission, Daily Epidemic Report of Shanghai Corona Virus Disease. 2022. Available online: https://wsjkw.sh.gov.cn/yqtb/index.html (accessed on 3 January 2024).
- Shanghai Municipal Commission of Health and Family Planning, 2022 Shanghai Statistics Yearbook. 2022. Available online: https://tjj.sh.gov.cn/tjnj/nj22.htm?d1=2022tjnj/C0201.htm (accessed on 3 January 2024).
- Comprehensive Group of State Council Joint Prevention and Control Mechanism, Diagnosis and Treatment Protocol for Novel Coronavirus Pneumonia (Tenth Edition). 2023. Available online: http://www.nhc.gov.cn/xcs/zhengcwj/202301/bdc1ff75feb94934ae1dade176d30936.shtml (accessed on 3 January 2024).
- Chen, Z.; Deng, X.; Fang, L.; Sun, K.; Wu, Y.; Che, T.; Zou, J.; Cai, J.; Liu, H.; Wang, Y.; et al. Epidemiological characteristics and transmission dynamics of the outbreak caused by the SARS-CoV-2 Omicron variant in Shanghai, China: A descriptive study. Lancet Reg. Health 2022, 29, 100592. [Google Scholar] [CrossRef]
- Life Times, How Long Will It Take to Recover from Clearing the Virus to Symptom Disappearing? 2023. Available online: https://mp.weixin.qq.com/s/ftChcf4AklPfb-jtX4DREA (accessed on 3 January 2024).




| Parameter | Value | Source |
|---|---|---|
| 24,894,300 | [43] | |
| 0 | Estimated | |
| 14 | Estimated | |
| 2 | Estimated | |
| 10 | [42] | |
| 1 | [42] | |
| 1 | [42] | |
| 0 | Estimated |
| Parameter | Value | Source | Parameter | Value | Source |
|---|---|---|---|---|---|
| [44] | Estimated | ||||
| 0.0192 | [42] | Estimated | |||
| 0.4458 | [42] | a | 1 | Estimated | |
| Estimated | Estimated | ||||
| 1 | Estimated | Estimated | |||
| 0.02693 | [42] | 100 | Estimated | ||
| [46] | 0.8 | Estimated | |||
| [12] | 0.2 | Estimated | |||
| Estimated | Estimated | ||||
| Estimated | Estimated |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
|---|---|---|---|---|---|
| 1 | 28 | 451 | 1158 | 1258 | |
| 1 | 1 | 1 | 1 | 1 | |
| 92.7395% | 50.1279% | 10% | 4.9980% | 4.6941% | |
| 655,816 | 359,886 | 73,119 | 36,700 | 34,466 | |
| 0.0002 | 0.0440 | 0.5146 | 0.8742 | 0.9116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y. Optimal Control for an Epidemic Model of COVID-19 with Time-Varying Parameters. Mathematics 2024, 12, 1484. https://doi.org/10.3390/math12101484
Li Y. Optimal Control for an Epidemic Model of COVID-19 with Time-Varying Parameters. Mathematics. 2024; 12(10):1484. https://doi.org/10.3390/math12101484
Chicago/Turabian StyleLi, Yiheng. 2024. "Optimal Control for an Epidemic Model of COVID-19 with Time-Varying Parameters" Mathematics 12, no. 10: 1484. https://doi.org/10.3390/math12101484
APA StyleLi, Y. (2024). Optimal Control for an Epidemic Model of COVID-19 with Time-Varying Parameters. Mathematics, 12(10), 1484. https://doi.org/10.3390/math12101484








