Dynamics Behavior of a Predator-Prey Diffusion Model Incorporating Hunting Cooperation and Predator-Taxis
Abstract
1. Introduction
2. Global Existence of Classical Solution
2.1. Local Existence and Preliminary
- (i)
- There exists a positive constant such that model (2) admits a unique local-in-time classical solution , which satisfies;
- (ii)
- There exists a constant such that;
- (iii)
- There exists a constant such that;
- (iv)
- If , we have.
2.2. Global Existence of Solution
3. Stability/Instability Caused by Predator-Taxis
- (i)
- If , then for all , is always locally asymptotically stable;
- (ii)
- If and , then is locally asymptotically stable when and it is unstable when ;
- (iii)
- If , then is locally asymptotically stable when and it is unstable when or .
- (i)
- If and , it is evident that for any , then exhibits locally asymptotically stability;
- (ii)
- If , together with , one has for any . When , then for any , thus is locally asymptotically stability. When , we have for some , which implies is unstable;
- (iii)
- If , then is unstable for the corresponding reaction–diffusion model. From , it follows that for any . When , we observe that for any , and then is locally asymptotically stability. When and , we have for some , then is unstable.
- Next, we show that can reach its maximum on . Set
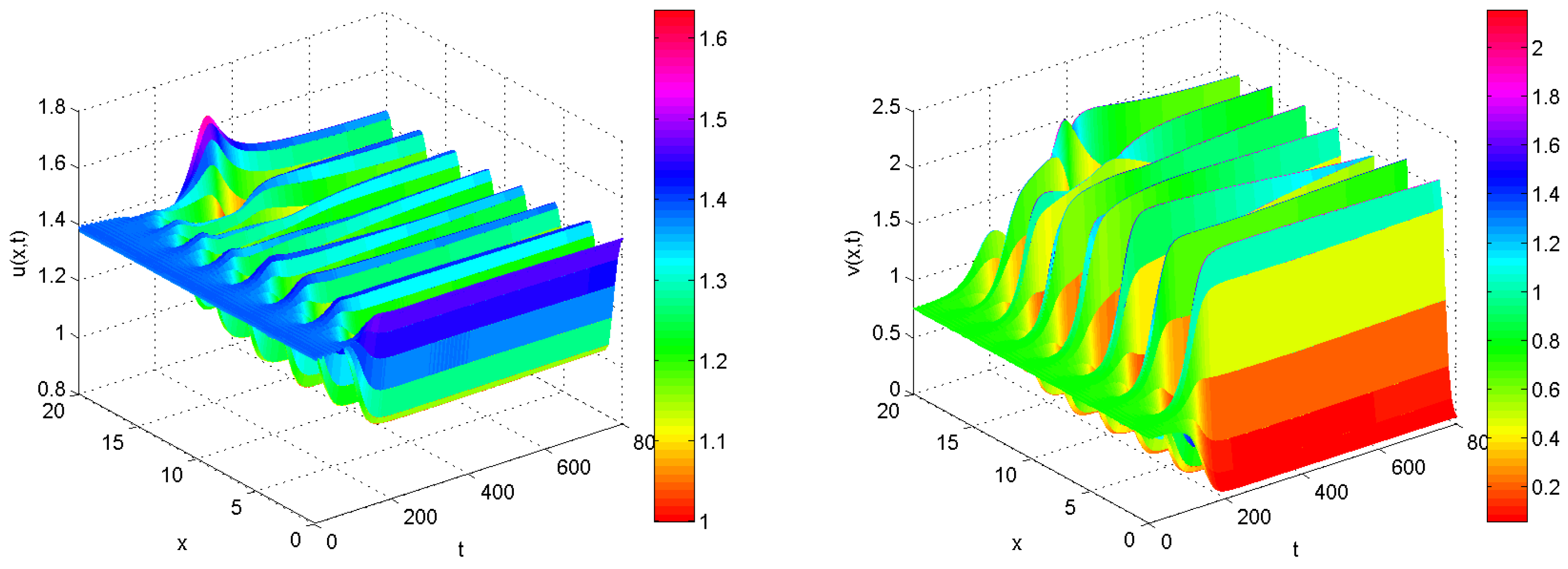
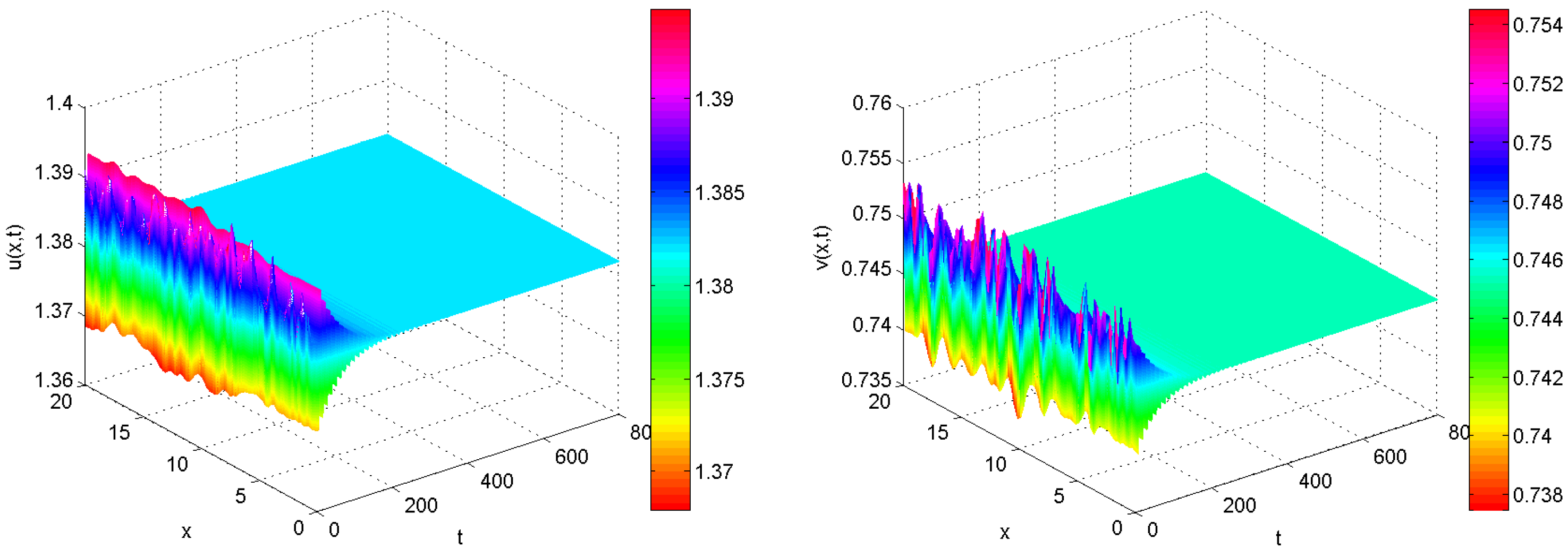
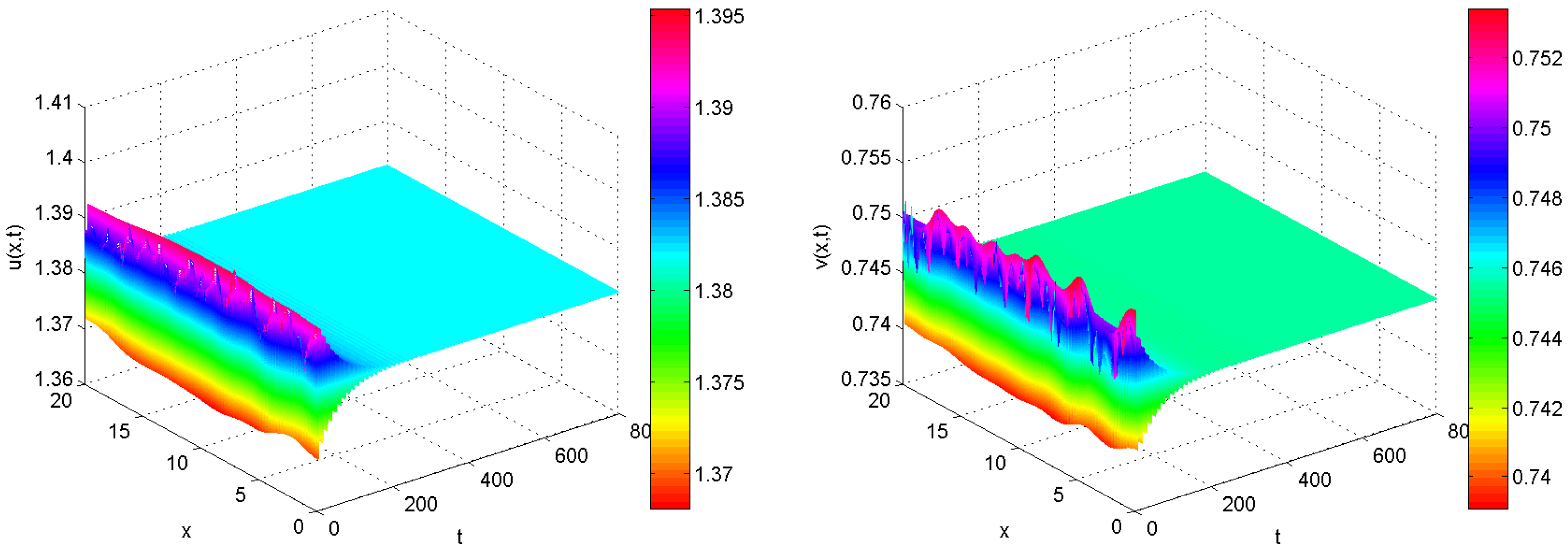
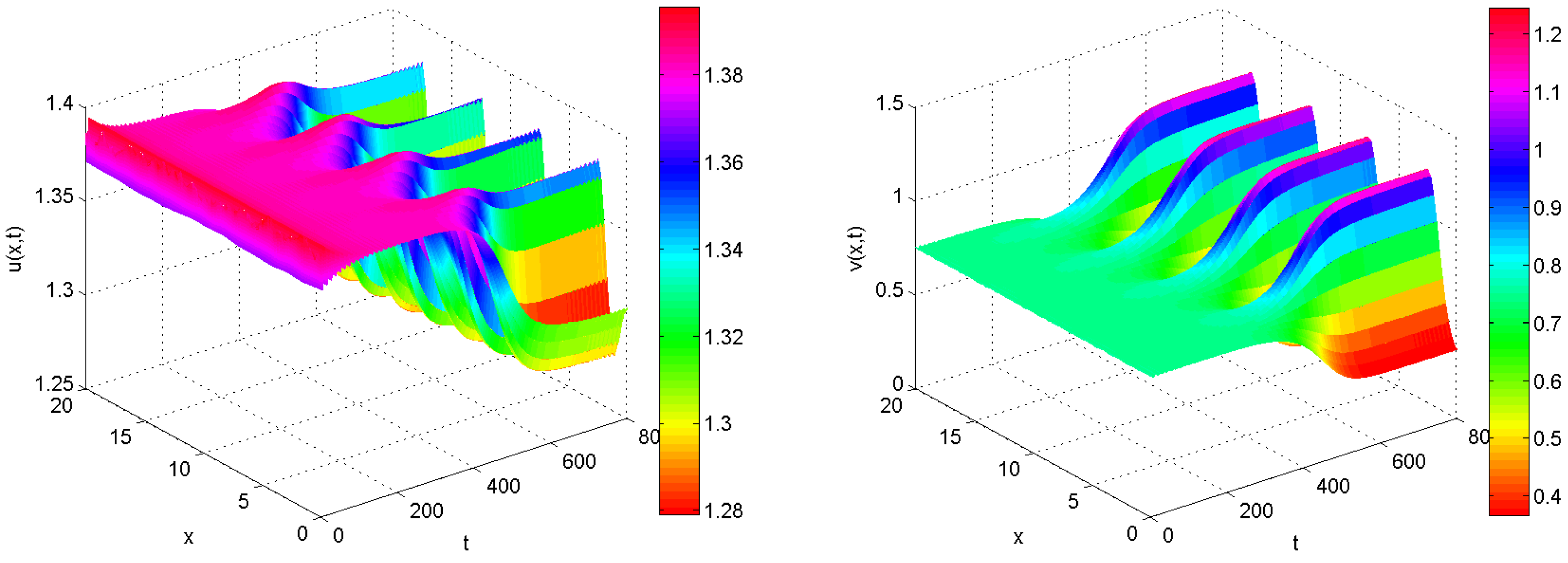
4. Numerical Simulations
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scheel, D.; Packer, C. Group hunting behaviour of lions: A search for cooperation. Anim. Behav. 1991, 41, 697–709. [Google Scholar] [CrossRef]
- Boesch, C.; Boesch, H.; Vigilant, L. Cooperation in Primates and Humans: Mechanisms of Evolution; Kappeler, P.M., van Schaik, C.P., Eds.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Cook, W.L.; Streams, F.A. Fish predation on Notonecta (Hemiptera): Relationship between prey risk and habitat utilization. Oecologia 1984, 64, 177–183. [Google Scholar] [CrossRef] [PubMed]
- Hector, D.P. Cooperative hunting and its relationship to foraging success and prey size in an avian predator. Ethology 1986, 73, 247–257. [Google Scholar] [CrossRef]
- Moffett, M.W. Foraging dynamics in the group-hunting myrmicine ant, pheidologeton diversus. J. Insect. Behav. 1988, 1, 309–331. [Google Scholar] [CrossRef]
- Goodale, E.; Beauchamp, G.; Ruxton, G.D. Mixed-Species Groups of Animals: Behavior, Community Structure, and Conservation; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Duarte, J.; Januario, C.; Martins, N.; Sardanyes, J. Chaos and crises in a model for cooperative hunting: A symbolic dynamics approach. Chaos 2009, 19, 043102. [Google Scholar] [CrossRef]
- Berec, L. Impacts of foraging facilitation among predators on predator-prey dynamics. Bull. Math. Biol. 2010, 72, 94–121. [Google Scholar] [CrossRef] [PubMed]
- Alves, M.T.; Hilker, F.M. Hunting cooperation and Allee effects in predators. J. Theo. Biol. 2017, 419, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.M.; Zhang, H.S. Effect of hunting cooperation on the dynamic behavior for a diffusive Holling type II predator-prey model. Commun. Nonlinear Sci. Numer. Simulat. 2021, 99, 105807. [Google Scholar] [CrossRef]
- Kareiva, P.; Odell, G. Swarms of predators exhibit “preytaxis” if individual predators use area-restricted search. Am. Nat. 1987, 130, 233–270. [Google Scholar] [CrossRef]
- Jin, H.Y.; Wang, Z.A. Global stability of prey-taxis systems. J. Differ. Equ. 2017, 262, 1257–1290. [Google Scholar] [CrossRef]
- Choi, W.; Ahn, I. Predator invasion in predator-prey model with prey-taxis in spatially heterogeneous environment. Nonlinear Anal. Real World Appl. 2022, 65, 103495. [Google Scholar] [CrossRef]
- Zuo, W.J.; Song, Y.L. Stability and double-Hopf bifurcations of a Gause-Kolmogorov-type predator-prey system with indirect prey-taxis. J. Dyn. Diff. Equat. 2021, 33, 1917–1957. [Google Scholar] [CrossRef]
- Banda, H.; Chapwanya, M.; Dummani, P. Pattern formation in the Holling-Tanner predator-prey model with predator-taxis. A nonstandard finite difference approach. Math. Compu. Simul. 2022, 196, 336–353. [Google Scholar] [CrossRef]
- Chen, M.X.; Zheng, Q.Q. Predator-taxis creates spatial pattern of a predator-prey model. Chaos Solitons Fractals 2022, 161, 112332. [Google Scholar] [CrossRef]
- Gao, X.Y. Global solution and spatial patterns for a ratio-dependent predator-prey model with predator-taxis. Results Math. 2022, 77, 66. [Google Scholar] [CrossRef]
- Amann, H. Dynamic theory of quasilinear parabolic equations. II. Reaction-diffusion systems. Differ. Integral Equ. 1990, 3, 13–75. [Google Scholar] [CrossRef]
- Amann, H. Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems. In Function Spaces, Differential Operators and Nonlinear Analysis; Teubner–Taxte Math: Stuttgart, Germany, 1993; Volume 133, pp. 9–126. [Google Scholar]
- Alikakos, N.D. Lp bounds of solutions of reaction-diffusion equations. Commun. Part. Diff. Equ. 1979, 4, 827–868. [Google Scholar] [CrossRef]
- Horstmann, D.; Winkler, M. Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 2005, 215, 52–107. [Google Scholar] [CrossRef]
- Friedman, A. Patial Differential Equations; Holt Rinehart Winston: New York, NY, USA, 1969. [Google Scholar]
- Burnside, W.S.; Panton, A.W. The Theory of Equations: With an Introduction to the Theory of Binary Algebraic Forms, 2nd ed.; Dublin University Press Series: Dublin, Ireland, 1886. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H. Dynamics Behavior of a Predator-Prey Diffusion Model Incorporating Hunting Cooperation and Predator-Taxis. Mathematics 2024, 12, 1474. https://doi.org/10.3390/math12101474
Zhang H. Dynamics Behavior of a Predator-Prey Diffusion Model Incorporating Hunting Cooperation and Predator-Taxis. Mathematics. 2024; 12(10):1474. https://doi.org/10.3390/math12101474
Chicago/Turabian StyleZhang, Huisen. 2024. "Dynamics Behavior of a Predator-Prey Diffusion Model Incorporating Hunting Cooperation and Predator-Taxis" Mathematics 12, no. 10: 1474. https://doi.org/10.3390/math12101474
APA StyleZhang, H. (2024). Dynamics Behavior of a Predator-Prey Diffusion Model Incorporating Hunting Cooperation and Predator-Taxis. Mathematics, 12(10), 1474. https://doi.org/10.3390/math12101474