Abstract
The level of difficulty of mathematical test items is a critical aspect for evaluating test quality and educational outcomes. Accurately predicting item difficulty during test creation is thus significantly important for producing effective test papers. This study used more than ten years of content and score data from China’s Henan Provincial College Entrance Examination in Mathematics as an evaluation criterion for test difficulty, and all data were obtained from the Henan Provincial Department of Education. Based on the framework established by the National Center for Education Statistics (NCES) for test item assessment methodology, this paper proposes a new framework containing eight features considering the uniqueness of mathematics. Next, this paper proposes an XGBoost-based SHAP model for analyzing the difficulty of mathematics tests. By coupling the XGBoost method with the SHAP method, the model not only evaluates the difficulty of mathematics tests but also analyzes the contribution of specific features to item difficulty, thereby increasing transparency and mitigating the “black box” nature of machine learning models. The model has a high prediction accuracy of 0.99 for the training set and 0.806 for the test set. With the model, we found that parameter-level features and reasoning-level features are significant factors influencing the difficulty of subjective items in the exam. In addition, we divided senior secondary mathematics knowledge into nine units based on Chinese curriculum standards and found significant differences in the distribution of the eight features across these different knowledge units, which can help teachers place different emphasis on different units during the teaching process. In summary, our proposed approach significantly improves the accuracy of item difficulty prediction, which is crucial for intelligent educational applications such as knowledge tracking, automatic test item generation, and intelligent paper generation. These results provide tools that are better aligned with and responsive to students’ learning needs, thus effectively informing educational practice.
Keywords:
mathematics item difficulty; assessment methods; XGBoost; SHAP; secondary education; computer-based assessment MSC:
97U40; 97D60; 97N80; 97P50
1. Introduction
The difficulty of mathematics items is important in assessing the quality of examinations and the value of educational outcomes [1]. It is generally determined by several features, including the knowledge required, the depth of thinking, the problem-solving ability, and the time constraints [2,3,4]. Understanding item difficulty has practical implications for intelligent educational applications such as knowledge tracking [5,6], automatic test item generation [7,8,9], intelligent paper generation [10] and personalized recommendations [11,12]. By accurately assessing the difficulty of exam items, these applications can be improved and provide effective support for teaching practice.
Methods for assessing item difficulty can be divided into two categories: post-test determination based on students’ scores [13,14], and pre-test prediction [15]. The former is prone to hindsight bias and lacks usefulness for developing new test items. The latter has three approaches: expert judgment, pre-testing, and text-based feature extraction using machine learning [16,17]. Expert judgment lacks strong interpretability with accuracy depending on the experience of the expert. Pre-testing is not only laborious and costly but can also lead to question leakage in traditional paper-and-pencil tests with fixed length and content [18]. Text-based feature extraction is a popular method for determining the difficulty of language-related items such as reading comprehension [3]. However, for disciplines such as mathematics and physics, which involve logic, symbolic language and a systematic knowledge system, text-based feature extraction may not fully capture the unique features of these subjects. As a result, it may not effectively reveal students’ logic and reasoning abilities [19,20,21,22]. In addition, machine learning models suffer from an inherent opacity problem, commonly known as the ‘black box’ problem, which makes it crucial to understand how the model is making predictions [23]. In this article, item difficulty prediction refers only to the prediction of item difficulty before the exam.
In this paper, we present an interpretable model called XGBoost-based SHAP, which predicts the difficulty of test questions [24,25]. By analyzing the contribution of each feature to the difficulty of the item and improving the interpretability of the model, it can provide an estimate of the difficulty of the item before the exam [26]. To develop the model, we utilized information on math questions that contain subjective elements and corresponding test results gathered from the college admissions assessments taken by numerous Chinese students during recent decades as the study data. In addition, the model improves the accuracy and interpretability of item difficulty estimates. The model also supports the creation of scientific mathematics test items, the modernization of the item bank system, and the improvement of student knowledge tracking and teacher evaluation. It can also help to assess students’ ability to learn mathematics and to provide targeted help and guidance to students.
The contribution of this paper concerns three main aspects of item difficulty estimation: feature extraction method, model building, and feature contribution analysis for subjective difficulty of mathematics items.
- Firstly, we provide a rigorous framework for assessing the difficulty of mathematics items by listing several features necessary for this task, based on the relevant literature and the features of mathematics items. In particular, the requirements of mathematics in cognition and ability and the construction of the mathematical knowledge system are taken into account. The research data are then subjected to feature extraction, followed by data analysis of the extracted features.
- Secondly, we present the XGBoost-based SHAP model, which is a prediction model for estimating item difficulty that employs classification features and is highly interpretable, based on the above framework. The features are used as a base and combined in a linear fashion. The improved XGBoost model is then applied to train and predict the feature combinations. The SHAP model is then utilized to obtain a quantitative analysis of the contribution of each feature to the difficulty of the exam, through the marginal contribution rate of each feature for each exam item and the accumulation of the marginal contributions. The hyperparameters of the model are then optimized using a grid search algorithm to improve classification accuracy.
- Finally, the model is trained and evaluated using actual test scores from millions of Chinese test takers. In order to comply with the Chinese curriculum standards, the subjective questions of the Chinese math test are divided into nine knowledge units. As a complement, we further analyze the representation of the eight features in the nine knowledge units.
In summary, the three main research questions of this study are as follows:
Q1. Feature Extraction Methodology of Mathematics Items: What methodologies can be deployed to identify the critical features that determine the difficulty of mathematics items and to conduct an effective analysis of the data?
Q2. XGBoost-based SHAP Model Application: How does the XGBoost-based SHAP model function in predicting item difficulty, and what is the role of each identified feature in contributing to this prediction?
Q3. How many knowledge units can the subjective questions of the Chinese college entrance examination be classified into? How do the eight features influence the difficulty of test items in different knowledge units?
The paper is organized as follows: In the initial section of this study, we present the background and content of the research. In the second section, we provide a comprehensive overview of current methods used to assess exam difficulty and delve into the practical application of both the XGBoost and SHAP models in different domains. The third section delves into the specifics of feature extraction rules and data analysis to address the first research question. Following this, the fourth section meticulously outlines the process of model construction, including the incorporation of relevant formulas and parameter optimization efforts, thus addressing the second research question. Then, in the fifth section, we delve deeper into the analysis by evaluating the individual contributions of the features, thereby increasing the transparency of the model and further addressing the second research question. In addition, we classify the knowledge units of the Chinese college entrance examination and study the distribution of each knowledge unit in eight characteristics, which solves the third research problem. In the last section, we discussed possible future directions and limitations of our model.
2. The Related Work
2.1. A Summary and Classification of Item Difficulty Estimation Methods
Current methods of estimating item difficulty prior to testing include pre-testing [27] and expert judgment [3,28]. Pre-testing has been widely used and has promising applications in Computer Adaptive Testing (CAT) and the Programme for International Student Assessment (PISA) [29]. In educational psychology, Classical Test Theory (CTT) [30,31,32] often uses students’ scores or pass rates on exam items as data and uses statistical methods to quantify the difficulty of exam items. However, its disadvantages are obvious: (1) the unfairness caused by the leakage of examination papers; (2) the difference in the level of knowledge and ability between the pre-test takers and the actual exam takers [33]; and (3) the waste of resources and money. As for expert judgment, it may be affected by individual differences and subjective bias.
Data-driven machine learning methods have been widely used to estimate item difficulty. Mainstream methods use textual information, such as the stem and options of exam items, as features [3]. Using the known difficulty information of the exam items as labels, a machine learning model is constructed to predict item difficulty. Traditional machine learning models include regression analysis [3], support vector machines (SVMs) [34], decision trees [35,36], Random Forests [37], and shallow BP neural networks [38]. On the other hand, deep learning models such as Convolutional Neural Networks (CNNs) [39], Recurrent Neural Networks (RNNs) [40] and Long Short-Term Memory (LSTM) [41] neural networks are also used. Feature extraction based on text content is widely used in disciplines with rich text information, such as language. Lexical and syntactic features of texts can help to estimate the difficulty of language-related tasks [42,43]. However, in mathematics and physics, the difficulty of test items is influenced by the amount of computation, the knowledge background, and the correlation between knowledge items, which cannot be determined by lexical and syntactic features alone [19,20,21,22].
In summary, traditional methods, statistical methods and machine learning methods have achieved high accuracy in predicting the difficulty of exam items (Figure 1), This study employed the XGBoost model in machine learning, which has been demonstrated to exhibit high accuracy and generalizability [25].
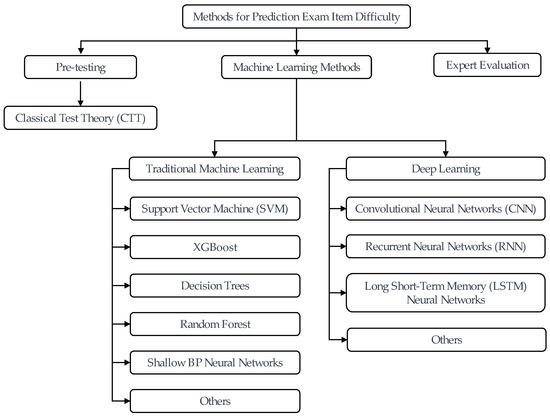
Figure 1.
A classification of methods for item difficulty estimation.
However, the XGBoost model was not designed with interpretability in mind and is therefore a “black-box” model [44,45]. Thus, in this study, we further use SHAP to increase the interpretability of XGBoost results. We can then reveal what features are primary contributors to the exam difficulty. Accuracy is a critical metric in machine learning, but focusing solely on accuracy while ignoring interpretability can lead to misinterpretation of predictions, ultimately affecting final decisions. That is why it is critical to understand the process by which models make predictions in order to accurately interpret and apply them. While previous researchers have summarized the impact of input features on the entire model using global interpretation methods, little consideration has been given to local interpretation, specifically, the impact of input features on the prediction of individual samples or sample data [46]. In order to explain the influence of individual features on the assessment of test difficulty, this paper introduces the SHAP model, which provides more detailed and accurate explanations and reveals the contribution of each feature to an individual sample. Only by interpreting the prediction model in a reasonable way, i.e., by identifying the features that influence the evaluation of test difficulty and by analyzing the importance of these features, can the model of test difficulty evaluation be better understood. This will give examiners and teachers confidence in the predicted results so that timely adjustments and corrections can be made in exam design and teaching.
2.2. XGBoost-Based SHAP Model
In [25], a new ensemble learning method, called eXtreme Gradient Boosting (XGBoost), is proposed by Chen and Guestrin by introducing a scalable end-to-end tree boosting system. As one of the commonly used nonlinear models, XGBoost is applied by machine learning practitioners as an independent predictor [47] for prediction based on input feature sets [48] in areas such as finance, medicine, biology, customer loyalty, advertising, supply chain management, manufacturing, public health, and others [26,49]. Compared to other algorithms, it is a practicable model in classification and nonlinear problem solving in related fields [25] because it can deal with overfitting in the model, allowing faster learning and faster model exploration. As for the prediction of confusion attempting algebra homework [50] and student performance [51], the scalable XGBoost model was superior to other evaluation models and significantly improved its prediction performance. In conclusion, although the XGBoost model has never been used to judge the difficulty of test questions, it can provide accurate and highly interpretable predictions of input features and has good applicability for judging the difficulty of test questions based on subject features.
The SHapley Additive exPlanations (SHAP) is a mathematical method proposed by Shapley L. S. in 1953 [24] for calculating the contribution of each feature in a shared feature space. It is commonly used to allocate benefits between collaborators. The SHAP value of a feature is the marginal contribution of that feature to the feature mix [52,53,54], i.e., the impact of that feature on the final output value is calculated. SHAP is widely used. The Catboost SHAP method is used to visualize and analyze the factors that influence students’ grades, which can both predict student performance and help administrators better understand the factors that influence student performance [55]. SHAP values are incorporated into the Student Achievement Prediction Framework model to make it more intuitive to determine which factors have an impact on test scores, and to aid the interpretation and understanding of the overall model. In this article, we will use SHAP to explain the importance of individual features in assessing the difficulty of exam items.
Based on the analysis of XGBoost model and SHAP method, we can find that the XGBoost model has a better generalization ability than other machine learning methods. It can deal with the overfitting problem of the model more effectively to achieve faster learning and faster model exploration. Therefore, it is a very good model for classification and nonlinear problem solving in related fields. In terms of model interpretation, the SHAP method can rank the importance of the features that affect the model and help researchers better understand the factors that affect the model. Although no researchers have combined the XGBoost and SHAP model in the field of mathematics education, the combination of these two models has been applied to real-time accident detection and feature analysis in the aspect of traffic safety factors [26] and traffic accident feature detection [56].
In summary, this paper proposes a SHAP model based on XGBoost, which is a kind of machine learning model. This model combines and improves the two previous models to accurately evaluate the complexity of mathematics test questions. In fact, the XGBoost-based SHAP strategy used in this paper is effective in improving the interpretability of the model as well as the accuracy of test difficulty prediction while taking into account the generalization performance of the model [52,53,54,55]. Firstly, it improves interpretability by revealing the contribution of each feature to the prediction results. In addition, this integration also allows a ranking of feature importance to be derived, which helps to identify influential features. This is valuable for understanding the impact of data and features, as well as for feature selection, and improves model performance [26].
3. Framework Building and Data Analysis
3.1. Feature Extraction Rules for Item Difficulty Estimation Framework
In 2001, the National Center for Education Statistics (NCES) established a framework for test item assessment methodology [57]. The NCES framework evaluates test items based on eight aspects, including content categories, scientific vocabulary, response type, context, multi-step reasoning, mathematical skills, computation, and interpretation or use of figures and graphs. Although this framework can, to a certain extent, effectively assess the overall situation of test papers, it still has some shortcomings. The framework has some limitations when applied to mathematics. It lacks features that accurately reflect the unique features of the mathematical knowledge system and the level of mathematical exploration. In addition, the framework’s evaluation criteria are somewhat crude and do not provide sufficient quantitative rules for analyzing the difficulty of examination items in the era of big data. Furthermore, within the eight features evaluated by the NCES framework, we does not know the contribution of each characteristic to the overall difficulty of an exam item.
In order to address the first research question of this study, a novel framework for the evaluation of the difficulty of test items is proposed, which will overcome the aforementioned limitations. We identified eight features that significantly influence the difficulty level of Chinese high school math exam items, namely, Parameter Level Features (PLFs) [57], Reasoning Level Features (RLFs) [57], Thinking Mode Features (TMFs), Calculate Rank Features (CRFs) [57], Background Information Features (BIFs) [57], Character Count Features (CCFs), Knowledge Content Features (KCFs), and Cognitive Level Features (CLFs). The four selected features, PLF, RLF, CRF and BIF, are based on the framework of NCES [19,20,21,22,57]. However, the specific extraction rules for these features have been defined differently from those proposed by NCES as shown in Table 1. Furthermore, this study considers TMF, CCF, CLF, and KCF to be important features that affect the difficulty of math tests. TMF reflects the mathematical thinking mode needed to solve the problem. CCF reflects the amount of information and complexity of the test. CLF represents the cognitive depth required by the test. KCF involves the specific mathematical knowledge content and quantity involved in the test as shown in the Table 1. These features directly affect the way students understand and respond to the questions, and thus, they are crucial in assessing the difficulty of the questions. Next, we provided extraction rules and defined four levels for each feature based on Bloom’s cognitive target classification and the nature of mathematics as shown in Table 1. Each level was assigned a rank variable from high to low (1, 2, 3, and 4).

Table 1.
Extraction rules for item difficulty features.
Taking the 17th item (12 points) in the 2019 Chinese National College Entrance Examination (C-NCEE) Volume 1 exam as an example, this item contains two parameters, requires five to six steps of reasoning, and mainly tests reverse thinking. The computation involves both simple symbol operations and simple numerical operations, without specific contextual factors. There are 42 printed characters, and the item covers 5 knowledge units, with a total cognitive level of 14 across these units. The item is shown as follows, and the original data are shown in Table 2.

Table 2.
Features of the 17th item (12 points) in the 2019 C-NCEE1 Mathematics paper.
Q17. We are given a parallelogram in which and . Also, and . We need to find the following:
- (a)
- (b)
- Length of if .
3.2. Item Difficulty Levels
In this paper, we introduce a difficulty coefficient (DC) to measure and quantify the difficulty level of actual test questions, where AS and TS are the average score and total score of the test items, respectively [58]:
Specifically, items with DC falling within the ranges of , , and were classified as Level 0, Level 1, and Level 2. These levels correspond to easy, moderate, and difficult items, respectively.
To calculate the DC and DL of each item, Table 3 presents the TS and AS of the seven subjective math items in the 2019 C-NCEE1 exam. These data were provided by the Information Management Department of a provincial admissions office in China.

Table 3.
Normalized values, DC and DL of features in the 2019 C-NCEE1 math paper items.
3.3. Data Analysis
In this section, we apply Principal Component Analysis (PCA) to decrease the dataset’s dimensionality, while still keeping the most significant characteristics that influence variance. In order to better construct the model, all the data are normalized. The mathematics paper from the 2019 C-NCEE is taken as an example, referring to Table 3.
Principal Component Analysis is an unsupervised learning algorithm that is used for the dimensionality reduction in machine learning. It is a statistical process that converts the observations of correlated features into a set of linearly uncorrelated features with the help of orthogonal transformation. These new transformed features are called the Principal Components. It is one of the popular tools that is used for exploratory data analysis and predictive modeling. It is a technique to draw strong patterns from the given dataset by reducing the variances. In general, PCA tries to find the lower-dimensional surface to project the high-dimensional data. Figure 2 depicts the distribution of abnormal features in PCA dimensionality reduction, with blue data points representing these abnormal features. Abnormal features are defined as those that differ from or deviate from the normal pattern during the dimensionality reduction process. They may affect the PCA results, causing changes in the principal variance or distorting the data distribution. Consequently, it is of paramount importance to monitor the distribution of abnormal features during PCA dimensionality reduction, evaluate their influence on the results, and implement appropriate corrective measures, such as the removal of outliers.
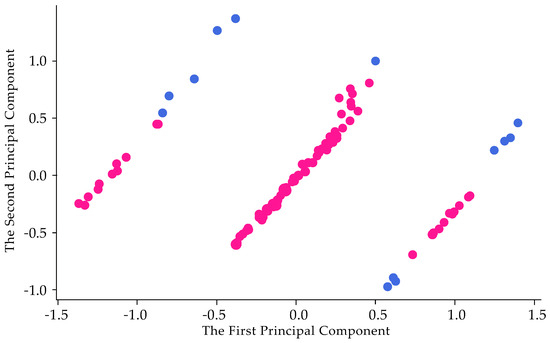
Figure 2.
Distribution of abnormal features in dimensionality reduction by PCA.
4. Methodology
4.1. Model Building
The test question difficulty prediction model we developed consists of the following parts: in the model development phase, we utilized and improved the XGBoost model; in the model parameterization phase, we improved it using the grid search method; and in the model interpretation phase, we integrated the SHAP model. We trained the model using the mathematics test questions from China’s college entrance exams over the past decade. These test questions are evaluated based on the actual scores of millions of test takers. The model uses 263 sets of samples, each consisting of 8 features and a DL.
In constructing the model, we referred to the model construction process by Chen and Guestrin [25]. Motivated by Gradient Boosting Decision Tree (GBDT), XGBoost adopts a tree-shaped structure containing decision nodes (root nodes), chance nodes (internal nodes), and terminal nodes (leaf nodes). Starting from the decision node, each internal node represents a judgment on a feature, each branch represents an output of the judgment result, and each leaf node represents a classification result. The XGBoost algorithm consists of multiple decision trees, where each tree is trained on the residual of the previous tree and influences the next tree. The conclusions of all decision trees are accumulated to obtain the final conclusion.
In this work, we investigated a dataset containing n sets of data, each set including an independent variable and a dependent variable . Each independent variable contains 8 features. , while . To generate predictions, the model employs K decision tree functions , and these functions are summed to denote the prediction on the K-th boost result [25]:
where denotes the set of all decision tree functions . It is important to note that XGBoost utilizes a specific type of base learner in the form of a decision tree, where each tree can be represented as , , and T is the total number of leaves in the tree. Here, q represents the decision rules of the tree, which classify the samples into corresponding leaves, and is a vector indicating the weight of each leaf node (i.e., leaf scores). Essentially, q and together describe how the samples are classified into leaves and the corresponding weights assigned to each leaf node in the tree.
To prevent overfitting, we introduce a regularization term that limits the complexity of the algorithm [59]. Here, and are regularization coefficients, and is the L2 norm of leaf weights. We use to represent the deviation between predicted values and true values in order to minimize the following objective function:
XGBoost approximates (3) using Taylor expansion [60], allowing for fast computation. Let be the set of instances of leaf j. After removing the constant term, we simplify and obtain the objective function after k iterations as follows:
where and are first- and second-order gradient statistics on the loss function.
By using a fixed tree structure and the optimal leaf weights on each leaf node, the optimal solution for and the extreme value of can be obtained by Equations (2)–(4):
XGBoost’s primary challenge is finding the optimal tree structure, which can be approached through an intuitive search algorithm that involves enumerating all possible tree structures, computing their scores using (6), and selecting the one with the highest score. Nonetheless, due to the infinite number of possible tree structures, this approach is impractical. So, we use the greedy algorithm to change the objective function to [25]:
Here, is the instances set of left nodes after the split, is the instances set of right nodes after the split, and .
4.2. Model Parameters
To improve the classification accuracy of the model in this study, we employed grid search to determine the optimal hyperparameters. Typically, learning algorithms are trained to optimize parameters for improved data fitting, while hyperparameters are used to regulate the complexity of the model or introduce regularization techniques to enhance performance. The credit-scoring models discussed in this paper (SVM, CNN, RNN, and the proposed model) have various hyperparameters that greatly affect the accuracy of the models [61].
Grid search is a method that optimizes model performance by traversing a given set of parameter combinations. Within the specified parameter range, the parameters are adjusted step by step, and every possible combination is tried through a loop traversal to find the parameters that produce the highest accuracy on the training set. The adjusted parameters are then used to train the base and ensemble learners. Grid search effectively prevents overfitting of the model. However, since it essentially traverses all combinations, it is time-consuming. Therefore, this study sets other irrelevant optimization model parameters to their default values (Table 4).

Table 4.
Hyperparameters combination.
The procedure for setting parameters is as follows. The study first determined the number of base learners through a fitting score curve, then utilized grid search to identify the optimal hyperparameters [26], and finally trained the model on a 7:3 ratio training and test set, generating a curve graph to illustrate the classification accuracy of the model as the number of base learners varied. To ensure the rigor of this study, the model was trained on the training set, and a curve graph showing the classification accuracy (number of correctly classified samples/total number of samples) of the model as the number of base learners changes was plotted as shown in Figure 3. In Figure 3, the classification accuracy of the training set reaches its highest value of when the number of base learners exceeds 18.
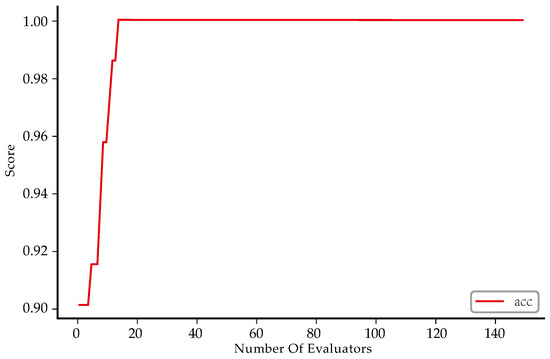
Figure 3.
The relationship between number of evaluators and scores.
The data show that the most accurate model is achieved by establishing the hyperparameters illustrated in Table 4.
4.3. Model Interpretation
This article utilizes the SHAP value method for model interpretation. The SHAP value method, introduced by Shapley L. S. in 1952 [24], is a mathematical approach used to calculate the contribution rate of individual features under the joint action of multiple features [62]. It is commonly used to allocate benefits among collaborators [63]. The Shapley value of a certain feature is the average marginal contribution of it to the combination of features.
Combining the relevant data of the difficulty estimation of exam items, the specific principles of SHAP are briefly introduced as follows:
The set I is composed of eight test question difficulty features, denoted as through , where , , , , , , , and . For any subset s of I, which represents any combination of the eight features, there exists a corresponding combination contribution represented by the real-valued function . For instance, when , denotes the combined contribution of features and to the exam item difficulty. Assuming that there is only one tree in the model, given a sample x and its feature subset s, if all features are considered, i.e., s is equal to the entire feature set, then the combination contribution is the output value of the model under that feature. On the other hand, if the subset is empty, the combination contribution is calculated as the weighted average of the predicted values of all leaf nodes, which are used as the output value. If the subset contains some features, only leaf nodes that can be reached after removing the features excluded are considered. The weighted average of the predicted values from the remaining leaf nodes is then taken as the output value. In summary, this process defines how the model generates output values based on different feature subsets [26].
The SHAP value is calculated as follows:
where represents the number of elements in subset s; represents all subsets of features that include ; i is the number of features, .
5. Results
5.1. Model Evaluation
In this section, we compare our proposed model with two other models and summarize the results in Table 5. We evaluate the correlation model using five metrics: training set fit accuracy, test set fit accuracy, recall, F1 score, and precision (see Table 5). We divide the datasets into training and test sets to train the models with the former and evaluate their performance with the latter. Following the standard industry practice advocated by [64,65], we adopt a 70/30 split for training and testing. Specifically, of the samples are utilized for model development and the remaining for evaluation. Following the optimization of five parameters and the consideration of eight features, we subsequently continue with model training.

Table 5.
Evaluation metrics for the three classification models.
Precision, recall, accuracy, and score are commonly used metrics to evaluate the performance of a classification model [66,67]. Precision is especially important in assessing positive instance predictions. A higher precision corresponds to better accuracy in detecting positive cases and reducing the risk of false positives. However, precise measurement alone cannot fully capture the model’s efficacy in identifying positive instances missed, or false negatives. Therefore, when evaluating the model’s performance, it is crucial to consider additional metrics such as recall, score, and accuracy, which offer a more comprehensive assessment of the model’s effectiveness. Accuracy measures the proportion of accurately predicted samples out of the total sample size, providing an overall measure of correctness. A higher level of accuracy indicates that the model can make more precise predictions. Recall measures the model’s ability to correctly identify true positive samples, showing the ratio of accurately predicted positive samples to the total number of true positive samples. A higher recall indicates that the model captures a greater portion of true positive samples. The score calculates a harmonic mean of accuracy and recall, providing an objective evaluation of the model’s performance based on both prediction accuracy and its ability to efficiently capture positive instances (Table 5).
As Table 5 shows, the proposed model always yields the best result. It outperforms Light GBM with a significant improvement of 0.2123 in training set fitting accuracy, surpassing Random Forest by 0.1496. It also beats the other two models in terms of test set fitting accuracy with a score of 0.8064. Additionally, its F1 score reaches 0.9419, 0.2640 higher than Light GBM and 0.2932 higher than Random Forest. When considering the weighted average recall, the proposed model surpasses Light GBM and Random Forest by 0.2656 and 0.2983 respectively. Moreover, precision increases from 0.5600 to 0.9435.
In Figure 4, we show the confusion matrix [68] of the proposed model in the test set, and the overall data. In this confusion matrix, each cell represents the model’s prediction results for a certain class. The elements on the diagonal represent the number of correct predictions for a certain class by the model, while those off the diagonal represent the number of instances where the model incorrectly predicted a certain class as another class. In the test set, the proposed model achieved a weighted average accuracy of 0.8312 for item-level deep learning. Additionally, in the overall data, the proposed model demonstrated a weighted average accuracy of 0.9435 for item-level deep learning.
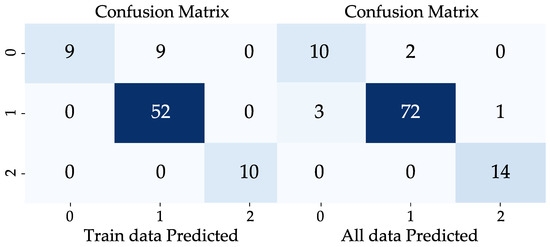
Figure 4.
The confusion matrix of the proposed model.
In a word, the proposed model outperforms Light GBM and Random Forest in terms of training and test set fitting accuracy, as well as the score, weighted average recall, and precision.
5.2. Model Interpretability
In the preceding sections, in order to address the initial research question of this study, we presented a novel framework for evaluating the difficulty of test items (Table 1). In order to address the second research question of this study, this section offers an objective interpretation of the results, ranking their importance based on eight features. Interpretability holds the same importance in credit scoring as accuracy. However, it receives little attention in many studies for two reasons [61]. Firstly, popular base models like SVM are inherently black-box systems [69]. Secondly, global explanations adopted by ensemble methods like bagging, boosting, and stacking face challenges when it comes to establishing comprehensive credit-scoring models. To overcome the constraints, this paper utilizes the SHAP model to emphasize localized explanations. It focuses on the impact of individual features on test difficulty assessment. By employing the SHAP model, this study provides in-depth and accurate insights, uncovering the precise contribution of each feature to a single sample in Figure 5.

Figure 5.
Shap summary plot.
Figure 6 shows the SHAP summary plot obtained by accumulating the precise contribution of each feature to the 116 sample sets. These features sorted by their relative importance scores in descending order are PLF, RLF, KCF, CCF, CLF, TMF, CRF, and BIF. Therefore, PLF is the most significant feature that affects test difficulty, while BIF is the least important and can be removed to improve learning speed and accuracy.
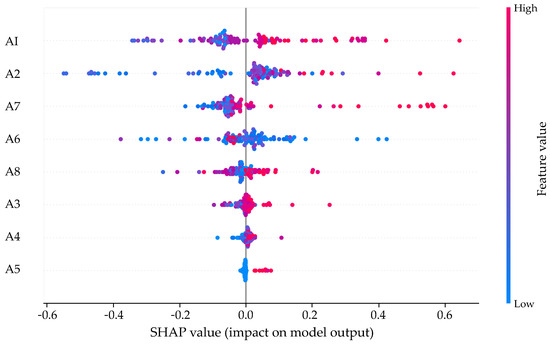
Figure 6.
Shap summary plot.
By removing the BIF, we observed a notable enhancement in XGBoost model accuracy on the test set, with an improvement of 7.5% compared to predictions made using all features. Additionally, we conducted an analysis where we systematically constructed 256 combinations of eight features. Subsequently, the accuracy of these combinations was evaluated on the training and test sets using the XGBoost model.
5.3. Distribution of Features in Different Knowledge Units
In order to address the third research question of this study, in this section, the subjective items in CNCEE mathematics are categorized into nine distinct knowledge units based on the Chinese curriculum standards [70], then the distribution of each knowledge unit across the eight features is analyzed. The identified knowledge units include probability and statistics, trigonometric functions, coordinate systems and parametric equations, plane analytic geometry, solid geometry, selected topics in geometric proofs, derivatives, selected topics in inequalities, and sequences. The results show that different knowledge units have different levels of emphasis on the eight characteristics (Figure 7).
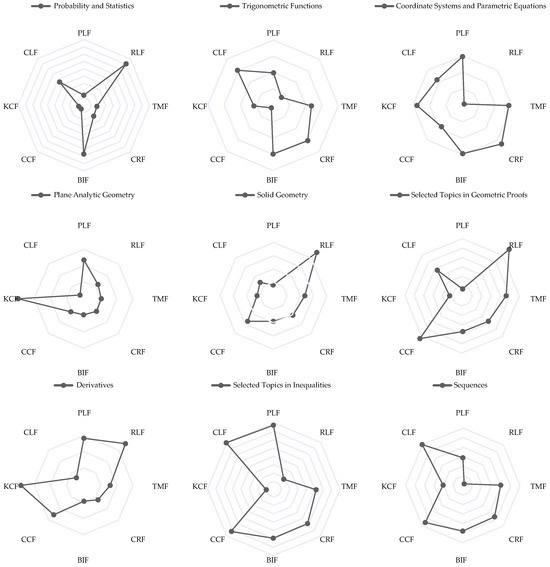
Figure 7.
Distribution of features in different knowledge units.
Figure 7 illustrates the distribution of each knowledge unit across eight features, which reveals varying levels of importance and focus. The distribution of knowledge units across different features reveals varying levels of importance and focus. For the “Inequality” knowledge unit, the distribution is relatively balanced, with a primary emphasis on the PLF, TMF, and CRF features. On the other hand, the “Derivative” knowledge unit exhibits a higher concentration in the PLF, TMF, CRF, CCF, and KCF features, particularly in the TMF and CRF features. Geometric proofs are mainly associated with the TMF feature, while analytic geometry demonstrates a significant presence in the PLF, TMF, CRF, CCF, and CLF features, particularly with higher distribution in the CRF and CLF features. Solid geometry shows a relatively balanced distribution across the PLF, TMF, CRF, and KCF features. Trigonometric functions and sequences exhibit a similar balanced distribution across the PLF, CRF, and CLF features. Statistics and probability are primarily associated with the CCF and KCF features, while coordinate and parametric equations are prominent in the PLF, CRF, KCF, and CLF features, with higher distribution in the CRF and CLF features. These findings contribute to a comprehensive understanding of the importance and distribution of features within each knowledge unit, providing valuable insights for further research and instructional.
6. Discussion
In this study, we utilized the past ten years’ subjective math items from the Chinese National College Entrance Examination and combined them with millions of students’ exam scores to establish an interpretable model, XGBoost-based SHAP, for predicting the difficulty of exam items. The training set and test set achieved accuracy rates of 0.99 and 0.806, respectively. We hypothesized that the item difficulty is determined by eight features and used SHAP model analysis to determine the importance of each feature relative to the item difficulty. We found that PLF and RLF were two significant factors influencing the difficulty of subjective items in the Chinese National College Entrance Examination. Additionally, we divided high school mathematics knowledge according to the Chinese curriculum standards into nine units [70]. We further analyzed the distribution of these nine knowledge units across the eight features to gain deeper insights into whether the influencing features on item difficulty vary across different knowledge units. Through this analysis, we reveal notable differences in the distribution of the eight features across different units of the textbook, which can assist teachers in placing different emphasis on different units during the instructional process. These findings have the potential to inform classroom practice by providing tools that are better aligned with and responsive to students’ learning needs.
6.1. Feature Analysis
Figure 6 gives a SHAP summary plot ranking the importance of features for item difficulty estimation. We can observe the features associated with item difficulty estimates and their importance ranking. This approach highlights the importance of each feature in determining item difficulty, reducing the ’black box’ of the model and increasing its interpretability compared to other models. The first and second research objectives of this study are solved. This section presents a detailed discussion of the first and second research objectives of this study.
PLF has the greatest influence on the model. Higher PLE value and higher SHAP value indicate that the item is more difficult. This is easy to understand because the more that unknown parameters are involved in the problem-solving process, the more information students need to solve the problem. This could increase the complexity of the question, as students have to consider more variables and factors. In addition, students may need to perform more calculation and analysis to solve the problem, which could also increase the difficulty of the item.
RLF and TMF are the next two most important features, with higher feature values indicating more difficult questions. Indeed, more complex reasoning steps and the examination of more knowledge points may require more thinking and calculation, thus making the question more difficult [71]. Especially when multiple knowledge items are integrated, students need to carefully distinguish the differences between them and practice, which may pose some challenge to their own knowledge thinking system [72]. At the same time, when multiple knowledge points are integrated, students may need to think creatively about how to solve the problem. This is because this type of question requires students to combine different knowledge points to generate new ideas and methods, thereby increasing the creativity and complexity of the item.
As for CCF, Figure 6 shows us an interesting result: the more characters an item has, the easier it is, and the fewer characters it has, the harder it is. This result is not difficult to understand and demonstrates a characteristic of mathematics itself: the effect of the use of symbolic language on the difficulty of questions. The use of symbolic mathematical language can make questions more concise and precise. At the same time, however, it can increase the abstractness of mathematical questions for students and thus increase their difficulty. Mathematical symbols make the mathematical expression of questions more abstract and symbolic, which can make mathematical questions more obscure and difficult for students to understand. It therefore poses a greater challenge to students’ mathematical and comprehension skills.
Subsequently, CLF also has a significant impact on question difficulty. The higher the cognitive level of the knowledge itself, the more difficult the question [73]. This may be because the Chinese Curriculum Standards require students to achieve a certain level of knowledge. Ref. [70] presents a SHAP summary plot ranking the importance of features for difficulty estimation of examination items.We can observe the features that are relevant for the difficulty estimation of examination questions, as well as their ranking of importance. And the higher the standard required, the deeper the examination of the questions by the test makers, thus making the questions more difficult.
The results for TMF show that, overall, the use of reverse thinking in the process of answering questions increases the difficulty of the question, but the effect is not significant. We can see that TMF has both positive and negative contributions to the difficulty of the question. This may be because the use of reverse thinking can lead to finding different perspectives and methods of solving problems, which can make some seemingly complex problems simpler and more direct than traditional methods, thereby reducing the amount of calculation and reasoning steps needed in the process of answering the question and thus reducing the difficulty of the question. We therefore conclude that backward and forward thinking do not have a direct effect on the difficulty of the question but rather depend on the nature of the question and the mathematical ability level of students.
In terms of CRF, as the computational complexity required to solve a problem increases, so does the difficulty of the problem [74,75]. Different types of mathematical operations are associated with different levels of difficulty in problems. In general, problems involving more complex operations are more difficult.
Finally, the BIF is the least important feature, which is very interesting and unexpected. In the Chinese GCE Mathematics examination, the context of the problem has relatively little effect on the difficulty of the problem. This may be because Chinese mathematics examiners focus on testing students’ basic concepts, skills and methods, emphasizing their problem-solving skills, and are relatively weak in testing the ability to identify and analyze problems [76]. As a result, items tend to lack background information and complexity.
In short, over the past decade, a variety of features have influenced the difficulty of subjective math questions on Chinese college entrance exam to varying degrees as illustrated in Figure 6. The figure provides a comprehensive overview of the relative importance of various features in estimating the test items’ difficulty. Educators can utilize the factors that have been identified to enhance the design of test papers and regulate the overall difficulty of test papers in order to better align with the diverse learning needs of students. Furthermore, this approach could facilitate the development of more targeted teaching strategies that would ultimately improve learning outcomes in mathematics education.
6.2. Distribution of Features in Different Knowledge Units
In this section, we divide high school mathematics knowledge into nine units [70] based on the Chinese curriculum standards, and further analyze the distribution of these eight features on the nine knowledge units to gain insights into whether there are differences in the influence of these characteristics on the difficulty of different knowledge units. In this section, we address the third research objective of this study; the results are shown in Figure 7.
In the realm of probability and statistics, it assumes paramount importance to cultivate students’ proficiency beyond fundamental concepts and mere probability computations. The focus should be directed towards nurturing their comprehension of statistical data, data organization and acquisition, data analysis and its interpretation, problem formulation and resolution, and fostering sound critical thinking skills. Our research findings indicate that within the domain of Chinese mathematics, questions pertaining to probability and statistics underscore the augmentation of question complexity in relation to features such as RLF, CLF, and BIF. This implies that China places a premium on evaluating students’ aptitude for data analysis, interpretation of statistical information, as well as the capacity to model and resolve problems in the context of probability and statistics inquiries. Nonetheless, there may exist certain lacunae in the domain of critical thinking.
Trigonometric functions, sequences, inequalities, and derivatives are typically categorized within the domain of functions. In the subjective question segment of the Chinese National College Entrance Examination for mathematics, there is a heightened emphasis on evaluating students’ grasp of and proficiency in handling functions. The incorporation of numerous variables in the examination questions elevates the intricacy of the computations involved. However, to a certain extent, this examination approach tends to neglect students’ capacity to employ functions for resolving real-world issues. This encompasses their ability to convert practical problems into functional models and to apply their functional knowledge in the process of problem resolution.
Coordinate systems and parametric equations, plane analytical geometry, solid geometry, and geometric proofs can be classified as part of the geometry section. In the subjective question section of the Chinese National College Entrance Examination Mathematics Test, there is a detailed examination of spatial visualization ability, graph analysis and judgment ability, geometric reasoning and proof ability, and geometric calculation and measurement ability. However, there is relatively little emphasis on the ability to apply geometric knowledge to solve practical problems.
Despite the curriculum reforms in China in 2017 and 2021 as highlighted by the Ministry of Education of P.R.o.C [70], which underscored the development of mathematical modeling skills encompassing the utilization of mathematical knowledge for practical problem-solving, this emphasis is not conspicuously manifested in the subjective question segment of the National College Entrance Examination. Mathematical modeling skills receive only modest assessment within the probability and statistics section, whereas they are scarcely addressed within the functions and geometry sections. This suggests that the current Chinese college entrance examination mathematics questions still lack the ability to examine mathematical modeling.
This analysis has revealed significant disparities in the distribution of the eight features across various units of the textbook. Overall, this study presents considerable potential for the field of mathematics education. It can equip teachers with more effective instructional support, enabling them to navigate the differences in teaching between distinct knowledge units. Moreover, it aids in comprehending the focal points and challenges of different knowledge units, assisting teachers in better understanding and addressing students’ learning needs.
6.3. Limitations and Future Directions
An important consideration to bear in mind pertains to the constraint imposed by our data sample in this study, which may not offer a comprehensive representation of all forms of assessments. Our research primarily centers on subjective mathematics items featured in the CNCEE. Consequently, the findings may not be readily extrapolated to various educational systems or diverse examination formats, such as those applicable to language subjects. Subsequent research endeavors could delve into assessing the suitability of the proposed approach across a broader spectrum of contexts and examination structures. This could involve the training of the model using items sourced from different countries and of various types, thereby validating the generalizability of the outcomes across student samples both within and outside of China.
Another noteworthy limitation pertains to the constraint imposed on the set of features. The paper’s focus on eight prominent features that exert an influence on the difficulty of mathematics test items signifies a significant starting point. Nevertheless, it is imperative to acknowledge that the complexity associated with item difficulty extends beyond the purview of these specific features alone. There may exist other pertinent factors that have not been incorporated into the analysis, potentially leaving crucial dimensions of difficulty unexplored. In order to mitigate this limitation, forthcoming research endeavors could consider an expansion of the feature set by incorporating additional variables or exploring the interplay among various features. By widening the spectrum of features under consideration, researchers can attain a more comprehensive grasp of the diverse factors that contribute to item difficulty. This expanded feature set may encompass cognitive factors such as problem-solving strategies, as well as critical aspects like item presentation format or language requirements.
The paper highlights the potential applications of the proposed approach in automatic test item generation and intelligent paper generation. However, it does not address the practical implementation or future directions for integrating the item difficulty assessment model into these systems. This provides an avenue for future research to explore and develop practical frameworks that utilize the proposed approach for automated item generation. Future research can explore the integration of the item difficulty assessment model into automated item generation systems to optimize the generation of well-balanced test items of varying difficulty levels. In addition, integrating the item difficulty rating model into intelligent paper generation systems can be explored to enable the dynamic assembly of test papers based on difficulty ratings, desired levels of challenge, and other relevant features. This integration enables educators and test administrators to create customized assessments that are aligned with educational objectives and take into account the diverse needs and abilities of students.
Author Contributions
Conceptualization, X.Y. and J.S.; methodology, X.Y. and J.S.; software, X.Y. and J.S.; validation, X.Y.; formal analysis, X.Y. and J.S.; investigation, X.Y. and J.S.; resources, X.W. and J.S.; data curation, X.Y.; writing—original draft preparation, X.Y.; writing—review and editing, X.W. and J.S.; supervision, X.W. and J.S.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (2021YFA1003400), Fundamental Research Funds for the Central Universities (2412023YQ006). This work was also support by China Industry-University-Research Innovation Fund (2022MU031).
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The author(s) declare that the manuscript has not been published in any journal, and there are no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Kurdi, G.; Leo, J.; Matentzoglu, N.; Parsia, B.; Sattler, U.; Forge, S.; Donato, G.; Dowling, W. A comparative study of methods for a priori prediction of MCQ difficulty. Semant. Web 2021, 12, 449–465. [Google Scholar] [CrossRef]
- El Masri, Y.H.; Ferrara, S.; Foltz, P.W.; Baird, J.A. Predicting item difficulty of science national curriculum tests: The case of key stage 2 assessments. Curric. J. 2017, 28, 59–82. [Google Scholar] [CrossRef]
- Choi, I.C.; Moon, Y. Predicting the Difficulty of EFL Tests Based on Corpus Linguistic Features and Expert Judgment. Lang. Assess. Q. 2020, 17, 18–42. [Google Scholar] [CrossRef]
- Sun, L.; Liu, Y.; Luo, F. Automatic Generation of Number Series Reasoning Items of High Difficulty. Front. Psychol. 2019, 10, 884. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Kang, B.; Zhou, L. Object Tracking by Unified Semantic Knowledge and Instance Features. IEICE Trans. Inf. Syst. 2019, E102.D, 680–683. [Google Scholar] [CrossRef]
- Gauezere, B.; Ritrovato, P.; Saggese, A.; Vento, M. Human Tracking Using a Top-Down and Knowledge Based Approach. In Proceedings of the 18th International Conference on Image Analysis and Processing (ICIAP), Genoa, Italy, 7–11 September 2015; Murino, V., Puppo, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9279, pp. 257–267. [Google Scholar] [CrossRef]
- Gierl, M.J.; Lai, H. Using Automatic Item Generation to Create Solutions and Rationales for Computerized Formative Testing. Appl. Psychol. Meas. 2018, 42, 42–57. [Google Scholar] [CrossRef]
- Attali, Y. Automatic Item Generation Unleashed: An Evaluation of a Large-Scale Deployment of Item Models. In Proceedings of the 19th International Conference on Artificial Intelligence in Education (AIED), London, UK, 27–30 June 2018; Rose, C., Martinez-Maldonado, R., Hoppe, H., Luckin, R., Mavrikis, M., Porayska-Pomsta, K., McLaren, B., DuBoulay, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10947, pp. 17–29. [Google Scholar] [CrossRef]
- Arendasy, M.E.; Sommer, M. Using automatic item generation to meet the increasing item demands of high-stakes educational and occupational assessment. Learn. Individ. Differ. 2012, 22, 112–117. [Google Scholar] [CrossRef]
- Stancheva, N.; Stoyanova-Doycheva, A.; Stoyanov, S.; Popchev, I.; Ivanova, V. An Environment for Automatic Test Generation. Cybern. Inf. Technol. 2017, 17, 183–196. [Google Scholar] [CrossRef]
- Klasnja-Milicevic, A.; Vesin, B.; Ivanovic, M.; Budimac, Z. E-Learning personalization based on hybrid recommendation strategy and learning style identification. Comput. Educ. 2011, 56, 885–899. [Google Scholar] [CrossRef]
- Tarus, J.K.; Niu, Z.; Mustafa, G. Knowledge-based recommendation: A review of ontology-based recommender systems for e-learning. Artif. Intell. Rev. 2018, 50, 21–48. [Google Scholar] [CrossRef]
- Fan, X. Item response theory and classical test theory: An empirical comparison of their item/person statistics. Educ. Psychol. Meas. 1998, 58, 357–381. [Google Scholar] [CrossRef]
- Zhan, P.; Jiao, H.; Liao, D. Cognitive diagnosis modelling incorporating item response times. Br. J. Math. Stat. Psychol. 2018, 71, 262–286. [Google Scholar] [CrossRef]
- Conejo, R.; Guzman, E.; Perez-de-la Cruz, J.L.; Barros, B. An empirical study on the quantitative notion of task difficulty. Expert Syst. Appl. 2014, 41, 594–606. [Google Scholar] [CrossRef]
- AlKhuzaey, S.; Grasso, F.; Payne, T.R.; Tamma, V. A Systematic Review of Data-Driven Approaches to Item Difficulty Prediction. In Proceedings of the 23rd International Conference, AIED 2022, Durham, UK, 27–31 July 2022; Roll, I., McNamara, D., Sosnovsky, S., Luckin, R., Dimitrova, V., Eds.; Springer: Cham, Switzerland, 2021; pp. 29–41. [Google Scholar]
- Pandarova, I.; Schmidt, T.; Hartig, J.; Boubekki, A.; Jones, R.D.; Brefeld, U. Predicting the Difficulty of Exercise Items for Dynamic Difficulty Adaptation in Adaptive Language Tutoring. Int. J. Artif. Intell. Educ. 2019, 29, 342–367. [Google Scholar] [CrossRef]
- Lim, E.C.H.; Ong, B.K.C.; Wilder-Smith, E.P.V.; Seet, R.C.S. Computer-based versus pen-and-paper testing: Students’ perception. Ann. Acad. Med. Singap. 2006, 35, 599–603. [Google Scholar] [CrossRef] [PubMed]
- Wei, T.; Fei, W.; Qi, L.; Enhong, C. Data Driven Prediction for the Difficulty of Mathematical Items. J. Comput. Res. Dev. 2019, 56, 1007–1019. [Google Scholar]
- Pollitt, A.; Marriott, C.; Ahmed, A. Language, Contextual and Cultural Constraints on Examination Performance. Presented at the International Association for Educational Assessment, Jerusalem, Israel, 14–19 May 2000. [Google Scholar]
- Kubinger, K.D.; Gottschall, C.H. Item difficulty of multiple choice tests dependant on different item response formats—An experiment in fundamental research on psychological assessment. Psychol. Sci. 2007, 49, 1–8. [Google Scholar]
- Susanti, Y.; Nishikawa, H.; Tokunaga, T.; Obari, H. Item Difficulty Analysis of English Vocabulary Questions. In Proceedings of the International Conference on Computer Supported Education (CSEDU 2016), Rome, Italy, 21–23 April 2016. [Google Scholar]
- Zhong, S.; Zhang, K.; Wang, D.; Zhang, H. Shedding light on “Black Box” machine learning models for predicting the reactivity of HO center dot radicals toward organic compounds. Chem. Eng. J. 2021, 405, 126627. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for N-Person Games; RAND Corporation: Santa Monica, CA, USA, 1952. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Janelli, M.; Lipnevich, A.A. Effects of pre-tests and feedback on performance outcomes and persistence in Massive Open Online Courses. Comput. Educ. 2021, 161, 104076. [Google Scholar] [CrossRef]
- Sreelatha, V.K.; Manjula, V.D.; Kumar, R.S. Pre-Test as a Stimulant to Learning for Undergraduates in Medicine. J. Evol. Med. Dent. Sci. 2019, 8, 3886–3889. [Google Scholar] [CrossRef]
- Harrison, S.; Kroehne, U.; Goldhammer, F.; Luedtke, O.; Robitzsch, A. Comparing the score interpretation across modes in PISA: An investigation of how item facets affect difficulty. Large-Scale Assess. Educ. 2023, 11, 8. [Google Scholar] [CrossRef]
- DeVellis, R.F. Classical test theory. Med. Care 2006, 44, S50–S59. [Google Scholar] [CrossRef] [PubMed]
- Kohli, N.; Koran, J.; Henn, L. Relationships Among Classical Test Theory and Item Response Theory Frameworks via Factor Analytic Models. Educ. Psychol. Meas. 2015, 75, 389–405. [Google Scholar] [CrossRef] [PubMed]
- Garcia Pinzon, I.; Olivera Aguilar, M. Noncognitive factors related to academic performance. Rev. Educ. 2022, 398, 161–192. [Google Scholar] [CrossRef]
- Yaneva, V.; Ha, L.A.; Baldwin, P.; Mee, J. Predicting Item Survival for Multiple Choice Questions in a High-stakes Medical Exam. In Proceedings of the 12th International Conference on Language Resources and Evaluation (LREC), Marseille, France, 11–16 May 2020; Calzolari, N., Bechet, F., Blache, P., Choukri, K., Cieri, C., Declerck, T., Goggi, S., Isahara, H., Maegaard, B., Mariani, J., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 6812–6818. [Google Scholar]
- Fu-Yuan, H.; Hahn-Ming, L.; Tao-Hsing, C.; Yao-Ting, S. Automated estimation of item difficulty for multiple-choice tests: An application of word embedding techniques. Inf. Process. Manag. 2018, 54, 969–984. [Google Scholar] [CrossRef]
- Zhang, S.; Bergner, Y.; DiTrapani, J.; Jeon, M. Modeling the interaction between resilience and ability in assessments with allowances for multiple attempts. Comput. Hum. Behav. 2021, 122, 106847. [Google Scholar] [CrossRef]
- Wu, S.F.; Kao, C.H.; Lu, Y.L.; Lien, C.J. A Method Detecting Student’s Flow Construct during School Tests through Electroencephalograms (EEGs): Factors of Cognitive Load, Self-Efficacy, Difficulty, and Performance. Appl. Sci. 2022, 12, 12248. [Google Scholar] [CrossRef]
- Golino, H.F.; Gomes, C.M.A. Random forest as an imputation method for education and psychology research: Its impact on item fit and difficulty of the Rasch model. Int. J. Res. Method Educ. 2016, 39, 401–421. [Google Scholar] [CrossRef]
- Wang, C.D.; Xi, W.D.; Huang, L.; Zheng, Y.Y.; Hu, Z.Y.; Lai, J.H. A BP Neural Network Based Recommender Framework With Attention Mechanism. IEEE Trans. Knowl. Data Eng. 2022, 34, 3029–3043. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Shang, J.S. PAENL: Personalized attraction enhanced network learning for recommendation. Neural Comput. Appl. 2023, 35, 3725–3735. [Google Scholar] [CrossRef]
- von Davier, M. Automated Item Generation with Recurrent Neural Networks. Psychometrika 2018, 83, 847–857. [Google Scholar] [CrossRef]
- Hachmann, W.M.; Bogaerts, L.; Szmalec, A.; Woumans, E.; Duyck, W.; Job, R. Short-term memory for order but not for item information is impaired in developmental dyslexia. Ann. Dyslexia 2014, 64, 121–136. [Google Scholar] [CrossRef] [PubMed]
- Gorin, J.S.; Embretson, S.E. Item difficulty modeling of paragraph comprehension items. Appl. Psychol. Meas. 2006, 30, 394–411. [Google Scholar] [CrossRef]
- Stiller, J.; Hartmann, S.; Mathesius, S.; Straube, P.; Tiemann, R.; Nordmeier, V.; Krueger, D.; Belzen, A.U.Z. Assessing scientific reasoning: A comprehensive evaluation of item features that affect item difficulty. Assess. Eval. High. Educ. 2016, 41, 721–732. [Google Scholar] [CrossRef]
- Rodriguez-Perez, R.; Bajorath, J. Interpretation of machine learning models using shapley values: Application to compound potency and multi-target activity predictions. J. Comput.-Aided Mol. Des. 2020, 34, 1013–1026. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zheng, K.; Yang, Y.; Wang, X. An Explainable Machine Learning Framework for Intrusion Detection Systems. IEEE Access 2020, 8, 73127–73141. [Google Scholar] [CrossRef]
- Saleem, R.; Yuan, B.; Kurugollu, F.; Anjum, A.; Liu, L. Explaining deep neural networks: A survey on the global interpretation methods. Neurocomputing 2022, 513. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip.-Rev.-Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Abidi, S.M.R.; Hussain, M.; Xu, Y.; Zhang, W. Prediction of Confusion Attempting Algebra Homework in an Intelligent Tutoring System through Machine Learning Techniques for Educational Sustainable Development. Sustainability 2019, 11, 105. [Google Scholar] [CrossRef]
- Asselman, A.; Khaldi, M.; Aammou, S. Enhancing the prediction of student performance based on the machine learning XGBoost algorithm. Interact. Learn. Environ. 2023, 31, 3360–3379. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 30. [Google Scholar]
- Giannakas, F.; Troussas, C.; Voyiatzis, I.; Sgouropoulou, C. A deep learning classification framework for early prediction of team-based academic performance. Appl. Soft Comput. 2021, 106, 107355. [Google Scholar] [CrossRef]
- Zhai, M.; Wang, S.; Wang, Y.; Wang, D. An interpretable prediction method for university student academic crisis warning. Complex Intell. Syst. 2022, 8, 323–336. [Google Scholar] [CrossRef]
- Sahlaoui, H.; Alaoui, E.A.A.; Nayyar, A.; Agoujil, S.; Jaber, M.M. Predicting and Interpreting Student Performance Using Ensemble Models and Shapley Additive Explanations. IEEE Access 2021, 9, 152688–152703. [Google Scholar] [CrossRef]
- Kashani, H.; Movahedi, A.; Morshedi, M.A. An agent-based simulation model to evaluate the response to seismic retrofit promotion policies. Int. J. Disaster Risk Reduct. 2019, 33, 181–195. [Google Scholar] [CrossRef]
- Nohara, D. A Comparison of the National Assessment of Educational Progress (NAEP), the Third International Mathematics and Science Study Repeat (TIMSS-R), and the Programme for International Student Assessment (PISA); National Center for Education Statistics: Washington, DC, USA, 2001.
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests. In Achievement Tests; American Psychological Association: Washington, DC, USA, 1993; p. 199. [Google Scholar]
- Johnson, R.; Zhang, T. Learning Nonlinear Functions Using Regularized Greedy Forest. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 942–954. [Google Scholar] [CrossRef] [PubMed]
- Rubin, W. Principles of Mathematical Analysis; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining Prediction Models and Individual Predictions with Feature Contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Ala’raj, M.; Abbod, M.F. Classifiers consensus system approach for credit scoring. Knowl.-Based Syst. 2016, 104, 89–105. [Google Scholar] [CrossRef]
- Finlay, S. Multiple classifier architectures and their application to credit risk assessment. Eur. J. Oper. Res. 2011, 210, 368–378. [Google Scholar] [CrossRef]
- Mujahid, M.; Lee, E.; Rustam, F.; Washington, P.B.; Ullah, S.; Reshi, A.A.; Ashraf, I. Sentiment Analysis and Topic Modeling on Tweets about Online Education during COVID-19. Appl. Sci. 2021, 11, 8438. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Hand, D.J. Classifier technology and the illusion of progress. Stat. Sci. 2006, 21, 1–14. [Google Scholar] [CrossRef]
- Ministry of Education of the People’s Republic of China. Curriculum Standard for Mathematics in Senior High School (2017 Edition, Revised 2020); China People’s Education Press: Beijing, China, 2020. [Google Scholar]
- Knight, J.K.; Wise, S.B.; Southard, K.M. Understanding Clicker Discussions: Student Reasoning and the Impact of Instructional Cues. CBE-Life Sci. Educ. 2013, 12, 645–654. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.L. Trends of mobile learning: A review of the top 100 highly cited papers. Br. J. Educ. Technol. 2020, 51, 721–742. [Google Scholar] [CrossRef]
- van de Weijer-bergsma, E.; van der Ven, S.H.G. Why and for whom does personalizing math problems enhance performance? Testing the mediation of enjoyment and cognitive load at different ability levels. Learn. Individ. Differ. 2021, 87, 101982. [Google Scholar] [CrossRef]
- Grover, S.; Pea, R. Computational Thinking in K-12: A Review of the State of the Field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Wing, J.M. Computational thinking and thinking about computing. Philos. Trans. R. Soc.-Math. Phys. Eng. Sci. 2008, 366, 3717–3725. [Google Scholar] [CrossRef] [PubMed]
- Ozkan, G.; Selcuk, G.S. The effectiveness of conceptual change texts and context-based learning on students’ conceptual achievement. J. Balt. Sci. Educ. 2015, 14, 753–763. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).