Enhanced Efficiency of MHD-Driven Double-Diffusive Natural Convection in Ternary Hybrid Nanofluid-Filled Quadrantal Enclosure: A Numerical Study
Abstract
1. Introduction
2. Physical Model
3. Mathematical Formulations
3.1. Governing Equations
3.2. Thermophysical Properties of Ternary Hybrid Nanofluid
4. Numerical Technique
5. Result and Discussion
6. Conclusions
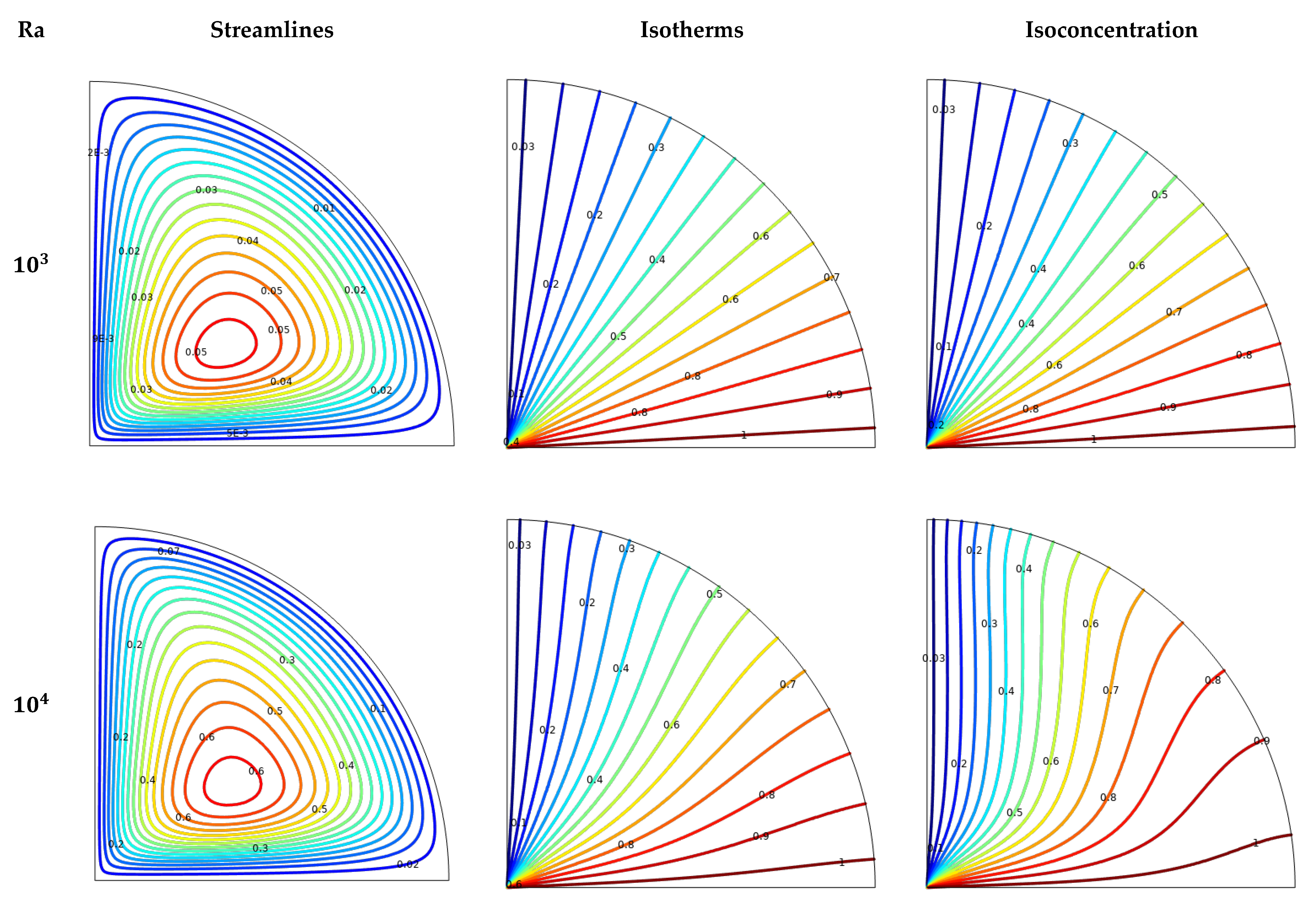
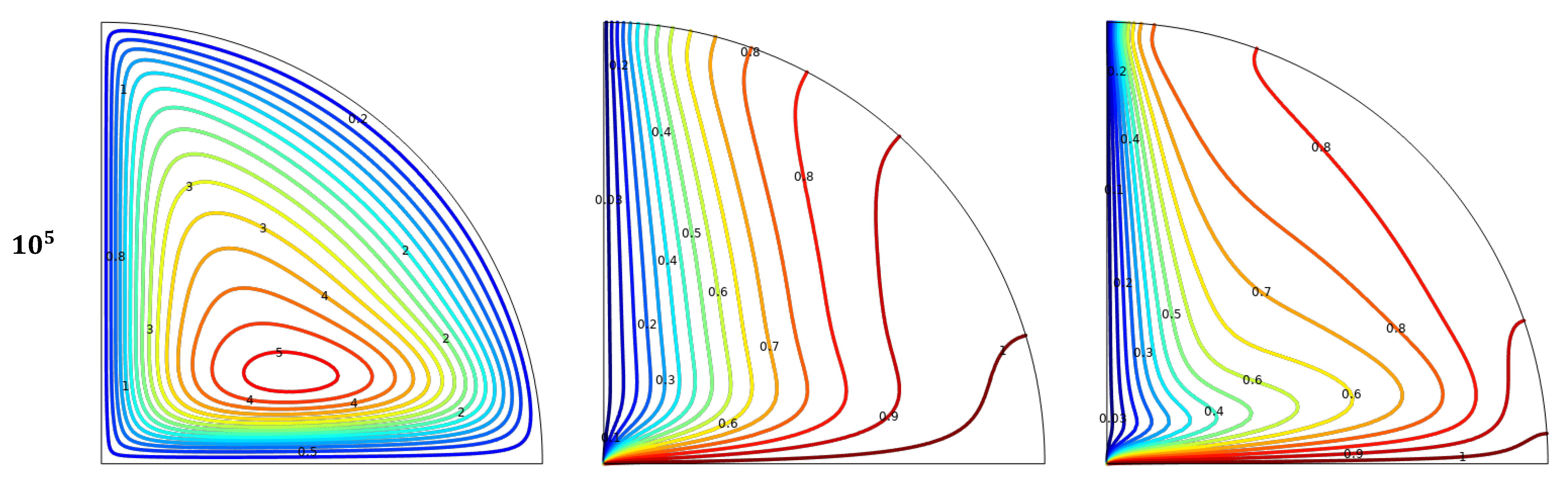
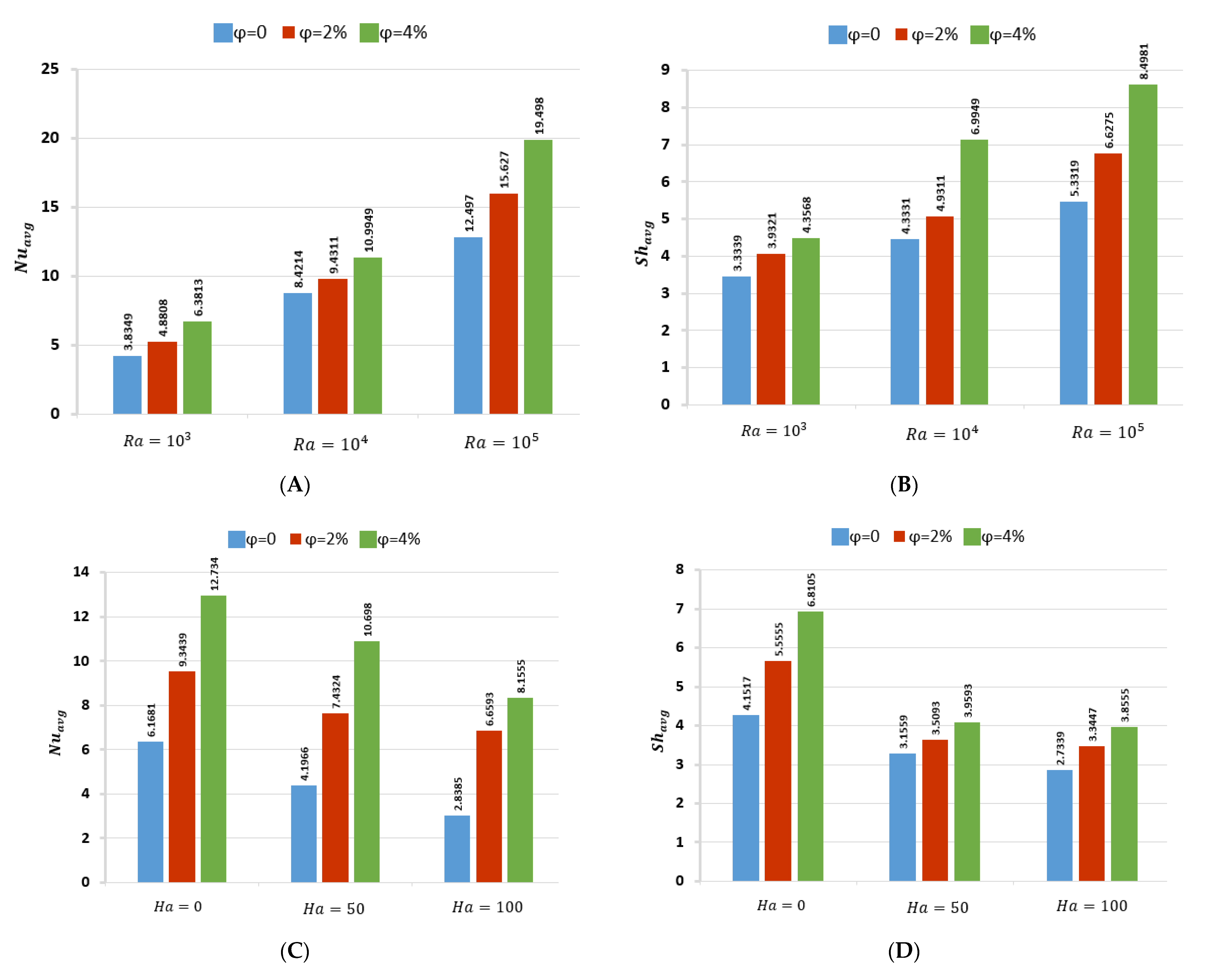
- Increasing the Rayleigh number from to results in a marked enhancement of buoyancy-induced flow within the cavity;
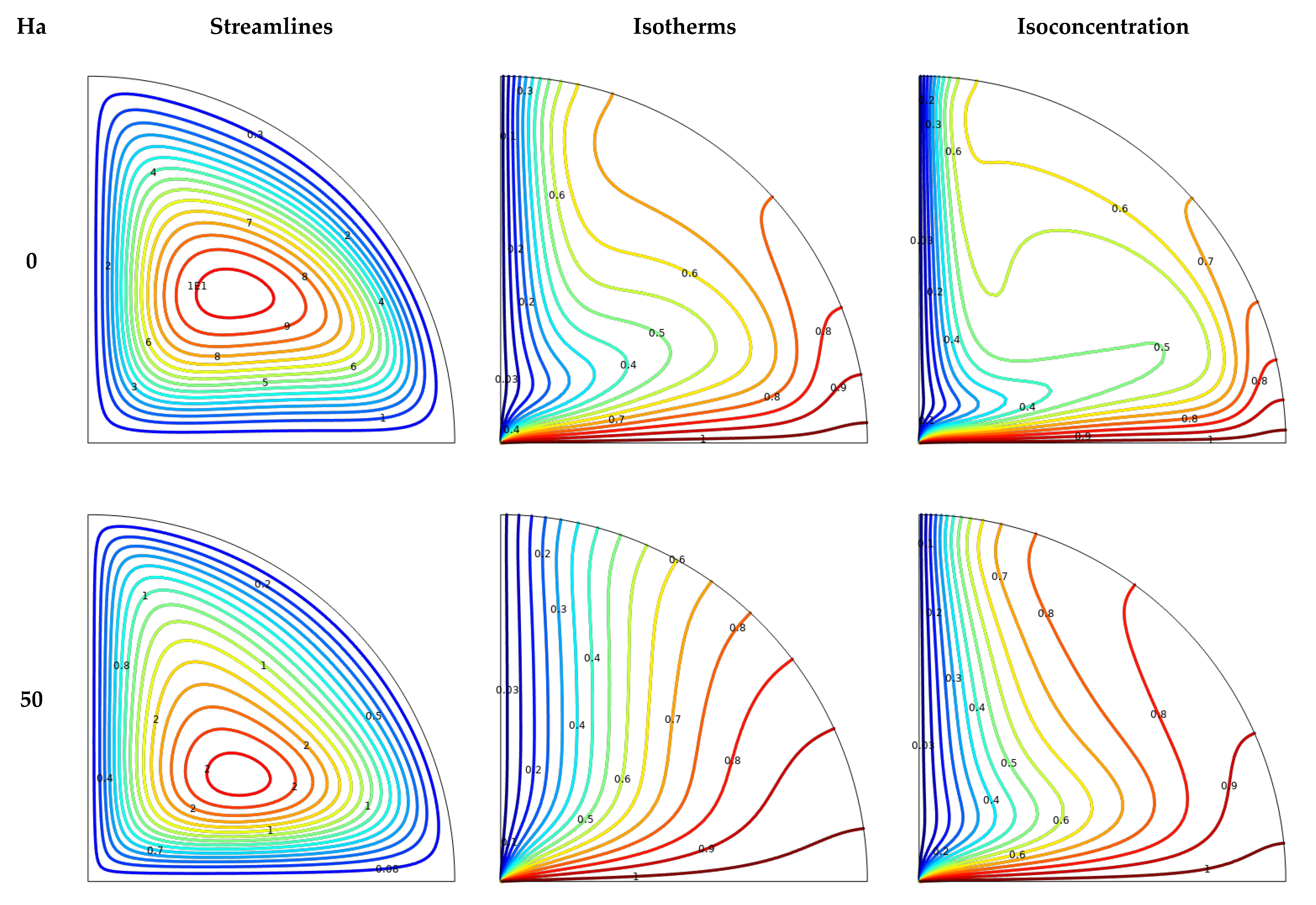
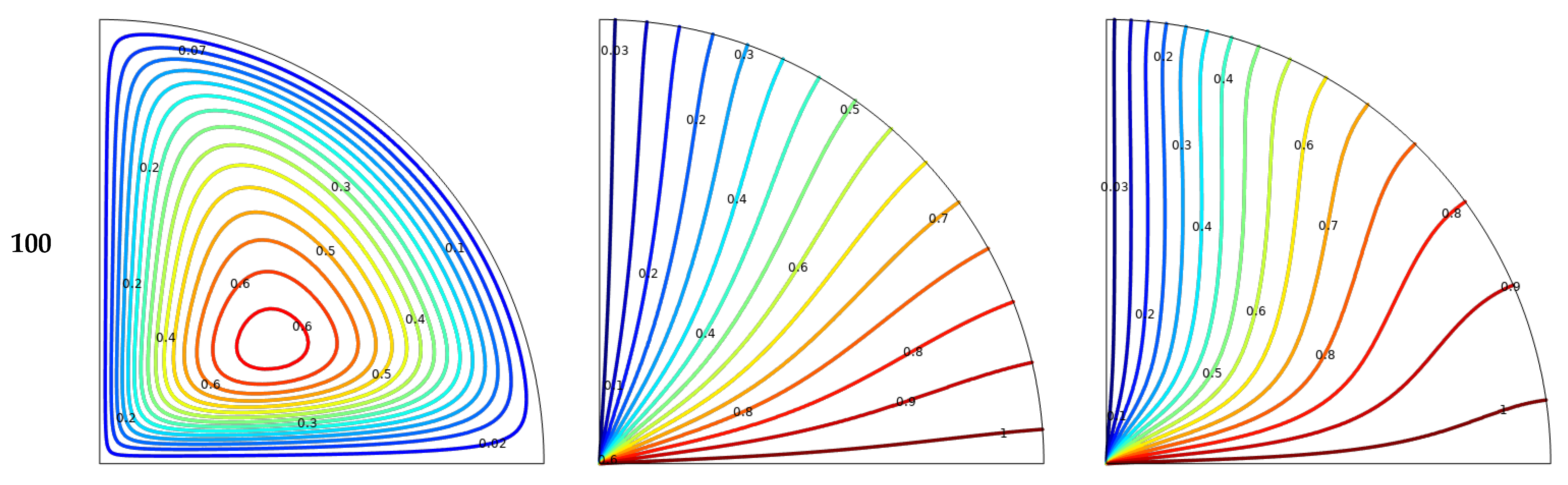
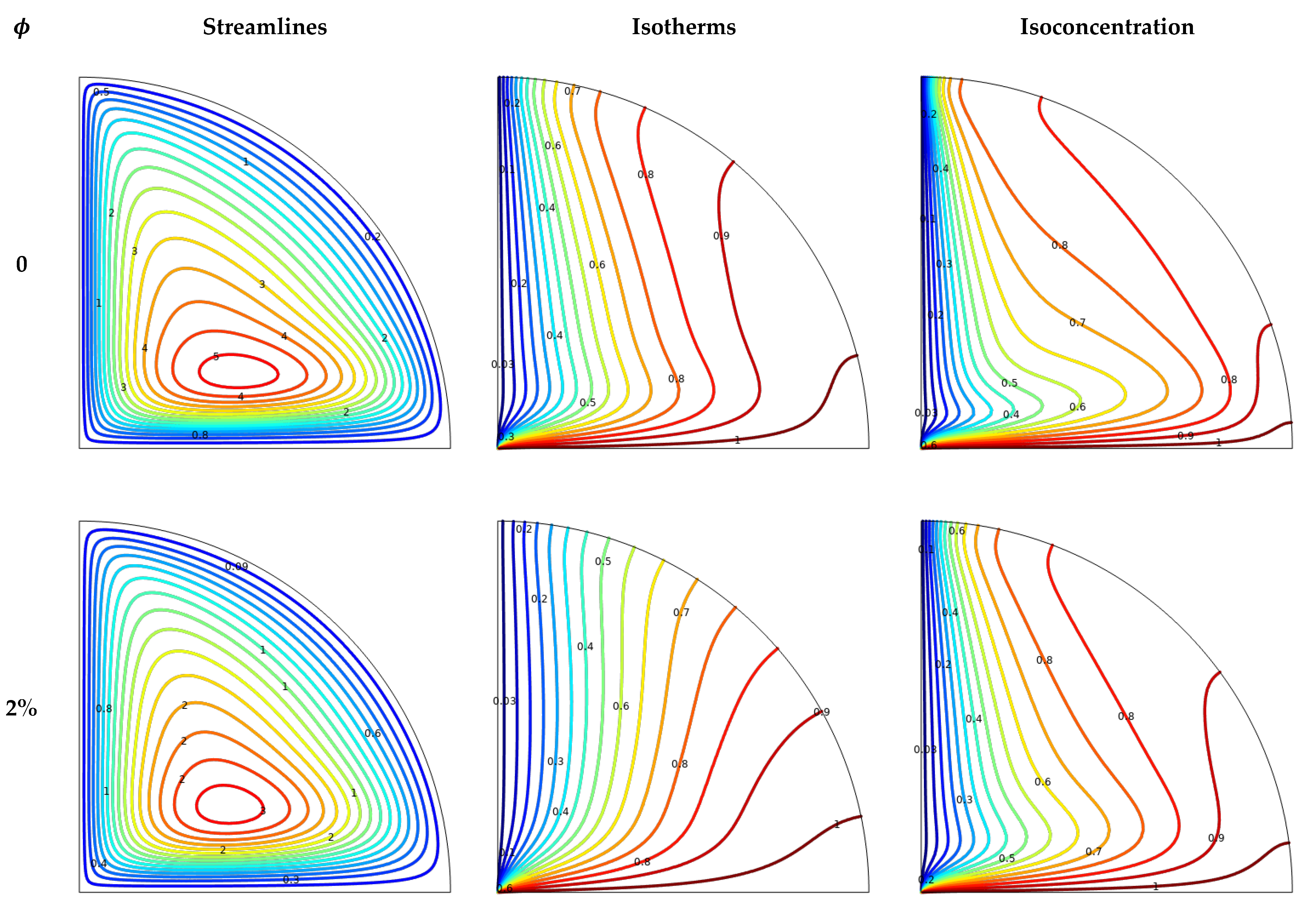
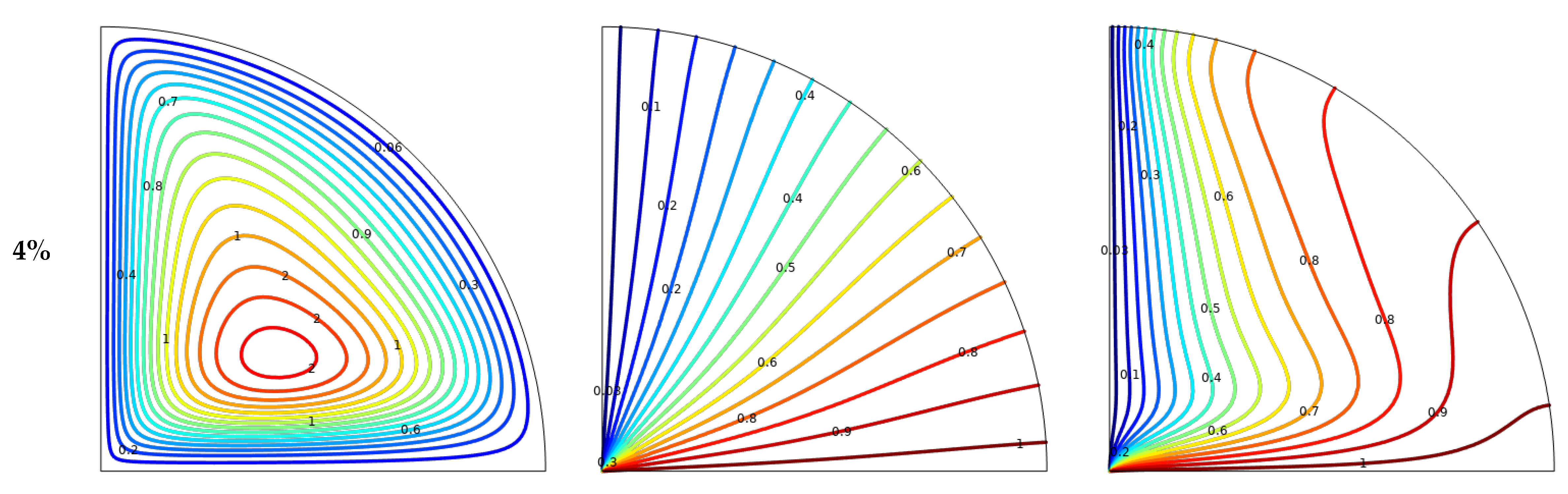
- Fluid flow intensity significantly increases with the rise in Rayleigh number (Ra) values, yet it diminishes with an increase in magnetic field strength and nanoparticle volume fraction. Moreover, under conditions of higher Ra and lower Hartmann number (Ha) and volume fraction (ϕ), isotherms and particle distributions become more concentrated;
- The and numbers show an upward trend with higher Rayleigh numbers and nanoparticle volume fractions. However, these average values decrease as the Hartmann number increases;
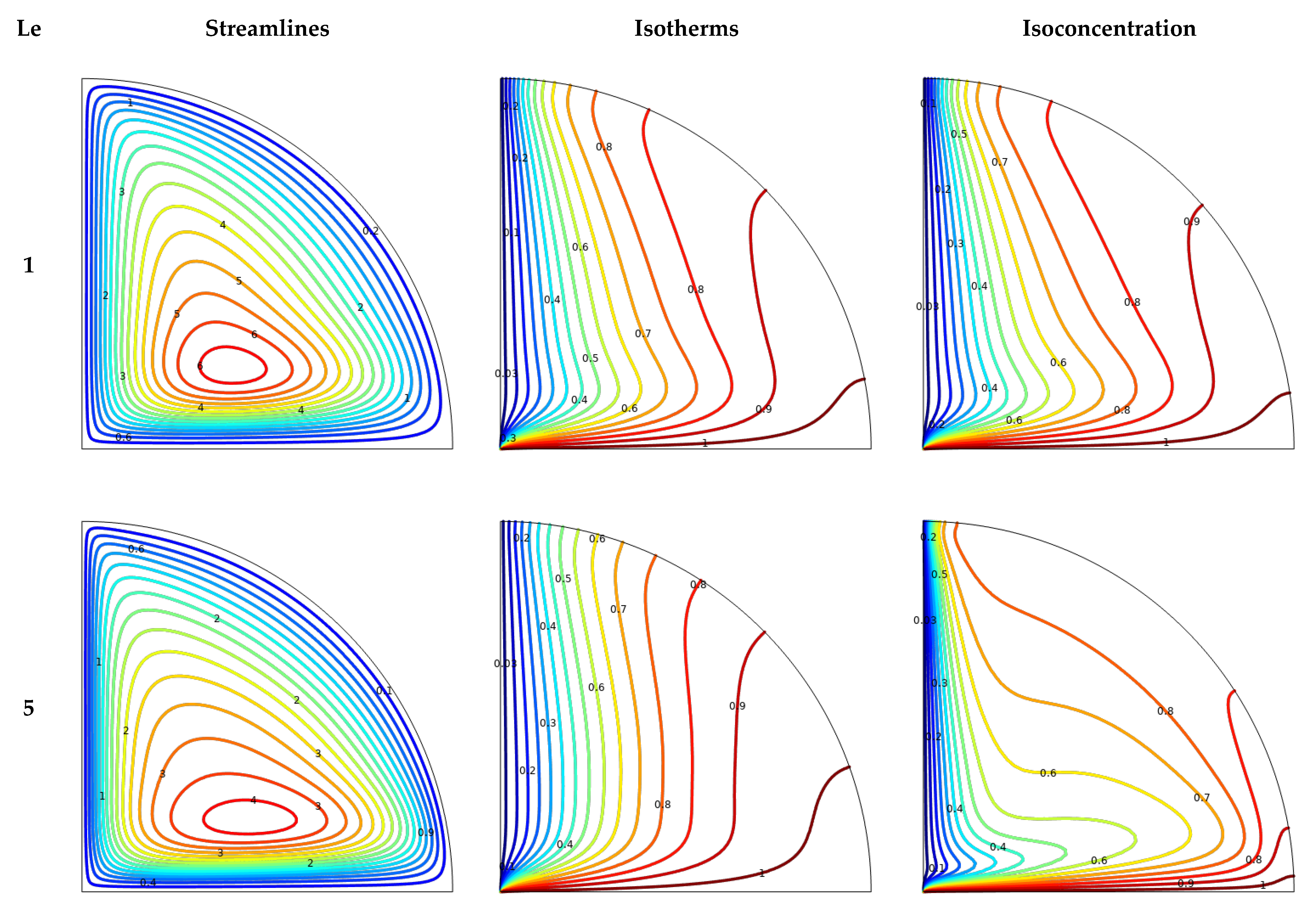
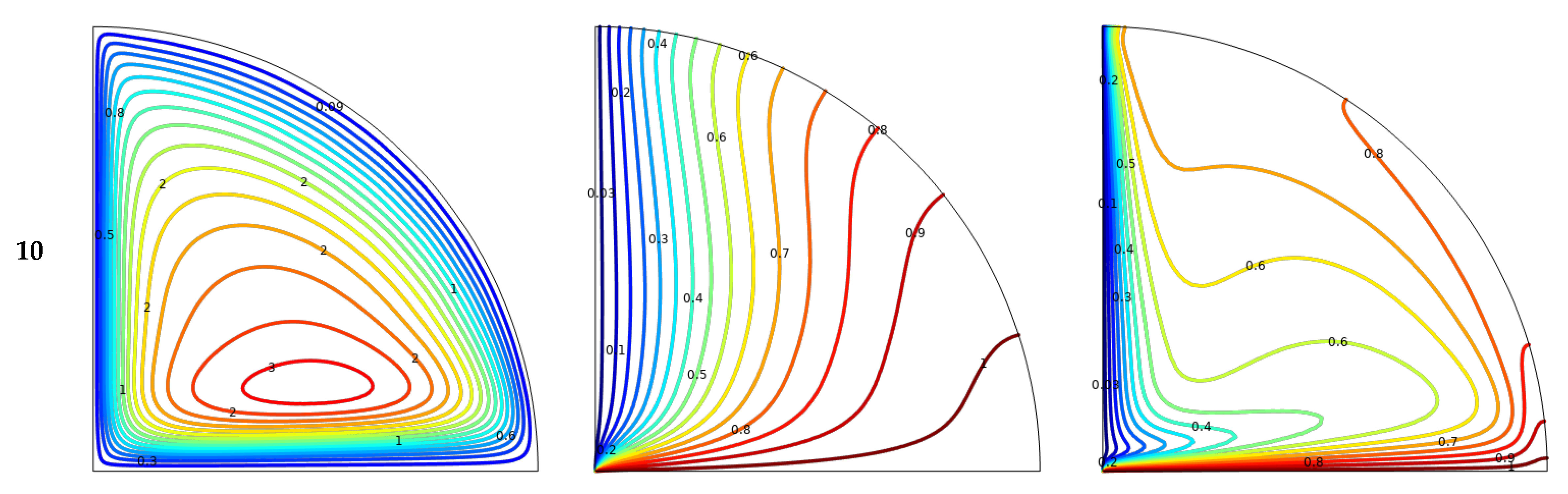
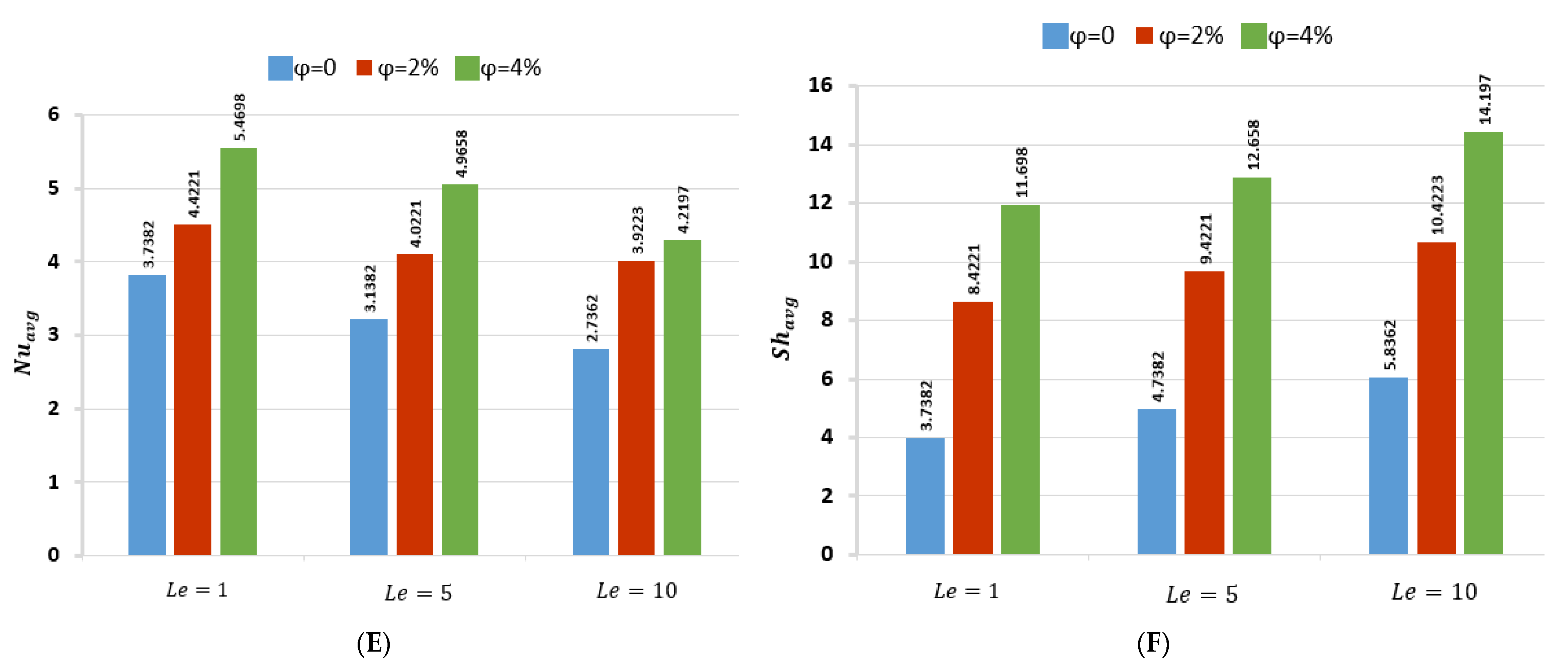
- With an increase in the Lewis number, the rate of heat transfer decreases, while the mass transfer rate increases;
- The introduction of Cu-CuO-Al2O3 nanoparticles into the base fluid (water) reduces the intensity of convective flow but is notably effective in enhancing heat and mass transfer rates, exceeding the performance achievable without nanoparticles;
- The study reveals that increasing the concentration of Cu-CuO-Al2O3 nanoparticles in the base fluid significantly boosts heat transfer efficiency, potentially enhancing it by up to 78% compared to the base fluid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Copper | Copper(II) oxide | ||
| Al2O3 | Alumina | Sherwood number | |
| g | Gravitational acceleration | Magnetic field strength | |
| Cartesian coordinates | Dynamic viscosity | ||
| Dimensionless coordinates | Dimensionless temperature | ||
| Dimensionless concentration | concentration | ||
| Velocity components in directions | T | Temperature | |
| Dimensionless velocity components | Fluid pressure | ||
| Density | Dimensionless pressure | ||
| Enclosure length | Thermal conductivity | ||
| Pr | Prandtl number | Thermal diffusivity | |
| Kinematic viscosity | Nu | Nusselt number | |
| Cu nanoparticles volume fraction | CuO nanoparticles volume fraction | ||
| Al2O3 nanoparticles volume fraction | |||
| Ra | Rayleigh number | Subscripts | |
| Ha | Hartmann number | Cold wall | |
| Solid volume fraction | Hot wall | ||
| Shape of nanoparticle | Fluid (pure water) | ||
| Specific heat | Nanofluid | ||
| Thermal expansion coefficient | Hybrid nanofluid | ||
| Electrically conductivity | Ternary hybrid nanofluid | ||
References
- Rashed, Z.Z.; Ahmed, S.E. Unsteady three dimensional radiative-convective flow and heat transfer of dusty nanofluid within porous cubic enclosures. J. Dispersion Sci. Technol. 2023, 44, 189–203. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Tian, Z. A fourth-order compact difference algorithm for numerical solution of natural convection in an inclined square enclosure. Numer. Heat Transf. Part A Appl. 2021, 80, 255–290. [Google Scholar] [CrossRef]
- Ostrach, S. Natural convection in enclosures. ASME J. Heat Transfer. 1988, 110, 1175–1190. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; United States; Department of Energy: Washington, DC, USA, 1995. [Google Scholar]
- Mozafari, B.; Arani, A.; Sheikhzadeh, G.A.; Salimi, M. Brownian models effect on turbulent fluid flow and heat transfer and entropy generation of water/boehmite alumina nanofluid inside enclosure. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 2305–2327. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Alsaedi, A. Optimization of entropy generation in motion of magnetite-Fe3O4 nanoparticles due to curved stretching sheet of variable thickness. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3347–3365. [Google Scholar] [CrossRef]
- Bibi, A.; Xu, H.; Sun, Q.; Pop, I.; Zhao, Q. Free convection of a hybrid nanofluid past a vertical plate embedded in a porous medium with anisotropic permeability. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4083–4101. [Google Scholar] [CrossRef]
- Shadloo, M.S. Application of support vector machines for accurate prediction of convection heat transfer coefficient of nanofluids through circular pipes. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 2660–2679. [Google Scholar] [CrossRef]
- Roşca, C.N.; Roşca, A.V.; Pop, I. Axisymmetric flow of hybrid nanofluid due to a permeable non-linearly stretching/shrinking sheet with radiation effect. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2330–2346. [Google Scholar] [CrossRef]
- Thirumalaisamy, K.; Ramachandran, S.; Ramachandra Prasad, V.; Bég, O.A.; Leung, H.; Kamalov, F.; Vajravelu, K. Comparative heat transfer analysis of γ-Al2O3−C2H6O2 and γ-Al2O3−H2O electroconductive nanofluids in a saturated porous square cavity with Joule dissipation and heat source/sink effects. Phys. Fluids 2022, 34, 072001. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Toghraie, D.; Mashayekhi, R.; Akbari, O.A. Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single-and two-phase approaches. J. Therm. Anal. Calor. 2019, 138, 779–794. [Google Scholar] [CrossRef]
- Mashaei, P.R.; Hosseinalipour, S.M.; Bahiraei, M. Numerical investigation of nanofluid forced convection in channels with discrete heat sources. J. Appl. Math. 2012, 2012, 259284. [Google Scholar]
- Mousavi, S.M.; Esmaeilzadeh, F.; Wang, X.P. Effects of temperature and particles volume concentration on the thermophysical properties and the rheological behavior of CuO/MgO/TiO2 aqueous ternary hybrid nanofluid: Experimental investigation. J. Therm. Anal. Calorim. 2019, 137, 879–901. [Google Scholar] [CrossRef]
- Cakmak, N.K.; Said, Z.; Sundar, L.S.; Ali, Z.M.; Tiwari, A.K. Preparation, characterization, stability, and thermal conductivity of rGO-Fe3O4-TiO2 hybrid nanofluid: An experimental study. Powder Technol. 2020, 372, 235–245. [Google Scholar] [CrossRef]
- Sahoo, R.R. Heat transfer and second law characteristics of radiator with dissimilar shape nanoparticle-based ternary hybrid nanofluid. J. Therm. Anal. Calorim. 2021, 146, 827–839. [Google Scholar] [CrossRef]
- Dezfulizadeh, A.; Aghaei, A.; Joshaghani, A.H.; Najafizadeh, M. An experimental study on dynamic viscosity and thermal conductivity of water-Cu-SiO2-MWCNT ternary hybrid nanofluid and the development of practical correlations. Powder Technol. 2021, 389, 215–234. [Google Scholar] [CrossRef]
- Das, S.; Ali, A.; Jana, R.N.; Makinde, O.D. EDL impact on mixed magneto-convection in a vertical channel using ternary hybrid nanofluid. Chem. Eng. J. Adv. 2022, 12, 100412. [Google Scholar] [CrossRef]
- Huppert, E.H.; Turner, J.S. Double-diffusive convection. J. Fluid Mech. 1981, 106, 299–329. [Google Scholar] [CrossRef]
- Lee, J.W.; Hyun, J.M. Double-diffusive convection in a rectangle with opposing horizontal temperature and concentration gradients. Int. J. Heat Mass Transfer 1990, 33, 1619–1632. [Google Scholar] [CrossRef]
- Ghorayeb, K.; Mojtabi, A. Double diffusive convection in a vertical rectangular cavity. Phys. Fluids 1997, 9, 2339–2348. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Pal, D.; Mondal, S. Effects of buoyancy ratio on double-diffusive natural convection in a lid-driven cavity. Int. J. Heat Mass Transfer 2013, 57, 771–785. [Google Scholar] [CrossRef]
- Ghasemi, B.; Aminossadati, S.M.; Raisi, A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int. J. Therm. Sci. 2011, 50, 1748–1756. [Google Scholar] [CrossRef]
- Teamah, M.A. Numerical simulation of double diffusive natural convection in rectangular enclosure in the presences of magnetic field and heat source. Int. J. Therm. Sci. 2008, 47, 237–248. [Google Scholar] [CrossRef]
- Teamah, M.A.; Shehata, A.I. Magnetohydrodynamic double diffusive natural convection in trapezoidal cavities. Alexandria Eng. J. 2016, 55, 1037–1046. [Google Scholar] [CrossRef]
- Rahman, M.M.; Saidur, R.; Rahim, N.A. Conjugated effect of joule heating and magneto-hydrodynamic on double-diffusive mixed convection in a horizontal channel with an open cavity. Int. J. Heat Mass Transfer 2011, 54, 3201–3213. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Saha, B.C.; Pal, D. Magnetohydrodynamic double-diffusive natural convection for nanofluid within a trapezoidal enclosure. Comput. Appl. Math. 2018, 37, 6132–6151. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, X.; Zhang, H. A BDF3 and new nonlinear fourth-order difference scheme for the generalized viscous Burgers’ equation. Appl. Math. Lett. 2024, 151, 109002. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Zhou, Z.; Yang, X. A fast compact finite difference scheme for the fourth-order diffusion-wave equation. Int. J. Comput. Math. 2024, 101, 170–193. [Google Scholar] [CrossRef]
- Xiao, W.; Yang, X.; Zhou, Z. Pointwise-in-time α-robust error estimate of the ADI difference scheme for three-dimensional fractional subdiffusion equations with variable coefficients. Commun. Anal. Mech 2024, 16, 53–70. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, H.; Yang, X. CN ADI fast algorithm on non-uniform meshes for the three-dimensional nonlocal evolution equation with multi-memory kernels in viscoelastic dynamics. Appl. Math. Comput. 2024, 474, 128680. [Google Scholar] [CrossRef]
- Yang, X.; Qiu, W.; Chen, H.; Zhang, H. Second-order BDF ADI Galerkin finite element method for the evolutionary equation with a nonlocal term in three-dimensional space. Appl. Numer. Math. 2022, 172, 497–513. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, H.; Yang, X.; Wang, F. A second-order finite difference method for the multi-term fourth-order integral–differential equations on graded meshes. Comput. Appl. Math. 2022, 41, 313. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z. On conservative, positivity preserving, nonlinear FV scheme on distorted meshes for the multi-term nonlocal Nagumo-type equations. Appl. Math. Lett. 2024, 150, 108972. [Google Scholar] [CrossRef]
- Wang, F.; Yang, X.; Zhang, H.; Wu, L. A time two-grid algorithm for the two dimensional nonlinear fractional PIDE with a weakly singular kernel. Math. Comput. Simul. 2022, 199, 38–59. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Yang, X. A new nonlinear compact difference scheme for a fourth-order nonlinear Burgers type equation with a weakly singular kernel. J. Appl. Math. Comput. 2024, 1–33. [Google Scholar] [CrossRef]
- Eshaghi, S.; Izadpanah, F.; Dogonchi, A.S.; Chamkha, A.J.; Hamida, M.B.B.; Alhumade, H. The optimum double diffusive natural convection heat transfer in H-Shaped cavity with a baffle inside and a corrugated wall. Case Stud. Therm. Eng. 2021, 28, 101541. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Unsteady convection flow of some nanofluids past a moving vertical flat plate with heat transfer. J. Heat Transfer 2014, 136, 031704. [Google Scholar] [CrossRef]
- Rajesh, V.; Sheremet, M. Free Convection in a Square Ternary Hybrid Nanoliquid Chamber with Linearly Heating Adjacent Walls. Nanomaterials 2023, 13, 2860. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics®, version 5.2; COMSOL AB: Stockholm, Sweden, 1998. Available online: www.comsol.com (accessed on 5 March 1998).
- Dutta, S.; Pati, S.; Baranyi, L. Numerical analysis of magnetohydrodynamic natural convection in a nanofluid filled quadrantal enclosure. Case Stud. Therm. Eng. 2021, 28, 101507. [Google Scholar] [CrossRef]
- Bilal, S.; Shah, I.A.; Khan, I.; Al-Otaibi, S.; Rahimzai, A.A. FEM simulations for double diffusive transport mechanism hybrid nano fluid flow in corrugated enclosure by installing uniformly heated and concentrated cylinder. Sci. Rep. 2024, 14, 766. [Google Scholar] [CrossRef]
- Shah, I.A.; Bilal, S.; Muhammad, T.; Eldin, S.M. Computational assessment about hydrothermal attributes with induction of MWNT’s-Fe3O4 in water saturated in hexagonal enclosure. Case Stud. Therm. Eng. 2023, 47, 103036. [Google Scholar]


| Physical Properties | Water (f) (Base Fluid) | |||
|---|---|---|---|---|
| 4179 | 385 | 6320 | 765 | |
| 997.1 | 8933 | 531.8 | 3970 | |
| 0.613 | 401 | 76.5 | 40 | |
| 0.05 | 34.5 |
| Properties of the Ternary Hybrid Nanofluid | |
|---|---|
| Nanoparticles concentration | |
| Density | |
| Dynamic viscosity | |
| Thermal conductivity | |
| Thermal volume capacity | |
| Thermal expansion | |
| Thermal diffusivity | |
| Electrical conductivity |
| Boundary Wall | Temperature | Concentration |
|---|---|---|
| Left | ||
| Bottom | ||
| Curved wall |
| Boundary Wall | Temperature | Concentration |
|---|---|---|
| Left | ||
| Bottom | ||
| Curved wall |
| Case | Mesh Size | Name | ||
|---|---|---|---|---|
| 1 | 833 | Coarse | 5.7970 | 2.1501 |
| 2 | 2056 | Fine | 6.4264 | 2.4366 |
| 3 | 14,723 | Extra fine | 8.4221 | 3.3447 |
| 4 | 21,539 | Extremely fine | 8.4215 | 3.3444 |
| Dutta et al. [40] | Present Work | Relative Difference % | |
|---|---|---|---|
| 0 | 9.82 | 9.74 | 0.8 |
| 20 | 9.04 | 9.01 | 0.3 |
| 40 | 7.49 | 7.37 | 1.3 |
| 60 | 6.03 | 6.01 | 0.3 |
| 120 | 3.39 | 3.3 | 1.1 |
| Base Fluid (Water) | % Increase in Heat Transfer Rate | % Increase in Heat Transfer Rate | Ternary Hybrid Nanofluid | % Increase in Heat Transfer Rate | |||
|---|---|---|---|---|---|---|---|
| 3.8349 | 5.8465 | 34.40% | 10.128 | 62.13% | 17.698 | 78.33% | |
| 3.8808 | 5.8542 | 33.70% | 10.130 | 61.69% | 17.789 | 78.18% | |
| 5.3813 | 6.4274 | 16.27% | 10.307 | 47.78% | 17.846 | 69.84% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, S.M.; Alzahrani, T.A. Enhanced Efficiency of MHD-Driven Double-Diffusive Natural Convection in Ternary Hybrid Nanofluid-Filled Quadrantal Enclosure: A Numerical Study. Mathematics 2024, 12, 1423. https://doi.org/10.3390/math12101423
Alzahrani SM, Alzahrani TA. Enhanced Efficiency of MHD-Driven Double-Diffusive Natural Convection in Ternary Hybrid Nanofluid-Filled Quadrantal Enclosure: A Numerical Study. Mathematics. 2024; 12(10):1423. https://doi.org/10.3390/math12101423
Chicago/Turabian StyleAlzahrani, Saleh Mousa, and Talal Ali Alzahrani. 2024. "Enhanced Efficiency of MHD-Driven Double-Diffusive Natural Convection in Ternary Hybrid Nanofluid-Filled Quadrantal Enclosure: A Numerical Study" Mathematics 12, no. 10: 1423. https://doi.org/10.3390/math12101423
APA StyleAlzahrani, S. M., & Alzahrani, T. A. (2024). Enhanced Efficiency of MHD-Driven Double-Diffusive Natural Convection in Ternary Hybrid Nanofluid-Filled Quadrantal Enclosure: A Numerical Study. Mathematics, 12(10), 1423. https://doi.org/10.3390/math12101423






