Low-Carbon Optimization Design of Grinding Machine Spindle Based on Improved Whale Algorithm
Abstract
:1. Introduction
2. Spindle Carbon Emissions and Performance Analysis
2.1. Carbon Emissions Function
2.2. Static and Dynamic Performance Analysis
2.2.1. Static Performance
2.2.2. Dynamic Performance
3. Low-Carbon Design Approach for Spindles
3.1. Structural and Objective Selection
3.1.1. Structural Parameters
3.1.2. Design Variables
3.1.3. Determination of Design Variables
3.2. Integrated Optimization Objectives
3.2.1. Establishment of Test Methods
3.2.2. Response Surface Modeling
3.2.3. Establishment of Response Surface Model
- Carbon emissions regression equation.
- 2.
- Solving the maximum deformation regression equation.
- 3.
- Solving the first-order natural frequency regression equation.
3.2.4. Comprehensive Optimization Modeling
4. Algorithms and Results of Optimization
4.1. Algorithm for Optimization
- In comparison to similar classical algorithms, this algorithm has the more important ability to jump out of local optimization.
- The algorithm offers three search methods: surrounding, random, and bubble net, demonstrating robust local search capabilities. Finding discrete and discontinuous optimal solutions is the key to spindle optimization.
4.2. Improvement of the Whale Algorithm
4.2.1. Initialization of the Cat Chaotic Map
4.2.2. Golden Sine Algorithm
4.3. Analyses and Results of Optimization
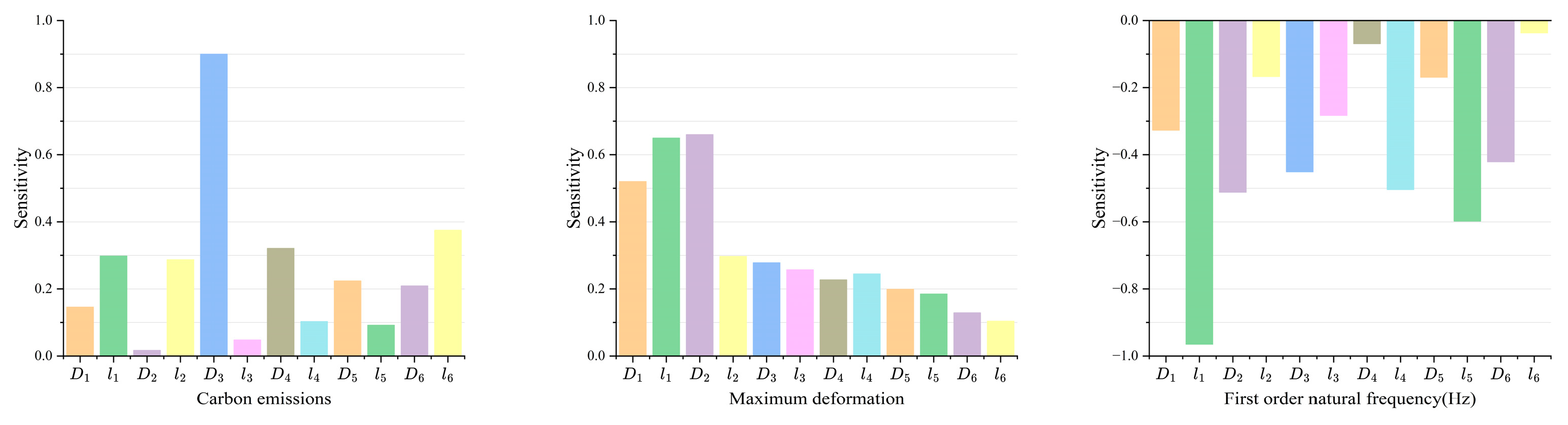
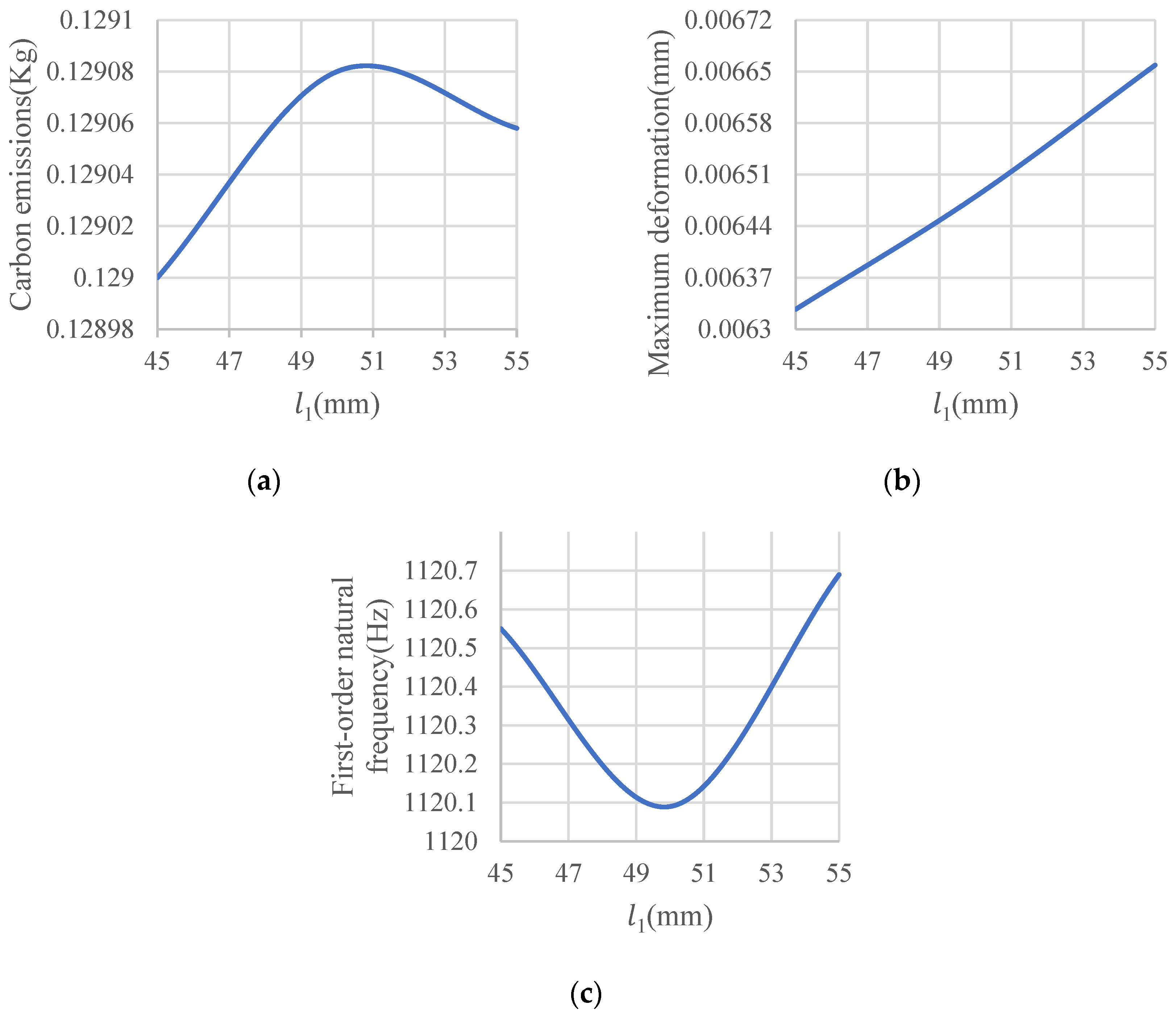
4.4. Design Variables and Their Impact on Goals
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ji, Q.; Li, C.; Zhu, D.; Jin, Y.; Lv, Y.; He, J. Structural design optimization of moving component in CNC machine tool for energy saving. J. Clean. Prod. 2020, 246, 118976. [Google Scholar] [CrossRef]
- Bilga, P.; Singh, S.; Kumar, R. Optimization of energy consumption response parameters for turning operation using Taguchi method. J. Clean. Prod. 2016, 137, 1406–1417. [Google Scholar] [CrossRef]
- Gavrus, C.; Ivan, N.; Oancea, G. Machining Parameters Optimization Based on Objective Function Linearization. Mathematics 2022, 10, 803. [Google Scholar] [CrossRef]
- García-Hernández, C.; Garde-Barace, J.-J.; Valdivia-Sánchez, J.-J.; Ubieto-Artur, P.; Bueno-Pérez, J.-A.; Cano-Álvarez, B.; Alcázar-Sánchez, M.Á.; Valdivia-Calvo, F.; Ponz-Cuenca, R.; Huertas-Talón, J.L.; et al. Trochoidal Milling Path with Variable Feed. Application to the Machining of a Ti-6Al-4V Part. Mathematics 2021, 9, 2701. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, G.; Yang, F.; Zheng, Y.; Zhai, F. Prediction of Tool Remaining Useful Life Based on NHPP-WPHM. Mathematics 2023, 11, 1837. [Google Scholar] [CrossRef]
- Popișter, F.; Popescu, D.; Păcurar, A.; Păcurar, R. Mathematical Approach in Complex Surfaces Toolpaths. Mathematics 2021, 9, 1360. [Google Scholar] [CrossRef]
- Liu, Z.; Sealy, M.; Li, W.; Zhang, D.; Fang, X.; Guo, Y.; Liu, Z. Energy consumption characteristics in finish hard milling. J. Manuf. Process. 2018, 35, 500–507. [Google Scholar] [CrossRef]
- Liu, F.; Xie, J.; Liu, S. A method for predicting the energy consumption of the main driving system of a machine tool in a machining process. J. Clean. Prod. 2015, 105, 171–177. [Google Scholar] [CrossRef]
- Wójcicki, J.; Bianchi, G. Electric load management in spindle run-up and run-down for multi-spindle machine tools via optimal power-torque trajectories and peak load synchronization. Int. J. Adv. Manuf. Technol. 2018, 95, 1819–1835. [Google Scholar] [CrossRef]
- Albertelli, P. Energy saving opportunities in direct drive machine tool spindles. J. Clean. Prod. 2017, 165, 855–873. [Google Scholar] [CrossRef]
- Lv, J.; Tang, R.; Tang, W.; Liu, Y.; Zhang, Y.; Jia, S. An investigation into reducing the spindle acceleration energy consumption of machine tools. J. Clean. Prod. 2016, 143, 794–803. [Google Scholar] [CrossRef]
- Ben, J.; Hentati, T.; Bellacicco, A.; Khabou, M.; Riviere, A.; Haddar, M. Energy consumed by a bearing supported spindle in the presence of a dynamic cutting force and of defects. C. R. Mec. 2019, 347, 685–700. [Google Scholar]
- Hu, L.; Liu, Y.; Lohse, N.; Tang, R.; Lv, J.; Peng, C.; Evans, S. Sequencing the features to minimize the non-cutting energy consumption in machining considering the change of spindle rotation speed. Energy 2017, 139, 935–946. [Google Scholar] [CrossRef]
- Hu, L.; Zheng, H.; Shu, L.; Jia, S.; Cai, W.; Xu, K. An investigation into the method of energy monitoring and reduction for machining systems. J. Manuf. Syst. 2020, 57, 390–399. [Google Scholar] [CrossRef]
- Avram, O.; Xirouchakis, P. Evaluating the use phase energy requirements of a machine tool system. J. Clean. Prod. 2011, 19, 699–711. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, Z.; Sun, X.; Xu, J.; Dong, L.; Zhu, G. Investigation on specific milling energy and energy efficiency in high-speed milling based on energy flow theory. Energy 2020, 192, 116596. [Google Scholar] [CrossRef]
- Han, F.; Li, L.; Cai, W.; Li, C.; Deng, X.; Sutherland, J. Parameters optimization considering the trade-off between cutting power and MRR based on linear decreasing particle swarm algorithm in milling. J. Clean. Prod. 2020, 262, 121388. [Google Scholar] [CrossRef]
- Sealy, M.; Liu, Z.; Zhang, D.; Guo, Y.; Liu, Z. Energy consumption and modeling in precision hard milling. J. Clean. Prod. 2016, 135, 1591–1601. [Google Scholar] [CrossRef]
- Li, L.; Deng, X.; Zhao, J.; Zhao, F.; Sutherland, J. Multi-objective optimization of tool path considering efficiency, energy-saving and carbon-emission for free-form surface milling. J. Clean. Prod. 2018, 172, 3311–3322. [Google Scholar] [CrossRef]
- Li, B.; Hong, J.; Liu, Z. A novel topology optimization method of welded box-beam structures motivated by low- carbon manufacturing concerns. J. Clean. Prod. 2017, 142, 2792–2803. [Google Scholar] [CrossRef]
- Liu, H.; Li, B.; Tang, W. Manufacturing oriented topology optimization of 3D structures for carbon emission reduction in casting process. J. Clean. Prod. 2019, 225, 755–770. [Google Scholar] [CrossRef]
- Chen, G. Research on Dynamic Characteristics and Structural Optimization Design of High-Speed Grinding Machine. Ph.D. Thesis, Hunan University, Changsha, China, 2018. [Google Scholar]
- Liu, S.; Li, Y.; Liao, Y.; Guo, Z. Structural optimization of the cross-beam of a gantry machine tool based on grey relational analysis. Struct. Multidiscipl. Optim. 2014, 50, 297–311. [Google Scholar] [CrossRef]
- Chen, T.; Wang, C. Topological and sizing optimization of reinforced ribs for a machining centre. Eng. Optim. 2008, 40, 33–45. [Google Scholar] [CrossRef]
- Law, M.; Altintas, Y.; Srikantha, P. Rapid evaluation and optimization of machine tools with position-dependent stability. Int. J. Mach. Tools Manuf. 2013, 68, 81–90. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, H.; Yao, Y.; Diao, G. A new approach to improving the machining precision based on dynamic sensitivity analysis. Int. J. Mach. Tools Manuf. 2016, 102, 9–21. [Google Scholar] [CrossRef]
- 2019 Annual Emission Reduction Projects China Regional Power Grid Baseline Emission Factors. Available online: https://www.mee.gov.cn/ywgz/ydqhbh/wsqtkz/202012/W020201229610353340851.pdf (accessed on 7 November 2023).
- Yang, S. A study of the static stiffness of machine tool spindles. Int. J. Mach. Tool Des. 1981, 21, 23–40. [Google Scholar]
- Liu, S. Multi-objective optimization design method for the machine tool’s structural parts based on computer-aided engineering. Int. J. Adv. Manuf. Technol. 2015, 78, 1053–1065. [Google Scholar] [CrossRef]
- He, B.; Tang, W.; Huang, S.; Hou, S.; Cai, H. Towards low-carbon product architecture using structural optimization for lightweight. Int. J. Adv. Manuf. Technol. 2016, 83, 1419–1429. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, S.; Fu, W. Sensitivity analysis and optimal design of a dual mechanic- al port bidirectional flux-modulated machine. IEEE Trans. Ind. Electron. 2017, 65, 211–220. [Google Scholar] [CrossRef]
- Tan, Z.; Liao, Y.; Jiang, J. Multi-objective optimization design of five-axis grinder’s spindle based on second-order response surface method. J. Mech. Design 2022, 39, 122–128. [Google Scholar]
- Seyedali, M.; Andrew, L. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
- Nadimi-Shahraki, M.H.; Zamani, H.; Mirjalili, S. Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study. Comput. Biol. Med. 2022, 148, 105858. [Google Scholar] [CrossRef] [PubMed]
- Tanyildizi, E.; Demir, G. Golden Sine Algorithm: A Novel Math-Inspired Algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]








| References | Energy Consumption | Static Characteristic | Dynamic Characteristic | Optimization Method |
|---|---|---|---|---|
| Reference [9] | 10% reduction | Not considered | Not considered | Optimize motor parameters |
| Reference [10] | 7% reduction | Not considered | Not considered | Optimized spindle drive mode |
| Reference [11] | 10.6% reduction | Not considered | Not considered | Optimize processing time |
| Reference [21] | 17.6% reduction | The maximum deformation is reduced by 0.8% | Not considered | Optimize topology |
| Reference [23] | Not considered | Not considered | The first four natural frequencies increased by 17% | Optimize structure |
| District | Chinese North | Chinese Northeast | Chinese East | Chinese Central | Chinese Northwest | Chinese South |
|---|---|---|---|---|---|---|
| Carbon emissions factor () | 0.9419 | 1.0826 | 0.792 | 0.8587 | 0.8922 | 0.804 |
| Objectives | D1 | l1 | D2 | l2 | D3 | l3 | D4 | l4 | D5 | l5 | D6 | l6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Carbon emissions | 0.146 | 0.289 | 0.017 | 0.287 | 0.9 | 0.048 | 0.321 | 0.103 | 0.224 | 0.092 | 0.209 | 0.357 |
| Maximum deformation | 0.52 | 0.65 | 0.66 | 0.297 | 0.278 | 0.257 | 0.227 | 0.245 | 0.199 | 0.185 | 0.129 | 0.104 |
| First-order frequency | −0.327 | −0.965 | −0.512 | −0.167 | −0.451 | −0.283 | −0.069 | −0.504 | −0.169 | −0.598 | −0.421 | −0.037 |
| Serial Number | /mm | /mm | /mm | /Kg | /mm | /Hz |
|---|---|---|---|---|---|---|
| 1 | 50.00 | 65.00 | 70.00 | 0.129 | 6.489 × 10−3 | 1120.09 |
| 2 | 50.00 | 65.00 | 63.00 | 0.127 | 6.493 × 10−3 | 1119.82 |
| 3 | 50.00 | 65.00 | 77.00 | 0.131 | 6.489 × 10−3 | 1120.55 |
| 4 | 50.00 | 58.50 | 70.00 | 0.117 | 6.072 × 10−3 | 1120.38 |
| 5 | 50.00 | 71.50 | 70.00 | 0.141 | 6.778 × 10−3 | 1119.97 |
| 6 | 45.00 | 65.00 | 70.00 | 0.129 | 6.327 × 10−3 | 1120.55 |
| 7 | 55.00 | 65.00 | 70.00 | 0.129 | 6.659 × 10−3 | 1120.69 |
| 8 | 45.93 | 59.72 | 64.31 | 0.118 | 6.032 × 10−3 | 1120.47 |
| 9 | 45.93 | 59.72 | 75.69 | 0.121 | 6.029 × 10−3 | 1120.82 |
| 10 | 45.93 | 70.28 | 64.31 | 0.137 | 6.579 × 10−3 | 1120.50 |
| 11 | 45.93 | 70.28 | 75.69 | 0.141 | 6.575 × 10−3 | 1120.53 |
| 12 | 54.07 | 59.72 | 64.31 | 0.118 | 6.279 × 10−3 | 1120.50 |
| 13 | 54.07 | 59.72 | 75.69 | 0.121 | 6.277 × 10−3 | 1121.33 |
| 14 | 54.07 | 70.28 | 64.31 | 0.137 | 6.859 × 10−3 | 1120.64 |
| 15 | 54.07 | 70.28 | 75.69 | 0.141 | 6.848 × 10−3 | 1120.24 |
| Carbon Emissions | ||||
|---|---|---|---|---|
| 1.097 × 10−3 | 9 | 4.74 × 10−9 | 5 |
| Maximum Deformation | ||||
|---|---|---|---|---|
| 1.084 × 10−6 | 9 | 2.672 × 10−10 | 5 |
| First-Order Natural Frequency | ||||
|---|---|---|---|---|
| 1.84 | 9 | 0.19 | 5 |
| Design Variables/ Objectives | Before Optimization | Lightweight Optimization | Traditional Whale Algorithm | Improved Whale Algorithm |
|---|---|---|---|---|
| /mm | 50 | 51.4 | 46.2 | 44.5 |
| /mm | 65 | 61.5 | 62.5 | 61 |
| /mm | 70 | 67 | 66.4 | 65.5 |
| /Kg | 0.129 | 0.1143 | 0.1232 | 0.1184 |
| U/mm | 0.0065 | 0.00706 | 0.00614 | 0.00601 |
| /Hz | 1120.09 | 1119.64 | 1120.52 | 1120.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Gao, X.; Chan, F.T.S. Low-Carbon Optimization Design of Grinding Machine Spindle Based on Improved Whale Algorithm. Mathematics 2024, 12, 69. https://doi.org/10.3390/math12010069
Lu Q, Gao X, Chan FTS. Low-Carbon Optimization Design of Grinding Machine Spindle Based on Improved Whale Algorithm. Mathematics. 2024; 12(1):69. https://doi.org/10.3390/math12010069
Chicago/Turabian StyleLu, Qi, Xubo Gao, and Felix T. S. Chan. 2024. "Low-Carbon Optimization Design of Grinding Machine Spindle Based on Improved Whale Algorithm" Mathematics 12, no. 1: 69. https://doi.org/10.3390/math12010069
APA StyleLu, Q., Gao, X., & Chan, F. T. S. (2024). Low-Carbon Optimization Design of Grinding Machine Spindle Based on Improved Whale Algorithm. Mathematics, 12(1), 69. https://doi.org/10.3390/math12010069







