Physics-Informed Neural Networks with Periodic Activation Functions for Solute Transport in Heterogeneous Porous Media
Abstract
:1. Introduction
2. Underlying Physics
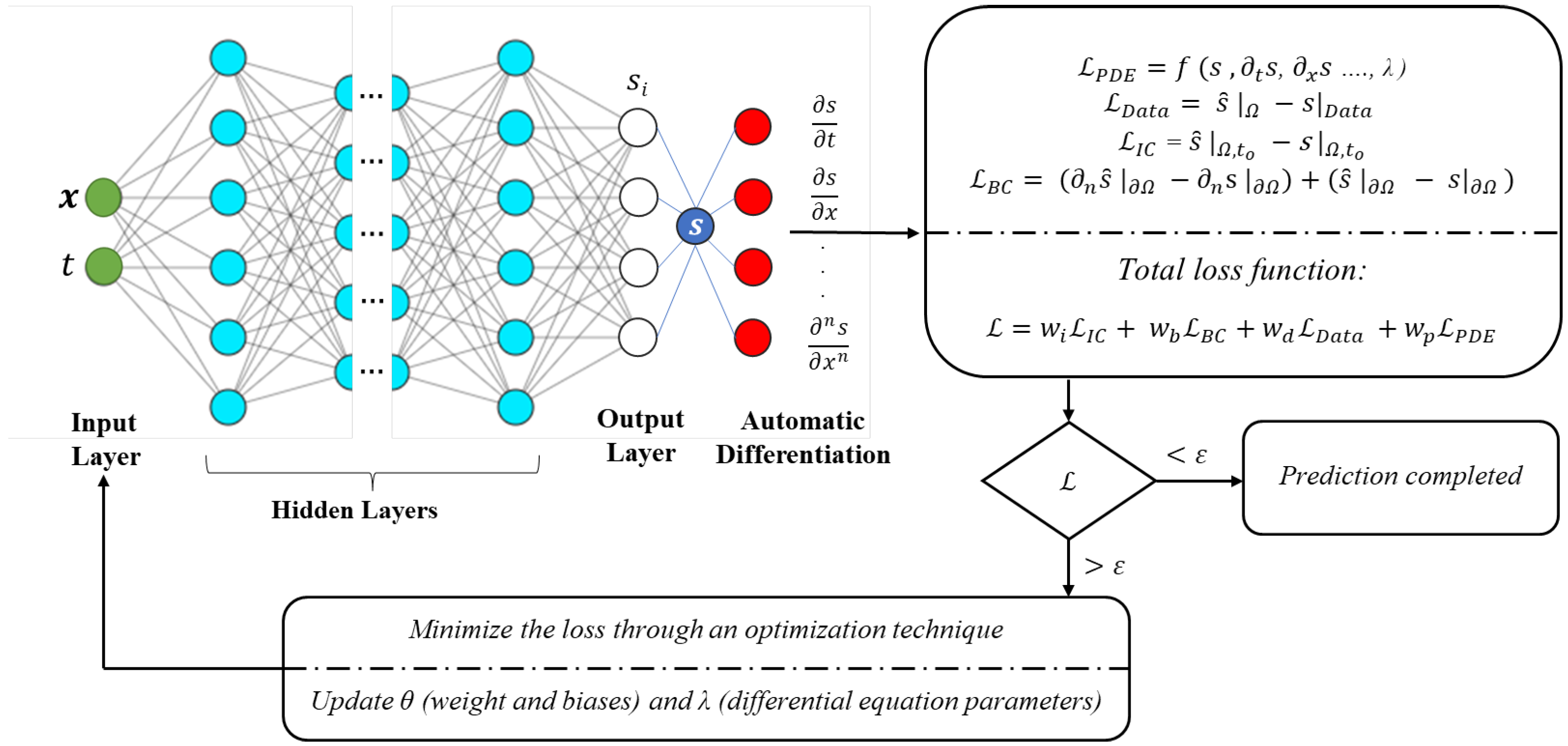
3. Methodology
4. Computational Experiments
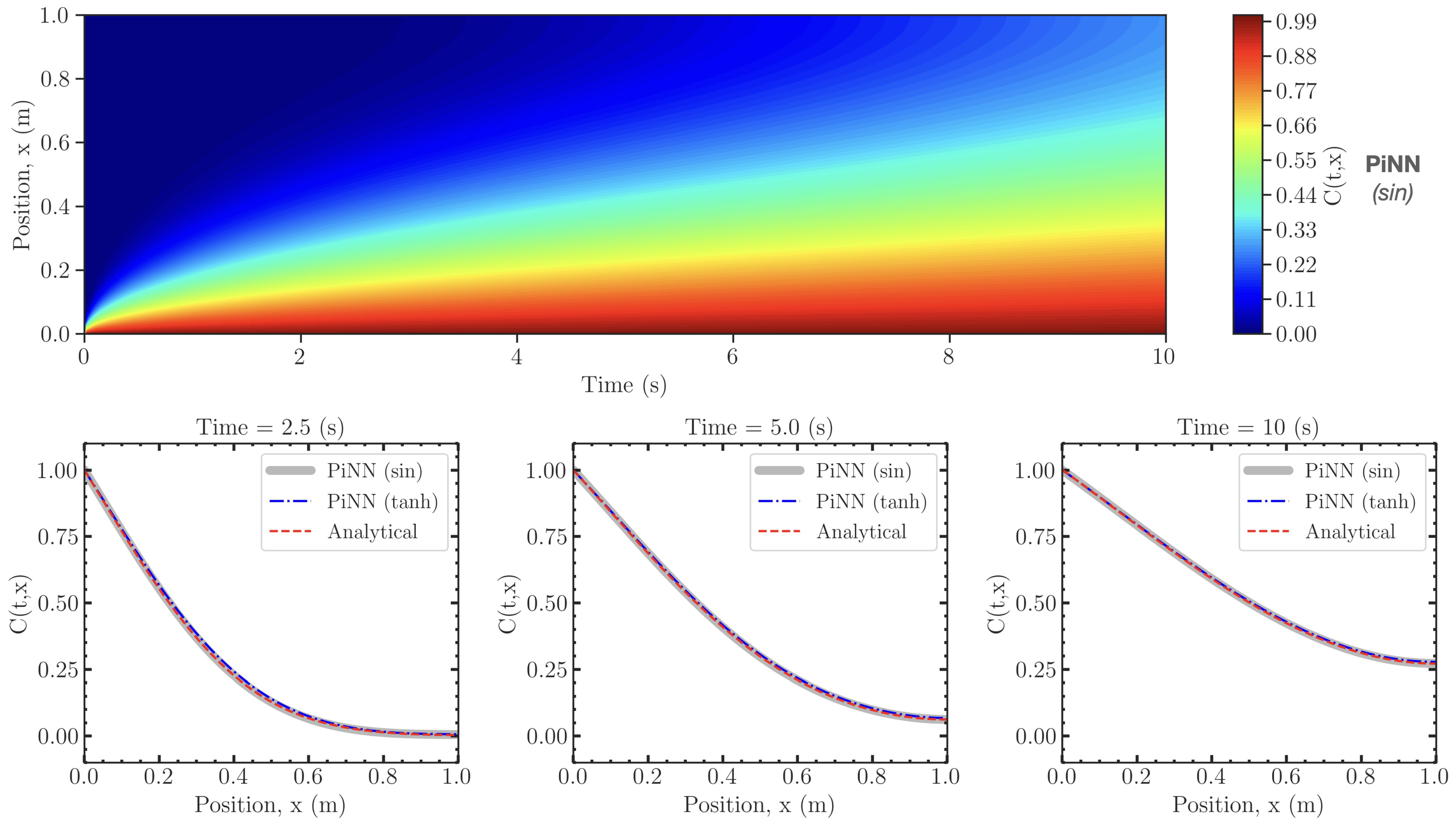
4.1. Case 1: 1D Solute Transport with Constant Velocity
4.2. Case 2: 2D Solute Transport with Constant Velocity
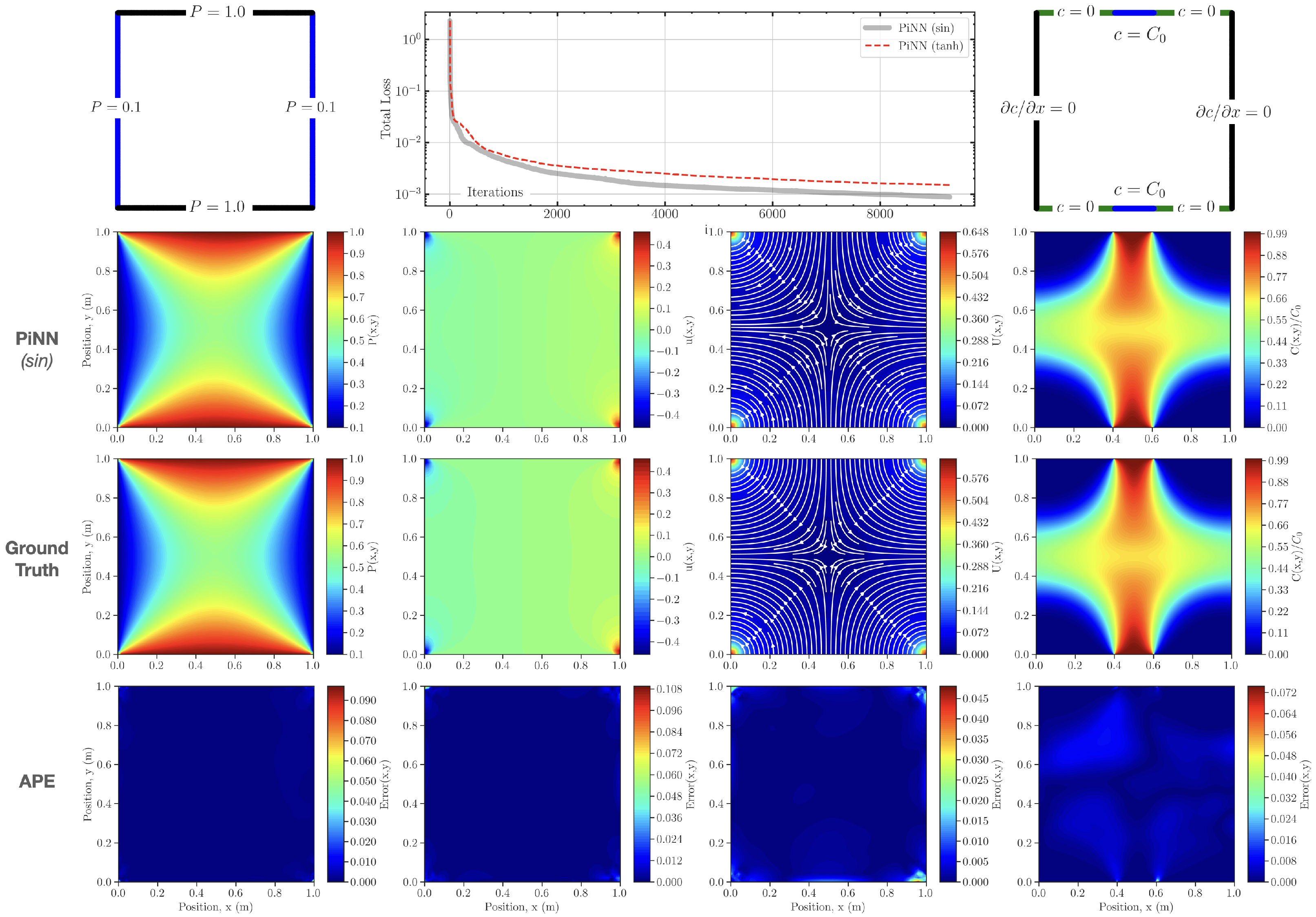
4.3. Case 3: 2D Solute Transport in Homogeneous Porous Media
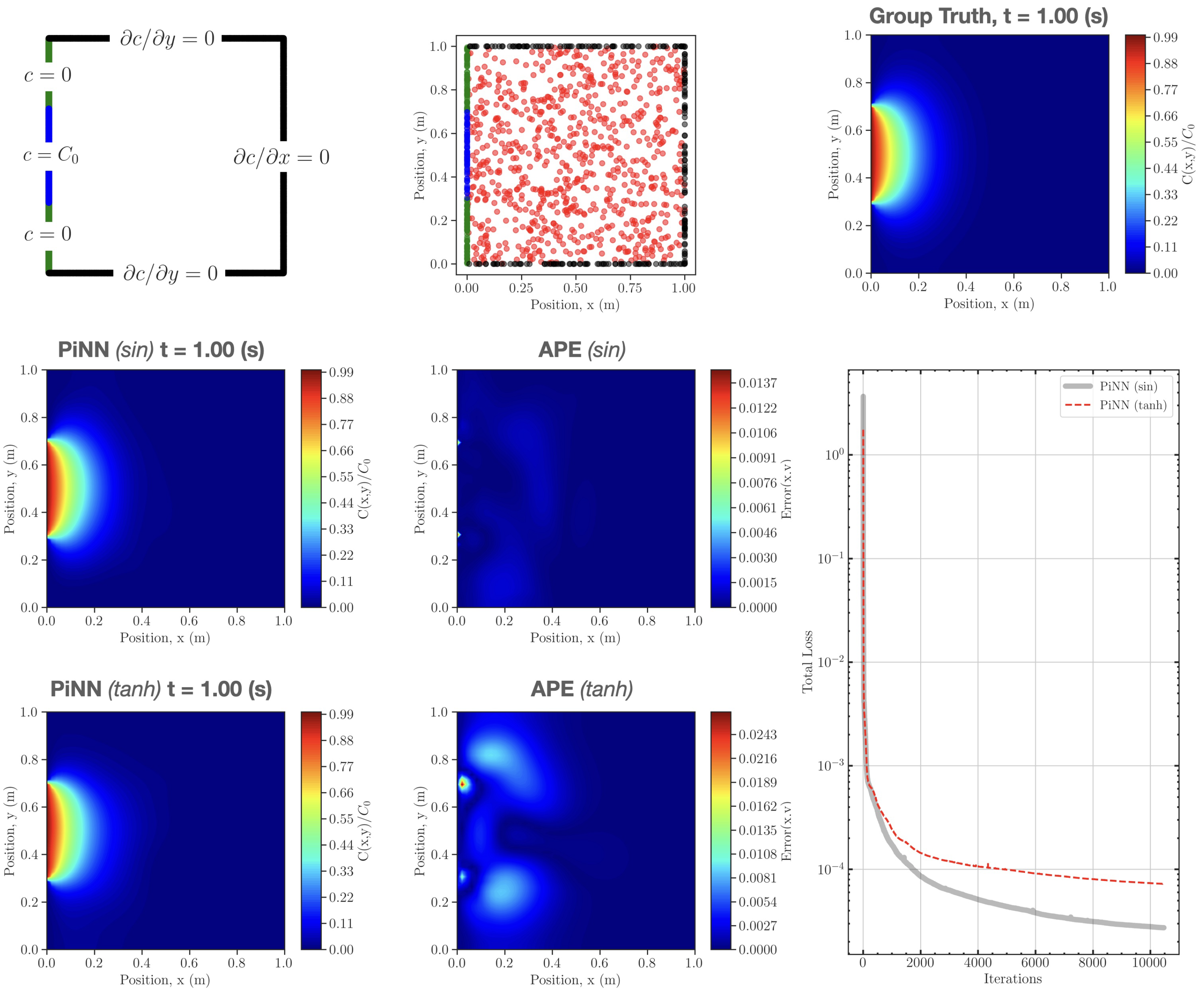
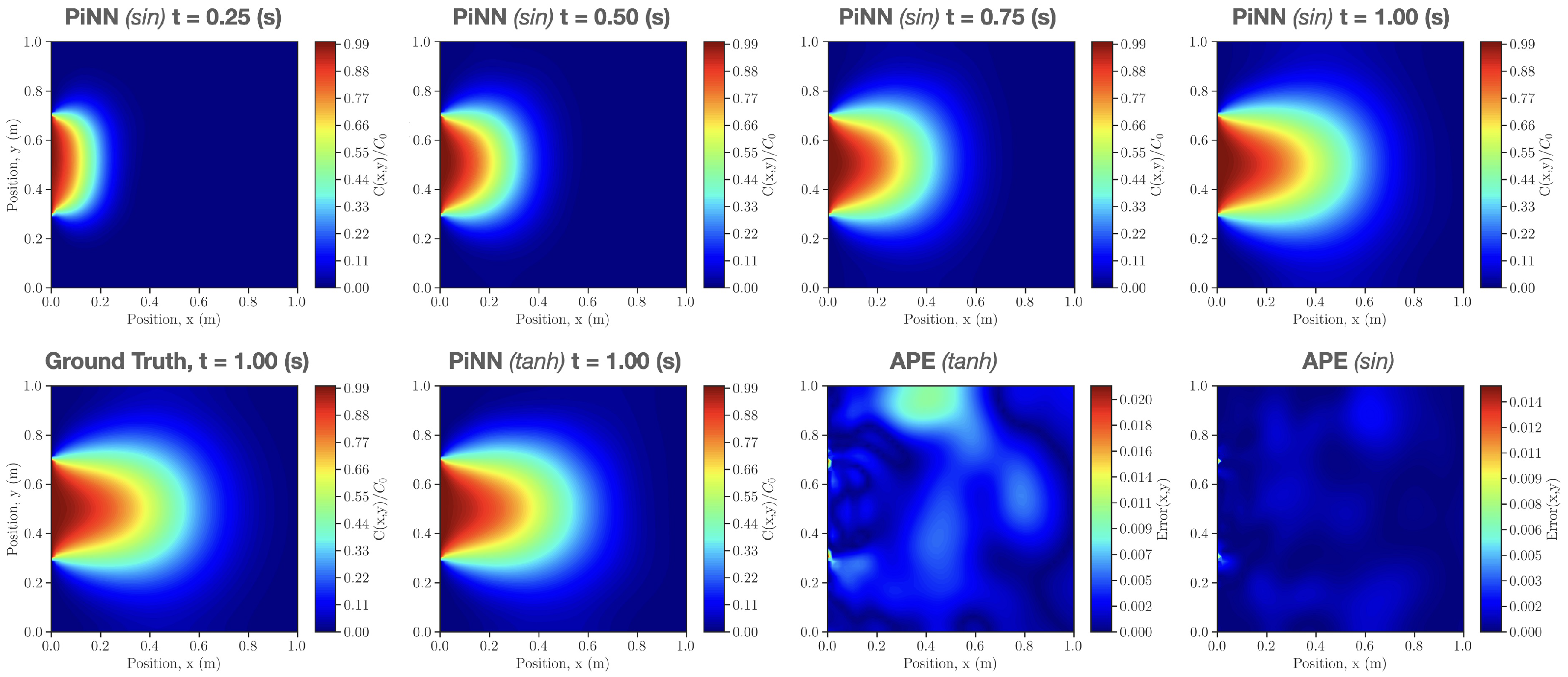
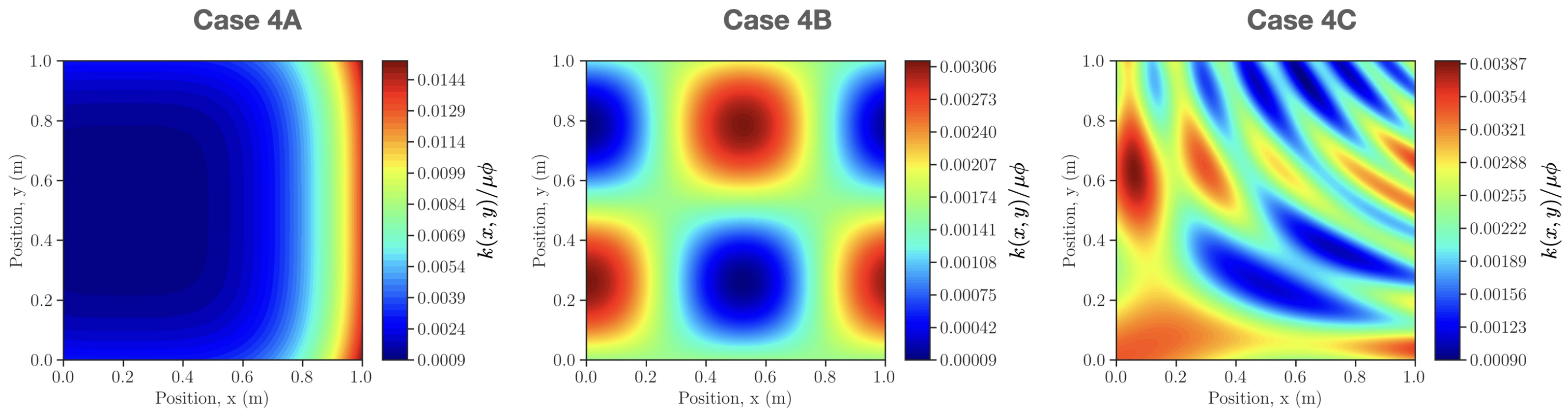
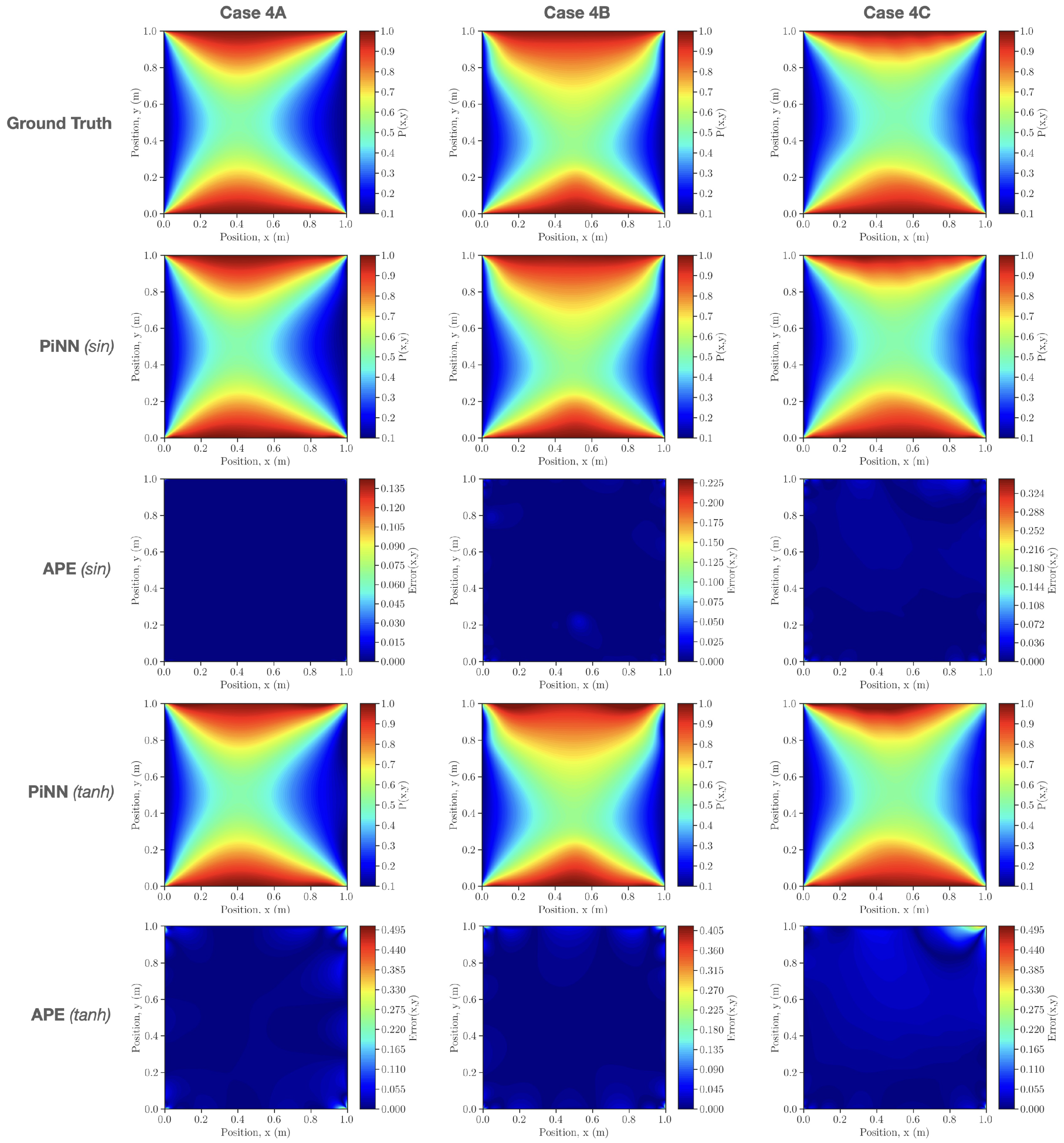
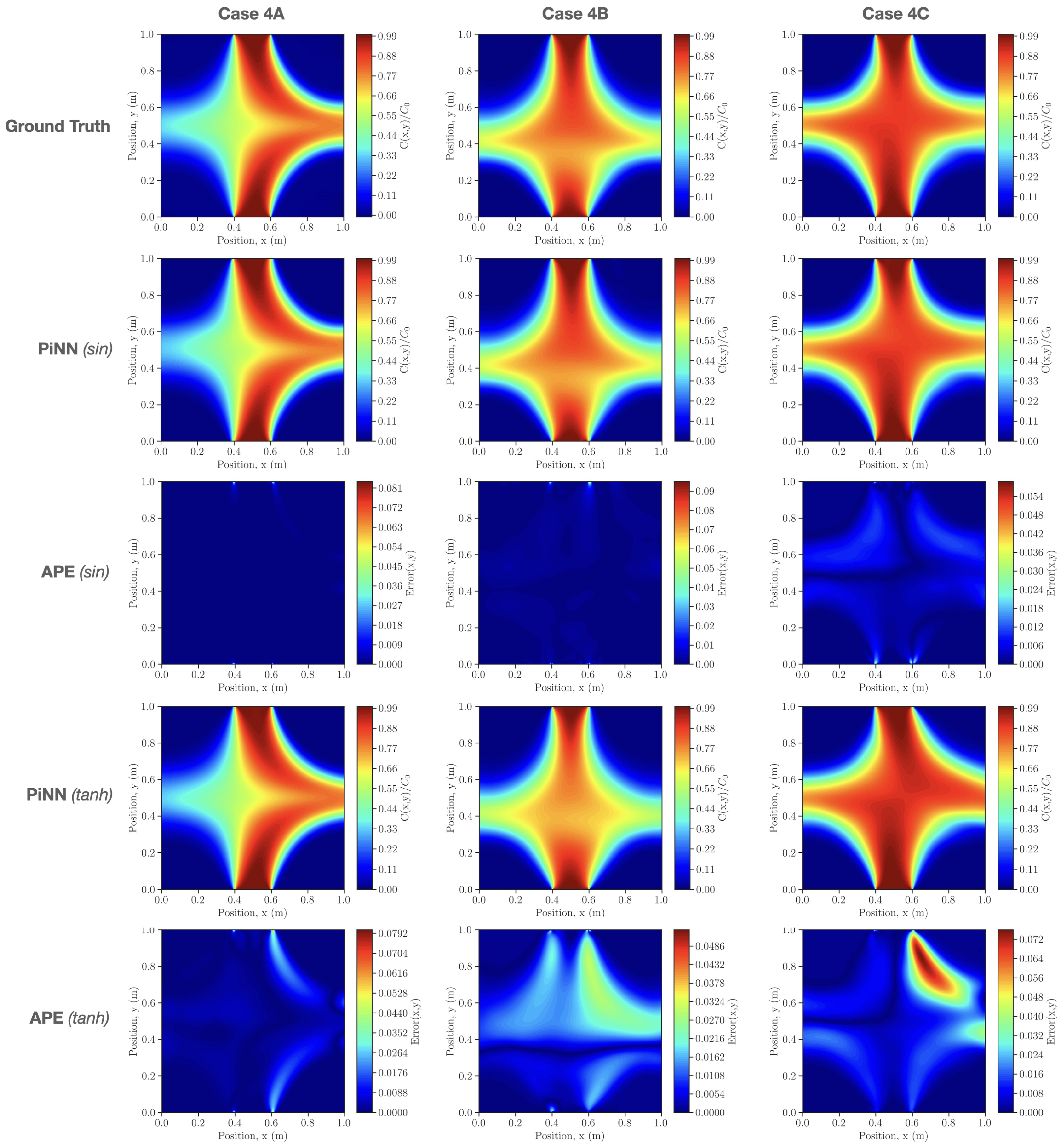
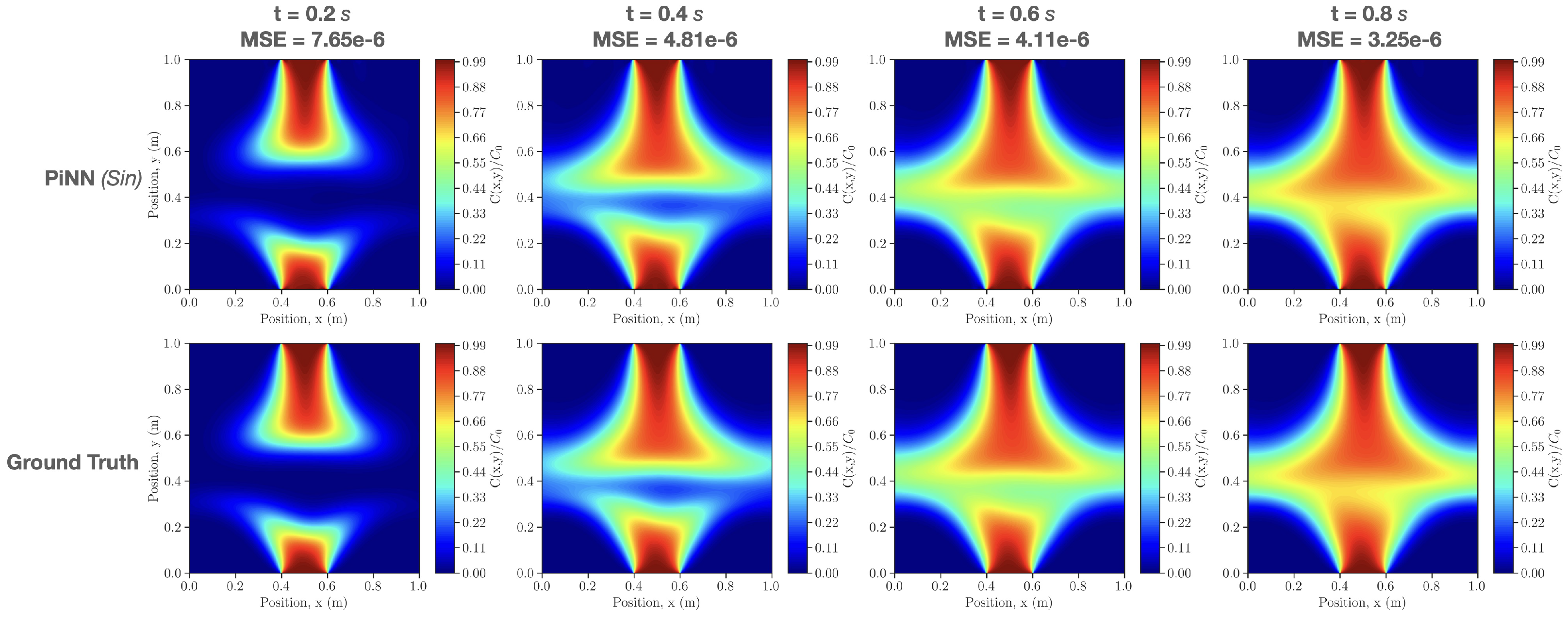
4.4. Case 4: 2D Solute Transport in Heterogeneous Porous Media
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cook, P.G.; Böhlke, J.K. Determining timescales for groundwater flow and solute transport. In Environmental Tracers in Subsurface Hydrology; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–30. [Google Scholar] [CrossRef]
- Gaus, I.; Audigane, P.; André, L.; Lions, J.; Jacquemet, N.; Durst, P.; Czernichowski-Lauriol, I.; Azaroual, M. Geochemical and solute transport modelling for CO2 storage, what to expect from it? Int. J. Greenh. Gas Control. 2008, 2, 605–625. [Google Scholar] [CrossRef]
- Pruess, K.; Yabusaki, S.; Steefel, C.; Lichtner, P. Fluid flow, heat transfer, and solute transport at nuclear waste storage tanks in the Hanford vadose zone. Vadose Zone J. 2002, 1, 68–88. [Google Scholar] [CrossRef]
- Bienert, G.P.; Schjoerring, J.K.; Jahn, T.P. Membrane transport of hydrogen peroxide. Biochim. Biophys. Acta (BBA)-Biomembr. 2006, 1758, 994–1003. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, E.; Hansen, K. Transport of carbon dioxide and ammonium in bioturbated (Nereis diversicolor) coastal, marine sediments. Biogeochemistry 1999, 45, 147–168. [Google Scholar] [CrossRef]
- Li, X.; Li, D.; Xu, Y.; Feng, X. A DFN based 3D numerical approach for modeling coupled groundwater flow and solute transport in fractured rock mass. Int. J. Heat Mass Transf. 2020, 149, 119179. [Google Scholar] [CrossRef]
- Hasan, S.; Niasar, V.; Karadimitriou, N.K.; Godinho, J.R.; Vo, N.T.; An, S.; Rabbani, A.; Steeb, H. Direct characterization of solute transport in unsaturated porous media using fast X-ray synchrotron microtomography. Proc. Natl. Acad. Sci. USA 2020, 117, 23443–23449. [Google Scholar] [CrossRef] [PubMed]
- Faraji, M.; Mazaheri, M. Mathematical model of solute transport in rivers with storage zones using nonlinear dispersion flux approach. Hydrol. Sci. J. 2022, 67, 1656–1668. [Google Scholar] [CrossRef]
- Yang, X.R.; Wang, Y. Ubiquity of anomalous transport in porous media: Numerical evidence, continuous time random walk modelling, and hydrodynamic interpretation. Sci. Rep. 2019, 9, 4601. [Google Scholar] [CrossRef]
- Zhao, Z.; Jing, L.; Neretnieks, I.; Moreno, L. Numerical modeling of stress effects on solute transport in fractured rocks. Comput. Geotech. 2011, 38, 113–126. [Google Scholar] [CrossRef]
- Zhang, Z.h.; Zhang, J.p.; Ju, Z.y.; Zhu, M. A one-dimensional transport model for multi-component solute in saturated soil. Water Sci. Eng. 2018, 11, 236–242. [Google Scholar] [CrossRef]
- Bagalkot, N.; Suresh Kumar, G. Effect of nonlinear sorption on multispecies radionuclide transport in a coupled fracture-matrix system with variable fracture aperture: A numerical study. ISH J. Hydraul. Eng. 2015, 21, 242–254. [Google Scholar] [CrossRef]
- Mostaghimi, P.; Liu, M.; Arns, C.H. Numerical simulation of reactive transport on micro-CT images. Math. Geosci. 2016, 48, 963–983. [Google Scholar] [CrossRef]
- Maheshwari, P.; Ratnakar, R.; Kalia, N.; Balakotaiah, V. 3-D simulation and analysis of reactive dissolution and wormhole formation in carbonate rocks. Chem. Eng. Sci. 2013, 90, 258–274. [Google Scholar] [CrossRef]
- Noetinger, B.; Roubinet, D.; Russian, A.; Le Borgne, T.; Delay, F.; Dentz, M.; De Dreuzy, J.R.; Gouze, P. Random walk methods for modeling hydrodynamic transport in porous and fractured media from pore to reservoir scale. Transp. Porous Media 2016, 115, 345–385. [Google Scholar] [CrossRef]
- Im, S.; Lee, J.; Cho, M. Surrogate modeling of elasto-plastic problems via long short-term memory neural networks and proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2021, 385, 114030. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Han, J.; Jentzen, A.; E, W. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Pawar, N.; Fernandes, C.; Das, S.; Kalantari, N.K.; Mahjour, S.K. Physics-Guided, Physics-Informed, and Physics-Encoded Neural Networks in Scientific Computing. arXiv 2022, arXiv:2211.07377. [Google Scholar] [CrossRef]
- Van Merriënboer, B.; Breuleux, O.; Bergeron, A.; Lamblin, P. Automatic differentiation in ML: Where we are and where we should be going. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Marchine Learn. Res. 2018, 18, 1–43. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: A Navier-Stokes informed deep learning framework for assimilating flow visualization data. arXiv 2018, arXiv:1808.04327. [Google Scholar] [CrossRef]
- Almajid, M.M.; Abu-Al-Saud, M.O. Prediction of porous media fluid flow using physics informed neural networks. J. Pet. Sci. Eng. 2022, 208, 109205. [Google Scholar] [CrossRef]
- Hanna, J.M.; Aguado, J.V.; Comas-Cardona, S.; Askri, R.; Borzacchiello, D. Residual-based adaptivity for two-phase flow simulation in porous media using Physics-informed Neural Networks. Comput. Methods Appl. Mech. Eng. 2022, 396, 115100. [Google Scholar] [CrossRef]
- Haghighat, E.; Amini, D.; Juanes, R. Physics-informed neural network simulation of multiphase poroelasticity using stress-split sequential training. Comput. Methods Appl. Mech. Eng. 2022, 397, 115141. [Google Scholar] [CrossRef]
- He, Q.; Barajas-Solano, D.; Tartakovsky, G.; Tartakovsky, A.M. Physics-informed neural networks for multiphysics data assimilation with application to subsurface transport. Adv. Water Resour. 2020, 141, 103610. [Google Scholar] [CrossRef]
- He, Q.; Tartakovsky, A.M. Physics-Informed neural network method for forward and backward advection-dispersion equations. Water Resour. Res. 2021, 57, e2020WR029479. [Google Scholar] [CrossRef]
- Vadyala, S.R.; Betgeri, S.N.; Betgeri, N.P. Physics-informed neural network method for solving one-dimensional advection equation using PyTorch. Array 2022, 13, 100110. [Google Scholar] [CrossRef]
- Rodriguez-Torrado, R.; Ruiz, P.; Cueto-Felgueroso, L.; Green, M.C.; Friesen, T.; Matringe, S.; Togelius, J. Physics-informed attention-based neural network for hyperbolic partial differential equations: Application to the Buckley–Leverett problem. Sci. Rep. 2022, 12, 7557. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Al Kobaisi, M. On the Monotonicity and Positivity of Physics-Informed Neural Networks for Highly Anisotropic Diffusion Equations. Energies 2022, 15, 6823. [Google Scholar] [CrossRef]
- Fuks, O.; Tchelepi, H.A. Limitations of physics informed machine learning for nonlinear two-phase transport in porous media. J. Mach. Learn. Model. Comput. 2020, 1, 19–37. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, X.; Liu, P.; Zhang, K.; Han, R.; Wang, S. A physics-informed convolutional neural network for the simulation and prediction of two-phase Darcy flows in heterogeneous porous media. J. Comput. Phys. 2023, 477, 111919. [Google Scholar] [CrossRef]
- Jagtap, A.; Karniadakis, G.E. How important are activation functions in regression and classification? A survey, performance comparison, and future directions. J. Mach. Learn. Model. Comput. 2022, 4, 21–75. [Google Scholar] [CrossRef]
- Parascandolo, G.; Huttunen, H.; Virtanen, T. Taming the waves: Sine as activation function in deep neural networks. In Proceedings of the ICLR 2017 Conference Track, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhang, C.; Kaito, K.; Hu, Y.; Patmonoaji, A.; Matsushita, S.; Suekane, T. Influence of stagnant zones on solute transport in heterogeneous porous media at the pore scale. Phys. Fluids 2021, 33, 036605. [Google Scholar] [CrossRef]
- Khan, S.; Alhazmi, S.E.; Alotaibi, F.M.; Ferrara, M.; Ahmadian, A. On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media. Fractal Fract. 2022, 6, 445. [Google Scholar] [CrossRef]
- Zhao, X.; Toksoz, M.N. Solute transport in heterogeneous porous media. Mass. Inst. Technol. Earth Resour. Lab. 1994, 145, 151–177. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Alves, W. Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation; Technical Bulletin (USA); United States Department of Agriculture: Washington, DC, USA, 1982. [Google Scholar] [CrossRef]
- Sun, L.; Qiu, H.; Wu, C.; Niu, J.; Hu, B.X. A review of applications of fractional advection–dispersion equations for anomalous solute transport in surface and subsurface water. Wiley Interdiscip. Rev. Water 2020, 7, e1448. [Google Scholar] [CrossRef]
- Haigh, M.; Sun, L.; McWilliams, J.C.; Berloff, P. On eddy transport in the ocean. Part II: The advection tensor. Ocean. Model. 2021, 165, 101845. [Google Scholar] [CrossRef]
- Lou, S.; Chen, S.s.; Lin, B.x.; Yu, J.; Yan, C. Effective high-order energy stable flux reconstruction methods for first-order hyperbolic linear and nonlinear systems. J. Comput. Phys. 2020, 414, 109475. [Google Scholar] [CrossRef]
- Talon, L. On the statistical properties of fluid flows with transitional power-law rheology in heterogeneous porous media. J. Non-Newton. Fluid Mech. 2022, 304, 104789. [Google Scholar] [CrossRef]
- Baioni, E.; Mousavi Nezhad, M.; Porta, G.M.; Guadagnini, A. Modeling solute transport and mixing in heterogeneous porous media under turbulent flow conditions. Phys. Fluids 2021, 33, 106604. [Google Scholar] [CrossRef]
- Berkowitz, B.; Klafter, J.; Metzler, R.; Scher, H. Physical pictures of transport in heterogeneous media: Advection-dispersion, random-walk, and fractional derivative formulations. Water Resour. Res. 2002, 38, 9-1–9-12. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended Physics-informed Neural Networks (XPINNs): A Generalized Space-Time Domain Decomposition based Deep Learning Framework for Nonlinear Partial Differential Equations. Commun. Comput. Phys. 2020, 8, 2002–2041. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What’s next. arXiv 2022, arXiv:2201.05624. [Google Scholar] [CrossRef]
- Depina, I.; Jain, S.; Mar Valsson, S.; Gotovac, H. Application of physics-informed neural networks to inverse problems in unsaturated groundwater flow. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 21–36. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Sitzmann, V.; Martel, J.N.P.; Bergman, A.W.; Lindell, D.B.; Wetzstein, G. Implicit Neural Representations with Periodic Activation Functions. arXiv 2020, arXiv:2006.09661. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving partial differential equations using deep learning and physical constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2022, 37, 1727–1738. [Google Scholar] [CrossRef]
- Strelow, E.L.; Gerisch, A.; Lang, J.; Pfetsch, M.E. Physics informed neural networks: A case study for gas transport problems. J. Comput. Phys. 2023, 481, 112041. [Google Scholar] [CrossRef]
- Cuomo, S.; Giampaolo, F.; Izzo, S.; Nitsch, C.; Piccialli, F.; Trombetti, C. A physics-informed learning approach to Bernoulli-type free boundary problems. Comput. Math. Appl. 2022, 128, 34–43. [Google Scholar] [CrossRef]
- Shah, K.; Stiller, P.; Hoffmann, N.; Cangi, A. Physics-Informed Neural Networks as Solvers for the Time-Dependent Schrödinger Equation. arXiv 2022, arXiv:2210.12522. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Bengio, Y. Gradient-based optimization of hyperparameters. Neural Comput. 2000, 12, 1889–1900. [Google Scholar] [CrossRef]
- Kylasa, S.; Roosta, F.; Mahoney, M.W.; Grama, A. GPU accelerated sub-sampled Newton’s method for convex classification problems. In Proceedings of the 2019 SIAM International Conference on Data Mining, SIAM, Calgary, AB, Canada, 2–4 May 2019; pp. 702–710. [Google Scholar] [CrossRef]
- Richardson, A. Seismic full-waveform inversion using deep learning tools and techniques. arXiv 2018, arXiv:1801.07232. [Google Scholar] [CrossRef]
- Olmo, A.; Zamzam, A.; Glaws, A.; King, R. Physics-Driven Convolutional Autoencoder Approach for CFD Data Compressions. arXiv 2022, arXiv:2210.09262. [Google Scholar] [CrossRef]
- Escapil-Inchauspé, P.; Ruz, G.A. Hyper-parameter tuning of physics-informed neural networks: Application to Helmholtz problems. Neurocomputing 2023, 561, 126826. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-Informed Neural Networks (PINNs) for Wave Propagation and Full Waveform Inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Zhou, J.G. A lattice Boltzmann method for solute transport. Int. J. Numer. Methods Fluids 2009, 61, 848–863. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Meng, X.; Karniadakis, G.E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114823. [Google Scholar] [CrossRef]
- Chiu, P.H.; Wong, J.C.; Ooi, C.; Dao, M.H.; Ong, Y.S. CAN-PINN: A fast physics-informed neural network based on coupled-automatic–numerical differentiation method. Comput. Methods Appl. Mech. Eng. 2022, 395, 114909. [Google Scholar] [CrossRef]
- Atmakidis, T.; Kenig, E.Y. A study on the Kelvin-Helmholtz instability using two different computational fluid dynamics methods. J. Comput. Multiph. Flows 2010, 2, 33–45. [Google Scholar] [CrossRef]
| Case 1 | Case 2 | |||
|---|---|---|---|---|
| sin | tanh | sin | tanh | |
| Collocation Points, | 5000 | 5000 | 8000 | 8000 |
| Weights: , , | 1.0, 1.0, 1.0 | 1.0, 1.0, 0.9 | 1.0, 1.0, 1.0 | 1.0, 1.0, 0.8 |
| Accuracy (MSE) | 1.15e-06 | 1.21e-06 | 1.54e-06 | 2.37e-05 |
| Training Time (s) | ||||
| Case 3 | ||
|---|---|---|
| sin | tanh | |
| Collocation Points, | 12,000 | 12,000 |
| Initial and Boundary Loss Weights: , | 1.0, 1.0 | 1.0, 1.0 |
| Pressure and Concentrations PDE Loss Weights: , | 1.0, 1.0 | 0.7, 0.9 |
| Pressure MSE | 2.84e-06 | 4.36e-05 |
| Concentration MSE | 1.22e-06 | 1.51e-05 |
| Training Time (s) | ||
| Case 4A | Case 4B | Case 4C | ||||
|---|---|---|---|---|---|---|
| sin | tanh | sin | tanh | sin | tanh | |
| 15,000 | 15,000 | 18,000 | 18,000 | 20,000 | 20,000 | |
| , | 1.0, 1.0 | 1.0, 1.0 | 1.0, 1.0 | 1.0, 1.0 | 1.0, 1.0 | 1.0, 1.0 |
| , | 0.20, 0.70 | 0.25, 0.65 | 0.15, 0.80 | 0.25, 0.70 | 0.15, 0.80 | 0.3, 0.90 |
| Pressure MSE | 1.13e-05 | 1.38e-04 | 2.48e-05 | 1.96e-04 | 5.38e-05 | 2.08e-04 |
| Concentration MSE | 1.12e-06 | 1.10e-04 | 3.62e-06 | 1.25e-04 | 9.86e-06 | 2.72e-04 |
| Training Time (s) | ||||||
| FEM | PiNN (sin) | Speed-Up Factor | |
|---|---|---|---|
| (s) | (s) | (—) | |
| 2D Homogeneous | 1458.7× | ||
| 2D Heterogeneous-Case 4A | 1402.3× | ||
| 2D Heterogeneous-Case 4B | 1399.6× | ||
| 2D Heterogeneous-Case 4C | 1401.9× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faroughi, S.A.; Soltanmohammadi, R.; Datta, P.; Mahjour, S.K.; Faroughi, S. Physics-Informed Neural Networks with Periodic Activation Functions for Solute Transport in Heterogeneous Porous Media. Mathematics 2024, 12, 63. https://doi.org/10.3390/math12010063
Faroughi SA, Soltanmohammadi R, Datta P, Mahjour SK, Faroughi S. Physics-Informed Neural Networks with Periodic Activation Functions for Solute Transport in Heterogeneous Porous Media. Mathematics. 2024; 12(1):63. https://doi.org/10.3390/math12010063
Chicago/Turabian StyleFaroughi, Salah A., Ramin Soltanmohammadi, Pingki Datta, Seyed Kourosh Mahjour, and Shirko Faroughi. 2024. "Physics-Informed Neural Networks with Periodic Activation Functions for Solute Transport in Heterogeneous Porous Media" Mathematics 12, no. 1: 63. https://doi.org/10.3390/math12010063
APA StyleFaroughi, S. A., Soltanmohammadi, R., Datta, P., Mahjour, S. K., & Faroughi, S. (2024). Physics-Informed Neural Networks with Periodic Activation Functions for Solute Transport in Heterogeneous Porous Media. Mathematics, 12(1), 63. https://doi.org/10.3390/math12010063







