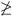Open Quantum Dynamics: Memory Effects and Superactivation of Backflow of Information
Abstract
1. Introduction
2. Non-Markovianity: Divisibility and BFI
2.1. Non-Markovianity: Lack of CP-Divisibility
2.2. Non-Markovianity: Backflow of Information
2.3. General Tensor Families
3. Mixtures of Pure Dephasing Processes: Two-Qubit Divisibility Diagram
3.1. One-Qubit Divisibility Diagram
- (i)
- P-divisibility. As one can easily check from (30),as well as for cyclic permutations of the indices. Thus (see Example 1), is P-divisible for all p.
- (ii)
- Eternal and quasi-eternal non-Markovianity. From (30), one hasIf , thenfor instance, letting and ,while , as a consequence of Property (i). Such a dynamics is clearly not CP-divisible and is usually labeled as eternally non-Markovian (ENM). For instance, choosing , , we end up with the ENM evolution first introduced in [26], with and . Similarly, if andThis is checked explicitly in Appendix B. It also follows that, for a given p, at most one rate can become negative: indeed, if for and for , for , violating P-divisibility condition (32).
- (iii)
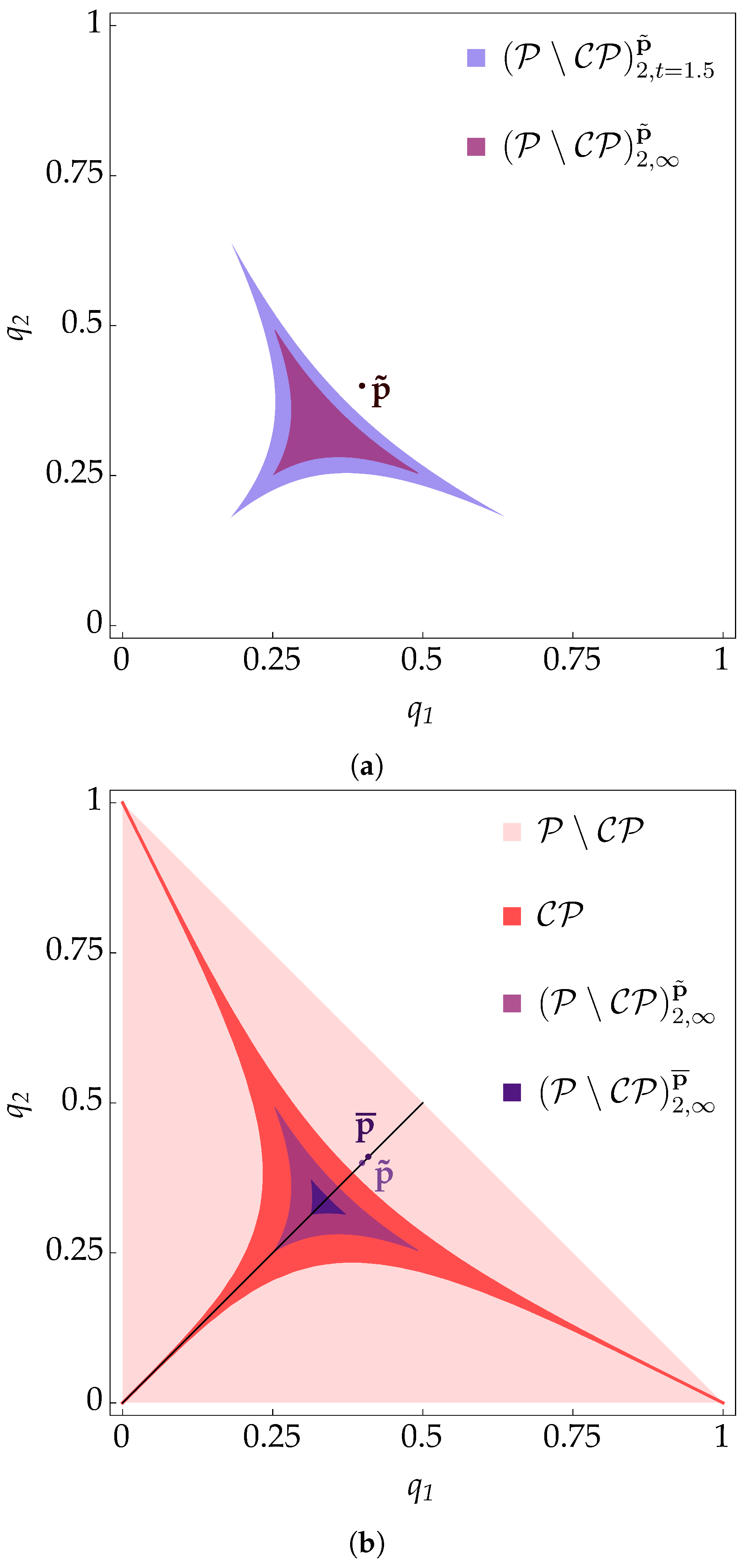
- One-qubit divisibility diagram. The above properties allow one to characterize the one-qubit “divisibility diagram” [31] of the mixtures in terms of the parameters p. Let us denote by the set of weights . As remarked in point (i) above, each corresponds to a P-divisible map . Therefore, the set of divisible maps is the union of the disjoint subsetsnamely, of the subsets of weights corresponding to CP-divisible maps, respectively, and to P-divisible but not CP-divisible maps , respectively. The subset can be identified by means of Property (ii); indeed, if is not CP-divisible, there must exist exactly one such that . On the other hand, if and only if it has positive rates, so that:Assuming , the asymptotic behavior of the rates for is as follows:makes the region identified using the following inequalitieswhere was used, making it possible to represent as a two-dimensional, triangular-like region in the plane, as in Figure 1. Conversely, maps which are only P-divisible are identified with points that violate one and only one of the inequalities (39). Such maps are all examples of so-called weakly non-Markovian evolutions: in fact, as stated in Proposition 3, they do not display BFI. The situation is remarkably different when taking the tensor product of two such maps: in such a case, parameter regions with associated BFI appear.
3.2. Divisibility Diagram of Tensor Product Dynamics
- CP-divisibility. Since the tensor product of CP-divisible maps is still CP-divisible,On the other hand, if , consider arbitrary rank-1 projectors ; since is a CPTP map for all ,(superscripts denote only to which qubits the matrices refer) showing that has to be completely positive. The same holds for , so that
- Lack of P-divisibility. In view of Proposition 2,Also, as we have seen, all single-dynamical maps labeled by p are P-divisible; thus, if is not P-divisible, cannot be CP-divisible, and thenFurthermore, for a sufficiently small but not vanishing perturbation , , one also hasIndeed, a small perturbation cannot in general restore the P-divisibility of the tensor product (see Remark 3). Moreover, we can also assert thatIndeed, if both p and q are in , then two rates, say, and , would become negative and stay negative asymptotically: , , by Property (ii). In particular, so will their sum, . Thus, cannot be P-divisible, due to Proposition 6. As a consequence, all will give rise to a tensor product map displaying SBFI.
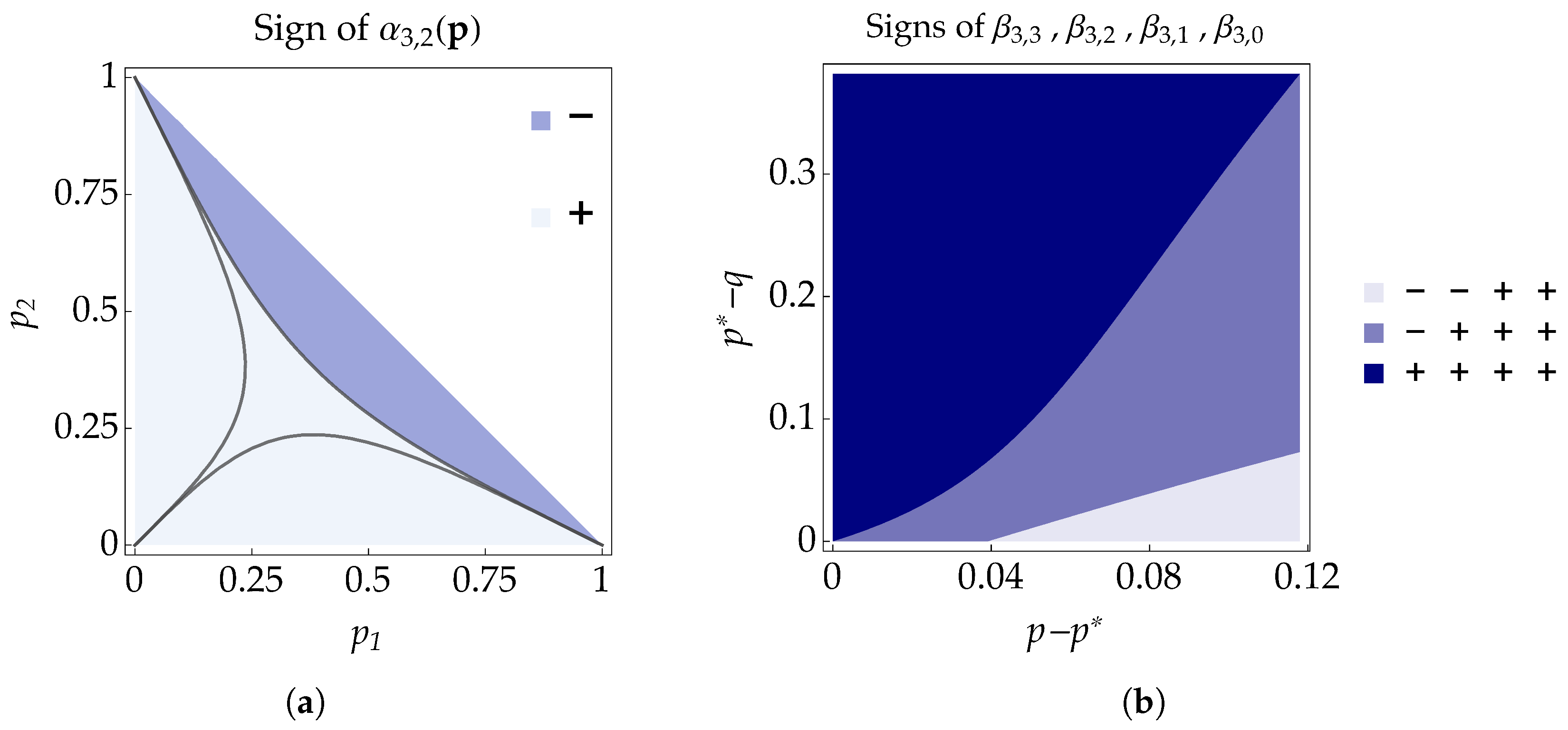
- P-divisibility without CP-divisibility. We now prove the existence of a non-trivial region of maps which are P-divisible, without , being both CP-divisible. From (41), such a region can only consist of points with and or and . In order to show that the region is not empty, we restrict to p of the form , . These are the points lying along the line in Figure 1. With this choice, the Pauli rates becomeThus, only might become negative. If , then the inequality (39c) must be satisfied. For , it readsThen, if and only if , with . Conversely, for , is not a positive function of time and is not CP-divisible.Setting so that , we then look for parameters such that is P-divisible. From Proposition 6, necessary and sufficient conditions areFirst, let us look for a q on the line , with . Then, a simpler condition can be inferred, namely,Indeed, can have at most one zero for (see Appendix B). In turn, the following holds:so that one can look only at the asymptotic behavior. Then, (44) enforces the following conditions on the pair :Hence, if and satisfy (46a) and (46b), then ; otherwise, they belong to . Regions defined by (46a) and (46b) are displayed in Figure 2: it shows that, for values of p increasingly greater than , the following are true:
- The largest value such that is P-divisible is increasingly smaller than (and p). Thus, what also increases is the minimal departure of q from p in the second party such that is P-divisible;
- The subset of such that is P-divisible progressively reduces, up to , for which only can make P-divisible (that is, the only q making the map P-divisible is the centroid of ).
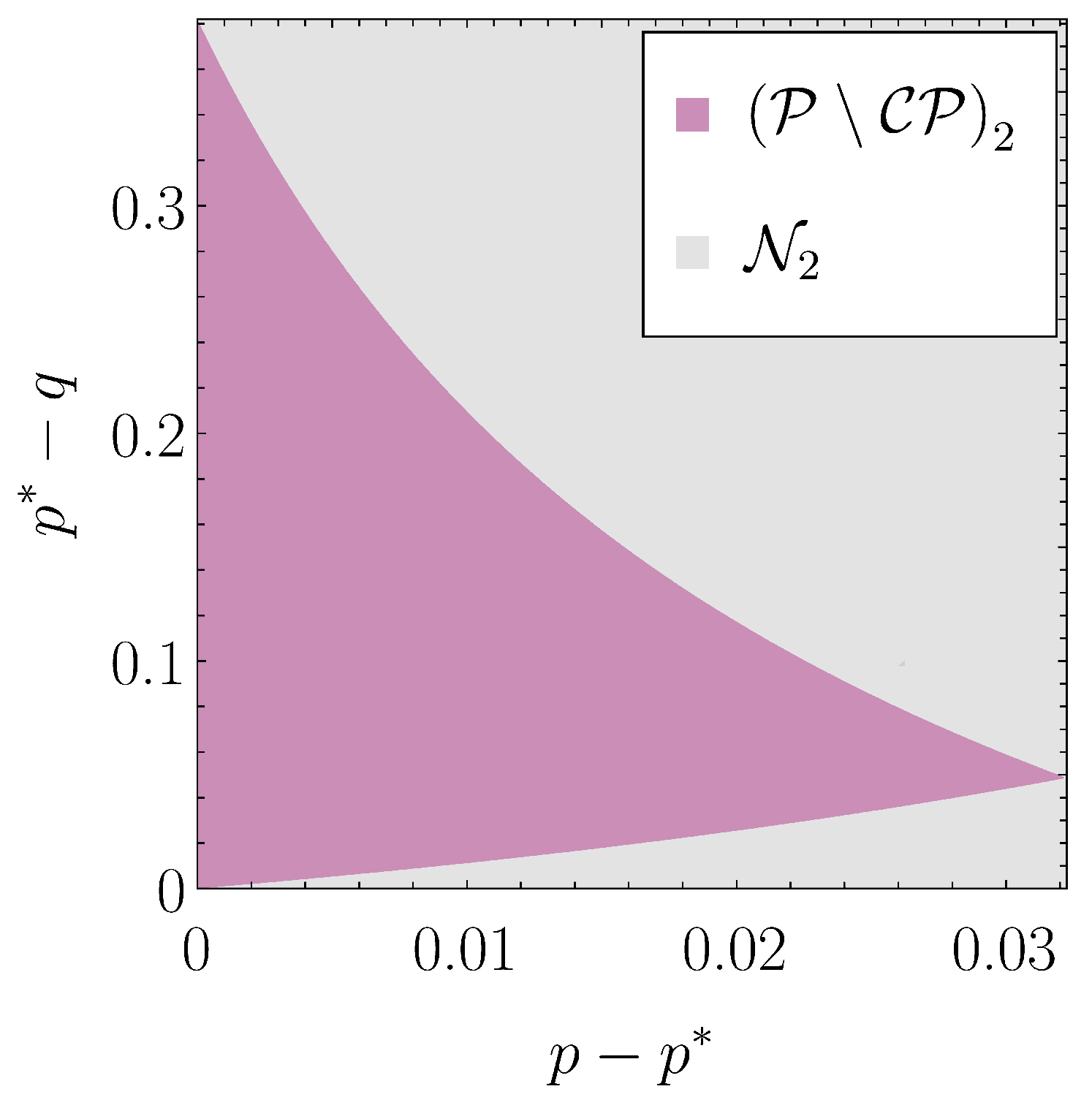
To have more insight about the structure of the region , let us now allow , while keeping fixed. Define then a regionAt , , so . In Figure 3a, is depicted for ; it shrinks for increasing t, but it survives the limit . Points q within the asymptotic region will give rise to maps , which are P-divisible. Numerical evidence indeed shows that (44) is still necessary and sufficient for having the P-divisibility of the tensor product, since the sum will have at most one zero if (this can be checked by studying the numerator of , which will be a polynomial in , and studying the pattern of coefficients to apply the Descartes rule of signs. This is carried out explicitly in Appendix B for the case of taken along the lines and ).In addition, for p along the line and progressively further away from , the size of will reduce, as already noted for the case. The regions for and are compared in Figure 3b.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs of Propositions 5 and 6
Appendix B. Properties of the Quasi-ENM Dynamics
- (I)
- If and for some , , then .Proof.Suppose that is the rate turning negative at some . Then, by means of Descartes’s sign rule [32], we show that can have at most one zero, so if it turns negative, it stays negative for all subsequent times. Using (30) and (31), we rewritewherewithThus, and for all p, while can turn negative. By the Descartes rule of signs (recall that the rule states that for a polynomial with real coefficients, the number of its positive roots P is given by , where S is the number of sign changes between its nonzero coefficients ordered in descending order of the powers, and . In particular, if the number of sign changes is or , there are, respectively, one or zero roots), will have only one zero when turns negative. Points p for which turn negative are shown in Figure A1a. □Figure A1. In (a), the subset of p that makes negative corresponds to the subregion of for which
0. In (b), the sign patterns of , , , are functions of , and , . Since there is only one sign flip, can then have up to one zero.
Figure A1. In (a), the subset of p that makes negative corresponds to the subregion of for which0. In (b), the sign patterns of , , , are functions of , and , . Since there is only one sign flip, can then have up to one zero.
- (II)
- Let and , with and , . If for some , , then for all .Proof.The reasoning is the same as in (I). Letwhere andFocusing only on the numerator, for , one has , and coefficients readCoefficients and are always positive, while and may become negative. Nevertheless, there can be at most one change of sign in the pattern of coefficients (considered in increasing order with the powers of ), as shown in Figure A1b. Again, by the Descartes rule of signs, one concludes that can have at most one real zero. The same reasoning applies for , for which andwhere , so that can have at most one zero for , depending on the sign of . □
References
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Davies, E.B. Markovian master equations. Commun. Math. Phys. 1974, 39, 91–110. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A. N-level system in contact with a singular reservoir. J. Math. Phys. 1976, 17, 1298–1305. [Google Scholar] [CrossRef]
- Dümcke, R. The low density limit for an N-level system interacting with a free Bose or Fermi gas. Commun. Math. Phys. 1985, 97, 331–359. [Google Scholar] [CrossRef]
- Li, C.F.; Guo, G.C.; Piilo, J. Non-Markovian quantum dynamics: What is it good for? Europhys. Lett. 2020, 128, 30001. [Google Scholar] [CrossRef]
- Bylicka, B.; Chruściński, D.; Maniscalco, S. Non-Markovianity and Reservoir Memory of Quantum Channels: A Quantum Information Theory Perspective. Sci. Rep. 2014, 4, 5720. [Google Scholar] [CrossRef]
- Chin, A.W.; Huelga, S.F.; Plenio, M.B. Quantum Metrology in Non-Markovian Environments. Phys. Rev. Lett. 2012, 109, 233601. [Google Scholar] [CrossRef]
- Laine, E.M.; Breuer, H.P.; Piilo, J. Nonlocal memory effects allow perfect teleportation with mixed states. Sci. Rep. 2014, 4, 4620. [Google Scholar] [CrossRef]
- Chruściński, D. Dynamical maps beyond Markovian regime. Phys. Rep. 2022, 992, 1–85. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef] [PubMed]
- Benatti, F.; Chruściński, D.; Filippov, S. Tensor power of dynamical maps and positive versus completely positive divisibility. Phys. Rev. A 2017, 95, 012112. [Google Scholar] [CrossRef]
- Hastings, M.B. Superadditivity of Communication Capacity Using Entangled Inputs. Nat. Phys. 2009, 5, 255–257. [Google Scholar] [CrossRef]
- Smith, G.; Yard, J. Quantum communication with zero-capacity channels. Science 2008, 321, 1812–1815. [Google Scholar] [CrossRef] [PubMed]
- Benatti, F.; Nichele, G. Superactivation of Backflow of Information: Microscopic derivation. 2024; in press. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum System; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Rivas, Á.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef]
- Rivas, Á.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef]
- Kossakowski, A. On Necessary and sufficient conditions for a generator of a quantum dynamical semi-group. Bull. Acad. Pol. Sci. Ser. Math. Astr. Phys. 1972, 20, 1021. [Google Scholar]
- Chruściński, D.; Wudarski, F.A. Non-Markovian random unitary qubit dynamics. Phys. Lett. A 2013, 377, 1425–1429. [Google Scholar] [CrossRef]
- Chruściński, D.; Wudarski, F.A. Non-Markovianity degree for random unitary evolution. Phys. Rev. A 2015, 91, 012104. [Google Scholar] [CrossRef]
- Choi, M.D. Completely positive linear maps on complex matrices. Linear Algebra Its Appl. 1975, 10, 285–290. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Romano, R. Complete positivity and dissipative factorized dynamics. J. Phys. A Math. Gen. 2002, 35, L551. [Google Scholar] [CrossRef]
- Wissmann, S.; Breuer, H.P.; Vacchini, B. Generalized trace-distance measure connecting quantum and classical non-Markovianity. Phys. Rev. A 2015, 92, 042108. [Google Scholar] [CrossRef]
- Chruściński, D.; Maniscalco, S. Degree of Non-Markovianity of Quantum Evolution. Phys. Rev. Lett. 2014, 112, 120404. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.J.W.; Cresser, J.D.; Li, L.; Andersson, E. Canonical form of master equations and characterization of non-Markovianity. Phys. Rev. A 2014, 89, 042120. [Google Scholar] [CrossRef]
- Chruściński, D.; Kossakowski, A.; Rivas, Á. Measures of non-Markovianity: Divisibility versus backflow of information. Phys. Rev. A 2011, 83, 052128. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Piani, M. Non-Decomposable Quantum Dynamical Semigroups and Bound Entangled States. Open Syst. Inf. Dyn. 2004, 11, 325–338. [Google Scholar] [CrossRef][Green Version]
- Benatti, F.; Floreanini, R.; Piani, M. Quantum dynamical semigroups and non-decomposable positive maps. Phys. Lett. A 2004, 326, 187–198. [Google Scholar] [CrossRef][Green Version]
- Megier, N.; Chruściński, D.; Piilo, J.; Strunz, W.T. Eternal non-Markovianity: From random unitary to Markov chain realisations. Sci. Rep. 2017, 7, 6379. [Google Scholar] [CrossRef]
- Chen, H.B.; Lien, J.Y.; Chen, G.Y.; Chen, Y.N. Hierarchy of Non-Markovianity and k -Divisibility Phase Diagram of Quantum Processes in Open Systems. Phys. Rev. A 2015, 92, 042105. [Google Scholar] [CrossRef]
- Meserve, B. Fundamental Concepts of Algebra; Dover Books on Advanced Mathematics; Dover Publications: Mineola, NY, USA, 1982. [Google Scholar]
| CP-d | |
| P-d | , |
| P-d | |
| P-d | P-d, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benatti, F.; Nichele, G. Open Quantum Dynamics: Memory Effects and Superactivation of Backflow of Information. Mathematics 2024, 12, 37. https://doi.org/10.3390/math12010037
Benatti F, Nichele G. Open Quantum Dynamics: Memory Effects and Superactivation of Backflow of Information. Mathematics. 2024; 12(1):37. https://doi.org/10.3390/math12010037
Chicago/Turabian StyleBenatti, Fabio, and Giovanni Nichele. 2024. "Open Quantum Dynamics: Memory Effects and Superactivation of Backflow of Information" Mathematics 12, no. 1: 37. https://doi.org/10.3390/math12010037
APA StyleBenatti, F., & Nichele, G. (2024). Open Quantum Dynamics: Memory Effects and Superactivation of Backflow of Information. Mathematics, 12(1), 37. https://doi.org/10.3390/math12010037