Power System Operation Mode Calculation Based on Improved Deep Reinforcement Learning
Abstract
:1. Introduction
- (1)
- The power flow adjustment problem in OMC is expressed as a Markov decision process (MDP), in which the generator power adjustment and line switching in power systems are considered. The state space, action space, and reward function are designed to conform to the rules of a power system, and the minimum adjustment value of the generator output power is set as 5% of the upper limit;
- (2)
- An improved deep Q-network (improved DQN) method is proposed and introduced to solve the MDP problem, which improves the action mapping strategy for generator power adjustment to reduce the number of adjustments and speed up the DQN training process;
- (3)
- OMC experiments with a power system with eight basic load levels and six N-1 faults are designed; the simulation verification is realized in an IEEE-118 bus system and the robustness of the algorithm after generator fault disconnection is verified.
2. Problem Formulation
2.1. Introduction of the MDP
2.2. Power Flow Convergence MDP Model
- (1)
- State space S: The state space at time step t is defined aswhere is the active power of the generator i; is the line status of the number i; m is the total number of adjustable generators; n is the total number of lines; and is a set of binary codes to represent the number of operating modes at different load levels. For example, k = 4 represents a total of 16 load levels; represents the operation mode of the first target load level, and represents the operation mode of the 16th target load level. In order to simplify the model, we discretized the value of the active generator power into 21 types. The maximum active power of generator i was taken as 1.0. Thus, the allowed value of was . The line status is a binary variable representing the connection () and disconnection () of line i.
- (2)
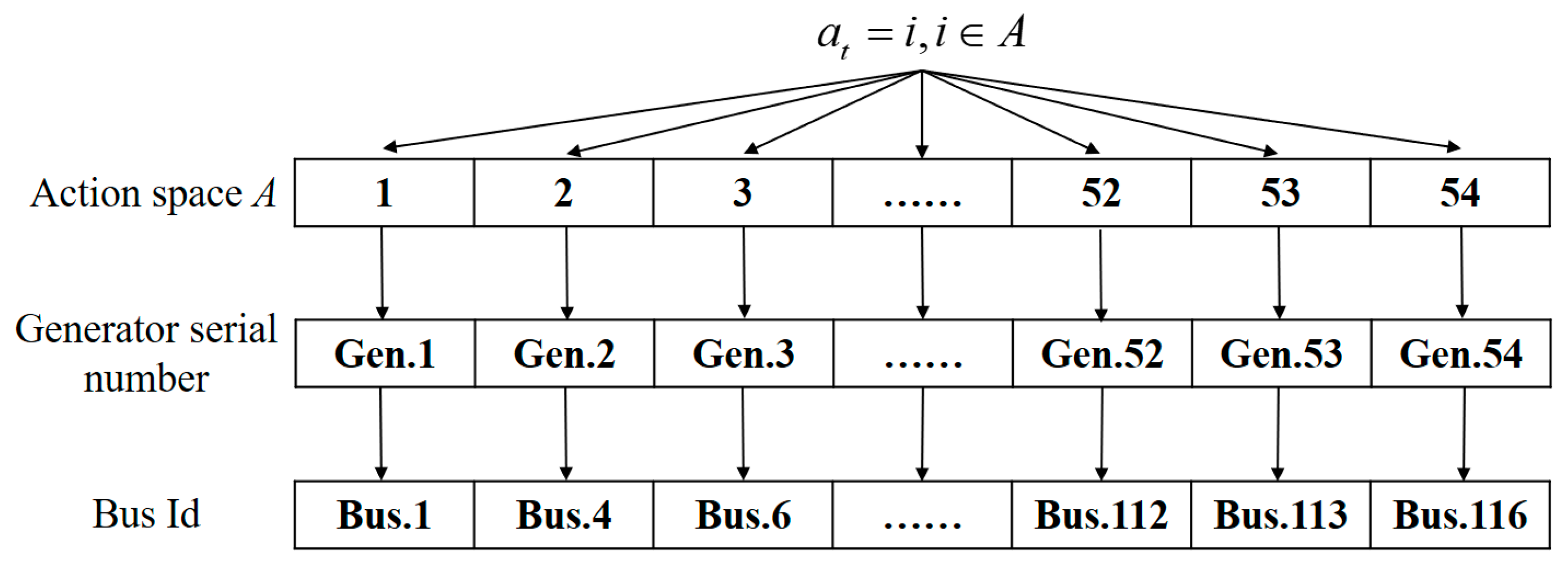
- Action space A: The action space A is discrete and associated with positive integers, defined as , where m is the number of adjustable generators. As is shown in Figure 1 (taking the IEEE-118 bus system as an example), represents the respective serial numbers of the adjustable generators. represents the power adjustment of generator i at time step t. For different sizes of grids, t takes on different values. The action adjustment strategy of generator i is shown in Section 3.2.
- (3)
- State transition: The state transition formula of the system is defined asThe state transition between the system states and at adjacent moments is determined by the transfer function f and the action . Since the power flow calculation function f remains unchanged, the state transition result is only determined by .
- (4)
- Reward function R: Start by defining two indicators in the OMC power flow convergence problem as follows: (a) the convergence of power flow calculation, denoted by ; and (b) the output power of the slack bus generator, which does not exceed the limit and is denoted by . The reward function is thus defined as
3. The Improved DQN Model for OMC
3.1. Introduction of DQN
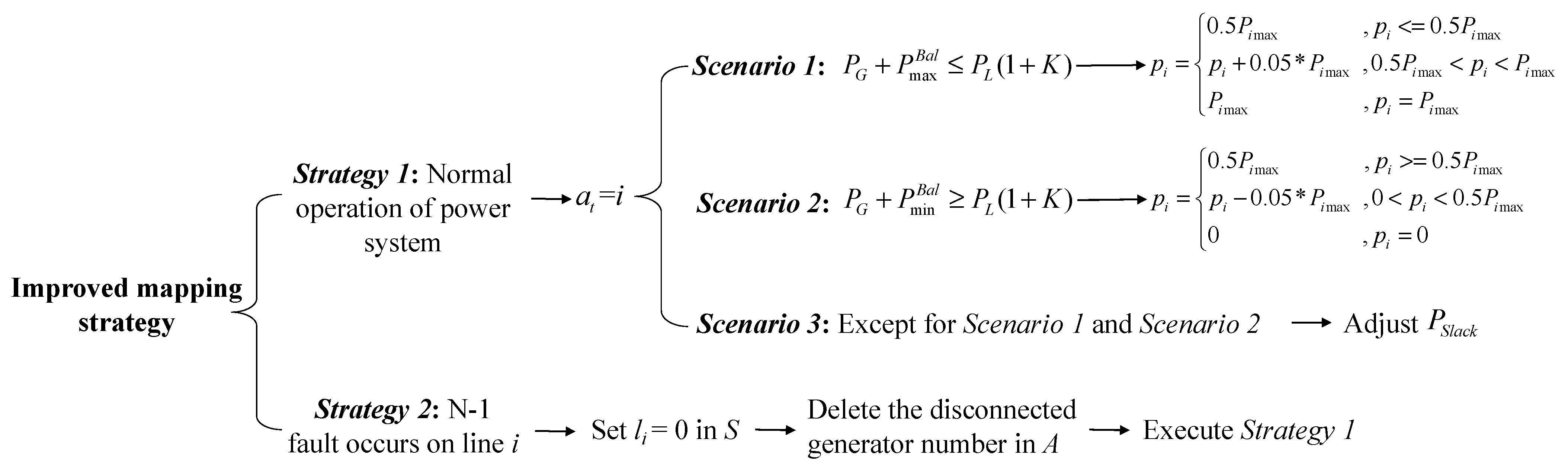
3.2. Improved Mapping Strategy
3.3. Training of the Improved DQN
| Algorithm 1: Training of the improved DQN method | |
| Input: All target load levels. | |
| Output: Trained parameters . | |
| 1 | Initialize reply memory D to capacity N. |
| 2 | Initialize online Q-network with random weight , set target Q-network weight . |
| 3 | For episode = 1, M do |
| 4 | Initialize of power system with generator, load and bus data. |
| 5 | For t = 1, T do |
| 6 | With probability select a random action . |
| 7 | Otherwise select . |
| 8 | Execute action in MATPOWER and observe reward and state . |
| 9 | Store transition in D. |
| 10 | Sample random minibatch of transitions from D. |
| 11 | Set . |
| 12 | Perform a gradient descent step on with the parameters . |
| 13 | Every C step, reset . |
| 14 | If |
| 15 | Reset the power flow state and randomly initialize the target load level. |
| 16 | End If |
| 17 | End For |
| 18 | End For |
4. Experimental Verification and Analyses
4.1. Experimental Setup
4.2. Training Process
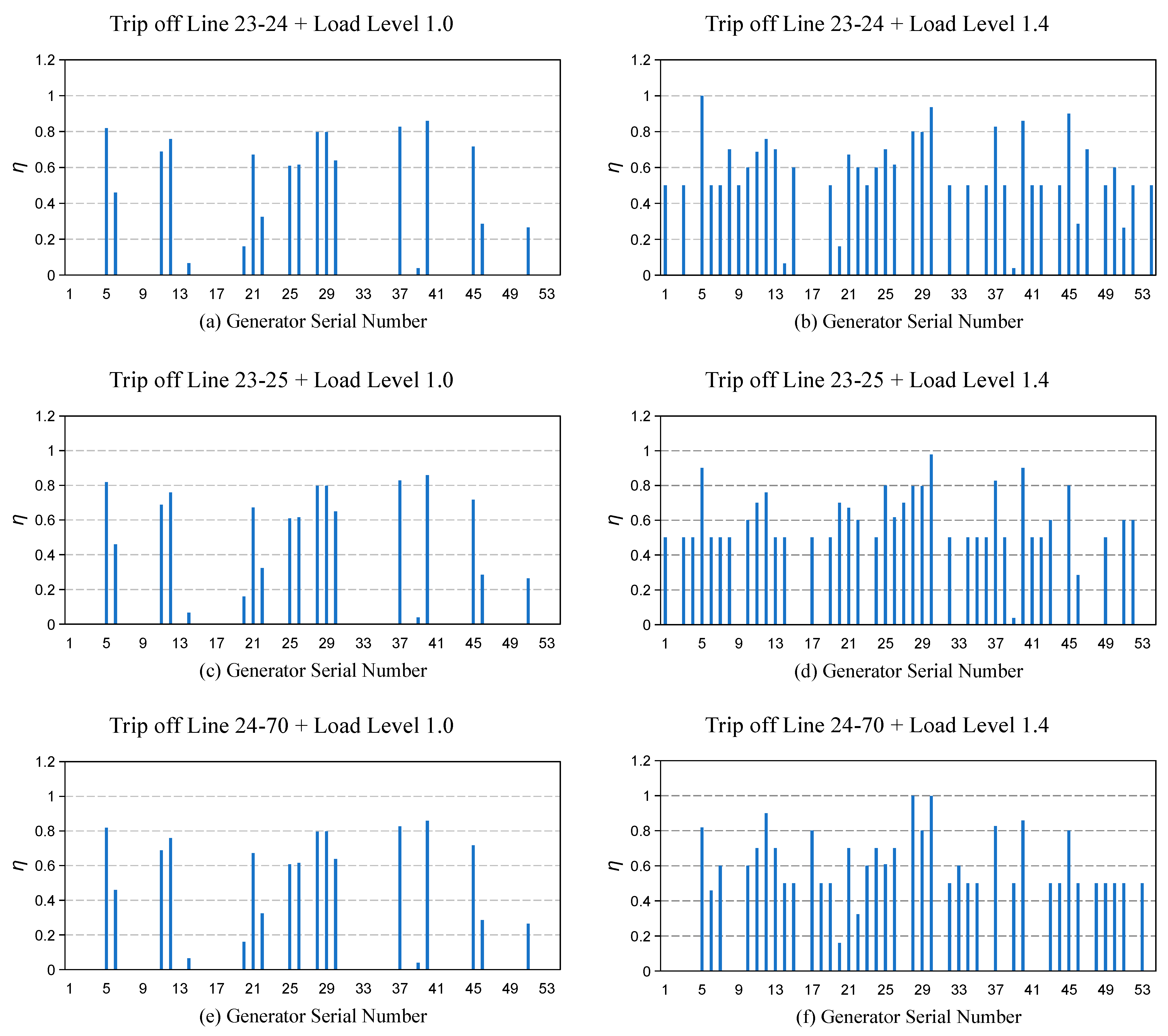
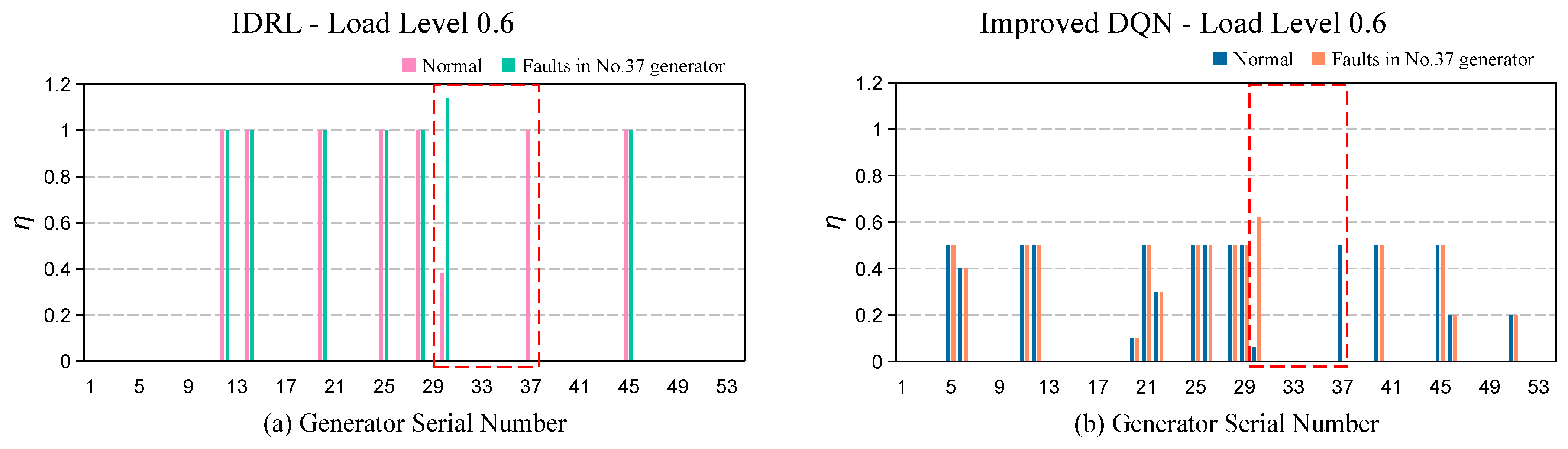
4.3. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.T.; Sun, W.G.; Chen, Z.Y.; Meng, H.F.; Chen, G.R. Backwards square completion MPC solution for real-time economic dispatch in power networks. IET Control Theory Appl. 2019, 13, 2940–2947. [Google Scholar] [CrossRef]
- Xu, H.T.; Yu, Z.H.; Zheng, Q.P.; Hou, J.X.; Wei, Y.W.; Zhang, Z.J. Deep Reinforcement Learning-Based Tie-Line Power Adjustment Method for Power System Operation State Calculation. IEEE Access 2019, 7, 156160–156174. [Google Scholar] [CrossRef]
- Gong, C.; Cheng, R.; Ma, W. Available transfer capacity model and algorithm of the power grid with STATCOM installation. J. Comput. Methods Sci. Eng. 2021, 21, 185–196. [Google Scholar] [CrossRef]
- Jabr, R.A. Polyhedral Formulations and Loop Elimination Constraints for Distribution Network Expansion Planning. IEEE Trans. Power Syst. 2013, 28, 1888–1897. [Google Scholar] [CrossRef]
- Vaishya, S.R.; Sarkar, V. Accurate loss modelling in the DCOPF calculation for power markets via static piecewise linear loss approximation based upon line loading classification. Electr. Power Syst. Res. 2019, 170, 150–157. [Google Scholar] [CrossRef]
- Farivar, M.; Low, S.H. Branch Flow Model: Relaxations and Convexification-Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Fan, Z.X.; Yang, Z.F.; Yu, J.; Xie, K.G.; Yang, G.F. Minimize Linearization Error of Power Flow Model Based on Optimal Selection of Variable Space. IEEE Trans. Power Syst. 2021, 36, 1130–1140. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Saber, A.; Ammar, M.E.; Zeineldin, H.H. A multi-objective planning approach for optimal DG allocation for droop based microgrids. Electr. Power Syst. Res. 2021, 200, 107474. [Google Scholar] [CrossRef]
- Ren, L.Y.; Zhang, P. Generalized Microgrid Power Flow. IEEE Trans. Smart Grid 2018, 9, 3911–3913. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, Y.X.; Li, X.L.; Wang, Z.G.; Liu, Y.X.; Bai, L.Q.; Wang, C.S. Data-Driven Power Flow Calculation Method: A Lifting Dimension Linear Regression Approach. IEEE Trans. Power Syst. 2022, 37, 1798–1808. [Google Scholar] [CrossRef]
- Huang, W.J.; Zheng, W.Y.; Hill, D.J. Distributionally Robust Optimal Power Flow in Multi-Microgrids with Decomposition and Guaranteed Convergence. IEEE Trans. Smart Grid 2021, 12, 43–55. [Google Scholar] [CrossRef]
- Smadi, A.A.; Johnson, B.K.; Lei, H.T.; Aljahrine, A.A. A Lnified Hybrid State Estimation Approach for VSC HVDC lines Embedded in Ac Power Grid. In Proceedings of the IEEE-Power-and-Energy-Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023. [Google Scholar]
- Khodayar, M.; Liu, G.Y.; Wang, J.H.; Khodayar, M.E. Deep learning in power systems research: A review. CSEE J. Power Energy Syst. 2021, 7, 209–220. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Zhang, D.X.; Qiu, R.C. Deep Reinforcement Learning for Power System Applications: An Overview. CSEE J. Power Energy Syst. 2020, 6, 213–225. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Dehghanpour, K.; Wang, Z.Y.; Qiu, F.; Zhao, D.B. Multi-Agent Safe Policy Learning for Power Management of Networked Microgrids. IEEE Trans. Smart Grid 2021, 12, 1048–1062. [Google Scholar] [CrossRef]
- Ye, Y.J.; Wang, H.R.; Chen, P.L.; Tang, Y.; Strbac, G.R. Safe Deep Reinforcement Learning for Microgrid Energy Management in Distribution Networks with Leveraged SpatialTemporal Perception. IEEE Trans. Smart Grid 2023, 14, 3759–3775. [Google Scholar] [CrossRef]
- Massaoudi, M.; Chihi, I.; Abu-Rub, H.; Refaat, S.S.; Oueslati, F.S. Convergence of Photovoltaic Power Forecasting and Deep Learning: State-of-Art Review. IEEE Access 2021, 9, 136593–136615. [Google Scholar] [CrossRef]
- Yin, L.F.; Zhao, L.L.; Yu, T.; Zhang, X.S. Deep Forest Reinforcement Learning for Preventive Strategy Considering Automatic Generation Control in Large-Scale Interconnected Power Systems. Appl. Sci. 2018, 8, 2185. [Google Scholar] [CrossRef]
- Yin, L.F.; Yu, T.; Zhou, L. Design of a Novel Smart Generation Controller Based on Deep Q Learning for Large-Scale Interconnected Power System. J. Energy Eng. 2018, 144, 04018033. [Google Scholar] [CrossRef]
- Xi, L.; Chen, J.F.; Huang, Y.H.; Xu, Y.C.; Liu, L.; Zhou, Y.M.; Li, Y.D. Smart generation control based on multi-agent reinforcement learning with the idea of the time tunnel. Energy 2018, 153, 977–987. [Google Scholar] [CrossRef]
- Ali, M.; Mujeeb, A.; Ullah, H.; Zeb, S. Reactive Power Optimization Using Feed Forward Neural Deep Reinforcement Learning Method: (Deep Reinforcement Learning DQN algorithm). In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020; pp. 497–501. [Google Scholar]
- Yan, Z.M.; Xu, Y. Data-Driven Load Frequency Control for Stochastic Power Systems: A Deep Reinforcement Learning Method with Continuous Action Search. IEEE Trans. Power Syst. 2019, 34, 1653–1656. [Google Scholar] [CrossRef]
- Yan, Z.M.; Xu, Y. A Multi-Agent Deep Reinforcement Learning Method for Cooperative Load Frequency Control of a Multi-Area Power System. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Claessens, B.J.; Vrancx, P.; Ruelens, F. Convolutional Neural Networks for Automatic State-Time Feature Extraction in Reinforcement Learning Applied to Residential Load Control. IEEE Trans. Smart Grid 2018, 9, 3259–3269. [Google Scholar] [CrossRef]
- Lin, L.; Guan, X.; Peng, Y.; Wang, N.; Maharjan, S.; Ohtsuki, T. Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things J. 2020, 7, 6288–6301. [Google Scholar] [CrossRef]
- Nian, R.; Liu, J.F.; Huang, B. A review On reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- IEEE 118-Bus System; Illinois Center for a Smarter Electric Grid (ICSEG): Champaign, IL, USA, 2022.
- Xu, H.; Yu, Z.; Zheng, Q.; Hou, J.; Wei, Y. Improved deep reinforcement learning based convergence adjustment method for power flow calculation. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Virtual, 2–3 July 2020; pp. 1898–1903. [Google Scholar]
- Jie, W.; Ming, D.; Lei, S.; Liubing, W. An improved clustering algorithm for searching critical transmission sections. Electr. Power China 2022, 55, 86–94. [Google Scholar]



| Layer | Input | Output | Activation |
|---|---|---|---|
| Conv1 | 242 × 1 × 1 × minibatch | 128 × 128 × 128 × 32 | ReLu |
| Conv2 | 128 × 128 × 128 × 32 | 256 × 256 × 256 × 64 | ReLu |
| Conv3 | 256 × 256 × 256 × 64 | 128 × 128 × 128 × 128 | ReLu |
| Conv4 | 128 × 128 × 128 × 128 | 64 × 64 × 64 × 54 | ReLu |
| FC | 64 × 64 × 64 × 54 | 54 | Linear |
| Load Level | Tripped-Off Line | (MW) | (MW) | m | K | |
|---|---|---|---|---|---|---|
| Operation Mode 1 | 1.0 | None | 3861.0 | 513.9 | 19 | 3.03% |
| Operation Mode 2 | 0.6 | None | 2456.5 | 49.9 | 17 | 1.97% |
| Operation Mode 3 | 0.8 | None | 3413.1 | 87.3 | 18 | 3.05% |
| Operation Mode 4 | 1.2 | None | 4455.6 | 802.1 | 27 | 3.18% |
| Operation Mode 5 | 1.4 | None | 5252.8 | 797.4 | 38 | 2.83% |
| Operation Mode 6 | 1.6 | None | 6150.6 | 780.2 | 47 | 2.94% |
| Operation Mode 7 | 1.8 | None | 6959.9 | 802.3 | 53 | 2.79% |
| Operation Mode 8 | 2.0 | None | 7843.8 | 783.7 | 53 | 2.82% |
| Operation Mode 9 | 1.0 | 23–24 | 3861.0 | 514.2 | 19 | 3.04% |
| Operation Mode 10 | 1.4 | 23–24 | 5349.4 | 752.9 | 42 | 2.68% |
| Operation Mode 11 | 1.0 | 23–25 | 3861.0 | 521.8 | 19 | 3.21% |
| Operation Mode 12 | 1.4 | 23–25 | 5322.6 | 787.0 | 40 | 2.80% |
| Operation Mode 13 | 1.0 | 24–70 | 3861.0 | 513.8 | 19 | 3.04% |
| Operation Mode 14 | 1.4 | 24–70 | 5302.1 | 803.3 | 38 | 2.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Zhou, B.; Yang, D.; Wu, W.; Lv, C.; Cui, Y. Power System Operation Mode Calculation Based on Improved Deep Reinforcement Learning. Mathematics 2024, 12, 134. https://doi.org/10.3390/math12010134
Yu Z, Zhou B, Yang D, Wu W, Lv C, Cui Y. Power System Operation Mode Calculation Based on Improved Deep Reinforcement Learning. Mathematics. 2024; 12(1):134. https://doi.org/10.3390/math12010134
Chicago/Turabian StyleYu, Ziyang, Bowen Zhou, Dongsheng Yang, Weirong Wu, Chen Lv, and Yong Cui. 2024. "Power System Operation Mode Calculation Based on Improved Deep Reinforcement Learning" Mathematics 12, no. 1: 134. https://doi.org/10.3390/math12010134
APA StyleYu, Z., Zhou, B., Yang, D., Wu, W., Lv, C., & Cui, Y. (2024). Power System Operation Mode Calculation Based on Improved Deep Reinforcement Learning. Mathematics, 12(1), 134. https://doi.org/10.3390/math12010134








