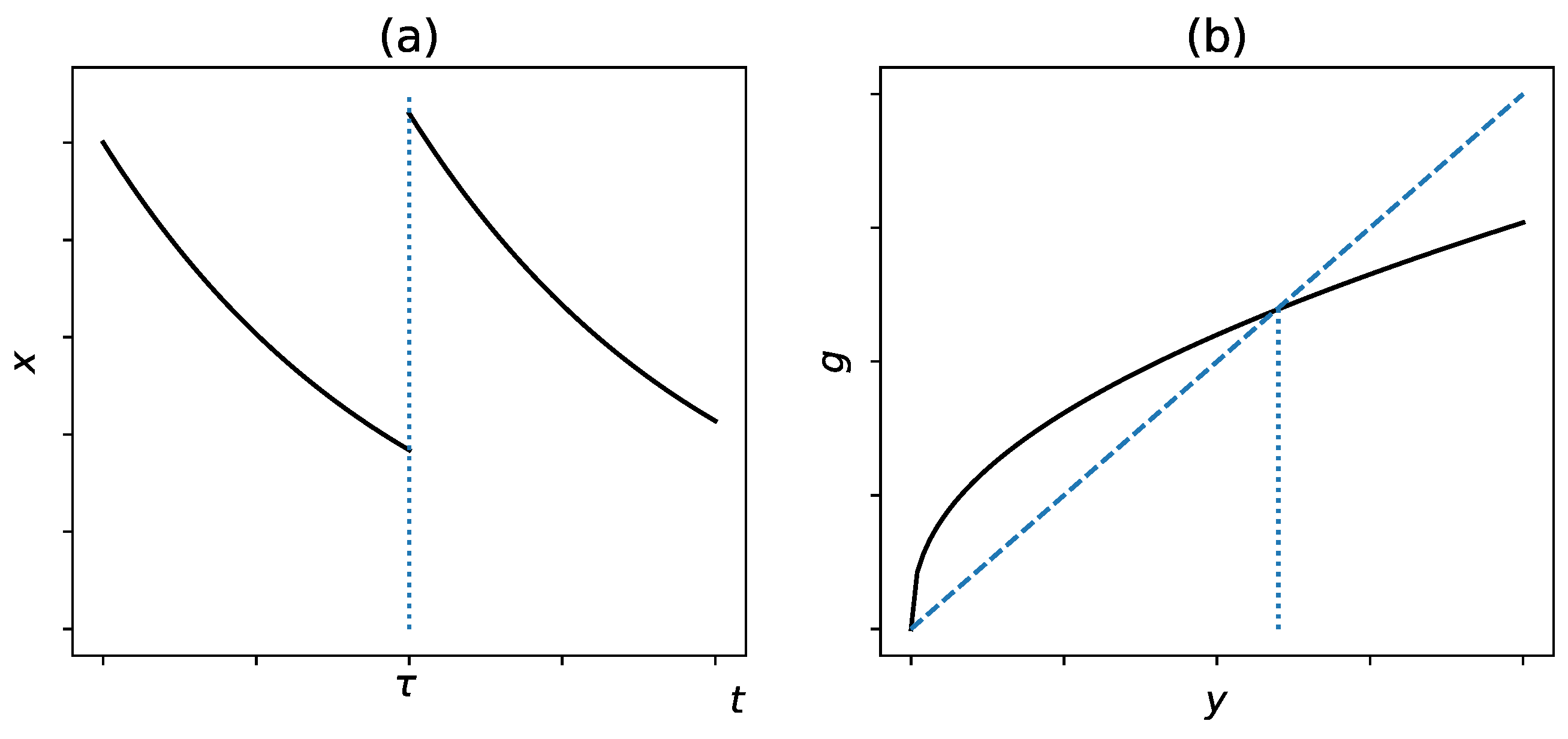1. Introduction
Simulation models are widely used in the study of environmental, economic, and social systems, see, for instance, classical references [
1,
2]. An important feature of such objects is the possibility of an ambiguous description: the interaction of their elements can be represented by many “plausible” nonlinear dependencies. This “uncertainty” (freedom) allows us in some cases to choose a special structure of the model that allows for a fairly complete study. To study the population evolution in a periodic environment, in the present paper, we propose the design of competition models, i.e.,
δ-systems, in which population growth coefficients are periodic delta functions.
Periodicity often reflects seasonality, which is an important factor affecting population dynamics [
3,
4]. More precisely, there are a lot of periodic factors, e.g., temperature, rainfall, human activity, etc., which can essentially affect evolution [
3], species coexistence [
5,
6], infectious diseases [
7,
8,
9], etc. Taking into account seasonality can qualitatively change the conclusions regarding population dynamics, since parameter periodicity can, in particular, produce quasi-periodic and chaotic solution behavior [
10,
11]. Interestingly, seasonality can have a stabilizing as well as destabilizing effect on dynamics [
12,
13,
14].
In this paper, we follow the approach which was first used in [
15] that can be classified as semi-discrete modeling [
16]. In fact, it utilizes differential equations with impulsive effects [
17,
18,
19]. We believe that the form of this approach which we use in the paper has a certain degree of novelty. Usually, impulses are used to reproduce some biological or environmental effects such as short-term reproduction processes [
15,
20], pulsed immigration [
16], impulsive harvesting [
21], etc. Our goal is somewhat different: the presented approach allows us to simplify the study of large time dynamics in systems with periodically changing parameters. We show that the study of such systems can be substantially simplified by the utilization of periodic delta functions as population growth rates. In the
-system framework, the search for periodic regimes is reduced to the solution of a certain system of linear algebraic equations. Moreover, the stability of equilibria can be justified by quite elementary means. In the corresponding
-systems, nonlinear interactions appear quite rarely; each population has only one growth point during a period. The last circumstance allows us to split the Poincaré mapping into a superposition of simple mappings by changing only one (“its own”) variable. Therefore, a certain “nonlinear skeleton” remains from a full-fledged nonlinear interaction. This skeleton preserves the competitive essence of the phenomena, while greatly simplifying the investigation. Therefore,
-systems represent a kind of “scout model” for obtaining plausible hypotheses related to the general case.
The aim of this paper is to demonstrate the capabilities of this approach using the Contois-type model [
22] as the main example. From the point of view of modeling ecosystems, we demonstrate that some interesting effects can be discovered with the use of the adopted approach: a low-productive population can displace a highly productive one, the displacement can be non-transitive, the coexistence can be non-transitive. We also show how delta functions can be utilized for the analysis of a “predator–prey” system.
The paper is organized as follows. In
Section 2, we introduce
-shaped periodic growth rates using an example of the Contois model for a single population. We derive the jump condition and carry out a simple study of the correspondent Poincaré mapping. In
Section 3, we generalize the jump condition to the case of two populations, underlying the “splitting effect” of the Poincaré mapping. We present some examples, demonstrating counter-intuitive properties of competition outcomes. In
Section 4, we present some results related to the stock constant, which is sufficient for the displacement of competitors.
Section 5 concludes the paper.
2. Single Population Dynamics in a Model with -Shaped Growth Rates
Formally, the dynamics of a single population are represented in the form [
23]:
where
x is the population biomass;
is a smooth function, which decreases in the first argument;
is the growth rate, depending on changing environmental factors (temperature, etc.). For example, the Contois model [
22] uses the dependence
where
k is the biomass of competitors at time moment
t, and
for all
t. If the environment is periodic, then
r is a periodic function,
,
, for some
. Growth rate functions are usually non-negative and may have one or several maxima on
. Some biologists suggest that for evolutionary mature communities of similar species, within common ecological niches, the areas under these graphs are approximately the same (over the same time period) [
24]. Without loss of generality, we assume that they are equal to 1.
The usage of
-shaped growth rate functions can be rationalized as follows. Consider the Laplace-like transform
The function
p is completely monotone:
,
, and
. Let
E be the locally compact space of infinitely differentiable functions on
, endowed with the topology of uniform convergence of functions and all their derivatives on compact subsets of
. As is mentioned in [
25], the set
K of all completely monotone functions such that
is compact in
E, and the exponents
,
are precisely its extreme points. Any function in
K can be represented as
with some non-negative Borel measure on
(the Bernstein theorem [
25]). Since
, from a heuristic point of view, delta functions turn out to be a kind of “basis” in the family of growth functions.
Let us construct the Poincaré mapping (the first recurrence mapping) for the following single population model with a
-shaped growth rate:
where
,
is a population productivity parameter, and
k is the biomass of competitors.
From now on, we assume that all delta functions δ are T-periodic. Roughly speaking, the solution of (
3) on
is a decreasing exponent, except of one point
, where there is a positive jump from
to
, see
Figure 1a.
To deduce the formula for this jump, we follow a well-known scheme [
26,
27]. Assume that the solution
x of Equation (
3) is a pointwise limit of the solutions
, corresponding to the growth rates
, where
is a smooth function concentrated in the interval
, and
We also assume that
. Such a definition of
x is correct if the limit does not depend on the sequence. For
, from (
1), (
2) we obtain
Integrating over
, we see that for
Finally, since
it follows that
is uniformly bounded:
and
,
. Collecting these assertions, we obtain the relation for the left and right limits
,
at the jump point
:
Importantly, the values
,
do not depend on the sequence. Note also that the nonlinearity in (
3) is related only to the jump at
. In particular,
Put
. Then,
where
. Indeed, for
, this relation coincides with (
5). In the general case, (
6) follows from the periodicity argument.
The relation (
6) implicitly determines the Poincaré mapping
where the function
g is monotone increasing and concave in the first argument (see
Appendix A). Note that functions of this kind constitute the simplest class of nonlinear dependencies. They are widely used in applied research in economics and ecology (see, e.g., [
28]).
Assume that
; then, there exists a unique equilibrium point
of (
7). From the properties
(see
Appendix B) and
Figure 1b, it follows that
is globally stable in
.
To show that the proposed approach is of general nature, consider the non-autonomous Volterra model [
29]:
where, as defined above,
is the
T-periodic delta function, which is zero everywhere except the points
,
. Clearly, the solution of this equation on the interval
is an increasing exponent. At the point
, there is a downward jump. Put
. Then,
. To find
, rewrite the Volterra equation as follows
Integrating this over a small interval
and passing to the limit as
, we get
. These related calculations are quite similar to those considered above. In general, the recursion takes the form [
30]:
3. Paradoxes in a -System of Two Competitors
If there are several populations with
T-periodic growth rates
, then to avoid the ambiguity in the jump outcomes, we always assume that all
are different. Furthermore, we consider the model of “similar” competitors:
Here, other competitors exert equal pressure on the growth rate of the i-th population. Sometimes, such competition is called neutral.
Consider a Contois-type model with two competitors and
T-periodic
-growth rates:
where
,
and
. Put
,
,
Using the “jump conditions” (
4), after a few calculations (see
Appendix C), we conclude that the Poincare mapping is implicitly determined by the equations
where
,
Furthermore, the Poincaré mapping
admits a decomposition
into two simple mappings
Each simple mapping is a monotone concave function, and it changes only “its own” coordinate. This gives rise to a “stepwise” movement of the state point, resembling the movement of a rook on a chessboard, see
Figure 2a. Without splitting, the movement of the state point resembles the “oblique” movement of the chess bishop, see
Figure 2b.
A key role in the study of the dynamics of the system (
11), (
12) is played by two isoclines
It is remarkable that each isocline is a straight line segment which gently attracts the state point along its own coordinate. If
is above
(see
Figure 2a), then the first population displaces the second one. If the isoclines intersect inside
, then a positive equilibrium
arises:
Note that the determinant
of the system of linear Equations (
13) is strictly positive for all
. In this case, it is easy to see that the positive equilibrium is asymptotically stable, see
Figure 2b.
If one of the components, say
, is negative, then the correspondent component
of the solution of (
9), (
10) tends to zero. Put
. The analysis of (
13) with
reveals the following “paradoxical” phenomena.
- 1.
A low-productive population can displace a highly productive one. Put
,
,
,
. From (
13), we get
,
.
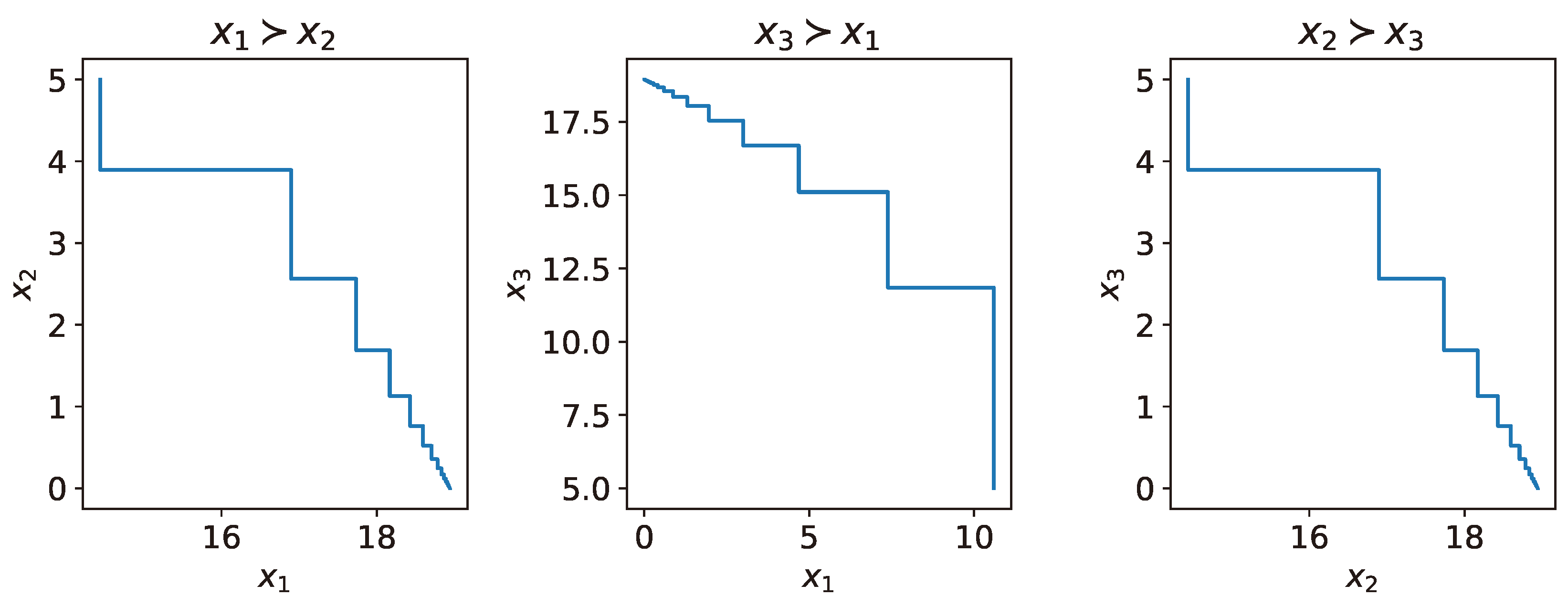
- 2.
The displacement can be non-transitive. Consider a set of three populations with parameters
Applying (
13) to any pair of these populations, we see that in a two-species community, one of the populations displaces the other. Formally,
where
is the binary relation, meaning that the
i-th population displaces the
j-th one. Iterations of the split Poincaré mapping are shown in
Figure 3.
In the three-dimensional Contois system, a stable periodic regime was discovered. However, in some other models, non-transitivity gives rise to a complex regime consisting of a cyclical change of dominant forms, see [
30].
- 3.
Coexistence can be non-transitive. Denote by
~
the coexistence relation. It appears that this relation need not be transitive. For
from the analysis of (
13), we get
Note that in a constant environment, the neutral competition is quite tough. In particular, it is not difficult to show that only one (the most productive) population survives in such a situation. The changing environment turns out to be less rigid, and here the coexistence of several competitors is possible, as mentioned above. It is natural to ask how many competitors can contain their community for a given period
T, reflecting the time capacity of the environment. This problem was investigated in [
31] for piecewise constant growth rates. After some quite cumbersome calculations, the authors deduced that the coexistence of any finite number of competitors is possible.
It turns out that this conclusion can be easily achieved for a
-system with
n similar competitors:
for
, and
,
. Put
and construct the Poincaré mapping, similarly to the two-dimensional case. Its equilibrium points
are determined by a system of linear equations. When a positive solution exists, its components are equal due to symmetry. Finally (see [
30]), this solution is globally asymptotically stable in
.
Note that even in simple oscillatory systems, periodic deformations of their parameters often lead to unexpected effects. For instance, at a certain frequency of oscillations of the suspension of a pendulum, the lower equilibrium becomes unstable (parametric resonance), and a “strange” stabilization of the upper equilibrium occurs at sufficiently high frequencies [
26]. Therefore, it is natural, for example, to investigate the influence of parameter periodicity on the oscillatory dynamics of the “predator–prey” system. To do this, we carry out a modification of the non-autonomous Volterra “predator–prey” model [
29]:
where
. Put
By the argument given above, we obtain the relations
Here, the equilibrium is unstable for all . In particular, for , a locally stable cycle of length 6 arises. So, the oscillatory process becomes more complex.
4. A Sufficient Condition for Competitive Displacement—Universal Stock Constant
Let us analyze paradox 1 from
Section 3 more carefully. Namely, we will find a sufficient condition for the displacement of the second population. Within the framework of system (
13), this is a constraint on
,
, ensuring the inequalities
and
for all
. The most severe option occurs when the parameters
and
are very close to each other. Put formally,
. Then,
,
. We will call
the
stock constant. Under the condition
we have
and
. This conclusion holds true for all other
and implies the following result.
Theorem 1 ([
30])
. Under condition (14), the first population displaces the second one within a community of two competitors. Sometimes, a cruder sufficient condition for competitive dominance is used [
30]:
. For
n competitors, the Contois
-system takes the form
where
. Surprisingly, the stock constant for a two-dimensional system remains valid in the general case as well.
Theorem 2 ([
30])
. Under the stock conditionthe first population displaces the others in system (15). The justification of this result is based on simple geometric considerations similar to
Figure 2a: For each variable in (
15), it is possible to construct a Poincaré mapping (see (
11), (
12) for its two-dimensional analogue), from which isoclines
can be found explicitly. All isoclines are hyperplanes. It turns out that under the stock condition (
16), the isocline
is located above the others. This implies the result of Theorem 2.
One can say that (
15) describes all vs. all competition. Here, for the dominance of the first population, the stock constant need not depend on the number of competitors. This universality is due to the fact that populations interfere with each other, and therefore cannot fully unite against the first one.
Let us consider an analogue of system (
15) with smooth growth coefficients:
where each
is a non-negative
T-periodic function. It appears that here, the inequalities (
16) with
still imply that the the first population displaces the others. The proof of this rather complex result is based of the principle of inheritance of local properties by the global Poincaré mapping [
32].
For comparison, consider Volterra’s competitive scheme:
It is natural to call the value of individual productivity of the i-th population.
Theorem 3 ([
30])
. Assume that the stock conditionis satisfied. Then, in the Volterra system, the first population displaces the others. This means that system (
18) also has a universal stock constant. Of course, the coincidence of the stock constants in the models (9) and (12) is accidental. Again, we stress that the existence of universal stock constants is due to the “all vs. all” competition scheme. It is expected that in “all vs. one” models, the stock constants depend on
n.