A Depth-Progressive Initialization Strategy for Quantum Approximate Optimization Algorithm

Abstract

The quantum approximate optimization algorithm (QAOA) is known for its capability and universality in solving combinatorial optimization problems on near-term quantum devices. The results yielded by QAOA depend strongly on its initial variational parameters. Hence, parameter selection for QAOA becomes an active area of research, as bad initialization might deteriorate the quality of the results, especially at great circuit depths. We first discuss the patterns of optimal parameters in QAOA in two directions: the angle index and the circuit depth. Then, we discuss the symmetries and periodicity of the expectation that is used to determine the bounds of the search space. Based on the patterns in optimal parameters and the bounds restriction, we propose a strategy that predicts the new initial parameters by taking the difference between the previous optimal parameters. Unlike most other strategies, the strategy we propose does not require multiple trials to ensure success. It only requires one prediction when progressing to the next depth. We compare this strategy with our previously proposed strategy and the layerwise strategy for solving the Max-cut problem in terms of the approximation ratio and the optimization cost. We also address the non-optimality in previous parameters, which is seldom discussed in other works despite its importance in explaining the behavior of variational quantum algorithms.

1. Introduction

The Quantum Approximate Optimization Algorithm (QAOA) was first introduced by Farhi et al. [1] as a quantum-classical hybrid algorithm, which consists of a quantum circuit with an outer classical optimization loop, to approximate the solution of combinatorial optimization problems. Since then, many studies have been conducted to discuss its quantum advantage and its implementability on near-term Noisy Intermediate Scale Quantum (NISQ) devices [2,3,4,5,6,7,8]. QAOA is shown to guarantee the approximation ratio $\alpha >0.6924$ for circuit depth $p=1$ in the Max-cut problem on 3-regular graphs [1]. Further studies have shown a lower bound of $\alpha >0.7559$ for $p=2$ and $\alpha >0.7924$ for $p=3$ [9].

Parameter selection in QAOA has been an active area of research due to the difficulties that lie within the classical optimization of QAOA, especially the barren plateaus problem [10,11,12]. Patterns in optimal parameters of QAOA have constantly been studied, and various strategies are proposed to improve the quality of the solution [13,14,15,16,17,18,19,20]. Machine learning methods are also employed to improve parameter selection [18,19,21,22]. For instance, it is found that for some classes of graphs, e.g., regular graphs, the optimal parameters of a smaller graph can be reused as they are on larger graphs to approximate the solution without solving them [23]. This characteristic is defined as the ‘parameter concentration’ in [24] and is found in some projectors as well. Recently, the transferability of parameters has also been studied with the discovery of parameter concentration in d-regular subgraphs with the same parity (odd or even) [25]. These works focused on the characteristics of the optimal parameters of QAOA in the direction of problem size n.

Another direction that is mostly concerned is the QAOA circuit depth p. It is discussed that we usually need a larger p to solve problems with a larger n with a higher $\alpha$. However, as p grows larger, the increased occurrence of local minima makes the optimization difficult. If the QAOA parameters are initialized randomly, there is a high chance that they will converge to an undesired local optimum. This is shown in our previous work [26], and we proposed to use the previous optimal parameters as starting points for the following depths. We found out that this improves the convergence of the approximation ratio towards optimality. This implies that there is some relationship between the previous optimum and the current optimum. This motivates us to study the relationship between the optimal parameters and circuit depths.

In this work, we study the patterns in the optimal parameters of QAOA Max-cut in two directions: the angle index j and the circuit depth p. We name the pattern exhibited by the optima with respect to j as the adiabatic path, and the pattern with respect to p as the non-optimality, which we explain each of them in detail in Section 3. Also, as the expectation function of QAOA Max-cut is highly periodic and symmetric, the landscape it produces will have multiple optima. Therefore, for the adiabatic path and the non-optimality patterns to be seen explicitly, it is required to restrict the bounds of the parameter search space, so that the redundant optimal points in the full search space can be removed.

Based on the adiabatic path and the non-optimality, we propose the bilinear initialization strategy (or simply bilinear strategy) which generates initial parameters at the new depth given the optimal parameters from the previous depths. This strategy aims to reproduce the optimal patterns at the new depth so that the initial parameters generated will be close to the optimal parameters, reducing the likelihood to converge to an undesired optimum. Since the previous parameters are used to predict the new parameters, this strategy requires optimization at every depth up to the desired depth. However, unlike most other strategies [27,28] which require multiple trials to ensure success, the bilinear strategy only requires one trial at each depth.

We then demonstrate the effect of the bilinear strategy on solving the Max-cut problem for 30 non-isomorphic instances composing different classes of graphs, including the 3-regular, the 4-regular, and the Erdös-Rényi graphs with different edge probabilities. We compare the strategy with our previously proposed parameters fixing strategy, and the layerwise strategy, in terms of approximation ratio and optimization cost.

We also study the case where the strategy might fail in odd-regular graphs with wrongly specified bounds. The result is interesting as it shows that there exists an optimum in the expectation function of odd-regular graphs that does not follow the adiabatic path pattern. Instead, the $\beta$ parameters (parameters associated with the mixer Hamiltonian) oscillate back and forth. We then explain this phenomenon using the symmetry in odd-regular graphs.

2. QAOA: Background and Notation

The objective of QAOA is to maximize the expectation of some cost Hamiltonian $H_z$ with respect to the ansatz state $\psi (\mathbf{\gamma },\mathbf{\beta })$ prepared by the evolution of the alternating operators:

$$|{\psi }_p(\mathbf{\gamma },\mathbf{\beta })\rangle =\prod _{j=1}^p{e}^{-i{\beta }_j{H}_x}{e}^{-i{\gamma }_j{H}_z}|+{\rangle }^{\otimes n}.$$

(1)

where $\mathbf{\gamma }=({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_p)$ and $\mathbf{\beta }=({\beta }_1,{\beta }_2,\dots ,{\beta }_p)$ are the $2p$ variational parameters, with $\mathbf{\gamma }\in {[0,2\pi )}^p$ and $\mathbf{\beta }\in {[0,\pi )}^p$. ${|+\rangle }^{⨂n}$ corresponds to n qubits in the ground state of $H_x={\sum }_{j=1}^n{X}_j$, where $X_j$ is the Pauli X operator acting on the j-th qubit.

In this paper, we consider the Max-cut problem, which aims to divide a graph into two parts, with the maximum number of edges between them. The Max-cut problem is an NP-complete problem due to its reducibility to the MAX-2-SAT problem [29]. The cost Hamiltonian $H_z$ for the Max-cut problem for an unweighted graph $G=(V,E)$ is given as

$$H_z=\frac{1}{2}\sum _{(j,k)\in E}(\mathrm{𝟙}-Z_j{Z}_k),$$

(2)

where $Z_j$ is the Pauli Z operator acting on the j-th qubit. The $Z_j{Z}_k$ operators are applied to qubits j and k for every edge $(j,k)$ in the graph. We define the expectation of $H_z$ with respect to the ansatz state in Equation (1):

$$F_p(\mathbf{\gamma },\mathbf{\beta })\equiv \langle {\psi }_p(\mathbf{\gamma },\mathbf{\beta })|H_z|{\psi }_p(\mathbf{\gamma },\mathbf{\beta })\rangle ,$$

(3)

where p is known as the circuit depth of QAOA. Solving the problem with QAOA is equivalent to maximizing Equation (3) with respect to the variational parameters $\mathbf{\gamma }$ and $\mathbf{\beta }$. This can be completed with a classical optimizer that searches for the maximum F and the parameters that maximize it:

$$({\mathbf{\gamma }}^{*},{\mathbf{\beta }}^{*})\equiv arg\underset{\mathbf{\gamma },\mathbf{\beta }}{max}F(\mathbf{\gamma },\mathbf{\beta }),$$

(4)

where the superscript * denotes optimal parameters. We also define the approximation ratio $\alpha$ as

$$\alpha \equiv \frac{F({\mathbf{\gamma }}^{*},{\mathbf{\beta }}^{*})}{C_{\max }},$$

(5)

where $C_{\max }$ is the maximum cut value for the graph. The approximation ratio is a typical evaluation metric indicating how close the solution given by QAOA is to the true solution, $0\le \alpha \le 1$, with the value of 1 nearer to the true solution.

Throughout the paper, we use the symbol $\varphi$ to generally denote either $\gamma$ or $\beta$ in situations where the distinction of both is not required. Also, we sometimes use ${\Phi }_p$ to denote the entire parameter vector at circuit depth p:

$${\Phi }_p\equiv {(\mathbf{\gamma },\mathbf{\beta })}_p=({\gamma }_1,\dots ,{\gamma }_p,{\beta }_1,\dots ,{\beta }_p).$$

(6)

For a single parameter, we use ${\varphi }_j^p$ to denote the parameter at circuit depth p with index j.

The maximum of $F_p$ in the p-level search space will approach $C_{max}$ as $p\to \infty$, thus the approximation ratio $\alpha$ will approach 1 [1]. However, due to the increased occurrence of local maxima in larger p, it gets more difficult to find the maximum $F_p$ [3,27]. If the parameters were initialized randomly, the optimizer is more likely to be trapped in local maxima for larger p [26]. The choice of initial points for the optimizer determines whether the optimizer converges to a global maximum. Hence, we would prefer to have “good” initial points for the optimizer to converge to the desired maximum.

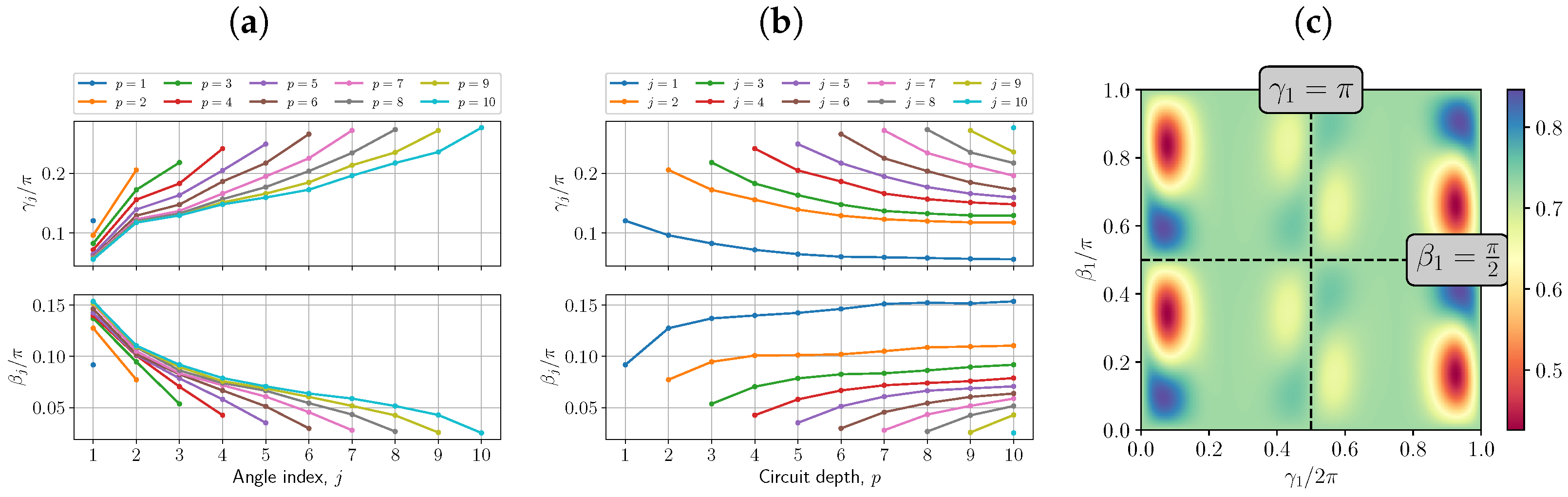
3. Patterns in the Optimal Parameters of QAOA

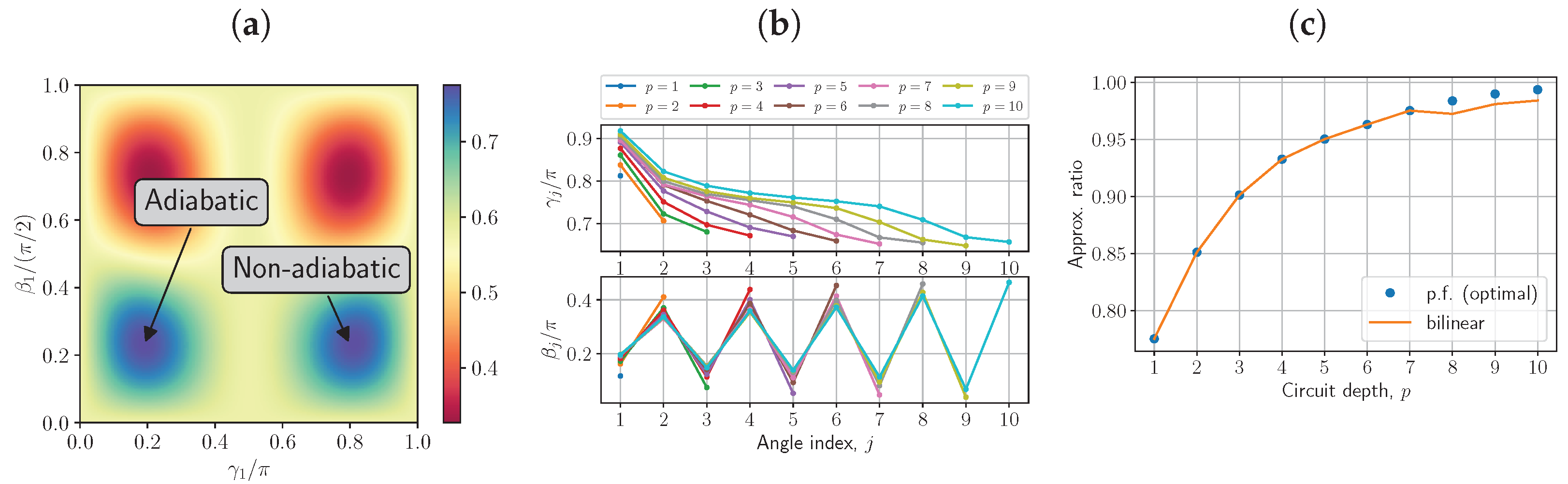
3.1. Resemblance to the Quantum Adiabatic Evolution

It has been repeatedly reported that the optimal parameters resemble the adiabatic quantum computation (AQC) process [30], where the mixer Hamiltonian $H_x$ is gradually turned off (decreasing $\beta$) and the cost Hamiltonian $H_z$ is slowly turned on (increasing $\gamma$) [27,31]. This comes from the fact that the angles $\gamma$ and $\beta$ is related to the discrete time step of the adiabatic process [1,15,30]. Consider the time-dependent Hamiltonian $H\left(t\right)=(1-t/T)H_x+(t/T)H_z$ going through a simple adiabatic evolution with total run time T. Discretizing the evolution gives

$$e^{-i{\int }_0^{T}H\left(t\right)dt}\approx \prod _{j=1}^p{e}^{-iH(j\Delta t)\Delta t},$$

(7)

with $t=j\Delta t$. Applying the first order Lie-Suzuki-Trotter decomposition to Equation (7) gives

$$\left(7\right)\approx \prod _{j=1}^p{e}^{-i(1-j\Delta t/T)H_x\Delta t}{e}^{-i(j\Delta t/T)H_z\Delta t}.$$

(8)

We can then substitute ${\gamma }_j=(j\Delta t/T)\Delta t$ and ${\beta }_j=(1-j\Delta t/T)\Delta t$ into Equation (8), and it leads to the QAOA form in Equation (1). Note that the discretization in Equation (7) divides the total run time T into p steps, i.e., $\Delta t=T/p$. Hence, we obtain the parameter-index-depth relation:

$${\gamma }_j^p=\frac{j}{p}\Delta t;{\beta }_j^p=\left(1-\frac{j}{p}\right)\Delta t.$$

(9)

It is obvious that ${\gamma }_j$ increases linearly with j and ${\beta }_j$ decreases linearly with j. Previous works [2,15,27,31,32] have shown that the optimal parameters of QAOA tend to follow this linear-like adiabatic path, and the pattern becomes nearer to linearity as p increases. Consequently, this pattern is exploited in devising various strategies. Figure 1a shows the adiabatic path taken by the optimal parameters at different p. Note that the patterns are not completely linear. This might be due to the discretization error and the Trotter error in our process of approximating the continuous evolution, and it is expected to approach linear as $p\to \infty$ [32].

3.2. Non-Optimality of Previous Parameters

Besides the adiabatic path, we also discovered the non-optimality of optimal parameters from previous depths, i.e., the optimal parameters for p are not optimal for $p+1$. The optimal parameters are shifted a little as the depth increases, as observed in Figure 1b. This phenomenon can also be inferred from Equation (9). As p increases, at the same index j, ${\gamma }_j$ will decrease and ${\beta }_j$ will increase. Also, we noticed that as p gets larger, the parameters at smaller indices have fewer changes compared with those with larger indices, e.g., it can be observed in Figure 1b that $|{\varphi }_8^{10}-{\varphi }_8^9|$ (rightmost two points of the gray line) is greater than $|{\varphi }_1^{10}-{\varphi }_1^9|$ (rightmost two of the blue line). We emphasize that the non-optimality is just the counterpart of the adiabatic path as they can be explained with the same relation, but it is seldom discussed in previous works. The patterns in the optimal parameters seem to be inherited from the time steps in the discrete adiabatic evolution. Note that Figure 1a,b are essentially plotted from the same set of parameters, viewed from different perspectives (j and p). They are both plotted for better visualization.

The results of layerwise training of QAOA also imply this non-optimality [28]. Layerwise training is an optimization strategy in which only the parameters of the current layer are optimized, the rest of the parameters are taken from the previous optimal parameters. The layerwise training has a relatively low training cost in exchange for a lower approximation ratio, as it suffers from premature saturation (saturation before the approximation ratio reaches 1). In [28], the authors discussed the premature saturation at $p=n$ for the rank-1 projector Hamiltonian $H_z=0^n$, where n is the number of qubits. Since the previous parameters in layerwise training are held constant and not allowed to move throughout the optimization, they will not reach the global minimum because of the non-optimality.

3.3. Bounded Optimization of QAOA

The adiabatic path and the non-optimality show that the optimal parameters exhibit some trends related to AQC. However, in the QAOA parameter space, not only the adiabatic path leads to the solution of the problem. There are redundant optimal points in the search space whose patterns do not follow the adiabatic path. This leads to the optimization of the bounded parameter space, where no redundancy exists. Therefore, the properties of the problem and its parameter space need to be studied beforehand to ensure only one optimum exists in the parameter space.

For instance, the bounds of the unweighted Max-cut problem were originally taken as $\mathbf{\gamma }\in {[0,2\pi )}^p$ and $\mathbf{\beta }\in {[0,\pi )}^p$ because of their periodicity [1]. However, it is further discussed in [27] that the operator $e^{-i(\pi /2)H_x}=X^{\otimes n}$ commutes through the operators in Equation (1), and due to the symmetry of the solutions, the period of $\beta$ becomes $\pi /2$. Also, QAOA has a time-reversal symmetry:

$$F_p(\mathbf{\gamma },\mathbf{\beta })=F_p(-\mathbf{\gamma },-\mathbf{\beta })=F_p\left(2\pi -\mathbf{\gamma },\frac{\pi }{2}-\mathbf{\beta }\right).$$

(10)

The second equality is due to the fact that $\gamma$ has a period of $2\pi$ and $\beta$ has a period of $\pi /2$. From Equation (10), one would expect that the landscape of $F_p$ beyond $\mathbf{\gamma }=\pi$ is the image of the rotation by ${180}^{\circ }$ of the landscape within $\mathbf{\gamma }=\pi$ (corresponding to the reflection of both $\mathbf{\gamma }=\pi$ and $\mathbf{\beta }=\pi /4$). Therefore, in general, the optimization can be completed in the bounds ${\Phi }_p\in {[0,\pi )}^p\times {[0,\pi /2)}^p$ due to the redundancies in the landscape, i.e., one part of the landscape being the image of another. Figure 1c shows the visualization of the $p=1$ expectation landscape for a 10-node Erdös-Rényi graph. It is observed that the maximum point (colored in blue) is redundant beyond ${\gamma }_1=\pi$ and ${\beta }_1=\pi /2$. Moreover, in regular graphs, there are symmetries in $e^{-i\pi H_z}=Z^{\otimes n}$ for odd-degree regular graphs and $e^{-i\pi H_z}=\mathrm{𝟙}$ for even-degree regular graphs. Thus, the optimization bounds can be further restricted to ${[0,\pi /2)}^p\times {[0,\pi /2)}^p$ for unweighted regular graphs. The details for the periodicity and symmetries are mainly discussed in [27,33,34], and we include the derivations in Appendix A.

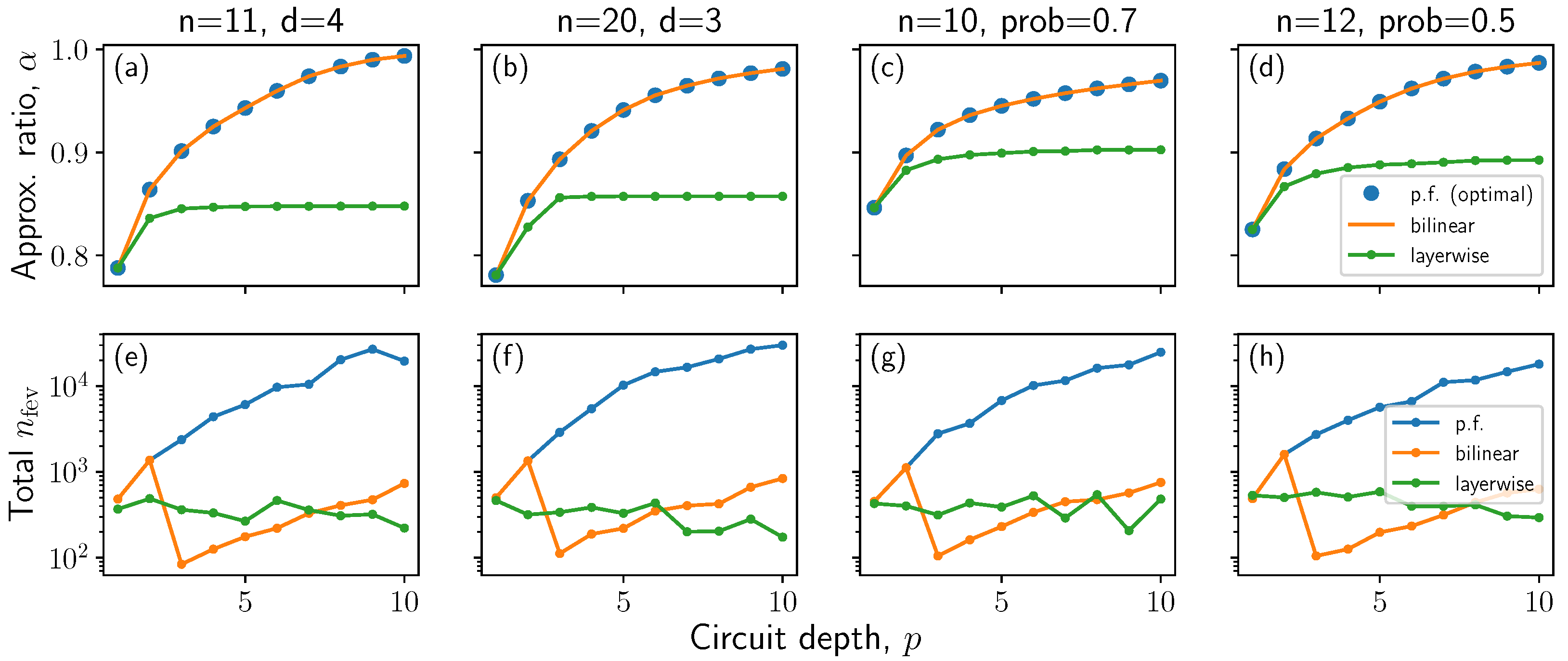
4. Bilinear Strategy

Using the properties discussed in Section 3, we devise a strategy that is depth-progressive, i.e., the optimization is completed depth-by-depth up to the desired depth p. We utilize the fact that in the bounded search space, the optimal parameters undergo smooth changes, as shown in the patterns of the adiabatic path and the non-optimality. Our strategy tries to reproduce the adiabatic path and the non-optimality patterns so that we can generate initial parameters that are near optimal. Therefore, we use the difference in previous optimal parameters to predict the initial points for the new parameters, i.e., the parameters for the next depth. Following the adiabatic path, we can predict ${\varphi }_{j+1}^p$ using ${\Delta }_{j,j-1}^p\equiv {\varphi }_j^p-{\varphi }_{j-1}^p$. For the non-optimality, we can predict ${\varphi }_j^{p+1}$ using ${\Delta }_j^{p,p-1}\equiv {\varphi }_j^p-{\varphi }_j^{p-1}$. We define ${\Delta }_{i,j}$ as the difference between the parameters ${\varphi }_i$ and ${\varphi }_j$, and this works the same way for the superscript. We call this the bilinear strategy as it involves the linear differences of two directions: j and p.

We explain the mechanism of our strategy. First, we can use any exhaustion method to find the optima for $p=1$ and $p=2$ within the specified bounds ${\Phi }_p\in {[{\gamma }_{\min },{\gamma }_{\max })}^p\times {[{\beta }_{\min },{\beta }_{\max })}^p$. This is to establish the base for our strategy, where we can take the difference between two sets of optimal parameters. The bounds are chosen such that there are no redundant optimals in the search space, as mentioned in Section 3.3, so that we can capture the pattern. We start applying the strategy from $p=3$. The parameters with indices up to $j=p-2$ are extrapolated using the pattern of non-optimality:

$$\begin{array}{cc}\hfill \forall j\le p-2,{\varphi }_j^p& ={\varphi }_j^{p-1}+{\Delta }_j^{p-1,p-2}\hfill \\ \hfill & =2{\varphi }_j^{p-1}-{\varphi }_j^{p-2}.\hfill \end{array}$$

(11)

The current parameter ${\varphi }_j^p$ is extended from the previous parameter ${\varphi }_j^{p-1}$ by adding the difference between the previous two parameters ${\Delta }_j^{p-1,p-2}={\varphi }_j^{p-1}-{\varphi }_j^{p-2}$. Note that $\Delta$ can be either positive or negative, which determines the direction of the extrapolation. This agrees with the monotonous change in optimal parameters. For the parameters with index $j=p-1$, we want to use a relation similar to Equation (11). However, the parameter ${\varphi }_{p-1}^{p-2}$ does not exist, so we take the difference from the previous index $j=p-2$ instead:

$${\varphi }_{p-1}^p={\varphi }_{p-1}^{p-1}+{\Delta }_{p-2}^{p-1,p-2}.$$

(12)

For the newly added parameter $j=p$, it is predicted using the adiabatic path pattern:

$$\begin{array}{cc}\hfill {\varphi }_p^p& ={\varphi }_{p-1}^p+{\Delta }_{p-1,p-2}^p\hfill \\ \hfill & =2{\varphi }_{p-1}^p-{\varphi }_{p-2}^p.\hfill \end{array}$$

(13)

If the parameters produced in Equations (11)–(13) are out of the bounds specified, we will take the boundary value of ${\varphi }_{\min }$ or ${\varphi }_{\max }$ (whichever is nearer) to replace them. After the process, the initial parameters ${\Phi }_p=({\gamma }_1,\dots ,{\gamma }_p,{\beta }_1,\dots ,{\beta }_p)$ for p will be obtained, and it is optimized to find the optimal at p. This entire process is summarized in Algorithm 1. A visualization diagram of the strategy is also shown in Figure 2.

Algorithm 1 Bilinear initialization

1: Input:${\Phi }_1^{*}$ and ${\Phi }_2^{*}$. ${\Phi }_p\in {[{\gamma }_{\min },{\gamma }_{\max })}^p\times {[{\beta }_{\min },{\beta }_{\max })}^p$. 2: for$p:=3\dots q$ do 3:     Build the initial parameters ${\Phi }_{\mathbf{p}}$: 4:     for $j:=1\dots p$ do 5:         if $j\le p-2$ then 6:            ${\varphi }_j^p\leftarrow {\varphi }_j^{p-1}+{\Delta }_j^{p-1,p-2}$ 7:         else if $j=p-1$ then 8:            ${\varphi }_j^p\leftarrow {\varphi }_j^{p-1}+{\Delta }_{j-1}^{p-1,p-2}$ 9:         else if $j=p$ then 10:            ${\varphi }_j^p\leftarrow {\varphi }_{j-1}^p+{\Delta }_{j-1,j-2}^p$ 11:         end if 12:     end for 13:     Initialize QAOA with ${\Phi }_p$ and perform bounded optimization. 14: end for 15: Output: ${\Phi }_p^{*}$ and $F_p\left({\Phi }_p^{*}\right)$ for each p up to q.

5. Results

We use statevector simulation and apply the bilinear strategy to solving the Max-cut problem for regular graphs and Erdös-Rényi graphs. The performance of the strategy is evaluated on 30 non-isomorphic instances of different classes of graphs up to the number of nodes $n=20$, which include the 3-regular, 4-regular graphs, and Erdös-Rényi graphs with different edge probabilities. For the regular graphs, we optimize the parameters within the bound ${[0,\pi /2)}^p\times {[0,\pi /2)}^p$, whereas the Erdös-Rényi graphs are optimized within ${[0,\pi )}^p\times {[0,\pi /2)}^p$. Here, we only show the results for 4 of the instances in Figure 3, but the trends discussed also apply to all other instances unless otherwise stated.

We compare the approximation ratio $\alpha$ obtained from the bilinear strategy with our previously proposed parameter fixing strategy [26]. From Figure 3a–d, it can be observed that the $\alpha$ produced by the bilinear strategy traces the optimal $\alpha$ (found by parameters fixing) with minimal error. The results of the layerwise strategy are also plotted. Besides the projectors completed in the previous work [28], we found out that for the Max-cut Hamiltonian, $\alpha$ also saturates at a certain p due to the non-optimality of the parameters.

In Figure 3e–h, we compare the number of function evaluations $n_{\mathrm{fev}}$ before the convergence of the Limited-memory BFGS Bounded (L-BFGS-B) [35] optimizer for the strategies. It is the number of function calls to the quantum circuit to compute the expectation in Equation (3), and less $n_{\mathrm{fev}}$ usually means less quantum and classical resources used. For parameter fixing and layerwise, which need multiple trials to ensure success, we consider the total $n_{\mathrm{fev}}$ for 20 trials. The results show that the $n_{\mathrm{fev}}$ required by the bilinear initial points is always less than that of the parameters fixed by an order of ${10}^2$ to ${10}^3$ for $p\ge 3$. This clearly shows the advantage of the bilinear strategy on the optimization cost, as only a single trial is required. For $p=1$ and $p=2$, the $n_{\mathrm{fev}}$’s are the same, as we used parameter fixing to search for the optima. As for layerwise, the $n_{\mathrm{fev}}$’s are relatively small, as only two parameters are optimized for each p. It is observed that for small depths up to $p=6$, even the bilinear strategy costs less than layerwise, and the cost grows with p as the number of optimization variables increases.

On the other hand, we also consider the case where the bilinear strategy fails, where the initial points do not follow the monotonous trend of the adiabatic path. One of the examples is the odd-regular graph. We mentioned in Section 3.3 that one should take the bound ${[0,\pi /2)}^p\times {[0,\pi /2)}^p$ for regular graphs to avoid redundancies. However, if one tries to take the bound ${[0,\pi )}^p\times {[0,\pi /2)}^p$, which is considered the general bound for unweighted Max-cut, one has a chance to fall into the starting point in ${\gamma }_1\in [\pi /2,\pi )$ for $p=1$ (shown in Figure 4a). In this case, the optimal parameters will not follow the adiabatic path as shown in Figure 1a. Figure 4b shows that for this non-adiabatic starting point, the optimal $\beta$’s oscillate back and forth instead. In fact, this point is symmetric to the adiabatic start ${\gamma }_1\in [0,\pi /2)$. We explain this odd-regular symmetry, including the $\beta$ oscillation in Appendix B.

Figure 4c shows the result of a bilinear strategy with a non-adiabatic start for a 10-node 3-regular graph. The $\alpha$ produced by the bilinear strategy traces the optimal until $p=7$, where it deviates after $p=8$. This shows that the bilinear strategy is still effective to some extent, even for non-adiabatic starts.

6. Conclusions

To conclude, we have studied the patterns in the optimal parameters of QAOA for the unweighted Max-cut problem in two directions, namely the angle index j and the circuit depth p. We call the variation against j and p the adiabatic path and the non-optimality respectively. By leveraging these properties, we devise the depth-progressive bilinear strategy, in which the optimization is completed for each depth until the desired depth. The bilinear strategy utilizes the optimal parameters from the previous two depths, ${\Phi }_{p-2}^{*}$ and ${\Phi }_{p-1}^{*}$, to initialize the parameters for the current depth ${\Phi }_p$.

We have demonstrated the effectiveness of the bilinear strategy by comparing it with the parameter fixing strategy [26] and the layerwise [28] strategy on 30 non-isomorphic random regular and Erdös-Rényi graphs. The results show bilinear is able to trace the optimal approximation ratio $\alpha$ found by parameter fixing. While we have also observed premature saturation occurring in the Max-cut Hamiltonian for layerwise. It is also found out that the number of function evaluations $n_{\mathrm{fev}}$ of bilinear is less than that of parameter fixing due to its single prediction.

The bilinear strategy is advantageous against most other strategies [27,28] that usually require multiple trials to ensure success, including the parameter fixing strategy. It only requires the optimization of one set of initial parameters at each circuit depth. The bilinear strategy also requires knowledge of the bounds for the optimization to avoid redundancies in the search space, thereby ensuring success. However, we have considered the case where it fails when initialized from a “non-adiabatic” point. Numerically, for a particular 3-regular graph, it is still capable of tracing the optimal until circuit depth $p=7$.

We suggest some potential work that can be pursued in the future. Since the new prediction is extrapolated from the change in optimal parameters, we can increase the depth step of the bilinear strategy for less optimization cost. In this work, we have shown using the depth step of 1. One can, for example, increase the depth step to 2 ($p=2,4,6,\dots$) while progressing to larger circuit depths. Although not tested, the bilinear strategy is expected to perform on different kinds of problems (different $H_z$) in which their optimal parameters follow the adiabatic path and non-optimality, which is believed to be true for QAOA. This is also a good future work to explore.