Static Response of Nanocomposite Electromagnetic Sandwich Plates with Honeycomb Core via a Quasi 3-D Plate Theory
Abstract
1. Introduction
2. Configure of the Plate
2.1. GPLs-Type A
2.2. GPLs-Type B
2.3. GPLs-Type C
2.4. GPLs-Type D
3. Displacement Field
4. Governing Equations
5. Solution Method
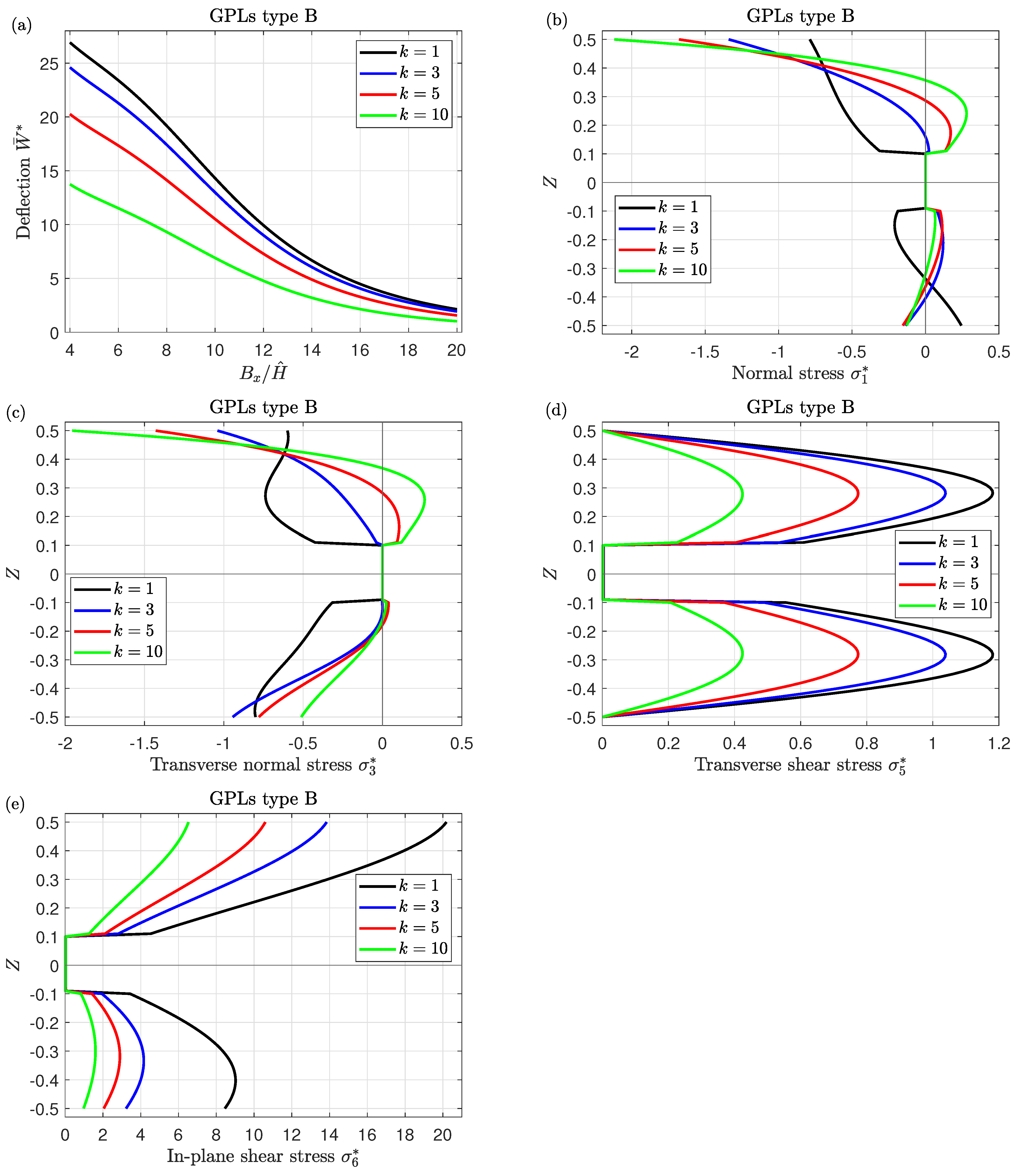
6. Numerical Analysis and Discussions
7. Conclusions
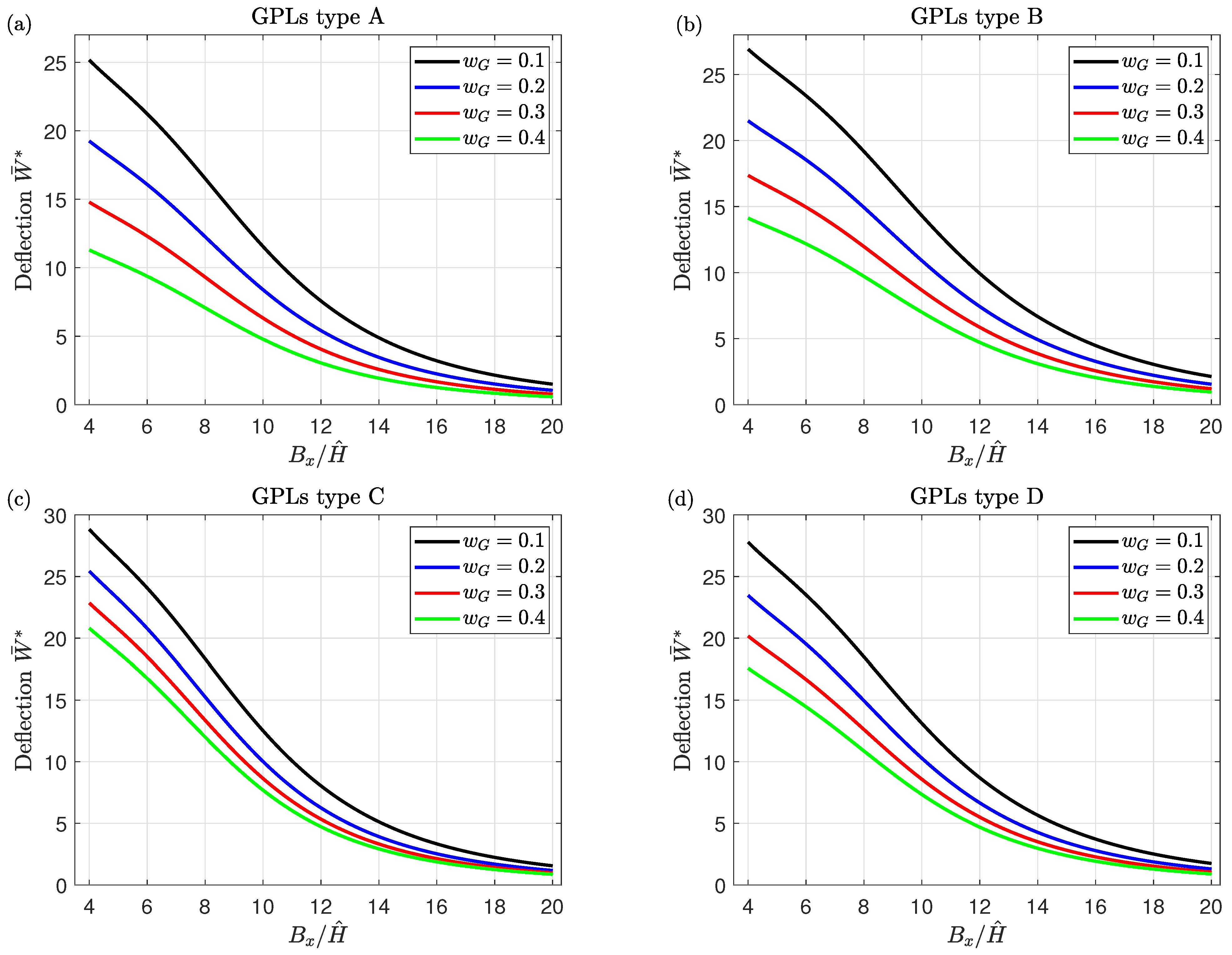
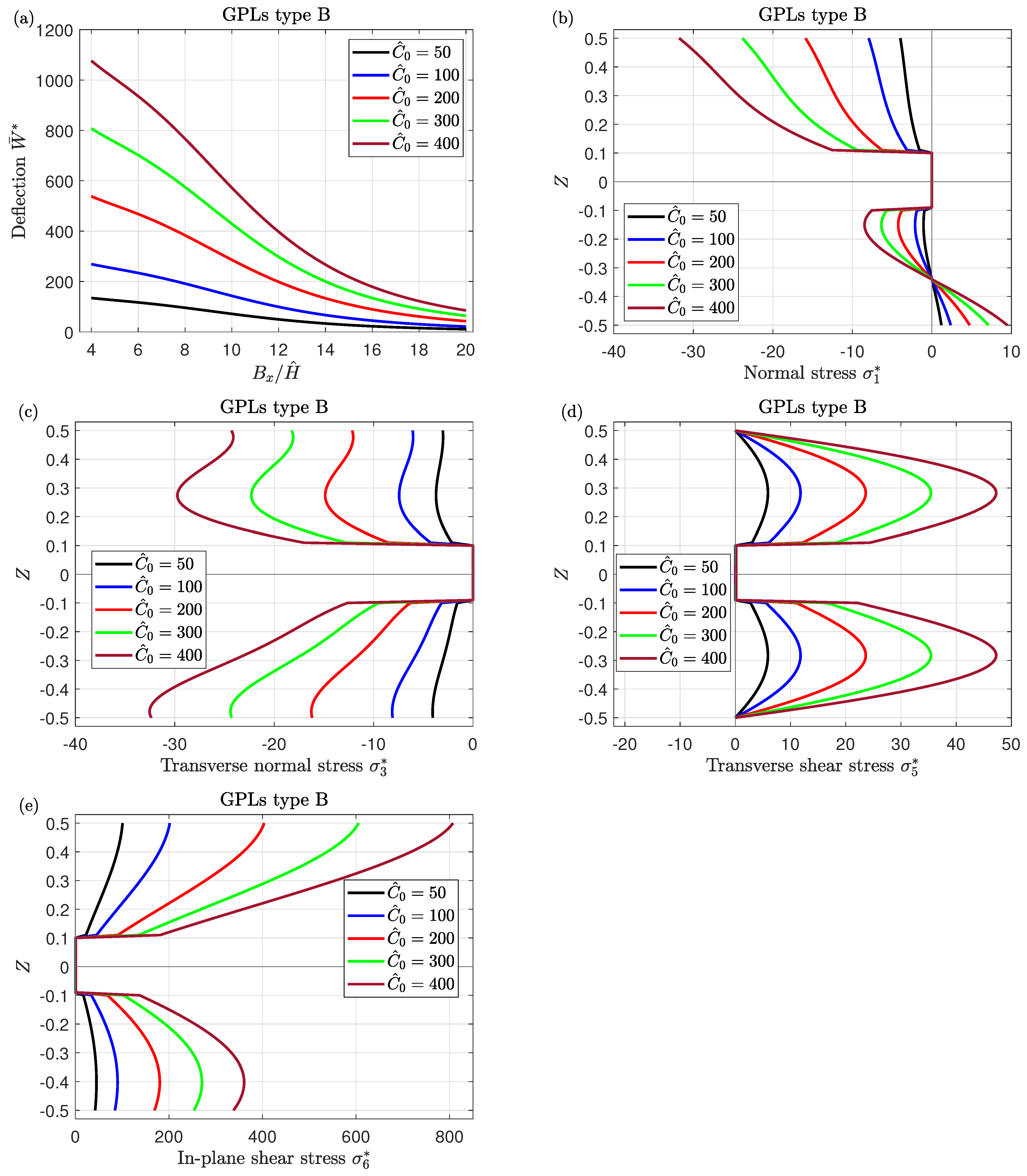
- The increment in graphene components enhances the strength of the sandwich nanocomposite piezoelectromagnetic plates leading to a reduction in the central deflection.
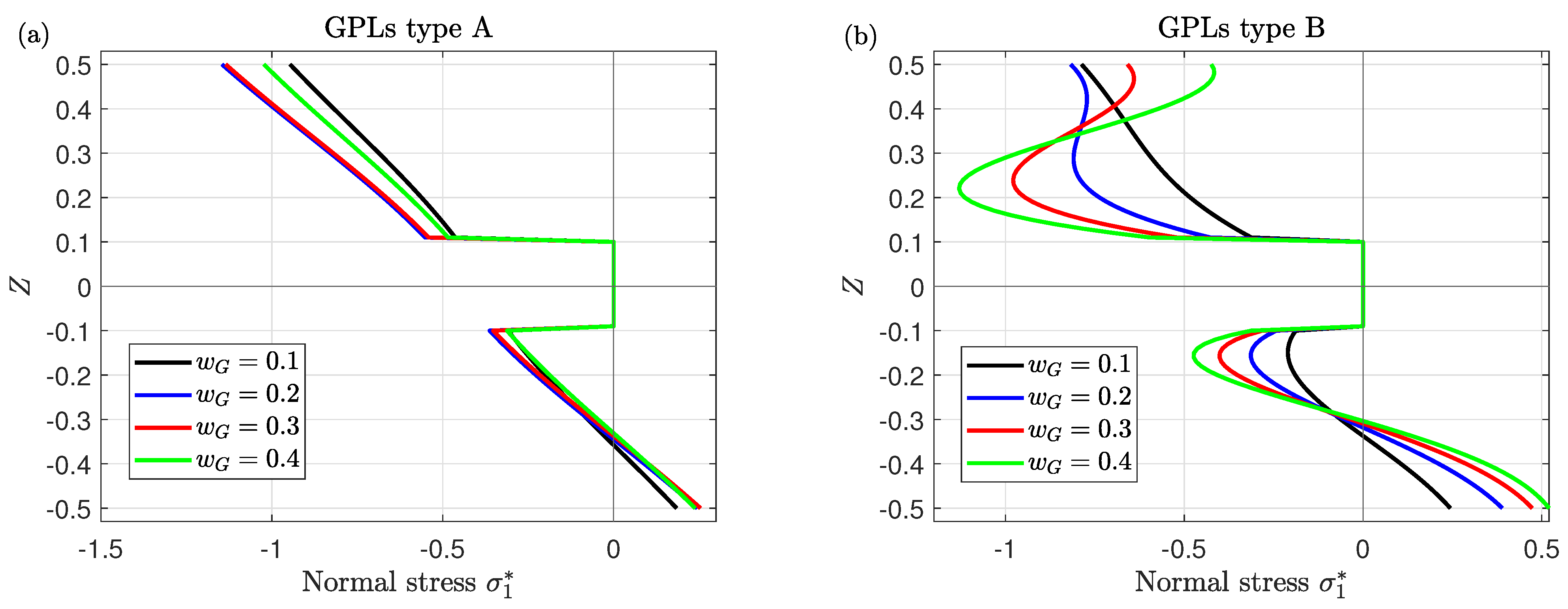
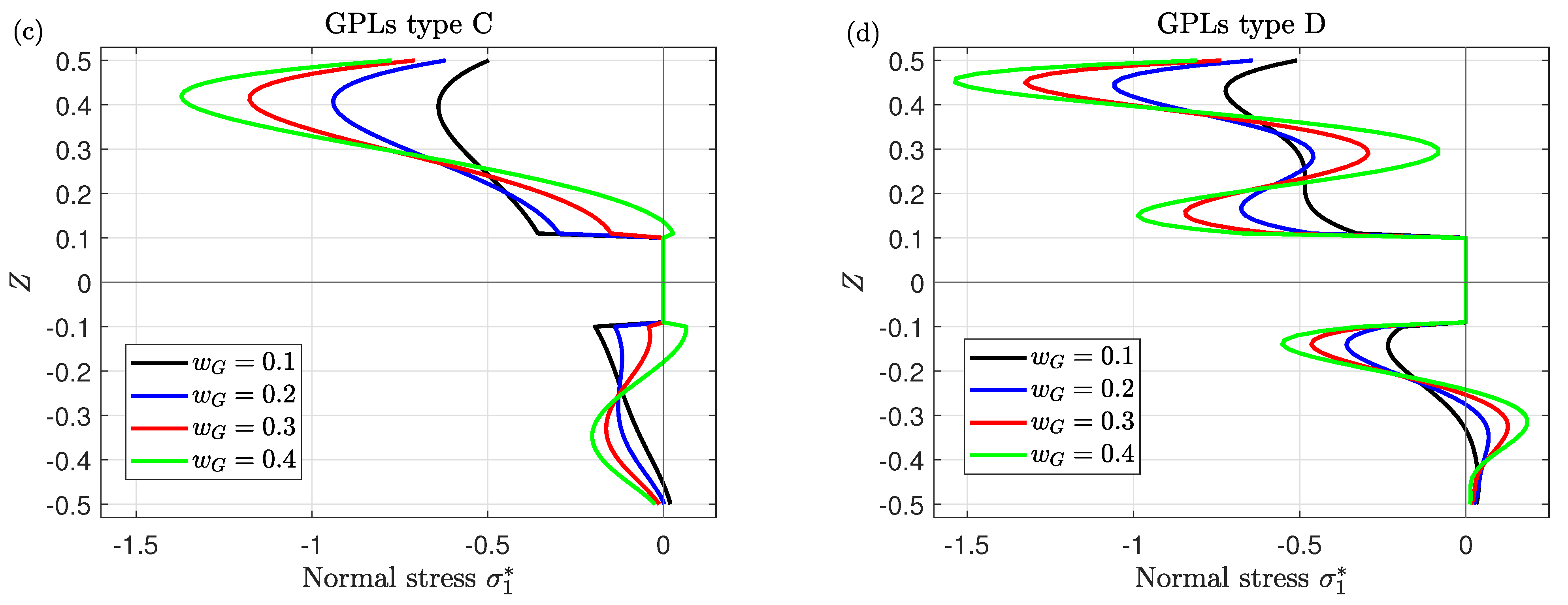
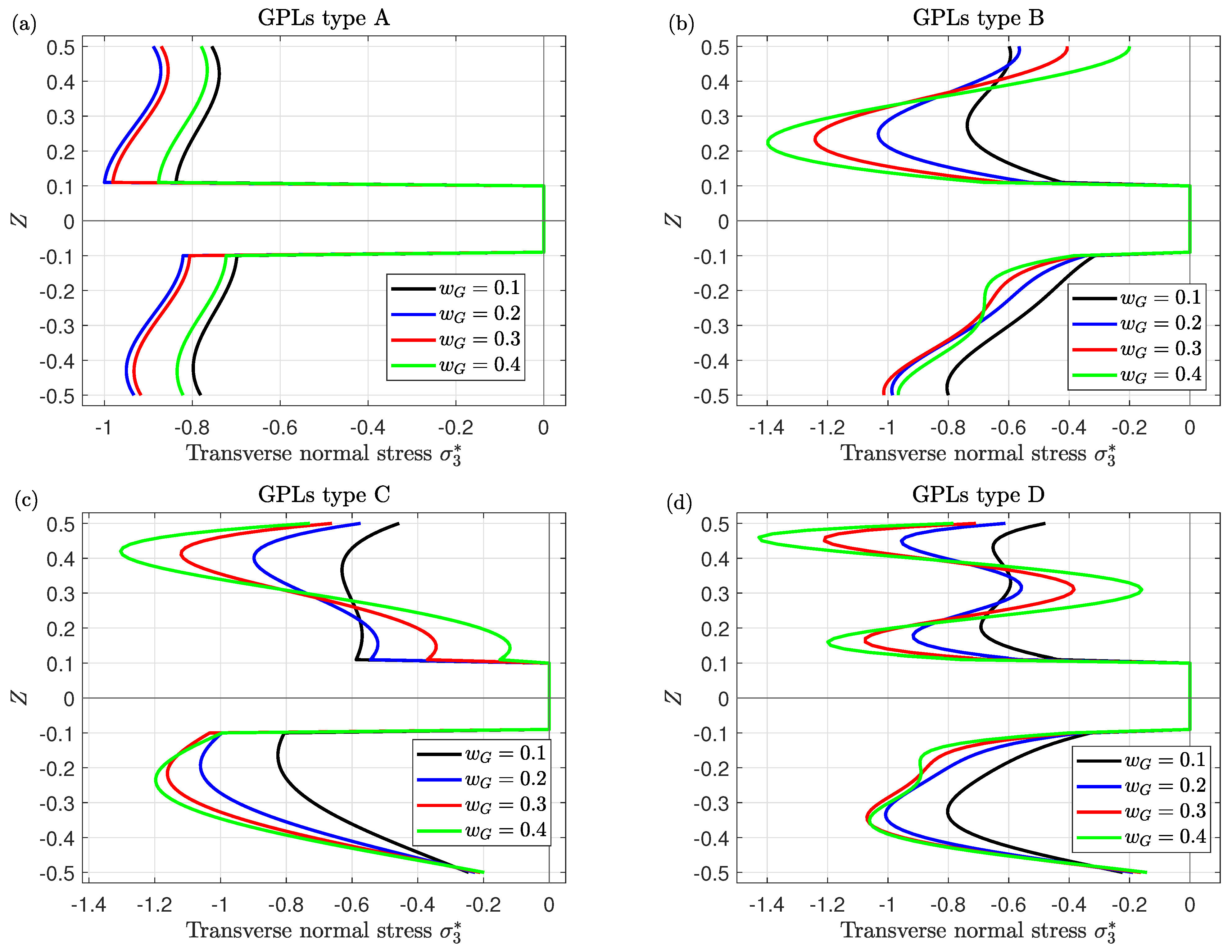
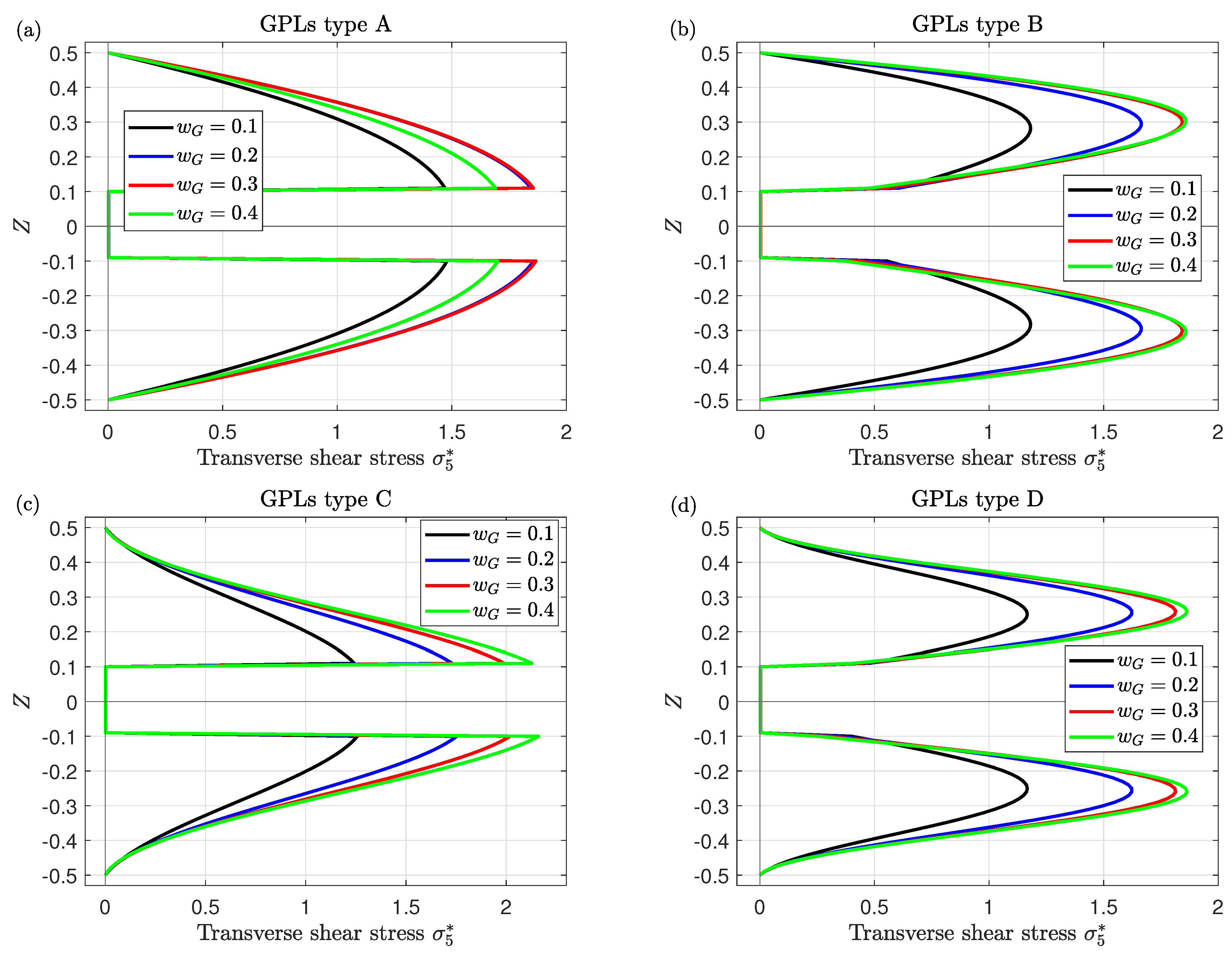
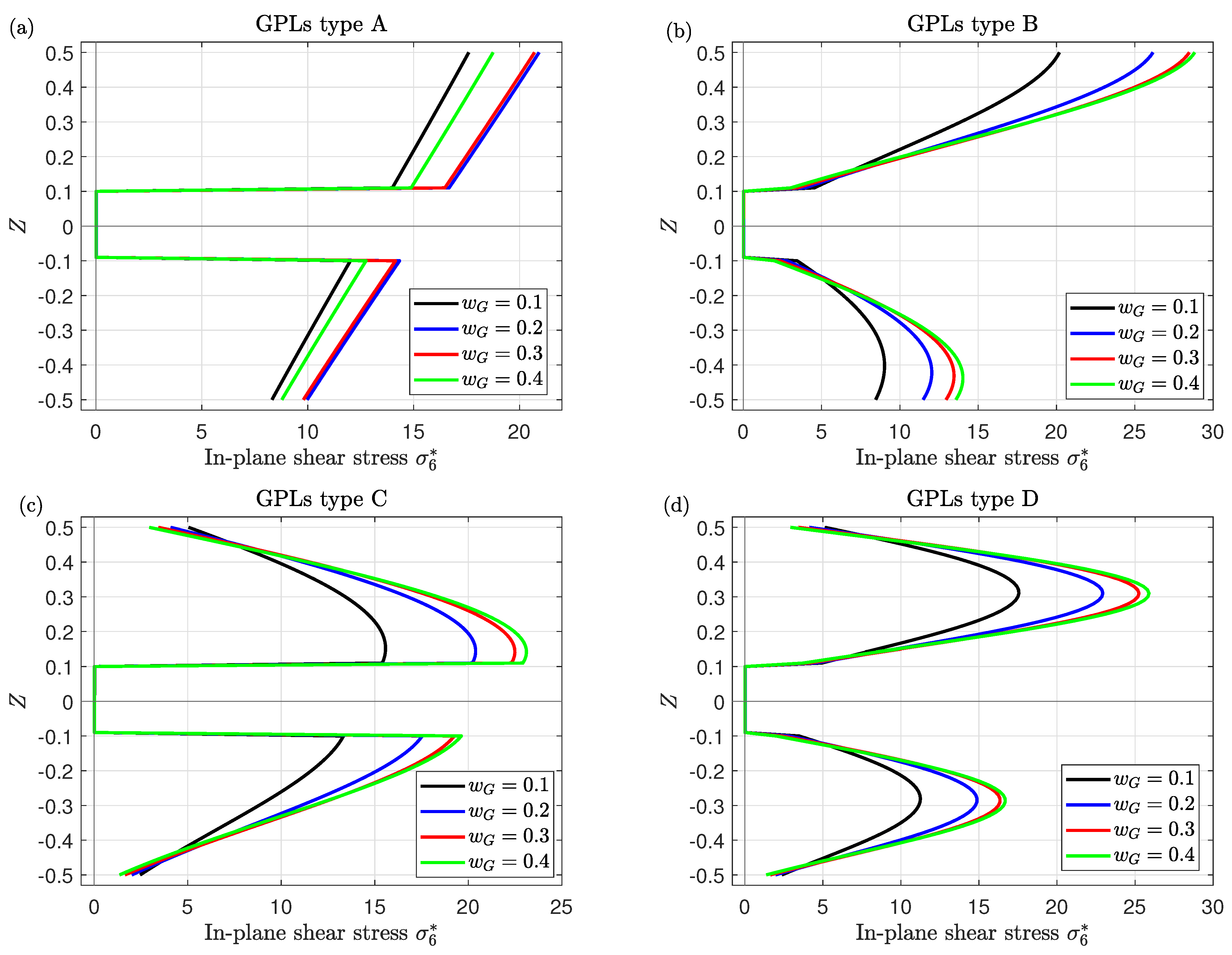
- The variation of the stresses through the thickness of the plate significantly depends on GPLs distribution types.
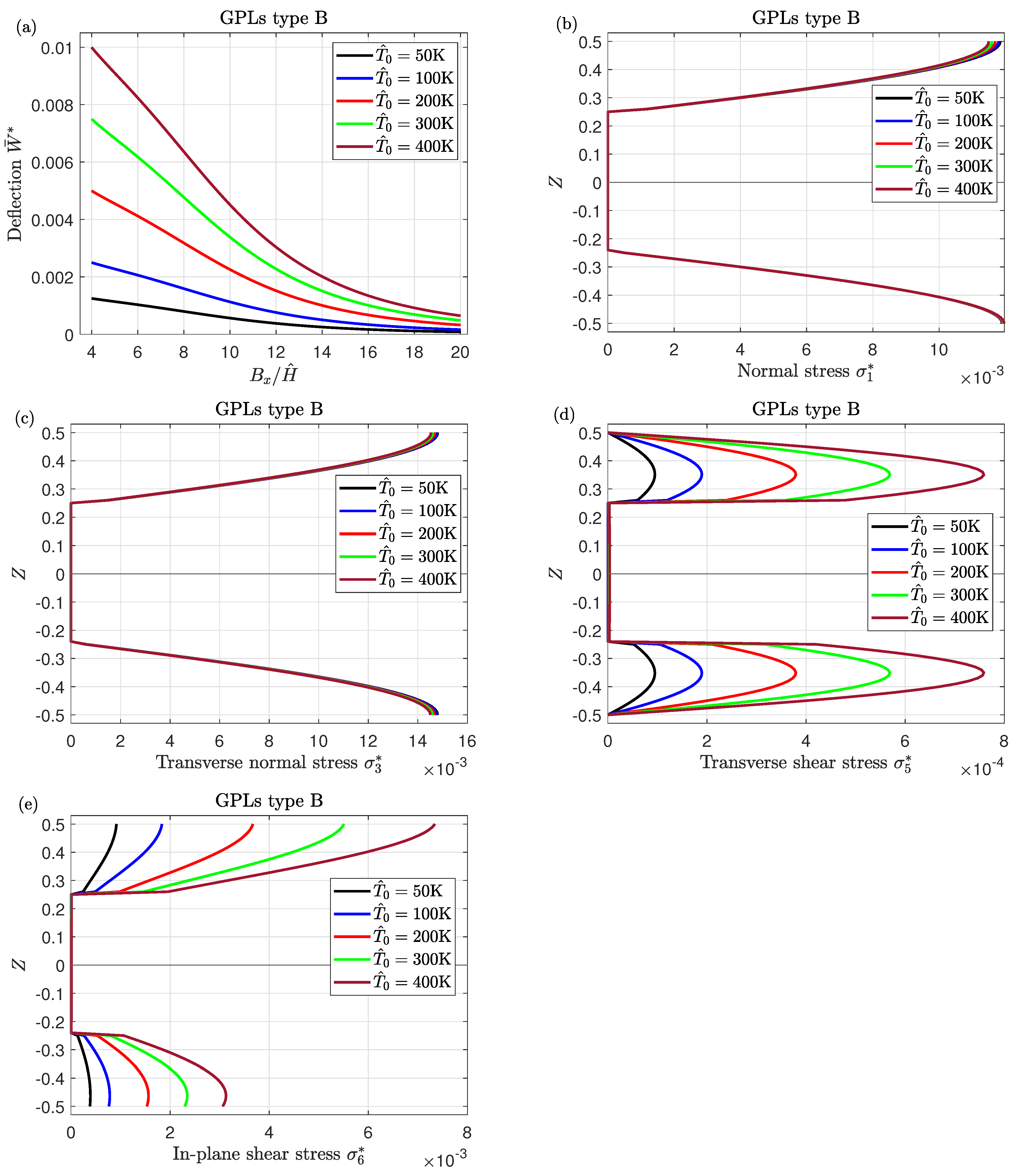
- While the moisture and temperature conditions weaken the plate stiffness, therefore, the central deflection and stresses rise as the moisture and temperature parameter increase; normal stresses appear to be independent of varying the temperature parameter.
- The existence of the honeycomb core results in the plate being more resistant to the thermal condition and the external electric voltage due to the low thermal and electrical conductivity of the honeycomb cells. Subsequently, the central deflection decreases with increasing the thickness of the honeycomb core.
- By varying the external electric and magnetic potentials, the deflection behavior of the sandwich structures can be managed. Increasing the electric and magnetic parameters leads to an increment and decrement in the deflection, respectively.
- This investigation illustrates that the current study can produce very accurate results compared with other theories in literature and, therefore, deserves particular attention and additional execution by using numerical techniques.
- The suggested model and our numerical findings could be very helpful for the design and production of many aerospace, automotive, or shipbuilding engineering applications. Honeycomb cells should be utilized in these applications due to their outstanding capacity to resist high pressures and stress despite their light structure.
Funding
Data Availability Statement
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Sobhy, M. Size-dependent hygro-thermal buckling of porous FGM sandwich microplates and microbeams using a novel four-variable shear deformation theory. Int. J. Appl. Mech. 2020, 12, 2050017. [Google Scholar] [CrossRef]
- Chen, A.; Davalos, J.F. A solution including skin effect for stiffness and stress field of sandwich honeycomb core. Int. J. Solids Struct. 2005, 42, 2711–2739. [Google Scholar] [CrossRef]
- Qing, T.D.; Zhi, C.Y. Wave propagation in sandwich panel with auxetic core. J. Solid Mech. 2010, 2, 393–402. [Google Scholar]
- Yu, S.D.; Cleghorn, W.L. Free flexural vibration analysis of symmetric honeycomb panels. J. Sound Vib. 2005, 284, 189–204. [Google Scholar] [CrossRef]
- Cong, P.H.; Khanh, N.D.; Khoa, N.D.; Duc, N.D. New approach to investigate nonlinear dynamic response of sandwich auxetic double curves shallow shells using TSDT. Compos. Struct. 2018, 185, 455–465. [Google Scholar] [CrossRef]
- Li, Y.Q.; Li, F.; He, Y.L. Geometrically nonlinear forced vibrations of the symmetric rectangular honeycomb sandwich panels with completed clamped supported boundaries. Compos. Struct. 2011, 93, 360–368. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, M.; Wang, T.; Zhang, Y. Nonlinear primary resonance with internal resonances of the symmetric rectangular honeycomb sandwich panels with simply supported along all four edges. Thin-Walled Struct. 2020, 147, 106480. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X.; Yang, X.; Zhang, W. Transient nonlinear responses of an auxetic honeycomb sandwich plate under impact loads. Inter. J. Impact Eng. 2019, 134, 103383. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R.; Aiello, M.A. Higher order formulations for doubly-curved shell structures with a honeycomb core. Thin-Walled Struct. 2021, 164, 107789. [Google Scholar] [CrossRef]
- Tan, P.; Tong, L. Modeling for the electro-magneto-thermo-elastic properties of piezoelectric-magnetic fiber reinforced composites. Compos. Part A Appl. Sci. Manuf. 2002, 33, 631–645. [Google Scholar] [CrossRef]
- Singh, S.; Singh, A.K.; Guha, S. Reflection of plane waves at the stress-free/rigid surface of a micro-mechanically modeled piezo-electro-magnetic fiber-reinforced half-space. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Sun, J.; Xu, X.; Lim, C.W.; Zhou, Z.; Xiao, S. Accurate thermo-electro-mechanical buckling of shear deformable piezoelectric fiber-reinforced composite cylindrical shells. Compos. Struct. 2016, 141, 221–231. [Google Scholar] [CrossRef]
- Zhu, S.; Tong, Z.; Sun, J.; Li, Q.; Zhou, Z.; Xu, X. Electro-thermo-mechanical post-buckling of piezoelectric functionally graded cylindrical shells. Appl. Math. Model. 2021, 98, 309–322. [Google Scholar] [CrossRef]
- Huang, X.; Zhi, C.; Lin, Y.; Bao, H.; Wu, G.; Jiang, P.; Mai, Y.W. Thermal conductivity of graphene-based polymer nanocomposites. Mater. Sci. Eng. R Rep. 2020, 142, 100577. [Google Scholar] [CrossRef]
- Potts, J.R.; Dreyer, D.R.; Bielawski, C.W.; Ruoff, R.S. Graphene-based polymer nanocomposites. Polymer 2011, 52, 5–25. [Google Scholar] [CrossRef]
- Alimirzaei, S.; Mohammadimehr, M.; Tounsi, A. Nonlinear analysis of viscoelastic micro-composite beam with geometrical imperfection using FEM: MSGT electro-magneto-elastic bending, buckling and vibration solutions. Struct. Eng. Mech. 2019, 71, 485–502. [Google Scholar]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Li, K.; Wu, D.; Chen, X.; Cheng, J.; Liu, Z.; Gao, W.; Liu, M. Isogeometric analysis of functionally graded porous plates reinforced by graphene platelets. Compos. Struct. 2018, 204, 114–130. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M. Nonlinear instability of axially loaded functionally graded multilayer graphene platelet-reinforced nanoshells based on nonlocal strain gradient elasticity theory. Int. J. Mech. Sci. 2017, 131, 95–106. [Google Scholar] [CrossRef]
- Sobhy, M. Buckling and vibration of FG graphene platelets/aluminum sandwich curved nanobeams considering the thickness stretching effect and exposed to a magnetic field. Results Phys. 2020, 16, 102865. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Tran, T.D.; Phung-Van, P. A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos. Struct. 2020, 234, 111695. [Google Scholar] [CrossRef]
- Al Mukahal, F.H.H.; Sobhy, M. Wave propagation and free vibration of FG graphene platelets sandwich curved beam with auxetic core resting on viscoelastic foundation via DQM. Arch. Civ. Mech. Eng. 2022, 22, 12. [Google Scholar] [CrossRef]
- Sobhy, M. Analytical buckling temperature prediction of FG piezoelectric sandwich plates with lightweight core. Mater. Res. Express 2021, 8, 095704. [Google Scholar] [CrossRef]
- Abazid, M.A.; Sobhy, M.; Zenkour, A.M. Wave propagation in FG porous GPLs-reinforced nanoplates under in-plane mechanical load and Lorentz magnetic force via a new quasi 3D plate theory. Mech. Based Des. Struct. Mach. 2022, 50, 1831–1850. [Google Scholar] [CrossRef]
- Abazid, M.A. 2D magnetic field effect on the thermal buckling of metal foam nanoplates reinforced with FG-GPLs lying on pasternak foundation in humid environment. Eur. Phys. J. Plus 2020, 135, 910. [Google Scholar] [CrossRef]
- Sobhy, M. 3-D elasticity numerical solution for magneto-hygrothermal bending of FG graphene/metal circular and annular plates on an elastic medium. Eur. J. Mech.-A/Solids 2021, 88, 104265. [Google Scholar] [CrossRef]
- Sobhy, M.; Abazid, M.A.; Al Mukahal, F.H.H. Electro-thermal buckling of FG graphene platelets-strengthened piezoelectric beams under humid conditions. Adv. Mech. Eng. 2022, 14, 1–12. [Google Scholar] [CrossRef]
- Al Mukahal, F.H.H.; Abazid, M.A.; Sobhy, M. Investigating Electromechanical Buckling Response of FG-GPL-Reinforced Piezoelectric Doubly Curved Shallow Shells Embedded in an Elastic Substrate. Materials 2023, 16, 2975. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Y.; Zhang, S.; Dimitri, R.; Tornabene, F.; Asemi, K. Numerical Study on the Buckling Behavior of FG Porous Spherical Caps Reinforced by Graphene Platelets. Nanomaterials 2023, 13, 1205. [Google Scholar] [CrossRef]
- Quang Hung, T.; Duc, D.M.; Minh Tu, T. Static bending mesh-free analysis of smart piezoelectric porous beam reinforced with graphene platelets. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 1595–1612. [Google Scholar] [CrossRef]
- Xu, K.; Wang, K.; Zhao, W.; Bao, W.; Liu, E.; Ren, Y.; Wang, M.; Fu, Y.; Zeng, J.; Li, Z.; et al. The positive piezoconductive effect in graphene. Nat. Commun. 2015, 6, 8119. [Google Scholar] [CrossRef] [PubMed]
- Abolhasani, M.M.; Shirvanimoghaddam, K.; Naebe, M. PVDF/graphene composite nanofibers with enhanced piezoelectric performance for development of robust nanogenerators. Compos. Sci. Technol. 2017, 138, 49–56. [Google Scholar] [CrossRef]
- Mao, J.J.; Lu, H.M.; Zhang, W.; Lai, S.K. Vibrations of graphene nanoplatelet reinforced functionally gradient piezoelectric composite microplate based on nonlocal theory. Compos. Struct. 2020, 236, 111813. [Google Scholar] [CrossRef]
- Sobhy, M.; Al Mukahal, F.H.H. Analysis of Electromagnetic Effects on Vibration of Functionally Graded GPLs Reinforced Piezoelectromagnetic Plates on an Elastic Substrate. Crystals 2022, 12, 487. [Google Scholar] [CrossRef]
- Sobhy, M.; Al Mukahal, F.H. Wave Dispersion Analysis of Functionally Graded GPLs-Reinforced Sandwich Piezoelectromagnetic Plates with a Honeycomb Core. Mathematics 2022, 10, 3207. [Google Scholar] [CrossRef]
- Khorasani, M.; Soleimani-Javid, Z.; Arshid, E.; Amir, S.; Civalek, Ö. Vibration analysis of graphene nanoplatelets’ reinforced composite plates integrated by piezo-electromagnetic patches on the piezo-electromagnetic media. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Zenkour, A.M.; Sobhy, M. Hygrothermal Buckling of Smart Graphene/Piezoelectric Nanocomposite Circular Plates on an Elastic Substrate via DQM. Mathematics 2022, 10, 2638. [Google Scholar] [CrossRef]
- Sobhy, M.; Al Mukahal, F.H.H. Magnetic control of vibrational behavior of smart FG sandwich plates with honeycomb core via a quasi-3D plate theory. Adv. Eng. Mater. 2023. [Google Scholar] [CrossRef]
- Mahesh, V. Nonlinear damping of auxetic sandwich plates with functionally graded magneto-electro-elastic facings under multiphysics loads and electromagnetic circuits. Compos. Struct. 2022, 290, 115523. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Vivio, F. Application of the Ritz method for the bending and stress analysis of thin rectilinear orthotropic composite sector plates. Thin-Walled Struct. 2023, 183, 110374. [Google Scholar] [CrossRef]
- Singh, A.; Karathanasopoulos, N. Three-dimensional analytical elasticity solution for the mechanical analysis of arbitrarily-supported, cross and angle-ply composite plates under patch loads. Compos. Struct. 2023, 310, 116752. [Google Scholar] [CrossRef]
- Attar, F.; Khordad, R.; Zarifi, A.; Modabberasl, A. Application of nonlocal modified couple stress to study of functionally graded piezoelectric plates. Phys. B Condens. Matter 2021, 600, 412623. [Google Scholar] [CrossRef]
- Li, J.; Xue, Y.; Li, F.; Narita, Y. Active vibration control of functionally graded piezoelectric material plate. Compos. Struct. 2019, 207, 509–518. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Thermoelastic vibration and buckling analysis of functionally graded piezoelectric cylindrical shells. Appl. Math. Model. 2010, 34, 2630–2643. [Google Scholar] [CrossRef]
- Sobhy, M.; Radwan, A.F. An axial magnetic field effect on frequency analysis of rotating sandwich cylindrical shells with FG graphene/AL face sheets and honeycomb core. Int. J. Appl. Mech. 2022, 14, 2250074. [Google Scholar] [CrossRef]
- Abdollahi, M.; Saidi, A.R.; Mohammadi, M. Buckling analysis of thick functionally graded piezoelectric plates based on the higher-order shear and normal deformable theory. Acta Mech. 2015, 226, 2497–2510. [Google Scholar] [CrossRef]
- Sobhy, M.; Abazid, M.A. Mechanical and thermal buckling of FG-GPLs sandwich plates with negative Poisson’s ratio honeycomb core on an elastic substrate. Eur. Phys. J. Plus 2022, 137, 93. [Google Scholar] [CrossRef]
- Zaitoun, M.W.; Chikh, A.; Tounsi, A.; Al-Osta, M.A.; Sharif, A.; Al-Dulaijan, S.U.; Al-Zahrani, M.M. Influence of the visco-Pasternak foundation parameters on the buckling behavior of a sandwich functional graded ceramic–metal plate in a hygrothermal environment. Thin-Walled Struct. 2022, 170, 108549. [Google Scholar] [CrossRef]
- Hebali, H.; Chikh, A.; Bousahla, A.A.; Bourada, F.; Tounsi, A.; Benrahou, K.H.; Hussain, M.; Tounsi, A. Effect of the variable visco-Pasternak foundations on the bending and dynamic behaviors of FG plates using integral HSDT model. Arch. Appl. Mech. 2022, 83, 177–191. [Google Scholar]
- Bakoura, A.; Bourada, F.; Bousahla, A.A.; Tounsi, A.; Benrahou, K.H.; Tounsi, A.; Al-Zahrani, M.M.; Mahmoud, S.R. Buckling analysis of functionally graded plates using HSDT in conjunction with the stress function method. Comput. Concr. Int. J. 2021, 27, 73–83. [Google Scholar]
- Tahir, S.I.; Tounsi, A.; Chikh, A.; Al-Osta, M.A.; Al-Dulaijan, S.U.; Al-Zahrani, M.M. The effect of three-variable viscoelastic foundation on the wave propagation in functionally graded sandwich plates via a simple quasi-3D HSDT. Steel Compos. Struct. 2022, 42, 501. [Google Scholar]
- Bouafia, K.; Selim, M.M.; Bourada, F.; Bousahla, A.A.; Bourada, M.; Tounsi, A.; Adda Bedia, E.A.; Tounsi, A. Bending and free vibration characteristics of various compositions of FG plates on elastic foundation via quasi 3D HSDT model. Steel Compos. Struct. 2021, 41, 487–503. [Google Scholar]
- Kouider, D.; Kaci, A.; Selim, M.M.; Bousahla, A.A.; Bourada, F.; Tounsi, A.; Tounsi, A.; Tounsi, A.; Hussain, M. An original four-variable quasi-3D shear deformation theory for the static and free vibration analysis of new type of sandwich plates with both FG face sheets and FGM hard core. Steel Compos. Struct. 2021, 41, 167–191. [Google Scholar]
- Hachemi, H.; Bousahla, A.A.; Kaci, A.; Bourada, F.; Tounsi, A.; Benrahou, K.H.; Tounsi, A.; Al-Zahrani, M.M.; Mahmoud, S.R. Bending analysis of functionally graded plates using a new refined quasi-3D shear deformation theory and the concept of the neutral surface position. Steel Compos. Struct. Int. J. 2021, 39, 51–64. [Google Scholar]
- Sobhy, M.; Alsaleh, F. Nonlinear bending of FG metal/graphene sandwich microplates with metal foam core resting on nonlinear elastic foundations via a new plate theory. Mech. Based Des. Struct. Mach. 2023; in press. [Google Scholar]
- Shimpi, R.P. Refined plate theory and its variants. AIAA J. 2002, 40, 137–146. [Google Scholar] [CrossRef]
- Zamani, M.H.; Heidari-Rarani, M.; Torabi, K. A novel graded auxetic honeycomb core model for sandwich structures with increasing natural frequencies. J. Sandw. Struct. Mater. 2022, 24, 1313–1339. [Google Scholar] [CrossRef]
- Cong, P.H.; Duc, N.D. Nonlinear dynamic analysis of porous eccentrically stiffened double curved shallow auxetic shells in thermal environments. Thin-Walled Struct. 2021, 163, 107748. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech. Sin. 2014, 30, 516–525. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Free vibration analysis of a three-layered microbeam based on strain gradient theory and three-unknown shear and normal deformation theory. Steel Compos. Struct. Int. J. 2018, 26, 421–437. [Google Scholar]
- Arshid, H.; Khorasani, M.; Soleimani-Javid, Z.; Dimitri, R.; Tornabene, F. Quasi-3D hyperbolic shear deformation theory for the free vibration study of honeycomb microplates with graphene nanoplatelets-reinforced epoxy skins. Molecules 2020, 25, 5085. [Google Scholar] [CrossRef] [PubMed]
- Hebali, H.; Tounsi, A.; Houari, M.S.A.; Bessaim, A.; Bedia, E.A.A. New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. J. Eng. Mech. 2014, 140, 374–383. [Google Scholar] [CrossRef]
- Alsebai, F.; Al Mukahal, F.H.; Sobhy, M. Semi-analytical solution for thermo-piezoelectric bending of FG porous plates reinforced with graphene platelets. Mathematics 2022, 10, 4104. [Google Scholar] [CrossRef]
- Abazid, M.A.; Sobhy, M. Thermo-electro-mechanical bending of FG piezoelectric microplates on Pasternak foundation based on a four-variable plate model and the modified couple stress theory. Microsyst. Technol. 2018, 24, 1227–1245. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A size-dependent functionally graded Reddy plate model based on a modified couple stress theory. Compos. Part B Eng. 2013, 45, 1636–1645. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. A refined plate theory for functionally graded plates resting on elastic foundation. Compos. Sci. Technol. 2011, 71, 1850–1858. [Google Scholar] [CrossRef]


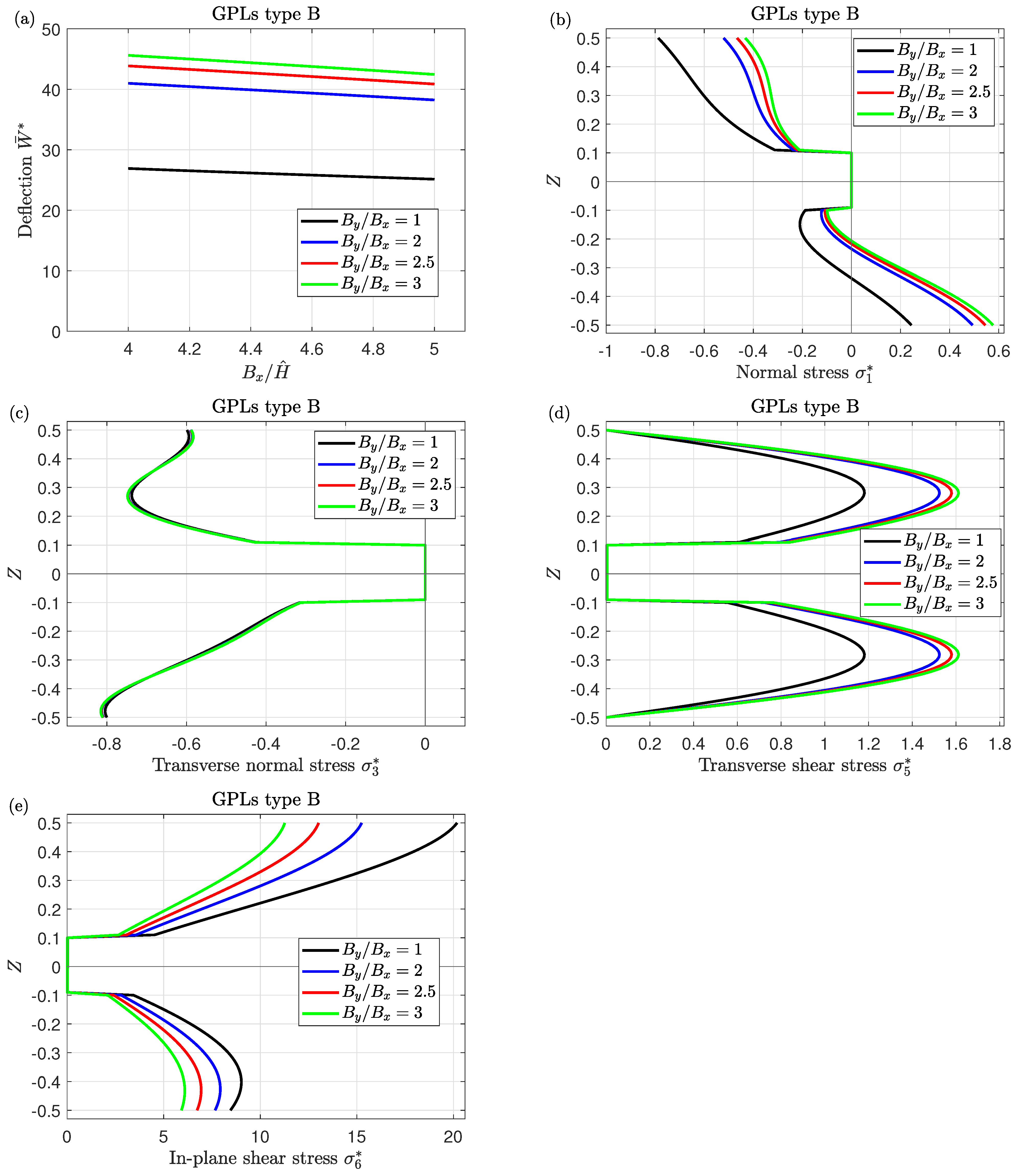
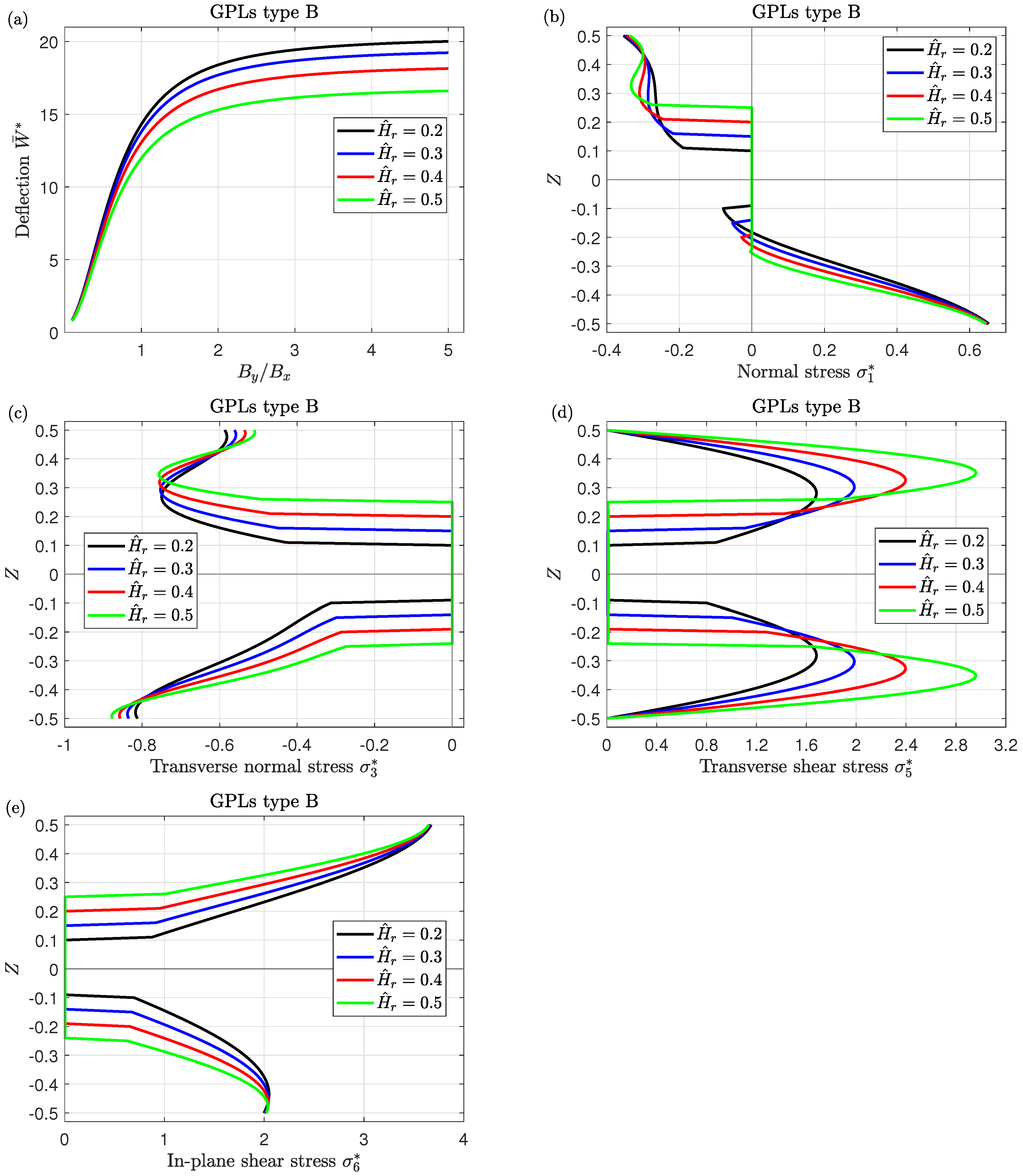
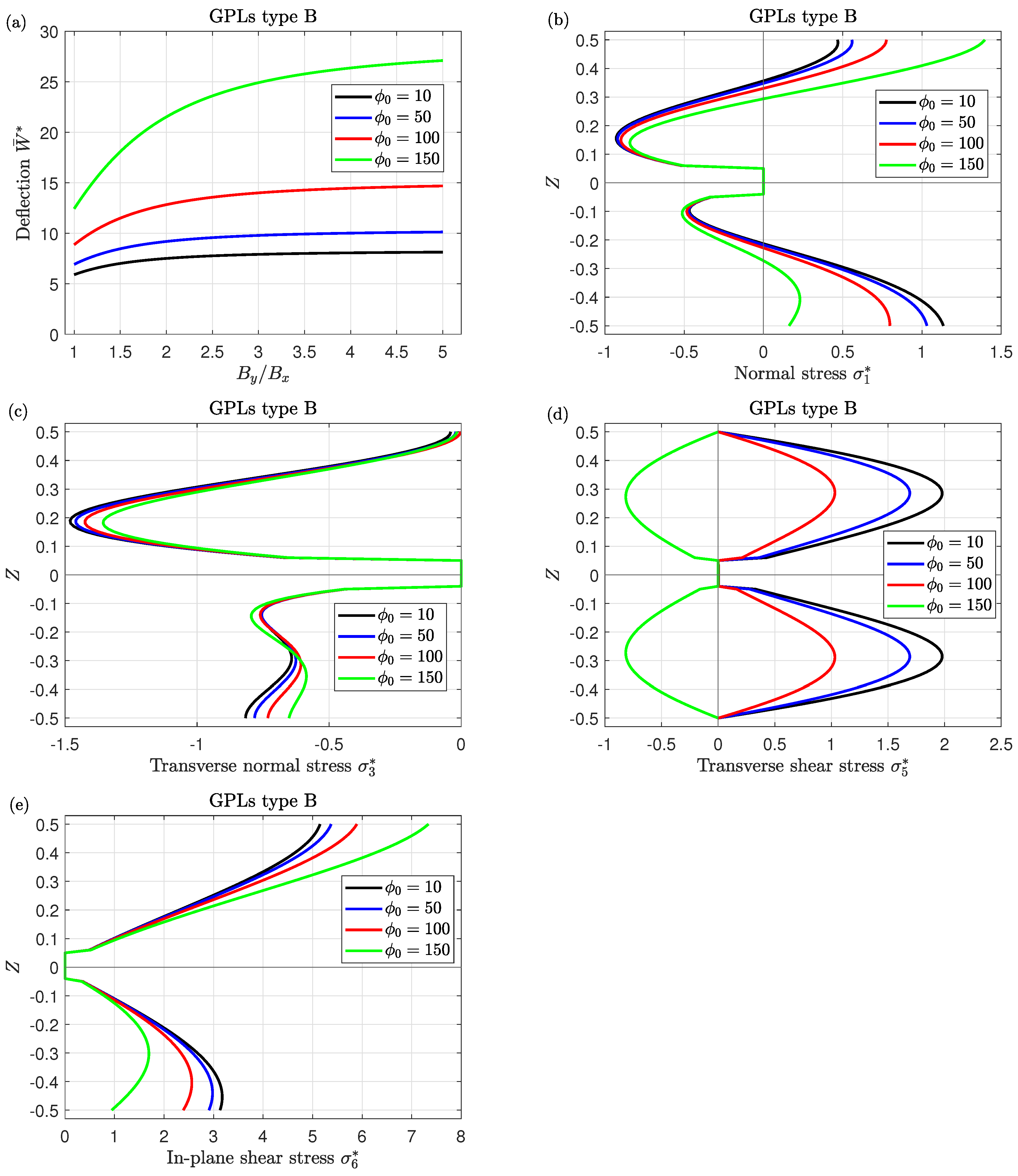
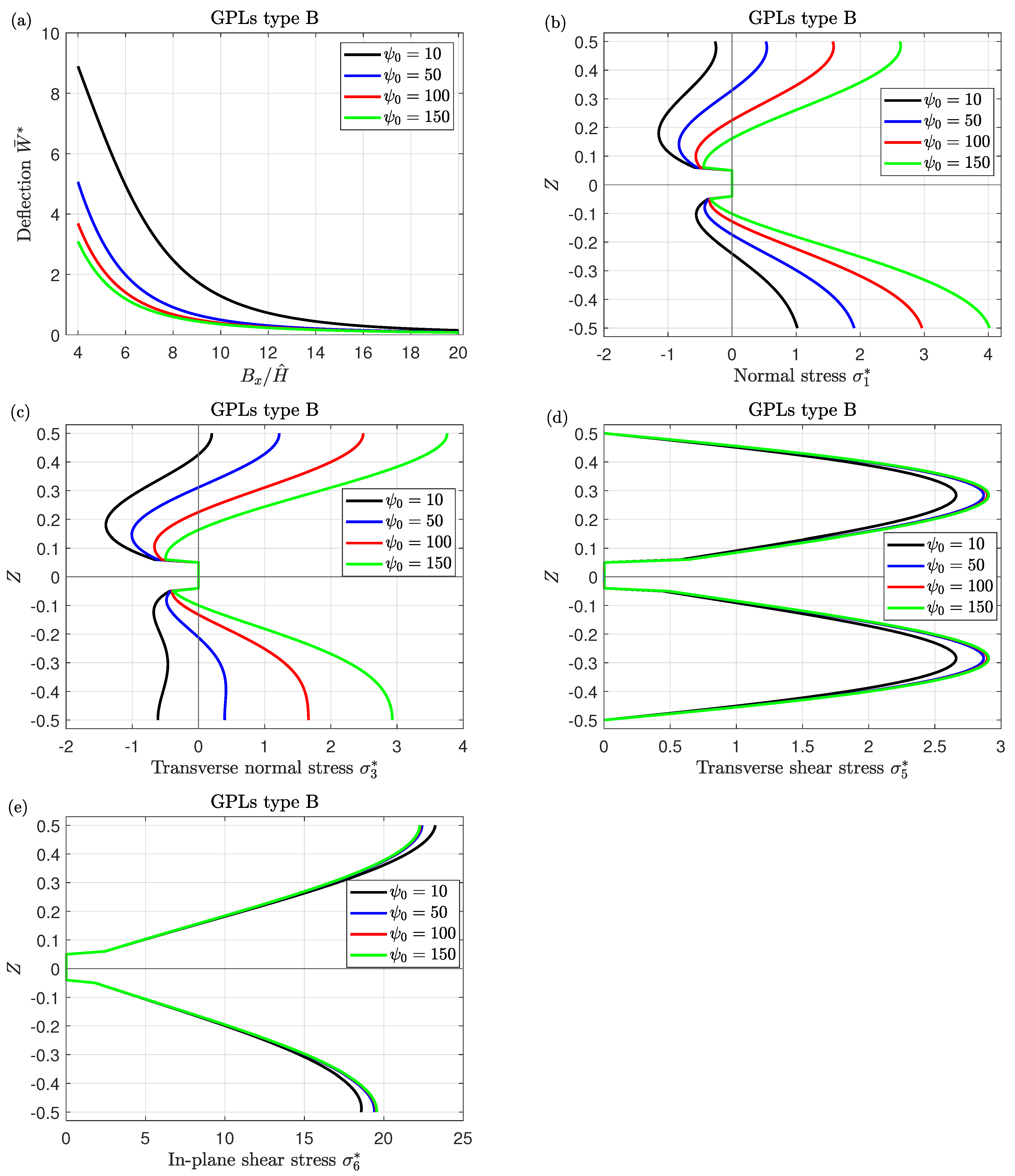
| Materials | Piezoelectromagnetic | GPLs |
|---|---|---|
| E(GPa) | 1.4 | 1010 |
| 0.29 | 0.186 | |
| (g/cm) | 1.92 | 1.06 |
| (K) | 3.06 | 5 |
| (wt.% | 0.44 | 0.00026 |
| () | −2.2 | −2.2 |
| () | 9.3 | 9.3 |
| () | 5.8 | 5.8 |
| 290.1 | 290.1 | |
| 349.9 | 349.9 | |
| 275 | 275 | |
| 5.64 | 5.64 | |
| ( | 6.35 | 6.35 |
| 5.367 | 5.367 | |
| 2737.5 | 2737.5 | |
| −297 | −297 | |
| 83.5 | 83.5 |
| Source | |||||||
|---|---|---|---|---|---|---|---|
| 5 | Ref. [66] | 0.3433 | 0.6688 | 0.8671 | 1.0885 | 1.2276 | |
| =0 | Present | 0.3433 | 0.6688 | 0.8671 | 1.0889 | 1.2277 | |
| ≠0 | Present | 0.3235 | 0.6189 | 0.7956 | 1.0037 | 1.1420 | |
| 10 | Ref. [66] | 0.2961 | 0.5890 | 0.7573 | 0.9114 | 1.0087 | |
| =0 | Present | 0.2961 | 0.5890 | 0.7573 | 0.9115 | 1.0088 | |
| ≠0 | Present | 0.2906 | 0.5635 | 0.7147 | 0.8640 | 0.9693 | |
| 20 | Ref. [66] | 0.2842 | 0.5689 | 0.7298 | 0.8669 | 0.9538 | |
| =0 | Present | 0.2842 | 0.5689 | 0.7298 | 0.8669 | 0.9538 | |
| ≠0 | Present | 0.2828 | 0.5502 | 0.6953 | 0.8301 | 0.9274 | |
| 100 | Ref. [66] | 0.2804 | 0.5625 | 0.7209 | 0.8527 | 0.9362 | |
| =0 | Present | 0.2804 | 0.5625 | 0.7209 | 0.8527 | 0.9362 | |
| ≠0 | Present | 0.2803 | 0.5461 | 0.6891 | 0.8193 | 0.9141 |
| k | Source | |||||
|---|---|---|---|---|---|---|
| 0 | Ref. [67] | 0.2961 | 1.9943 | 1.3124 | 0.7067 | |
| =0 | Present | 0.2961 | 1.9945 | 1.3123 | 0.7066 | |
| ≠0 | Present | 0.2914 | 2.0269 | 1.3126 | 0.7009 | |
| 1 | Ref. [67] | 0.5890 | 3.0850 | 1.4898 | 0.6111 | |
| =0 | Present | 0.5890 | 3.0854 | 1.4897 | 0.6111 | |
| ≠0 | Present | 0.5647 | 3.1121 | 1.4481 | 0.5659 | |
| 2 | Ref. [67] | 0.7573 | 3.6067 | 1.3960 | 0.5442 | |
| =0 | Present | 0.7573 | 3.6072 | 1.3959 | 0.5442 | |
| ≠0 | Present | 0.7166 | 3.6399 | 1.3419 | 0.4943 | |
| 3 | Ref. [67] | 0.8375 | 3.8709 | 1.2756 | 0.5526 | |
| =0 | Present | 0.8375 | 3.8715 | 1.2755 | 0.5526 | |
| ≠0 | Present | 0.7917 | 3.9015 | 1.2177 | 0.5005 | |
| 4 | Ref. [67] | 0.8815 | 4.0655 | 1.1794 | 0.5669 | |
| =0 | Present | 0.8816 | 4.0662 | 1.1792 | 0.5669 | |
| ≠0 | Present | 0.8358 | 4.0915 | 1.1220 | 0.5146 | |
| 5 | Ref. [67] | 0.9114 | 4.2447 | 1.1041 | 0.5757 | |
| =0 | Present | 0.9115 | 4.2455 | 1.1039 | 0.5756 | |
| ≠0 | Present | 0.8673 | 4.2665 | 1.0495 | 0.5246 | |
| 6 | Ref. [67] | 0.9351 | 4.4201 | 1.0428 | 0.5806 | |
| =0 | Present | 0.9352 | 4.4209 | 1.0426 | 0.5805 | |
| ≠0 | Present | 0.8931 | 4.4387 | 0.9919 | 0.5313 | |
| 7 | Ref. [67] | 0.9558 | 4.5928 | 0.9915 | 0.5836 | |
| =0 | Present | 0.9559 | 4.5937 | 0.9913 | 0.5836 | |
| ≠0 | Present | 0.9158 | 4.6093 | 0.9442 | 0.5363 | |
| 8 | Ref. [67] | 0.9746 | 4.7619 | 0.9477 | 0.5858 | |
| =0 | Present | 0.9747 | 4.727 | 0.9475 | 0.5858 | |
| ≠0 | Present | 0.9364 | 4.7771 | 0.9041 | 0.5405 | |
| 9 | Ref. [67] | 0.9921 | 4.9261 | 0.9103 | 0.5878 | |
| =0 | Present | 0.9922 | 4.9269 | 0.9101 | 0.5877 | |
| ≠0 | Present | 0.9556 | 4.9407 | 0.8700 | 0.5443 |
| Ref. [65] | Present | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 53.61227 | −0.69981 | 0.02431 | 53.68555 | −0.69826 | 0.08231 |
| 10 | 30.11324 | 0.43018 | 0.28122 | 30.11930 | 0.43095 | 0.31548 | |
| 20 | 20.59210 | 0.84383 | 0.42313 | 20.58718 | 0.84338 | 0.44638 | |
| 30 | 15.51250 | 1.04298 | 0.52254 | 15.50585 | 1.04257 | 0.53920 | |
| 50 | 0 | 44.74203 | −0.22953 | 0.09075 | 44.78091 | −0.22797 | 0.14095 |
| 10 | 26.85012 | 0.59960 | 0.30675 | 26.84963 | 0.60007 | 0.33799 | |
| 20 | 18.91641 | 0.92909 | 0.43682 | 18.90952 | 0.92887 | 0.45845 | |
| 30 | 14.49721 | 1.09370 | 0.53118 | 14.48983 | 1.09316 | 0.54681 | |
| 100 | 0 | 38.19967 | 0.11483 | 0.14044 | 38.21763 | 0.11618 | 0.18480 |
| 10 | 24.15575 | 0.73833 | 0.32817 | 24.15061 | 0.73853 | 0.35688 | |
| 20 | 17.45993 | 1.00256 | 0.44892 | 17.45155 | 1.00216 | 0.46912 | |
| 30 | 13.58837 | 1.13871 | 0.53904 | 13.58043 | 1.13805 | 0.55374 | |
| 150 | 0 | 33.17936 | 0.37694 | 0.17918 | 33.18390 | 0.37798 | 0.21897 |
| 10 | 21.89475 | 0.85371 | 0.34645 | 21.88627 | 0.85365 | 0.37300 | |
| 20 | 16.18287 | 1.06639 | 0.45971 | 16.17337 | 1.06582 | 0.47864 | |
| 30 | 12.77039 | 1.17886 | 0.54623 | 12.76203 | 1.17808 | 0.56009 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Mukahal, F.H.H. Static Response of Nanocomposite Electromagnetic Sandwich Plates with Honeycomb Core via a Quasi 3-D Plate Theory. Mathematics 2023, 11, 2046. https://doi.org/10.3390/math11092046
Al Mukahal FHH. Static Response of Nanocomposite Electromagnetic Sandwich Plates with Honeycomb Core via a Quasi 3-D Plate Theory. Mathematics. 2023; 11(9):2046. https://doi.org/10.3390/math11092046
Chicago/Turabian StyleAl Mukahal, Fatemah H. H. 2023. "Static Response of Nanocomposite Electromagnetic Sandwich Plates with Honeycomb Core via a Quasi 3-D Plate Theory" Mathematics 11, no. 9: 2046. https://doi.org/10.3390/math11092046
APA StyleAl Mukahal, F. H. H. (2023). Static Response of Nanocomposite Electromagnetic Sandwich Plates with Honeycomb Core via a Quasi 3-D Plate Theory. Mathematics, 11(9), 2046. https://doi.org/10.3390/math11092046






