Analytical Modelling of an Active Vibration Absorber for a Beam
Abstract
1. Introduction
2. Materials and Methods
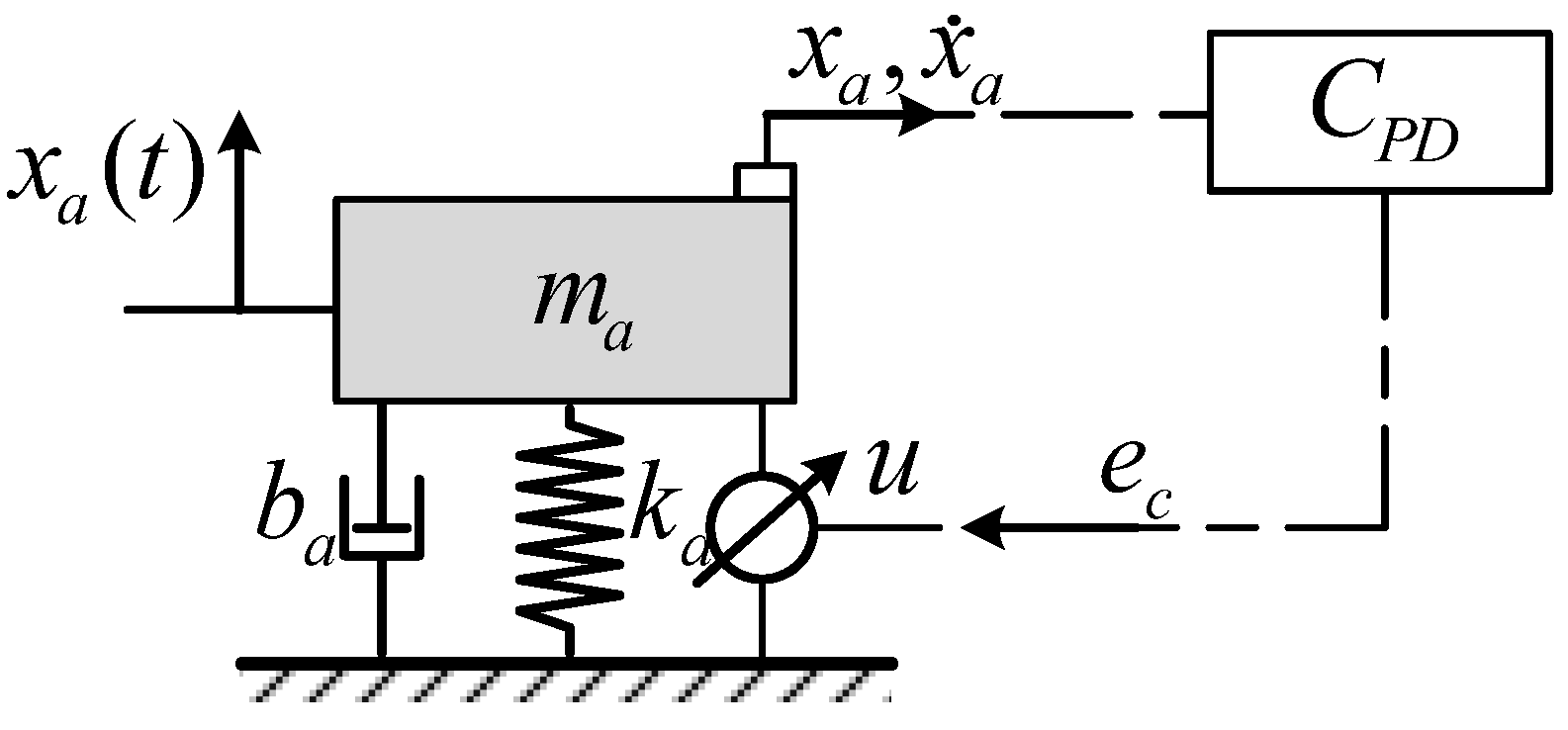
2.1. Active Vibration Absorber Model
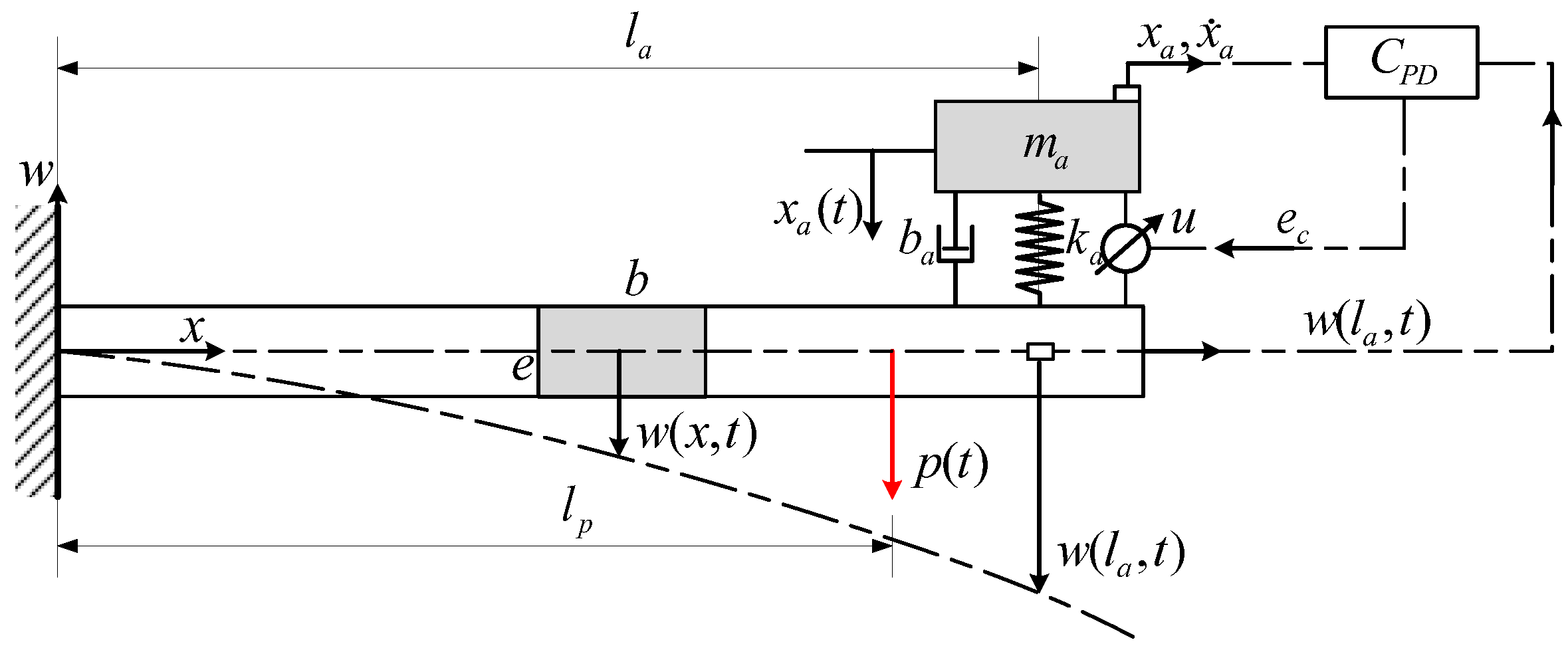
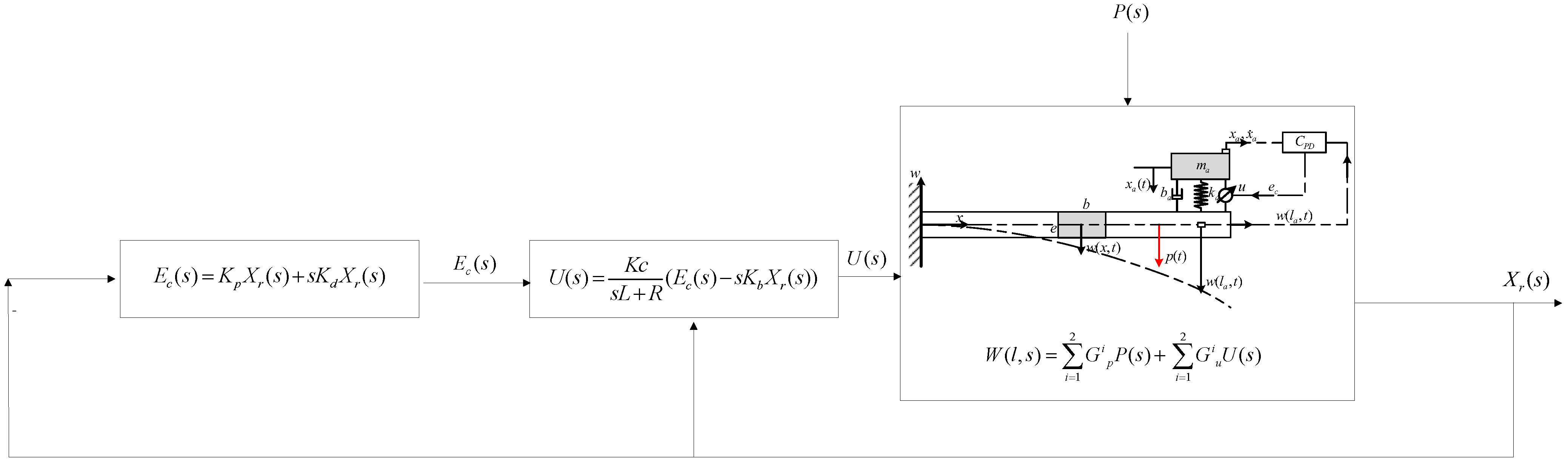
2.2. Active Control for a Cantilever Beam
2.3. Simulation
2.3.1. Dynamic Characteristics of the AVA
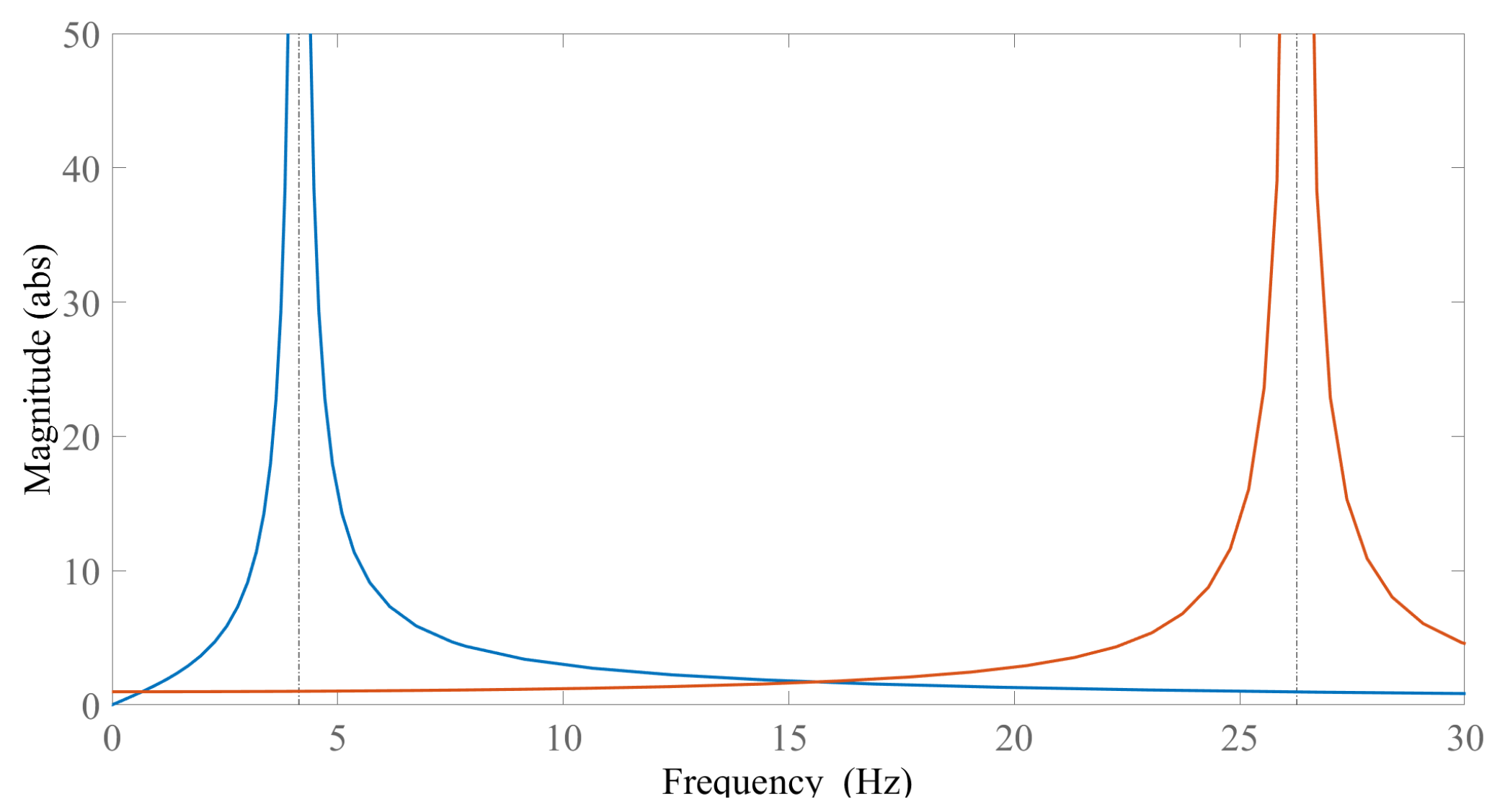
2.3.2. Natural Frequencies of the Cantilever Beam
2.3.3. Dynamic Response of the Cantilever Beam
3. Results
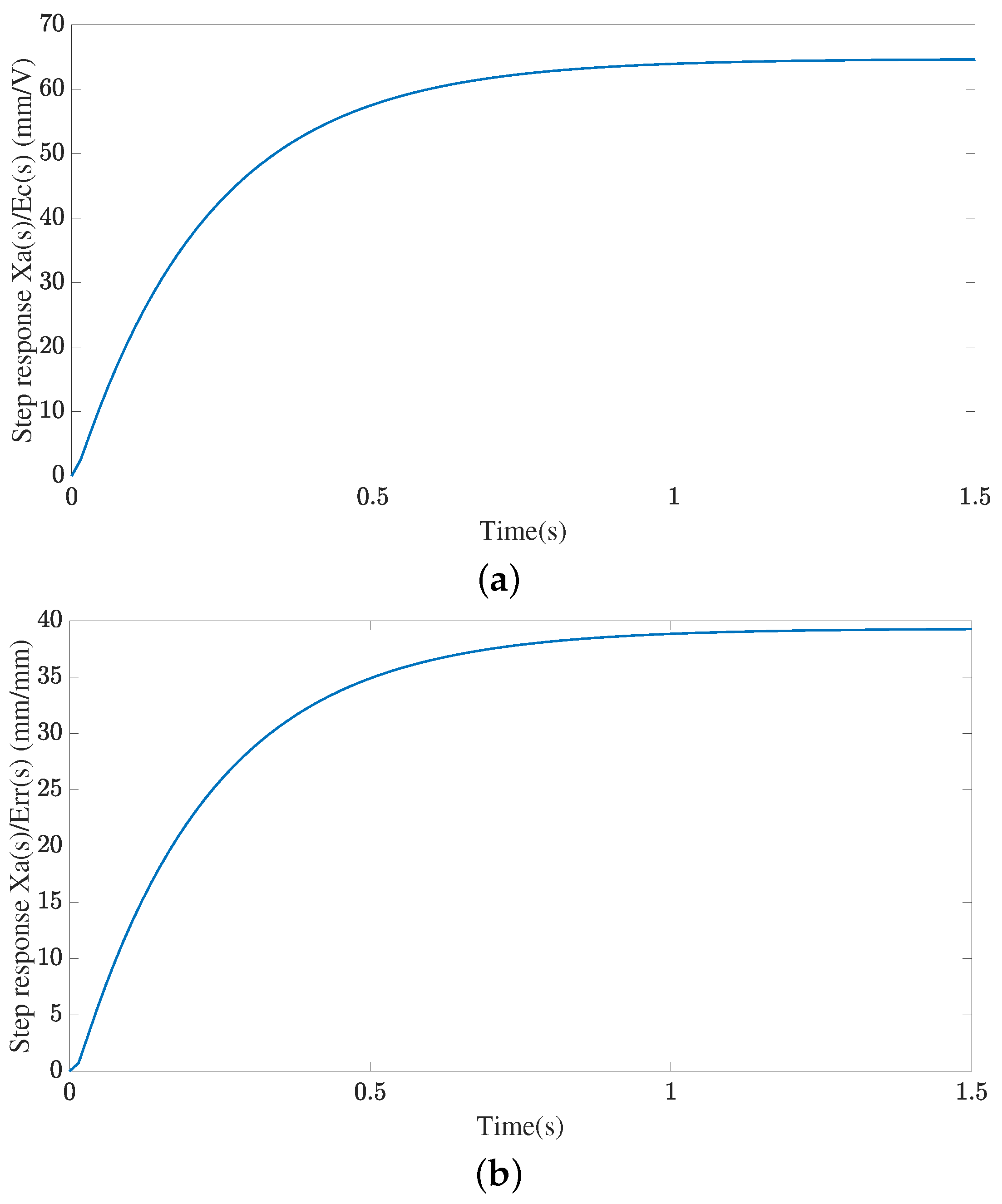
3.1. AVA Dynamic Characteristics
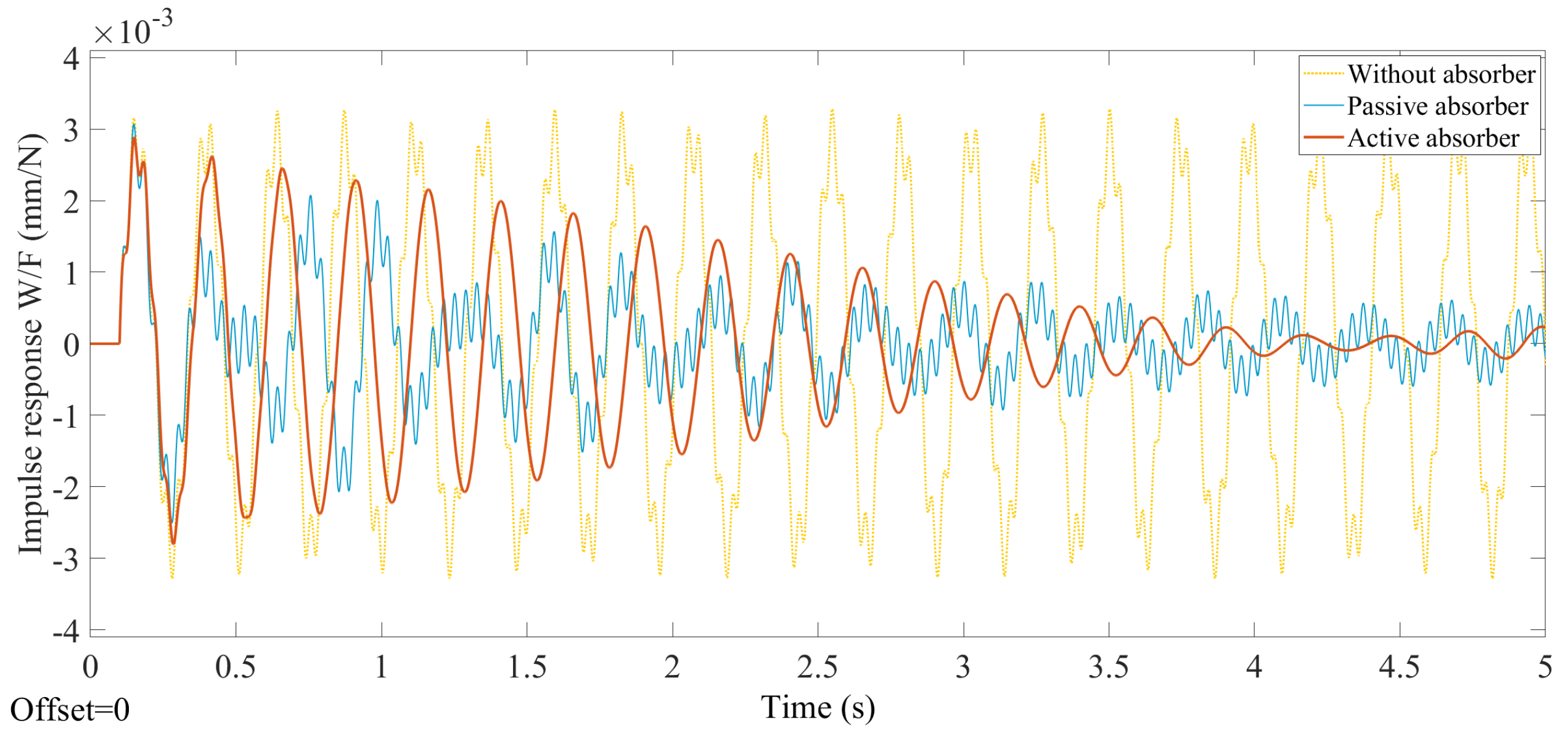
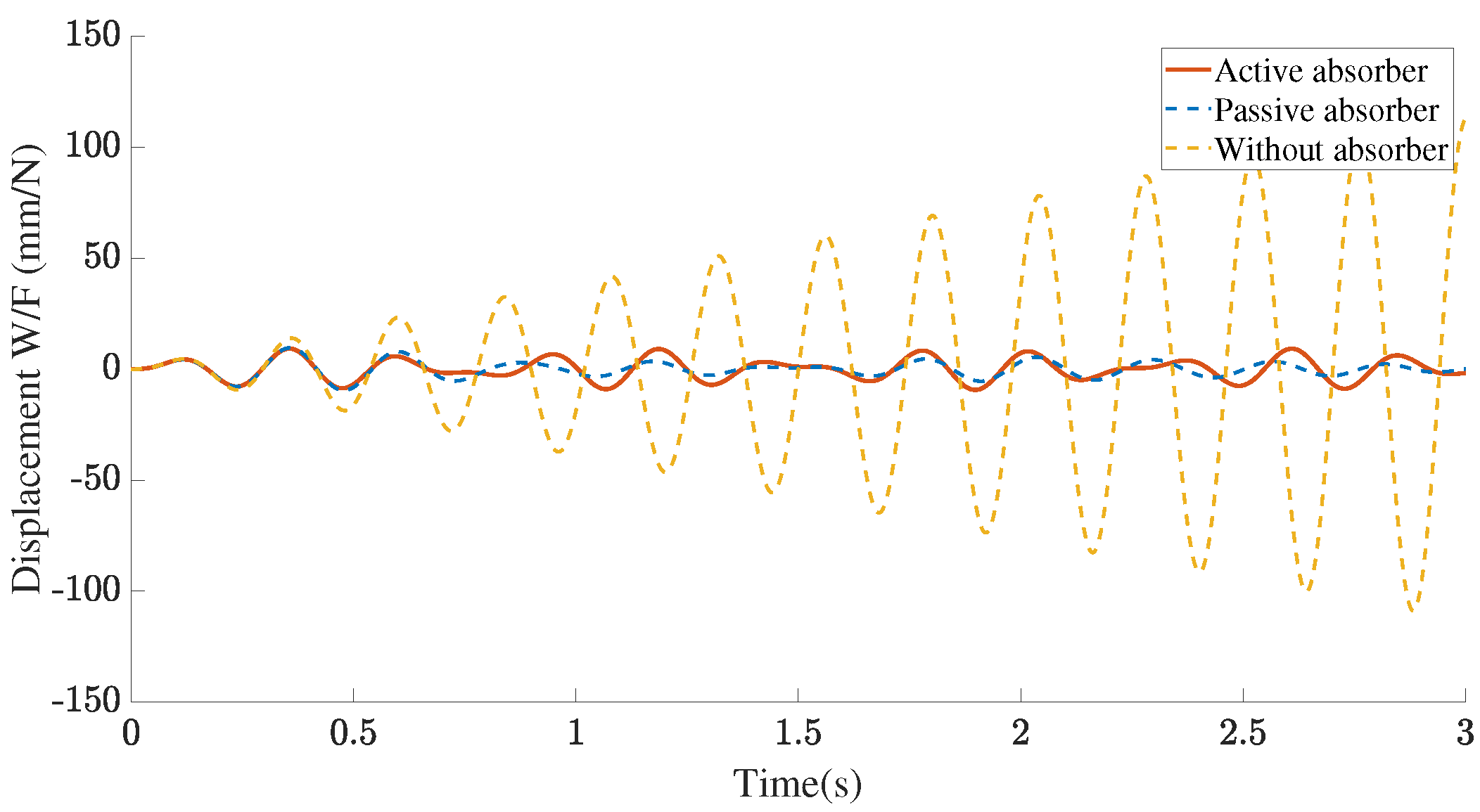
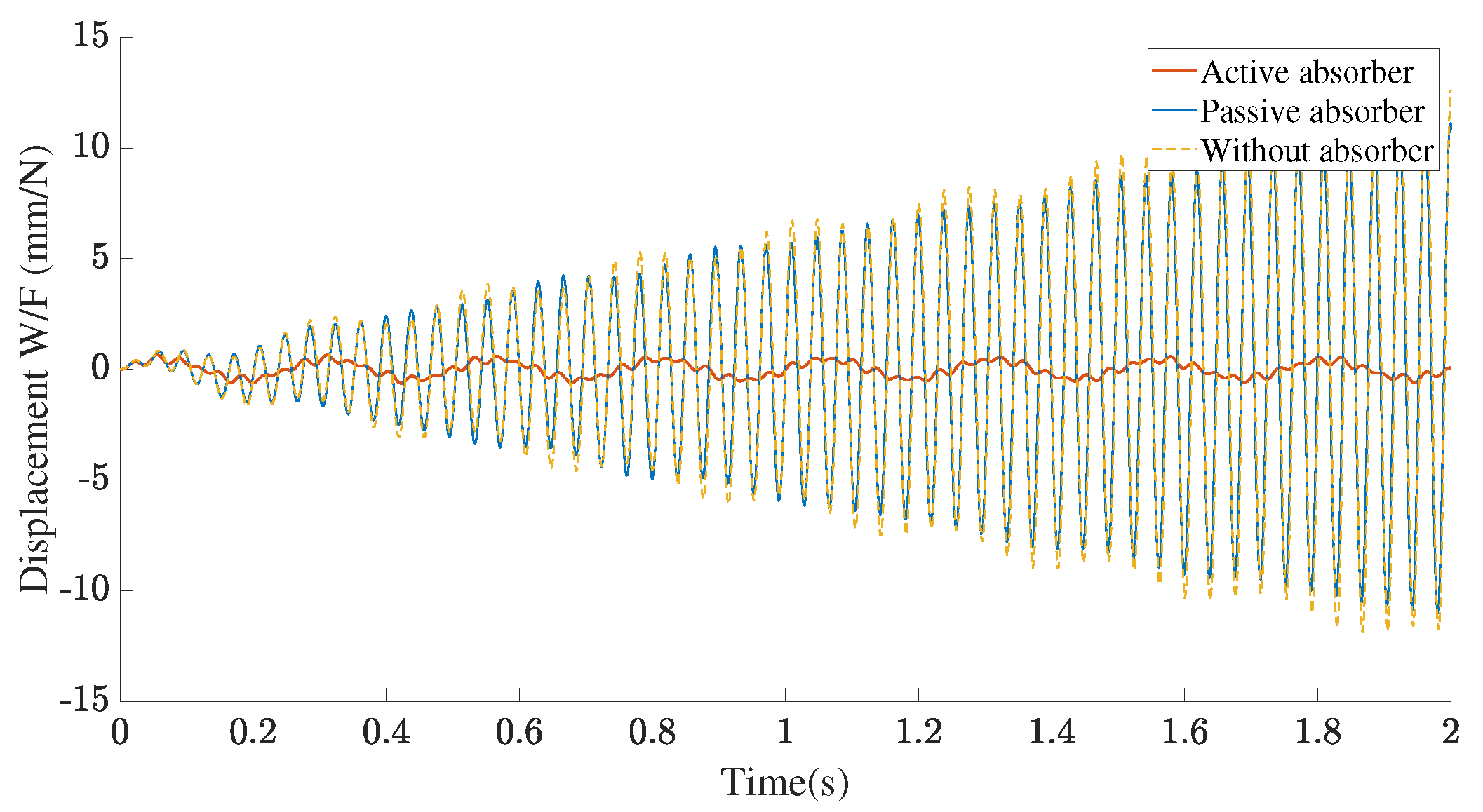
3.2. Dynamic Response
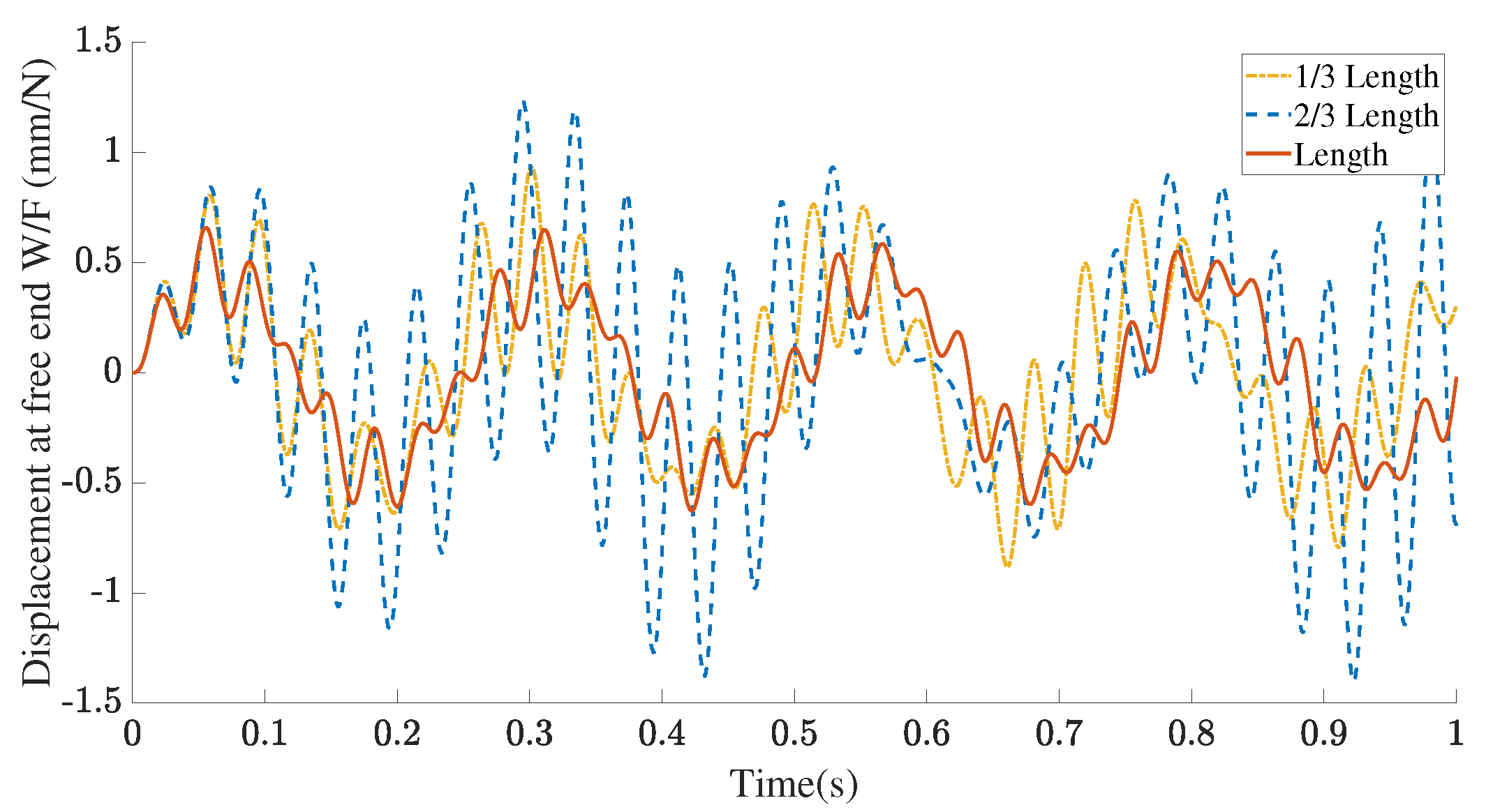
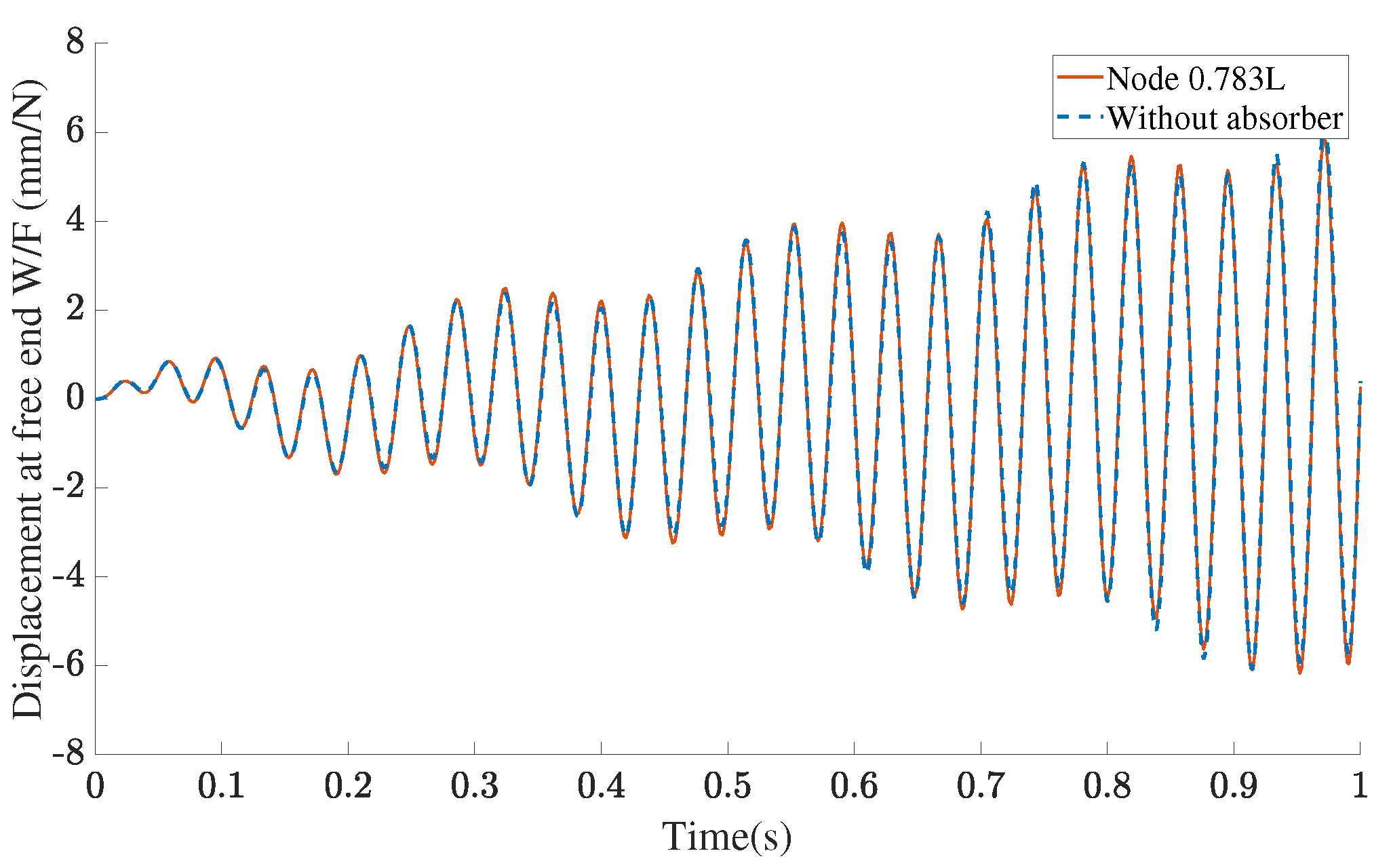
3.3. Position Influence
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Orhan, S.; Aktürk, N.; Çelik, V. Vibration monitoring for defect diagnosis of rolling element bearings as a predictive maintenance tool: Comprehensive case studies. NDT E Int. 2006, 39, 293–298. [Google Scholar] [CrossRef]
- Sofronas, A. Case Histories in Vibration Analysis and Metal Fatigue for the Practicing Engineer; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 245–268. [Google Scholar]
- Frahm, H. A Device for Damping Vibrations of Bodies. US Patent 989958A, 18 April 1911. [Google Scholar]
- Hartog, J.D. Mechanical Vibrations, 4th ed.; McGraw-Hill: New York, NY, USA, 1956; Volume 1. [Google Scholar]
- Soong, T.T. Active structural control in civil engineering. Eng. Struct. 1988, 10, 74–84. [Google Scholar] [CrossRef]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T. Structural control: Past, present and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Kobori, T.; Koshika, N.; Yamada, K.; Ikeda, Y. Seismic-response-controlled structure with active mass driver system. Part 1: Design. Earthq. Eng. Struct. Dyn. 1991, 20, 133–149. [Google Scholar] [CrossRef]
- Kobori, T.; Koshika, N.; Yamada, K.; Ikeda, Y. Seismic-response-controlled structure with active mass driver system. Part 2: Verification. Earthq. Eng. Struct. Dyn. 1991, 20, 151–166. [Google Scholar] [CrossRef]
- Chang, C.; Yang, H.T. Control of Buildings Using Active Tuned Mass Dampers. J. Eng. Mech. 1995, 121, 355–366. [Google Scholar] [CrossRef]
- Kwak, M.K.; Yang, D.H.; Shin, J.H. Active vibration control of structures using a semi-active dynamic absorber. Noise Control Eng. J. 2015, 63, 287–299. [Google Scholar] [CrossRef]
- Yu, W.; Thenozhi, S.; Li, X. Stable active vibration control system for building structures using PD/PID control. IFAC Proc. Vol. 2014, 47, 4760–4765. [Google Scholar] [CrossRef]
- Yang, D.H.; Shin, J.H.; Lee, H.W.; Kim, S.K.; Kwak, M.K. Active vibration control of structure by Active Mass Damper and Multi-Modal Negative Acceleration Feedback control algorithm. J. Sound Vib. 2017, 392, 18–30. [Google Scholar] [CrossRef]
- Chang, S. Active mass damper for reducing wind and earthquake vibrations of a long-period bridge. Actuators 2020, 9, 66. [Google Scholar] [CrossRef]
- Kumar, K.R.; Narayanan, S. Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs. Smart Mater. Struct. 2008, 17, 055008. [Google Scholar] [CrossRef]
- Cao, H.; Li, Q.S. New control strategies for active tuned mass damper systems. Comput. Struct. 2004, 82, 2341–2350. [Google Scholar] [CrossRef]
- Zhou, K.; Li, Q.S.; Li, X. Dynamic Behavior of Supertall Building with Active Control System during Super Typhoon Mangkhut. J. Struct. Eng. 2020, 146, 04020077. [Google Scholar] [CrossRef]
- Babaei, M.; Asemi, K.; Safarpour, P. Natural Frequency and Dynamic Analyses of Functionally Graded Saturated Porous Beam Resting on Viscoelastic Foundation Based on Higher Order Beam Theory. J. Solid Mech. 2019, 11, 615–634. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Qin, Z.; Ma, L.; Chu, F. Dynamic performance of a novel integral magnetorheological damper-rotor system. Mech. Syst. Signal Process. 2022, 172, 109004. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, W.; Jing, J. An electromagnetic torsion active vibration absorber based on the FxLMS algorithm. J. Sound Vib. 2022, 524, 116734. [Google Scholar] [CrossRef]
- Mo, J.; Priefer, R. Medical Devices for Tremor Suppression: Current Status and Future Directions. Biosensors 2021, 11, 99. [Google Scholar] [CrossRef]
- Fromme, N.P.; Camenzind, M.; Riener, R.; Rossi, R.M. Design of a lightweight passive orthosis for tremor suppression. J. Neuroeng. Rehabil. 2020, 17, 47. [Google Scholar] [CrossRef]
- Tremelo for Essential Tremor | Effective Hand Tremor Device. Available online: https://fivemicrons.com/tremelo/ (accessed on 25 February 2023).
- Rudraraju, S. Wearable tremor reduction device (trd) for human hands and arms. In Frontiers in Biomedical Devices; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar]
- Palomera-Arias, R.; Connor, J.J.; Ochsendorf, J.A. Feasibility Study of Passive Electromagnetic Damping Systems. J. Struct. Eng. 2008, 134, 109–158. [Google Scholar] [CrossRef]
- Diez-Jimenez, E.; Rizzo, R.; Gómez-García, M.J.; Corral-Abad, E. Review of Passive Electromagnetic Devices for Vibration Damping and Isolation. Shock Vib. 2019, 2019, 1250707. [Google Scholar] [CrossRef]
- Elmali, H.; Renzulli, M.; Olgac, N. Experimental comparison of delayed resonator and PD controlled vibration absorbers using electromagnetic actuators. J. Dyn. Syst. Meas. Control. Trans. ASME 2000, 122, 514–520. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Pearson: London, UK, 2010; Volume 169, p. 641. [Google Scholar] [CrossRef]
- Łatas, W. Application of the continuous dynamic absorbers in local and global vibration reduction problems in beams. Vib. Phys. Syst. 2016, 27, 245–254. [Google Scholar]
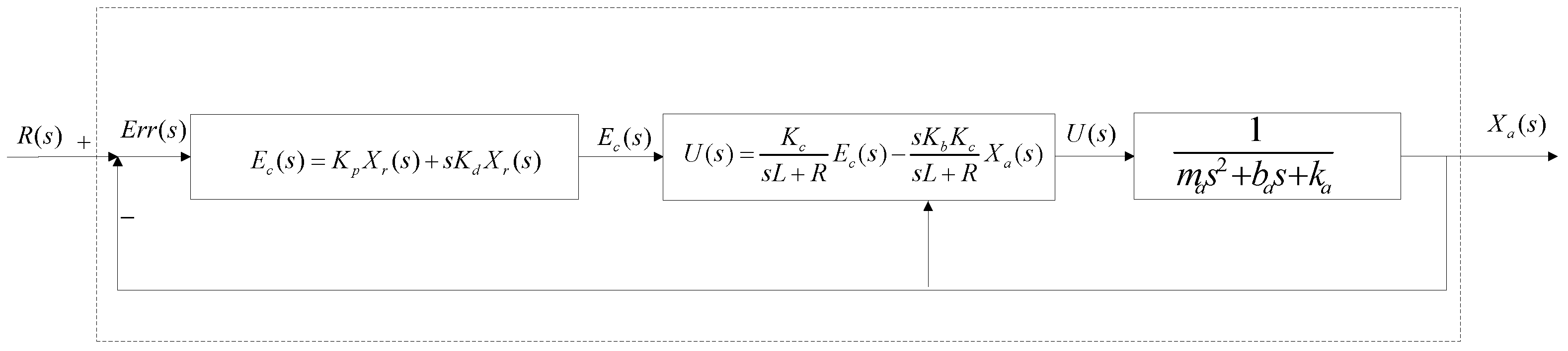

| Description | Parameter | Value |
|---|---|---|
| Cantilever beam | b | 50 mm |
| e | 5 mm | |
| 7850 kg/m3 | ||
| A | 250 mm2 | |
| E | 210 GPa | |
| I | 5000 mm4 | |
| l | 1 m | |
| Active vibration absorber | 0.05 kg | |
| 141.8 N/m | ||
| 0.1 N.s/m | ||
| R | 1.6 Ohm | |
| L | 0.75 mH | |
| 3.5 N/A | ||
| 3.5 V.s/m |
| Natural Frequency | Without Absorber | With Absorber |
|---|---|---|
| First | 4.14 Hz | 3.50 Hz |
| Second | 26.26 Hz | 4.93 Hz |
| Third | 73.53 Hz | 26.26 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rincon, C.; Alencastre, J.; Rivera, R. Analytical Modelling of an Active Vibration Absorber for a Beam. Mathematics 2023, 11, 2009. https://doi.org/10.3390/math11092009
Rincon C, Alencastre J, Rivera R. Analytical Modelling of an Active Vibration Absorber for a Beam. Mathematics. 2023; 11(9):2009. https://doi.org/10.3390/math11092009
Chicago/Turabian StyleRincon, Carlos, Jorge Alencastre, and Richard Rivera. 2023. "Analytical Modelling of an Active Vibration Absorber for a Beam" Mathematics 11, no. 9: 2009. https://doi.org/10.3390/math11092009
APA StyleRincon, C., Alencastre, J., & Rivera, R. (2023). Analytical Modelling of an Active Vibration Absorber for a Beam. Mathematics, 11(9), 2009. https://doi.org/10.3390/math11092009










