Estimations of Covering Functionals of Convex Bodies Based on Relaxation Algorithm

Abstract

Estimating covering functionals of convex bodies is an important part of Chuanming Zong’s program to attack Hadwiger’s covering conjecture, which is a long-standing open problem from convex and discrete geometry. In this paper, we transform this problem into a vertex p-center problem (VPCP). An exact iterative algorithm is introduced to solve the VPCP by making adjustments to the relaxation-based algorithm mentioned by Chen and Chen in 2009. The accuracy of this algorithm is tested by comparing numerical and exact values of covering functionals of convex bodies including the Euclidean disc, simplices, and the regular octahedron. A better lower bound of the covering functional with respect to 7 of 3-simplices is presented.

1. Introduction

Let ${\mathbb{R}}^n$ be the n-dimensional Euclidean space and $e_1,e_2,\cdots ,e_n$ be the standard orthogonal basis of ${\mathbb{R}}^n$. A compact convex subset K of ${\mathbb{R}}^n$ having interior points is called a convex body. The set of extreme points of K is denoted by $extK$. Let ${\mathcal{K}}^n$ be the set of convex bodies in ${\mathbb{R}}^n$. For each $K\in {\mathcal{K}}^n$, we denote by $c\left(K\right)$ the smallest number of translates of $intK$ (the interior of K) needed to cover K. Concerning the least upper bound of $c\left(K\right)$ in ${\mathcal{K}}^n$, there is a long-standing conjecture:

Conjecture 1 

(Hadwiger’s covering conjecture). For each $K\in {\mathcal{K}}^n$, we have

$$c\left(K\right)\le 2^n,$$

and the equality holds if and only if K is a parallelotope.

Classical results concerning this conjecture can be found in the monograph [1] and the survey [2]. See also the monograph [3] and the survey [4]. Although many in-depth studies have been conducted, this conjecture is completely solved only in the two-dimensional case (cf. [5]). M. Lassak proved that $c\left(K\right)\le 8$ holds for each centrally symmetric three-dimensional convex body in [6]. I. Papadoperakis showed that $c\left(K\right)\le 16$ holds for each $K\in {\mathcal{K}}^3$ (cf. [7]). A. Prymak and V. Shepelska obtained (cf. [8])

$$c\left(K\right)\le 96,\forall K\in {\mathcal{K}}^4,c\left(K\right)\le 1091,\forall K\in {\mathcal{K}}^5, \mathrm{and} c\left(K\right)\le \mathrm{15,373},\forall K\in {\mathcal{K}}^6.$$

Clearly, we are still far away from the complete solution of Conjecture 1 even in the three-dimensional situation.

By Theorem 34.3 in [1] or [9], $c\left(K\right)$ equals the least number of smaller homothetic copies of K (i.e., a set of the form $\gamma K+x$ with $\gamma \in (0,1)$ and $x\in {\mathbb{R}}^n$) needed to cover K. Therefore, $c\left(K\right)\le p$ for some $p\in {\mathbb{Z}}^{+}$ if and only if

$${\Gamma }_p\left(K\right):=min\left\{\gamma >0\mid \exists \left\{x_i\mid i\in \left[p\right]\right\}\subseteq {\mathbb{R}}^n\mathrm{s}.\mathrm{t}.K\subseteq \bigcup _{i\in \left[p\right]}(\gamma K+x_i)\right\}<1,$$

where $\left[p\right]=\left\{i\in {\mathbb{Z}}^{+}\mid 1\le i\le p\right\}$. The map

$$\begin{array}{cc}\hfill {\Gamma }_p(·):{\mathcal{K}}^n& \to [0,1]\hfill \\ \hfill K& \mapsto {\Gamma }_p\left(K\right)\hfill \end{array}$$

is called the covering functional with respect to p. For each $p\in {\mathbb{Z}}^{+}$, ${\Gamma }_p(·)$ is an affine invariant. More precisely, ${\Gamma }_p\left(K\right)={\Gamma }_p\left(T\left(K\right)\right)$ holds for each non-degenerate affine transformation T on ${\mathbb{R}}^n$. For $K\in {\mathcal{K}}^n$ and $p\in {\mathbb{Z}}^{+}$, a set C of p points satisfying

$$K\subseteq {\Gamma }_p\left(K\right)K+C=\bigcup _{c\in C}({\Gamma }_p\left(K\right)K+c)$$

is called a p-optimal configuration of K.

Estimating ${\Gamma }_p\left(K\right)$ for special convex bodies $K\in {\mathcal{K}}^n$ plays an important role in Chuanming Zong’s quantitative program to attack Conjecture 1 (cf. [10]), which is the first attempt at a computer-based resolution of Conjecture 1, and is theoretically feasible if this conjecture admits an affirmative answer. Motivated by Zong’s program, many results concerning the estimation of ${\Gamma }_p(·)$ appeared in the literature. For example, it is shown that ${\Gamma }_{2^n}\left(K\right)\ge 1/2,\forall K\in {\mathcal{K}}^n$ (cf. [11]); covering functionals of convex polytopes and of convex hulls of compact sets are estimated in [12,13]. However, known results are still insufficient for choosing a suitable $\widehat{{\gamma }_n}\in [{\gamma }_n,1)$, where

$${\gamma }_n=sup\left\{{\Gamma }_{2^n}\left(K\right)\mid K\in {\mathcal{K}}^n\right\}.$$

The main difficulty in estimating ${\Gamma }_p(·)$ is finding a p-optimal configuration of K, which is not easy even for the Euclidean disk (cf. Figure 6 in [4]). It is the aim of this paper to design a feasible algorithm for finding approximate p-optimal configurations.

For each $K\in {\mathcal{K}}^n$, let $P_K$ be a subset of ${\mathbb{R}}^n$ that contains at least one p-optimal configuration of K. In Section 2, we show that when S and V are fine discretizations of K and $P_K$, respectively, the solution of a vertex p-center problem (VPCP) will provide a good approximation of ${\Gamma }_p\left(K\right)$. In such a problem, S and V are viewed as the set of demand points (clients) and the set of candidate centers (candidate facilities), respectively; the dissimilarity $d(u,v)$ between $u\in S$ and $v\in V$ is the least non-negative number $\gamma$ such that $u\in v+\gamma K$; the problem, which is denoted by VPCP($S,V,p$), looks for a p-element subset $V\left(S\right)$ of V such that the maximum dissimilarity between every point in S and its closest center in $V\left(S\right)$ is minimized, i.e.,

$$\underset{V\left(S\right)\subseteq V,\left|V\left(S\right)\right|=p}{min}\underset{u\in S}{max}\underset{v\in V\left(S\right)}{min}d(u,v).$$

Optimal value and optimal set are synonyms of optimal dissimilarity and optimal center set of VPCP, respectively. The combination of the optimal value and optimal set is called an optimal solution of VPCP.

As one of the first to study VPCP, Hakimi suggested that VPCP is NP-hard (cf. [14,15]). Minieka proposed an iterative algorithm in 1970 to solve VPCP, each iteration of the algorithm solves a set covering problem (SCP): for a fixed number $\gamma$ > 0, find the minimum number of facilities such that the dissimilarity from each demand point to its nearest facility is less than or equal to $\gamma$ (cf. [16]). Daskin [17] limited the set of candidate centers to the set of vertices of a graph and solved the VPCP about a graph by Binary Search (BS) algorithm in 1995. In 2001, Ilhan and Pınar proposed a restricted set covering problem (R-SCP) that limits the cardinality of the optimal center set of SCP to less than or equal to p, and VPCP is solved by solving a sequence of R-SCPs (cf. [18]). In order to reduce the number of iterations, Al-Khedhairi and Salhi improved the results of [17] and [18] in [19].

As shown in Section 2, better estimation of ${\Gamma }_p\left(K\right)$ needs finer discretizations of K and $P_K$, which will lead to large-scale VPCPs. In 1987, Chen and Handler put forward a relaxation-based iterative algorithm that approaches an optimal solution of a VPCP step by step by solving some subproblems which only consider a subset of the demand point set (cf. [20]). In 2009, Chen and Chen improved this algorithm and proposed three new relaxation algorithms (cf. [21]). Irawan et al. adopted the idea of simplified subproblem in 2015. By gathering the set of demand points and solving the result of the aggregation via a heuristic algorithm, a VPCP with up to 71,009 demand points (see [22]) is solved. In [23], Claudio Contardo et al. introduced a scalable exact algorithm that can solve a VPCP with up to one million demand points when p is very small.

In Section 2, the problem of estimating ${\Gamma }_p\left(K\right)$ is transformed to a VPCP, and an error estimation is provided. Using ideas mentioned in [21], a relaxation-based algorithm for solving such a VPCP is designed in Section 3. Results of computational experiments showing the effectiveness of our algorithm are presented in Section 4.

2. Covering Functional and the Optimal Value of a VPCP

Let $K\in {\mathcal{K}}^n$, $S\subseteq K$, and $V\subseteq {\mathbb{R}}^n$ be a set with $\left|V\right|\ge p$. Put

$${\Gamma }_p(K,S,V)=min\left\{\gamma \ge 0\mid \exists \left\{x_i\mid i\in \left[p\right]\right\}\subseteq V \mathrm{s}.\mathrm{t}. S\subseteq \bigcup _{i\in \left[p\right]}(x_i+\gamma K)\right\}.$$

For $s\in S$ and $v\in V$, if the dissimilarity $d(s,v)$ of VPCP($S,V,p$) is defined by

$$d(s,v)=min\left\{\gamma \ge 0\mid s\in \gamma K+v\right\},$$

(1)

then ${\Gamma }_p(K,S,V)$ equals the optimal value of VPCP($S,V,p$).

Theorem 1. 

Let $p\in {\mathbb{Z}}^{+}$, $K\in {\mathcal{K}}^n$, $S\subseteq K$, $P_K$ be a set containing a p-optimal configuration of K, and $V\subseteq P_K$. If there exist two numbers ${\epsilon }_1$, ${\epsilon }_2>0$ such that $K\subseteq S+{\epsilon }_{1}K$ and $P_K\subseteq V+{\epsilon }_{2}K$, then

$${\Gamma }_p(K,S,V)-{\epsilon }_2\le {\Gamma }_p\left(K\right)\le {\Gamma }_p(K,S,V)+{\epsilon }_1.$$

(2)

Proof. 

By the definition of ${\Gamma }_p(K,S,V)$, there exists a set $C_S\subseteq V$ with $|C_S|=p$ such that

$$S\subseteq C_S+{\Gamma }_p(K,S,V)K.$$

Then

$$K\subseteq S+{\epsilon }_{1}K\subseteq C_S+{\Gamma }_p(K,S,V)K+{\epsilon }_{1}K=C_S+({\Gamma }_p(K,S,V)+{\epsilon }_1)K,$$

which implies that

$${\Gamma }_p\left(K\right)\le {\Gamma }_p(K,S,V)+{\epsilon }_1.$$

(3)

Similarly, there exists a set $C_S^{\prime }\subseteq P_K$ of p points such that

$$S\subseteq C_S^{\prime }+{\Gamma }_p(K,S,P_K)K.$$

Since $P_K\subseteq V+{\epsilon }_{2}K$, there exists a set $C^{\prime }\subseteq V$ with $|C^{\prime }|\le p$ such that $C_S^{\prime }\subseteq C^{\prime }+{\epsilon }_{2}K$, which shows that

$$\begin{array}{cc}\hfill S\subseteq C_S^{\prime }+{\Gamma }_p(K,S,P_K)K& \subseteq C^{\prime }+{\epsilon }_{2}K+{\Gamma }_p(K,S,P_K)K\hfill \\ \hfill & =C^{\prime }+({\epsilon }_2+{\Gamma }_p(K,S,P_K))K.\hfill \end{array}$$

Hence

$${\Gamma }_p(K,S,V)\le {\epsilon }_2+{\Gamma }_p(K,S,P_K).$$

(4)

Since $S\subseteq K$, we have

$${\Gamma }_p(K,S,P_K)\le {\Gamma }_p(K,K,P_K)={\Gamma }_p\left(K\right).$$

(5)

From (3), (4), and (5), (2) follows.    □

Theorem 1 shows that, when S and V are fine discretizations of K and $P_K$, respectively, then the optimal value of VPCP($S,V,p$) with the dissimilarity defined by (1) is a good approximation of ${\Gamma }_p\left(K\right)$. When the dimension is high, such discretizations of K and $P_K$ will produce S and V with large cardinality. Consequently, we have to solve a large-scale VPCP efficiently.

A suitable choice of $P_K$ is important to reduce the computational complexity of the corresponding VPCP. When there is less information about p-optimal configurations of K, we can use the set

$$Q_K=\left\{c\in {\mathbb{R}}^n\mid (c+K)\cap K\ne \varnothing \right\}$$

as $P_K$. Since $Q_K$ always contains a p-optimal configuration of K, we have

$${\Gamma }_p(K,K,Q_K)={\Gamma }_p\left(K\right).$$

Since $\left\{c\in {\mathbb{R}}^n\mid (c+K)\cap S\ne \varnothing \right\}\subseteq Q_K$, we also have

$${\Gamma }_p(K,S,Q_K)={\Gamma }_p(K,S,{\mathbb{R}}^n).$$

Theorem 2. 

Let $K\in {\mathcal{K}}^n$, $p\in {\mathbb{Z}}^{+}$, $U\subseteq S\subseteq K$ and V be a set with $\left|V\right|\ge p$. Then,

$${\Gamma }_p(K,U,V)\le {\Gamma }_p(K,S,V),$$

(6)

and the equality holds if and only if there exists a set $C_U\subseteq V$ of p points satisfying

$$S\subseteq C_U+{\Gamma }_p(K,U,V)K.$$

(7)

Proof. 

Let $C_S\subseteq V$ be a p-element set satisfying $S\subseteq C_S+{\Gamma }_p(K,S,V)K$. Clearly,

$$U\subseteq C_S+{\Gamma }_p(K,S,V)K.$$

Thus, ${\Gamma }_p(K,U,V)\le {\Gamma }_p(K,S,V)$. If $C_U$ is a p-element subset of V satisfying (7), then

$${\Gamma }_p(K,S,V)\le {\Gamma }_p(K,U,V).$$

Hence, ${\Gamma }_p(K,S,V)={\Gamma }_p(K,U,V)$. Conversely, if the equality in (6) holds, then there exists a set $C^{\prime }\subseteq V$ with $|C^{\prime }|=p$ such that

$$S\subseteq C^{\prime }+{\Gamma }_p(K,S,V)K=C^{\prime }+{\Gamma }_p(K,U,V)K.$$

   □

3. A Relaxation-Based Algorithm for VPCP($\mathit{S},\mathit{V},\mathit{p}$)

Relaxation-based algorithms are useful to attack a large-scale location problem (see [21] for a clear description of relaxation-based algorithms). An algorithm of this type tries to solve the original problem by solving a series of subproblems. In each of these subproblems, only a subset of the set of demanding points is taken into consideration. Thus, the optimal value of a subproblem provides a lower bound of the optimal value of the original problem. Moreover, if the optimal set of a subproblem is feasible for the original one, then it is also optimal to the original problem (cf. Theorem 2). Otherwise, it is necessary to find a suitable subset of the violated points, add them in, and solve the new subproblem. The worst situation is that we do not obtain the optimal value until the subproblem expands to the original one.

3.1. The Relaxation-Based Algorithm about VPCP

Let $K\in {\mathcal{K}}^n$, $p\in {\mathbb{Z}}^{+}$, $P_K$ be a set containing at least one p-optimal configuration of K and S and V be suitable discretizations of K and $P_K$, respectively. Let $k\in {\mathbb{Z}}^{+}$, $\left\{S_i\mid i\in \left[k\right]\right\}$ be a sequence of sets such that

$$S_1\subseteq S_2\subseteq \cdots \subseteq S_k=S,$$

and ${\epsilon }_1\left(i\right)$ and ${\epsilon }_2$ be positive real numbers satisfying $K\subseteq S_i+{\epsilon }_1\left(i\right)K$ and $P_K\subseteq V+{\epsilon }_{2}K$, respectively.

Let U be a subset of $S_1$ (also a subset of $S_i$) with small cardinality. Choose an initial lower bound $LB$ (take, e.g., $LB=0$) for VPCP($U,V,p$) and an initial upper bound $UB$ (take, e.g., $UB=1$) for VPCP($S_1,V,p$). As the first step, the procedure BS_SolveVPCP($U,V,p,LB,UB,e$) (see Algorithm 1) is invoked to solve VPCP($U,V,p$) and yields the optimal value $r^{*}\left(U\right)$ and an optimal set $V^{*}\left(U\right)$. Put

$$W=\left\{u\in S_1\backslash U\mid d(u,V^{*}\left(U\right))>r^{*}\left(U\right)\right\},$$

where $d(u,V^{*}\left(U\right))=min\left\{d(u,v)\mid v\in V^{*}\left(U\right)\right\}$. If $W=\varnothing$, then VPCP($S_1,V,p$) is solved. Otherwise, we can update $LB$ by $r^{*}\left(U\right)$ (by Theorem 2, $r^{*}\left(U\right)$ is a lower bound of $r^{*}\left(S_1\right)$), select some points from W to update U by SelectPointsFromW ($W,$$\epsilon ,V^{*}\left(U\right)$) (see Algorithm 2), and invoke BS_SolveVPCP($U,V,p,LB,UB,e$) again. The iteration continues until ($r^{*}\left(U\right),$$V^{*}\left(U\right)$) is a feasible solution of VPCP($S_1,V,p$).

Algorithm 1 A binary search algorithm BS_SolveVPCP($U,V,p,LB,UB,e$)

Require:  U, V, p, $LB$, $UB$e Ensure:  $r^{*}\left(U\right),V^{*}\left(U\right)$ 1: if R-SCP($U,V,p,LB$) has a feasible solution then 2:     $V^{*}\left(U\right)\leftarrow$ SolveR-SCP($U,V,p,LB$)                                ▹ Solve R-SCP by ILP 3:     $r^{*}\left(U\right)\leftarrow LB$ 4:     return $r^{*}\left(U\right),V^{*}\left(U\right)$ 5: else: 6:     $V^{*}\left(U\right)\leftarrow$ SolveR-SCP($U,V,p,UB$) 7:     $r^{*}\left(U\right)\leftarrow UB$ 8:     repeat 9:         $\gamma \leftarrow \frac{LB+UB}{2}$ 10:         if R-SCP($U,V,p,\gamma$) has a feasible solution then 11:            $V^{*}\left(U\right)\leftarrow$ SolveR-SCP($U,V,p,\gamma$) 12:            $r^{*}\left(U\right)\leftarrow UB\leftarrow \gamma$ 13:         else: 14:            $LB\leftarrow \gamma$ 15:         end if 16:     until $UB-LB\le e$ 17:     return $r^{*}\left(U\right),V^{*}\left(U\right)$ 18: end if

Algorithm 2 $\epsilon$-separated sequence algorithm SelectPointsFromW($W,\epsilon ,V^{*}\left(U\right)$)

Require:  W, $\epsilon$, $V^{*}\left(U\right)$ Ensure:  $W^{\prime }$ 1: select a point u in W such that $d(u,V^{*}\left(U\right))$ is maximal 2: $W^{\prime }\leftarrow${u} 3: for$w\in W$do 4:     if $d(w,v)>\epsilon$ for each $v\in W^{{}^{\prime }}$ then 5:         $W^{\prime }\leftarrow W^{\prime }\cup \left\{w\right\}$ 6:     end if 7: end for 8: return  $W^{\prime }$

Subsequently, suppose that, for some $1\le i<k$, $r^{*}\left(S_i\right)$ and $V^{*}\left(S_i\right)$ have been obtained. By Theorem 1, we have

$$r^{*}\left(S_{i+1}\right)-{\epsilon }_2\le {\Gamma }_p\left(K\right)\le r^{*}\left(S_i\right)+{\epsilon }_1\left(i\right).$$

So update $UB$ of $r^{*}\left(S_{i+1}\right)$ with $r^{*}\left(S_i\right)+{\epsilon }_1\left(i\right)+{\epsilon }_2$. Let

$$W=\left\{u\in S_{i+1}\backslash U\mid d(u,V^{*}\left(S_i\right))>r^{*}\left(S_i\right)\right\}.$$

If $W=\varnothing$, then $r^{*}\left(S_i\right)$ and $V^{*}\left(S_i\right)$ are also optimal for VPCP($S_{i+1},V,p$), see Theorem 2 again. Otherwise, select a subset $W^{\prime }$ of W to update U by applying the procedure SelectPointsFromW($W,\epsilon ,V^{*}\left(U\right)$) and then solve VPCP($S_{i+1},V,p$) with the new U. This process, as described in Algorithm 3, stops after we obtain an optimal solution of VPCP($S_k,V,p$).

3.2. Sub-Routine BS_SolveVPCP$(U,V,p,LB,UB,e)$: A Binary Search Algorithm for VPCP

The procedure BS_SolveVPCP($U,V,p,LB,UB,e$) solves VPCP($U,V,p$) by a binary search, which is based on whether a R-SCP has a feasible solution. Given U, V, p, and a positive number $\gamma$, the restricted set covering problem R-SCP($U,V,p,\gamma$) asks whether it is possible to find a subset $V^{*}\left(U\right)$ of V with cardinality less than or equal to p such that $max\left\{d(s,V^{*}\left(U\right))\mid s\in U\right\}\le \gamma$. Let I and J be the index sets of U and V, respectively. Put, for each pair $(i,j)\in I\times J$,

$$\begin{array}{cc}\hfill a_{ij}& =\left\{\begin{array}{cc}1,\hfill & d(u_i,v_j)\le \gamma ,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

Then, R-SCP($U,V,p,\gamma$) can be transformed to the following integer linear programming (ILP):

$$\begin{array}{}\mathrm{(8a)}& \min \sum _{j\in J}{x}_j\hfill \mathrm{(8b)}& \hfill \mathrm{s}.\mathrm{t}.\sum _{j\in J}{a}_{ij}{x}_j\ge 1, \forall i\in I,\mathrm{(8c)}& \sum _{j\in J}{x}_j\le p,\hfill \mathrm{(8d)}& \hfill x_j\in \left\{0,1\right\}, \forall j\in J.\end{array}$$

It can be verified that $x_j=1$ for some $j\in J$ if and only if $v_j$ is used as a center (cf. [23]). The objective function (8a) minimizes the number of centers. The constraint (8b) ensures that each demand point in U is covered by at least one center. The constraint (8c) means that the number of centers does not exceed p. Note that if $\gamma$ is too small, the problem (8a)–(8d) might be infeasible.

Algorithm 3 A relaxation-based algorithm to solve VPCP($S_k,V,p$)

Require:  $S_1,\cdots ,S_k$, V, p, $LB$, $UB$, two positive real numbers e and $\epsilon$ Ensure:  $r^{*}\left(S_k\right),V^{*}\left(S_k\right)$ 1: $U\leftarrow$ a subset of $S_1$ 2: $i\leftarrow 0$ 3: repeat 4:     repeat 5:         $(r^{*}\left(U\right),V^{*}\left(U\right))\leftarrow$BS_SolveVPCP($U,V,p,LB,UB,e$)          ▹ Algorithm 1 6:         $LB\leftarrow r^{*}\left(U\right)$ 7:         $W\leftarrow \left\{u\in S_{i+1}\backslash U\mid d(u,V^{*}\left(U\right))>r^{*}\left(U\right)\right\}$ 8:         if $W\ne \varnothing$ then 9:            $W^{{}^{\prime }}\leftarrow$SelectPointsFromW($W,\epsilon ,V^{*}\left(U\right)$)                                 ▹Algorithm 2 10:            $U\leftarrow U\cup W^{{}^{\prime }}$ 11:         end if 12:     until $W=\varnothing$ 13:     $i\leftarrow i+1$ 14:     while $i\ne k$ and $W=\varnothing$ do: 15:         $UB\leftarrow min\{r^{*}\left(U\right)+{\epsilon }_1\left(i\right)+{\epsilon }_2,1\}$ 16:         $W\leftarrow \left\{u\in S_{i+1}\backslash U\mid d(u,V^{*}\left(U\right))>r^{*}\left(U\right)\right\}$ 17:         if $W\ne \varnothing$ then 18:            $W^{{}^{\prime }}\leftarrow$ SelectPointsFromW($W,\epsilon ,V^{*}\left(U\right)$) 19:            $U\leftarrow U\cup W^{{}^{\prime }}$ 20:         else 21:            $i\leftarrow i+1$ 22:         end if 23:     end while 24: until$i=k$ 25: $(r^{*}\left(S_k\right),V^{*}\left(S_k\right))\leftarrow (r^{*}\left(U\right),V^{*}\left(U\right))$ 26: return  $r^{*}\left(S_k\right),V^{*}\left(S_k\right)$

If R-SCP($U,V,p,LB$) has a feasible solution $V^{*}\left(U\right)$, then $V^{*}\left(U\right)$ and $LB$ are returned. Otherwise, we set $r^{*}\left(U\right)=UB$ and $V^{*}\left(U\right)$ to be a feasible solution of R-SCP($U,V,p,UB$). Put

$$\gamma =\frac{LB+UB}{2}.$$

(9)

If R-SCP($U,V,p,\gamma$) is feasible, then update $UB$ and $r^{*}\left(U\right)$ with $\gamma$, and $V^{*}\left(U\right)$ with the feasible solution. Otherwise, update $LB$ with $\gamma$. Subsequently, replace $\gamma$ by (9) and try to solve R-SCP($U,V,p,\gamma$) again. As Algorithm 1 illustrates, this procedure continues whenever $UB-LB>e$.

Let $(r^{*}\left(U\right),V^{*}\left(U\right))$ be the optimal solution of VPCP($U,V,p$) and $(r^{*}{\left(U\right)}^{\prime },V^{*}{\left(U\right)}^{\prime })$ be an approximate optimal solution obtained by Algorithm 1. Then,

$${r^{*}\left(U\right)}^{\prime }-e\le r^{*}\left(U\right)\le {r^{*}\left(U\right)}^{\prime }.$$

If (${r^{*}\left(U\right)}^{\prime },{V^{*}\left(U\right)}^{\prime }$) is also a feasible solution of VPCP($S,V,p$) for $U\subseteq S$, then

$${r^{*}\left(U\right)}^{\prime }-e\le r^{*}\left(U\right)\le r^{*}\left(S\right)\le {r^{*}\left(U\right)}^{\prime }.$$

Therefore, by (2), we have

$${r^{*}\left(U\right)}^{\prime }-e-{\epsilon }_2\le r^{*}\left(S\right)-{\epsilon }_2\le {\Gamma }_p\left(K\right)\le r^{*}\left(S\right)+{\epsilon }_1\le {r^{*}\left(U\right)}^{\prime }+{\epsilon }_1.$$

(10)

3.3. Sub-Routine SelectPointsFromW$(W,\epsilon ,V^{*}\left(U\right))$: An $\epsilon$-Separated Sequence Generating Algorithm

The rule for choosing and updating U is critical to the efficiency of Algorithm 3. One can randomly or uniformly select some points from S to be the initial U. After several iterations, the cardinality of U might be large, which will lead to high computational complexity. To avoid this situation, Chen and Handler selected a single node in W which is most dissimilar to $V^{*}$ and added it to U (cf. [20]). This method cannot ensure the increasing of lower bounds of $r^{*}\left(S\right)$ in the next iteration (cf. [23]). Other methods for updating U can be found in [21,23].

Let $\epsilon$ be a positive number,

$$W=\left\{u\in S\backslash U\mid d(u,V^{*}\left(U\right))>r^{*}\left(U\right)\right\},$$

u be a point in W such that $d(u,V^{*}\left(U\right))$ is maximal and $W^{\prime }=\left\{u\right\}$. If there exists a point $w\in W$ satisfying $d(w,W^{\prime })>\epsilon$, then we update $W^{\prime }$ with $W^{\prime }\cup \left\{w\right\}$. Repeat this process until no point in W can be added into $W^{\prime }$. See Algorithm 2. Note that

$$W\subseteq \bigcup _{w\in W^{\prime }}\left\{v\in {\mathbb{R}}^n\mid d(w,v)\le \epsilon \right\},$$

and $d(x,y)>\epsilon$ holds for any two distinct points x and y in $W^{\prime }$.

4. Computational Experiments

All algorithms were coded in Python 3.8. ILPs involved in Algorithm 1 were solved by Gurobi 9.1.2.

4.1. Covering Functionals of the Euclidean Unit Disc

Let D be the Euclidean unit disc. For each $x,y\in D$, $d(x,y)$ is the Euclidean distance between x and y. For positive integers i and j, set

$$S_{i,j}=\left\{\rho (cos2\pi \theta ,sin2\pi \theta )\mid \rho \in \left\{\frac{k}{2^i}\mid k\in \left[2^i\right]\right\},\theta \in \left\{\frac{k}{2^j}\mid k\in \left[2^j\right]\right\}\right\}\cup \left\{o\right\}.$$

Let $\gamma$ be a positive number. For two points x and y in $\partial \left(\gamma D\right)$ satisfying $x\ne -y$, we denote by $arc(x,y)$ the minor arc of $\partial \left(\gamma D\right)$ connecting x and y. Let

$$R({\rho }_1,{\rho }_2,{\theta }_1,{\theta }_2)=\left\{\rho (cos2\pi \theta ,sin2\pi \theta )\mid \rho \in [{\rho }_1,{\rho }_2],\theta \in [{\theta }_1,{\theta }_2]\right\}.$$

$R({\rho }_1,{\rho }_2,{\theta }_1,{\theta }_2)$ is a circular sector when ${\rho }_1=0$, and a circular ring sector when ${\rho }_1>0$. Each point in

$$\left\{\rho (cos2\pi \theta ,sin2\pi \theta )\mid \rho \in {\rho }_1,{\rho }_2,\theta \in {\theta }_1,{\theta }_2\right\}$$

is called a vertex of $R({\rho }_1,{\rho }_2,{\theta }_1,{\theta }_2)$.

Theorem 3. 

Let i and j be two positive integers. Then,

$$D\subseteq S_{i,j}+\alpha D,$$

where

$$\alpha =max\left\{{(2+\frac{1-2^{i+2}}{2^{2i+2}}-\left(\frac{2^{i+1}-1}{2^i}\right)cos\left(\frac{\pi }{2^j}\right))}^{\frac{1}{2}},2sin\frac{\pi }{2^{j+1}}\right\}.$$

Proof. 

Let ${\rho }^{\prime }=2^{-i},{\theta }^{\prime }=2^{-j}$. Clearly, D is divided into a collection of circular sectors

$$A_1=\left\{R(0,{\rho }^{\prime },\theta ,\theta +{\theta }^{\prime })\mid \theta \in \left\{{\theta }^{\prime }·k\mid k\in \left[2^j\right]\right\}\right\}$$

and a set of circular ring sectors

$$A_2=\left\{R(\rho ,\rho +{\rho }^{\prime },\theta ,\theta +{\theta }^{\prime })\mid \rho \in \left\{{\rho }^{\prime }·k\mid k\in [2^i-1]\right\},\theta \in \left\{{\theta }^{\prime }·k\mid k\in \left[2^j\right]\right\}\right\}.$$

For $x\in D$, there are two possible cases.

Case 1: x lies in a circular ring sector $R(\rho ,\rho +{\rho }^{\prime },\theta ,\theta +{\theta }^{\prime })$, where

$$\rho \in \left\{{\rho }^{\prime }·k\mid k\in [2^i-1]\right\} \mathrm{and} \theta \in \left\{{\theta }^{\prime }·k\mid k\in \left[2^j\right]\right\}.$$

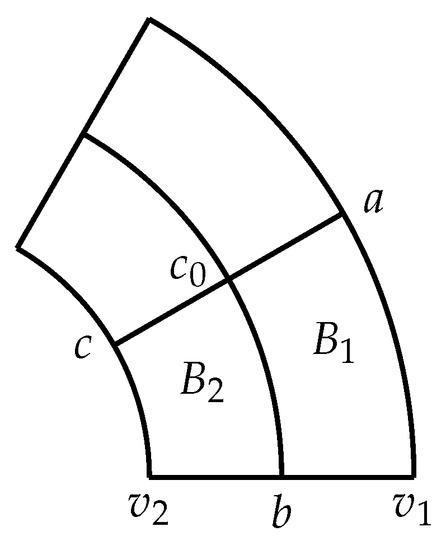
To show that $x\in S_{i,j}+\alpha D$, we only need to prove that there exists a vertex v of $R(\rho ,\rho +{\rho }^{\prime },\theta ,\theta +{\theta }^{\prime })$ such that $d(x,v)\le \alpha$. It suffices to consider the case when $x\in B:=R(1-{\rho }^{\prime },1,0,{\theta }^{\prime })$. We divide B into four circular ring sectors, see Figure 1. By symmetry, we only need to consider the case when $x\in B_1\cup B_2$, where

$$B_1=R(1-\frac{{\rho }^{\prime }}{2},1,0,\frac{{\theta }^{\prime }}{2}) \mathrm{and} B_2=R(1-{\rho }^{\prime },1-\frac{{\rho }^{\prime }}{2},0,\frac{{\theta }^{\prime }}{2}).$$

Let

$$\begin{array}{c}{v}_1=(1,0),b=(1-\frac{{\rho }^{\prime }}{2},0),v_2=(1-{\rho }^{\prime },0),a=(cos{\theta }^{\prime }\pi ,sin{\theta }^{\prime }\pi ),\\ c_0=(1-\frac{{\rho }^{\prime }}{2})(cos{\theta }^{\prime }\pi ,sin{\theta }^{\prime }\pi ), \mathrm{and} c=(1-{\rho }^{\prime })(cos{\theta }^{\prime }\pi ,sin{\theta }^{\prime }\pi ).\end{array}$$

Clearly, $v_1,v_2\in S_{i,j}$. First, we show that $x\in v_1+\alpha D$ when $x\in B_1$. It suffices to consider the case when $x\in bd{B}_1$. If $x\in arc(a,v_1)$, then $d(x,v_1)\le d(a,v_1)$; if $x\in [c_0,a]$, then $d(x,v_1)\le max\left\{d(a,v_1),d(c_0,v_1)\right\}$; if $x\in arc(c_0,b)$, then $d(x,v_1)\le max\left\{d(c_0,v_1),d(b,v_1)\right\}=d(c_0,v_1)$; if $x\in [b,v_1]$, then $d(x,v_1)\le d(b,v_1)\le d(c_0,v_1)$. Thus

$$\begin{array}{cc}\hfill d(x,v_1)& \le max\left\{d(c_0,v_1),d(a,v_1)\right\}\hfill \\ \hfill & =max\left\{{(2+\frac{1-2^{i+2}}{2^{2i+2}}-\left(\frac{2^{i+1}-1}{2^i}\right)cos\left(\frac{\pi }{2^j}\right))}^{\frac{1}{2}},2sin\frac{\pi }{2^{j+1}}\right\}=\alpha .\hfill \end{array}$$

Figure 1. A circular ring sector is divided into four circular rings sectors.

For $x\in B_2$, if $x\in arc(c_0,b)\backslash \{c_0,b\}$, then o, $c_0$, x, and $v_2$ are vertices of a convex quadrilateral wuth $[o,x]$ and $[v_2,c_0]$ as diagonals. Therefore,

$$d(o,c_0)+d(x,v_2)\le d(c_0,v_2)+d(o,x),$$

which implies $d(x,v_2)\le d(c_0,v_2)$. Using similar arguments as above, one can show that $x\in v_2+{\alpha }^{\prime }D$, $\forall x\in B_2$, where ${\alpha }^{\prime }=max\left\{d(b,v_2),d(c_0,v_2)\right\}$. Since

$$\begin{array}{c}\hfill {\alpha }^{\prime }=max\left\{d(b,v_2),d(c_0,v_2)\right\}\le max\left\{d(c_0,v_1),d(v_1,b)\right\}=d(c_0,v_1)\le \alpha ,\end{array}$$

we have $x\in v_2+\alpha D,\forall x\in B_2$.

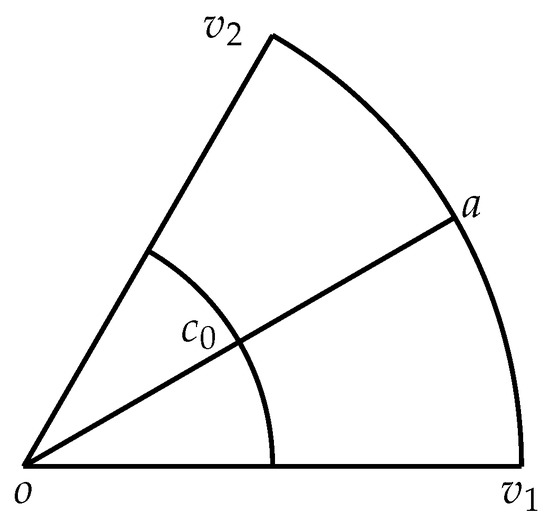
Case 2. x lies in a circular sector $R(0,{\rho }^{\prime },\theta ,\theta +{\theta }^{\prime })$ (see Figure 2). We only need to consider the case when $x\in R(0,{\rho }^{\prime },0,{\theta }^{\prime })$. Set

$$a={\rho }^{\prime }(cos{\theta }^{\prime }\pi ,sin{\theta }^{\prime }\pi ),c_0=\frac{1}{2}a,v_1=({\rho }^{\prime },0), \mathrm{and} v_2={\rho }^{\prime }(cos2\pi {\theta }^{\prime },sin2\pi {\theta }^{\prime }).$$

Then,

$$x\in \frac{{\rho }^{\prime }}{2}D\cup (v_1+max\left\{d(a,v_1),d(c_0,v_1)\right\}D)\cup (v_2+max\left\{d(a,v_2),d(c_0,v_2)\right\}D).$$

Clearly, ${\rho }^{\prime }/2\le d(c_0,v_1)\le \alpha$. It follows that $x\in S_{i,j}+\alpha D$. □

Figure 2. A circular sector is divided into two circular sectors and two circular ring sectors.

By Lemma 13 in [24], we can choose D as $P_D$. Let $S=S_{i_1,j_1}$ and $V=S_{i_2,j_2}$. If $r^{*}\left(S\right)$ is the optimal value of VPCP($S,V,p$) obtained by our algorithm, then, by Theorem 3 and Equation (10), we have

$$r^{*}\left(S\right)-e-{\alpha }_2\le {\Gamma }_p\left(D\right)\le r^{*}\left(S\right)+{\alpha }_1,$$

where, for each $k\in 1,2$,

$${\alpha }_k=max\left\{{(2+\frac{1-2^{i_k+2}}{2^{2i_k+2}}-\left(\frac{2^{i_k+1}-1}{2^{i_k}}\right)cos\left(\frac{\pi }{2^{j_k}}\right))}^{\frac{1}{2}},2sin\frac{\pi }{2^{j_k+1}}\right\}.$$

Computational results providing estimations of ${\Gamma }_p\left(D\right)$ are summarized in Table 1. In Table 1, column 6 provides an interval which contains ${\Gamma }_p\left(D\right)$.

Table 1. The estimation results of ${\Gamma }_p\left(D\right)$.

e	p	$({\mathit{i}}_1,{\mathit{j}}_1)$	$({\mathit{i}}_2,{\mathit{j}}_2)$	${\mathit{r}}^{*}\left(\mathit{S}\right)$	Ranges of ${\Gamma }_{\mathit{p}}\left(\mathit{D}\right)$	Known Exact Values
0.002	5	(8, 10)	(6, 9)	0.610644⋯	[0.5987⋯, 0.6142⋯]	0.609⋯ [4]
0.002	6	(8, 10)	(6, 8)	0.557473⋯	[0.5409⋯, 0.5611⋯]	0.555⋯ [4]
0.002	7	(8, 10)	(6, 8)	0.504028⋯	[0.4895⋯, 0.5076⋯]	0.5 [25]
0.002	8	(8, 10)	(6, 8)	0.447640⋯	[0.4311⋯, 0.4512⋯]	0.445⋯ [25]

4.2. Covering Functionals of the Simplex

The convex hull of $n+1$ affinely independent vectors in ${\mathbb{R}}^n$ is called an n-simplex, which is denoted by $S_n$. Without loss of generality, let

$$S_n={\Delta }_n-\frac{1}{n+1}\sum _{i\in \left[n\right]}{e}_i,$$

where

$${\Delta }_n=\left\{({\alpha }_1,\cdots ,{\alpha }_n)\in {\mathbb{R}}^n\mid {\alpha }_i\ge 0,\forall i\in \left[n\right] \mathrm{and} \sum _{j\in \left[n\right]}{\alpha }_j\le 1\right\}.$$

We denote the i-th coordinate of x in ${\mathbb{R}}^n$ by $p_i\left(x\right)$. Let x and c be two points in ${\mathbb{R}}^n$ and $\gamma \in (0,1)$. By Lemma 3 in [26], it can be proved that $x\in c+\gamma S_n$ if and only if

$$p_i\left(x\right)-p_i\left(c\right)\ge \frac{-\gamma }{n+1},\forall i\in \left[n\right] \mathrm{and} \sum _{j\in \left[n\right]}(p_j\left(x\right)-p_j\left(c\right))\le \frac{\gamma }{n+1}.$$

Therefore, the dissimilarity between a demand point x and a candidate center c is defined as

$$\begin{array}{cc}\hfill d(x,c):& =min\left\{\gamma \ge 0\mid x\in c+\gamma S_n\right\}\hfill \\ \hfill & =min\left\{\gamma \ge 0\mid p_j\left(x\right)-p_j\left(c\right)\ge \frac{-\gamma }{n+1},\forall j\in \left[n\right],\sum _{i\in \left[n\right]}(p_i\left(x\right)-p_i\left(c\right))\le \frac{\gamma }{n+1}\right\}\hfill \\ \hfill & =max\left\{max\left\{(n+1)(p_j\left(c\right)-p_j\left(x\right))\mid j\in \left[n\right]\right\},(n+1)\sum _{i\in \left[n\right]}(p_i\left(x\right)-p_i\left(c\right))\right\}.\hfill \end{array}$$

For each $\delta \in (0,1)$, $K\in {\mathcal{K}}^n$, and $a=({\eta }_1,\cdots ,{\eta }_n)$, where ${\eta }_i=min\left\{p_i\left(x\right)\mid x\in K\right\}$, set

$$K\left(\delta \right)=K\cap (a+\delta ·{\mathbb{Z}}^n).$$

Theorem 4. 

For each $\delta \in (0,1)$ and $\gamma >0$, we have

$$\gamma S_n\subseteq \gamma \left(S_n\left(\delta \right)\right)+(n+1)\delta \gamma S_n.$$

Proof. 

We only need to prove that

$$S_n\subseteq S_n\left(\delta \right)+(n+1)\delta S_n.$$

Clearly,

$$S_n\left(\delta \right)=S_n\cap (-\frac{1}{n+1}\sum _{i\in \left[n\right]}{e}_i+\delta ·{\mathbb{Z}}^n).$$

Let $C={[0,1]}^n$ and $\mathcal{B}=\left\{x+\delta C\mid x\in S_n\left(\delta \right)\right\}$. Then,

$$S_n\subseteq \bigcup _{B\in \mathcal{B}}B.$$

For each $x\in S_n$, there exists $y\in S_n\left(\delta \right)$ such that $x\in B:=y+\delta C$. Let

$$k=\underset{v\in (extB)\cap S_n}{max}\left|\left\{i\in \left[n\right]\mid p_i\left(v\right)=p_i\left(y\right)+\delta \right\}\right|$$

(11)

and $v_1$ be the point in $(extB)\cap S_n$ that corresponds to the maximum value for (11). Hence, $v_1\in S_n\left(\delta \right)$. Moreover,

$$\sum _{i\in \left[n\right]}{p}_i\left(x\right)<\sum _{i\in \left[n\right]}{p}_i\left(y\right)+(k+1)\delta .$$

Otherwise, since $v^{\prime }:=(p_1\left(y\right)+\delta ,\cdots ,p_{k+1}\left(y\right)+\delta ,p_{k+2}\left(y\right),\cdots ,p_n\left(y\right))\in extB$, we have

$$\sum _{i\in \left[n\right]}{p}_i\left(v^{\prime }\right)=\sum _{i\in \left[n\right]}{p}_i\left(y\right)+(k+1)\delta \le \sum _{i\in \left[n\right]}{p}_i\left(x\right)\le \frac{1}{n+1}$$

and

$$p_j\left(v^{\prime }\right)\ge p_j\left(y\right)\ge \frac{-1}{n+1},\forall j\in \left[n\right].$$

Therefore, $v^{\prime }\in S_n$, a contradiction to the choice of k. Since, for each $i\in \left[n\right]$, $p_i\left(x\right)\ge p_i\left(y\right)$, $p_i\left(v_1\right)\le p_i\left(y\right)+\delta$, and ${\displaystyle \sum _{j\in \left[n\right]}}{p}_j\left(v_1\right)={\displaystyle \sum _{j\in \left[n\right]}}{p}_j\left(y\right)+k\delta$, we have

$$\begin{array}{c}{p}_i\left(x\right)-p_i\left(v_1\right)\ge p_i\left(y\right)-(p_i\left(y\right)+\delta )\ge -\delta ,\forall i\in \left[n\right]\end{array}$$

and

$$\sum _{j\in \left[n\right]}(p_j\left(x\right)-p_j\left(v_1\right))\le \sum _{j\in \left[n\right]}{p}_j\left(y\right)+(k+1)\delta -(\sum _{j\in \left[n\right]}{p}_j\left(y\right)+k\delta )=\delta .$$

Hence, $x\in v_1+(n+1)\delta S_n$. Consequently, $S_n\subseteq S_n\left(\delta \right)+(n+1)\delta S_n$. □

Let $C\subseteq {\mathbb{R}}^n$ be a set satisfying $S_n\subseteq C+\gamma S_n$. By Lemma 3 in [26], it can be proved that there exists a set $C^{\prime }\subseteq (1-\gamma )S_n$ such that $\left|C\right|=|C^{\prime }|$ and $S_n\subseteq C^{\prime }+\gamma S_n$. Then, there exists a p-optimal configuration of $S_n$ in $(1-{\Gamma }_p\left(S_n\right))S_n$. It follows that $(1-LB)S_n$ can be seen as $P_{S_n}$ since $o\in int{S}_n$, where $LB$ is a lower bound ${\Gamma }_p\left(S_n\right)$. Let $S=S_n\left({\delta }_1\right)$, $V=(1-LB)\left(S_n\left({\delta }_2\right)\right)$, and $r^{*}\left(S\right)$ be the optimal value obtained by Algorithm 3 of VPCP($S,V,p$). By Theorem 4 and Equation (10),

$$r^{*}\left(S\right)-(n+1)(1-LB){\delta }_2-e\le {\Gamma }_p\left(S_n\right)\le r^{*}\left(S\right)+(n+1){\delta }_1.$$

(12)

Estimations of ${\Gamma }_p\left(S_n\right)$ via our algorithm are summarized in Table 2.

Table 2. Estimations of ${\Gamma }_p\left(S_n\right)$.

n	e	p	$\mathbf{LB}$	${\mathit{\delta }}_1$	${\mathit{\delta }}_2$	${\mathit{r}}^{*}\left(\mathit{S}\right)$	Ranges of ${\Gamma }_{\mathit{p}}\left({\mathit{S}}_{\mathit{n}}\right)$	Known Exact Values or Estimations
3	0.001	4	$0.7$	0.002	0.01	0.75632⋯	[0.7433⋯, 0.7643⋯]	$3/4$ [10]
3	0.001	5	$0.65$	0.002	0.01	0.69241⋯	[0.6774⋯, 0.7004⋯]	$9/13$ [10]
3	0.001	6	$0.65$	0.002	0.01	0.67233⋯	[0.6573⋯, 0.6803⋯]	$2/3$ [26]
3	0.001	7	$0.6$	0.002	0.02	0.64031⋯	[0.6073⋯, 0.6483⋯]	$[0.6,11/17]$ [26]
3	0.001	8	$0.5$	0.002	0.02	0.62040⋯	[0.5794⋯, 0.6284⋯]	≤8/13 [26]
4	0.001	5	$0.75$	0.008	0.04	0.80058⋯	[0.7495⋯, 0.8405⋯]	$0.8$
4	0.001	6	$0.7$	0.008	0.04	0.76012⋯	[0.6991⋯, 0.8001⋯]	$16/21$ [26]

Remark 5. 

Let $\gamma \in (0,1)$ and $P(S_n,\gamma )=S_n\backslash ((1-\gamma )ext{S}_n+\gamma S_n)$. It can be verified that

$$min\gamma ,\beta \le {\Gamma }_{p+n+1}\left(S_n\right)\le max\left\{\gamma ,\beta \right\},$$

where $\beta ={\Gamma }_p(S_n,P(S_n,\gamma ),S_n)$. Consequently, if $\beta =\gamma$, then ${\Gamma }_{p+n+1}\left(S_n\right)=\gamma$. Based on this fact, we can estimate covering functionals of n-simplices by adding a binary search to Algorithm 3. More precisely, we can obtain firstly an estimation ${\beta }^{\prime }$ of ${\Gamma }_p(S_n,P(S_n,\gamma ),S_n)$ by Algorithm 3. Subsequently, update $\gamma$ by $({\beta }^{\prime }+\gamma )/2$ and return to the previous step. This procedure ends when $|{\beta }^{\prime }-\gamma |$ is less than a given positive number $\epsilon$ and an estimation of ${\Gamma }_{p+n+1}\left(S_n\right)$ is obtained. Note that the scale of demand point set involved in the adjusted algorithm is smaller than the one in Algorithm 3.

4.3. Covering Functionals of the Regular Octahedron

Let

$$B_1^n=\left\{x\in {\mathbb{R}}^n\mid \sum _{i\in \left[n\right]}\left|p_i\left(x\right)\right|\le 1\right\}.$$

Thus, $B_1^3$ is a regular octahedron. For a demand point x and a candidate center c, the dissimilarity between x and c is defined as

$$d(x,c)=\sum _{i\in \left[3\right]}\left|p_i\left(x\right)-p_i\left(c\right)\right|.$$

For each $\beta >0$, it is clear that

$$\beta B_1^3\subseteq \left(\beta B_1^3\right)\left(\delta \right)+3\delta B_1^3.$$

(13)

Example 1. 

Let $c=(1/2,-1/2,1/2)$. Then,

$$\left\{(\frac{1}{2},-\frac{1}{2},0),(0,-\frac{1}{2},\frac{1}{2}),(\frac{1}{2},0,\frac{1}{2})\right\}\subseteq (c+\frac{1}{2}{B}_1^3)\cap B_1^3.$$

In the following, we want to find the smallest positive number $\gamma$ and $c^{\prime }\in B_1^3$ satisfying

$$\left\{(\frac{1}{2},-\frac{1}{2},0),(0,-\frac{1}{2},\frac{1}{2}),(\frac{1}{2},0,\frac{1}{2})\right\}\subseteq c^{\prime }+\gamma B_1^3.$$

(14)

The problem can be transformed to the following optimization problem:

$$\begin{array}{}\mathrm{(15a)}& \min \gamma \hfill \mathrm{(15b)}& \mathrm{s}.\mathrm{t}. \sum _{i\in \left[3\right]}|p_i\left(c^{\prime }\right)|\le 1\hfill \mathrm{(15c)}& \hfill \left|p_1\left(c^{\prime }\right)-\frac{1}{2}\right|+\left|p_2\left(c^{\prime }\right)+\frac{1}{2}\right|+|p_3\left(c^{\prime }\right)|-\gamma \le 0\mathrm{(15d)}& \hfill |p_1\left(c^{\prime }\right)|+|p_2\left(c^{\prime }\right)+\frac{1}{2}|+|p_3\left(c^{\prime }\right)-\frac{1}{2}|-\gamma \le 0\mathrm{(15e)}& \hfill \left|p_1\left(c^{\prime }\right)-\frac{1}{2}|+\right|p_2\left(c^{\prime }\right)|+\left|p_3\left(c^{\prime }\right)-\frac{1}{2}\right|-\gamma \le 0\end{array}$$

This problem is solved by Lingo 18.0 and the optimal value is ${\gamma }_{opt}=2/3$. It shows that there exists no point $c^{\prime }\in B_1^3$ such that $(c+(1/2)B_1^3)\cap B_1^3\subseteq c^{\prime }+(1/2)B_1^3$. Therefore, we are not sure whether $B_1^3$ can be chosen as $P_{B_1^3}$ in the same way as simplices.

For $p\in {\mathbb{Z}}^{+}$ and an upper bound $UB$ of ${\Gamma }_p\left(B_1^3\right)$, we use $(1+UB)B_1^3$ as $P_{B_1^3}$. Let $S=B_1^3\left({\delta }_1\right)$ and $V=\left((1+UB)B_1^3\right)\left({\delta }_2\right)$, where ${\delta }_1,{\delta }_2\in (0,1)$. By (10) and (13), we have

$$r^{*}\left(S\right)-3{\delta }_2-e\le {\Gamma }_p\left(B_1^3\right)\le r^{*}\left(S\right)+3{\delta }_1,$$

where $r^{*}\left(S\right)$ is the optimal value obtained by Algorithm 3 of VPCP($S,V,p$). Estimations of ${\Gamma }_p\left(B_1^3\right)$ are summarized in Table 3.

Table 3. The estimation results of ${\Gamma }_p\left(B_1^3\right)$.

e	p	$\mathbf{UB}$	${\mathit{\delta }}_1$	${\mathit{\delta }}_2$	${\mathit{r}}^{*}\left(\mathit{S}\right)$	Ranges of ${\Gamma }_{\mathit{p}}\left({\mathit{B}}_1^3\right)$	Known Exact Values
0.001	6	0.7	0.004	0.025	0.67556⋯	[0.5995⋯, 0.6875⋯]	$2/3$ [10] or [27]
0.001	7	0.7	0.004	0.025	0.67573⋯	[0.5997⋯, 0.6877⋯]	$2/3$ [10] or [27]
0.001	8	0.7	0.004	0.025	0.67555⋯	[0.5995⋯, 0.6875⋯]	$2/3$ [10] or [27]

Remark 6. 

Let $\gamma \in (0,1)$, $c\in {\mathbb{R}}^n$, and $v\in ext{B}_1^n$. We can prove that if $v\in c+\gamma B_1^n$, then

$$(c+\gamma B_1^n)\cap B_1^n\subseteq (1-\gamma )v+\gamma B_1^n.$$

Put $P(B_1^n,\gamma )=B_1^n\backslash ((1-\gamma )ext{B}_1^n+\gamma B_1^n)$. It can be also verified that

$$min\left\{\gamma ,\beta \right\}\le {\Gamma }_{p+n+1}\left(B_1^n\right)\le max\left\{\gamma ,\beta \right\},$$

where $\beta ={\Gamma }_p(B_1^n,P(B_1^n,\gamma ),2B_1^n)$. Consequently, if $\beta =\gamma$, then ${\Gamma }_{p+n+1}\left(B_1^n\right)=\gamma$. Similar to the situation of n-simplices, one can use this observation to reduce the computational complexity.

5. Conclusions

This paper transforms the problem of estimating covering functionals of convex bodies to a VPCP and presents an exact algorithm to obtain an approximate p-optimal configuration and calculate the corresponding covering functional. The theoretical accuracy of our algorithm is given by (10). When the cardinality of the candidate center set is large or the dimension is high, the large-scale VPCP is hard to solve. Future research could be conducted to find better methods to update the subset to reduce the number of iterations. In addition, our algorithm can also be optimized by combining with heuristic algorithms.

Our algorithm can be adjusted to estimate covering functionals of an arbitrary three-dimensional convex polytope. One just needs to measure the dissimilarity with the gauge function (or the Minkowski functional) of a suitable convex polytope containing the origin in its interior. To continue with Chuanming Zong’s program to attack Conjecture 1 in the three-dimensional situation, we need to choose a suitable $\epsilon >0$, to construct an $\epsilon$-net ${\mathcal{N}}_{\epsilon }$ of ${\mathcal{K}}^3$ consisting of convex polytopes, and to show that

$$e^{\epsilon }-1+max\left\{{\Gamma }_8\left(K\right)\mid K\in {\mathcal{N}}_{\epsilon }\right\}<1.$$

In this sense, we are now closer to the complete solution of Conjecture 1 when $n=3$.