Abstract
In both theoretical and applied research, it is often of interest to assess the strength of an observed association. Existing guidelines also frequently recommend going beyond null-hypothesis significance testing and reporting effect sizes and their confidence intervals. As such, measures of effect sizes are increasingly reported, valued, and understood. Beyond their value in shaping the interpretation of the results from a given study, reporting effect sizes is critical for meta-analyses, which rely on their aggregation. We review the most common effect sizes for analyses of categorical variables that use the (chi-square) statistic and introduce a new effect size—פ (Fei, pronounced “fay”). We demonstrate the implementation of these measures and their confidence intervals via the effectsize package in the R programming language.
MSC:
62-01; 62-04; 62-08; 62H17; 62P99
1. Introduction
Over the last two decades, there have been growing concerns about the so-called replication crisis in psychology and other fields [1,2]. As a result, the scientific community has paid increasing attention to the issue of replicability in science as well as to good research and statistical practices.
In this context, many have highlighted the limitations of null-hypothesis significance testing and called for more modern approaches to statistics. One such recommendation, for example, from the “New Statistics” initiative is to report effect sizes and their corresponding confidence intervals and to increasingly rely on meta-analyses to increase confidence in those estimations [3]. These recommendations are meant to complement (or even replace, according to some) null-hypothesis significance testing and would help transition toward a “cumulative quantitative discipline”.
These so-called “New Statistics” are synergistic because effect sizes are not only useful for interpreting study results in themselves but also because they are necessary for meta-analyses, which aggregate effect sizes and their confidence intervals to create a summary effect size of their own [4,5]. (The title of this paper is an allusion to the rhyme spoken by the giant in the English fairy tale Jack and the Beanstalk (“Fee-fi-fo-fum”).)
Unfortunately, popular software applications do not always offer the necessary implementations of the specialized effect sizes necessary for a given research design and their confidence intervals. In this paper, we want to focus on effect sizes for categorical data that are probably less well known than popular effect sizes like Cohen’s d or Pearson’s r [6,7]. For categorical data, d and r are inappropriate measures of an effect size. Cohen’s d refers to the standardized difference between the means of two populations, while Pearson’s correlation coefficient r measures linear correlations. Hence, both measures refer to continuous, not categorical, data.
To compare categorical data, for instance, where associations can be presented as contingency tables, several effect size metrics are available. Common effect sizes for 2-by-2 tables are odds ratios (OR), risk ratios (RR), or the phi () coefficient. While phi can be interpreted similarly to a correlation coefficient, OR and RR are harder to interpret as they are not bounded between zero and one. Furthermore, RR is not symmetrical [8]. The size of the effect can change when columns and rows are exchanged. For tables with larger dimensions than 2-by-2, other effect sizes (like Cramér’s V) are available that share the property of phi of being able to be interpreted like a correlation coefficient and which are discussed later.
The observed distribution of categorical data—usually measured as multinomial variables—can also be compared to an expected distribution. Again, effect sizes to measure the strength of such associations show some limitations regarding ease of interpretation. What is missing here is an effect size whose metric is comparable to those for contingency tables.
This paper aims to review the most commonly used effect sizes for analyses of categorical variables that use the (chi-square) test statistic and introduce a new effect size, פ (Fei, pronounced “fay”), which closes the gap of a missing effect size measure in a correlation-like metric that is appropriate for categorical data.
Importantly, we offer researchers an applied walkthrough on how to use these effect sizes in practice thanks to the effectsize package in the R programming language, which implements these measures and their confidence intervals [9,10]. The presented effectsize package closes another gap related to the aforementioned effect sizes because the uncertainty of such measures—expressed by their confidence intervals—is often not included in the output of statistical software. We cover, in turn, tests of independence (φ/phi, Cramér’s V) and tests of goodness-of-fit (Cohen’s w, Tschuprow’s T, and a new proposed effect size, פ/Fei).
2. Effect Sizes for Tests of Independence
The test of independence between two categorical variables examines if the frequency distribution of one of the variables is dependent on the other. That is, are the two variables correlated such that, for example, members of group 1 on variable X are more likely to be members of group A on variable Y rather than evenly spread across Y variable groups A and B. Formally, the test examines how likely the observed conditional frequencies (cell frequencies) are under the null hypotheses of independence. This is done by examining the degree to which the observed cell frequencies deviate from the frequencies that would be expected if the variables were indeed independent. The test statistic for these tests is the , which is computed as:
where are the observed frequencies and are the frequencies expected under independence, and and are the number of rows and columns, respectively, in the contingency table.
Instead of the deviations between the observed and expected frequencies, we can write in terms of observed and expected cell probabilities and the total sample size (since ):
where are the observed cell probabilities and the probabilities expected under independence.
Table 1 gives a short example in R to demonstrate whether the probability of survival is dependent on the sex of the passenger aboard the Titanic. The null hypothesis tested here is that the probability of survival is independent of the passenger’s sex.

Table 1.
test of survival of Titanic passengers by sex, Titanic dataset from R.
The performed -test is statistically significant. Thus, we can reject the hypothesis of independence. However, the output includes no effect size, and we cannot conclude the strength of the association between sex and survival.
2.1. Phi
For a 2-by-2 contingency table analysis, as the one used above, the (phi) coefficient is a correlation-like measure of effect size indicating the strength of association between the two binary variables. One possibility to compute this effect size is to recode the binary variables as dummy (“0” and “1”) variables and compute the Pearson correlation between them [11]:
Another way to compute is by using the statistic:
This value ranges between 0 (no association) and 1 (complete dependence), and its values can be interpreted the same as Pearson’s correlation coefficient. Table 2 shows the correlation coefficient and the effect size for the data shown in Table 1.

Table 2.
Correlation and effect size (phi) for the survival of Titanic passengers by sex, Titanic dataset from R.
Note that cannot be negative, so we will take the absolute value of Pearson’s correlation coefficient. Also note that the effectsize package gives a one-sided confidence interval by default, to match the positive direction of the associated test at (that the association is larger than zero at a 95% confidence level).
2.2. Cramér’s V (and Tschuprow’s T)
When the contingency table is larger than 2-by-2, using can produce values larger than 1, which loses its interpretability as a correlation-like effect size. Cramér showed that while for 2-by-2 the maximal possible value of is , for larger tables the maximal possible value for is [12]. Therefore, he suggested the effect size (also sometimes known as Cramér’s phi and denoted as ):
where is 1 when the columns are completely dependent on the rows or the rows are completely dependent on the columns (and 0 when rows and columns are completely independent).
Table 3 gives a short example in R to demonstrate whether the probability of survival is dependent on the person’s travel class or position aboard the Titanic. The null hypothesis tested here is that the probability of survival is independent of the travel class or position.

Table 3.
Effect size Cramér’s V for the survival of Titanic passengers by class/position, Titanic dataset from R.
Tschuprow devised an alternative value, at
which is 1 only when the columns are completely dependent on the rows and the rows are completely dependent on the columns, which is only possible when the contingency table is a square [13].
For example, in Table 4, each row is dependent on the column value; that is, if we know if the food is a soy, milk, or meat product, we also know whether the food is vegan or not. However, the columns are not fully dependent on the rows: knowing the food is vegan tells us the food is soy-based; however, knowing it is not vegan does not allow us to classify the food—it can be either a milk product or a meat product.

Table 4.
Cramér’s V and Tschuprow’s T for food classes, example dataset from R.
We can generalize , , and to: . That is, they express the square root of a proportion of the sample- to the maximum possible given the study design.
These coefficients can also be used for confusion matrices, which are 2-by-2 contingency tables used to assess machine learning algorithms’ classification abilities by comparing true outcome classes with the model-predicted outcome class. A popular metric is the Matthews correlation coefficient (MCC) for binary classifiers, which is often presented in terms of true and false positives and negatives but is nothing more than [14].
3. Effect Sizes for the Goodness-of-Fit Tests
These tests compare the observed distribution of a multinomial variable to the expected distribution using the same statistic. Here, in addition, we can compute an effect size as ; all we need to find is .
3.1. Cohen’s w
Cohen defined an effect size—w—for the goodness-of-fit test [7]:
Thus, .
Unfortunately, w has an upper bound of 1 only when the variable is binomial (has two categories) and the expected distribution is uniform (). When the distribution is non-uniform or if there are more than two classes, then , and so w can be larger than 1 [15,16]. Examples are shown in Table 5.

Table 5.
Effect size Cohen’s w for variables with different numbers of categories and distributions.
Although Cohen suggested that w can also be used for such designs, we believe that this hinders the interpretation of w since it can be arbitrarily large [7].
3.2. Fei
We present here a new effect size, פ (Fei, pronounced “fay”), which normalizes goodness-of-fit by the proper for non-uniform and/or multinomial variables.
The largest deviation from the expected probability distribution would occur when all observations are in the cell with the smallest expected probability. That is:
We can find for each of these values:
Therefore,
So,
Finally, an effect size can be derived as:
We call this effect size פ (Fei), which represents the voiceless bilabial fricative in Hebrew, keeping in line with (which in modern Greek marks the same sound) and (which in English marks a voiced bilabial fricative; being derived from the letter V in the modern Latin alphabet). פ will be 0 when the observed distribution perfectly matches the one expected (under the null hypothesis) and will be 1 when the sample contains only one class of observations—the one with the smallest expected probability (under the null hypothesis). That is, פ is 1 (its maximal value) only when we observe only the least expected class. When there are only two cells with uniform expected probabilities (50%), the expression reduces to and so פ . Table 6 shows the effect size Fei for the same vectors and distributions as seen for Cohen’s w in Table 5. As can be seen, unlike Cohen’s w, all effect size values of Fei (and their confidence intervals) are within the range from 0 to 1. (See Section 6 below for how to type the פ symbol on various computer systems.)

Table 6.
Effect size Fei for variables with different numbers of categories and distributions.
The computation of פ (Fei) can be achieved with the Fei() function of the effectsize package—fei(c(90, 10), p = c(0.35, 0.65)). This function here computes confidence intervals using the non-centrality parameter method (also called the “pivot method”) by finding values for the non-centrality parameter (“ncp”) of a noncentral distribution that place the observed test statistic at the desired probability point of the distribution (e.g., p = 0.025 and p = 0.975 for a two-sided 95% confidence interval). The two ncps (for the lower and upper bounds) are then converted back to פ using the same scale-and-root formula as with the sample :
where and are the non-centrality parameters corresponding to the desired tail probabilities, and and are the bounds of the confidence intervals for פ (Fei) (See also the next section).
4. Simulation Study of the Distributional Form of the Fei Effect Size
In the previous section, we showed some results for the effect size פ (Fei) and its confidence intervals for different distributions of a multinomial variable. Like all effect sizes discussed in this paper, פ follows a scaled non-central distribution: the statistic follows a non-central distribution, and its square root follows a non-central distribution; this random variable is then scaled by a constant that is a function of the sample size and the study design. The noncentrality parameter of the non-central distribution can be found by applying the inverse of the scale to the population effect size. Therefore,
where is the inverse of the to פ conversion:
פ is the population effect size, k is the number of classes, and is the random variable of possible observed effect sizes in a random sample. This can also be formulated in terms of a non-central distribution:
where is the inverse of the to פ conversion:
To validate our assumptions, we conducted a simulation study, where we simulated data of multinomial distributions for known true effect sizes of 0.1, 0.3, and 0.5, respectively. The datasets contained 500 simulations per effect size, for three different expected probabilities (same as in Table 6), and 3 different sample sizes of 50, 100, and 350, resulting in 13,500 simulated data points (500 simulations × 3 effect sizes × 3 expected probabilities × 3 different sample sizes). Figure 1 shows the results from the simulation study.
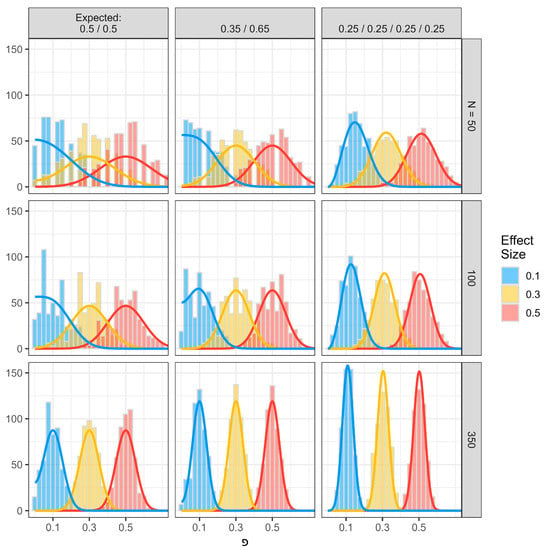
Figure 1.
Comparison of true and simulation-based actual effect size פ (Fei) for different expected proportions, true effect sizes, and sample sizes. Histograms represent the distributions of the sample פ’s from the simulated datasets, and the plotted lines represent density functions for (scaled) non-central distributions for the corresponding effect sizes and sample sizes.
The smallest sample size is more affected by noise, and results show more variation (and less continuity) of simulation-based פ (Fei) values around the true effect sizes. For sample sizes N = 100 and N = 350, פ values closely replicate the true effect sizes and clearly follow a non-central distribution, indicating that Fei, like , V, T, and w, is a scaled value.
פ (Fei) following a non-central distribution also allows for power calculation. For example, if the null probabilities are [0.35, 0.65] and the alternative probabilities are [0.545, 0.455], the scaling constant is:
and the population effect size is
Therefore, the sample פ will follow the following distribution:
One must then find the N that produces the desired power for the significance level that will be used to reject the null. For example, for a significant level of 0.01 and a power of at least 0.85, an N of at least 78 is required.
The pwr package in R provides a function (pwr.chisq.test()) that can be used to calculate the power for goodness-of-fit tests. Although the function uses Cohen’s w as input/output, פ can easily be converted to Cohen’s w (e.g., by using the fei_to_w() function from effectsize), allowing for the pwr function to be used with פ. An example can be found in the accompanying R code.
5. Conclusions
Effect sizes are essential to interpreting the magnitude of observed effects; they are frequently required in scientific journals; and they are necessary for a cumulative quantitative science relying on meta-analyses. In this paper, we have covered the mathematics and implementation in R of four different effect sizes for analyses of categorical variables that specifically use the (chi-square) statistic. Furthermore, with our proposal of the effect size פ (Fei), we fill in the missing effect size for all cases of a test, as can be seen in Table 7.

Table 7.
Effect size for tests for differently sized contingency tables.
Thus, we now have effect sizes to accompany any sized 1-dimensional or 2-dimensional contingency tables that represent the sample’s relative to the maximally possible , ranging from 0 to 1, that can be easily interpreted on the scale of a correlation coefficient.
6. How to Type the פ Symbol
The Hebrew character can be inserted into documents via several methods:
- By copying the character from https://util.unicode.org/UnicodeJsps/character.jsp?a=05E4 (access date: 9 March 2023) or similar webpages.
- In R, by typing the string “\u05e4”.
- In LaTeX, by typing \char”05e4 and using a Unicode-compatible compiler, such as XeTeX or LuaLaTeX.
- In Microsoft Word, from the Hebrew character of the Symbols window (Insert → Symbol…) or by typing 05e4, followed by Alt + X on the keyboard (Windows only).
- On Windows, using the Character Map application or by holding down Alt and typing +1508 on the numeric keypad.
- On macOS, by enabling the Unicode Hex Input language from System Settings… → Keyboard, then typing Opt + 05e4.
Author Contributions
M.S.B.-S. conceptualized and developed the Fei effect size and its implementation in effectsize, conducted the simulation study, and drafted the paper; D.L. prepared the revised manuscript; I.P., R.T., B.M.W. and D.L. contributed to both the writing of the paper and the conception of the software. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The R code to reproduce the results from the tables and the simulation study in this article can be downloaded at https://osf.io/cg64s/ (doi: 10.17605/osf.io/cg64s).
Acknowledgments
The {effectsize} package is part of the collaborative R easystats ecosystem. Thus, we thank all members of easystats, contributors, and users alike.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Open Science Collaboration. Estimating the Reproducibility of Psychological Science. Science 2015, 349, aac4716. [Google Scholar] [CrossRef] [PubMed]
- Camerer, C.F.; Dreber, A.; Holzmeister, F.; Ho, T.-H.; Huber, J.; Johannesson, M.; Kirchler, M.; Nave, G.; Nosek, B.A.; Pfeiffer, T.; et al. Evaluating the Replicability of Social Science Experiments in Nature and Science between 2010 and 2015. Nat. Hum. Behav. 2018, 2, 637–644. [Google Scholar] [CrossRef] [PubMed]
- Cumming, G. The New Statistics: Why and How. Psychol. Sci. 2014, 25, 7–29. [Google Scholar] [CrossRef] [PubMed]
- Wiernik, B.M.; Dahlke, J.A. Obtaining Unbiased Results in Meta-Analysis: The Importance of Correcting for Statistical Artifacts. Adv. Methods Pract. Psychol. Sci. 2020, 3, 94–123. [Google Scholar] [CrossRef]
- DeGeest, D.S.; Schmidt, F.L. The Impact of Research Synthesis Methods on Industrial-Organizational Psychology: The Road from Pessimism to Optimism about Cumulative Knowledge. Res. Synth. Methods 2010, 1, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K., VII. Note on Regression and Inheritance in the Case of Two Parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: Oxfordshire, UK, 1988; ISBN 978-0-203-77158-7. [Google Scholar]
- Cummings, P. The Relative Merits of Risk Ratios and Odds Ratios. Arch. Pediatr. Adolesc. Med. 2009, 163, 438. [Google Scholar] [CrossRef] [PubMed]
- Ben-Shachar, M.; Lüdecke, D.; Makowski, D. Effectsize: Estimation of Effect Size Indices and Standardized Parameters. J. Open Source Softw. 2020, 5, 2815. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Olvera Astivia, O.L. The Relationship between the Phi Coefficient and the Chi-Square Test of Association. Psychometroscar 2022. Available online: https://psychometroscar.com/2022/04/21/the-relationship-between-the-phi-coefficient-and-the-chi-square-test-of-association/ (accessed on 9 March 2023).
- Cramér, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1999; ISBN 978-0-691-00547-8. [Google Scholar]
- Tschuprow, A.A. Principles of the Mathematical Theory of Correlation; W. Hodge, Limited: London, UK, 1939. [Google Scholar]
- Chicco, D.; Jurman, G. The Advantages of the Matthews Correlation Coefficient (MCC) over F1 Score and Accuracy in Binary Classification Evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, M.S. A Generalized Formula for Converting Chi-Square Tests to Effect Sizes for Meta-Analysis. PLoS ONE 2010, 5, e10059. [Google Scholar] [CrossRef] [PubMed]
- Johnston, J.E.; Berry, K.J.; Mielke, P.W. Measures of Effect Size for Chi-Squared and Likelihood-Ratio Goodness-of-Fit Tests. Percept. Mot. Skills 2006, 103, 412–414. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).