CPPE: An Improved Phasmatodea Population Evolution Algorithm with Chaotic Maps
Abstract
1. Introduction
- We combine chaos theory with the PPE algorithm for the first time to propose a new Chaotic-based PPE algorithm called CPPE.
- We select 12 different chaotic maps and 28 popular benchmark functions to evaluate the performance of the proposed CPPE algorithm. The experimental results demonstrate that the performance and convergence of CPPE are greatly enhanced.
2. Related Work
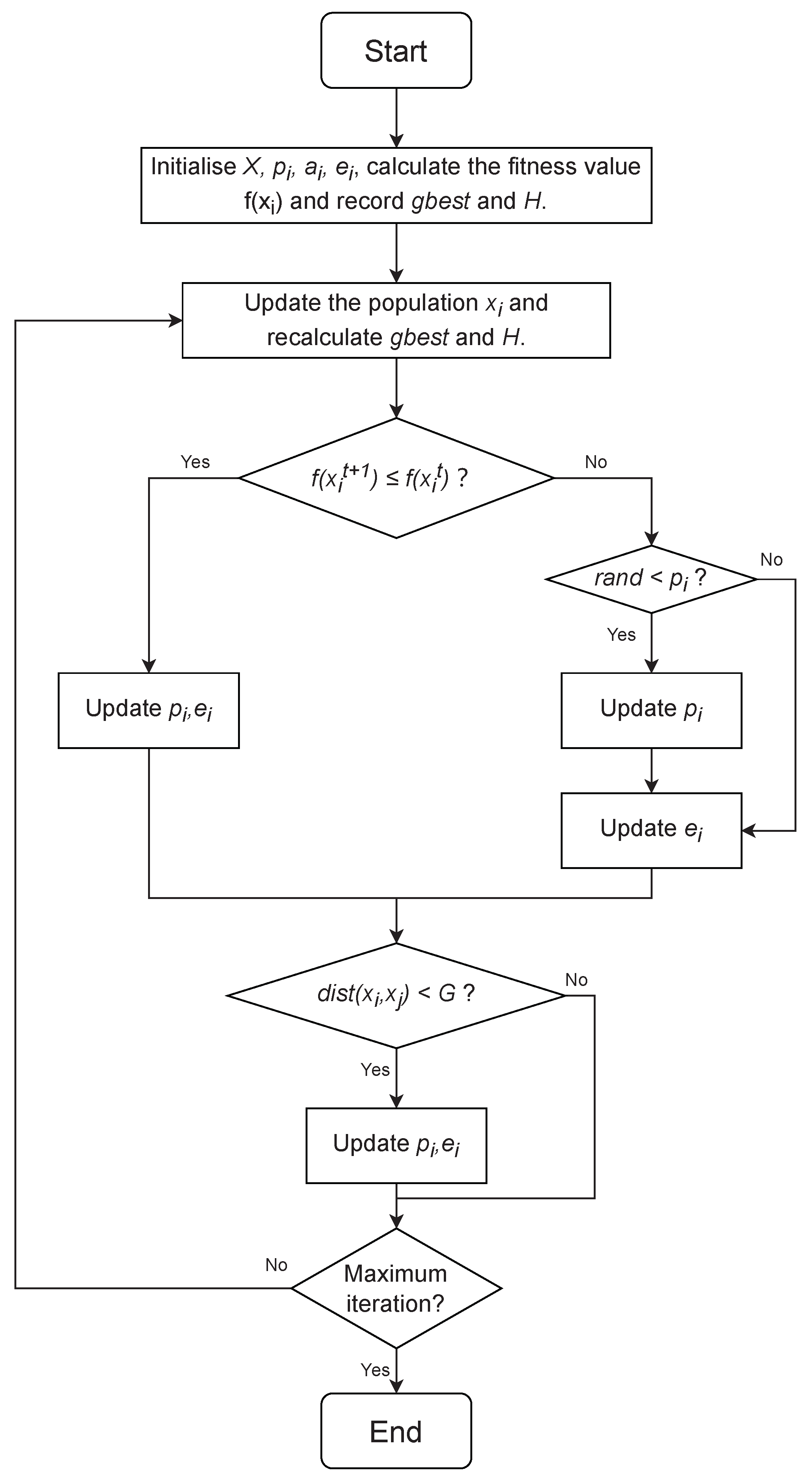
3. Chaotic-Based Phasmatodea Population Evolution (CPPE) Algorithm
3.1. Phasmatodea Population Evolution (PPE) Algorithm
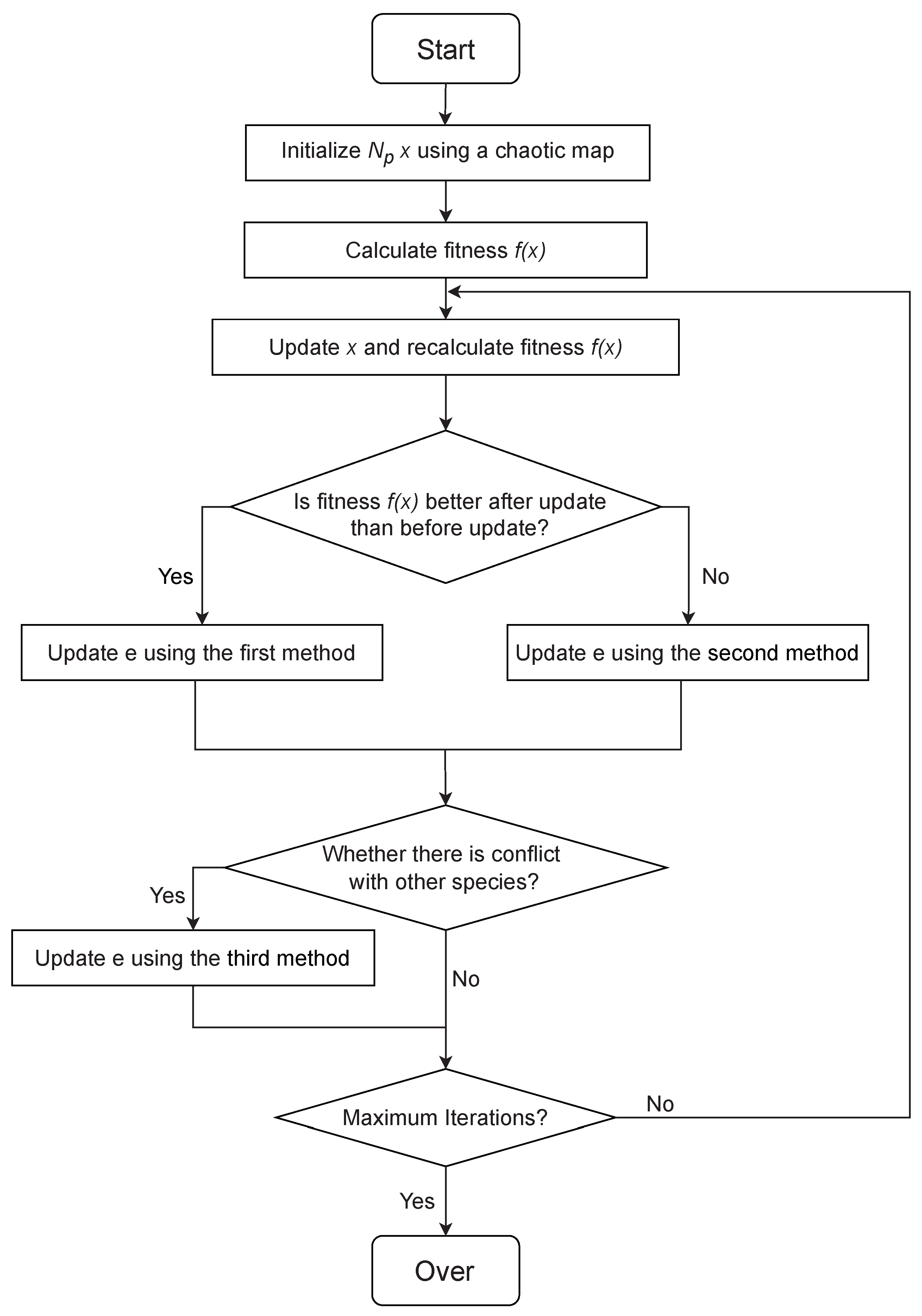
3.2. The Proposed CPPE Algorithm
- Initialize a matrix Z with dimension , where all elements are zero, that is,Z = , ;
- Using the method to randomly generate a vector, and replace the vector in the first row of the matrix Z;
- Traversing the second to -th rows of the matrix Z, and using the chaotic map to generate vectors, each of which is ;
- Traversing the first to -th rows of the matrix Z, and mapping each element to the interval. The mapping formula is Equation (8), where represents an element in the matrix Z.
- Use the chaotic map to initialize the matrix, in which each element represents a population, and initialize the two attributes and of the population. Initialize the evolution trend is set 0. Calculate the fitness value, and use to represent the global optimal solution, and use H to store k historical global optimal solutions;
- Entering the iterative process, update each population, recalculate the fitness value, and update and H;
- For the updated fitness value, if , then update and use the first method to update , if , and, then, judge the first. The value generated by the method is compared with . If it is less than , the population size needs to be updated, otherwise it need not be updated. Then use the second method to update ;
- Use the distance between and to compare with the threshold G. If it is less than G, this confirms that there is competition between the two populations, and the third method is used to update ;
- Determine whether the maximum number of iterations has been achieved. If the maximum number of iterations is not reached, proceed to step 2 and repeat the process until the maximum number is attained.
| Algorithm 1: Pseudo-code of the CPPE algorithm. |
| Initialize populations using a chaotic map; Initialize , , ; Initialize ; Calculate fitness , set and H;  |
4. Experimental Results and Discussions
4.1. Benchmark Functions and Experimental Environments
4.2. Performance Comparison between PPE and CPPEs
4.3. Convergence Comparison between PPE and CPPEs
4.4. Discussions
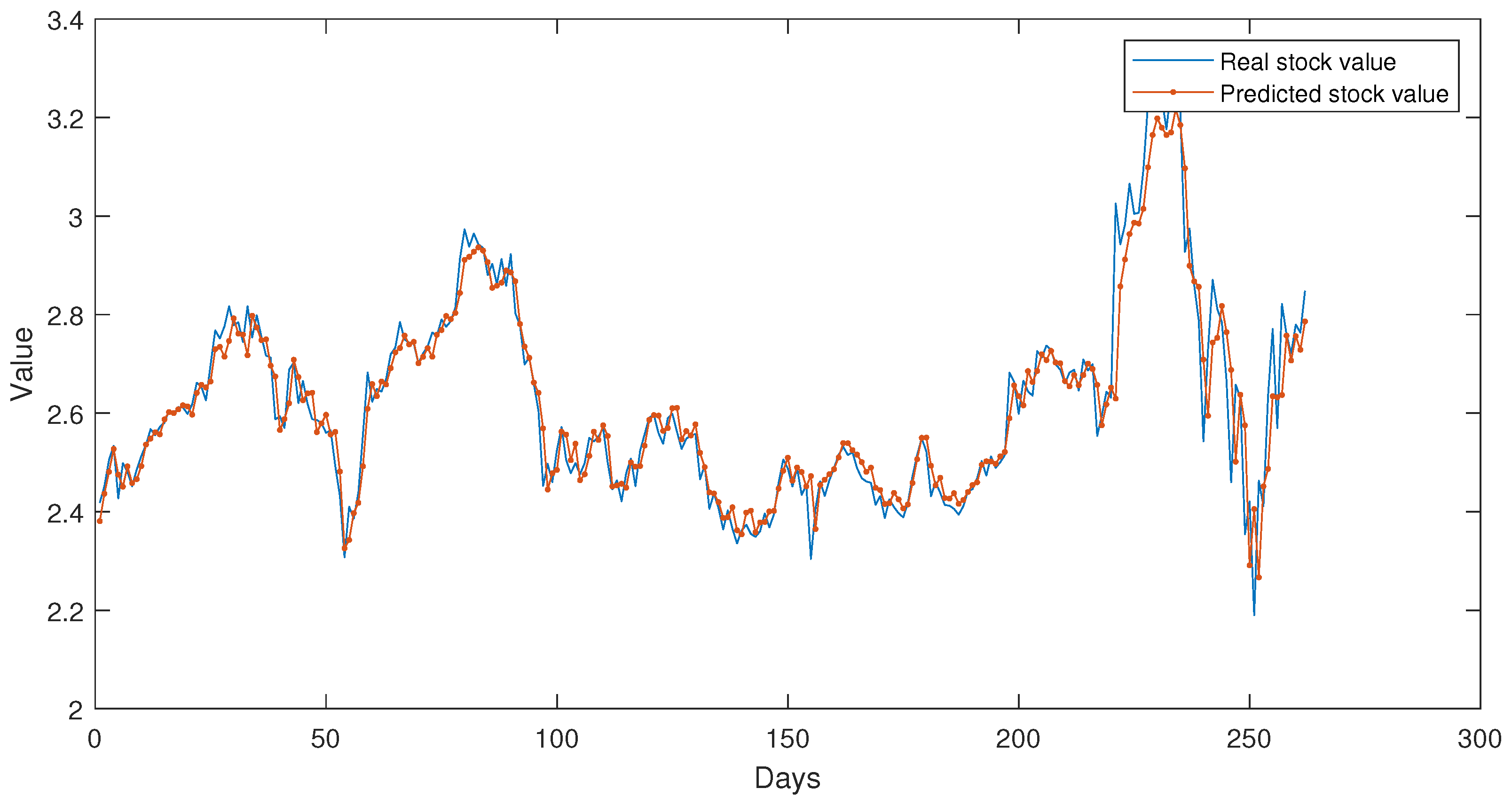
4.5. Real-Life Problem: Stock Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPE | Phasmatodea Population Evolution |
| CPPE | Chaotic-based Phasmatodea Population Evolution |
| GA | Generic Algorithm |
| DE | Differential Evolution |
| PSO | Particle Swarm Optimization |
| WOA | Whale Optimization Algorithm |
| BOA | Butterfly Optimization Algorithm |
| GOA | Grasshopper Optimization Algorithm |
| CMBSA | Bird Swarm Algorithm with Chaotic Mapping |
| BSA | Bird Swarm Algorithm |
| SSA | Sparrow Search Algorithm |
| CLS | Chaotic Local Search |
| GWO | Gray Wolf Optimization |
| CHHO | Chaotic Harris Hawks Optimization |
| HHO | Harris Hawks Optimization |
| CQFFA | Chaotic Quasi-oppositional Farmland Fertility Algorithm |
| CSBOA | Chaotic Satin Bowerbird Optimization Algorithm |
| CSGO | Chaotic Social Group Optimization |
| SGO | Social Group Optimization |
| MPPE | Multigroup-based Phasmatodea Population Evolution Algorithm with Multistrategy |
| APPE | Advanced Phasmatodea Population Evolution Algorithm |
References
- Wu, T.Y.; Lin, J.C.W.; Zhang, Y.; Chen, C.H. A grid-based swarm intelligence algorithm for privacy-preserving data mining. Appl. Sci. 2019, 9, 774. [Google Scholar] [CrossRef]
- Kang, L.; Chen, R.S.; Chen, Y.C.; Wang, C.C.; Li, X.; Wu, T.Y. Using cache optimization method to reduce network traffic in communication systems based on cloud computing. IEEE Access 2019, 7, 124397–124409. [Google Scholar] [CrossRef]
- Leardi, R. Application of genetic algorithm–PLS for feature selection in spectral data sets. J. Chemom. 2000, 14, 643–655. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Poursamad, A.; Ghalichi, B. Application of genetic algorithm for optimization of control strategy in parallel hybrid electric vehicles. J. Frankl. Inst. 2006, 343, 420–435. [Google Scholar] [CrossRef]
- Baldo, A.; Boffa, M.; Cascioli, L.; Fadda, E.; Lanza, C.; Ravera, A. The polynomial robust knapsack problem. Eur. J. Oper. Res. 2023, 305, 1424–1434. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, T.Y.; Wang, Y.; Xiong, R.; Ding, G.; Mei, P.; Liu, L. Application of quantum genetic optimization of LVQ neural network in smart city traffic network prediction. IEEE Access 2020, 8, 104555–104564. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Saravanan, M.; Slochanal, S.M.R.; Venkatesh, P.; Abraham, P.S. Application of PSO technique for optimal location of FACTS devices considering system loadability and cost of installation. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; pp. 716–721. [Google Scholar]
- Assareh, E.; Behrang, M.; Assari, M.; Ghanbarzadeh, A. Application of PSO (particle swarm optimization) and GA (genetic algorithm) techniques on demand estimation of oil in Iran. Energy 2010, 35, 5223–5229. [Google Scholar] [CrossRef]
- Meng, F.Q.; Wei, S.; Wang, J.D.; Wang, P.F.; Li, B. An Information Feedback-based Particle Swarm Optimization Algorithm for Multi-regional Image Segmentation. J. Netw. Intell. 2023, 8, 194–210. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Saremi, S.; Mirjalili, S. Whale optimization algorithm: Theory, literature review, and application in designing photonic crystal filters. Nat.-Inspired Optim. 2020, 811, 219–238. [Google Scholar]
- Liu, X.K.; Li, P.Q.; Zhang, Z.K.; Zen, J.J. Location and Capacity Determination of Energy Storage System Based on Improved Whale Optimization Algorithm. J. Netw. Intell. 2023, 8, 35–46. [Google Scholar]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Rezaee Jordehi, A. A chaotic artificial immune system optimisation algorithm for solving global continuous optimisation problems. Neural Comput. Appl. 2015, 26, 827–833. [Google Scholar] [CrossRef]
- Chen, C.M.; Hao, Y.; Wu, T.Y. Discussion of “Ultra Super Fast Authentication Protocol for Electric Vehicle Charging Using Extended Chaotic Maps”. IEEE Trans. Ind. Appl. 2023, 59, 2091–2092. [Google Scholar] [CrossRef]
- Gao, J.M.L.Y.L. Chaos particle swarm optimization algorithm. J. Comput. Appl. 2008, 28, 322. [Google Scholar]
- Talatahari, S.; Azar, B.F.; Sheikholeslami, R.; Gandomi, A. Imperialist competitive algorithm combined with chaos for global optimization. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1312–1319. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Talatahari, S.; Alavi, A.H. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 89–98. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Ozsoydan, F.B. Adaptive firefly algorithm with chaos for mechanical design optimization problems. Appl. Soft Comput. 2015, 36, 152–164. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S. Chaotic bat algorithm. J. Comput. Sci. 2014, 5, 224–232. [Google Scholar] [CrossRef]
- Snaselova, P.; Zboril, F. Genetic algorithm using theory of chaos. Procedia Comput. Sci. 2015, 51, 316–325. [Google Scholar] [CrossRef]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Sayed, G.I.; Tharwat, A.; Hassanien, A.E. Chaotic dragonfly algorithm: An improved metaheuristic algorithm for feature selection. Appl. Intell. 2019, 49, 188–205. [Google Scholar] [CrossRef]
- Arora, S.; Anand, P. Chaotic grasshopper optimization algorithm for global optimization. Neural Comput. Appl. 2019, 31, 4385–4405. [Google Scholar] [CrossRef]
- Varol Altay, E.; Alatas, B. Bird swarm algorithms with chaotic mapping. Artif. Intell. Rev. 2020, 53, 1373–1414. [Google Scholar] [CrossRef]
- Li, M.W.; Wang, Y.T.; Geng, J.; Hong, W.C. Chaos cloud quantum bat hybrid optimization algorithm. Nonlinear Dyn. 2021, 103, 1167–1193. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S. A stochastic configuration network based on chaotic sparrow search algorithm. Knowl.-Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, H.; Li, J.; Zhang, X.; Lu, B.; Gao, S. Comparative Study on Single and Multiple Chaotic Maps Incorporated Grey Wolf Optimization Algorithms. IEEE Access 2021, 9, 77416–77437. [Google Scholar] [CrossRef]
- Hao, P.; Sobhani, B. Application of the improved chaotic grey wolf optimization algorithm as a novel and efficient method for parameter estimation of solid oxide fuel cells model. Int. J. Hydrog. Energy 2021, 46, 36454–36465. [Google Scholar] [CrossRef]
- Song, P.C.; Chu, S.C.; Pan, J.S.; Yang, H. Phasmatodea population evolution algorithm and its application in length-changeable incremental extreme learning machine. In Proceedings of the 2020 2nd international conference on industrial artificial intelligence (IAI), Shenyang, China, 23–25 October 2020; pp. 1–5. [Google Scholar]
- Song, P.C.; Chu, S.C.; Pan, J.S.; Yang, H. Simplified Phasmatodea population evolution algorithm for optimization. Complex Intell. Syst. 2022, 8, 2749–2767. [Google Scholar] [CrossRef]
- Gezici, H.; Livatyalı, H. Chaotic Harris hawks optimization algorithm. J. Comput. Des. Eng. 2022, 9, 216–245. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Nadimi-Shahraki, M.H.; Barshandeh, S.; Abdollahzadeh, B.; Zamani, H. CQFFA: A Chaotic Quasi-oppositional Farmland Fertility Algorithm for Solving Engineering Optimization Problems. J. Bionic Eng. 2022, 20, 158–183. [Google Scholar] [CrossRef]
- Chen, X.; Cao, B.; Pouramini, S. Energy cost and consumption reduction of an office building by Chaotic Satin Bowerbird Optimization Algorithm with model predictive control and artificial neural network: A case study. Energy 2023, 270, 126874. [Google Scholar] [CrossRef]
- Naik, A. Chaotic Social Group Optimization for Structural Engineering Design Problems. J. Bionic Eng. 2023. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, F.; Pan, J.S.; Yu, L.; Bai, Y.; Wang, W.; He, C.; Shi, Z. Mutigroup-based phasmatodea population evolution algorithm with mutistrategy for iot electric bus scheduling. Wirel. Commun. Mob. Comput. 2022, 2022, 1500646. [Google Scholar] [CrossRef]
- Zhuang, J.; Chu, S.C.; Hu, C.C.; Liao, L.; Pan, J.S. Advanced Phasmatodea Population Evolution Algorithm for Capacitated Vehicle Routing Problem. J. Adv. Transp. 2022, 2022. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Seyedzadeh, S.M.; Mirzakuchaki, S. A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map. Signal Process. 2012, 92, 1202–1215. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Oliva, D.; Ewees, A.A.; Lu, S. Feature selection based on improved runner-root algorithm using chaotic singer map and opposition-based learning. In Proceedings of the Neural Information Processing: 24th International Conference, ICONIP 2017, Guangzhou, China, 14–18 November 2017; Proceedings, Part V 24. Springer: Cham, Switzerland, 2017; pp. 156–166. [Google Scholar]
- Belazi, A.; Abd El-Latif, A.A. A simple yet efficient S-box method based on chaotic sine map. Optik 2017, 130, 1438–1444. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Chikushi, R.T.M.; de Barros, R.S.M.; da Silva, M.G.N.M.; Maciel, B.I.F. Using spectral entropy and bernoulli map to handle concept drift. Expert Syst. Appl. 2021, 167, 114114. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Image encryption using Chebyshev map and rotation equation. Entropy 2015, 17, 2117–2139. [Google Scholar] [CrossRef]
- Mennis, J.; Viger, R.; Tomlin, C.D. Cubic map algebra functions for spatio-temporal analysis. Cartogr. Geogr. Inf. Sci. 2005, 32, 17–32. [Google Scholar] [CrossRef]
- Jiteurtragool, N.; Ketthong, P.; Wannaboon, C.; San-Um, W. A topologically simple keyed hash function based on circular chaotic sinusoidal map network. In Proceedings of the 2013 15th International Conference on Advanced Communications Technology (ICACT), Pyeongchang, Republic of Korea, 27–30 January 2013; pp. 1089–1094. [Google Scholar]
- Liu, W.; Sun, K.; He, Y.; Yu, M. Color image encryption using three-dimensional sine ICMIC modulation map and DNA sequence operations. Int. J. Bifurc. Chaos 2017, 27, 1750171. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.; Suganthan, P.N.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2013; Volume 201212, pp. 281–295. [Google Scholar]
- Huang, R.; Wei, C.; Wang, B.; Yang, J.; Xu, X.; Wu, S.; Huang, S. Well performance prediction based on Long Short-Term Memory (LSTM) neural network. J. Pet. Sci. Eng. 2022, 208, 109686. [Google Scholar] [CrossRef]
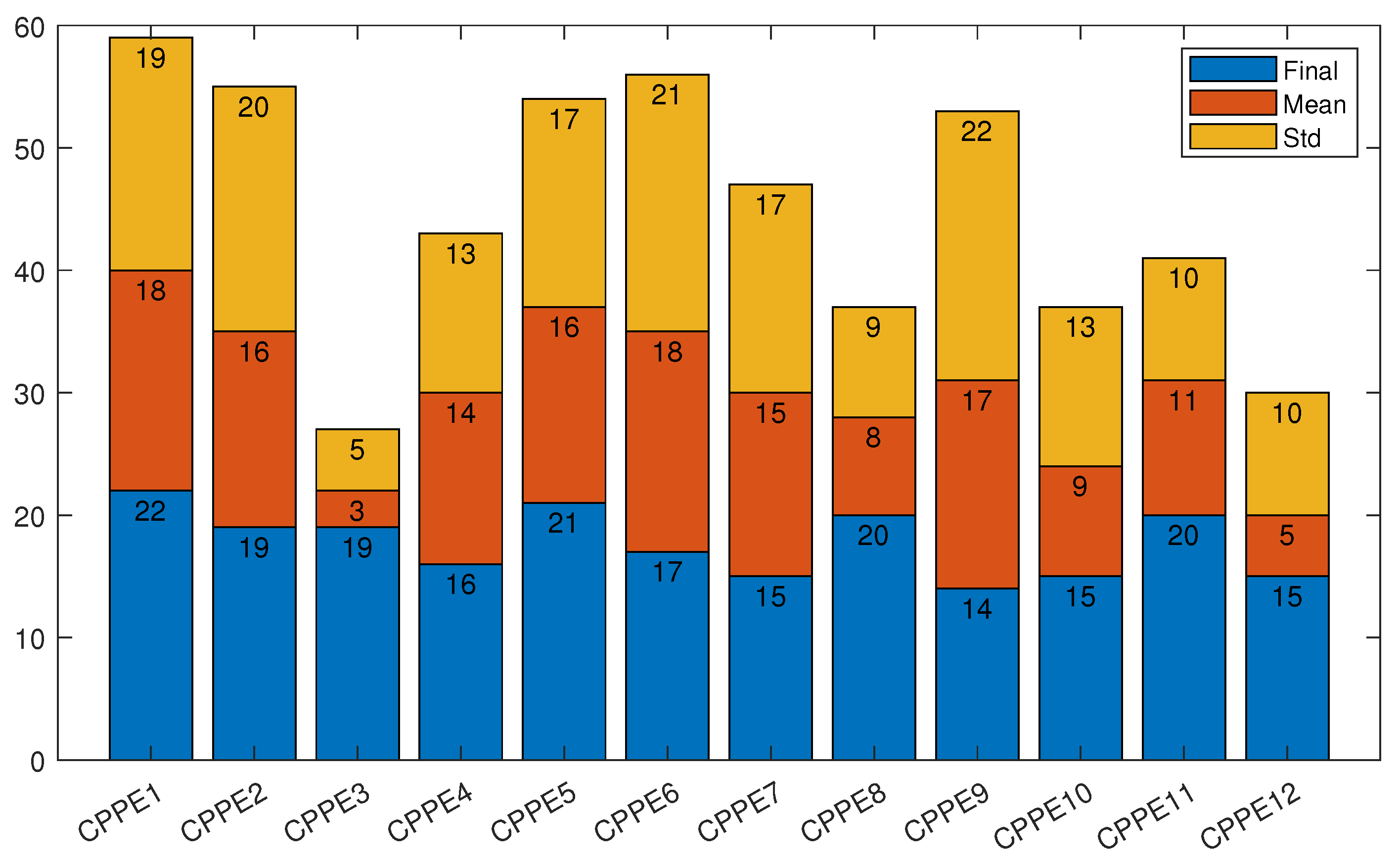
| Symbols | Interpretation of Symbols |
|---|---|
| The total population size | |
| d | The dimensionality |
| i-th population | |
| The size of | |
| The growth rate of | |
| The evolution trend of | |
| The fitness value of | |
| m | Mutation factor |
| A method to generate random numbers in the range (0, 1) | |
| Impact factor | |
| U, L | The upper and lower bounds |
| Total iterations | |
| t | Current iteration count |
| Symbols | Explains |
|---|---|
| CPPE1 | PPE + Logistic map [39] |
| CPPE2 | PPE + Piecewise map [40] |
| CPPE3 | PPE + Singer map [41] |
| CPPE4 | PPE + Sine map [42] |
| CPPE5 | PPE + Gauss map [19] |
| CPPE6 | PPE + Tent map [43] |
| CPPE7 | PPE + Bernoulli map [44] |
| CPPE8 | PPE + Chebyshev map [45] |
| CPPE9 | PPE + Circle map [23] |
| CPPE10 | PPE + Cubic map [46] |
| CPPE11 | PPE + Sinusoidal map [47] |
| CPPE12 | PPE + ICMIC map [48] |
| Benchmark Function | Dimension | Optimal |
|---|---|---|
| 10 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 5 | 0 | |
| 5 | 0 | |
| 5 | 0 | |
| 2 | 0 | |
| 10 | 0 | |
| 10 | 0 | |
| 5 | 0 | |
| 5 | 0 | |
| 5 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 10 | 0 | |
| 5 | 0 | |
| 5 | 0 | |
| 10 | 0 | |
| 10 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 | |
| 2 | 0 |
| Parameters | Values |
|---|---|
| Population_Number | 100 |
| Max_Gen | 100 |
| Run_Nums | 50 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 9.99E-02 | 3.89E-01 | 2.94E-01 | PPE | 2.33E-02 | 5.66E+01 | 1.11E+02 | PPE | 5.88E-03 | 4.08E+00 | 1.29E+01 |
| CPPE1 | 5.18E-02 | 2.64E-01 | 1.43E-01 | CPPE1 | 1.26E-02 | 1.68E+02 | 3.28E+02 | CPPE1 | 3.05E-03 | 2.69E+00 | 5.81E+00 |
| CPPE2 | 6.39E-02 | 3.29E-01 | 2.40E-01 | CPPE2 | 3.10E-02 | 1.11E+02 | 2.08E+02 | CPPE2 | 1.78E-02 | 2.95E+00 | 4.41E+00 |
| CPPE3 | 6.39E-02 | 7.41E-01 | 3.97E-01 | CPPE3 | 3.10E-02 | 3.47E+02 | 5.46E+02 | CPPE3 | 1.78E-02 | 1.36E+00 | 2.61E+00 |
| CPPE4 | 4.41E-02 | 3.36E-01 | 2.05E-01 | CPPE4 | 5.47E-03 | 1.17E+02 | 2.76E+02 | CPPE4 | 1.10E-02 | 4.52E+00 | 7.25E+00 |
| CPPE5 | 9.47E-02 | 3.63E-01 | 1.98E-01 | CPPE5 | 1.15E-02 | 1.41E+02 | 2.55E+02 | CPPE5 | 2.30E-03 | 3.50E+00 | 6.33E+00 |
| CPPE6 | 2.69E-02 | 3.38E-01 | 2.01E-01 | CPPE6 | 6.13E-02 | 9.08E+01 | 2.35E+02 | CPPE6 | 5.43E-03 | 2.93E+00 | 6.14E+00 |
| CPPE7 | 5.00E-02 | 3.99E-01 | 2.36E-01 | CPPE7 | 4.03E-03 | 7.59E+01 | 1.33E+02 | CPPE7 | 1.61E-02 | 3.66E+00 | 6.01E+00 |
| CPPE8 | 9.46E-02 | 3.90E-01 | 2.36E-01 | CPPE8 | 4.60E-03 | 6.86E+01 | 1.19E+02 | CPPE8 | 4.52E-04 | 4.61E+00 | 9.50E+00 |
| CPPE9 | 5.95E-02 | 4.37E-01 | 2.49E-01 | CPPE9 | 1.83E-02 | 2.53E+01 | 5.59E+01 | CPPE9 | 1.36E-03 | 3.07E+00 | 1.18E+01 |
| CPPE10 | 4.74E-02 | 3.89E-01 | 2.08E-01 | CPPE10 | 2.24E-02 | 7.64E+01 | 1.56E+02 | CPPE10 | 4.93E-03 | 2.11E+00 | 3.52E+00 |
| CPPE11 | 5.80E-02 | 3.29E-01 | 2.13E-01 | CPPE11 | 8.68E-02 | 1.64E+02 | 3.00E+02 | CPPE11 | 6.02E-03 | 4.75E+00 | 1.37E+01 |
| CPPE12 | 2.87E-02 | 3.95E-01 | 2.34E-01 | CPPE12 | 2.95E-02 | 6.63E+01 | 1.11E+02 | CPPE12 | 4.11E-03 | 7.05E+00 | 2.49E+0 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 4.44E-03 | 7.66E+01 | 2.44E+02 | PPE | 2.10E-04 | 3.00E-03 | 3.39E-03 | PPE | 3.22E-04 | 1.11E+00 | 1.77E+00 |
| CPPE1 | 1.69E-02 | 9.47E+01 | 1.63E+02 | CPPE1 | 5.20E-05 | 2.97E-03 | 2.96E-03 | CPPE1 | 5.27E-06 | 1.14E+00 | 1.75E+00 |
| CPPE2 | 2.36E-02 | 8.54E+01 | 2.09E+02 | CPPE2 | 5.47E-05 | 3.80E-03 | 5.20E-03 | CPPE2 | 4.17E-05 | 7.00E-01 | 1.40E+00 |
| CPPE3 | 2.36E-02 | 7.23E+01 | 1.90E+02 | CPPE3 | 5.47E-05 | 2.27E-02 | 2.85E-02 | CPPE3 | 4.17E-05 | 4.10E+00 | 1.19E+00 |
| CPPE4 | 1.83E-02 | 1.43E+02 | 2.39E+02 | CPPE4 | 7.80E-04 | 5.00E-03 | 5.74E-03 | CPPE4 | 6.81E-06 | 7.04E-01 | 1.39E+00 |
| CPPE5 | 9.05E-04 | 6.24E+01 | 1.85E+02 | CPPE5 | 3.20E-04 | 5.07E-03 | 7.87E-03 | CPPE5 | 3.02E-05 | 8.88E-01 | 1.58E+00 |
| CPPE6 | 1.65E-02 | 1.82E+02 | 3.43E+02 | CPPE6 | 1.53E-04 | 3.24E-03 | 2.58E-03 | CPPE6 | 5.39E-04 | 9.89E-01 | 1.64E+00 |
| CPPE7 | 3.93E-02 | 8.55E+01 | 1.95E+02 | CPPE7 | 1.91E-04 | 3.38E-03 | 3.38E-03 | CPPE7 | 1.34E-04 | 5.88E-01 | 1.26E+00 |
| CPPE8 | 1.45E-01 | 1.40E+02 | 2.65E+02 | CPPE8 | 3.35E-04 | 4.99E-03 | 5.54E-03 | CPPE8 | 2.02E-03 | 2.88E+00 | 1.93E+00 |
| CPPE9 | 3.82E-03 | 2.43E+01 | 5.28E+01 | CPPE9 | 5.43E-04 | 4.30E-03 | 3.35E-03 | CPPE9 | 2.04E-02 | 3.48E-01 | 6.07E-01 |
| CPPE10 | 4.69E-02 | 9.29E+01 | 2.20E+02 | CPPE10 | 2.96E-04 | 7.14E-03 | 7.37E-03 | CPPE10 | 1.31E-03 | 3.56E+00 | 1.59E+00 |
| CPPE11 | 1.27E-01 | 1.65E+02 | 2.61E+02 | CPPE11 | 1.44E-04 | 4.44E-03 | 5.40E-03 | CPPE11 | 3.02E-05 | 1.04E+00 | 1.68E+00 |
| CPPE12 | 3.53E-04 | 8.67E+01 | 1.88E+02 | CPPE12 | 4.42E-04 | 7.36E-03 | 9.66E-03 | CPPE12 | 2.19E-03 | 2.86E+00 | 1.97E+00 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 3.15E-02 | 7.70E-01 | 1.23E+00 | PPE | 6.42E-05 | 1.61E-03 | 8.21E-03 | PPE | 2.59E+00 | 5.21E+00 | 1.27E+00 |
| CPPE1 | 3.61E-02 | 7.08E-01 | 1.17E+00 | CPPE1 | 5.00E-05 | 6.37E-04 | 6.79E-04 | CPPE1 | 1.98E+00 | 5.62E+00 | 1.22E+00 |
| CPPE2 | 2.70E-02 | 8.54E-01 | 1.63E+00 | CPPE2 | 4.44E-05 | 4.20E-04 | 3.07E-04 | CPPE2 | 2.53E+00 | 5.26E+00 | 1.25E+00 |
| CPPE3 | 2.70E-02 | 1.04E+00 | 1.36E+00 | CPPE3 | 4.44E-05 | 2.06E+00 | 6.03E+00 | CPPE3 | 2.53E+00 | 5.70E+00 | 1.74E+00 |
| CPPE4 | 2.93E-02 | 1.06E+00 | 2.30E+00 | CPPE4 | 3.75E-05 | 4.17E-04 | 2.88E-04 | CPPE4 | 2.61E+00 | 5.22E+00 | 1.20E+00 |
| CPPE5 | 2.40E-02 | 1.06E+00 | 2.11E+00 | CPPE5 | 3.42E-05 | 3.69E-04 | 3.63E-04 | CPPE5 | 2.95E+00 | 5.57E+00 | 1.24E+00 |
| CPPE6 | 1.08E-02 | 5.14E-01 | 1.16E+00 | CPPE6 | 5.51E-05 | 4.14E-04 | 3.55E-04 | CPPE6 | 2.52E+00 | 5.49E+00 | 1.14E+00 |
| CPPE7 | 2.35E-02 | 7.07E-01 | 1.55E+00 | CPPE7 | 7.07E-05 | 4.00E-01 | 2.83E+00 | CPPE7 | 2.95E+00 | 5.09E+00 | 1.16E+00 |
| CPPE8 | 1.43E-02 | 1.35E+00 | 2.21E+00 | CPPE8 | 1.29E-05 | 4.68E-01 | 2.83E+00 | CPPE8 | 2.35E+00 | 5.20E+00 | 1.31E+00 |
| CPPE9 | 1.58E-02 | 6.38E-01 | 9.98E-01 | CPPE9 | 1.58E-05 | 4.34E-04 | 3.91E-04 | CPPE9 | 2.61E+00 | 5.88E+00 | 1.11E+00 |
| CPPE10 | 5.88E-02 | 1.82E+00 | 2.82E+00 | CPPE10 | 2.63E-05 | 4.90E-04 | 4.41E-04 | CPPE10 | 1.88E+00 | 5.46E+00 | 1.37E+00 |
| CPPE11 | 2.09E-02 | 8.63E-01 | 1.70E+00 | CPPE11 | 7.62E-05 | 3.92E-01 | 2.77E+00 | CPPE11 | 2.05E+00 | 5.68E+00 | 1.46E+00 |
| CPPE12 | 5.03E-02 | 1.11E+00 | 1.20E+00 | CPPE12 | 6.32E-05 | 8.56E-04 | 2.47E-03 | CPPE12 | 3.06E+00 | 5.54E+00 | 1.29E+00 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 1.02E+00 | 3.79E+00 | 3.15E+00 | PPE | 2.86E-04 | 8.57E-01 | 9.29E-01 | PPE | 1.00E+00 | 6.27E+00 | 3.20E+00 |
| CPPE1 | 3.41E-01 | 3.63E+00 | 2.19E+00 | CPPE1 | 1.83E-04 | 6.00E-01 | 7.10E-01 | CPPE1 | 2.07E-03 | 4.97E+00 | 2.77E+00 |
| CPPE2 | 9.34E-01 | 2.81E+00 | 1.62E+00 | CPPE2 | 2.72E-03 | 5.97E-01 | 6.04E-01 | CPPE2 | 1.99E+00 | 5.52E+00 | 2.73E+00 |
| CPPE3 | 9.34E-01 | 2.37E+01 | 9.73E+00 | CPPE3 | 2.72E-03 | 3.97E+00 | 2.47E+00 | CPPE3 | 1.99E+00 | 1.49E+01 | 7.33E+00 |
| CPPE4 | 1.13E+00 | 4.14E+00 | 3.52E+00 | CPPE4 | 5.08E-04 | 7.68E-01 | 9.91E-01 | CPPE4 | 1.89E-03 | 5.28E+00 | 2.93E+00 |
| CPPE5 | 8.46E-01 | 3.52E+00 | 2.46E+00 | CPPE5 | 1.36E-04 | 6.13E-01 | 6.64E-01 | CPPE5 | 1.99E+00 | 6.15E+00 | 3.38E+00 |
| CPPE6 | 1.03E+00 | 3.30E+00 | 2.15E+00 | CPPE6 | 2.08E-04 | 8.17E-01 | 9.67E-01 | CPPE6 | 1.99E+00 | 5.66E+00 | 2.49E+00 |
| CPPE7 | 8.74E-01 | 3.62E+00 | 2.08E+00 | CPPE7 | 1.50E-04 | 5.80E-01 | 6.44E-01 | CPPE7 | 9.95E-01 | 5.00E+00 | 2.80E+00 |
| CPPE8 | 1.41E+00 | 6.76E+00 | 3.81E+00 | CPPE8 | 9.87E-05 | 1.13E+00 | 1.19E+00 | CPPE8 | 8.62E-03 | 8.82E+00 | 5.06E+00 |
| CPPE9 | 1.15E+00 | 3.33E+00 | 1.66E+00 | CPPE9 | 3.76E-03 | 9.77E-01 | 7.03E-01 | CPPE9 | 9.96E-01 | 7.97E+00 | 4.15E+00 |
| CPPE10 | 1.11E+00 | 8.50E+00 | 5.68E+00 | CPPE10 | 7.28E-04 | 1.25E+00 | 1.54E+00 | CPPE10 | 9.95E-01 | 8.88E+00 | 4.92E+00 |
| CPPE11 | 1.11E+00 | 4.84E+00 | 3.37E+00 | CPPE11 | 1.06E-03 | 6.36E-01 | 9.28E-01 | CPPE11 | 9.96E-01 | 5.76E+00 | 3.10E+00 |
| CPPE12 | 1.04E+00 | 5.23E+00 | 2.87E+00 | CPPE12 | 7.14E-04 | 9.17E-01 | 1.03E+00 | CPPE12 | 9.96E-01 | 7.45E+00 | 3.61E+00 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 1.59E+00 | 8.17E+00 | 4.15E+00 | PPE | 3.60E-06 | 5.78E-02 | 1.21E-01 | PPE | 1.26E-05 | 1.17E+00 | 5.25E+00 |
| CPPE1 | 1.00E+00 | 6.89E+00 | 3.39E+00 | CPPE1 | 1.09E-07 | 4.68E-02 | 1.09E-01 | CPPE1 | 3.14E-06 | 3.61E+00 | 1.73E+01 |
| CPPE2 | 5.17E-04 | 7.30E+00 | 3.59E+00 | CPPE2 | 1.82E-06 | 5.34E-02 | 1.31E-01 | CPPE2 | 7.14E-06 | 2.07E-01 | 2.32E-01 |
| CPPE3 | 5.17E-04 | 1.42E+01 | 8.33E+00 | CPPE3 | 1.82E-06 | 7.94E-01 | 3.30E+00 | CPPE3 | 7.14E-06 | 8.84E+00 | 2.87E+01 |
| CPPE4 | 1.39E+00 | 6.76E+00 | 3.73E+00 | CPPE4 | 4.32E-07 | 5.09E-02 | 1.15E-01 | CPPE4 | 1.68E-05 | 1.78E+00 | 4.60E+00 |
| CPPE5 | 9.95E-01 | 8.12E+00 | 3.04E+00 | CPPE5 | 2.99E-06 | 6.56E-02 | 1.24E-01 | CPPE5 | 8.55E-07 | 8.92E-01 | 3.31E+00 |
| CPPE6 | 1.59E+00 | 8.20E+00 | 3.17E+00 | CPPE6 | 3.09E-08 | 5.22E-02 | 1.16E-01 | CPPE6 | 5.26E-07 | 1.19E+00 | 3.98E+00 |
| CPPE7 | 1.59E+00 | 8.22E+00 | 2.96E+00 | CPPE7 | 2.78E-06 | 4.52E-02 | 1.09E-01 | CPPE7 | 6.87E-07 | 5.42E-01 | 2.35E+00 |
| CPPE8 | 1.39E+00 | 8.63E+00 | 3.80E+00 | CPPE8 | 2.63E-06 | 4.24E-01 | 2.36E+00 | CPPE8 | 1.80E-06 | 4.97E+00 | 2.36E+01 |
| CPPE9 | 2.19E+00 | 1.09E+01 | 4.30E+00 | CPPE9 | 5.03E-06 | 4.27E-02 | 1.03E-01 | CPPE9 | 4.05E-06 | 1.40E-01 | 2.11E-01 |
| CPPE10 | 5.03E+00 | 9.67E+00 | 4.49E+00 | CPPE10 | 5.20E-08 | 1.05E-01 | 1.49E-01 | CPPE10 | 1.49E-05 | 4.95E+00 | 2.36E+01 |
| CPPE11 | 1.39E+00 | 8.00E+00 | 4.33E+00 | CPPE11 | 2.82E-06 | 7.64E-02 | 1.49E-01 | CPPE11 | 3.53E-06 | 2.22E+00 | 5.46E+00 |
| CPPE12 | 2.03E+00 | 7.68E+00 | 3.37E+00 | CPPE12 | 2.54E-08 | 1.05E-01 | 1.43E-01 | CPPE12 | 3.05E-06 | 3.43E+00 | 1.72E+01 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 5.62E-01 | 9.91E-01 | 2.55E-01 | PPE | 8.77E-01 | 6.14E+00 | 1.80E+00 | PPE | 1.82E+00 | 9.10E+00 | 3.13E+00 |
| CPPE1 | 4.44E-01 | 9.44E-01 | 3.00E-01 | CPPE1 | 3.89E-01 | 5.59E+00 | 2.06E+00 | CPPE1 | 3.71E+00 | 8.59E+00 | 2.28E+00 |
| CPPE2 | 3.49E-01 | 9.59E-01 | 2.29E-01 | CPPE2 | 4.94E-01 | 6.32E+00 | 1.67E+00 | CPPE2 | 1.80E+00 | 8.87E+00 | 2.63E+00 |
| CPPE3 | 3.49E-01 | 8.84E-01 | 3.25E-01 | CPPE3 | 4.94E-01 | 8.97E+00 | 1.87E+00 | CPPE3 | 1.80E+00 | 1.48E+01 | 5.10E+00 |
| CPPE4 | 4.34E-01 | 9.02E-01 | 2.77E-01 | CPPE4 | 1.49E-01 | 5.88E+00 | 2.27E+00 | CPPE4 | 2.58E+00 | 8.54E+00 | 3.02E+00 |
| CPPE5 | 5.00E-01 | 9.96E-01 | 2.61E-01 | CPPE5 | 1.08E+00 | 6.35E+00 | 1.73E+00 | CPPE5 | 5.60E+00 | 8.81E+00 | 1.80E+00 |
| CPPE6 | 3.73E-01 | 9.02E-01 | 2.92E-01 | CPPE6 | 6.76E-01 | 6.16E+00 | 1.84E+00 | CPPE6 | 1.87E+00 | 9.10E+00 | 2.76E+00 |
| CPPE7 | 5.74E-01 | 9.83E-01 | 2.51E-01 | CPPE7 | 7.27E-01 | 6.30E+00 | 1.81E+00 | CPPE7 | 4.49E+00 | 1.02E+01 | 2.76E+00 |
| CPPE8 | 3.32E-01 | 9.01E-01 | 2.89E-01 | CPPE8 | 1.51E+00 | 7.00E+00 | 1.85E+00 | CPPE8 | 3.38E+00 | 1.06E+01 | 3.97E+00 |
| CPPE9 | 2.60E-01 | 8.42E-01 | 2.86E-01 | CPPE9 | 5.31E+00 | 6.95E+00 | 1.11E+00 | CPPE9 | 6.19E+00 | 1.07E+01 | 3.00E+00 |
| CPPE10 | 3.80E-01 | 9.45E-01 | 2.51E-01 | CPPE10 | 1.78E+00 | 7.14E+00 | 1.51E+00 | CPPE10 | 5.39E+00 | 1.01E+01 | 2.65E+00 |
| CPPE11 | 3.74E-01 | 9.63E-01 | 2.85E-01 | CPPE11 | 4.72E-01 | 6.31E+00 | 2.18E+00 | CPPE11 | 4.00E+00 | 9.81E+00 | 2.77E+00 |
| CPPE12 | 4.37E-01 | 8.80E-01 | 2.57E-01 | CPPE12 | 3.55E-01 | 6.42E+00 | 1.85E+00 | CPPE12 | 5.95E+00 | 1.06E+01 | 3.22E+00 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 7.65E-01 | 2.67E+00 | 1.11E+00 | PPE | 2.27E+00 | 3.31E+00 | 3.97E-01 | PPE | 3.84E-04 | 7.86E-03 | 6.25E-03 |
| CPPE1 | 1.19E+00 | 2.20E+00 | 7.19E-01 | CPPE1 | 2.54E+00 | 3.33E+00 | 3.59E-01 | CPPE1 | 1.81E-04 | 6.24E-03 | 5.49E-03 |
| CPPE2 | 9.94E-01 | 2.52E+00 | 8.09E-01 | CPPE2 | 1.99E+00 | 3.34E+00 | 4.42E-01 | CPPE2 | 4.51E-04 | 2.01E+00 | 1.41E+01 |
| CPPE3 | 9.94E-01 | 4.60E+00 | 2.51E+00 | CPPE3 | 1.99E+00 | 3.78E+00 | 1.86E-01 | CPPE3 | 4.51E-04 | 8.75E-03 | 8.53E-03 |
| CPPE4 | 8.55E-01 | 2.17E+00 | 8.48E-01 | CPPE4 | 2.18E+00 | 3.36E+00 | 4.21E-01 | CPPE4 | 9.22E-04 | 2.01E+00 | 1.41E+01 |
| CPPE5 | 8.06E-01 | 2.86E+00 | 1.01E+00 | CPPE5 | 2.20E+00 | 3.37E+00 | 4.36E-01 | CPPE5 | 1.76E-04 | 6.36E-03 | 4.91E-03 |
| CPPE6 | 7.53E-01 | 2.64E+00 | 9.52E-01 | CPPE6 | 2.50E+00 | 3.31E+00 | 3.31E-01 | CPPE6 | 1.09E-03 | 6.53E-03 | 5.99E-03 |
| CPPE7 | 1.12E+00 | 2.89E+00 | 1.27E+00 | CPPE7 | 2.50E+00 | 3.30E+00 | 4.11E-01 | CPPE7 | 4.56E-04 | 4.01E+00 | 1.98E+01 |
| CPPE8 | 5.88E-01 | 2.74E+00 | 1.32E+00 | CPPE8 | 2.35E+00 | 3.46E+00 | 3.49E-01 | CPPE8 | 4.26E-04 | 6.81E-03 | 4.90E-03 |
| CPPE9 | 1.78E+00 | 3.43E+00 | 9.62E-01 | CPPE9 | 2.02E+00 | 3.28E+00 | 5.32E-01 | CPPE9 | 4.45E-04 | 6.16E-03 | 4.22E-03 |
| CPPE10 | 7.16E-01 | 3.03E+00 | 1.43E+00 | CPPE10 | 3.07E+00 | 3.69E+00 | 2.56E-01 | CPPE10 | 2.10E-04 | 6.71E-03 | 6.54E-03 |
| CPPE11 | 7.23E-01 | 2.23E+00 | 8.45E-01 | CPPE11 | 1.54E+00 | 3.30E+00 | 5.19E-01 | CPPE11 | 2.42E-04 | 4.01E+00 | 1.98E+01 |
| CPPE12 | 5.20E-01 | 3.35E+00 | 1.45E+00 | CPPE12 | 2.58E+00 | 3.53E+00 | 2.90E-01 | CPPE12 | 1.03E-03 | 7.21E-03 | 5.00E-03 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 9.26E-05 | 2.51E+00 | 1.24E+01 | PPE | 3.03E-04 | 7.19E-03 | 3.19E-02 | PPE | 2.79E-05 | 5.12E-01 | 2.72E+00 |
| CPPE1 | 6.80E-05 | 9.60E-04 | 7.66E-04 | CPPE1 | 7.24E-05 | 2.00E+00 | 1.41E+01 | CPPE1 | 6.98E-06 | 1.88E+00 | 5.70E+00 |
| CPPE2 | 1.14E-04 | 2.51E+00 | 1.24E+01 | CPPE2 | 9.60E-05 | 6.43E-01 | 3.17E+00 | CPPE2 | 3.42E-06 | 8.78E-01 | 3.75E+00 |
| CPPE3 | 1.14E-04 | 9.59E+00 | 2.43E+01 | CPPE3 | 9.60E-05 | 3.16E+01 | 4.78E+01 | CPPE3 | 3.42E-06 | 2.22E+00 | 8.03E+00 |
| CPPE4 | 5.06E-05 | 2.51E+00 | 1.24E+01 | CPPE4 | 1.19E-04 | 6.50E-01 | 3.19E+00 | CPPE4 | 3.56E-06 | 5.02E-01 | 2.71E+00 |
| CPPE5 | 6.93E-05 | 1.11E-03 | 8.06E-04 | CPPE5 | 3.29E-05 | 3.58E+00 | 1.78E+01 | CPPE5 | 1.21E-05 | 9.46E-01 | 3.76E+00 |
| CPPE6 | 5.84E-05 | 1.21E-03 | 1.06E-03 | CPPE6 | 1.72E-04 | 1.60E+00 | 1.11E+01 | CPPE6 | 6.13E-06 | 5.02E-01 | 2.71E+00 |
| CPPE7 | 1.25E-04 | 1.25E+00 | 8.86E+00 | CPPE7 | 1.82E-04 | 2.33E-03 | 2.54E-03 | CPPE7 | 7.00E-06 | 8.39E-01 | 2.94E+00 |
| CPPE8 | 8.38E-05 | 1.25E+00 | 8.86E+00 | CPPE8 | 9.04E-05 | 4.33E+00 | 1.99E+01 | CPPE8 | 2.45E-05 | 1.89E-01 | 7.55E-01 |
| CPPE9 | 9.54E-05 | 1.08E-03 | 8.44E-04 | CPPE9 | 2.21E-04 | 1.58E+00 | 1.11E+01 | CPPE9 | 6.21E-06 | 8.15E-01 | 3.74E+00 |
| CPPE10 | 4.11E-05 | 1.20E-03 | 9.59E-04 | CPPE10 | 2.19E-04 | 5.11E+00 | 2.23E+01 | CPPE10 | 1.62E-05 | 4.40E-01 | 2.69E+00 |
| CPPE11 | 3.67E-05 | 1.07E-03 | 9.33E-04 | CPPE11 | 1.38E-04 | 1.00E+01 | 3.03E+01 | CPPE11 | 9.83E-06 | 5.71E-01 | 2.74E+00 |
| CPPE12 | 1.38E-04 | 2.86E+00 | 1.26E+01 | CPPE12 | 9.71E-05 | 3.68E+00 | 1.83E+01 | CPPE12 | 1.56E-05 | 7.52E-01 | 3.72E+00 |
| Final | Mean | Std | Final | Mean | Std | Final | Mean | Std | |||
| PPE | 9.41E-05 | 9.72E-04 | 7.71E-04 | PPE | 2.07E-08 | 1.40E-01 | 2.04E-01 | PPE | 2.83E-03 | 3.95E+01 | 4.88E+01 |
| CPPE1 | 3.44E-05 | 8.99E-04 | 6.42E-04 | CPPE1 | 1.81E-08 | 2.26E-01 | 2.59E-01 | CPPE1 | 1.82E-02 | 5.73E+01 | 4.91E+01 |
| CPPE2 | 7.25E-05 | 8.78E-04 | 6.66E-04 | CPPE2 | 8.16E-08 | 1.57E-01 | 2.38E-01 | CPPE2 | 6.27E-05 | 3.91E+01 | 4.86E+01 |
| CPPE3 | 7.25E-05 | 1.32E+01 | 3.33E+01 | CPPE3 | 8.16E-08 | 4.81E-01 | 1.29E+00 | CPPE3 | 6.27E-05 | 7.94E+01 | 4.05E+01 |
| CPPE4 | 3.03E-05 | 2.09E+00 | 1.41E+01 | CPPE4 | 2.51E-07 | 2.07E-01 | 2.60E-01 | CPPE4 | 3.04E-03 | 4.89E+01 | 4.96E+01 |
| CPPE5 | 5.75E-05 | 8.96E-04 | 7.81E-04 | CPPE5 | 1.58E-08 | 1.66E-01 | 2.40E-01 | CPPE5 | 3.27E-01 | 3.56E+01 | 4.68E+01 |
| CPPE6 | 7.88E-05 | 7.72E-04 | 6.25E-04 | CPPE6 | 1.51E-08 | 1.72E-01 | 2.23E-01 | CPPE6 | 4.53E-03 | 3.16E+01 | 4.58E+01 |
| CPPE7 | 2.35E-05 | 2.00E+00 | 1.41E+01 | CPPE7 | 7.94E-08 | 1.34E-01 | 1.83E-01 | CPPE7 | 9.17E-04 | 4.78E+01 | 4.93E+01 |
| CPPE8 | 8.98E-06 | 7.29E-04 | 6.83E-04 | CPPE8 | 8.04E-09 | 1.19E-01 | 1.83E-01 | CPPE8 | 1.30E-04 | 5.54E+01 | 4.97E+01 |
| CPPE9 | 4.34E-05 | 6.38E-04 | 5.22E-04 | CPPE9 | 2.59E-08 | 6.16E-02 | 1.52E-01 | CPPE9 | 9.76E-03 | 2.15E+00 | 2.28E+00 |
| CPPE10 | 1.02E-04 | 7.46E-04 | 6.38E-04 | CPPE10 | 1.14E-08 | 7.49E-01 | 4.45E+00 | CPPE10 | 1.59E-02 | 5.37E+01 | 4.88E+01 |
| CPPE11 | 2.85E-05 | 8.42E-04 | 7.63E-04 | CPPE11 | 2.36E-08 | 2.10E-01 | 2.45E-01 | CPPE11 | 2.04E-03 | 6.48E+01 | 4.74E+01 |
| CPPE12 | 5.87E-05 | 4.00E+00 | 1.98E+01 | CPPE12 | 7.30E-08 | 2.12E-01 | 6.17E-01 | CPPE12 | 6.20E-04 | 5.47E+01 | 4.91E+01 |
| Final | Mean | Std | |||||||||
| PPE | 4.48E-04 | 4.42E-03 | 3.09E-03 | ||||||||
| CPPE1 | 4.15E-04 | 3.64E-03 | 3.28E-03 | ||||||||
| CPPE2 | 1.16E-04 | 3.11E-03 | 2.50E-03 | ||||||||
| CPPE3 | 1.16E-04 | 2.00E+00 | 1.41E+01 | ||||||||
| CPPE4 | 2.94E-04 | 3.90E-03 | 3.60E-03 | ||||||||
| CPPE5 | 3.60E-04 | 3.43E-03 | 2.30E-03 | ||||||||
| CPPE6 | 4.55E-04 | 3.92E-03 | 2.85E-03 | ||||||||
| CPPE7 | 8.54E-04 | 3.91E-03 | 3.26E-03 | ||||||||
| CPPE8 | 3.09E-04 | 3.80E-03 | 3.65E-03 | ||||||||
| CPPE9 | 7.55E-05 | 3.56E-03 | 2.56E-03 | ||||||||
| CPPE10 | 2.70E-04 | 4.02E-03 | 4.28E-03 | ||||||||
| CPPE11 | 2.77E-04 | 3.76E-03 | 3.03E-03 | ||||||||
| CPPE12 | 1.23E-04 | 3.12E-03 | 2.27E-03 |
| CPPE1 | CPPE2 | CPPE3 | CPPE4 | CPPE5 | CPPE6 | CPPE7 | CPPE8 | CPPE9 | CPPE10 | CPPE11 | CPPE12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Final | 22 | 19 | 19 | 16 | 21 | 17 | 15 | 20 | 14 | 15 | 20 | 15 |
| Mean | 18 | 16 | 3 | 14 | 16 | 18 | 15 | 8 | 17 | 9 | 11 | 5 |
| Std | 19 | 20 | 5 | 13 | 17 | 21 | 17 | 9 | 22 | 13 | 10 | 10 |
| Final | Mean | Std | |
|---|---|---|---|
| CPPE1 | |||
| CPPE2 | |||
| CPPE3 | |||
| CPPE4 | |||
| CPPE5 | |||
| CPPE6 | |||
| CPPE7 | |||
| CPPE8 | |||
| CPPE9 | |||
| CPPE10 | |||
| CPPE11 | |||
| CPPE12 |
| Final | Mean | Std | |
|---|---|---|---|
| CPPE1 | 12.2222% | −16.1146% | −3.8127% |
| CPPE2 | −28.3925% | 6.0912% | 10.2575% |
| CPPE3 | −28.3925% | −61,464.2086% | −194,171.1520% |
| CPPE4 | −33.2308% | −8601.8259% | −73,153.7043% |
| CPPE5 | −447.3261% | −2.7712% | 3.2219% |
| CPPE6 | 8.9647% | 10.4633% | 14.6716% |
| CPPE7 | −6.9034% | −9211.8529% | −74,512.3505% |
| CPPE8 | 7.5525% | −1212.8028% | −1469.2995% |
| CPPE9 | −329.5657% | 16.9592% | 26.3463% |
| CPPE10 | −46.3178% | −56.9641% | −105.2342% |
| CPPE11 | −0.1405% | −984.1307% | −1354.9638% |
| CPPE12 | −35.6815% | −16,492.6669% | −102,746.3320% |
| Parameters | Values |
|---|---|
| Population_Number | 100 |
| Max_Gen | 50 |
| Run_Nums | 50 |
| PPE | 2.87E+02 | 3.94E+04 | 6.97E+04 | 2.16E+04 | 4.11E+01 | 2.86E+00 | 3.76E+00 | 3.51E-01 | 1.52E-01 | 3.79E+01 | 1.38E+00 |
| CPPE1 | 4.43E+02 | 7.76E+04 | 1.13E+05 | 4.98E+04 | 6.85E+01 | 3.72E+00 | 3.29E+00 | 3.64E-01 | 1.48E-01 | 4.83E+01 | 1.74E+00 |
| CPPE2 | 2.81E+02 | 1.92E+04 | 8.76E+04 | 2.68E+04 | 4.40E+01 | 2.70E+00 | 5.91E+00 | 3.51E-01 | 1.43E-01 | 3.30E+01 | 1.33E+00 |
| CPPE3 | 4.73E+02 | 4.22E+04 | 1.85E+06 | 1.33E+05 | 7.26E+01 | 4.75E+00 | 3.02E+02 | 3.18E-01 | 1.39E-01 | 4.49E+01 | 1.94E+00 |
| CPPE4 | 4.12E+02 | 2.77E+04 | 1.42E+05 | 1.90E+04 | 6.89E+01 | 3.37E+00 | 4.01E+00 | 3.81E-01 | 1.44E-01 | 4.86E+01 | 1.65E+00 |
| CPPE5 | 2.91E+02 | 2.62E+04 | 5.02E+04 | 3.42E+04 | 4.34E+01 | 2.78E+00 | 3.94E+00 | 3.67E-01 | 1.43E-01 | 3.53E+01 | 1.35E+00 |
| CPPE6 | 2.95E+02 | 2.48E+04 | 1.16E+05 | 2.69E+04 | 3.35E+01 | 2.80E+00 | 3.03E+00 | 3.59E-01 | 1.55E-01 | 3.42E+01 | 1.38E+00 |
| CPPE7 | 2.79E+02 | 2.89E+04 | 4.08E+04 | 1.54E+04 | 3.52E+01 | 2.78E+00 | 3.07E+00 | 3.50E-01 | 1.45E-01 | 3.37E+01 | 1.34E+00 |
| CPPE8 | 3.45E+02 | 6.47E+04 | 2.22E+05 | 4.06E+04 | 5.84E+01 | 4.01E+00 | 1.02E+01 | 3.68E-01 | 1.50E-01 | 4.11E+01 | 1.45E+00 |
| CPPE9 | 2.08E+02 | 8.04E+03 | 2.44E+04 | 7.86E+03 | 7.14E+01 | 2.39E+00 | 1.26E+02 | 2.37E-01 | 1.25E-01 | 2.18E+01 | 1.23E+00 |
| CPPE10 | 3.77E+02 | 3.05E+04 | 2.66E+05 | 2.91E+04 | 5.85E+01 | 3.62E+00 | 1.31E+01 | 3.65E-01 | 1.52E-01 | 4.12E+01 | 1.59E+00 |
| CPPE11 | 3.90E+02 | 3.37E+04 | 1.34E+05 | 1.16E+04 | 5.04E+01 | 4.34E+00 | 3.05E+00 | 3.87E-01 | 1.45E-01 | 5.11E+01 | 1.63E+00 |
| CPPE12 | 3.28E+02 | 4.05E+04 | 1.12E+05 | 2.69E+04 | 4.48E+01 | 2.59E+00 | 1.47E+01 | 3.75E-01 | 1.49E-01 | 4.00E+01 | 1.46E+00 |
| PPE | 1.22E+00 | 1.29E+00 | 3.65E+00 | 3.79E+00 | 5.12E-02 | 1.84E+00 | 1.76E+00 | 2.40E+03 | 3.00E-02 | 3.60E+00 | 4.82E+00 |
| CPPE1 | 1.80E+00 | 1.55E+00 | 4.54E+00 | 4.39E+00 | 4.66E-02 | 2.76E+00 | 2.66E+00 | 8.82E+03 | 2.80E-02 | 4.30E+00 | 5.34E+00 |
| CPPE2 | 1.35E+00 | 1.28E+00 | 3.79E+00 | 3.97E+00 | 5.19E-02 | 1.71E+00 | 1.77E+00 | 2.66E+03 | 2.92E-02 | 3.37E+00 | 4.15E+00 |
| CPPE3 | 2.04E+00 | 1.89E+00 | 4.37E+00 | 4.31E+00 | 5.20E-02 | 3.11E+00 | 2.63E+00 | 4.30E+04 | 2.00E-02 | 4.22E+00 | 5.17E+00 |
| CPPE4 | 1.61E+00 | 1.66E+00 | 5.19E+00 | 3.91E+00 | 5.54E-02 | 2.86E+00 | 2.68E+00 | 8.39E+03 | 2.83E-02 | 4.06E+00 | 5.96E+00 |
| CPPE5 | 1.26E+00 | 1.20E+00 | 4.03E+00 | 3.62E+00 | 5.15E-02 | 1.78E+00 | 1.81E+00 | 2.84E+03 | 3.09E-02 | 3.37E+00 | 4.87E+00 |
| CPPE6 | 1.29E+00 | 1.26E+00 | 3.86E+00 | 3.73E+00 | 5.72E-02 | 1.78E+00 | 1.73E+00 | 2.61E+03 | 3.06E-02 | 3.54E+00 | 4.44E+00 |
| CPPE7 | 1.37E+00 | 1.28E+00 | 3.96E+00 | 3.94E+00 | 4.86E-02 | 1.81E+00 | 1.70E+00 | 2.87E+03 | 2.89E-02 | 3.41E+00 | 5.37E+00 |
| CPPE8 | 1.67E+00 | 1.46E+00 | 4.05E+00 | 4.54E+00 | 4.96E-02 | 2.31E+00 | 2.20E+00 | 1.38E+04 | 2.44E-02 | 3.80E+00 | 5.34E+00 |
| CPPE9 | 9.29E-01 | 9.12E-01 | 2.81E+00 | 2.21E+00 | 5.61E-02 | 9.47E-01 | 8.61E-01 | 3.81E+02 | 2.38E-02 | 1.77E+00 | 3.30E+00 |
| CPPE10 | 1.79E+00 | 1.72E+00 | 3.98E+00 | 4.48E+00 | 5.33E-02 | 2.46E+00 | 2.27E+00 | 1.62E+04 | 2.48E-02 | 3.95E+00 | 4.86E+00 |
| CPPE11 | 1.69E+00 | 1.61E+00 | 5.19E+00 | 3.80E+00 | 5.07E-02 | 2.63E+00 | 2.73E+00 | 6.41E+03 | 2.65E-02 | 4.10E+00 | 6.83E+00 |
| CPPE12 | 1.48E+00 | 1.55E+00 | 4.19E+00 | 4.61E+00 | 4.78E-02 | 1.98E+00 | 2.19E+00 | 7.88E+03 | 2.63E-02 | 3.79E+00 | 5.18E+00 |
| PPE | 5.75E+00 | 1.71E+00 | 2.00E+00 | 1.77E+00 | 3.69E+00 | 2.23E+00 | |||||
| CPPE1 | 6.35E+00 | 1.89E+00 | 2.20E+00 | 1.72E+00 | 3.72E+00 | 2.80E+00 | |||||
| CPPE2 | 5.53E+00 | 1.59E+00 | 2.07E+00 | 1.53E+00 | 3.31E+00 | 2.23E+00 | |||||
| CPPE3 | 5.99E+00 | 1.92E+00 | 1.94E+00 | 2.01E+00 | 2.73E+00 | 2.59E+00 | |||||
| CPPE4 | 6.03E+00 | 1.91E+00 | 2.09E+00 | 1.87E+00 | 4.20E+00 | 2.73E+00 | |||||
| CPPE5 | 5.16E+00 | 1.67E+00 | 2.07E+00 | 1.35E+00 | 4.28E+00 | 2.41E+00 | |||||
| CPPE6 | 6.45E+00 | 1.54E+00 | 2.18E+00 | 1.42E+00 | 3.31E+00 | 2.24E+00 | |||||
| CPPE7 | 5.99E+00 | 1.63E+00 | 2.18E+00 | 1.60E+00 | 3.60E+00 | 2.46E+00 | |||||
| CPPE8 | 6.27E+00 | 1.81E+00 | 2.04E+00 | 1.71E+00 | 2.75E+00 | 2.62E+00 | |||||
| CPPE9 | 3.90E+00 | 1.03E+00 | 1.45E+00 | 7.03E-01 | 3.62E+00 | 1.53E+00 | |||||
| CPPE10 | 5.58E+00 | 1.87E+00 | 2.11E+00 | 1.72E+00 | 2.90E+00 | 2.60E+00 | |||||
| CPPE11 | 7.08E+00 | 1.93E+00 | 2.28E+00 | 1.75E+00 | 3.25E+00 | 2.64E+00 | |||||
| CPPE12 | 6.12E+00 | 1.70E+00 | 2.08E+00 | 1.41E+00 | 3.02E+00 | 2.47E+00 |
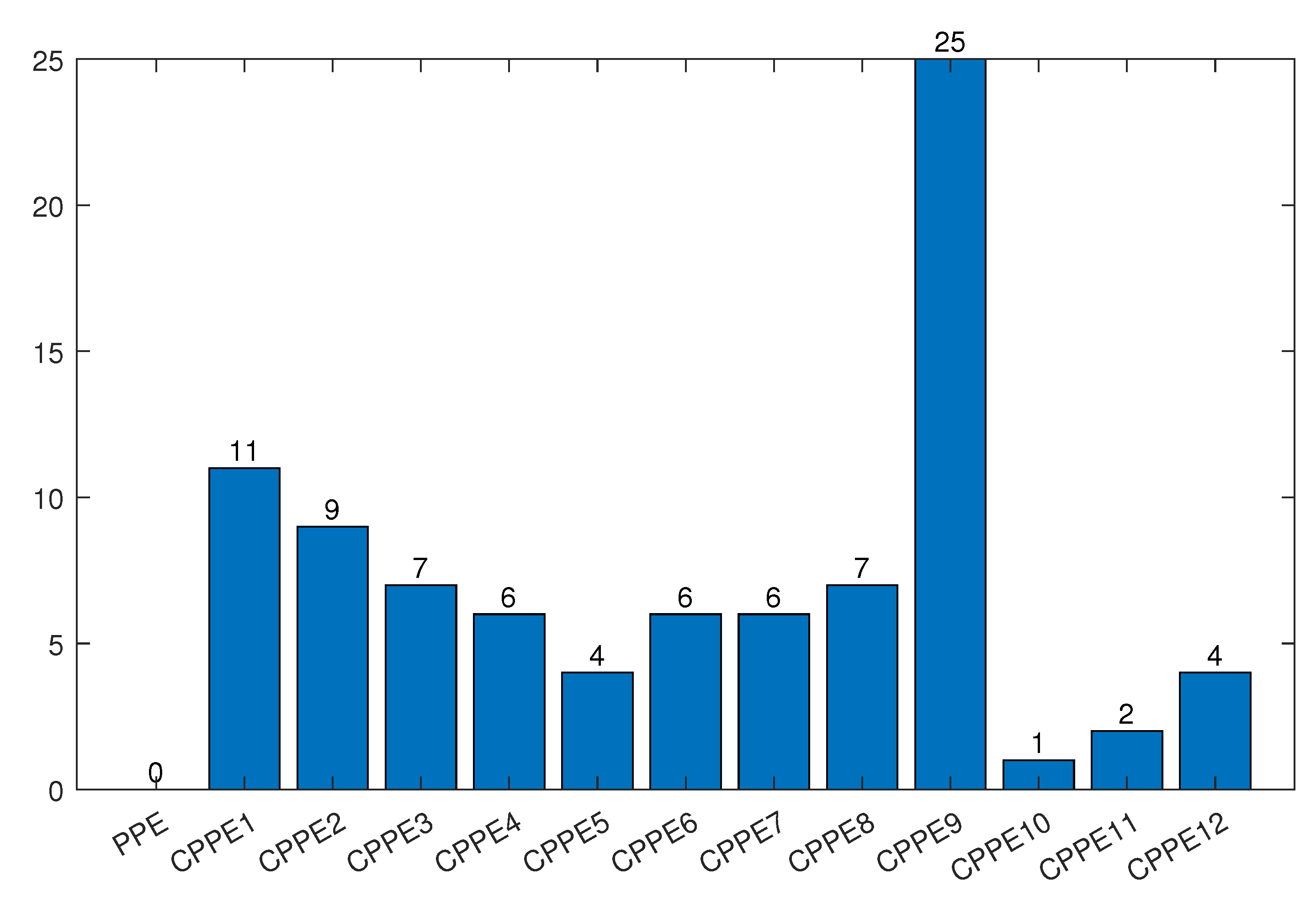
| The Average Change Rate of Fitness Value | |
|---|---|
| CPPE1 | 3.1636% |
| CPPE2 | −0.0739% |
| CPPE3 | 65.1776% |
| CPPE4 | 2.3946% |
| CPPE5 | −1.1542% |
| CPPE6 | 1.1324% |
| CPPE7 | −1.3921% |
| CPPE8 | 6.7471% |
| CPPE9 | −2.8102% |
| CPPE10 | 7.2003% |
| CPPE11 | 2.2421% |
| CPPE12 | 1.7341% |
| Parameters | Values |
|---|---|
| Population_Number | 10 |
| Max_Gen | 10 |
| Dimension | 3 |
| L, U | 1, 300 |
| Time_step | 5 |
| Solver | “adam” |
| Learning_rate | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.-Y.; Li, H.; Chu, S.-C. CPPE: An Improved Phasmatodea Population Evolution Algorithm with Chaotic Maps. Mathematics 2023, 11, 1977. https://doi.org/10.3390/math11091977
Wu T-Y, Li H, Chu S-C. CPPE: An Improved Phasmatodea Population Evolution Algorithm with Chaotic Maps. Mathematics. 2023; 11(9):1977. https://doi.org/10.3390/math11091977
Chicago/Turabian StyleWu, Tsu-Yang, Haonan Li, and Shu-Chuan Chu. 2023. "CPPE: An Improved Phasmatodea Population Evolution Algorithm with Chaotic Maps" Mathematics 11, no. 9: 1977. https://doi.org/10.3390/math11091977
APA StyleWu, T.-Y., Li, H., & Chu, S.-C. (2023). CPPE: An Improved Phasmatodea Population Evolution Algorithm with Chaotic Maps. Mathematics, 11(9), 1977. https://doi.org/10.3390/math11091977








